Калейдоскоп формул для пи
Калейдоскоп формул для пи«…я считал, что есть две математики — алгебраическая и геометрическая, и что геометрическая математика принципиально “трансцендентна” для алгебраической. Возьмите, например, формулу длины окружности — там есть “геометрическое” число $\pi$. Или, скажем, синус — он определяется чисто геометрически.
Когда я обнаружил, что синус можно записать алгебраически в виде ряда, барьер обрушился, математика стала единой.»
— из интервью И. М. Гельфанда
«Калейдоскоп» ниже состоит из нескольких «алгебраических» формул для $\pi$ с краткими комментариями. Он также опубликован (с сокращениями) в журнале «Квант» (№5 за 2020 год).
1. Формула Виета
Одна из первых алгебраических формул для $\pi$ — это открытое в XVI веке Виетом бесконечное произведение
$$
\frac\pi2=\frac2{\sqrt2}\cdot\frac2{\sqrt{2+\sqrt2}}\cdot\frac2{\sqrt{2+\sqrt{2+\sqrt2}}}\cdot\ldots
$$
Это равенство не очень сложно доказать. Идея состоит в следующем.
4. Формула Валлиса
Если подставить $x=\pi/2$ в разложение Эйлера синуса в бесконечное произведение, то получается равенство $$ \frac\pi2= \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots} $$ Впрочем, Джон Валлис нашел эту формулу уже в середине XVII века, почти за 100 лет до формулы Эйлера, вычисляя некоторые интегралы.
В упоминавшейся выше статье Ягломов при помощи элементарной тригонометрии доказывается и формула Валлиса. А J. Wästlund нашел и доказательство (в духе «геометрического суммирования»), непосредственно связывающее произведение Валлиса с площадью круга — см. его статью (AMM, 2007) или лекцию Д. Кнута.
При помощи формулы Валлиса можно доказать, что если подкинуть монету $2n$ раз, то вероятность того, что орлов и решек выпадет в точности поровну, приблизительно равна $1/\sqrt{\pi n}$.
Пространства с иным числом Пи / Хабр
Недавно на Хабре в одной статье упомянули про вопрос «Что было бы с миром, если бы число Пи равнялось 4?» Я решил слегка поразмышлять на эту тему, используя некоторые (пусть и не самые обширные) знания в соответствующих областях математики. Кому интересно – прошу под кат.
Чтобы представить такой мир, нужно математически реализовать пространство с иным соотношением длины окружности к ее диаметру. Это я и попытался сделать.
Попытка №1.
Оговорим сразу, что рассматривать я буду только двумерные пространства. Почему? Потому что окружность, собственно, определена в двумерном пространстве (если рассмотреть размерность n>2, то отношение меры (n-1)-мерной окружности к ее радиусу даже не будет константой).
Так что для начала я попытался придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого я взял метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат (т.
е. расстояние Чебышева).
Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле.
Да, в некоторой метрике это — окружность!
Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2. Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2. Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4. Получилось! Но нужно ли сильно радоваться? Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты.
Попытка №2.
Осознав, что я получил хоть и интересный, но абсолютно бесполезный (в смысле понимания строения мира с иным числом Пи) результат, я решил попытаться построить модель пространства с определенными понятиями углов и поворотов (то есть пространство с заданным невырожденным скалярным произведением). Разумеется, мне хотелось, чтобы метрика осталась метрикой в классическом понимании этого слова (т.е. чтобы расстояние между двумя точками было вещественным и неотрицательным). Но тогда скалярное произведение должно быть положительно определено, откуда вытекает, что пространство должно быть евклидовым. Или хотя бы локально евклидовым, то есть многообразием. Можно не забивать себе голову всеми этими понятиями, а просто читать дальше 🙂
Признаюсь, я убил некоторое время, пытаясь придумать хитрую евклидову метрику с нехорошим числом Пи.
Попытка №3.
Раз нам по-прежнему желательно наличие углов и поворотов, но евклидово пространство нас не устраивает, попробуем рассмотреть псевдоевклидово типа (1,1) (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками (а, как следствие, и скалярное произведение двух векторов) может быть отрицательным. Чтобы особо не мучиться, я взял метрику в которой скалярное произведение в декартовых координатах будет иметь вид . Какой же вид примет окружность единичного радиуса? Это будет множество точек, задаваемых уравнением , то есть… Гипербола.
Да-да! В определенном пространстве и это — окружность.
Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. После некоторых поисков информации в интернете, я пришел к выводу, что в псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.
Если кто-нибудь в комментариях расскажет мне, как формально считать длину кривой в псевдоевклидовом пространстве, я буду очень рад, ибо моих познаний в дифференциальной геометрии, топологии (а также усердного гугления) для этого не хватило.
Выводы:
Не знаю, можно ли писать о выводах после таких не сильно продолжительных исследований, но кое-что сказать можно. Во-первых, попытавшись представить пространство с иным числом Пи, я понял, что оно будет слишком абстрактно, чтобы быть моделью реального мира. Во-вторых, когда если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным.
Upd. Узнал точно. Длина кривой в псевдоевклидовом пространстве может быть определена только на каком-либо его евклидовом подпространстве. То есть, в частности, для получившейся в попытке N3 «окружности» вовсе не определено такое понятие как «длина». Соответственно, Пи там тоже посчитать нельзя.
чему равна окружность круга площадью 4 пи см?
Вот ответ на вопросы типа: как найти периметр круга площадью 4 пи сантиметра?
Круговой калькулятор
| ||||||||||||
Длина окружности с площадью 4π равна 12,57 (*) | ||||||||||||
| ||||||||||||
| ||||||||||||
Используйте этот калькулятор длины окружности выше, чтобы найти периметр круга, учитывая его площадь или другие параметры.
Формула для расчета длины окружности
Вот три способа нахождения длины окружности или периметра круга:
Формула длины окружности через радиус
C = 2·π·r
Формула длины окружности через диаметр
C = π·d
Формула длины окружности через площадь
C = √4·π·A
Вопросы, на которые может ответить этот калькулятор:
- Как найти периметр круга с радиусом 2 сантиметра?
- Круг имеет диаметр 4 сантиметра. Какова его окружность?
- Если площадь круга равна 12,57 квадратных сантиметров.
Каков его периметр?
Каков его периметр?Примеры решений окружности окружности
- Окружность площадью 17 пи м
- Окружность радиусом 6,8 фута
- Окружность площадью 5 пи
- 901 901 57
- Окружность площадью 4 п. см
- Окружность с радиусом 6,1
- Окружность с радиусом 7,82 мм
- Окружность площадью 7 пи сантиметров
- Окружность диаметром 92 см
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Почему PI не 4, математика великолепна и другие загадки.
Почему число пи не равно 4, математика великолепна и прочие загадки.
На днях я столкнулся с интересной задачей аппроксимации окружности окружающим ее квадратом, что, кажется, доказывает, что pi = 4.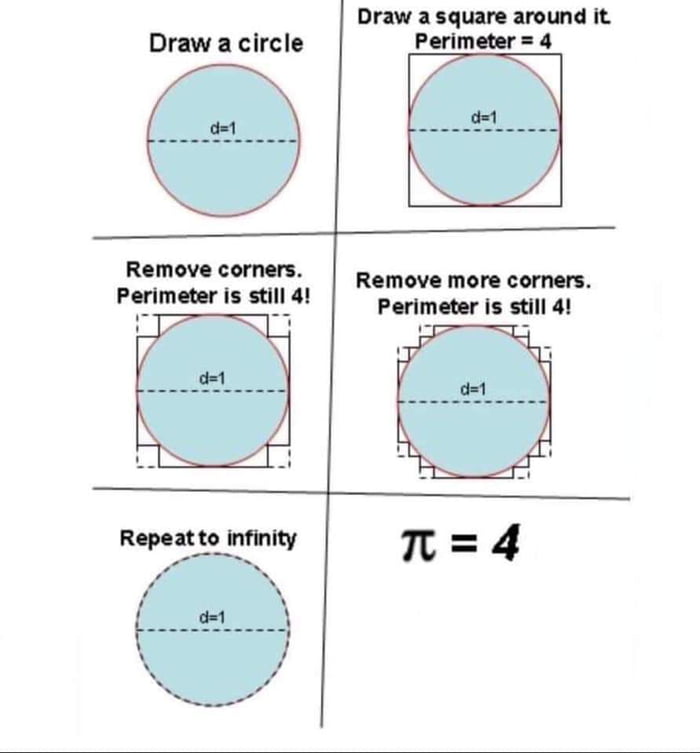
долгое вдохновение. См. «Сонату для черепахи без сопровождения», чтобы узнать, почему!
Вот оскорбительный парадокс:
Это пример того, как можно ответить на парадоксальные вопросы с помощью небольшого расчета.
Суть в том, чтобы понять, что независимо от того, насколько близко мы приближаемся к окружности, ортогональных линий приближения, образованных инвертированием квадратных углов , никогда не будут касаться окружности.
Внимательно отметьте, что по мере приближения к 90 градусам горизонтальная линия становится намного длиннее вертикальной. То же самое и с аппроксимацией при 0 и 180 — вертикальная линия намного больше, чем горизонтальная составляющая.
Если мы возьмем квадрант окружности — скажем, верхний левый квадрант, двигаясь против часовой стрелки сверху вниз — мы можем представить, что каждая бесконечно малая дуга ( под углом тета) аппроксимируется горизонтальной линией, которая приблизительная длина дуги умножается на косинус угла , а вертикальная линия равна той же дуге умножается на синус угла.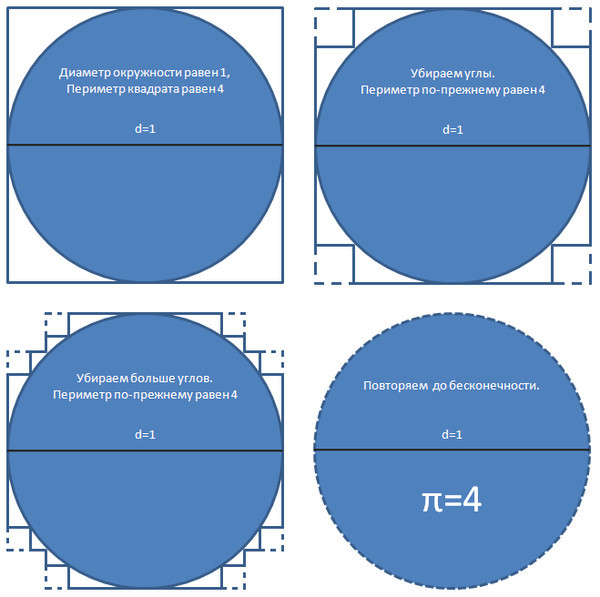
Вот примерное изображение:
Таким образом, каждая дуга аппроксимируется двумя линиями, и мы просто складываем все аппроксимации. Вот где в дело вступают исчисление и пределы. Для одного квадранта от 0 до 90 градусов вот результат:
Умножьте на четыре, и вы получите 8*r (или 4*диаметр).
Вуаля!
PI не равно 4, , потому что приблизительная фигура никогда не совпадает с окружностью, даже в пределе бесконечного числа приближений.
Отсюда вытекает интересный результат: большинство кругов в цифровом представлении (ч/б) должны иметь яркость (или плотность цвета) 4/pi, или примерно на 27% ярче, чем реальный круг того же размера в реальном мире. .
Кроме того, можно ли сделать сглаживание более умным способом, чтобы не только сгладить края, но и уменьшить яркость, чтобы относительная яркость круга была такой же, как физическая реальность — когда разрешение изображения меньше человеческого разрешение глаза?
Является ли это одной из причин, почему переход Apple на дисплей Retina, где разрешение в пикселях лучше, чем разрешение сетчатки глаза, отличает iPhone (а теперь и iPad3)?
Больше вопросов, чем ответов.
Популярные посты из этого блога
Архитектура, проектирование, эксплуатация — 1
В современном мире бесконечно много вещей, которые нужно «сделать». По крайней мере, в смысле создания/управления учреждением, использующим технологии, есть много ролей, которые участвуют в том, чтобы все работало. Мир информационных технологий и технологий в целом делает возможной скорость и разнообразие. Теперь у нас есть ИТ-платформа, которую можно масштабировать в глобальном масштабе, если мы сможем по-новому взглянуть на старые проблемы «достижения цели». Есть отличные организации, которые хорошо с этим справляются, и для этого они используют современные принципы ИТ. Основой проектирования современной ИТ (или организации инфраструктуры) являются три роли: архитектура, проектирование и эксплуатация.
Кто-то скажет, что архитектура — это закодированная инженерная история, но пока мы будем держать их отдельно. Популярные определения этих ролей касаются поставленных результатов или сферы дискурса. Насколько я понимаю, личностные побуждения, определяющие реальную производительность, не обсуждаются целостно.0003
Амбиции против страха.
Самые важные вещи в жизни не приходят к нам. И мы не получаем их, ища/желая их. Это происходит из-за того, что вы отпускаете неважные вещи. Самое сложное — это избавиться от тенденции принимать мир таким, какой он есть. Это привычка наших прошлых успехов. Но успех — это не пункт назначения, это знак СТОП. Вы останавливаетесь, ждете и идете дальше. Слишком часто успех парализует нас, превращая в страх перед новым. Мы останавливаемся на пути к новой жизни. Нам нужно сломать нашу инерцию и двигаться. Наши мысли и мыслительные привычки трудно сломать. Но именно на это нам приходится тратить больше всего энергии. Мысли всегда представляют собой соперничающие нити: заботы о прошлом и тревоги о будущем.