Кубические уравнение: Решение кубических уравнений, онлайн сервис для решения кубических уравнений, решение уравнений, решение уравнений третьей степени.

Кубические уравнения в школе

ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ

ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»

Учитель Математики Высшей категории

Как решать кубические уравнения

3 метода: Решение при помощи формулы для решения квадратного уравнения. Нахождение целых решений при помощи разложения на множители. Использование дискриминанта.

Кубические уравнения имеют вид ax3 + bx2 + cx + d = 0. Способ решения таких уравнений известен уже несколько столетий (он был открыт в 16 веке итальянскими математиками). Решить некоторые кубические уравнения довольно сложно, но при правильном подходе (и хорошем уровне теоретических знаний) вы сможете решать даже самые сложные кубические уравнения.

 

Метод 1 из 3: Решение при помощи формулы для решения квадратного уравнения

1. Проверьте, имеет ли данное вам кубическое уравнение свободный член.Как отмечалось выше, кубические уравнения имеют вид ax3 + bx2 + cx + d = 0, где коэффициенты «b», «с» и «d» могут быть равны 0, то есть кубическое уравнение может состоять только из одного члена (с переменной в третьей степени). Сначала проверьте, имеет ли данное вам кубическое уравнение свободный член, то есть «d». Если свободного члена нет, вы можете решить данное кубическое уравнение при помощи формулы для решения квадратного уравнения.

Если свободный член есть, используйте другой метод решения (смотрите следующие разделы).

 

2. Так как в данном уравнении свободного члена нет, то все члены этого уравнения содержат переменную «х», которую можно вынести за скобки:x(ax2 + bx + c).

Пример. 3×3 + -2×2 + 14x = 0. Если вынести «х» за скобки, вы получите x(3×2+ -2x + 14) = 0.

 

3. Обратите внимание, что уравнение в скобках – это квадратное уравнение вида ax2 + bx + c, которое можно решить при помощи формулы ({-b +/-√ (b2— 4ac)}/2a). Решите квадратное уравнение, и вы решите кубическое уравнение.

В нашем примере подставьте значения коэффициентов «а», «b», «с» (3, -2, 14) в формулу:

{-b +/-√ (b2- 4ac)}/2a

{-(-2) +/-√ ((-2)2- 4(3)(14))}/2(3)

{2 +/-√ (4 — (12)(14))}/6

{2 +/-√ (4 — (168)}/6

{2 +/-√ (-164)}/6

Решение 1:

{2 + √(-164)}/6

{2 + 12,8i}/6

Решение 2:

{2 – 12,8i}/6

 

4. Помните, что квадратные уравнения имеют два решения, а кубические – три решения. Вы нашли два решения квадратного, а следовательно и кубического уравнения. В случаях, когда вы выносите «х» за скобки, третье решение всегда равно 0.

Это верно, так как любое число или выражение, умноженное на 0, равно 0. Так как вы вынесли «х» за скобки, то вы разложили кубическое уравнение на два множителя («х» и квадратное уравнение), один из которых должен быть равен 0, чтобы все уравнение равнялось 0.

 

Метод 2 из 3: Нахождение целых решений при помощи разложения на множители

1. Проверьте, имеет ли данное вам кубическое уравнение свободный член.Описанный в предыдущем разделе метод не годится для решения кубических уравнений, в которых присутствует свободный член. В этом случае вам придется воспользоваться методом, который описан в этом или следующем разделах.

Пример. 2×3 + 9×2 + 13x = -6. Здесь перенесите свободный член d = -6 на левую сторону уравнения, чтобы на правой стороне получить 0: 2×3 + 9×2 + 13x + 6 = 0.

 

2. Найдите множители коэффициента «а» (коэффициент при x3) и свободного члена «d». Множители числа – это числа, которые при перемножении дают исходное число. Например, множителями числа 6 являются числа 1, 2, 3, 6 (1*6 = 6 и 2*3 = 6).

В нашем примере а = 2 и d = 6 . Множители 2 – это числа 1 и 2. Множители 6 – это числа 1, 2, 3 и 6.

 

3. Разделите множители коэффициента «а» на множители свободного члена «d». Вы получите дроби и целые числа. Целым решением данного вам кубического уравнения будет либо одно из этих целых чисел, либо отрицательное значение одного из этих целых чисел.

В нашем примере разделите множители «а» (1, 2) на множители «d» (1, 2, 3, 6) и получите: 1, 1/2, 1/3, 1/6, 2, 2/3. Теперь добавьте к этому ряду чисел их отрицательные значения: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3, -2/3. Целые решения данного вам кубического уравнения находятся в этом ряду чисел.

 

4. Теперь вы можете найти целые решения вашего кубического уравнения, подставив в него целые числа из найденного ряда чисел.  Но если вы не хотите тратить время на это, воспользуйтесь делением по схеме Горнера. Такая схема подразумевает деление целых чисел на значения «а», «b», «с», «d» данного кубического уравнения. Если остаток равен 0, целое число является одним из решений кубического уравнения.

Деление по схеме Горнера – непростая тема; для получения дополнительной информации по ней перейдите по ссылке, указанной выше. Вот пример того, как найти одно из решений данного вам кубического уравнения при помощи деления по схеме Горнера:

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Так как остаток 0, то одним из решений уравнения является целое число -1.

 

Метод 3 из 3: Использование дискриминанта

1. В этом методе вы будете работать со значениями коэффициентов «а», «b», «с», «d». Поэтому лучше выписать значения этих коэффициентов заранее.

Пример. x3 — 3×2 + 3x — 1. Здесь a = 1, b = -3, c = 3, d = -1. Не забывайте, что когда перед «х» коэффициента нет, то это значит, что коэффициент равен 1.

 

2. Вычислите Δ0 = b2 — 3ac. В этом методе потребуется провести несколько сложных вычислений, но если вы уясните его, вы сможете решать самые сложные кубические уравнения.

В нашем примере:

b2 — 3ac

(-3)2 — 3(1)(3)

9 — 3(1)(3)

9 — 9 = 0 = Δ0

 

3. Вычислите Δ1= 2b3 — 9abc + 27a2d.

В нашем примере:

2(-3)3 — 9(1)(-3)(3) + 27(1)2(-1)

2(-27) — 9(-9) + 27(-1)

-54 + 81 — 27

81 — 81 = 0 = Δ1

 

4. Вычислите Δ = Δ12 — 4Δ03) ÷ -27a2. Теперь вычислите дискриминант уравнения при помощи найденных значений Δ0 и Δ1. Дискриминант – это число, дающее вам информацию о корнях многочлена (вы, возможно, уже знаете, что дискриминант квадратного уравнения равен b2 — 4ac). В случае кубического уравнения, если дискриминант положительный, то уравнение имеет три решения; если дискриминант равен нулю, то уравнение имеет одно или два решения; если дискриминант отрицательный, то уравнение имеет только одно решение. Кубическое уравнение всегда имеет по крайней мере одно решение, потому что график такого уравнения пересекает ось X по крайней мере в одной точке.

В нашем примере Δ0 = 0 и Δ1 = 0, поэтому найти Δ не составит труда.

Δ12 — 4Δ03) ÷ -27a2

(0)2 — 4(0)3) ÷ -27(1)2

0 — 0 ÷ 27

0 = Δ, поэтому данное вам уравнение имеет одно или два решения.

 

5. Вычислите C = 3√(√((Δ12 — 4Δ03) + Δ1)/ 2). Эта величина позволит вам найти корни кубического уравнения.

В нашем примере:

3√(√((Δ12 — 4Δ03) + Δ1)/ 2)

3√(√((02 — 4(0)3) + (0))/ 2)

3√(√((0 — 0) + (0))/ 2)

0 = C

 

6. Корни (решения) кубического уравнения вычисляются по формуле (b +unC + (Δ0/unC)) / 3a, где u = (-1 + √(-3))/2, а n равно либо 1, либо 2, либо 3.

Если подставить в эту формулу соответствующие значения величин, вы получите возможные решения данного вам кубического уравнения. Подставьте их в исходное уравнение и если равенство соблюдено, то решения правильные. Например, если, подставив значения в формулу, вы получили 1, подставьте 1 в x3 — 3×2 + 3x — 1 и получите 0. То есть равенство соблюдено, и 1 является одним из решений данного вам кубического уравнения.

Математика и ее история

Математика и ее история

Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 580 с. Оглавление Предисловие ко второму изданию Глава 1. Теорема Пифагора 1.2. Пифагоровы тройки 1.3. Рациональные точки на круге 1.4. Прямоугольные треугольники 1.5. Иррациональные числа 1.6. Определение расстояния 1.7. Биографические заметки: Пифагор Глава 2. Греческая геометрия 2.9. Правильные многогранники 2.10. Построения с помощью линейки и циркуля 2.11. Конические сечения 2.12. Кривые более высокой степени 2.13. Биографические заметки: Евклид Глава 3. Греческая теория чисел 3.15. Многоугольные, простые и совершенные числа 3.16. Евклидов алгоритм 3.17. Уравнение Пелля 3.18. Методы хорд и касательных 3.19. Биографические заметки: Диофант Глава 4. Бесконечность в греческой математике 4.21. Теория пропорций Евдокса 4.22. Метод исчерпывания 4.23. Площадь параболического сегмента 4.24. Биографические заметки: Архимед Глава 5. Теория чисел в Азии 5.26. Китайская теорема об остатках 5.27. Линейные диофантовы уравнения 5.28. Уравнение Пелля у Брахмагупты 5.29. Уравнение Пелля у Бхаскары II 5.30. Рациональные треугольники 5.31. Биографические заметки: Брахмагупта и Бхаскара Глава 6. Полиномиальные уравнения 6.33. Линейные уравнения и исключение 6. 34. Квадратные уравнения 6.35. Квадратные иррациональные числа 6.36. Решение кубических уравнений 6.37. Деление углов 6.38. Уравнения более высокой степени 6.39. Биографические заметки: Тарталья, Кардано и Виет Глава 7. Аналитическая геометрия 7.41. Ферма и Декарт 7.42. Алгебраические кривые 7.43. Классификация кубических кривых Ньютона 7.44. Построение уравнений и теорема Безу 7.45. Арифметизация геометрии 7.46. Биографические заметки: Декарт Глава 8. Проективная геометрия 8.48. Анаморфоза 8.49. Проективная геометрия Дезарга 8.50. Проективный вид кривых 8.51. Однородные координаты 8.52. Снова теорема Везу 8.53. Теорема Паскаля 8.54. Биографические заметки: Дезарг и Паскаль Глава 9. Исчисление 9.55. Что такое исчисление? 9.56. Ранние результаты о площадях и объемах 9.57. Максимумы, минимумы и касательные 9.58. Arithmetica Infinitorum Валлиса 9.59. Исчисление ряда Ньютона 9.60. Исчисление Лейбница 9. 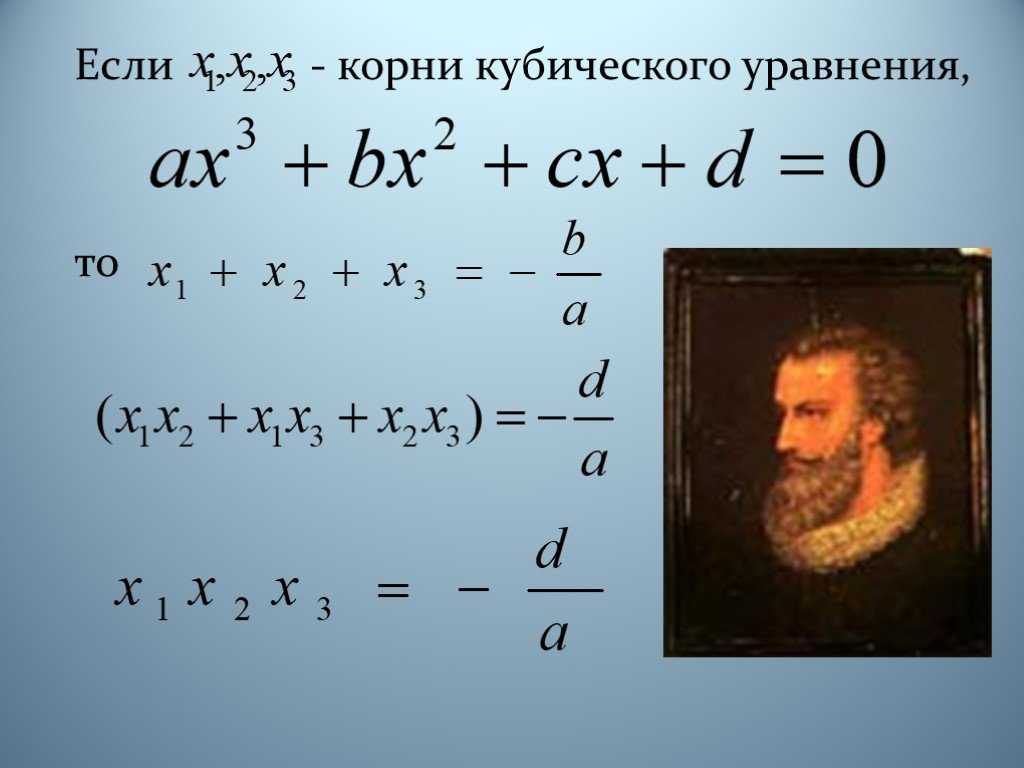61. Биографические заметки: Валлис, Ньютон и Лейбниц Глава 10. Бесконечные ряды 10.63. Степенные ряды 10.64. Интерполяция на интерполяции 10.65. Суммирование рядов 10.66. Дробно-степенные ряды 10.67. Производящие функции 10.68. Дзета-функция 10.69. Биографические заметки: Грегори и Эйлер Глава 11. Возрождение теории чисел 11.71. Малая теорема Ферма 11.72. Последняя теорема Ферма 11.73. Рациональные прямоугольные треугольники 11.74. Рациональные точки на кубических кривых 0-го рода 11.76. Биографические заметки: Ферма Глава 12. Эллиптические функции 12.77. Эллиптические и круговые функции 12.78. Параметризация кубических кривых 12.79. Эллиптические интегралы 12.80. Удвоение дуги лемнискаты 12.81. Общие теоремы сложения 12.82. Эллиптические функции 12.83. Постскриптум о лемнискате 12.84. Биографические заметки: Абель и Якоби Глава 13. Механика 13.85. Механика до исчисления 13.86. Небесная механика 13. 87. Механические кривые 13.88. Колеблющаяся струна 13.89. Гидродинамика 13.90. Биографические заметки: семья Бернулли Глава 14. Комплексные числа в алгебре 14.92. Квадратные уравнения 14.93. Кубические уравнения 14.94. Попытка Валлиса при геометрическом представлении 14.95. Деление угла 14.96. Основная теорема алгебры 14.97. Доказательства Даламбера и Гаусса 14.98. Биографические заметки: Даламбер Глава 15. Комплексные числа и кривые 15.100. Комплексная проективная линия 15.101. Точки ветвления 15.102. Топология комплексных проективных кривых 15.103. Биографические заметки: Риман Глава 16. Комплексные числа и функции 16.104. Комплексные функции 16.105. Конформное отображение 16.106. Теорема Коши 16.107. Двойная периодичность эллиптических функций 16.108. Эллиптические кривые 16.109. Униформизация 16.110. Биографические заметки: Лагранж и Коши Глава 17. Дифференциальная геометрия 17.111. Трансцендентные кривые 17.112. Кривизна плоских кривых 17.113. Кривизна поверхностей 17.114. Поверхности постоянной кривизны 17.115. Геодезические линии 17.116. Теорема Гаусса-Бонне 17.117. Биографические заметки: Гарриот и Гаусс Глава 18. Неевклидова геометрия 18.119. Сферическая геометрия 18.120. Геометрия Бойяи и Лобачевского 18.121. Проективная модель Бельтрами 18.122. Конформные модели Бельтрами 18.123. Комплексные интерпретации 18.124. Биографические заметки: Бойяи и Лобачевский Глава 19. Теория групп 19.126. Перестановки и теория уравнений 19.127. Группы подстановок 19.128. Группы многогранников 19.129. Группы и геометрии 19.130. Комбинаторная теория групп 19.131. Биографические заметки: Галуа Глава 20. Гиперкомплексные числа 20.133. Арифметика пар 20.134. Свойства «сложения» и «умножения» 20.135. Арифметические тройки и четверки 20.136. Кватернионы, геометрия и физика 20.137. Октонионы 20.138. Почему C, H и O особенные 20.139. Биографические заметки: Гамильтон Глава 21. Алгебраическая теория чисел 21.141. Гауссовы целые числа 21.142. Алгебраические целые числа 21.143. Идеалы 21.144. Разложение идеала 21.145. Вновь суммы квадратов 21.146. Кольца и поля 21.147. Биографические заметки: Дедекинд, Гильберт и Нётер Глава 22. Топология 22.148. Геометрия и топология 22.149. Формулы многогранника Декарта и Эйлера 22.150. Классификация поверхностей 22.151. Декарт и Гаусс-Бонне 22.152. Эйлерова характеристика и кривизна 22.153. Поверхности и плоскости 22.154. Фундаментальная группа 22.155. Биографические заметки: Пуанкаре Глава 23. Множества, логика и вычисление 23.157. Множества 23.158. Мера 23.159. Аксиома о выборе и большие кардинальные числа 23.160. Диагональная аргументация 23.161. Вычислимость 23.162. Логика и теорема Гёделя 23.163. Доказуемость и истина 23. 164. Биографические заметки: Гёдель

Быстрое решение кубического уравнения? — Определенные домены

longemen3000 6 ноября 2019 г., 5:38

1

Я просто хочу знать, есть ли из всех существующих пакетов для решения полиномиальных корней тот, который решает кубические уравнения с точной формулой (метод Кардано)

jling 6 ноября 2019 г., 5:42

2

лонжемен3000:

Я просто хочу знать, является ли из всех существующих пакетов решения полиномиальных корней

да https://github. com/giordano/PolynomialRoots.jl

3 лайков

6 ноября 2019 г., 5:48

3

я смотрел исходный код и вот он, xD

longemen3000 6 ноября 2019 г., 5:52

4

из кода, кубический решатель не вызывается при использовании функции root , но метод здесь, и это все, что мне нужно знать

jling 6 ноября 2019 г., 6:05

5

лонжемен3000:

кардано

не звонит? https://github. com/giordano/PolynomialRoots.jl/blob/196154b7ff97e4310509e1e32290cc80aad83d65/src/PolynomialRoots.jl#L655

longemen3000 6 ноября 2019 г., 6:07

6

из файла readme:

root можно использовать для решения полиномов любой степени, root5 предназначен (и работает только для) для полиномов степени 5.

вызов находится в root5 , а не в roots , но в любом случае я использовал эту функцию напрямую

джлинг 6 ноября 2019 г., 6:09

7

ах, я понимаю, что вы имеете в виду, подпрограмма solve_cubic_eq не используется, если не вызывается roots5 .

Кубические уравнения состояния — IDAES v1.4.0

Этот пакет свойств реализует общую форму кубического уравнения состояния, которое можно использовать для большинства уравнений состояния кубического типа. Этот пакет поддерживает расчеты фазового равновесия с формулировкой плавного фазового перехода, что делает его пригодным для оптимизации, ориентированной на уравнения. В настоящее время поддерживаются следующие уравнения состояния:

• Пенг-Робинсон
• Соаве-Редлих-Квонг

Основа : Молярный

Единицы : единицы SI

Переменные состояния :

Блок состояния использует следующие переменные состояния:

• Общая частота потока Molar (Mol/s) — .
• Температура (К) - температура
• Давление (Па) - давление
• Мольная доля смеси - mole_frac_comp

Входы

При создании экземпляра блока параметров, который использует этот конкретный блок состояний, может быть передан 1 необязательный аргумент:

• valid_phase - "Liq" или "Vap" или ("Liq", "Vap") или («Вап», «Лик»)

Аргумент valid_phase обозначает допустимые фазы для заданного набора входных условий. Например, если пользователь априори знает, что это будет только одна фаза (например, только жидкость), то лучше не включать в модель сложные ограничения мгновенного равновесия. Если пользователь не указывает какую-либо опцию, пакет по умолчанию использует предположение о двух фазах, что означает, что будут вычислены ограничения для вычисления фазового равновесия.

Степени свободы

В общем случае общее кубическое уравнение состояния имеет число степеней свободы, равное 2 + количество компонентов в системе (общий расход, температура, давление и N-1 мольных долей). В некоторых случаях (в первую очередь на входе в установки) это значение увеличивается на 1 из-за снятия ограничения на сумму мольных долей.

Общее кубическое уравнение состояния

Все уравнения взяты из «Свойства газов и жидкостей, 4-е издание» Рейда, Праусница и Полинга. Общее кубическое уравнение состояния представляется следующими уравнениями: 92}\]

\[B = \frac{b_mP}{RT}\]

где \(Z\) - коэффициент сжимаемости смеси, \(a_m\) и \(b_m\) - свойства смесь и \(u\) и \(w\) являются параметрами, которые зависят от конкретного используемого уравнения состояния, как показано в таблице ниже.

Уравнение	\(у\)	\(ж\)	\(Омега_А\)	\(Омега_Б\)	\(каппа_j\) 9{1/2}(1-k_{ij})}}\] \[b_m = \sum_i{y_ib_i}\] где \(P_{c,j}\) и \(T_{c, j}\) — критические давления и температуры компонентов, \(y_j\) — мольная доля компонента :math`j`, \(k_{ij}\) — набор параметров бинарного взаимодействия, характерных для уравнения состояния и \(\Omega_A\), \(\Omega_B\) и \(\kappa_j\) взяты из таблицы выше. \(\omega_j\) - ацентрический фактор Питцера каждого компонента. Кубическое уравнение состояния решается для каждой фазы посредством вызова внешней функции, которая автоматически определяет правильный кубический корень и возвращает значение \(Z\) как функцию \(A\) и \( Б\) вместе с первой и второй частными производными. 9{1/2}(1-k_{ij})}\] Решается кубическое уравнение состояния, чтобы найти \(Z\) для каждой фазы в зависимости от состава этой фазы. Обычно расчеты вспышки рассчитываются при заданной температуре \(T\). Однако расчеты вспышки становятся тривиальными, если заданные условия не попадают в двухфазную область. Для исследований только с помощью моделирования пользователь может априори знать состояние потока, но когда тот же набор уравнений используется для оптимизации, существует высокая вероятность того, что спецификации могут выйти за пределы фазовой огибающей, и, следовательно, включенные уравнения вспышки могут быть тривиальными. в однофазной области (т.е. только жидкость или пар). Чтобы обойти эту проблему, пакеты свойств в IDAES, поддерживающие VLE, ​​будут выполнять расчеты флэш-памяти при «равновесной» температуре \(T_{eq}\). Равновесная температура рассчитывается следующим образом: \[T_{1} = max(T_{пузырь}, T)\] \[T_{экв} = min(T_{1}, T_{роса})\] где \(T_{ eq}\) — равновесная температура, при которой рассчитываются мгновенные расчеты, \(T\) — температура потока, \(T_{1}\) — переменная промежуточной температуры, \(T_{bubble}\) — пузырьковый температура точки росы смеси, а \(T_{dew}\) - температура точки росы смеси. Обратите внимание, что в приведенных выше уравнениях используются аппроксимации для функций max и min следующим образом: 92}]}\] где \(\epsilon_1\) и \(\epsilon_2\) параметры сглаживания (изменяемые). Значения по умолчанию — 0,01 и 0,0005 соответственно. Рекомендуется, чтобы \(\epsilon_1\) > \(\epsilon_2\). Пожалуйста, обратитесь к ссылке 4 для более подробной информации. Следовательно, можно видеть, что если температура потока меньше температуры точки насыщения, расчеты VLE будут выполняться в точке насыщения. Точно так же, если температура потока больше, чем температура точки росы, то расчеты VLE выполняются при температуре точки росы. Для всех других условий расчеты равновесия будут выполняться при фактической температуре. Другие ограничения В модель включены дополнительные ограничения для расчета термодинамических свойств на основе кубического уравнения состояния, таких как энтальпии и энтропии. Обратите внимание, что эти ограничения добавляются только в том случае, если переменная вызывается при построении модели. Это устраняет добавление ненужных ограничений для вычислительных свойств, которые не нужны в модели. Все теплофизические свойства рассчитываются с использованием идеального и остаточного членов, так что: 9{1/2}(1-k_{ij})}\] Энергия Гиббса Энергия Гиббса системы рассчитывается с использованием определения энергии Гиббса: \[g_i = h_i - T \Delta s_i\ ] Список переменных Имя переменной Описание Единиц поток_моль Общий молярный расход моль/с mole_frac_comp Мольная доля смеси, индексированная по компоненту Нет температура Температура К давление Давление Па поток_моль_фаза Молярный расход, индексированный по фазе моль/с mole_frac_phase_comp Молярная доля, индексированная по фазам и компонентам Нет давление_нас Насыщение или давление паров, индексированное компонентом Па dens_mol_phase Молярная плотность, индексированная по фазе моль/м3 dens_mass_phase Массовая плотность, индексированная по фазе кг/м3 enth_mol_phase Молярная энтальпия, индексированная по фазе Дж/моль энт_моль Молярная энтальпия смеси Дж/моль энтр_мол_фаза Молярная энтропия, индексированная по фазе Дж/моль. К энтр_мол Молярная энтропия смеси Дж/моль.К fug_phase_comp Фугитивность индексируется по фазам и компонентам Па fug_coeff_phase_comp Коэффициент фугитивности, индексированный по фазам и компонентам Нет гиббс_мол_фаза Молярная энергия Гиббса, индексированная по фазе Дж/моль МВт Молекулярная масса смеси кг/моль мВт_фаза Молекулярная масса по фазам кг/моль температура_пузырька Температура точки насыщения К температура_росы Температура точки росы К давление_пузырь Давление насыщения Па давление_росы Давление точки росы Па _тек Температура, при которой рассчитывается VLE К Список параметров Название параметра Описание Единиц кубический_тип Используемый тип кубического уравнения состояния из CubicEoS Enum Нет давление_ссылка Эталонное давление Па температура_ссылка Эталонная температура К омега Коэффициент ацентричности Питцера Нет каппа Параметры бинарного взаимодействия для EoS (обратите внимание, что параметры специфичны для данного EoS Нет mw_comp Молекулярные массы компонентов кг/моль cp_ig Параметры для расчета теплоемкости компонентов варьируется dh_form Стандартная теплота образования компонента (используется для энтальпии в исходном состоянии) Дж/моль ds_form Компонентная стандартная энтропия образования (используется для энтропии в исходном состоянии) Дж/моль. К Антуан Компонентные коэффициенты Антуана (используются для инициализации расчета пузырьков и точки росы) бар, К Документация блока конфигурации класс idaes.property_models.cubic_eos.cubic_prop_pack. CubicParameterData ( компонент )[источник] Класс блока параметров общего свойства сборка ()[источник] Вызываемый метод для построения блока. метод класса define_metadata ( объект )[источник] Определение поддерживаемых свойств и единиц измерения. класс idaes.property_models.cubic_eos.cubic_prop_pack. CubicStateBlock ( *args , **kwargs ) Параметры: Возвраты: (CubicStateBlock) Новый экземпляр класс idaes. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт