\(x_1=\frac{-b+\sqrt{D}}{2a}\) \(x_1=\frac{-b-\sqrt{D}}{2a}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Карина Рафаэльевна Сайфулина
Репетитор по математике
Стаж (лет)
Образование:
Крымский федеральный университет им. Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юлия Сергеевна Слива
Репетитор по математике
Стаж (лет)
Образование:
Кубанский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ольга Яновна Савинова
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет имени Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по олимпиадной математике
- Репетитор по геометрии
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор по русскому языку для подготовки к ЕГЭ
- Английский язык для начинающих
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ВПР по английскому языку
- Репетитор для подготовки к ВПР по русскому языку
- Scratch
Похожие статьи
- Диаграммы
- Накрест лежащие углы
- Как складывать числа в столбик?
- Основные формулы: треугольник, параллелограмм и четырехугольник
- Значения обратных тригонометрических функций y=arctg(x) и y=arcctg
- Нахождение числа по его части
- Что делать, если в гости неожиданно пришли одноклассники
- Стресс, гены, питание: когда возникает седина и что с этим делать
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
формула, как найти координаты, вывод уравнения, абсцисса и ордината
Содержание:
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Содержание
- Что такое вершина параболы
- Вывод формулы координат вершины параболы
- Как найти координаты, основные способы
- Примеры решения задач
Что такое вершина параболы
Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.
2-7\times3,5+3=-9,25.\)
Ответ: (3,5; -9,25).
Насколько полезной была для вас статья?
Рейтинг: 2.29 (Голосов: 7)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Бесплатный калькулятор форм вершин
Что такое форма вершин?
Вершинная форма является специальной формой квадратичной функции. По форме вершины легко видно, где находится максимальная или минимальная точка (вершина) параболы: Число в скобках дает (проблемное место: с точностью до знака!) x-координату вершины, число в конец формы дает координату y. Это означает: если форма вершины , то вершина находится в (h|k) .
Как преобразовать функцию в вершинную форму?
Вы должны заполнить квадрат: возьмите число перед x, разделите его на и возведите результат в квадрат. Вот пример:
| Работа с этой функцией: SO, вертекс форма вашей фу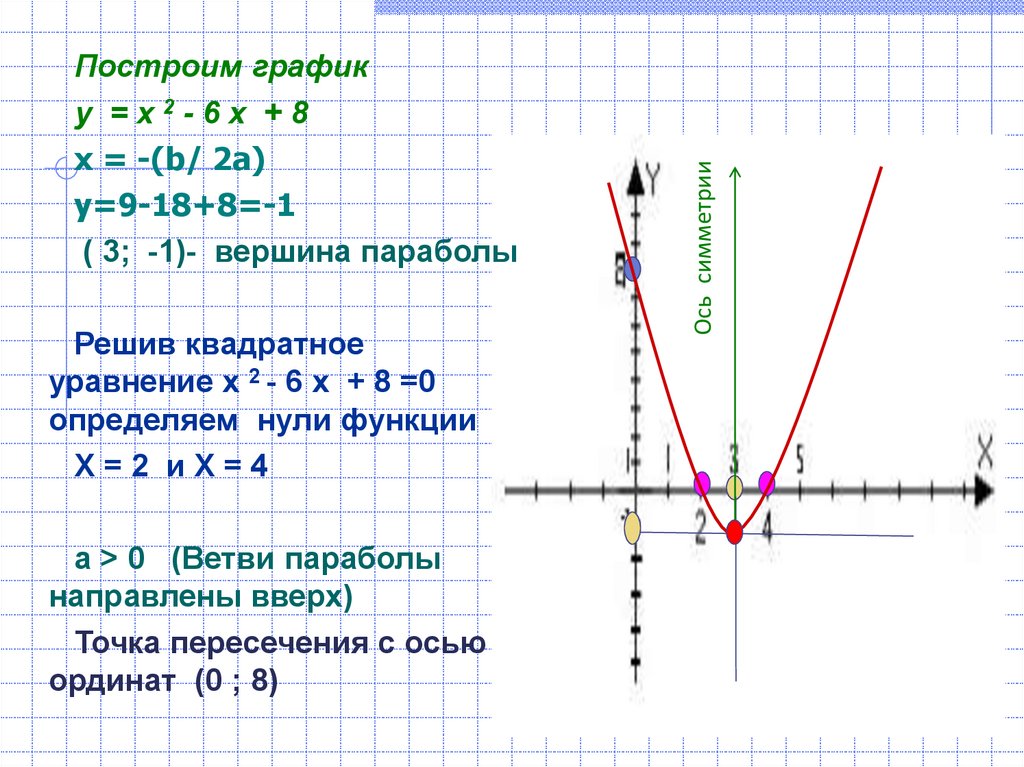нкции — .  график вашей функции.
|
Как видите, x-координата вершины равна числу в скобках, но только с точностью до смены знаков. Кроме того, из этого расчета видно, что вам просто нужно использовать биномиальную формулу в обратном порядке: построить биномиальную формулу из функционального члена. Это работает, только если есть правильное число (число, завершающее квадрат). Так что просто добавьте нужное число и вычтите его одновременно.
А если перед ?
Затем вы должны разложить это число. Пример:
| Mathepower Works с этой функцией:
 Это график вашей функции.
|
Важно сначала разложить по множителям, а затем завершить квадрат. Иначе могут быть неприятные ошибки. (К сожалению, многие люди не думают о таких вещах и просто используют биномиальную формулу, даже если это невозможно. К сожалению, термины не могут кричать «Ой!», но только учителя математики могут, когда видят такой расчет.)
А если перед ?
Просто факторизовать. Кстати: всякий раз, когда перед , есть отрицательное число, парабола открыта вниз.
Пример:
| Mathepower Works с этой функцией:
Это график вашей функции.
|
А как общая формула для точки вершины?
Нет проблем для Mathepower. Просто введите функцию.
| Mathepower Works с этой функцией: Итак, форма вершины — . 
|
Могу ли я увидеть еще больше примеров?
Конечно. Это бесплатный калькулятор форм вершин. Просто введите свой пример, и он будет решен.
Формула вершин — Что такое формула вершин? Примеры
Формула вершины параболы используется для нахождения координат точки, в которой парабола пересекает свою ось симметрии. Вершина — это точка (h,k). Как мы знаем, стандартное уравнение параболы: y = ax 2 +bx+c. Если коэффициент x 2 положительный, то вершина находится в нижней части U-образной кривой, а если он отрицателен, вершина является вершиной U-образной кривой.
Вершина, в которой парабола минимальна (когда парабола раскрывается вверх) или максимальна (когда парабола раскрывается вниз) и парабола поворачивается (или) меняет свое направление. Давайте узнаем больше о формуле вершины и решим примеры.
Что такое вершинная формула?
Формула вершины помогает найти координаты вершины параболы. Стандартная форма параболы: y = ax 2 + bx + c. Вершинная форма параболы y = a(x — h) 2 + k. Есть два способа определить вершину (h, k). Они таковы:
- (h, k) = (-b/2a, -D/4a), где D(дискриминант) = b 2 — 4ac
- (h,k), где h = -b / 2a, и оцените y в h, чтобы найти k.
Формула вершины
Две формулы вершины для нахождения вершины:
Формула 1: (h, k) = (-b/2a, -D/4a)
где
- D — это знаменатель
- h,k — координаты вершины
Формула 2: x-координата вершины = -b / 2a
Вывод формул вершин
Формула 1
Мы знаем, что стандартная форма параболы: y = ax 2 + bx + в.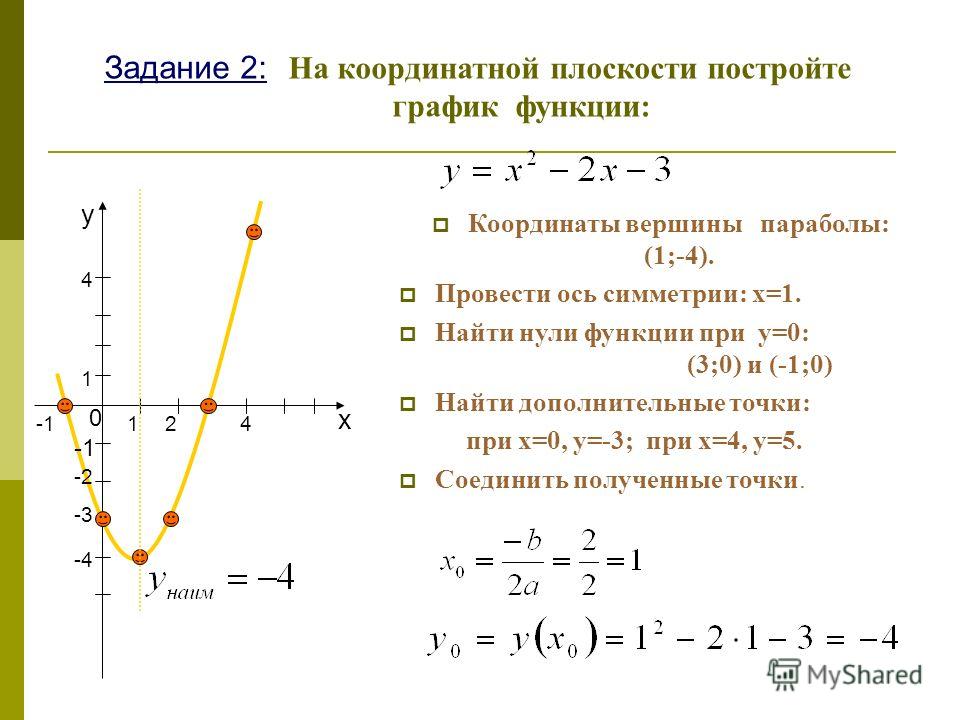
Преобразуем его к вершинной форме y = a(x — h) 2 + k, заполнив квадраты.
Вычитание c с обеих сторон:
y — c = ax 2 + bx
Принятие «a» в качестве общего множителя:
y — c = a (x 2 + b/a x)
5
Здесь половина коэффициента при x равна b/2a, а его квадрат равен b 2 /4a 2 . Прибавляя и вычитая это справа (в скобках):
y — c = a (x 2 + b/a x + b 2 /4a 2 — b 2 /4a 2 )
Мы можем записать x 2 + b/a x + b 2 /4a 2 как (x + b/2a) 2 . Таким образом, приведенное выше уравнение принимает вид:
y — c = a ( (x + b/2a) 2 — b 2 /4a 2 )
Распределив «a» в правой части и добавив «c » с обеих сторон:
y = a (x + b/2a) 2 — b 2 /4a + c
y = a (x + b/2a) 2 — (b 2 — 4ас) / (4а)
Сравнивая это с y = a (x — h) 2 + k, мы получаем:
h = -b/2a
k = -(b 2 — 4ac) / (4a)
Мы знаем что b 2 — 4ac является дискриминантом (D).
Таким образом, формула вершины: (h, k) = (-b/2a, -D/4a) где D = b 2 — 4ac
Формула 2
Если вам трудно запомнить выше формулы, вы можете просто запомнить формулу для x-координаты вершины, а затем просто подставить ее в данное уравнение y = ax 2 + bx + c, чтобы получить y-координату вершины.
x-координата вершины (h) = -b / 2a
В качестве альтернативы, если вы не хотите использовать какую-либо из приведенных выше формул для нахождения вершины, вы можете просто заполнить квадрат для преобразования y = ax 2 + bx + c вида y = a(x — h) 2 + k вручную и найти вершину (h, k).
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Примеры использования формулы вершин
Пример 1: Найти вершину y = 3x 2 — 6x + 1.
Решение:
Найти: Вершину заданного уравнения (параболы).
Сравнивая данное уравнение с y = ax 2 + bx + c, получаем
a = 3, b = -6, c = 1.
Тогда дискриминант равен D = b 2 — 4ac = (-6) 2 — 4(3)(1) = 36 — 12 = 24,
Используя формулу вершины (формула 1),
Вершина, (h, k) = (-b/2a, -D/4a)
(h, k) = (-(-6) / (2× 3), -24 / (4×3) ) = (6/6, -24/12) = (1, -2)
Следовательно, вершина данной параболы = (1, -2).
Пример 2. Найдите вершину параболы, у которой точки пересечения по оси x равны (2, 0) и (3, 0), а точка пересечения по оси y равна (0, 6).
Решение:
Найти: вершину параболы.
Поскольку (2, 0) и (3, 0) являются точками пересечения по оси x данной параболы, то (x — 2) и (x — 3) являются множителями уравнения параболы. Таким образом, уравнение параболы имеет вид:
y = a (x — 2) (x — 3) .
… (1)Ее точка пересечения y равна (0, 6). Подставьте x = 0 и y = 6 в приведенное выше уравнение:
6 = a (0 — 2) (0 — 3)
6 = 6a
a = 1
Подставьте a = 1 в (1):
у = 1 (х — 2) (х — 3) = х 2 — 5x + 6… (2)
Сравнивая вышеприведенное уравнение с y = ax 2 + bx + c, получаем
a = 1; б = -5; c = 6
Используя формулу вершины (формула 2),
x-координата вершины = -b / 2a = -(-5) / (2×1) = 5/2
Подставим это в (2 ), чтобы найти y-координату вершины.
y = (5/2) 2 — 5 (5/2) + 6 = -1/4
Следовательно, Вершина данной параболы = (5/2, -1/4)
Пример 3: Определить координаты вершины для заданного уравнения параболы: y= 4x 2 + 16x -16
Решение:
Заданное уравнение: y= 4x 50 — 909311 2 9063×1 2 9063x
Здесь a = 4, b = 16
Мы знаем, что формула для нахождения координаты x имеет вид -b/2a
= -16/2(4)
= -2
Следовательно, x — координата -2
Теперь подставим значение x в данное уравнение, получим
y = 4(-2) 2 +16(-2) -16
y= -32
Следовательно, координаты вершины (h, k) равны (-2, -32)
… (1)перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о формуле вершин
Что такое формула вершин?
Формула вершины параболы используется для определения координат точки, в которой парабола пересекает свою ось симметрии.
Координаты задаются как (h,k). Вершина параболы – это точка, в которой парабола минимальна (когда парабола раскрывается вверх) или максимальна (когда парабола раскрывается вниз) и парабола поворачивает (или) меняет свое направление.
Какая формула для нахождения вершины в координатах X?
Используя стандартную форму параболы y = ax 2 + bx + c и уравнение вершины y = a(x — h) 2 + k, мы можем вывести первую формулу вершины, т.е.
формула вершины: (h, k) = (-b/2a, -D/4a) , где D = b 2 — 4ac
Как использовать формулу вершин?
Формулу вершин можно использовать для нахождения вершины любой параболы с помощью уравнения параболы. Формула вершины для уравнения параболы y = ax 2 + bx + c задается как (h, k) = (-b/2a, -D/4a) , где D = b 2 — 4ac
Какова формула для нахождения вершины на Координаты Y?
Чтобы найти вершину (h, k), получите h(x-координата вершины) = -b/2a из стандартного уравнения y = ax 2 + bx + c, а затем найдите y в точке h, чтобы получить k (y-координата вершины).