Умножение: по-японски, по-итальянски и методом майя
- Аналия Йоренте
- BBC Mundo
Подпишитесь на нашу рассылку ”Контекст”: она поможет вам разобраться в событиях.
Автор фото, Getty Images
Подпись к фото,Не заболела бы голова…
«Математика такая трудная…» Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.
Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.
Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.
Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.
Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.
Но тут пригодятся некоторые художественные навыки.
Давайте порисуем!
Как минимум три способа умножения связаны с рисованием пересекающихся линий.
1. Способ индейцев майя, или японский метод
Относительно происхождения этого способа существует несколько версий.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Попробуйте метод майя и японцев
Пропустить Подкаст и продолжить чтение.
Подкаст
Что это было?
Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.
эпизоды
Конец истории Подкаст
Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.
Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.
Давайте умножим 23 на 41.
Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.
Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.
Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.
Ну как, неужели трудно?
2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»
Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.
«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.
Автор фото, Getty Images
Подпись к фото,Индийская или итальянская система умножения похожа на венецианские жалюзи
Давайте снова возьмем пример с умножением 23 на 41.
Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру.
Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.
Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.
Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.
Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.
Проделаем то же самое и с другими двумя цифрами.
Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Попробуйте индийский метод
Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.
Как вам показалось, проще этот способ или нет?
Давайте попробуем еще один метод умножения с помощью рисунка.
3. «Массив», или метод таблицы
Как и в предыдущем случае, для этого потребуется нарисовать таблицу.
Возьмем тот же пример: 23 x 41.
Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.
По вертикали мы запишем наверху 40, а внизу 1 .
Затем мы перемножим числа по горизонтали и вертикали.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Нарисуйте таблицу.
Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.
То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.
Проделаем то же самое с нижним рядом.
Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.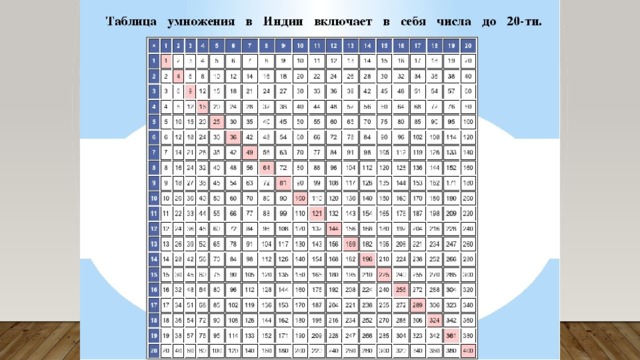
В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.
Сделаем так же со всеми прочими удержанными нулями.
И наконец, мы складываем все четыре числа, полученных умножением в таблице.
Результат? 943. Ну как, помогло?
Важно разнообразие
Автор фото, Getty Images
Подпись к фото,Все способы хороши, главное — чтобы ответ сошелся
Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!
Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.
Так почему же мало где в мире в обычных школах учат этим методам вычисления?
Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.
Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.
«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.
Автор фото, Getty Images
Подпись к фото,Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры
Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.
«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.
Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.
Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.
«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.
Таблица умножения на 13 — Выучить таблицу 13
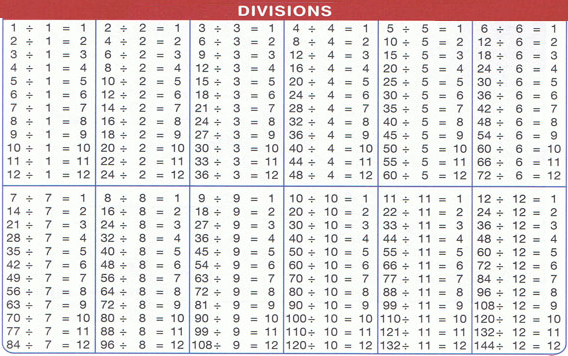
Таблица 13 состоит из умножения 13 на целые числа. Знание таблицы умножения на 13 облегчает обучение в средней школе и за ее пределами. Вместе с таблицей 13 дети должны усвоить факты ее деления. Например, факты деления для таблицы умножения на 13 таковы: 39 ÷ 13 = 3, 52 ÷ 13 = 4, 65 ÷ 13 = 5. Это заложит прочную основу для деления больших чисел.
13 Таблица умножения Таблица умножения:
1. | Таблица умножения 13 |
| 2. | Советы по 13-кратному столу |
| 3. | Часто задаваемые вопросы о таблице умножения на 13 |
Таблица умножения 13
Таблица 13 помогает в расчетах длинного умножения и деления, кратных 13. Итак, давайте посмотрим на первые 10 кратных таблицы 13 умножить.
Таблица умножения на 13
| Таблица умножения на 13 до 10 | |
|---|---|
| 13 × 1 = 13 | 13 × 6 = 78 |
| 13 × 2 = 26 | 13 × 7 = 91 |
| 13 × 3 = 39 | 13 × 8 = 104 |
| 13 × 4 = 52 | 13 × 9 = 117 |
| 13 × 5 = 65 | 13 × 10 = 130 |
Вы можете распечатать или сохранить таблицу 13 в формате PDF, нажав на ссылку ниже.
☛ Таблица умножения на 13
Советы для 13-кратного стола
1.
Чтобы запомнить таблицу умножения на 13, сначала нам нужно запомнить таблицу умножения на 3. Число, кратное 3, равно 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. . . .
2. Чтобы получить числа, кратные 13, прибавьте натуральные числа к цифре десятков, кратных 3. Таким образом, таблица умножения на 13 получается следующим образом: (1+0)3, (2+0)6 , (3+0)9, (4+1)2, (5+1)5, (6+1)8, (7+2)1, (8+2)4, (9+2)7, (10+3)0 = 13, 26, 39, 52, 65, 78, 91, 104, 117, 130.
3. 13 не имеет правил, облегчающих запоминание таблицы умножения 13, но есть шаблон для каждые десять кратных трем: 13, 26, 39, 52, 65, 78, 91, 104, 117, 130. Последняя цифра этих кратных всегда повторяется, что означает, что учащиеся могут запомнить эти цифры, чтобы помочь им с 13 раз стол.
Таблица от 13 до 20
В таблице ниже вы можете увидеть следующие 10 кратных 13, до 20.
| 13 × 11 = 143 | 13 × 16 = 208 |
| 13 × 12 = 156 | 13 × 17 = 221 |
| 13 × 13 = 169 | 13 × 18 = 234 |
| 13 × 14 = 182 | 13 × 19 = 247 |
| 13 × 15 = 195 | 13 × 20 = 260 |
Часто задаваемые вопросы о таблице 13 Times Table
В чем хитрость Таблицы 13?
Один из самых важных приемов для запоминания таблицы умножения на 13 — это запоминание таблицы 3, т. е. 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. Они будут повторяться в таблице умножения.
Что такое Таблица умножения на 13?
| 13 × 1 = 13 | 13 × 6 = 78 |
| 13 × 2 = 26 | 13 × 7 = 91 |
| 13 × 3 = 39 | 13 × 8 = 104 |
| 13 × 4 = 52 | 13 × 9 = 117 |
| 13 × 5 = 65 | 13 × 10 = 130 |
Сколько будет 13 умножить на 12?
13 умножить на 12 = 13 × 12 = 156
Сколько будет 13 умножить на 13?
13 раз 13 = 13 × 13 = 169
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| + | знак плюс | сложение | 1/2 + 1/3 | |||||||
| — | знак минус | вычитание | 3 2 0/390 1||||||||
| * | звездочка | умножение | 2/3 * 3/4 | |||||||
| × | знак умножения | умножение | 2/3 × |
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций . BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
|