10 умножить на 10 в минус 6: 3,6 умножить на 10 в минус 6 степени делить на 12 умножить на 10 в…

alexxlab / / Разное

Единица Длины, Равная 10 В Минус 6 Степени 6 Букв

Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы М

Ниже вы найдете правильный ответ на Единица длины, равная 10 в минус 6 степени 6 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Среда, 19 Июня 2019 Г.


МИКРОН

предыдущий следующий

ты знаешь ответ ?

ответ:

связанные кроссворды

  1. Микрон
    1. Единица длины — миллионная часть метра 6 букв
    2. Миллионная часть метра 6 букв
    3. Одна миллионная доля метра 6 букв
    4. 1/1000000 метра 6 букв
    5. Мера длины 6 букв
    6. Единица длины 6 букв

2500000 минус 6 процентов — сколько будет? Онлайн калькулятор и решение по шагам

Содержание

  1. Способ №1
  2. Способ №2
  3. Считаем проценты с помощью калькулятора
  4. Способ №1
  5. Способ №2
  6. Упрощённый способ

Способ №1

  1. Для начала нужно вычислить процент от числа, для этого необходимо умножить число на нужное количество процентов и поделить на сто.
  2. Затем отнять полученное число от исходного.

Шаг 1: 2500000 умножаем на 6 и делим на 100:

2500000*6/100 = 15000000/100 = 150000

Шаг 2: Отнимаем полученное число 150000 от исходного 2500000:

2500000 — 150000 = 2350000.

Расчёт минус процентов онлайн

минус процентов …

Для добавления сайта в закладки нажмите Ctrl+D

2500000 — 6% = 2350000

2500000 — 6% = 2500000 — (2500000*6)/100 = 2500000 — 150000/100 = 2500000 — 150000 = 2350000

Итак, сколько будет 2500000 минус 6 процентов? Ответ: 2350000.

Способ №2

Если количество процентов, которые необходимо вычесть, меньше ста, можно воспользоваться данным способом:

  1. Сначала отнимаем от ста количество начальных процентов и получаем необходимый процент от числа.
  2. Затем умножаем полученное количество процентов на исходное число и делим на сто. То есть получаем число, равное процентам от нашего числа.

Шаг 1: От 100 процентов отнимаем 6 процентов:

100% — 6% = 94%.

Шаг 2: 94 умножаем на 2500000 и делим на 100:

94*2500000/100 = 235000000/100 = 2350000.

Считаем проценты с помощью калькулятора

Способ №1

Шаг 1: Вычисляем число, которое нужно отнять:

  1. Вводим число «2500000»;
  2. затем нажимаем на умножение «Х»;
  3. затем вводим «6»;
  4. нажимаем равно «=», будет показано «150000»;
  5. нажимаем «÷»;
  6. вводим «100»;
  7. нажимаем равно «=», будет показано «150000».

Шаг 2: Отнимаем число от исходного:

  1. Вводим число «2500000»;
  2. нажимаем «-»;
  3. вводим число «150000»;
  4. нажимаем равно «=», будет показано «2350000».

Способ №2

Шаг 1: Вычисляем проценты:

  1. Вводим «100»;
  2. нажимаем минус «-»;
  3. вводим «6»;
  4. нажимаем равно «=», калькулятор покажет «94».

Шаг 2: Считаем, какое число равно этому числу процентов:

  1. Вводим «2500000»;
  2. нажимаем на умножение «Х»;
  3. вводим полученные на прошлом этапе «94»;
  4. нажимаем «=», видим «235000000»;
  5. нажимаем разделить «÷»;
  6. вводим «100»;
  7. нажимаем «=», получится «2350000».

Упрощённый способ

На некоторых калькуляторах есть кнопка «%», которую можно использовать:

  1. Вводим «2500000»;
  2. нажимаем минус «-»;
  3. вводим «6»;
  4. нажимаем «%»; калькулятор выведет «150000», продвинутый калькулятор выведет в строке «2500000 — 150000»;
  5. нажимаем «=», получаем «2350000».

Калькулятор дробей


Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями.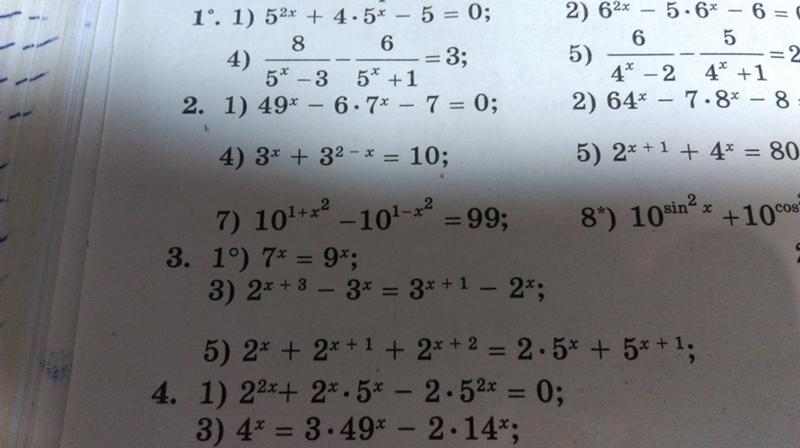 Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражения с дробями:

Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Math Symbols


Symbol Symbol name Symbol Meaning Example
+ plus sign addition 1/2 + 1/3
— знак минус вычитание 1 1/2 — 2/3
* asterisk multiplication 2/3 * 3/4 ​​
× times sign multiplication 2 /3 × 5/6
: division sign division 1/2 : 3
/ division slash division 1/3 / 5 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4 ​​
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.

  • Дробями
    Муравей за первый час поднимается на 2/5 шеста, а за следующий час – на 1/4 шеста. Какую часть шеста преодолевает муравей за два часа?
  • Младенцы
    Двое взрослых, двое детей и четверо младенцев едут в автобусе. Какую часть населения составляют младенцы?
  • Кто-то
    Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите?
  • Знаменатель 2
    Знаменатель дроби равен пяти, а числитель равен 7. Запишите дробь.
  • Корзина с фруктами
    Если в корзине семь яблок и пять апельсинов, какая часть апельсинов в корзине с фруктами?
  • Вычислить выражение
    Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2
  • Out 550,000,00
    Из 550,000,00 было использовано количество 325,000,00. Какая часть от общей суммы была использована?
  • Наименьшие члены 2
    Мы можем записать выражение 4/12 в его наименьшем члене как 1/3. Чему равно 3/15 в наименьшем члене?
  • Петрушка
    Бабушка Милки посадила 12 рядов овощей. 1/6 рядов — морковь. Остальное петрушка. Сколько рядов засажено петрушкой?
  • Четверть
    Четверть числа 72:
  • В столовой
    В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой?

more math problems »

  • decimals
  • fractions
  • triangle ΔABC
  • percentage %
  • permille ‰
  • prime factors
  • complex numbers
  • LCM
  • GCD
  • LCD
  • combinatorics
  • equations
  • статистика
  • … все математические калькуляторы

Как записывать числа в экспоненциальном представлении

Автор: Марк Зегарелли и

Обновлено: 17 августа 2022 г.

Из книги: Базовая математика и предварительная алгебра для чайников

Базовая математика и предварительная алгебра для чайников

Исследовать книгу Стандартно Купить на Amazon

способ записи очень больших и очень маленьких чисел, чтобы их было легче сравнивать и использовать в вычислениях. Чтобы писать в экспоненциальном представлении, используйте форму

, где N — это число от 1 до 10, но не само 10, а 9.0292 a — целое число (положительное или отрицательное число).

Вы перемещаете десятичную точку числа до тех пор, пока новая форма не станет числом от 1 до 10 ( N ), а затем записываете показатель степени ( a ) как количество знаков, на которое была перемещена десятичная точка . Является ли степень числа 10 положительной или отрицательной, зависит от того, сдвинете ли вы десятичную дробь вправо или влево. Перемещение десятичной дроби вправо делает показатель степени отрицательным; перемещение его влево дает положительный показатель степени. Чтобы увидеть положительную экспоненту, напишите

312 000 000 000 в научной записи:

  1. Переместите десятичный разряд к влево , чтобы создать новое число от 1 до 10.

    Где находится десятичная точка в числе 312 000 000 000? Поскольку это целое число, десятичная точка понимается как в конце числа: 312 000 000 000 .

    Итак, Н = 3,12.

  2. Определить показатель степени, то есть количество раз, которое вы передвинули десятичную дробь.

    В этом примере вы переместили десятичную дробь 11 раз; кроме того, поскольку вы переместили десятичную дробь влево, показатель степени положительный. Следовательно, = 11, и вы получите

    .

  3. Введите число в правильной форме для экспоненциального представления

Чтобы увидеть отрицательную экспоненту, напишите .00000031 в научном представлении.

  1. Переместите десятичный разряд вправо , чтобы создать новое число от 1 до 10.

    Итак, N = 3,1.

  2. Определить показатель степени, то есть количество раз, которое вы передвинули десятичную дробь.

    В этом примере вы переместили десятичную дробь 7 раз; кроме того, поскольку вы переместили десятичную дробь вправо, показатель степени будет отрицательным. Следовательно, a = –7, и вы получите

    .

  3. Введите число в правильной форме для экспоненциального представления

Когда вы привыкнете записывать числа в экспоненциальном представлении, вы сможете сделать все это за один шаг. Вот несколько примеров:

Порядок величины

Почему в научной записи всегда используется десятичная дробь от 1 до 10? Ответ связан с

порядком величины , что является простым способом примерно отследить, насколько велико число, чтобы вам было легче сравнивать числа. Порядок величины числа является его показателем степени в научной записи. Например,

703 = 7,03 х 10 2 — порядок величины 2 600 000 = 6 x 10 5 — порядок величины 5 0,00095 = 9.5 x 10 –4 — порядок величины –4

Каждое число от 10 до 100 имеет порядок величины 1. Каждое число от 100 до 1000 имеет порядок величины 2.

Об этой статье

Для чайников ,

Об авторе книги:

Марк Зегарелли — профессиональный писатель, получивший степень по английскому языку и математике в Университете Рутгерса.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта