Простейшее объяснение парадокса Монти Холла | by Андрей Шагин | NOP::Nuances of Programming
Парадокс Монти Холла — это одна из тех математических задач, над решением которой уже долгое время бьются многие умы, и даже всемирно известных математиков она приводит в затруднение. Хотя идея, лежащая в основе этого парадокса, предельно ясна и понятна. Задача эта, строго говоря, и не парадокс вовсе, но называется так из-за неочевидности и парадоксальности предлагаемых решений и объяснений, которые становятся поводом для самых жарких дискуссий в Интернете. Их накал уступает, пожалуй, лишь спорам из-за оптической иллюзии так называемого «платья раздора» и аудиоиллюзии «Янни и Лорел». Предлагаемое здесь объяснение призвано раз и навсегда развеять все связанные с этим парадоксом вопросы и очень доходчиво разъяснить всем интересующимся его суть.
Парадокс впервые был сформулирован американским математиком Стивом Селвином ещё в 1975 году, но широкую известность он приобрёл благодаря популярному игровому шоу «Давайте заключим сделку». В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В чём же суть парадокса Монти Холла?
Представьте, что перед вами три двери, как показано на рисунке ниже. За двумя дверьми находятся козы, за одной — автомобиль. Надо угадать дверь с автомобилем, и он ваш.
Казалось бы, ничего сложного. Но, как говорилось в одном фильме: «Если бы задача так просто решалась, то армянское радио этим бы не занималось». В своей передаче, после того как участник выбирал дверь, Монти всегда открывал одну из дверей с козой и предлагал ему поменять свой выбор. А вы поменяли бы или нет?
Этот вопрос многих ставит в тупик. Люди обычно думают: «Ну какая разница: остались две двери, и машина может с одинаковой вероятностью 50% оказаться как за одной, так и за другой дверью?». … И оказываются неправы. Правильный ответ — всегда менять первоначальный выбор. Поступая так, вы удваиваете свои шансы на победу.
Удивлены? Такой ответ для многих становится откровением: мало кто ожидает этого. Давайте подробно разберёмся, как так получается.
Давайте подробно разберёмся, как так получается.
Итак, вы выбрали одну из трёх дверей. Вероятность того, что машина окажется именно за ней, составляет 1/3. А вероятность того, что она окажется за одной из двух оставшихся (то есть не выбранных вами) дверей, будет 2/3. Это должно быть понятно.
На рисунке у нас наглядно показаны эти вероятности: 1/3 слева и 2/3 справа.
Теперь Монти открывает одну из невыбранных дверей — тех, что справа. И открывает он всегда ту, за которой коза.
Вероятности остаются неизменными: 1/3 слева (ваш первоначальный выбор) и 2/3 справа. Изменилось лишь то, что справа одна дверь теперь открыта, но вероятность для оставшейся неоткрытой двери здесь та же, что была прежде для обеих.
Если не совсем понятно, попробуем объяснить на примере с десятью дверьми.
Выбранная вами дверь будет слева, остальные девять — справа (как на рисунке ниже). Вероятность того, что вы угадали дверь с машиной, будет 1/10. Вероятность того, что вы не угадали и машина окажется за одной из оставшихся девяти дверей, будет 9/10.
Дальше Монти открывает восемь из этих невыбранных девяти дверей, причем за всеми восемью — козы. Как поступить теперь: поменять свой выбор или нет? Конечно, поменять! Ведь теперь восемь из девяти дверей справа открыты, а вероятность того, что машина окажется за оставшейся девятой дверью (как мы уже посчитали ранее), равна 9/10.
Ответ на вопрос станет ещё очевиднее, если представить, что Монти даёт вам возможность открыть не одну оставшуюся справа неоткрытой дверь, а сразу все девять!
Вот и всё. Это так просто! Однако важно не забывать, что всегда есть вероятность проигрыша. Верное решение определяется стратегией. Правильная стратегия — делать так, чтобы шансы на победу были максимальными или хотя бы такими, которые позволяют больше выигрывать, чем проигрывать.
Предположим, Монти хочет усложнить для вас задачу и открывает лишь одну дверь с правой стороны. Как вы поступите теперь: выберите одну из восьми закрытых дверей справа или не станете менять свой выбор?
Здесь придётся кое-что посчитать. Вероятность того, что машина окажется за одной из девяти дверей справа, равна 9/10. Разделим её на количество оставшихся неоткрытыми дверей (8):
Вероятность того, что машина окажется за одной из девяти дверей справа, равна 9/10. Разделим её на количество оставшихся неоткрытыми дверей (8):
Это будет вероятность того, что машина окажется за одной из восьми остающихся закрытыми дверей справа. И она чуть больше вероятности 0,1 (1/10), что первоначально выбранная вами дверь слева окажется с машиной. Поэтому вам всё же предпочтительнее поменять свой выбор, хотя шансы выиграть машину и в этом случае будут очень низкими. По этой же формуле можно посчитать вероятность для любого количества неоткрытых дверей.
Вот и весь парадокс Монти Холла вкратце. Не знаю, можно ли придумать более простое его объяснение? Я лишь выношу на ваш суд свой взгляд, отличный от тех, что изложены в большинстве других объяснений, в которых вы можете тоже почерпнуть много полезного. Надеюсь, что после прочтения статьи вы приблизились к пониманию парадокса Монти Холла.
Читайте также:
- Руководство по машинному обучению для новичков
- JavaScript Essentials: числа и математика
- Завораживающая последовательность Фибоначчи
Читайте нас в телеграмме, vk и Яндекс. Дзен
Дзен
Перевод статьи Anup Sebastian: The easiest explanation to the Monty Hall problem
Парадокс Монти Холла — подготовка к ЕГЭ по Математике
Анна Малкова
Один из парадоксов теории вероятностей назван, как ни странно, не в честь ученого, а в честь ведущего телевизионного шоу. Это знаменитый парадокс Монти Холла.
Вот как он формулируется:
Вы — участник игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1.
После этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не хотите ли изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Чтобы ведущий не схитрил, сразу оговариваются следующие правила:
- автомобиль равновероятно размещён за любой из трёх дверей;
- ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор;
- если у ведущего есть выбор, какую из двух дверей открыть, он выбирает любую из них с одинаковой вероятностью.

Итак, вы выбрали одну из дверей, но не знаете, что за ней. Возможно, там автомобиль. И если вы, приняв предложение ведущего, измените свой выбор, — вы променяете автомобиль на козу!
А если там коза? Тогда, приняв предложение ведущего, вы выиграете автомобиль! Так менять выбор или не менять? Или шансы останутся такими же?
Вспомним основные принципы теории вероятностей.
Случайным называется событие, которое невозможно точно предсказать заранее. Оно может либо произойти, либо нет. Теория вероятностей изучает случайные события и их закономерности, а также случайные величины и действия над ними.
Благоприятным мы называем исход, способствующий наступлению данного события.
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Очевидно, что вероятность – величина положительная и не может быть больше единицы.
Представьте, что вы – участник игры. С вероятностью вы выбрали дверь, за которой автомобиль. С вероятностью – дверь, за которой коза.
С вероятностью – дверь, за которой коза.
После этого ведущий спрашивает вас, не хотите ли вы поменять свой выбор.
Изобразим возможные исходы. В задачах по теории вероятностей мы часто рисуем такие схемы.
Если вы решили не менять свой выбор – вероятность выиграть автомобиль равна . Вы просто сразу выбрали дверь, за которой автомобиль, с вероятностью (одна благоприятная дверь из трех возможных).
А если вы поменяли свой выбор после того, как ведущий показал вам козу? Тогда вероятность выиграть автомобиль равна .
Все просто. Даже проще, чем в задачах ЕГЭ, которые мы рассматривали
Предложите эту задачу людям, не знающим теории вероятностей. Вы услышите самые разные ответы. Задача потому и называется «парадоксом», что первые пришедшие в голову «интуитивные» решения могут быть неверными.
Больше задач по теории вероятностей здесь:
Задачи по теории вероятности
— а также в бесплатном видеокурсе по теории вероятностей
Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Парадокс Монти Холла» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Информация на странице «Парадокс Монти Холла» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 08.04.2023
Понимание проблемы Монти Холла – BetterExplained
Задача Монти Холла представляет собой нелогичную статистическую головоломку:
- Есть 3 двери, за которыми две козы и машина.
- Вы выбираете дверь (назовем ее дверь А). Вы, конечно, надеетесь на машину.
- Монти Холл, ведущий игрового шоу, осматривает другие двери (B и C) и открывает одну с помощью козла. (Если на обеих дверях есть козы, он выбирает случайным образом.)
Вот игра: Вы придерживаетесь двери А (первоначальная догадка) или переключаетесь на неоткрытую дверь? Это имеет значение?
Удивительно, но шансы не 50 на 50. Если вы поменяете дверь, вы выиграете в 2/3 случаев!
Если вы поменяете дверь, вы выиграете в 2/3 случаев!
Сегодня давайте поймем , почему простая игра может быть такой непонятной. На самом деле игра заключается в переоценке ваших решений по мере появления новой информации.
Играть в игру
Вы, наверное, бормочете, что две двери означают шансы 50 на 50. Хорошо, дружище, давай сыграем в игру:
Попробуйте сыграть в игру 50 раз, используя стратегию «выбери и держи». Просто выберите дверь 1 (или 2, или 3) и продолжайте нажимать. Щелкни, щелкни, щелкни. Посмотрите на свой процент выигрышей. Вы увидите, что он стабилизируется примерно на 1/3.
Теперь сбросьте и сыграйте 20 раз, используя подход «выбери и переключи». Выберите дверь, Монти покажет козла (серая дверь), и вы переключитесь на другую. Посмотрите на свой винрейт. Выше 50% Ближе к 60%? До 66%?
Есть шанс, что стратегия «остановись и держись» сработает на небольшом количестве испытаний (менее 20 или около того). Если бы у вас была монета, сколько бросков вам нужно, чтобы убедить себя, что она честная? Вы можете получить 2 орла подряд и подумать, что это было сфальсифицировано. Просто сыграйте в игру несколько десятков раз, чтобы выровнять ее и уменьшить шум.
Просто сыграйте в игру несколько десятков раз, чтобы выровнять ее и уменьшить шум.
Понимание того, почему переключение работает
Это сложный (но убедительный) способ реализации переключения. Вот более простой способ:
Если я выберу дверь и буду держать ее, у меня будет 1/3 шанса на победу.
Мое первое предположение — 1 из 3 — есть 3 случайных варианта, верно?
Если я буду твердо придерживаться своего первого выбора, несмотря ни на что, я не смогу улучшить свои шансы. Монти может добавить 50 дверей, взорвать остальные, станцевать танец дождя вуду — это не имеет значения. Лучшее, что я могу сделать со своим первоначальным выбором, это 1 из 3. Остальные шансы должны быть у другой двери, или 2/3.
Объяснение может иметь смысл, но не объясняет почему шансы на другой стороне «улучшаются». (Несколько читателей оставили свои объяснения в комментариях — попробуйте их, если переключатель 1/3 остаться против 2/3 не щелкает).
Понимание игрового фильтра
Давайте посмотрим, почему удаление дверей делает переключение привлекательным. Вместо обычной игры представьте такой вариант:
- В начале 100 дверей на выбор
- Вы выбираете одну дверь
- Монти смотрит на 99 других, находит козлов и открывает все, кроме 1
Вы придерживаетесь своей исходной двери (1/100) или другой двери, которая была отфильтрована из 99? (Попробуйте это в игре-симуляторе, используйте 10 дверей вместо 100).
Теперь немного понятнее: Монти берет набор из 99 вариантов и улучшает их , удаляя 98 козлов. Когда он закончит, у него будет лучшая дверь из 99, которую вы можете выбрать.
Ваше решение: Вы хотите случайных дверь из 100 (первоначальная догадка) или лучшая дверь из 99? Другими словами, вам нужен 1 случайный шанс или лучший из 99 случайных шансов?
Мы начинаем понимать, почему действия Монти помогают нам. Он позволяет нам выбирать между обычным, случайным выбором и отобранными, отфильтрованными вариантами. Фильтрованное лучше.
Фильтрованное лучше.
Но… но… разве два выбора не означают шансы 50 на 50?
Преодоление наших заблуждений
Предположение, что «два варианта означают 50 на 50 шансов», является нашим самым большим препятствием.
Да, два варианта равновероятны, если вы ничего не знаете о каждом из них. Если я выберу двух случайных японских кувшинов и спрошу: «У кого рейтинг выше?» ты бы не догадался. Вы выбираете имя, которое звучит круче, и 50 на 50 — это лучшее, что вы можете сделать. Вы ничего не знаете о ситуации.
Теперь предположим, что Питчер А — новичок, никогда не тестировался, а Питчер Б выигрывал награду «Самый ценный игрок» последние 10 лет подряд. Изменит ли это ваше предположение? Несомненно: вы выберете кувшин B (почти с уверенностью). Ваш несведущий друг все равно назвал бы это ситуацией 50 на 50.
Информация имеет значение.
Чем больше вы знаете…
Вот общая идея: Чем больше вы знаете, тем лучше ваше решение.
С японскими бейсболистами вы знаете больше, чем ваш друг, и у вас больше шансов. Да, да, есть шансов новый новичок — лучший игрок в лиге, но мы говорим здесь о вероятностях . Чем больше вы тестируете старый стандарт, тем меньше вероятность того, что новый выбор превзойдет его.
Вот что происходит с игрой 100 дверей. Ваш первый выбор — случайная дверь (1/100), а другой ваш выбор — чемпион, выбивший 99 других дверей (он же MVP лиги). Скорее всего, чемпион лучше, чем новая дверь.
Визуализация облака вероятности
Вот как я визуализирую процесс фильтрации. В начале у каждой двери равные шансы — я представляю бледно-зеленое облако, равномерно распределенное между всеми дверями.
Когда Монти начинает удалять плохих кандидатов (из 99, которые вы не выбрали), он «отталкивает» облако от плохих дверей к хорошим на той стороне. Это продолжается и продолжается — и оставшиеся двери получают более яркое зеленое облако.
После всей фильтрации есть ваша исходная дверь (все еще с бледно-зеленым облаком) и «дверь чемпиона», светящаяся ядерно-зеленым цветом, содержащая вероятности 98 дверей.
Вот ключ: Монти не пытается улучшить твою дверь!
Он целенаправленно , а не осматривает вашу дверь и пытается избавиться от коз там. Нет, он только «выдергивает сорняки» с соседского газона, а не с вашего.
Обобщение игры
Общий принцип заключается в переоценке вероятностей по мере добавления новой информации. Например:
Байесовский фильтр улучшается, поскольку он получает больше информации о том, являются ли сообщения спамом или нет. Вы не хотите оставаться статичными с вашим начальным обучающим набором данных.
Оценка теорий. Без каких-либо доказательств две теории равновероятны. Собрав дополнительные доказательства (и проведя больше испытаний), вы можете увеличить доверительный интервал того, что теория А или Б верна. Одним из аспектов статистики является определение того, «сколько» информации необходимо для уверенности в теории.
Это общие случаи, но смысл ясен: больше информации означает, что вы переоцениваете свой выбор. Фатальный недостаток парадокса Монти Холла заключается в том, что не принимает во внимание фильтрацию Монти , полагая, что шансы одинаковы до и после того, как он фильтрует другие двери.
Фатальный недостаток парадокса Монти Холла заключается в том, что не принимает во внимание фильтрацию Монти , полагая, что шансы одинаковы до и после того, как он фильтрует другие двери.
Резюме
Вот ключевые моменты для понимания головоломки Монти Холла:
- Два варианта 50-50, когда вы ничего о них не знаете
- Монти помогает нам, «отфильтровывая» плохие решения на другой стороне. Это выбор случайного предположения и «Чемпионской двери», которая является лучшей с другой стороны.
- Как правило, чем больше информации, тем больше вы переоцениваете свой выбор.
Фатальная ошибка в парадоксе Монти Холла заключается в том, что он не принимает во внимание фильтрацию Монти, думая, что шансы одинаковы до и после. Но цель не в том, чтобы понять эту головоломку, а в том, чтобы понять, как последующие действия и информация бросают вызов предыдущим решениям. Счастливая математика.
Приложение
Давайте подумаем о других сценариях, чтобы закрепить наше понимание:
Ваш приятель делает предположение
Предположим, ваш друг входит в игру после того, как вы выбрали дверь, и Монти показал козла, но он не знает рассуждений, которые использовал Монти.
Он видит две двери и ему говорят выбрать одну: у него шансы 50 на 50! Он не знает, почему та или иная дверь должна быть лучше (но вы знаете). Основная путаница заключается в том, что мы думаем, что мы похожи на нашего приятеля — мы забываем (или не осознаем) влияние фильтрации Монти.
Монти сходит с ума
Монти показывает козу, и у него случается припадок. Он закрывает дверь и перемешивает все призы, включая вашу дверь. Переключение помогает?
Нет. Монти начал фильтровать, но так и не завершил — у вас есть 3 случайных выбора, как и в начале.
Множественный Монти
Монти дает вам 6 дверей: вы выбираете 1, а он делит остальные 5 на группы из 2 и 3. Затем он убирает коз до тех пор, пока в каждой группе не останется по 1 двери. На что вы переключаетесь?
Группа, в которой изначально было 3 двери. В ней 3 двери «схлопнулись» в 1, т.к. 3/6 = 50% шанс. Ваша исходная догадка имеет 1/6 (16%), а группа, у которой было 2, имеет 2/6 = 33% верности.
Другие сообщения из этой серии
- Краткое введение в теорию вероятностей и статистику
- Интуитивное (и краткое) объяснение теоремы Байеса
- Понимание теоремы Байеса с отношениями
- Понимание проблемы Монти Холла
- Как анализировать данные с использованием среднего значения
- Понимание парадокса дня рождения
Почему вы всегда должны переключаться: проблема Монти Холла (наконец-то) объяснена — Стивен Пинкер
Одним из самых известных телевизионных игровых шоу периода расцвета жанра с 1950-х по 1980-е годы было Let’s Make a Deal . Его ведущий, Монти Холл, добился славы второго рода, когда в его честь была названа дилемма теории вероятностей, основанная на сериале. Участник сталкивается с тремя дверями. За одним из них стоит гладкий новый автомобиль. За двумя другими стоят козы. Участник выбирает дверь, скажем, Дверь 1. Чтобы создать интригу, Монти открывает одну из двух других дверей, скажем, Дверь 3, показывая козу.
Почти все остаются. Они подсчитали, что, поскольку машина была помещена за одну из трех дверей случайным образом, а дверь 3 была удалена, теперь существует пятьдесят на пятьдесят шансов, что машина окажется за дверью 1 или дверью 2. Хотя в этом нет ничего плохого. переключение, думают они, тоже ни к чему. Поэтому они придерживаются своего первого выбора из-за инерции, гордости или ожидания, что их сожаление после неудачного переключения будет более сильным, чем их радость после удачного.
Дилемма Монти Холла стала известной в 1990, когда он был представлен в колонке «Спросите Мэрилин» в журнале Parade , помещенном в воскресных выпусках сотен американских газет. Обозревателем была Мэрилин вос Савант, известная в то время как «самая умная женщина в мире» из-за ее записи в Книге рекордов Гиннеса за наивысший балл в тесте на интеллект. Вос Савант написал, что вам следует переключиться: вероятность того, что машина окажется за дверью 2, составляет два к трем, по сравнению с одним к трем для двери 1. Колонка привлекла десять тысяч писем, тысяча из них от докторов наук, в основном по математике и статистике. , большинство из которых сказали, что она была неправа. Вот несколько примеров:
Вос Савант написал, что вам следует переключиться: вероятность того, что машина окажется за дверью 2, составляет два к трем, по сравнению с одним к трем для двери 1. Колонка привлекла десять тысяч писем, тысяча из них от докторов наук, в основном по математике и статистике. , большинство из которых сказали, что она была неправа. Вот несколько примеров:
Ты все испортил, и ты все испортил! Поскольку вам, кажется, трудно уловить основной принцип работы, я объясню. После того, как ведущий показывает козла, у вас теперь есть один шанс из двух быть правым. Независимо от того, измените ли вы свой выбор или нет, шансы одинаковы. В этой стране достаточно математической неграмотности, и нам не нужно, чтобы самый высокий в мире IQ распространялся дальше. Стыд!
— Скотт Смит, доктор философии, Университет Флориды
Я уверен, что вы получите много писем на эту тему от старшеклассников и студентов колледжей. Возможно, вам следует сохранить несколько адресов для помощи в будущих колонках.
—В. Роберт Смит, доктор философии, Университет штата Джорджия
Возможно, женщины смотрят на математические задачи иначе, чем мужчины.
— Дон Эдвардс, Санривер, Орегон
Среди противников был Пол Эрдёш (1913–1996), известный математик, который был настолько плодовит, что многие ученые хвастаются своим «числом Эрдёша» — длиной кратчайшей цепочки соавторства, связывающей их великому теоретику.
Но математики-мэнсплейнеры ошибались, а самая умная женщина в мире была права. Вы должны переключиться. Нетрудно понять, почему. Есть три варианта того, где можно было разместить машину. Давайте рассмотрим каждую дверь и посчитаем, сколько раз из трех вы бы выиграли с каждой стратегией. Вы выбрали Дверь 1, но это, конечно, просто ярлык; пока Монти следует правилу «Открой невыбранную дверь козой; если у обоих есть козы, выберите одну наугад», шансы одинаковы, какую бы дверь вы ни выбрали.
Допустим, ваша стратегия «Остаться» (левая колонка на рисунке). Если машина находится за дверью 1 (вверху слева), вы выиграли. (Неважно, какую из других дверей открыл Монти, потому что вы не переключаетесь ни на одну из них.) Если машина находится за дверью 2 (посередине слева), вы проигрываете. Если машина находится за дверью 3 (внизу слева), вы проиграли. Так что шансы на победу со стратегией «Останься» составляют один к трем.
Если машина находится за дверью 1 (вверху слева), вы выиграли. (Неважно, какую из других дверей открыл Монти, потому что вы не переключаетесь ни на одну из них.) Если машина находится за дверью 2 (посередине слева), вы проигрываете. Если машина находится за дверью 3 (внизу слева), вы проиграли. Так что шансы на победу со стратегией «Останься» составляют один к трем.
Теперь предположим, что ваша стратегия — «Переключение» (правая колонка). Если машина находится за дверью 1, вы проиграли. Если машина находится за дверью 2, Монти открыл бы дверь 3, поэтому вы переключитесь на дверь 2 и выиграете. Если машина находится за дверью 3, он бы открыл дверь 2, поэтому вы переключитесь на дверь 3 и выиграете. Шансы на победу со стратегией «Переключиться» — два к трем, что вдвое больше шансов остаться.
Это не ракетная хирургия. Даже если вы не прорабатываете логические возможности, вы можете сами сыграть несколько раундов с фигурками и игрушками и подсчитать результаты, как это сделал сам Холл, чтобы убедить скептически настроенного журналиста. (Сегодня вы можете играть в нее онлайн.) Или вы можете следовать интуиции: «Монти знает ответ и дал мне подсказку; было бы глупо не действовать». Почему математики, профессора и другие шишки так ошибались?
(Сегодня вы можете играть в нее онлайн.) Или вы можете следовать интуиции: «Монти знает ответ и дал мне подсказку; было бы глупо не действовать». Почему математики, профессора и другие шишки так ошибались?
Многие настаивают на том, что все неизвестные альтернативы (в данном случае неоткрытые двери) должны иметь одинаковую вероятность. Это верно для симметричных игровых игрушек, таких как лицевая сторона монеты или стороны игральной кости, и это разумная отправная точка, когда вы абсолютно ничего не знаете об альтернативах. Но это не закон природы.
Определенно были неудачи критического мышления из-за сексизма, личных предубеждений и профессиональной зависти. Вос Савант — привлекательная и стильная женщина без инициалов после имени, которая писала для газеты, наполненной рецептами и сплетнями, и подшучивала на ночных ток-шоу. Она бросила вызов стереотипу математика, а ее знаменитость и право хвастаться Guinness сделали ее большой жирной мишенью для тейкдауна.
Но часть проблемы заключается в самой проблеме. Многие люди не могут проглотить правильное объяснение, даже когда им на него указывают. В том числе и Эрдёш, который, оскорбляя душу математика, убедился только тогда, когда увидел, как игра многократно моделируется. Многие упорствуют, даже когда видят, что это смоделировано, и даже когда постоянно играют на деньги. В чем несоответствие между нашей интуицией и законами случая?
Подсказка исходит из самонадеянных оправданий, которые всезнайки предлагали своим ошибкам, иногда бездумно перенесенных из других вероятностных головоломок. Многие настаивают на том, что каждая из неизвестных альтернатив (в данном случае неоткрытая дверь) должна иметь равную вероятность. Это верно для симметричных игровых игрушек, таких как лицевая сторона монеты или стороны игральной кости, и это разумная отправная точка, когда вы абсолютно ничего не знаете об альтернативах. Но это не закон природы.
Многие люди не могут проглотить правильное объяснение, даже когда им указывают на него.
В том числе и Эрдёш, который, оскорбляя душу математика, убедился только тогда, когда увидел, как игра многократно моделируется.
Многие визуализируют причинно-следственную цепочку. Машина и козы были размещены до раскрытия, и открытие двери не может перемещать их после факта. Указание на независимость причинно-следственных механизмов — это распространенный способ развенчать другие иллюзии, такие как заблуждение игрока, согласно которому люди ошибочно думают, что после выпадения красных цветов следующий спин рулетки выпадет черным, хотя на самом деле колесо уже выпало. нет памяти, поэтому каждый спин независим. Как сказал один из корреспондентов Вос Саванта: «Представьте себе скачки с участием трех лошадей, каждая из которых имеет равные шансы на победу. Если лошадь № 3 упадет замертво на 50 футах в гонке, шансы для каждой из оставшихся двух лошадей больше не один к трем, а теперь один к двум». Очевидно, заключил он, не имеет смысла переключать ставку с лошади №1 на лошадь №2. Но проблема работает не так. Представьте, что после того, как вы сделали ставку на №1, Бог объявляет: «Это не будет лошадь №3». Он мог бы предостеречь против лошади № 2, но не сделал этого. Изменение ставки не звучит так безумно. В Давай заключим сделку , Монти Холл — это Бог.
Но проблема работает не так. Представьте, что после того, как вы сделали ставку на №1, Бог объявляет: «Это не будет лошадь №3». Он мог бы предостеречь против лошади № 2, но не сделал этого. Изменение ставки не звучит так безумно. В Давай заключим сделку , Монти Холл — это Бог.
Богоподобный хозяин напоминает нам, насколько экзотична проблема Монти Холла. Для этого требуется всеведущее существо, которое бросает вызов обычной цели разговора — поделиться тем, что слушатель должен знать (в данном случае, какая дверь скрывает машину), — и вместо этого преследует цель усилить напряжение среди третьих лиц. И в отличие от мира, чьи подсказки безразличны к нашему расследованию, Монти Всемогущий знает правду и знает наш выбор и соответственно выбирает свое откровение.
Невосприимчивость людей к этой прибыльной, но эзотерической информации указывает на когнитивную слабость в основе головоломки: мы путаем вероятность с склонностью . Склонность – это предрасположенность объекта действовать определенным образом. Интуитивные представления о склонностях составляют основную часть наших ментальных моделей мира. Люди чувствуют, что согнутые ветки имеют тенденцию отскакивать назад, что куду может легко устать, что дикобразы обычно оставляют следы с двумя подушечками. Склонность нельзя воспринять напрямую (либо ветвь отскочила, либо нет), но ее можно вывести, внимательно изучив физическое строение объекта и работая с законами причины и следствия. Более сухая ветка может сломаться, куду более вынослив в сезон дождей, у дикобраза есть две проксимальные подушечки, которые оставляют отпечатки на мягкой земле, но не обязательно на твердой.
Интуитивные представления о склонностях составляют основную часть наших ментальных моделей мира. Люди чувствуют, что согнутые ветки имеют тенденцию отскакивать назад, что куду может легко устать, что дикобразы обычно оставляют следы с двумя подушечками. Склонность нельзя воспринять напрямую (либо ветвь отскочила, либо нет), но ее можно вывести, внимательно изучив физическое строение объекта и работая с законами причины и следствия. Более сухая ветка может сломаться, куду более вынослив в сезон дождей, у дикобраза есть две проксимальные подушечки, которые оставляют отпечатки на мягкой земле, но не обязательно на твердой.
Невосприимчивость людей к этой прибыльной, но эзотерической информации указывает на когнитивную слабость в основе загадки: мы путаем вероятность с склонностью .
Но вероятность другая; это концептуальный инструмент, изобретенный в семнадцатом веке. Слово имеет несколько значений, но одно из них имеет значение при принятии рискованных решений — это сила веры в неизвестное положение дел.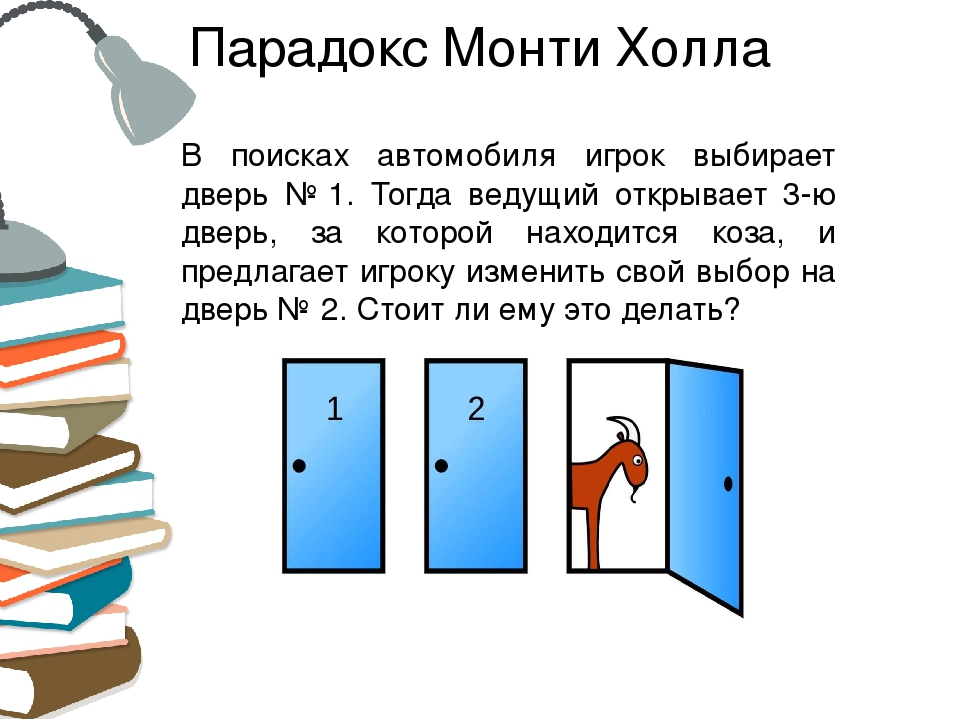 Любая крупица свидетельства, которая меняет нашу уверенность в исходе, изменит его вероятность и рациональный способ действовать в соответствии с ним. Зависимость вероятности от нематериальных знаний, а не просто от физического облика, помогает объяснить, почему люди терпят неудачу при решении этой дилеммы. Они интуитивно чувствуют склонность автомобиля к тому, чтобы оказаться за разными дверями, и знают, что открытие двери не могло изменить эти склонности. Но вероятности не касаются мира; они о наших невежество мира. Новая информация уменьшает наше невежество и изменяет вероятность. Если это звучит мистически или парадоксально, подумайте о вероятности того, что монета, которую я только что подбросил, выпадет решкой. Для вас это 0,5. Для меня это 1 (я заглянул). То же событие, другое знание, разная вероятность. В дилемме Монти Холла новая информация предоставляется всевидящим хозяином.
Любая крупица свидетельства, которая меняет нашу уверенность в исходе, изменит его вероятность и рациональный способ действовать в соответствии с ним. Зависимость вероятности от нематериальных знаний, а не просто от физического облика, помогает объяснить, почему люди терпят неудачу при решении этой дилеммы. Они интуитивно чувствуют склонность автомобиля к тому, чтобы оказаться за разными дверями, и знают, что открытие двери не могло изменить эти склонности. Но вероятности не касаются мира; они о наших невежество мира. Новая информация уменьшает наше невежество и изменяет вероятность. Если это звучит мистически или парадоксально, подумайте о вероятности того, что монета, которую я только что подбросил, выпадет решкой. Для вас это 0,5. Для меня это 1 (я заглянул). То же событие, другое знание, разная вероятность. В дилемме Монти Холла новая информация предоставляется всевидящим хозяином.
Один из выводов заключается в том, что когда уменьшение невежества, предоставленное носителем, более прозрачно связано с физическими обстоятельствами, решение проблемы становится интуитивно понятным.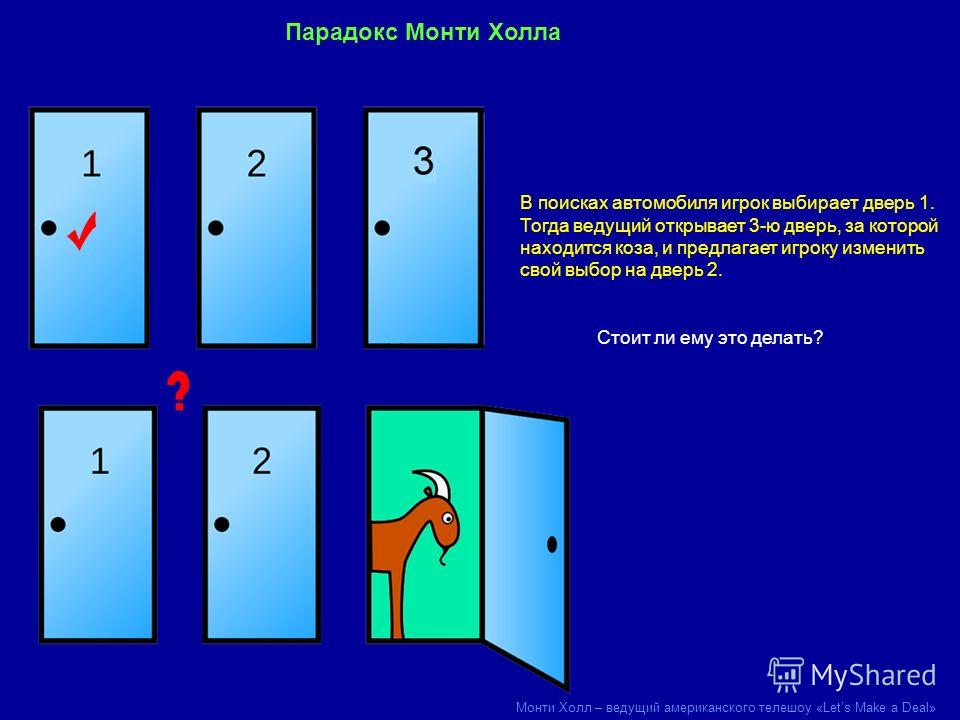


 В том числе и Эрдёш, который, оскорбляя душу математика, убедился только тогда, когда увидел, как игра многократно моделируется.
В том числе и Эрдёш, который, оскорбляя душу математика, убедился только тогда, когда увидел, как игра многократно моделируется.