Решение неравенства онлайн калькулятор: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

Решение абсолютных неравенств — MathCracker.com

Алгебра Учебники

---

Неравенство абсолютных ценностей — это неравенство, в котором есть одно или несколько абсолютная величина . Напомним, неравенство почти похоже на уравнение, но вместо знака «=» стоит «≤» или «≥».

Это различие приводит к тому, что набор решений обычно представляет собой область, как и для большинства неравенств.

И тот факт, что речь идет об абсолютных величинах, указывает на особый подход к их разрешению.

В этом руководстве мы сконцентрируемся на конкретных навыках, необходимых для разрешения этого типа неравенства, содержащего одно или несколько абсолютных значений. Также предположим, что в неравенстве участвуют одна или две переменные, \(x\) и / или \(y\).

---

Что такое абсолютное неравенство?

Для целей этого анализа мы будем рассматривать неравенство по абсолютной величине как неравенство, включающее одну или две переменные, по крайней мере, с одним абсолютным значением.

Например, ниже у нас есть неравенство абсолютных значений с двумя переменными \(x\) и \(y\):

\[|3x+2y-1| \ge 1\]

Или, кроме того, мы могли бы иметь следующее неравенство по абсолютным значениям только с одной переменной:

\[|3x-1| \le 2\]

Для наших целей и для целей методов, используемых для их разрешения, мы будем иметь дело с неравенствами обоих типов (одна и две переменные)

Как разрешить абсолютное неравенство ценностей?

При решении уравнений или неравенств на самом деле не существует серебряной пули, которая решает все. Каждая проблема индивидуальна и может иметь свои особенности.

Лучшее, что мы можем сделать, — это предложить серию шагов, которые помогут вам в процессе разрешения неравенства.

Шаг 1: Для каждого абсолютного значения определите области, в которых аргумент абсолютного значения отрицательный, а где неотрицательный.

Шаг 2: Если в неравенстве есть только одно абсолютное значение, решите его в обеих областях (где аргумент абсолютного значения отрицательный, а где он неотрицательный).

Шаг 3: Если в неравенстве более одного абсолютного значения, необходимо пересечь все регионы, чтобы получить набор меньших разделов. В каждом разделе нужно ТОЧНО знать знак каждого аргумента. Затем решите неравенство во всех областях.

Шаг 4: Как только вы получите частичное решение, которое находится в каждой из областей, окончательное решение будет простым объединением этих частичных решений.

Проще говоря: вам нужно выяснить области, в которых вы точно знаете знак аргумента абсолютных значений (чтобы от них можно было избавиться).

Несколько примеров должны прояснить эти шаги.

ПРИМЕР 1

Решите следующее неравенство

\[| 2x + 4y — 1 | \ge 2\]

ОТВЕЧАТЬ:

Чтобы решить неравенство, нам нужно использовать шаги, указанные выше.

Шаг 1: Существует только одно абсолютное значение, поэтому нам нужно определить, является ли аргумент отрицательным или неотрицательным. Следовательно, нам нужно сначала решить:

\[2x + 4y — 1 \ge 0\]

Есть несколько стратегий для решения вышеуказанного, но самый простой — сначала решить уравнение

\[2x + 4y — 1 = 0\]

что означает, что \(4y = -2x + 1\) или то же самое, что и \(y = -\frac{1}{2}x + \frac{1}{4}\), что соответствует линии с уклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\).

Теперь, чтобы позаботиться о \(2x + 4y — 1 \ge 0\), мы проверяем, удовлетворяет ли точка \((0,0)\) неравенству:

\[2(0) + 4(0) — 1 = -1 < 0\]

Итак, \((0,0)\) удовлетворяет или не удовлетворяет неравенству. Напрашивается вывод, что линия с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\) делит плоскость на две области:

Для точек ниже линии (мы называем эту область 1, \(R_1\)) мы получаем, что \(2x + 4y — 1 < 0\)

Для точек над линией, включая саму линию (мы называем эту область 2, \(R_2\)), мы получаем, что \(2x + 4y — 1 \ge 0\)

Почему это важно? Почему мы берем на себя все эти проблемы? Потому что на \(R_1\) мы получаем это с \( 2x + 4y — 1 < 0\), затем \(| 2x + 4y — 1 | = -(2x + 4y — 1) \).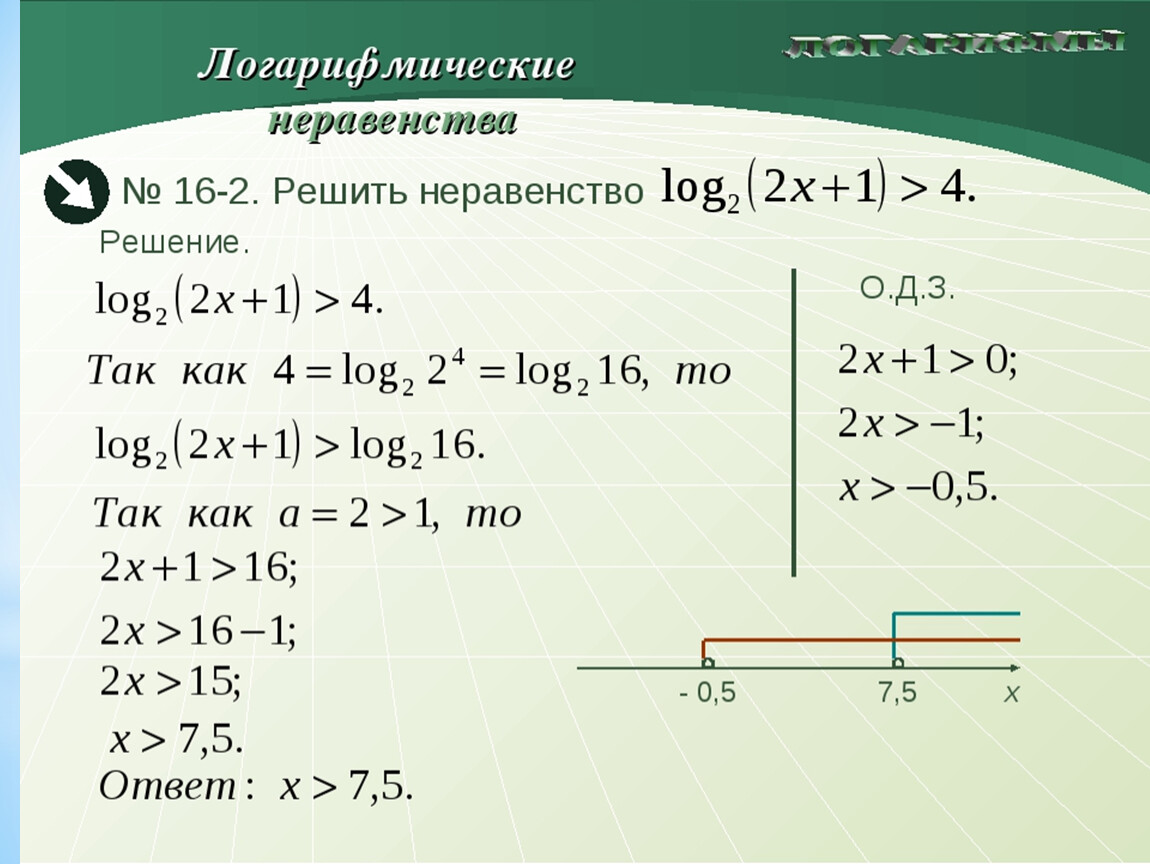 Точно так же на \(R_2\) мы получаем это, поскольку \( 2x + 4y — 1 \ge 0\), затем \(| 2x + 4y — 1 | = 2x + 4y — 1 \).

Шаг 2: Теперь нам нужно решить неравенство на участке 1, \(R_1\) :

\[| 2x + 4y — 1 | \ge 2\] \[\Rightarrow -(2x + 4y — 1) \ge 2\] \[\Rightarrow 2x + 4y — 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x — 1\] \[\Rightarrow y \le -\frac{1}{2}x — \frac{1}{4} \]

Это соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\). Но не забывайте, что вы находитесь на \(R_1\), и эта линия, которую мы обнаружили, находится НИЖЕ границы \(R_1\) (см. График ниже).

Чтобы уточнить, поскольку мы находимся в предположении, что мы находимся в \(R_1\), нам нужно, чтобы мы были НИЖЕ линией с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\). Исходя из этого предположения, мы решили исходное неравенство, и нам также необходимо находиться ниже линии с наклоном \(m = -\frac{1}{2}\) и точкой пересечения по оси Y \(n = -\frac{1}{4}\). Эти два условия должны выполняться одновременно, поэтому мы получаем пересечение двух областей.

Итак, частичное решение в этом случае соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\).

Теперь нам нужно решить неравенство в области 2, \(R_2\) :

\[| 2x + 4y — 1 | \ge 2\] \[\Rightarrow 2x + 4y — 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]

Это соответствует всем точкам выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\). Но не забывайте, что вы находитесь на \(R_2\), и эта линия находится НАД границей \(R_2\) (см. График ниже).

Находя пересечение между \(R_2\) и областью выше, мы получаем, что решение части в этом случае — это все точки выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\).

Шаг 4: Теперь окончательное решение — это объединение всех решений частей из предыдущих частей: окончательное решение — это все точки НИЖЕ или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\), ПЛЮС все точки НАДЕЖДА или на линии с наклоном \(m = -\frac{1}{2}\) и Y-перехват \(n = \frac{3}{4}\).

Графически получаем

что завершает разрешение неравенства.

ПРИМЕР 2

Решите следующее двойное неравенство абсолютных значений

\[| 2x — 1 | \ge |x + 3|\]

ОТВЕЧАТЬ:

Это двойное неравенство по абсолютным значениям, потому что существует 2 абсолютных значения. Это означает, что поиск регионов потребует немного больше работы (условно говоря).

Шаг 1: Для первого абсолютного значения мы решаем:

\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]

Итак, мы получаем \(2x- 1 \ge 0\) на \([\frac{1}{2}, +\infty)\) и \(2x- 1 < 0\) на \((-\infty, \frac{1}{2})\).

Для второго абсолютного значения решаем:

\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]

Итак, мы получаем \(x+3 \ge 0\) на \([-3, +\infty)\) и \(x+3 < 0\) на \((-\infty, -3)\).

Итак, мы определяем 4 региона:

\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). В этом регионе мы получаем: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).

\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). В этой области мы получаем: \(2x- 1 \ge 0\) AND \(x+3 < 0\), хотя эта область пуста.

\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). На этом участке получаем: \(2x- 1 < 0\) AND \(x+3 \ge 0\)

\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). В этом регионе мы получаем: \(2x- 1 < 0\) AND \(x+3 < 0\).

Шаг 2: Теперь нам нужно решить двойное неравенство по абсолютным значениям для каждой из четырех областей:

• \(R_1\):

Здесь мы получаем \(2x- 1 \ge 0\) AND \(x+3 \ge 0\), так что тогда

\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x — 1 \ge x + 3\] \[\Rightarrow \,\, 2x — x \ge 3 — (-1)\] \[\Rightarrow \,\, x \ge 4\]

Итак, чтобы получить частичное решение, нам нужно пересечь \(x \ge 4\) или \([4, +\infty)\) с \(R_1\).

Следовательно, соответствующее решение детали: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)

• \(R_2\):

Эта часть решения пуста (\(\varnothing\)).

• \(R_3\):

Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 \ge 0\), так что тогда

\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x — 1) \ge x + 3\] \[\Rightarrow \,\, 2x — 1 \le -x — 3\] \[\Rightarrow \,\, 2x — (-x) \le -3 — (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]

Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le -\frac{2}{3}\) или \( (-\infty, -\frac{2}{3}]\) с \(R_3\).

Следовательно, соответствующее решение детали: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)

• \(R_4\):

Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 < 0\), так что тогда

\[| 2x — 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x — 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x — 1 \le x + 3\] \[\Rightarrow \,\, 2x — x \le 3 — (-1)\] \[\Rightarrow \,\, x \le 4\]

Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le 4 \) или \((-\infty, 4]\) с \(R_4\).

Следовательно, соответствующее решение детали: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)

Шаг 4: Наконец, мы получаем объединение частичных решений, чтобы получить, что решение начального данного неравенства

\[(-\infty, -3) \cup [-3, -\frac{2}{3}] \cup [4, +\infty) = (-\infty, -\frac{2}{3}] \cup [4, +\infty) \]

Никто не сказал, что это будет коротко, правда? Хорошо. Это не очень сложно, просто нужно действовать систематически и придерживаться плана.

---

Подробнее о неравенствах с абсолютным значением

Почему мы вообще беспокоимся о подобном неравенстве? Нам это не безразлично, потому что у них действительно есть приложения на практике.

Например, в геометрии расстояния на реальной прямой должны быть представлены как абсолютные значения, поскольку они должны быть неотрицательными.

Может возникнуть определенная геометрическая ситуация, в которой вам нужно найти все точки на реальной прямой, которые находятся на расстоянии как минимум 2 от точки 3. Такая ситуация может быть описана следующим неравенством:

\[| x-3 |\ge 2\]

Давайте разберемся в указанном выше неравенстве. Точка \(x\) — это точка, в которой мы хотим удовлетворить неравенство. Расстояние от \(x\) до точки 3 обозначается как \(|x — 3|\).

Затем мы пытаемся найти точки, которые находятся на расстоянии не менее 2 от точки 3, поэтому расстояние \(|x — 3|\) должно быть не менее 2, что объясняет \(|x — 3| \ge 2.\)

Это всего лишь один из видов проблем неравенства абсолютных ценностей, с которыми вы можете столкнуться на практике.

Можете ли вы найти абсолютные неравенства без решения?

Вы делаете ставку. Вот вам один \(|2x| < |x|\). Неравенство может оказаться просто невыполнимым, как в случае с тем, которое я вам только что привел.

Как насчет графического отображения неравенства абсолютных значений?

Процесс их построения графиков по существу идет рука об руку с процессом их решения: вам нужно найти области, в которых вы точно знаете, являются ли аргументы абсолютных значений положительными или отрицательными, а затем неравенства абсолютных значений превращаются в простые неравенства, что тривиально изображено на графике. Затем все кусочки полученных областей просто соединяются.

---

Абсолютное неравенство проблемы абсолютного неравенства Учебники по алгебре

Калькулятор неравенства с шагами | Решатель неравенства

Калькулятор неравенства

Введите математическое выражение…

РАДДЕГ

Триггерные функции

Решить для:xyztabcdfghjklmnopqrsuvw

Решить для: xyztabcdfghjklmnopqrsuvw

Добро пожаловать в наш Калькулятор неравенства ! Этот мощный инструмент позволяет легко решить любое неравенство всего за несколько простых шагов. Просто введите неравенство в предоставленное поле ввода и нажмите кнопку «Рассчитать». Калькулятор неравенства предоставит вам пошаговое решение.

Независимо от того, являетесь ли вы студентом, пытающимся сдать экзамены по математике, или профессионалом, который ищет быстрый и точный способ решения неравенств, наш Калькулятор неравенства станет для вас идеальным инструментом. Попробуйте прямо сейчас и убедитесь, насколько это может быть полезно!

Допустимые функции и символы	Описание
квт()	Квадратный корень
лн()	Натуральный логарифм
лог()	Основание логарифма 10
^	Экспоненты
абс()	Абсолютное значение
sin(), cos(), tan(), csc(), sec(), кроватка()	Основные тригонометрические функции
asin(), acos(), atan(), acsc(), asec(), acot()	Обратные тригонометрические функции
sinh(), cosh(), tanh(), csch(), sech(), coth()	Гиперболические функции
asinh(), acosh(), atanh(), acsch(), asech(), acoth()	Обратные гиперболические функции
число пи	PI-номер (π = 3,14159. ..)
е	Число Непера (e= 2,71828…)
я	Для обозначения мнимой составляющей комплексного числа.

Таблица 1: Допустимые функции и символы

Содержание

• 1 Калькулятор неравенства
• 2 Определение неравенства | Что такое неравенство в математике?
• 3 Виды неравенств
• 4 Как решать неравенства
  • 4. 1 Решение линейных неравенств
  • 4.2 Решение квадратных неравенств
  • 4.3 Как решать абсолютные неравенства

Определение неравенства | Что такое неравенство в математике?

Неравенство в математике — это утверждение, в котором значение одного выражения сравнивается со значением другого с использованием одного из следующих символов неравенства :

• Меньше: <
• Меньше или равно: ≤
• Больше чем: >
• Больше или равно: ≥

Неравенства используются для описания ситуаций, когда одно значение не равно другому значению. Они часто используются в алгебре для описания условий, которые должны быть соблюдены, чтобы решение было действительным.

Например:

• x + 3 < 5 — это неравенство, говорящее, что «x + 3 меньше 5»
• y ≥ 10 — это неравенство, которое говорит, что «y больше или равно 10»

Решением неравенства является набор значений, которые делают неравенство верным.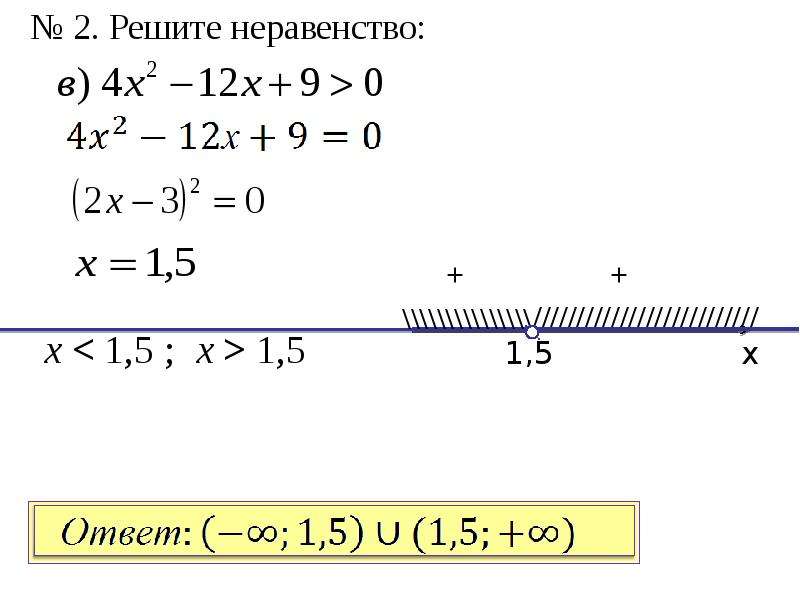 Например, решением неравенства x + 3 < 5 является множество всех значений x, меньших 2 (поскольку 5 – 3 = 2). Решением неравенства y ≥ 10 является множество всех значений y, которые больше или равны 10.

Типы неравенств

Существует несколько типов неравенств:

1. Линейные неравенства: Это неравенства, которые включают только одну переменную и могут быть представлены в виде «ax + b < c» или «ax + b > c», где a, b и c — константы, а x — переменная. Пример линейного неравенства: «2x + 3 < 7».

2. Квадратные неравенства: Это неравенства, которые включают переменную, возведенную во вторую степень, например «x ² + 2x + 1 < 0″. Квадратные неравенства можно решить, найдя значения x, которые делают неравенство верным, а затем проверив эти значения, чтобы определить, какие из них являются допустимыми решениями.

3. Неравенства абсолютного значения: это неравенства, которые включают абсолютное значение переменной, например «|x – 3| < 4”. Неравенства абсолютного значения можно решить, разбив их на два отдельных неравенства и решив каждое отдельно.

4. Рациональные неравенства: это неравенства, включающие рациональные выражения, такие как «1/x < 2». Рациональные неравенства можно решить, найдя значения x, которые делают неравенство верным, а затем проверив эти значения, чтобы определить, какие из них являются допустимыми решениями.

Это лишь несколько примеров существующих видов неравенства. Есть много других типов неравенств, которые можно использовать в различных математических контекстах и ​​при решении задач.

Как решать неравенства

Решение линейных неравенств

Большинство методов решения линейных уравнений применимы к вычислению линейных неравенств. Следовательно, чтобы найти решение действительного неравенства, вы можете прибавить или вычесть любое действительное число к обеим частям неравенства, а также умножить или разделить обе части на любое положительное вещественное число, чтобы получить эквивалентные неравенства.

Чтобы проиллюстрировать сказанное ниже, я представляю, как можно решить следующее линейное неравенство:

5x+3x−8>3

Шаг 1: Упростите обе части неравенства.

8x−8>3

Шаг 2: Добавьте 8 к обеим сторонам.

8x−8+8>3+8

8x>11

Шаг 3: Разделите обе части на 8. 02 Решение:

x>‌‌

Решение квадратных неравенств

Для решения квадратных неравенств необходимо выполнить следующие шаги:

1. Записать квадратное неравенство в стандартной форме, например: Ax ² +Bx+C>0
2. Определить критические точки: для этого найти решения соответствующего квадратного уравнения.
3. Используйте критические точки, чтобы определить интервалы, в которых неравенство верно. Запишите решение в интервальной записи.

Пример: решить квадратное неравенство x ² +5x-2>0

Как решить абсолютное неравенство

1. Чтобы решить абсолютное неравенство, вам нужно разделить неравенство на два отдельных неравенства и решить их по отдельности.
   • Если в неравенстве есть символ больше >, создайте два неравенства следующим образом:

(выражение внутри абсолютного значения) <- (число справа)

(выражение внутри абсолютного значения) > (число с правой стороны).

Та же настройка используется для знака больше или равно, >=.

• • Если знак неравенства «меньше», <, то составить два неравенства следующим образом:

(выражение по модулю) < (число справа) в пределах абсолютного значения) > – (число справа).

Та же настройка используется для неравенства со знаком меньше или равно, <=.

2. Затем решите созданные неравенства. Решением абсолютного неравенства является объединение решений.

Рассмотрим пример решения абсолютного неравенства:

Решим неравенство

|5x−8|≥3

Решить абсолютное значение.

|5x−8|≥3

Мы знаем либо 5x−8≥3, либо 5x−8≤−3

5x−8≥3 (A)

5x−8+8≥3+8(Добавить 8 к обе стороны)

5x≥11

‌‌≥‌‌(обе стороны разделить на 5)

x≥‌‌

5x−8≤−3 (B)

5x−8+8≤−3+8 (добавьте 8 с обеих сторон)

5x≤5

‌ ‌≤‌‌(Разделить оба сторон на 5)

x≤1

Решение:

x≥‌‌‌‌ или ‌‌x≤1

Сделано из ❤

Калькулятор неравенства | Решите уравнения неравенства легко

Наш инструмент калькулятора неравенства отображает результат данного уравнения. Этот онлайн-инструмент сделает ваши расчеты быстрее и решит уравнение неравенства за доли секунды. Просто введите уравнение неравенства в поле ввода и нажмите кнопку расчета, чтобы быстро сгенерировать результат. 9Калькулятор неравенства 019

Калькулятор неравенства: Если вам трудно решить уравнение неравенства, не волнуйтесь, вы можете воспользоваться помощью нашего простого и удобного калькулятора. Продолжайте читать, чтобы узнать больше о простой пошаговой процедуре решения уравнений и примерных вопросов.

Приведенные ниже простые рекомендации помогут вам легко решить уравнение неравенства. Взгляните на них и следуйте, чтобы получить мгновенные результаты.

• Возьмем любое уравнение неравенства.
• Удаление дробей путем умножения всех членов на наименьший общий знаменатель всех дробей.
• Упростите, объединив одинаковые члены с каждой стороны неравенства.
• Вычтите или прибавьте количества, чтобы получить неизвестные термины с одной стороны и числа с другой.
• Разделите каждое слагаемое на коэффициент переменной. Если коэффициент положительный, неравенство остается прежним. Если коэффициент отрицательный, неравенство будет обратным.
• Выполните необходимые математические операции на другой стороне, чтобы получить значение переменной.
• Для биномиальных, кубических или других уравнений необходимо найти множители, чтобы получить значение переменной.

Пример

Вопрос: Решите 4x+3 < 23?

Решение:

Учитывая, что

4x+3 < 23

Вычесть -3 с обеих сторон.

4x+3 -3 < 23 - 3

4x < 20

Разделить 4 с обеих сторон

4x/4 < 20/4

x < 5.

Взгляните на инструменты онлайн-калькулятора от Onlinecalculator .guru и улучшить свои математические навыки и легко понять концепции.

сообщите об этом объявлении

1. Как вы решаете неравенства с помощью калькулятора?

Введите неравенство в указанное поле ввода и нажмите кнопку расчета, которая находится рядом с полями ввода.