Найти ранг матрицы приведением к ступенчатому виду: определение, методы нахождения и примеры решения задач

Содержание

метод окаймляющих миноров, приведение к ступенчатому виду

В данной публикации мы рассмотрим определение ранга матрицы, а также методы, с помощью которых его можно найти. Также разберем примеры для демонстрации применения теории на практике.

Определение ранга матрицы
Нахождение ранга матрицы
- Метод окаймляющих миноров
- Приведение матрицы к ступенчатому виду

Определение ранга матрицы

Ранг матрицы – ранг ее системы строк или столбцов. В любой матрице есть ее строчный и столбцовый ранги, которые равны между собой.

Ранг системы строк – это максимальное количество линейно-независимых строк. Аналогичным образом определяется ранг системы столбцов.

Примечания:

Ранг нулевой матрицы (обозначается символом “θ“) любого размера равняется нулю.
Ранг любого ненулевого вектора-строки или вектора-столбца равняется единице.

Если в матрице любых размеров присутствует хотя бы один элемент, не равный нулю, значит ее ранг не меньше единицы.
Ранг матрицы не больше её минимальной размерности.
Элементарные преобразования, выполненные над матрицей, не меняют её ранга.

Нахождение ранга матрицы

Метод окаймляющих миноров

Ранг матрицы равняется максимальному порядку ненулевого минора.

Алгоритм следующий: находим миноры от низших порядков к высоким. Если минор n-го порядка не равняется нулю, а все последующие (n+1) равны 0, значит ранг матрицы равен n.

Пример
Чтобы было понятнее, давайте разберем практический пример и найдем ранг матрицы A ниже, пользуясь методом окаймляющих миноров.

Решение
Мы имеем дело с матрицей 4×4, следовательно, ее ранг не может быть выше 4. Также в матрице присутствуют ненулевые элементы, значит, ее ранг не меньше единицы.

Итак, приступим:

1. Начинаем проверять миноры второго порядка. Для начала берем две строки первого и второго столбцов.

Минор равняется нулю.

Следовательно переходим к следующему минору (первый столбец остается, а вместо второго берем третий).

Минор равен 54≠0, следовательно ранг матрицы не меньше двух.

Примечание: Если бы и этот минор оказался равным нулю, мы бы дальше проверили следующие комбинации:

Если требуется, перебор можно аналогичным образом продолжить со строками:

1 и 3;
1 и 4;
2 и 3;
2 и 4;
3 и 4.

Если бы все миноры второго порядка оказались равными нулю, то ранг матрицы равнялся бы одному.

2. Нам удалось почти сразу найти минор, который нам подходит. Поэтому переходим к минорам третьего порядка

К найденному минору второго порядка, который дал отличный от нуля результат, добавляем одну строку и один из столбцов, выделенных зеленым цветом (начнем со второго).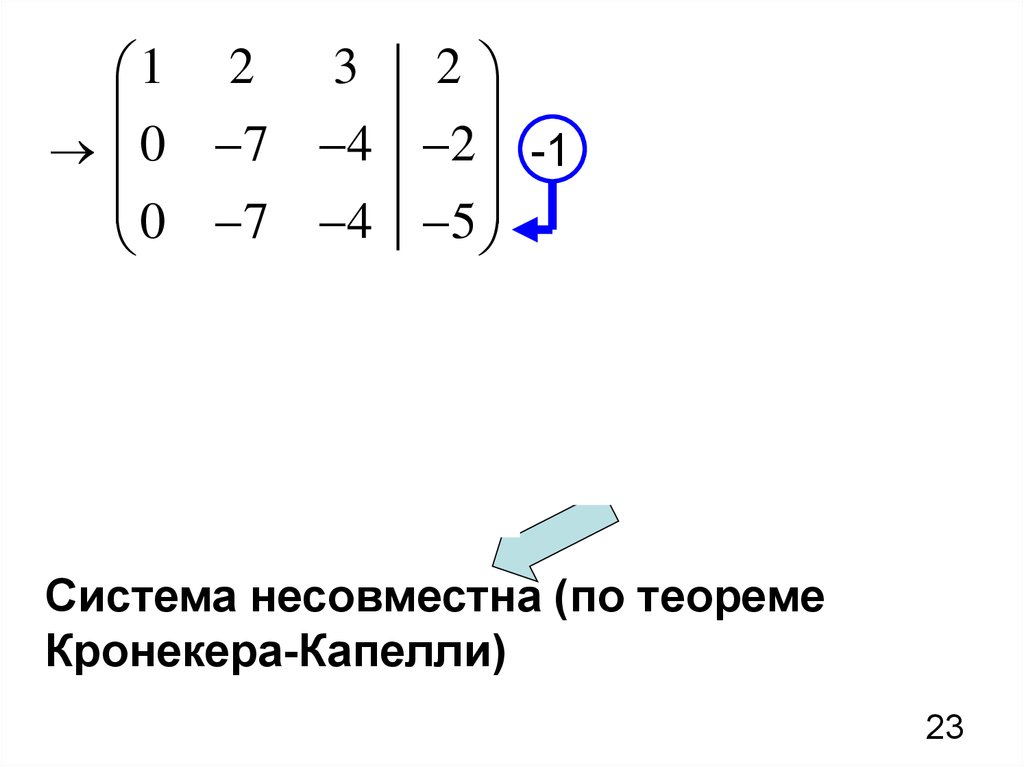

Минор оказался равным нулю.

Следовательно меняем второй столбец на четвертый. И со второй попытки нам удается найти минор, не равный нулю, значит ранг матрицы не может быть меньше 3.

Примечание: если бы результат снова оказался равным нулю, вместо второй строки мы бы дальше взяли четвертую и продолжили бы поиски “хорошего” минора.

3. Теперь остается определить миноры четвертого порядка с учетом найденного ранее. В данном случае он один, который совпадает с определителем матрицы.

Минор равняется 144≠0. А это значит, что ранг матрицы A равняется 4.

Приведение матрицы к ступенчатому виду

Ранг ступенчатой матрицы равняется количеству её ненулевых строк. То есть все, что нам нужно сделать – это привести матрицу к соответствующему виду, например, с помощью элементарных преобразований, которые, как мы уже упомянули выше, не меняют ее ранг.

Пример
Найдем ранг матрицы B ниже. Мы не берем слишком сложный пример, т.к. наша основная цель – это просто продемонстрировать применение метода на практике.

Решение
1. Сначала вычтем из второй строки удвоенную первую.

2. Теперь отнимем из третьей строки первую, умноженную на четыре.

Таким образом, мы получили ступенчатую матрицу, в которой количество ненулевых строк равняется двум, следовательно ее ранг, также, равен 2.

Онлайн калькулятор: Приведенные ступенчатые матрицы

УчебаМатематикаАлгебра

Этот онлайн калькулятор преобразует заданную матрицу к приведенному ступенчатому виду по строкам (каноническому виду по строкам) и показывает решение по шагам.

Этот онлайн калькулятор проводит пошаговое преобразование заданной матрицы к приведенному ступенчатому виду. Помимо решения — приведенной ступенчатой матрицы — калькулятор также показывает использованные на каждом шаге элементарные преобразования строк. Определения терминов, для тех, кто забыл, приведены, как обычно, под калькулятором.

Приведенные ступенчатые матрицы

1 2 0 1 0 0 0 0 0 3 0 0 0 0 1 3 1 0

Матрица

Точность вычисления

Округленно

Приведенный ступенчатый вид

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Ступенчатая матрица

Ступенчатой матрицей, или матрицей ступенчатого вида по строкам, называется матрица, такая что

все ненулевые строки (имеющие по крайней мере один ненулевой элемент) располагаются над всеми чисто нулевыми строками
ведущий элемент (первый, считая слева направо, ненулевой элемент строки) каждой ненулевой строки располагается строго правее ведущего элемента в строке, расположенной выше данной.

Примеры ступенчатых матриц:

нулевая матрица
однострочная матрица
единичная матрица
верхнетреугольная матрица

Матрица, приведенная ниже, также является ступенчатой матрицей:

Приведенная ступенчатая матрица

Ступенчатая матрица называется приведенной, если матрица, составленная из всех ее основных столбцов, является единичной матрицей (столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы).

То есть, приведенная ступенчатая матрица не имеет нулевых строк, и все ведущие элементы ее строк равны единице. При этом все элементы основных столбцов, помимо ведущих элементов, являются нулями.

Матрица, приведенная ниже, является приведенной ступенчатой матрицей:

Преобразование матрицы к приведенному ступенчатому виду по строкам (каноническому виду по строкам)

Для приведения матрицы к ступенчатому или приведенному ступенчатому виду используются элементарные преобразования строк. Каждая матрица может быть преобразована к уникальному приведенному ступенчатому виду.

Элементарные преобразования строк:

перестановка местами любых двух строк матрицы

умножение любой строки матрицы на ненулевую константу

прибавление к любой строке матрицы другой строки, умноженной на некоторую ненулевую константу

Эти преобразования и используются калькулятором выше для приведения матрицы к каноническому виду по строкам.

Ссылка скопирована в буфер обмена

Matrix Rank

Этот урок знакомит с концепцией матрицы ранга и объясняет, как ранг матрица раскрывается его эшелонированная форма.

Ранг матрицы

Матрицу r x c можно представить как набор из r строк векторы, каждый из c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых имеет

r элементов.

ранг матрицы определяется как (a) максимальное количество линейно независимые столбцов векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице. Оба определения эквивалентны.

Для матрицы r x c

Если r меньше c , то максимальный ранг матрицы р .
Если r больше c , то максимальный ранг матрицы это c .

Ранг матрицы был бы равен нулю только в том случае, если бы в матрице не было элементов. Если бы в матрице был хотя бы один элемент, ее минимальный ранг был бы равен единице.

Как найти ранг матрицы

В этом разделе мы опишем метод нахождения ранга любой матрицы. Этот метод предполагает знакомство с ступенчатые матрицы и ступенчатые преобразования.

Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его ступенчатая матрица строк. Поэтому, чтобы найти ранг матрицы, мы просто преобразовать матрицу в ступенчатую форму строки и подсчитать количество ненулевые строки.

Рассмотрим матрицу A и ее эшелон строк матрица, A _ref . Раньше мы показывали как найти эшелонированную форму строки для матрицы А .

0	1	2
1	2	1
2	7	8

⇒

1	2	1
0	1	2
0	0	0

А _№

Потому что форма эшелона ряда A _ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; и мы знаем, что ранг матрицы A равен 2.

Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы A линейно независимый. Тем не менее, строка 3 является линейная комбинация рядов 1 и 2. В частности, ряд 3 = 3*(строка 1) + 2*(строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.

Полноранговые матрицы

Когда все векторы в матрице линейно независимый, говорят, что матрица полный ранг . Рассмотрим матрицы A и B ниже.

А =

	1	2	3
	2	4	6

В =

1	0	2
2	1	0
3	2	1

Обратите внимание, что строка 2 матрицы A является скалярным числом, кратным ряд 1; то есть строка 2 вдвое больше строки 1. Следовательно, строки 1 и 2 равны линейно зависимы. Матрица А имеет только один линейно независимый строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.

Теперь посмотрим на матрицу B . Все его строки линейно независимы, поэтому ранг матрицы В это 3. Матрица B имеет полный ранг.

Проверьте свое понимание

Задача 1

Рассмотрим матрицу X , показанную ниже.

X =

	1	2	4	4
	3	4	8	0

Каков его ранг?

(А) 0
(Б) 1
(К) 2
(Д) 3
(Э) 4

Решение

Правильный ответ (С). Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку у него меньше строк, чем столбцов, его максимальный ранг равен максимальному количеству линейно независимые строки. И поскольку ни одна строка не зависит линейно от другой строки, матрица имеет 2 линейно независимых строки; поэтому его ранг равен 2,9.0005

Задача 2

Рассмотрим матрицу Y , показанную ниже.

Д =

1	2	3
2	3	5
3	4	7
4	5	9

Каков его ранг?

(А) 0
(Б) 1
(К) 2
(Д) 3
(Э) 4

Решение

Правильный ответ (С). Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку у него меньше столбцов, чем строк, его максимальный ранг равен максимальному числу линейно независимых столбцы.

Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярно кратно другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу с максимум двумя линейными независимые столбцы; то есть., столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2.

Последний урок Следующий урок

Сокращение строк с помощью калькулятора TI83 или TI84 (rref)

Сокращение строки матрицы может помочь нам найти решение системы уравнений (в случае расширенных матриц), понять свойства набора векторов и многое другое. Знание того, как использовать операции со строками для уменьшения матрицы вручную, важно, но во многих случаях нам просто нужно знать, как выглядит уменьшенная матрица. В этих случаях такие технологии, как графический калькулятор, являются отличным инструментом для использования!

[adsenseWide]

Мы пройдем шаги, используя эту матрицу: 9-1], чтобы войти в матричное меню. Обратите внимание, что на некоторых старых калькуляторах есть кнопка с простой надписью [MATRX]. Нажимайте стрелку вправо, пока не окажетесь в меню EDIT.

Нажмите [ENTER] и теперь вы можете редактировать матрицу A.

Шаг 2: Введите вашу матрицу в калькулятор.

Первая информация, которую вас спросят, это размер матрицы. Эта матрица имеет 3 строки и 3 столбца, так что это матрица 3 х 3. Введите эти числа, нажимая [ENTER] после каждого.

9-1], но оставайтесь в меню NAMES.

Теперь нажмите [ENTER], чтобы выбрать матрицу A.

Закройте скобки, нажав [ ) ] и затем нажав [ENTER], чтобы получить уменьшенную матрицу.

(примечание: вам не нужно закрывать скобки, чтобы это работало, но это хорошая привычка — или, может быть, просто не закрывая скобки сводит меня с ума… один из тех.