4 умножить на 33: Умножить столбиком 33 на 4

Содержание

Mathway | Популярные задачи

1	Найти объем	сфера (5)	
2	Найти площадь	окружность (5)	
3	Найти площадь поверхности	сфера (5)	
4	Найти площадь	окружность (7)	
5	Найти площадь	окружность (2)	
6	Найти площадь	окружность (4)	
7	Найти площадь	окружность (6)	
8	Найти объем	сфера (4)	
9	Найти площадь	окружность (3)	
10	Вычислить	(5/4(424333-10220^2))^(1/2)
11	Разложить на простые множители	741
12	Найти объем	сфера (3)	
13	Вычислить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	окружность (10)	
15	Найти площадь	окружность (8)	
16	Найти площадь поверхности	сфера (6)	
17	Разложить на простые множители	1162
18	Найти площадь	окружность (1)	
19	Найти длину окружности	окружность (5)	
20	Найти объем	сфера (2)	
21	Найти объем	сфера (6)	
22	Найти площадь поверхности	сфера (4)	
23	Найти объем	сфера (7)	
24	Вычислить	квадратный корень из -121
25	Разложить на простые множители	513
26	Вычислить	квадратный корень из 3/16* квадратный корень из 3/9
27	Найти объем	прямоугольный параллелепипед (2)(2)(2)	
28	Найти длину окружности	окружность (6)	
29	Найти длину окружности	окружность (3)	
30	Найти площадь поверхности	сфера (2)	
31	Вычислить	2 1/2÷22000000
32	Найти объем	прямоугольный параллелепипед (5)(5)(5)	
33	Найти объем	прямоугольный параллелепипед (10)(10)(10)	
34	Найти длину окружности	окружность (4)	
35	Перевести в процентное соотношение	1. 2-4*-1+2
45	Разложить на простые множители	228
46	Вычислить	0+0
47	Найти площадь	окружность (9)	
48	Найти длину окружности	окружность (8)	
49	Найти длину окружности	окружность (7)	
50	Найти объем	сфера (10)	
51	Найти площадь поверхности	сфера (10)	
52	Найти площадь поверхности	сфера (7)	
53	Определить, простое число или составное	5
54	Перевести в процентное соотношение	3/9
55	Найти возможные множители	8
56	Вычислить	(-2)^3*(-2)^9
57	Вычислить	35÷0. 2
60	Преобразовать в упрощенную дробь	2 1/4
61	Найти площадь поверхности	сфера (12)	
62	Найти объем	сфера (1)	
63	Найти длину окружности	окружность (2)	
64	Найти объем	прямоугольный параллелепипед (12)(12)(12)	
65	Сложение	2+2=
66	Найти площадь поверхности	прямоугольный параллелепипед (3)(3)(3)	
67	Вычислить	корень пятой степени из 6* корень шестой степени из 7
68	Вычислить	7/40+17/50
69	Разложить на простые множители	1617
70	Вычислить	27-( квадратный корень из 89)/32
71	Вычислить	9÷4
72	Вычислить	2+ квадратный корень из 21
73	Вычислить	-2^2-9^2
74	Вычислить	1-(1-15/16)
75	Преобразовать в упрощенную дробь	8
76	Оценка	656-521
77	Вычислить	3 1/2
78	Вычислить	-5^-2
79	Вычислить	4-(6)/-5
80	Вычислить	3-3*6+2
81	Найти площадь поверхности	прямоугольный параллелепипед (5)(5)(5)	
82	Найти площадь поверхности	сфера (8)	
83	Найти площадь	окружность (14)	
84	Преобразовать в десятичную форму	11/5
85	Вычислить	3 квадратный корень из 12*3 квадратный корень из 6
86	Вычислить	(11/-7)^4
87	Вычислить	(4/3)^-2
88	Вычислить	1/239
89	Вычислить	12/4-17/-4
90	Вычислить	2/11+17/19
91	Вычислить	3/5+3/10
92	Вычислить	4/5*3/8
93	Вычислить	6/(2(2+1))
94	Упростить	квадратный корень из 144
95	Преобразовать в упрощенную дробь	725%
96	Преобразовать в упрощенную дробь	6 1/4
97	Вычислить	7/10-2/5
98	Вычислить	6÷3
99	Вычислить	5+4
100	Вычислить	квадратный корень из 12- квадратный корень из 192

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 10 − 1 = 9

2) 9 + 2 = 11

3) 11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 3 + 5 = 8

2) 2 × 3 = 6

3) 8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1) 5 − 3 = 2

2) 5 × 2 = 10

3) 2 : 2 = 1

4) 10 + 1 = 11

11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1) 3250 − 2905 = 345

2) 345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1) 6 411 × 8 = 51 288

2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием.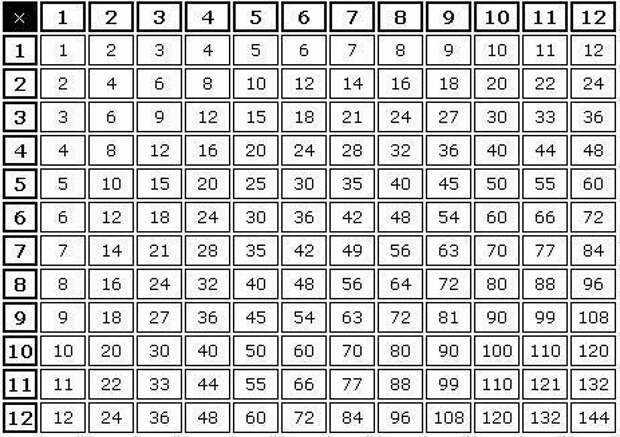 При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Показать решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Показать решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Показать решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Показать решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Как помочь ребенку быстро выучить таблицу умножения

Во втором классе школьники начинают учить таблицу умножения. Часто выучить ее наизусть задают на лето, перекладывая задание на плечи родителей. Если вы оказались в такой ситуации, наша статья поможет вам ответить на вопрос, как быстро выучить таблицу умножения.

Классические способы выучить таблицу умножения

Мы привыкли, что таблицу умножения печатают на оборотной стороне тетрадей в клетку.

Но на самом деле это таблица примеров по умножению, которые ребенку приходится бездумно заучивать наизусть, ведь в этих столбиках трудно найти логические связи и закономерности.

Намного проще учить таблицу умножения по таблице Пифагора.

В такой таблице легко можно найти закономерность, что поможет именно выучить её, а не временно зазубрить. В этой таблице видно симметрию.

Как учить

Умножение – это более быстрый и короткий способ вычислений, чем сложение. Например, 2 х 3 – это тоже самое, что 2+2+2, то есть три раза по 2.

Учить стоит постепенно, начиная от простого к сложному.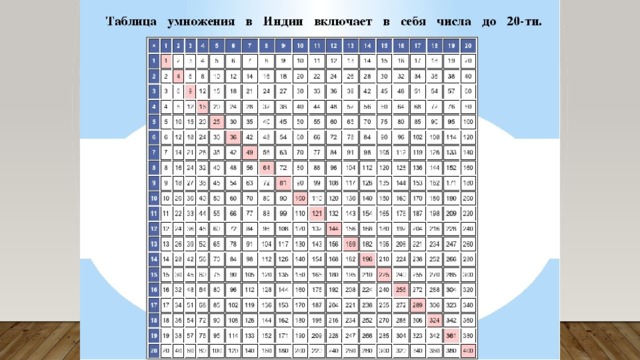 Легче всего выучить умножение на 1 (при умножении на него любое число остается прежним), добавляя каждый день новый столбик.

Распечатайте пустую таблицу Пифагора (без готовых ответов) и пусть ребенок самостоятельно заполняет ее, тогда подключится еще и зрительная память. На первом этапе ребенок может самостоятельно считать, чтобы получить результат.

Обратите внимание ребенка, если он сам не нашел эту закономерность, что от перестановки множителей произведение не меняется. Поэтому не нужно учить всю таблицу умножения, ведь половина примеров повторяется – 5 х 7 = 7 х 5!

Все примеры на 10 заканчиваются на 0, а начинаются на то число, на которое мы умножаем.

Все примеры на 5 заканчиваются на 0 (если умножали на четное число) или 5 (если умножали на нечетное число).

При умножении на 4, дважды удваивайте число. Например, 5 х 4 = 5+5, 5+5 = 20.

При умножении на 9, первая цифра в двузначном числе увеличивается на 1, а вторая – уменьшается на 1. 09-18-27-36-45-54-63-72-81-90.

Старайтесь чаще заниматься повторением. Пусть сначала вы будете спрашивать все по порядку, а когда появится стабильный результат, начинайте спрашивать в разнобой.

Неклассические методы выучить таблицу умножения

Каждый родитель задается вопросом, есть ли легкий способ выучить таблицу умножения. Таких способов несколько – китайский (японский метод), индийский, русский, Ферроля, итальянский. Обо всех этих методах можно почитать в интернете, но мы не будем их рассматривать, потому что они нужны для умножения больших чисел. Расскажем вам об одном интересном методе умножения на 9.

Умножение на 9 с помощью пальцев

Если пронумеровать мысленно каждый палец (смотри изображение) и загнуть тот палец, который соответствует цифре, на которую умножаем, то результат будет равен двум числам, первая из которых – количество пальцев до загнутого, а вторая – количество пальцев после загнутого.

Обучение через игру

Существует огромное количество методик по запоминанию таблицы умножения. Но дети любят познавать мир через игру. Поэтому для обучения можно использовать карточки с примерами без ответов и устроить викторину. Каждый день можно фиксировать количество правильных ответов и периодически делать какие-то поощрения за правильные ответы, например, если ребенок ответил правильно на все примеры.

Усложняйте игру. Подготовьте карточки с ответами без примеров. Пусть ребенок сам скажет, какие числа нужно умножить, чтобы получилось 25 или 90.

Используйте задания с примерами из жизни. Например, сколько лап у 6 кошек? Или сколько ножек у 8 стульев?

Стихи

Для того, чтобы освоить таблицу умножения, можно заучить веселые стихотворения. Андрей Усачев написал «Таблицу умножения в стихах». Покажем несколько примеров из этого сборника.

Что такое умножение?
Это умное сложение.
Ведь умней умножить раз,
Чем слагать все целый час.

Умножения таблица
Всем нам в жизни пригодиться.
И недаром названа
УМНОжением она!

1х1=1
Один пингвин гулял средь льдин.
Одиножды один — один.

1х2=2
Один в поле не воин.
Одиножды два — двое.

2х3=6
Сел петух до зари
На высокий шест:
— Кукареку!… Дважды три,
дважды три — шесть!

2х4=8
В пирог вонзилась пара вилок:
Два на четыре — восемь дырок.

3х4=12
Целый день твердит в квартире
Говорящий какаду:
— Трри умножить на четыре,
Трри умножить на четыре,
Трри умножить на четыре…
Двенадцать месяцев в году.

3х5=15
Школьник стал писать в тетрадь:
Сколько будет «трижды пять»?…
Был он страшно аккуратен:
Трижды пять- пятнадцать пятен!

4х5=20
Четыре учёных мартышки
Ногами листали книжки…
На каждой ноге — пять пальцев:
Четырежды пять – двадцать.

4х8=32
4х9=36
У Бабы Яги сломалась ступа:
Четырежды восемь — тридцать два зуба!
Беж жубов ей нечем есть:
-Четырежды девять — тридцать шешть!

6х6=36
Шесть старушек пряли шерсть:
Шестью шесть — тридцать шесть.

6х6=36
6х7=42
Шесть сетей по шесть ершей-
это тридцать шесть.
А попалась в сеть плотва:
Шестью семь — сорок два.

6х8=48
6х9=54
Бегемоты булок просят:
шестью восемь — сорок восемь…
Нам не жалко булок.
Рот откройте шире:
Шестью девять будет —
Пятьдесят четыре.

7х8=56
Раз олень спросил у лося:
— Сколько будет семью восемь?
Лось не стал в учебник лезть:
— Пятьдесят, конечно, шесть!

7х10=70
Учат в школе семь лисят —
Семью десять — семьдесят!

8х8=64
Пылесосит носом
Слон ковры в квартире:
Восемь на восемь —
Шестьдесят четыре.

8х10=80
Самый лучший в мире счет
Наступает в Новый год…
В восемь рядов игрушки висят:
Восемью десять — восемьдесят!

9х9=81
Свинка свинёнка решила проверить:
— Сколько получится девять на девять?
— Восемьдесят — хрю- один!-
Так ответил юный свин.

9х10=90
Невелик кулик, а нос-то:
девятью десять — девяносто.

10х10=100
На лугу кротов десяток,
Каждый роет десять грядок.
А на десять десять — сто:
Вся земля как решето!

Еще несколько рекомендаций, чтобы облегчить процесс обучения

Исключите напряжение. Перестаньте нервничать и ругать ребенка за допущенные ошибки. Со знанием таблицы умножения не рождаются.

Замотивируйте на обучение. Вместо того, чтобы заставлять ребенка заниматься, попробуйте его замотивировать, например отправив на курсы майнкрафт.

Не сравнивайте. Всем нам неприятно, когда нас с кем-то сравнивают, особенно в негативном ключе. Поэтому не стоит приводить в пример одноклассников и друзей, которые уже выучили все столбики таблицы.

Не давите. Старайтесь не переутомлять ребенка и даже если есть успехи, не учите всю таблицу сразу.

Не забывайте о похвале. Подбодрите и похвалите ребенка, если у него получается. Это придаст уверенности и желание учить дальше.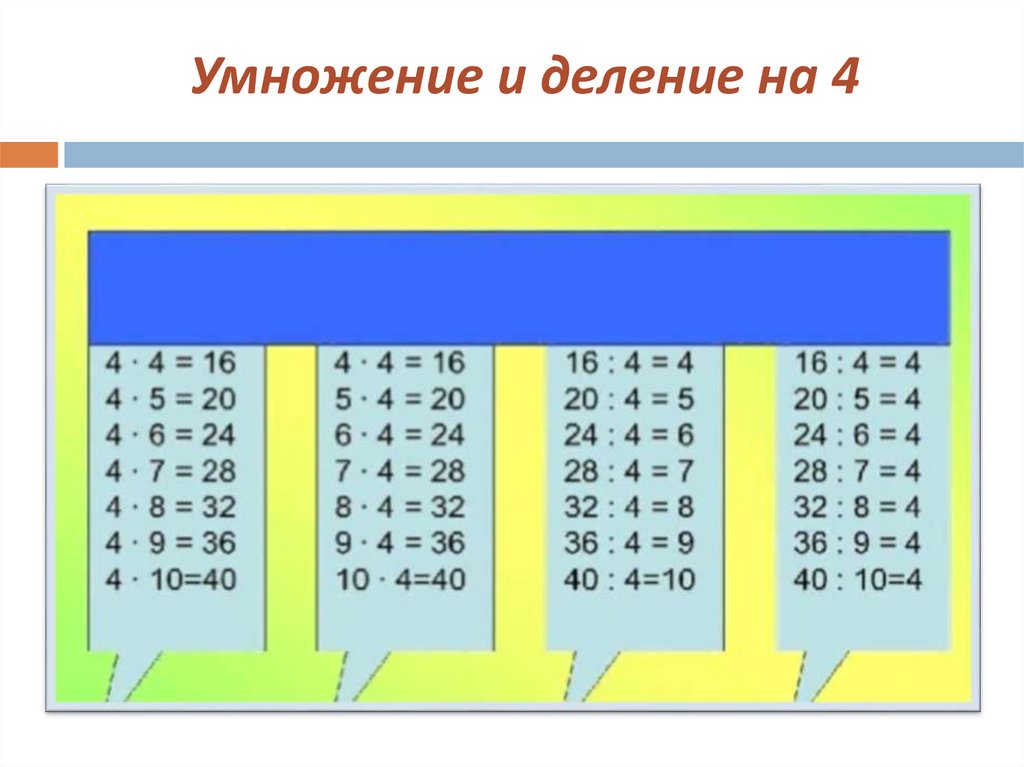

Примечание: Наш детский развивающий образовательный центр ведет подготовку ребят по информатике, робототехнике и инженерному делу. Рассказываем и показываем на практике, что такое Pyton, Scratch. Проводим программирование Arduino для начинающих.

72 умножить на 0 сколько будет. Что такое ноль

Впервые с таким арифметическим действием, как умножение, ученики знакомятся на школьной скамье. Учитель математики среди многочисленных правил поднимает тему «умножение на ноль». Несмотря на однозначность формулировки, у учащихся возникает множество вопросов. Давайте рассмотрим, что будет, если умножить на 0.

Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности.

В первую очередь акцентируется внимание на отсутствии достаточного уровня знаний у учеников средней общеобразовательной школы. Переступая порог учебного заведения, участник образовательного процесса в большинстве случаев не задумывается о главной цели, которую необходимо преследовать.

В течение обучения преподаватель освещает различные вопросы. В их число входит ситуация, что получится, если умножать на 0. Стремясь предвосхитить повествование преподавателя, некоторые ученики вступают в полемику. Они доказывают, по крайней мере, стараются, что умножение на 0 допустимо. Но, к сожалению, это не так. При умножении на 0 любого числа получается ровным счетом ничего. В некоторых литературных источниках даже встречается упоминание, что любое число, умноженное на ноль, образует пустоту.

Важно! Внимательные слушатели аудитории сразу схватывают, что если число умножить на 0, то в результате получится 0. Иное развитие событий прослеживается в случае тех учеников, кто систематически пропускает занятия. Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.

В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации.

Различие во взглядах на тему спора заключается в степени образованности на предмет того, можно умножать на 0 или все-таки нет. Единственный допустимый выход из сложившейся ситуации – попытаться воззвать к логическому мышлению для поиска верного ответа.

Для объяснения правила не рекомендуется использовать следующий пример. У Вани в сумке лежат 2 яблока на перекус. В обед он задумался о том, чтобы положить в портфель еще сколько-нибудь яблок. Но в тот момент рядом не оказалось ни одного фрукта. Ваня не положил ничего. Иными словами, к 2 яблокам он поместил 0 яблок.

В плане арифметики в данном примере получается, что если 2 умножить на 0, то не получается пустоты. Ответ в этом случае однозначный. Для этого примера правило умножения на ноль не актуально. Верное решение заключается в суммировании. Именно поэтому правильный ответ заключается в 2 яблоках.

В противном случае учителю не остается ничего иного, кроме как составить ряд заданий. Последняя мера – повторно задать прохождение темы и провести опрос на исключения в умножении.

Суть действия

Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия.

Сущность действия умножить изначально определялась исключительно для натурального числа. Если раскрывать механизм действия, то определенное число, участвующее в вычислении, прибавляется к самому себе.

При этом важно учитывать количество прибавлений. В зависимости от данного критерия получается различный результат. Прибавление числа относительно самого себя определяет такое его свойство, ка натуральность.

Рассмотрим на примере. Необходимо число 15 умножить на 3. При умножении на 3 число 15 троекратно увеличивается в своей величине. Иными словами, действие выглядит как 15 * 3 = 15 + 15 + 15 = 45. Основываясь на механизме расчета, становится очевидным, если число умножить на другое натуральное число, возникает подобие сложения в упрощенном виде.

Алгоритм действий при умножении на 0 целесообразно начинать с предоставления характеристики на ноль.

Обратите внимание! Согласно общепринятому мнению ноль обозначает целое ничто. Для пустоты подобного рода в арифметике предусмотрено обозначение. Несмотря на данный факт, нулевое значение не несет под собой ничего.

Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.

Иными словами, если умножить на ноль, то получится многообразие вариантов. В нулевом значении ученые рассматривали некое подобие глубины мироздания.

В качестве подтверждения возможности умножить на 0 математики приводили следующий факт. Если рядом с любым натуральным числом поставить 0, то получится значение, превышающее исходное в десятки раз.

Приведенный пример является одним из аргументов. Кроме доказательства подобного рода, существует множество других примеров.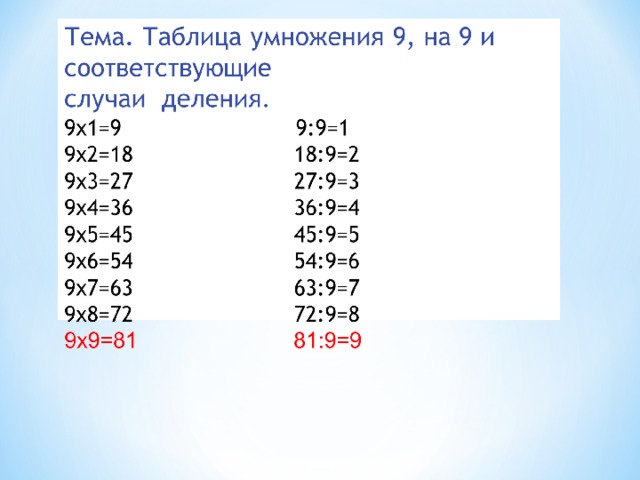 Именно они лежат в основе непрекращающихся споров при умножении на пустоту.

Целесообразность попыток

Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой.

По существу от таких попыток ничего не произойдет, но и пользы не будет. Если произвести умножение на нулевое значение, то получится в дневнике неудовлетворительная отметка.

Единственная мысль, которая должна возникать при умножении на пустоту, – невозможность действия. Запоминание в данном случае играет немаловажную роль. Выучив правило раз и навсегда, учащийся предотвращает появление спорных ситуаций.

В качестве примера, применяемого при умножении на нулевое значение, разрешается использовать следующую ситуацию. Саша решила купить яблоки. Пока она была в супермаркете, она остановила выбор на 5 крупных спелых яблоках. Сходив в отдел молочной продукции, она посчитала, что этого ей будет недостаточно. Девочка положила к себе в корзину еще 5 штук.

Поразмыслив еще чуть-чуть, она взяла еще 5. В результате на кассе у Саши получилось: 5 * 3 = 5 + 5 + 5 = 15 яблок. Если бы она положила по 5 яблок только 2 раза, то было бы 5 * 2 = 5 + 5 = 10. В том случае, если бы Саша не положила в корзинку ни разу по 5 яблок, было бы 5 * 0 = 0 + 0 + 0 + 0 + 0 = 0. Иными словами, купить яблоки 0 раз значит не купить ни одного.

Полезное видео

Подведем итоги

Правило умножения на нулевое значение порождает множество споров. Для понимания его сути достаточно рассмотреть пару примеров. Только запоминание формулировки позволит уяснить, можно умножать на 0 или нет.

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель:

Ввести частные случаи умножения с 0 и 1.
Закрепить смысл умножения и переместительное свойство умножения, отрабатывать вычислительные навыки.
Развивать внимание, память, мыслительные операции, речь, творческие способности, интерес к математике.

Оборудование: Слайдовая презентация: Приложение1.

Ход урока

1. Организационный момент.

Сегодня у нас необычный день. На уроке присутствуют гости. Порадуйте меня, друзей, гостей своими успехами. Откройте тетради, запишите число, классная работа. На полях отметьте свое настроение в начале урока. Слайд 2.

Устно весь класс повторяет таблицу умножения на карточках с проговариванием вслух (неправильные ответы дети отмечают хлопками).

Физкультминутка (“Мозговая гимнастика”, “Шапка для размышления”, на дыхание).

2. Постановка учебной задачи.

2.1. Задания на развитие внимания.

На доске и на столе у детей двухцветная картинка с числами:

– Что интересного в записанных числах? (Записаны разными цветами; все “красные” числа – четные, а “синие” – нечетные.)
– Какое число лишнее? (10 – круглое, а остальные нет; 10 – двузначное, а остальные однозначные; 5 – повторяется два раза, а остальные – по одному.)
– Закрою число 10. Есть ли лишнее среди остальных чисел? (3 – у него нет пары до 10, а у остальных есть.)
– Найдите сумму всех “красных” чисел и запишите ее в красном квадрате. (30.)
– Найдите сумму всех “синих” чисел и запишите ее в синем квадрате. (23.)
– На сколько 30 больше, чем 23? (На 7.)
– На сколько 23 меньше, чем 30? (Тоже на 7.)
– Каким действием искали? (Вычитанием.) Слайд 3.

2.2. Задания на развитие памяти и речи. Актуализация знаний.

а) – Повторите по порядку слова, которые я назову: слагаемое, слагаемое, сумма, уменьшаемое, вычитаемое, разность.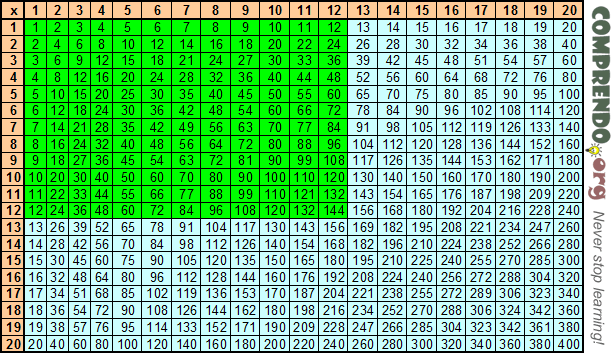 (Дети пытаются воспроизвести порядок слов.)
– Компоненты каких действий назвали? (Сложение и вычитание.)
– С каким действием вы еще знакомы? (Умножение, деление.)
– Назовите компоненты умножения. (Множитель, множитель, произведение.)
– Что обозначает первый множитель? (Равные слагаемые в сумме.)
– Что обозначает второй множитель? (Число таких слагаемых.)

Запишите определение умножения.

a + a +… + a = аn

б) – Рассмотрите записи. Какое задание будете выполнять?

12 + 12 + 12 + 12 + 12
33 + 33 + 33 + 33
а + а + а

(Заменить сумму произведением.)

Что получится? (В первом выражении 5 слагаемых, каждый из которых равен 12, поэтому оно равно 12 5. Аналогично – 33 4, а 3)

в) – Назовите обратную операцию. (Заменить произведение суммой.)

– Замените произведение суммой в выражениях: 99 2. 8 4. Ь 3. (99 + 99, 8 + 8 + 8 + 8, b + b + b) . Слайд 4.

г) На доске записаны равенства:

81 + 81 = 81 – 2
21 3 = 21 + 22 + 23
44 + 44 + 44 + 44 = 44 + 4
17 + 17 – 17 + 17 – 17 = 17 5

Рядом с каждым равенством помещаются картинки.

– Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили?

Дети устанавливают, что слон, тигр, заяц и белка ошиблись, объясняют, в чем их ошибки. Слайд 5.

д) Сравните выражения:

8 5… 5 8
5 6… 3 6
34 9… 31 2
а 3… а 2 + а

(8 5 = 5 8, так как от перестановки слагаемых сумма не изменяется;
5 6 > 3 6, так как слева и справа по 6 слагаемых, но слева слагаемые больше;
34 9 > 31 2. так как слева слагаемых больше и сами слагаемые больше;
а 3 = а 2 + а, так как слева и справа по 3 слагаемых, равных а.)

– Какое свойство умножения использовали в первом примере? (Переместительное.) Слайд 6.

2.3. Постановка проблемы. Целеполагание.

Верны ли равенства? Почему? (Верны, так как сумма 5 + 5 + 5 = 15. потом в сумме становится на одно слагаемое 5 больше, и сумма увеличивается на 5.)

5 3 = 15
5 4 = 20
5 5 = 25
5 6 = 30

– Продолжите эту закономерность направо. (5 7 = 35; 5 8 = 40…)
– Продолжите ее теперь налево. (5 2 = 10; 5 1=5; 5 0 = 0.)
– А что означает выражение 5 1? 5 0? (? Проблема!)

Итог обсуждения:

Однако выражения 5 1 и 5 0 не имеют смысла. Мы можем условиться считать эти равенства верными. Но для этого надо проверить, не нарушим ли мы переместительное свойство умножения.

Итак, цель нашего урока – установить, сможем ли мы считать равенства 5 1 = 5 и 5 0 = 0 верными?

– Проблема урока! Слайд 7.

3. “Открытие” детьми нового знания.

а) – Выполните действия: 1 7, 1 4, 1 5.

Дети решают примеры с комментированием в тетради и на доске:

1 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
1 4 = 1 + 1 + 1 + 1 = 4
1 5 = 1 + 1 + 1 + 1 +1 = 5

– Сделайте вывод: 1 а – ? (1 а = а. ) Выставляется карточка: 1 а = а

б) – Имеют ли смысл выражения 7 1, 4 1, 5 1? Почему? (Нет, так как в сумме не может быть одно слагаемое.)

– Чему они должны быть равны, чтобы не нарушалось переместительное свойство умножения? (7 1 тоже должно быть равно 7, поэтому 7 1 = 7.)

Аналогично рассматриваются 4 1 = 4; 5 1 = 5.

– Сделайте вывод: а 1 = ? (а 1 = а.)

Выставляется карточка: а 1 = а. Накладывается первая карточка на вторую: а 1 = 1 а = а.

– Совпадает наш вывод с тем, что у нас получилось на числовом луче? (Да.)
– Переведите это равенство на русский язык. (При умножении числа на 1 или 1 на число получается то же самое число.)
– Молодцы! Итак, будем считать: а 1 = 1 а = а. Слайд 8.

2) Аналогично исследуется случай умножения с 0. Вывод:

– при умножении числа на 0 или 0 на число получается нуль: а 0 = 0 а = 0. Слайд 9.
– Сравните оба равенства: что вам напоминают 0 и 1?

Дети высказывают свои версии. Можно обратить их внимание на образы:

1 – “зеркальце”, 0 – “страшный зверь” или “шапка-невидимка”.

Молодцы! Итак, при умножении на 1 получается то же самое число (1 – “зеркальце”) , а при умножении на 0 получается 0 (0 – “шапка-невидимка”).

4. Физкультминутка (для глаз – “круг”, “вверх – вниз”, для рук – “замок”, “кулачки”).

5. Первичное закрепление.

На доске записаны примеры:

23 1 =
1 89 =
0 925 =
364 1 =
156 0 =
0 1 =

Дети решают их в тетради и на доске с проговариванием в громкой речи полученных правил, например:

3 1 = 3, так как при умножении числа на 1 получается то же самое число (1 – “зеркальце”), и т.д.

а) 145 х = 145; б) х 437 = 437.

– При умножении 145 на неизвестное число получилось 145. Значит, умножали на 1 х = 1. И т.д.

a) 8 x = 0; б) х 1= 0.

– При умножении 8 на неизвестное число получился 0. Значит, умножали на 0 х = 0. И т.д.

6. Самостоятельная работа с проверкой в классе . Слайд 10.

Дети самостоятельно решают записанные примеры. Затем по готовому

образцу проверяют свои ответы с проговариванием в громкой речи, отмечают правильно решенные примеры плюсом, исправляют допущенные ошибки. Те, кто допустил ошибки, получают аналогичное задание на карточке и дорабатывают индивидуально, пока класс решает задачи на повторение.

7. Задачи на повторение. (Работа в парах). Слайд 11.

а) – Хотите узнать что вас ждет в будущем? Вы это узнаете, расшифровав запись:

г – 49:7 о – 9 8 н – 9 9 в – 45:5 й – 6 6 д – 7 8 ы – 24:3


81	72	5	8	36	7	72	56

–Так что же нас ждет? (Новый год. )

б) – “Я задумала число, вычла из него 7, прибавила 15, потом прибавила 4 и получила 45. Какое число я задумала?”

Обратные операции надо делать в обратном порядке: 45 – 4 – 15 + 7 = 31.

8. Итог урока. Слайд 12.

С какими новыми правилами познакомились?
Что понравилось? Что было трудно?
Можно ли применить эти знания в жизни?
На полях можно выразить свое настроение в конце урока.
Заполните таблицу самооценки:

Хочу знать больше
Хорошо, но могу лучше
Пока испытываю трудности

Спасибо за работу, вы хорошо потрудились!

9. Домашнее задание

С. 72–73 Правило, № 6.

Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!» , – но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.

Кто в итоге прав

Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй. Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!

Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.

Это интересно: Как найти разность чисел в математике?

Что такое умножение

Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:

25×3 = 75

25 + 25 + 25 = 75

25×3 = 25 + 25 + 25

Из этого уравнения следует вывод, что умножение — это упрощённое сложение .

Что такое ноль

Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.

Можно ли умножать на пустоту

Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.

Это интересно: что такое модуль числа?

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок

Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок

Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0

Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего , а когда у вас ничего нет , то сколько ни умножай — всё равно будет ноль . Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.

Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль – это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.

Расскажу тебе позволь,

Чтобы не делил на 0!

Режь 1 как хочешь, вдоль,

Только не дели на 0!

obrazovanie.guru

Деление на ноль. Увлекательная математика

Число 0 можно представить, как некую границу, отделяющую мир реальных чисел от мнимых или отрицательных. Благодаря двусмысленному положению, многие операции с этой числовой величиной не подчиняются математической логике. Невозможность деления на нуль – яркий тому пример. А разрешенные арифметические действия с нулем могут быть выполнены с помощью общепринятых определений.

История нуля

Ноль является точкой отсчета во всех стандартных системах исчисления. Европейцы стали использовать это число сравнительно недавно, но мудрецы Древней Индии пользовались нулем за тысячу лет до того, как пустое число стало регулярно использоваться европейскими математиками. Ещё раньше индийцев ноль являлся обязательной величиной в числовой системе майя. Этот американский народ использовал двенадцатеричную систему исчисления, а нулем у них начинался первый день каждого месяца. Интересно, что у майя знак, обозначающий «ноль», полностью совпадал со знаком, определяющим «бесконечность». Таким образом, древние майя делали вывод о тождественности и непознаваемости этих величин.

Математические действия с нулем

Стандартные математические операции с нулем можно свести к нескольким правилам.

Сложение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).

Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).

Умножение: любое число, умноженное на 0, дает в произведении 0 (a*0=0).

Деление: ноль можно разделить на любое число, не равное нулю. При этом значение такой дроби будет 0. А деление на ноль запрещено.

Возведение в степень. Это действие можно выполнить с любым числом. Произвольное число, возведенное в нулевую степень, даст 1 (x 0 =1).

Ноль в любой степени равен 0 (0 а =0).

При этом сразу возникает противоречие: выражение 0 0 не имеет смысла.

Парадоксы математики

О том, что деление на ноль невозможно, многие знают со школьной скамьи. Но объяснить причину такого запрета почему-то не получается. В самом деле, почему формула деления на ноль не существует, а вот другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.

Все дело в том, что привычные арифметические действия, которые школьники изучают в начальных классах, на самом деле далеко не так равноправны, как нам кажется. Все простые операции с числами могут быть сведены к двум: сложению и умножению. Эти действия составляют суть самого понятия числа, а остальные операции строятся на использовании этих двух.

Сложение и умножение

Возьмем стандартный пример на вычитание: 10-2=8. В школе его рассматривают просто: если от десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем по-другому. Ведь такой операции, как вычитание, для них не существует. Данный пример можно записать и другим способом: х+2=10. Для математиков неизвестная разность – это просто число, которое нужно добавить к двум, чтобы получилось восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.

Умножение и деление рассматриваются так же. В примере 12:4=3 можно понять, что речь идет о разделении восьми предметов на две равные кучки. Но в действительности это просто перевернутая формула записи 3х4=12.Такие примеры на деление можно приводить бесконечно.

Примеры на деление на 0

Вот тут и становится понемногу понятным, почему нельзя делить на ноль.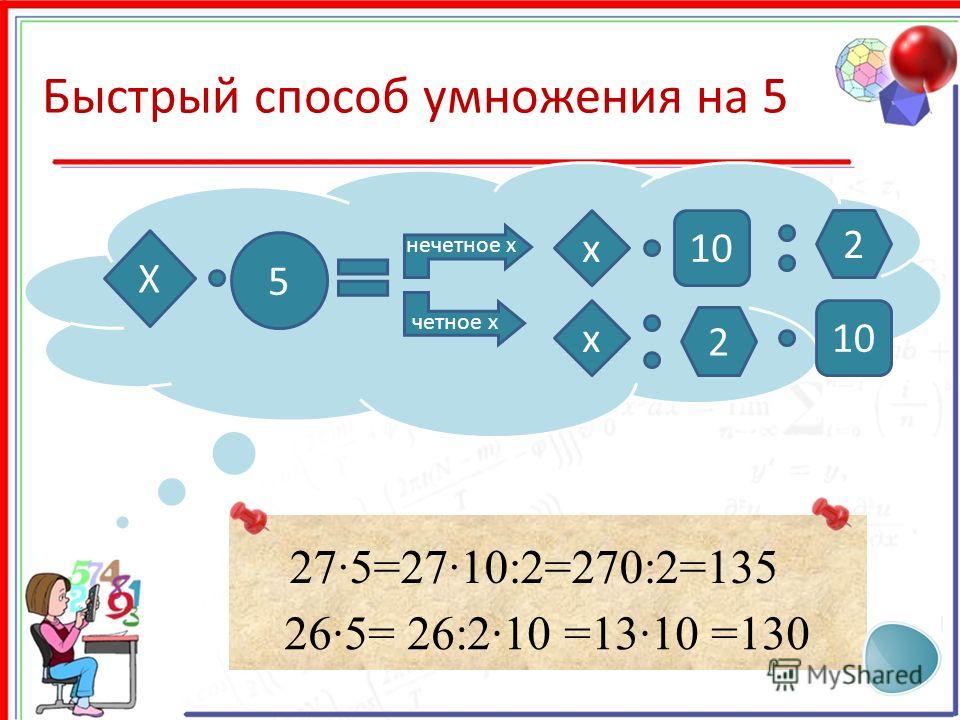 Умножение и деление на ноль подчиняется своим правилам. Все примеры на деление этой величины можно сформулировать в виде 6:0=х. Но это же перевернутая запись выражения 6 * х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевой величины.

Выходит, что такого числа, которое при умножении на 0 дает какую-либо осязаемую величину, не существует, то есть данная задача не имеет решения. Такого ответа бояться не следует, это естественный ответ для задач такого типа. Просто запись 6:0 не имеет никакого смысла, и она ничего не может объяснить. Кратко говоря, это выражение можно объяснить тем самым бессмертным «деление на ноль невозможно».

Существует ли операция 0:0? Действительно, если операция умножения на 0 законна, можно ли ноль разделить на ноль? Ведь уравнение вида 0х 5=0 вполне легально. Вместо числа 5 можно поставить 0, произведение от этого не поменяется.

Действительно, 0х0=0. Но поделить на 0 по-прежнему нельзя. Как было сказано, деление – это просто обратная операция умножения. Таким образом, если в примере 0х5=0, нужно определить второй множитель, получаем 0х0=5. Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это понравится?

Но если в выражение подходит любое число, то оно не имеет смысла, мы не можем из бесконечного множества чисел выбрать какое-то одно. А раз так, это значит и выражение 0:0 не имеет смысла. Получается, что на ноль нельзя делить даже сам ноль.

Высшая математика

Деление на ноль — это головная боль для школьной математики. Изучаемый в технических вузах математический анализ немного расширяет понятие задач, которые не имеют решения. Например, к уже известному выражению 0:0 добавляются новые, которые не имеют решения в школьных курсах математики:

бесконечность, разделенная на бесконечность: ∞:∞;

бесконечность минус бесконечность: ∞−∞;

единица, возведенная в бесконечную степень: 1 ∞ ;

бесконечность, умноженная на 0: ∞*0;

некоторые другие.

Элементарными методами решить такие выражения невозможно. Но высшая математика благодаря дополнительным возможностям для ряда подобных примеров дает конечные решения. Особенно это видно в рассмотрении задач из теории пределов.

Раскрытие неопределенности

В теории пределов значение 0 заменяется условной бесконечно малой переменной величиной. А выражения, в которых при подставлении нужного значения получается деление на ноль, преобразовываются. Ниже представлен стандартный пример раскрытия предела при помощи обычных алгебраических преобразований:

Как видно в примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.

При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подставлении предела, используют второй замечательный предел.

Метод Лопиталя

В некоторых случаях пределы выражений можно заменить пределом их производных. Гийом Лопиталь – французский математик, основоположник французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных этих выражений. В математической записи его правило выглядит следующим образом.

В настоящее время метод Лопиталя с успехом применяется при решении неопределенностей типа 0:0 или ∞:∞.

Математика: деление и умножение в столбик

Умножение и деление однозначных чисел не составит труда для любого школьника, выучившего таблицу умножения. Она входит в программу математики за 2 класс. Другое дело – когда необходимо произвести математические действия с многозначными числами. Начинают такие действия на уроках математики в 3 классе. Разбираем новую тему «Деление и умножение в столбик»

Умножение многозначных чисел

Делить и умножать сложные числа проще всего столбиком. Для этого нужно разряды числа: сотни, десятки, единицы:

235 = 200 (сотни) + 30 (десятки) + 5 (единицы).

Это нам понадобится для правильной записи чисел при умножении.

При записи двух чисел, которые нужно перемножить, их записывают друг под другом, размещая числа по разрядам (единицы — под единицами, десятки под десятками). При умножении многозначного числа на однозначное трудностей не возникнет:

Запись ведется так:

Вычисление ведут с конца – с разряда единиц. При умножении на первую цифру – из разряда единиц – запись тоже ведут с конца:

3 х 5 = 15, записываем 5 (единицы), десятки (1) запоминаем;
2 х 5 = 10 и 1 десяток, который мы запомнили, всего 11, записываем 1 (десятки), сотни (1) запоминаем;
поскольку дальше разрядов у нас в примере нет, записываем сотни (1 – которую запоминали).

Следующее действие – умножаем на вторую цифру (разряд десятков):

Поскольку умножали мы на цифру из разряда десятков, записывать начнем так же, с конца, начиная со второго места справа (там, где разряд десятков).

1. записывать столбиком умножение нужно по разрядам;

2. вычисления производить, начиная с единиц;

3. записывать итог по разрядам – если умножаем на цифру из разряда единиц – запись начинаем с последнего столбика, из разряда – десятков – с этого столбца и ведем запись.

Правило, действующее для умножения в столбик на двухзначное число, действует и для чисел с большим количеством разрядов.

Чтобы легче было запомнить правила записи примеров умножения многозначных чисел в столбик, можно сделать карточки, выделив разными цветами разные разряды.

Если производится в столбик умножение чисел с нулями на конце, их не принимают во внимание при вычислении, а запись ведут так, чтобы значащая цифра была под значащей, а нули остаются справа. После проведения вычислений их количество дописывают справа:

Математик Яков Трахтенберг разработал систему быстрого счета. Метод Трахтенберга облегчает умножение, если применять определенную систему вычислений. Например, умножение на 11. Для получения результата нужно прибавить цифру к соседней:

2,253 х 11 = (0 + 2) (2 + 2) (2 + 5) (5 + 3) (3 + 0) = 2 + 4 + 7 + 8 + 3 = 24,783.

Доказать истинность просто: 11 = 10 + 1

2,253 х 10 + 2,253 = 22,530 + 2,253 = 24,783.

Алгоритмы вычислений для разных чисел разные, но они позволяют производить вычисления быстро.

Видео «Умножение столбиком»

Деление многозначных чисел

Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215: 5 = ?
Записывается вычисление следующим образом:

Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20: 5 = 4 (остаток 1)

Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15: 5 = 3

Решение будет выглядеть таким образом:

Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.

Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.

Приведем примеры на деление:

Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853: 15 = 50 и (3) остаток
Обратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше.

Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.

Важно! Следите за записью: разряды должны записываться под разрядами, в столбик.

Видео «Деление в столбик»

Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.

razvitiedetei.info

Правила умножения и деления

После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.

Что такое умножение? Это умное сложение

При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:

В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.

Да какая разница?

Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?

Если мы будем выполнять действия по порядку, получим:

Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:

Пробуем решить двумя способами:

Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:

Другого решения у ответа у примера быть не должно.

Что важнее – умножение или сложение?

При решении примеров
Расставь порядок действий.
Умножить или разделить – на первом месте.

Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?

Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:

Значит, пример решен правильно. А если в нем будут скобки?

То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:

Раскрываем скобки. Если их несколько, делаем вычисления для каждых.

Умножение либо деление.

Вычисляем конечный результат, выполняя действия слева направо.

Пример:
81: 9 + (6 – 2) + 3 = ?

81: 9 + (6 – 2) + 3 = 16.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Алгоритм решения выражения:

Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.

Выполняем вычисления в скобках.

Делаем умножение и деление.

Выполняем сложение и вычитание.

28: (11 – 4) + 18 – (25 – 8) = ?

11 – 4 = 7;
25 – 8 = 17;
28: 7 = 4;
4 + 18 = 22;
22 – 17 = 5.

Ответ: 28: (11 – 4) + 18 – (25 – 8) = 5.

Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним.

Круглый нуль такой хорошенький,
Но не значит ничегошеньки.

В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:

При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:

0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;

Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:

0: 5 = 0.

Напомним другие арифметические действия с нулем:

Умножение и деление на единицу

Математические действия с единицей отличаются от действий с нулем. При умножении или делении числа на 1 получается само первоначальное число:

7 × 1 = 7;

7: 1 = 7.

Конечно, если у вас есть 7 друзей, и каждый подарил вам по конфете, у вас будет 7 конфет, а если вы их съели в одиночестве, то есть поделились лишь с самим собой, то все они и оказались в вашем желудке.

Вычисления с дробями, степенями и сложными функциями

Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.

Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:

2 × 3 = 6 — числитель

5 × 8 = 40 — знаменатель

После сокращения получаем:\(\) = \(\).

Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:

Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:

Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.

Действия с корнями, логарифмами, функциями

Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.

Главные правила по теме

Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:

В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:

При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.

Умножение и деление целых чисел

При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.

При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть, какое правило применять. Также необходимо изучить несколько законов умножения и деления. Изучение этих правил позволяет избежать некоторые досадные ошибки в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов, и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого , множителя и произведения . Например в выражении 3 × 2 = 6 , число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть, в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в данном случае будет показывать сколько раз нужно взять число 3:

Таким образом, если взять число 3 два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители . Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

Теперь поменяем местами сомножители:

В обоих случаях, мы получаем ответ 15, значит между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

А с помощью переменных переместительный закон умножения можно записать так:

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25 .

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть, во сколько раз увеличить ноль. Буквально это выражение читается как «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль?

Другими словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

Примеры применения закона умножения на ноль:

2 × 5 × 0 × 9 × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Далее рассмотрим умножение целых чисел.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают покороче: −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10, и мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно записывают короче: 12 × (−5) = −60

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Обычно записывают короче: 10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Обычно записывают короче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

Заключим его в скобки:

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

Всё это приравняем к нулю:

(4 × (−2)) + ((−4) × (−2)) = 0

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение (4 × (−2)) равно −8. Запишем в нашем выражении число −8 вместо произведения (4 × (−2))

Теперь вместо второго произведения временно поставим многоточие

Теперь внимательно смотрим на выражение −8 + […] = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

Пример 5. Найти значение выражения −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = (−2 × 6) + (−2 × 4)

Теперь вычислим выражения, находящиеся в скобках. Затем полученные результаты сложим. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

−2 × 6 = −(2 × 6) = −(12) = −12

−2 × 4 = −(2 × 4) = −(8) = −8

Третье действие:

Значит значение выражения −2 × (6 + 4) равно −20

Обычно записывают короче: −2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Значит значение выражения (−2) × (−3) × (−4) равно −24

Обычно записывают короче: (−2) × (−3) × (−4) = 6 × (−4) = −24

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого , делителя и частного . Например, в выражении 8: 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.

Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть, в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

На ноль делить нельзя

Любое число запрещено делить на ноль. Дело в том, что деление является обратной операцией умножению. Например, если 2 × 6 = 12, то 12: 6 = 2

Видно, что второе выражение записано в обратном порядке.

Теперь сделаем тоже самое для выражения 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

Если записать это выражение в обратном порядке, то получим:

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно и глупо.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть, каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8: 2 означает найти такое число, которое при умножении на 2 даст 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даёт ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

Теперь представим, что нужно найти значение выражения 5: 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даёт ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение […] × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение […] × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

При b ≠ 0

Число a можно разделить на число b , при условии, что b не равно нулю.

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12: 4. Значение этого выражения равно 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

(12 × 4) : (4 × 4)

(12 × 4) : (4 × 4) = 48: 16 = 3

Теперь попробуем не умножить, а разделить делимое и делитель на число 4

(12: 4) : (4: 4)

(12: 4) : (4: 4) = 3: 1 = 3

Получили ответ 3.

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

Деление целых чисел

Пример 1. Найти значение выражения 12: (−2)

Это деление чисел с разными знаками. 12 – это положительное число, (−2) – отрицательное. В таких случаях, нужно

12: (−2) = −(|12| : |−2|) = −(12: 2) = −(6) = −6

Обычно записывают короче 12: (−2) = −6

Пример 2. Найти значение выражения −24: 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. В таких случаях опять же нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак минус.

−24: 6 = −(|−24| : |6|) = −(24: 6) = −(4) = −4

Обычно записывают короче −24: 6 = −4

Пример 3. Найти значение выражения (−45) : (−5)

Это деление отрицательных чисел. В таких случаях, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

(−45) : (−5) = |−45| : |−5| = 45: 5 = 9

Обычно записывают короче (−45) : (−5) = 9

Пример 4. Найти значение выражения (−36) : (−4) : (−3)

Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим (−36) на (−4), и полученное число разделим на (−3)

Первое действие:

(−36) : (−4) = |−36| : |−4| = 36: 4 = 9

9: (−3) = −(|−9| : |−3|) = −(9: 3) = −(3) = −3

Обычно записывают короче (−36) : (−4) : (−3) = 9: (−3) = −3

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Кто в итоге прав

Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!

Что такое умножение

25×3 = 75
25 + 25 + 25 = 75
25×3 = 25 + 25 + 25

Из этого уравнения следует вывод, что умножение — это упрощённое сложение .

Что такое ноль

Можно ли умножать на пустоту

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0

Деление

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Расскажу тебе позволь,
Чтобы не делил на 0!
Режь 1 как хочешь, вдоль,
Только не дели на 0!

Презентация к уроку

Загрузить презентацию (489,5 кБ)

Ввести частные случаи умножения с 0 и 1.
Закрепить смысл умножения и переместительное свойство умножения, отрабатывать вычислительные навыки.
Развивать внимание, память, мыслительные операции, речь, творческие способности, интерес к математике.

Оборудование: Слайдовая презентация: Приложение1.

1. Организационный момент.

Физкультминутка (“Мозговая гимнастика”, “Шапка для размышления”, на дыхание).

2. Постановка учебной задачи.

2.1. Задания на развитие внимания.

На доске и на столе у детей двухцветная картинка с числами:

– Что интересного в записанных числах? (Записаны разными цветами; все “красные” числа – четные, а “синие” – нечетные.)
– Какое число лишнее? (10 – круглое, а остальные нет; 10 – двузначное, а остальные однозначные; 5 – повторяется два раза, а остальные – по одному. )
– Закрою число 10. Есть ли лишнее среди остальных чисел? (3 – у него нет пары до 10, а у остальных есть.)
– Найдите сумму всех “красных” чисел и запишите ее в красном квадрате. (30.)
– Найдите сумму всех “синих” чисел и запишите ее в синем квадрате. (23.)
– На сколько 30 больше, чем 23? (На 7.)
– На сколько 23 меньше, чем 30? (Тоже на 7.)
– Каким действием искали? (Вычитанием.) Слайд 3.

2.2. Задания на развитие памяти и речи. Актуализация знаний.

а) – Повторите по порядку слова, которые я назову: слагаемое, слагаемое, сумма, уменьшаемое, вычитаемое, разность. (Дети пытаются воспроизвести порядок слов.)
– Компоненты каких действий назвали? (Сложение и вычитание.)
– С каким действием вы еще знакомы? (Умножение, деление.)
– Назовите компоненты умножения. (Множитель, множитель, произведение.)
– Что обозначает первый множитель? (Равные слагаемые в сумме. )
– Что обозначает второй множитель? (Число таких слагаемых.)

Запишите определение умножения.

б) – Рассмотрите записи. Какое задание будете выполнять?

12 + 12 + 12 + 12 + 12
33 + 33 + 33 + 33
а + а + а

(Заменить сумму произведением.)

в) – Назовите обратную операцию. (Заменить произведение суммой.)

– Замените произведение суммой в выражениях: 99 2. 8 4. Ь 3. (99 + 99, 8 + 8 + 8 + 8, b + b + b) . Слайд 4.

г) На доске записаны равенства:

81 + 81 = 81 – 2
21 3 = 21 + 22 + 23
44 + 44 + 44 + 44 = 44 + 4
17 + 17 – 17 + 17 – 17 = 17 5

Рядом с каждым равенством помещаются картинки.

– Зверюшки лесной школы выполняли задание. Правильно ли они его выполнили?

Дети устанавливают, что слон, тигр, заяц и белка ошиблись, объясняют, в чем их ошибки. Слайд 5.

д) Сравните выражения:

8 5. 5 8
5 6. 3 6
34 9… 31 2
а 3. а 2 + а

– Какое свойство умножения использовали в первом примере? (Переместительное.) Слайд 6.

2.3. Постановка проблемы. Целеполагание.

5 3 = 15
5 4 = 20
5 5 = 25
5 6 = 30

– Продолжите эту закономерность направо. (5 7 = 35; 5 8 = 40.)
– Продолжите ее теперь налево. (5 2 = 10; 5 1=5; 5 0 = 0.)
– А что означает выражение 5 1? 5 0? (? Проблема!)

Итак, цель нашего урока – установить, сможем ли мы считать равенства 5 1 = 5 и 5 0 = 0 верными?

– Проблема урока! Слайд 7.

3. “Открытие” детьми нового знания.

а) – Выполните действия: 1 7, 1 4, 1 5.

Дети решают примеры с комментированием в тетради и на доске:

1 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1 = 7
1 4 = 1 + 1 + 1 + 1 = 4
1 5 = 1 + 1 + 1 + 1 +1 = 5

– Сделайте вывод: 1 а – ? (1 а = а.) Выставляется карточка: 1 а = а

б) – Имеют ли смысл выражения 7 1, 4 1, 5 1? Почему? (Нет, так как в сумме не может быть одно слагаемое.)

Аналогично рассматриваются 4 1 = 4; 5 1 = 5.

– Сделайте вывод: а 1 = ? (а 1 = а. )

Выставляется карточка: а 1 = а. Накладывается первая карточка на вторую: а 1 = 1 а = а.

2) Аналогично исследуется случай умножения с 0. Вывод:

Дети высказывают свои версии. Можно обратить их внимание на образы:

1 – “зеркальце”, 0 – “страшный зверь” или “шапка-невидимка”.

4. Физкультминутка (для глаз – “круг”, “вверх – вниз”, для рук – “замок”, “кулачки”).

5. Первичное закрепление.

На доске записаны примеры:

Дети решают их в тетради и на доске с проговариванием в громкой речи полученных правил, например:

3 1 = 3, так как при умножении числа на 1 получается то же самое число (1 – “зеркальце”), и т.д.

а) 145 х = 145; б) х 437 = 437.

– При умножении 145 на неизвестное число получилось 145. Значит, умножали на 1 х = 1. И т.д.

– При умножении 8 на неизвестное число получился 0. Значит, умножали на 0 х = 0. И т.д.

6. Самостоятельная работа с проверкой в классе . Слайд 10.

Дети самостоятельно решают записанные примеры. Затем по готовому

7. Задачи на повторение. (Работа в парах). Слайд 11.

а) – Хотите узнать что вас ждет в будущем? Вы это узнаете, расшифровав запись:

xn--i1abbnckbmcl9fb.xn--p1ai

Умножение на 1 и 0 правило

Согласно общепринятому определению, ноль — это число, отделяющее положительные числа от отрицательных на числовой прямой. Ноль — это самое проблематичное место в математике, которое не подчиняется логике, а все математические действия с нулём основаны не на логике, а на общепринятых определениях.

Первый пример проблематичности нуля — это натуральные числа. В русских школах ноль не является натуральным числом, в других школах ноль является натуральным числом. Поскольку понятие «натуральные числа» — это искусственное отделение некоторых чисел от всех остальных чисел по определённым признакам, то математического доказательства натуральности или не натуральности нуля быть не может. Ноль считается нейтральным элементом по отношению операций сложения и вычитания.

Ноль считается целым, беззнаковым числом. Также ноль считается чётным числом, поскольку при делении нуля на 2 получается целое число ноль .

Ноль является первой цифрой во всех стандартных системах счисления. В позиционных системах счисления, к которым принадлежит привычная нам десятичная система счисления, цифрой ноль обозначают отсутствие значения данного разряда при записи числа. Индейцы майя использовали ноль в принятой у них двенадцатиричной системе счисления за тысячу лет до индийских математиков. С нулевого дня в календаре майя начинался каждый месяц. Интересно, что тем же самым знаком ноль математики майя обозначали и бесконечность — вторую проблему современной математики.

Слово «ноль » в арабском языке звучит как «сыфр». От арабского слова ноль (сыфр) произошло слово «цифра».

Как правильно пишется — ноль или нуль ? Слова ноль и нуль совпадают в значении, но различаются употреблением. Как правило, ноль употребляется в обиходной речи и в ряде устойчивых сочетаний, нуль — в терминологии, в научной речи. Правильными будут оба варианта написания этого слова. Например: Деление на ноль. Ноль целых. Ноль внимания. Ноль без палочки. Абсолютный нуль. Ноль целых пять десятых.

В грамматике производные слова от слов ноль и нуль пишутся так: нолевой или нулевой, нолик или нулик, ноля или нуля, нулевой или реже встречающееся нолевой, ноль-ноль. Например: Ниже нуля. Равно нулю. Свести к нулю. Нулевой мередиан. Нулевой пробег. В двенадцать ноль-ноль.

В математических действиях с нулем на сегодняшний день определены следующие результаты:

сложение — если к любому числу прибавить ноль , число останется неизменным; если к нулю прибавить любое число результатом сложения будет то же самое любое число:

вычитание — если из любого числа вычесть ноль , число останется неизменным; если из нуля вычесть любое число в результате получится то же самое любое число с противоположным знаком:

умножение — если любое число умножить на ноль, результатом будет ноль; если ноль умножить на любое число в результате получится ноль :

деление — деление на ноль запрещено, поскольку результат не существует; общепринятый взгляд на проблему деления на ноль изложен в работе Александра Сергеева «Почему нельзя делить на ноль? » ; для любознательных написана другая статья, в которой рассматривается возможность деления на ноль:

a: 0 = делить на ноль запрещено , при этом а не равно нулю

ноль разделить на ноль — выражение не имеет смысла, так как не может быть определено:

0: 0 = выражение не имеет смысла

ноль разделить на число — если ноль разделить на число в результате всегда будет ноль , не зависимо от того, какое число находится в знаменателе (исключением из этого правила является число ноль , смотри выше):

0: a = 0 , при этом а не равно нулю

ноль в степени — ноль в любой степени равен нулю :

0 a = 0 , при этом а не равно нулю

возведение в степень — любое число в степени ноль равняется единице (число в степени 0):

a 0 = 1 , при этом а не равно нулю

ноль в степени ноль — выражение не имеет смысла, так как не может быть определено (ноль в нулевой степени, 0 в степени 0):

0 0 = выражение не имеет смысла

извлечение корня — корень любой степени из нуля равен нулю :

0 1/a = 0 , при этом а не равно нулю

факториал — факториал нуля, или ноль факториал, равняется единице:

распределение цифр — при подсчете распределения цифр ноль считается незначащей цифрой. Изменение подхода в правилах подсчета распределения цифр, когда ноль считается ЗНАЧАЩЕЙ цифрой позволит получать более точные результаты распределения цифр во всех стандартных системах счисления, в том числе в двоичной системе счисления.

Кому интересен вопрос возникновения нуля , предлагаю прочесть статью «История нуля» Дж. Дж. О’Коннора и Е. Ф. Робертсона в переводе И. Ю. Осмоловского.

Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.

Теперь маленький кусочек рекламы.Главная фильтры для воды помогут очистить воду и сделать её более безопасной для питья. Качество водопроводной воды сегодня не отвечает требованиям безопасности для здоровья человека. Применение фильтров для воды становится потребностью в каждом доме.

Создание сайта цены, изготовление сайта Москва. Создание и изготовление сайта пр. Мира. поможет вам обрести свое представительство в виртуальном мире. Красивые и функциональные сайты для самых разных нужд, создание сайта под ваши потребности.

Специальный проект «45 минут» организовывает постоянные конкурсы для педагогов по разным учебным дисциплинам. Создание собственных страничек, портфолио учителей, обмен педагогическим опытом, подготовка к экзаменам.

ndspaces.narod.ru

Как умножить на 0,1

Разберем правило и посмотрим на примерах, как умножить на 0,1 любое число.

Поэтому умножение числа на 0,1 можно заменить его делением на 10. В общем виде это можно записать так:

Отсюда следует правило.

Правило умножения на 0,1

Чтобы умножить число на 0,1, надо запятую в записи этого числа перенести на одну цифру влево.

В записи натурального числа запятую в конце не пишут:

Умножить натуральное число на 0,1 -значит, перенести эту запятую на один знак влево:

Если в записи натурального числа последняя цифра — нуль, в результате умножения этого числа на 0,1 получаем натуральное число (поскольку нуль после запятой в конце числа не пишут):

Чтобы умножить на 0,1 обыкновенную дробь, надо обе дроби привести к одному виду — либо обыкновенную дробь перевести в десятичную, либо десятичную — в обыкновенную.

www.for6cl.uznateshe.ru

Правило умножения любого числа на ноль

Кто в итоге прав

Это интересно: разрядные слагаемые – что это?

Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

Это интересно: Как найти разность чисел в математике?

Что такое умножение

25×3 = 75
25 + 25 + 25 = 75
25×3 = 25 + 25 + 25

Из этого уравнения следует вывод, что умножение — это упрощённое сложение .

Это интересно: что такое хорда окружности в геометрии, определение и свойства.

Что такое ноль

Можно ли умножать на пустоту

Это интересно: что такое модуль числа?

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Расскажу тебе позволь,

Чтобы не делил на 0!

Режь 1 как хочешь, вдоль,

Только не дели на 0!

obrazovanie.guru

Умножение с 0 и 1. 2-й класс

Презентация к уроку

Цели урока:

Образовательные :
- формировать умение выполнять умножение с нулем и единицей;
- формировать умение правильно читать математические выражения, называть компоненты умножения;
- закрепить умение заменять произведение чисел суммой и устно вычислять их значение; формировать начальные умения работы с тестом.
Развивающие :
- способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Воспитательные:
- воспитывать культуру поведения при фронтальной работе, индивидуальной работе; интерес к предмету.

Тип урока – урок открытия нового знания.

Формирование новых умений возможно только в деятельности, поэтому в разработке урока использована технология деятельностного метода. Использование данной технологии является существенным фактором повышения эффективности освоения учащимися предметных знаний, формирования учебных универсальных действий: регулятивных, коммуникативных, познавательных .

Разработанный урок имеет следующую структуру:

1. Приобретение первичного опыта выполнения действия и мотивация.
2. Формирование нового способа (алгоритма) действия, установление первичных связей с имеющимися способами.
3. Тренинг, уточнение связей, самоконтроль и коррекция.
4. Контроль.

Оборудование к уроку:

Стандартное: учебник, таблица для заполнения ответов теста, звездочки из цветной бумаги, памятки для учащихся.
Инновационное: мультимедийный проектор, интерактивная доска, мультимедийная презентация «Путешествие на планету Умножения»

Использование мультимедиа компонентов в уроке вносит элемент новизны, делает процесс работы наглядным, помогает учителю сконцентрировать внимание на основных моментах. Работа по каждому этапу урока строится как своеобразный диалог между учителем и учениками, в котором интерактивная доска служит демонстратором решения вопросов. Её использование в учебном процессе позволяет достигать высокой степени результативности.

Химия, Новые задания ЕГЭ, Доронькин В.Н., 2016 Химия, Новые задания ЕГЭ, Доронькин В.Н., 2016. Пособие составлено в соответствии с изменениями формулировок и содержания заданий в тестах ЕГЭ по новой спецификации и предназначено […]

Правила саймона на jailbreak 1. Использовать любые Скрипты/читы и прочее. [Бан на 1 Неделю/Навсегда] 2. Использовать баги игры,карт. [Бан на 30 мин/1 день] 3. Использовать программы, меняющие голос/воспроизводящие посторонние […]

Менеджмент. Пособие для подготовки к экзаменам. Сост. Руденко В.И. 4-е изд. — Ростов н / Д: Феникс, 2005. — 192 с. (Сер. «Зачет и экзамен») Учебное пособие содержит текст лекций на основе программы, соответствующей […]

Сокращение работника после выхода из декретного отпуска Добрый вечер!В соответствии с ТК РФ вас (до исполнения ребенку 3 лет) не могут уволить в связи с сокращением: Статья 261. Гарантии беременной женщине и лицам с […]

Математика Умножение числа 4 и на число 4, соответствующие случаи деления

Актуализация знаний

Устный счёт

Задание

Прочитайте выражение, найдите значение и соответствующую букву, и вы узнаете, какой герой придёт к нам на урок….

23 — 7
23 + 9
57 — 7
56 + 7
42 + 30
60 — 7
30 + 28

16	М
32	У
50	Р
63	А
72	В
53	Е
58	Й

К нам в гости пришёл муравей.
А что вы знаете о муравьях?
В хвойных лесах, а иногда в смешанных и в лиственных мы можем встретить конусы полутораметровой высоты – это муравейники рыжих лесных муравьёв. Эти конусы сооружаются из хвои, мелких веточек, мха и земли. Над землёй видна только часть муравьиного гнезда. Под конусом оно может уходить в землю на глубину до 2 м.

Задание

Выразите в других величинах.

2 м = □ см…….200 см
5 дм 1 см = □ см…….51 см
56 дм = □ м □ дм…….56 дм = 5 м 6 дм
75 мин = □ ч □ мин……75 мин = 1 ч 15 мин
1 ч 39 мин = □ мин…..1 ч 39 мин = 99 мин
101 см = □ дм □ см…..10 дм 1 см
1 м = □ дм…..1 м = 10дм

Большинство муравьёв – рабочие. Они выполняют множество дел: строят гнездо. Чистят и защищают его, ухаживают за потомством и снабжают гнездо пищей. Муравьи уничтожают множество вредных насекомых, поэтому их присутствие очень важно для здоровья лесов. Муравейники находятся под особой охраной, разрушать их запрещено.

Задание

7 муравьев могут нести одну травинку. Сколько травинок может нести 14 муравьев? 21 муравей?

14 : 7, будет 2, значит, 14 муравьёв могут нести 2 травинки.

21 : 7, будет 3, значит, 21 муравей может нести 3 травинки.

Задание

Посмотрите, ребята, муравей принёс нам задание:
Распределите числовые выражения в 3 группы. По какому признаку вы их распределили?

20 + 18 4 ∙ 8 40 + 20
85 — 80                     34 + 9                     4 ∙ 6
90 — 82                      4 ∙ 5    20 — 9

Числовые выражения на сложение, числовые выражения на вычитание, числовые выражения на умножение.

Найдите значение этих выражений.
Проверьте себя.

20 + 18 = 38 90 — 82 = 8 4 ∙ 5 = 20
34 + 9 = 43         85 — 80 = 5 4 ∙ 6 = 24
40 + 20 = 60       20 — 9 = 11 4 ∙ 8 = 32

Этап усвоения новых знаний

Уважаемый муравей, вы пришли на урок, где изучается табличное умножение и деление. Сегодня мы будем составлять таблицу умножения и деления с числом 4. А помогут нам Божьи коровки.

Ребята, рассмотрите рисунок, он поможет нам составить таблицу умножения.
Ребята, первая строчка — первый множитель, кружочки – второй множитель, произведение выделено голубым цветом.

Рассуждайте так:
Первый множитель единица, второй множитель четыре, произведение равно четырём.
Первый множитель 2, второй множитель четыре, произведение равно 8.
Первый множитель 3, второй множитель четыре, произведение равно 12.
Первый множитель 4, второй множитель четыре, произведение равно 16.
Первый множитель 4, второй множитель 5, произведение равно 20.
Первый множитель 4, второй множитель 6, произведение равно двадцати четырём.
Первый множитель 4, второй множитель 7, произведение равно двадцати восьми.
Первый множитель 4, второй множитель 8, произведение равно тридцати двум.
Первый множитель 4, второй множитель 9, произведение равно тридцати шести.

Зная таблицу умножения на 4, составьте таблицу деления на 4.
Для этого давайте вспомним правило, как найти множитель, зная произведение.
Чтобы найти множитель, нужно произведение разделить на второй множитель.

Рассуждайте так:
Произведение 16 делим на множитель 4, в ответе получаем 4.
Произведение 20 делим на множитель 4,в ответе получаем 5.
Произведение 24 делим на множитель 4, в ответе получаем 6.
Произведение 28 делим на множитель 4, в ответе получаем 7.
Произведение 32 делим на множитель 4, в ответе получаем 8.
Произведение 36 делим на множитель 4, в ответе получаем 9.

Закрепление знаний

Задание

Решите числовые выражения.

4 · 5
7 · 4
36 : 4
12 : 3
9 + 2 · 4
55 — 3 · 5
72 — 36 : 4
54 + 32 : 8
4 · (4 + 3)
24 : (3 · 2)

Проверьте себя и оцените свои успехи.

4 · 5 = 20
7 · 4 = 28
36 : 4 = 9
12 : 3 = 4
9 + 2 · 4 = 17 (сначала выполняем умножение: 2 умножить на 4, будет 8, к 9 прибавим 8, получим 17)
55 — 3 · 5 = 40 (сначала выполняем умножение: 3 умножить на 5, будет 15, из 55 вычтем 15, получим 40)
72 — 36 : 4 = 63 (сначала выполняем деление: 36 разделить на 4, будет 9, из 72 вычтем 9, получим 63)
54 + 32 : 8 = 58 (сначала выполняем деление: 32 разделить на 8, будет 4, к 54 прибавим 4, получим 58)
4 · (4 + 3) = 28 (сначала выполняем действия в скобках: 4 + 3 = 7, 4 умножаем на 7, будет 28)
24 : (3 · 2) = 4 (сначала выполняем действия в скобках 3 умножить на 2, будет 6, 24 : 6 = 4.

Задание

Решите задачу.
В киоске продали на 32 рубля ручки по цене 4 рубля за каждую. Сколько ручек продали?
Что известно в задаче?
Известна стоимость и цена.
Что нужно узнать в задаче?
Нужно узнать количество проданных ручек.
Как узнать, сколько ручек продали?
Чтобы узнать количество, нужно стоимость разделить на цену.
Решите задачу.

Цена	Кол-во	Стоимость
4 р.	?	32 р.

Проверьте себя и оцените свои успехи.

32 : 4 = 8 ручек.

Ответ: продали 8 ручек.

Задание

Решите уравнения.

х · 8 = 16
24 : у = 6
а — 17 = 54
33 + с = 99

Проверьте себя и оцените свои успехи.

х · 8 = 16
16 : 8 = 2
х = 2
Выполняем проверку.
2 · 8 = 16
16 = 16

24 : у = 6
24 : 6 = 4
у = 4
Выполняем проверку
24 : 4 = 6
6 = 6

а — 17 = 54
54 + 17 = 71
а = 71
Выполняем проверку
71 — 17 = 54
54 = 54

33 + с = 99
99 — 33 = 66
с = 66
Выполняем проверку
33 + 66 = 99
99 = 99

Задание

Назовите фигуры, изображенные на экране.
Круг, треугольник, квадрат, пятиугольник, треугольник.
Из каких двух фигур можно составить квадрат?
Вычислите периметр квадрата, если его сторона равна 4 см.
Проверьте себя и оцените свои успехи.

Периметр – сумма длин всех сторон.
Зная, что сторона квадрата равна 4 см, а все стороны квадрата равны, сложим длины их сторон:
4 + 4 + 4 + 4 = 16 см
Заменим сложение умножением:
4 · 4 = 16 см

Итог урока

Что нового узнали сегодня на уроке?
Сегодня на уроке мы познакомились с таблицей умножения и деления на 4.

Рефлексия

Оцените, как вы работали на уроке.
Поднимите красный кружок, кто считает, что всё понял и может объяснить другим, как составили, таблицу умножения и деления (отлично)
Поднимите желтый кружок, кто всё понял (я старался, но не всё получилось)
Зелёный – нужна помощь (нужно ещё поработать)

Говорит Муравей.

Молодцы ребята! Спасибо за урок!

Выбрасывай калькулятор: 17 полезных математических трюков

Собрали подборку классных математических трюков в помощь. С ними ты сможешь быстро считать в уме, не прибегая к калькулятору!

Привет!

Здесь 17 крутых математических трюков, которые полезны не только школьникам, но и взрослым. Они помогают производить сложные вычисления в голове. Освой эти техники, и будешь решать даже те задачи, которые когда-то казались непосильными.

А после можешь пройти наш быстрый математический тест 😉

Сложение крупных чисел в голове − намного более лёгкий процесс, чем кажется. А этот метод показывает, как упростить процесс, округлив все числа до десятка. Вот пример:

644 + 238

Чтобы было проще работать, округляем каждое из чисел. Итак, 644 превращаем в 650, а 238 становится 240.

Затем складываем 650 и 240. Получается 890. Чтобы найти ответ на исходное уравнение, нужно определить, сколько мы добавили к числам, чтобы их округлить.

650 — 644 = 6 и 240 — 238 = 2

Получается, что к первому числу (644) мы добавили 6, а ко второму (238) − 2. Складываем 6 и 2 вместе, получаем 8.

Остаётся вычесть из суммы округлённых чисел (890) лишнее (8):

890 — 8 = 882

Получаем, что 644 + 238 = 882. Это один из основных математических трюков, которые стоит знать.

Вот основное правило вычитания большого числа из 1000: раздели своё трёхзначное число на первую, вторую, третью цифру. Теперь вычти первую из 9, вторую из 9, а третью из 10. Например:

1000 — 556

Шаг 1: вычитаем 5 из 9 = 4

Шаг 2: вычитаем 5 из 9 = 4

Шаг 3: вычитаем 6 из 10 = 4

Ответ 444.

Умножая число 5 на четное число, можно быстро найти ответ. Например, 5 х 4:

Шаг 1: Берём число, которое хотим умножить на 5 и делим его пополам. В нашем случае, 4 превращаем в 2.

Шаг 2: Добавляем ноль к получившемуся числу, чтобы найти ответ. К числу 2 ставим рядом 0, получаем 20.

5 х 4 = 20

При умножении нечетного числа на 5 формула немного отличается. Например, рассмотрим 5 х 3:

Шаг 1: Вычитаем единицу из числа, которое хотим умножить на 5. В нашем случае, 3 превращаем в 2.

Шаг 2: Теперь делим получившееся число (2) пополам, получаем 1. Ставим последнее получившееся число на первое место, а число 5, на которое мы хотели умножать изначально, приставляем рядом. Получается, рядом с 1 ставим 5, становится 15.

5 х 3 = 15

Вот быстрый способ узнать, когда число может быть равномерно разделено на эти же числа:

10, если число заканчивается на 0.
9, когда цифры складываются вместе, а сумма делится поровну на 9.
8, если последние три цифры делятся на 8, или число оканчивается на 000.
6, если при сложении чётных чисел сумма делится на 3.
5, если число заканчивается на 0 или 5.
4, если число оканчивается на 00 или двузначное число, которое делится на 4.
3, если при сложении цифр числа результат делится на 3.
2, если оно заканчивается на 0, 2, 4, 6 или 8.

Это ещё один из математических трюков, который полезен в жизни. Нужен он для умножения любого числа на 9. Вот как это работает:

Покажем на примере умножения 9 на 3.

Шаг 1: Вычитаем 1 из числа, которое умножается на 9.

3 — 1 = 2

Число 2 является первым числом в ответе на уравнение.

Шаг 2: Вычитаем получившееся число из 9.

9 — 2 = 7

Число 7 является вторым числом в ответе на уравнение.

Итого, 9 х 3 = 27.

Хитрость в умножении любого числа на 10 состоит в добавлении нуля к концу числа. Например, 62 х 10 = 620.

Существует также простой способ умножения любого двузначного числа на 11. Вот оно:

11 х 25

Возьмём двузначное число и отделим первую часть числа от второй − из 25 сделаем 2 и 5.

Теперь складываем эти два числа вместе и помещаем результат в центр, между 2 и 5:

2 (2 + 5) 5

2 7 5

Ответ: 11 х 25 = 275.

Если число в центре содержит две цифры, добавь первое число из суммы к первой цифре итогового числа, а второе оставь на месте. Вот пример для уравнения 11 х 88:

8 (8 + 8) 8

8 (16) 8

(8 + 1) 6 8

9 6 8

Получаем ответ: 11 х 88 = 968.

Найти процент от числа может быть несколько сложно, если не подумать о способе решения, а просто считать. С этим методом всё проще. Чтобы узнать, сколько составляет 5% от 235, нужно:

Шаг 1: Переместить десятичную точку на одно значение вправо, 235 (235.0): становится 23.5.

Шаг 2: Разделить 23.5 на число 2, ответ − 11.75. Это ответ на исходное уравнение.

Используем число 35 в качестве примера:

Шаг 1: Умножим первую цифру на сумму единицы и первой цифры.

Шаг 2: В окончание поставим 25.

35 в квадрате = 3 x (3 + 1) & 25

3 x (3 + 1) = 12

12 и 25 = 1225

35 в квадрате = 1225.

Если при умножении больших чисел одно из них является четным, раздели первое число пополам, а второе умножь на 2. Например 20 х 120:

Шаг 1: Делим 20 на 2, получаем 10. Умножаем 120 на 2, получаем 240.

Затем умножаем два ответа вместе:

10 х 240 = 2400

Ответ: 20 х 120 = 2400.

Суть метода в том, чтобы умножить числа без 0, а потом добавить нули. Рассмотрим умножение 200 на 400:

Шаг 1: Умножаем первые числа − 2 на 4:

2 х 4 = 8

Шаг 2: Ставим рядом убранные нули:

80000

200 х 400 = 80000

Это похоже на метод со сложением − здесь тоже нужно округлять. Рассмотрим его на примере выражения 97 x 96:

Округлим каждое из чисел до 100. Получим 100 и 100.

Теперь из первых 100 вычитаем первое число (97) и получаем 3, из вторых 100 вычитаем второе число (96) и получаем 4. Складываем получившиеся числа:

3 + 4 = 7

Теперь из 100 вычитаем 7: получается 93. Это будут первые две цифры итогового результата. Чтобы получить оставшиеся две цифры, нужно не сложить, а умножить 3 и 4. Приписываем результат 12 к 93, получается 9312.

Посмотри на свои руки (в идеальном случае, должно быть 10 пальцев). Представим, что ты хочешь умножить 7 на 8.

Из 10 (как и пальцев на руках) вычти первое число (7), осталось 3. Запомни это число. Теперь вычти из 10 второе число (8), получается 2.

Теперь сложи получившиеся числа, результат (5) поставь на первое место. Затем, перемножь 3 и 2. Получится 6, цифру ставим на второе место, получается 56.

Казалось бы, как подборка математических трюков может помочь в таком серьёзном деле, как инвестирование? Может!

Если ты хочешь утроить свои инвестиции, запомни число 115. К примеру, инвестиции, которые дают 5% в год, утроятся через 23 года − 115 : 5 = 23.

Хотим посчитать 51 х 51. Возьмём одну из цифр, например, 1, к ней прибавим 25. Получается 26.

Теперь перемножим ту же цифру (1), получим 1 (01).

Соединим получившееся, 26 ставим первым числом, 01 вторым. Получается 2601.

Найти корень из таких чисел, как 49 или 81 достаточно просто, потому что корни являются целыми числами. Но как можно найти корень с остатком? Покажем на примере числа 420.

Шаг 1: Находим ближайшее число, которое можно получить возведением в квадрат. В данном случае, это число 400, которое получают возведением в квадрат числа 20.

Шаг 2: Делим наше число (420) на корень того, ближайшего числа (20). Получаем 21.

Шаг 3: Теперь находим среднее между результатом и корнем первого числа − среднее между 21 и 20 равно 20,5.

А корень числа 420 равен 20,494. Получается, что наш ответ максимально близок.

Допустим, мы хотим узнать, чему равно 81 в квадрате.

81 х 81 = ?

Округляем число до меньшего − 80, возводим его в квадрат. Получается 6400.

Теперь к сумме дважды прибавляем округленное число − 6400 + 80 + 80, а в конце добавляем ещё один.

Получается 6560 + 1 = 6561.

Как бы ты посчитал значение выражения 32 х 125? Лучше упростить его:

32 х 125 = ?

16 х 250 = ?

8 х 500 = ?

4 х 1000 = 4000

На этом наша подборка математических трюков заканчивается. Практика этих быстрых математических приемов может помочь как в жизни, так и в работе. А ещё, может быть, пробудит интерес к математике.

Понравилась подборка математических трюков? Тебя точно заинтересует следующее:

12 простых советов тем, кто самостоятельно учит математику
Математика для программистов: 7 крутых YouTube-каналов
Математика для программиста: советы, разделы, литература

Источник: 10 математических трюков в блоге Concorida University-Portland

Расскажи, какими математическими трюками пользуешься ты?

Калькулятор умножения

Создано Maciej Kowalski, кандидатом наук

Отзыв Стивена Вудинга

Последнее обновление: 3 сентября 2022 г.

Содержание:

Как умножать числа?
Умножение десятичных дробей
Пример: использование калькулятора умножения
Часто задаваемые вопросы

Добро пожаловать в Omni калькулятор умножения , где мы изучим одну из четырех основных арифметических операций: умножение . Короче говоря, мы используем его всякий раз, когда хотим добавить одно и то же число несколько раз. Например, 16 умножить на 7 (записано как 16 * 7 ) — это то же самое, что добавить 16 семь раз или, что то же самое, добавить 7 шестнадцать раз. Удобно, что наш инструмент работает также как калькулятор умножения десятичных дробей . Более того, даже если вам нужно умножить более двух чисел, вы все равно можете найти их произведение с помощью этого калькулятора.

Примечание : Если вы хотите увидеть пошаговые решения умножения больших чисел, воспользуйтесь калькулятором умножения длинных чисел Omni или калькулятором частичных произведений.

Давайте не будем терять ни секунды и посмотрим как умножать числа !

Как умножать числа?

Продукт и умножение — это одно и то же: они получаются в результате умножения чисел (или других объектов, если уж на то пошло). К счастью, процесс очень прост: он сводится к добавлению значения подходящее количество раз. Например, 24 умножить на 5 означает, что мы прибавляем 24 пять раз, т. е.

24 * 5 = 24 + 24 + 24 + 24 + 24 = 120 .

Аналогично, 12 умножить на 20 переводится как сложение 12 двадцать раз:

12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 1 + 12 + 122 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 240 .

Однако обратите внимание, что мы всегда можем обратить процесс нахождения произведения с умножением. Другими словами, 24 раза 5 может также означать добавление 5 двадцать четыре раза:

5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 120 ,

и мы можем получить 12 умножить на 20 , прибавив 20 двенадцать раз:

2 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 = 240 .

Мы всегда выбираем, как умножать числа, так как результат будет одинаковым в любом случае . В математических терминах это означает, что произведение или умножение является коммутативной операцией . Обратите внимание, что то же самое верно и для сложения. С другой стороны, оно не выполняется, скажем, для вычитания.

🔎 Знаете ли вы, что существует больше способов записи арифметических операций, чем «классический» оператор в среднем ? Попробуйте их с нашим конвертером польской нотации!

Кроме того, наш калькулятор умножения работает только с числами , но математики придумали, как умножать другие объекты. Ниже мы перечисляем несколько других калькуляторов умножения от Omni.

Калькулятор умножения матриц;
Калькулятор умножения дробей; и
Калькулятор умножения радикалов.

Однако не всегда мы имеем дело с целыми числами , такими как 2 , 18 или 2020 . Мы научились умножать их и что, скажем, 16 умножить на 7 , но как найти произведение десятичных дробей? Например, сколько будет 0,2 умножить на 1,25 ? Наш калькулятор умножения тоже калькулятор умножения десятичных дробей ?

О, еще бы!

🙋 Хотите научиться обрабатывать сложные математические выражения, включающие более одной арифметической операции? Проверьте наш калькулятор распределительной собственности.

Умножение десятичных дробей

По сути, десятичных дробей — это дроби . Таким образом, один из способов умножения десятичных дробей состоит в том, чтобы преобразовать их в правильные дроби, а затем использовать основное правило : числитель умножить на числитель на знаменатель, умножить на знаменатель 9.0155 . Например,

0,2 * 1,25 = (2/10) * (125/100) = (2 * 125) / (10 * 100) = 250/1000 = 0,25 .

Конечно, мы могли бы также найти более простые дроби, эквивалентные двум данным до умножения. В этом случае мы могли бы сказать, что 0,2 = 1/5 и 1,25 = 5/4 , поэтому

0,2 * 1,25 = (1/5) * (5/4) = (1 * 5) / (5 * 4) = 5/20 = 1/4 .

Оба ответа верны ; это всегда ваш выбор, как умножать десятичные дроби. Однако, кроме двух упомянутых, есть еще .

При умножении десятичных дробей, скажем, 0,2 и 1,25 , мы можем начать с , забыв о точках . Это означает, что для нахождения 0,2 * 1,25 мы начнем с нахождения 2 * 125 , что равно 250 . Затем подсчитываем, сколько цифр справа от точек у нас было всего в числах, с которых мы начали (в данном случае их три: одна в 0,2 и две в 1,25 ). Затем мы пишем точку, столько цифр справа в том, что мы получили. Для нас это означает поставить точку слева от 2 , что дает 0,250 = 0,25 (мы пишем 0 , если перед точкой нет числа).

В общем, мы видели как умножать десятичные дроби тремя способами . Честно говоря, первые два были почти одинаковыми; просто промежуточные шаги были в другом порядке. Тем не менее, на этом часть о том, как умножать без калькулятора, заканчивается. Теперь опишем подробно, как это сделать с одним, а если быть точным, то с с калькулятором умножения Omni .

Пример: с помощью калькулятора умножения

Найдем 2020 умножить на 12 с помощью калькулятора умножения. В верхней части нашего инструмента мы видим формулу:

результат = а₁ * а₂ .

Это означает, что для расчета 2020 * 12 нам нужно ввести:

a₁ = 2020 и a₂ = 12 .

В тот момент, когда мы даем второе число, калькулятор умножения выдает ответ в поле Результат .

результат = 2020 * 12 = 24240

Однако, скажем, вы хотите умножить результат еще на на 1,3 (помните, что наш инструмент также работает как калькулятор умножения десятичных дробей).

Мы могли бы просто очистить поля и записать ответ сверху в один из множителей, т.е. ввести a₁ = 24240 и a₂ = 1,3 . В качестве альтернативы, мы можем просто выбрать много чисел под Умножить… , что позволяет нам найти произведение умножения для большего количества чисел . Если мы это сделаем, мы получим возможность ввести a₁ , a₂ , a₃ и так далее до a₁₀ (обратите внимание, что изначально только a₁ и a₂4, переменные появляются, как только вы начинаете заполнять поля). Тогда достаточно ввести:

а₁ = 2020 , а₂ = 12 , а₃ = 1,3 ,

и читаем ответ снизу:

результат = 2020 * 12 * 1.3 = 31512 .

Ну, этот калькулятор умножения действительно экономит много времени. Можете ли вы представить, что пишет две тысячи двадцать раз число 12 , как мы это делали в первом разделе? Мы, например, нет.

`Часто задаваемые вопросы`

`Произведение совпадает с умножением?`

Умножение — одно из четырех основных арифметических действий (три других — сложение, вычитание и деление).

Произведение является результатом выполнения умножения: когда мы умножаем два числа (множимое и множитель), мы получаем их произведение.

`Какие части умножения?`

Два числа, которые мы перемножаем, называются множимым и множителем или просто множителями. Результат умножения называется произведением. Например, в задаче на умножение 3 × 5 = 15 число 3 является множимым, 5 — это множитель, 3 и 5 — множители, а 15 — произведение.

`Каковы свойства умножения?`

Арифметическая операция умножения двух чисел:

Ассоциативный;
Распределительный; и
Коммутативный.

`Что такое нейтральный элемент умножения?`

Нейтральный элемент (также известный как элемент идентичности) умножения — это число 9. 0023 1 . Это означает, что 1 — это (уникальное) число, такое, что при умножении любого числа на 1 мы получаем то же число, с которого начали.

Как умножить на 100?

Чтобы умножить любое число на 100 , выполните следующие действия:

Если у вас целое число, напишите два дополнительных нуля в правом конце вашего числа.
Если в вашем числе есть десятичная точка, вам нужно переместить десятичную точку на два знака вправо. Добавьте один или два нуля в конце, если десятичных цифр меньше двух.

Maciej Kowalski, кандидат PhD

Результат = A₁ * A₂

Умножение …

Факторы

РЕЗУЛЬТАТ

Проверьте свойство.

Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражений с дробями:

Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .

Математические символы

Символ Название символа Символ Значение Пример
+ plus sign addition 1/2 + 1/3
— minus sign subtraction 1 1/2 — 2/3
* asterisk multiplication 2/3 * 3/4 
× times sign multiplication 2/3 × 5/6
: division sign division 91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3
Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
Использование денег
Из 550 000,00, переданных школе, было использовано 325 000,00. Какая часть от общей суммы была использована?
Дети 9
В комнате 11 детей. 6 детей — девочки. Какую часть детей составляют девочки?
Одна суббота
Однажды субботним вечером в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки?
Дробями
Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа?
У Макса 2
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Младенцы
В автобусе двое взрослых, двое детей и четверо младенцев. Какую часть населения составляют младенцы?
Жениться
У Жени было полторы дюжины яиц в холодильнике. Использовала 1/3 яйца. Какая часть яиц использовалась?
Вычислить выражение
Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2
Ферма 6
На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.
Мэтью
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
more math problems »
decimals
fractions
triangle ΔABC
percentage %
permille ‰
prime factors
complex numbers
LCM
GCD
LCD
combinatorics
equations
статистика
… все математические калькуляторы
Таблица множителей и множителей
Вот множители (не включая отрицательные) и некоторые множители от 1 до 100:
9164 248 904 618 509 04 4 409 9 4 4 97 9
Коэффициенты Несколько
1 1 2 3 4 5 9 3 8 18
82
8 9 10
1, 2 9 2 4 6 8 10 12 14 16 18 20
1, 3 3 6 12 15 18 21 24 27 30
27 30
30
30
30
30
30
0419 4 8 12 16 20 24 28 32 36 40
1, 5 5 10 15 20 25 30 35 40 45 50
45 50
45 50 45 . 12 18 24 30 36 42 48 54 60
1, 7 7 14 21 28 35 42 49 56 63 70
1, 2, 4, 8 8 16 24 32 40 48 56 64 72 80
1, 3, 9 9 18 27 36 45 54 63 72 81 90
1, 2, 5, 10 10 20 30 40 50 60 70 80 90 100
1, 11 11 22 33 44 55 66 77 88 99 110
1, 2, 3, 4, 6, 12 12 24 36 48 60 72 84 96 108 120
1, 13 13 26 39 52 . 28 42 56 70 84 98 112 126 140
1, 3, 5, 15 15 30 45 60 75 90 105 120 135 150
1, 2, 4, 8, 16 16 32 48 64 80 96 112 128 144 160
1, 17 17 34 51 68 85 102 119 136 153 170
1, 2, 3, 6, 9, 18 18 36 54 72 90 108 126 144 162 180
1, 19 19 38 57 76 95 114 133 152 171 190
1, 2, 4, 5, 10, 20 20 40 60 80 100 120 140 40419 160 40419 180 200 180 200 180 200919 180 200 200 . 42 63 84 105 126 147 168 189 210
1, 2, 11, 22 90 2
44 66 88 110 132 154 176 198 220
1, 23 23 46 69 92 115 138 161 184 904 904 19 92
1, 2, 3, 4, 6, 8, 12, 24 24 48 72 96 120 144 168 192 216 240
1, 5, 25 25 50 75 100 125 150 175 200 225 250
1, 2, 13, 26 26 52 78 104 130 156 182 208 234 260
1, 3, 9, 27 27 54 81 108 135 162 189 216 243 270
1, 2, 4, 7, 14, 28 28 56 84 112 140 168 196 224 252 280
1, 29 29 58 87 116 145 174 203 232 261 290
1, 2, 3, 5, 6, 10, 15, 30 30 60 90 120 150 180 210 240 270 300
1, 31 31 62 93 124 155 186 217 248 279 310
1, 2, 4, 8, 16, 32 32 64 96 128 160 192 224 256 288 320
1, 3, 11, 33 33 66 99 132 165 198 231 264 297 330
1, 604 2, 904 394 68 102 136 170 204 238 272 306 340
1, 5, 7, 35 35 70 105 140 175 210 245 280 315 350
1, 2, 3, 4, 6, 9, 12, 18, 36 36 72 108 144 180 216 252 288 324 360
1, 37 37 74 111 148 185 222 259 296 333 370
1, 2, 19, 38 38 76 114 152 190 228 266 304 342 380
1, 3, 13, 39 39 78 117 156 195 234 273 312 351 390
1, 2, 4, 5, 8, 10, 20, 40 40 80 120 160 200 240 280 320 360 400
1, 41 091 901 82 123 164 205 246 287 328 369 410
1, 2, 3, 6, 7, 14, 21, 42 42 84 126 168 210 252 294 336 378 9041 420
1, 43 43 86 129 172 215 258 301 344 387 430
1, 2, 4, 11, 22, 44 44 88 132 176 220 264 308 352 396 440
1, 3, 5, 9, 15, 45 45 90 135 180 225 270 315 360 405 450
1, 2, 23, 46 46 92 138 184 230 276 322 368 414 460
1, 47 47 94 141 188 235 282 329 376 423 470
1, 2, 3, 4, 6, 8, 12, 16, 24, 48 48 96 144 192 240 288 336 384 432 480
1, 7, 49 49 98 147 196 245 294 343 392 441 490
1, 2, 5, 10, 25, 50 50 100 150 200 250 300 350 400 450 500
1, 3, 17, 51 51 102 153 204 255 306 357 408 459 510
1, 2, 4, 13, 26, 52 52 104 156 208 260 312 364 416 468 520
1, 53 53 106 159 212 265 318 371 424 477 530
1, 2, 3, 6, 9, 18, 27, 54 54 108 162 216 270 324 378 432 486 540
1, 5, 11, 55 55 110 165 220 275 330 385 440 495 550
1, 2, 4, 7, 8, 14, 28, 56 56 112 168 224 280 336 392 448
1, 3, 19, 57 57 114 171 228 285 342 399 456 513 570
1, 2, 29, 58 58 116 174 232 290 348 406 464 522 580
1, 59 59 118 177 236 295 354 413 472 531 590
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 60 120 180 240 300 360 420 480 540 600
1, 61 61 122 183 244 305 366 427 488 549 610
1, 2, 31, 62 62 124 186 248 310 372 434 496 558 620
1, 3, 7, 9, 21, 63 63 126 189 252 315 378 441 504 567 630
1, 2, 4, 8, 16, 32, 64 64 128 192 256 320 384 448 512 576 640
1, 5, 13, 65 65 130 195 260 325 390 455 520 585 650
1, 2, 3, 6, 11, 22, 33, 66 66 132 198 264 330 396 462 528 594 660
1, 67 67 134 201 268 335 402 469 536 603 670
1, 2, 4, 17, 34, 68 68 136 204 272 340 408 476 544 612 680
1, 3, 23, 69 69 138 207 276 345 414 483 552 621 690
1, 2, 5, 7, 10, 14, 35, 70 70 140 210 280 350 420 490 560 630 700
1, 71 71 142 213 284 355 426 497 568 639 710
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 72 144 216 288 360 432 504 576 648 648 648 9048 648 720 648 648 648 . 146 219 292 365 438 511 584 657 730
1, 2, 37, 74 74 148 222 296 370 444 518 592 666 740
1, 3, 5, 15, 25, 75 75 150 225 300 375 450 525 600 675 750
1, 2, 4, 19, 38, 76 76 152 228 304 380 456 532 608 684 760
1, 7, 11, 77 77 154 231 308 385 462 539 616 693 9 693 9 970189 8998 9 8 . 0659 1, 2, 3, 6, 13, 26, 39, 78 78 156 234 312 390 468 546 624 702 780
1, 79 79 158 237 316 395 474 553 632 711 790
1, 2, 4, 5, 8, 10, 16, 20, 40, 80 80 160 240 320 400 480 560 640 720 800
1, 3, 9, 27, 81 81 162 243 324 405 486 567 648 729 810
1, 2, 41, 82 82 164 246 328 410 492 574 656 738 820
1, 83 83 166 249 332 415 498 581 664 747 830
1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84 84 168 252 336 420 504 588 672 756 840
1, 5, 17, 85 85 170 255 340 425 510 595 680 765 850
1, 2, 43, 86 86 172 258 344 430 516 602 688 774 860
1, 3, 29, 87 87 174 261 348 435 522 609 696 783 870
1, 2, 4, 8, 11, 22, 44, 88 88 176 264 352 440 528 616 704 792 880
1, 89 89 178 267 356 445 534 623 712 801 890
1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90 90 180 270 360 450 540 630 720 810 900
1, 7, 13, 91 91 182 273 364 455 546 637 728 819 910
1, 2, 4, 23, 46, 92 92 184 276 368 460 552 644 736 828 920
1, 3, 31, 93 93 186 279 372 465 558 651 744 837 930
1, 2, 47, 94 94 188 282 376 470 564 658 752 846 940
1, 5, 19, 95 95 190 285 380 475 570 665 760 855 950
1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 96 192 288 384 480 576 672 768 864 960
194 291 388 485 582 679 776 873 970
1, 2, 7, 14, 49, 98 98 196 294 392 490 588 686 784 882 980
1, 3, 9, 11, 33, 99 99 198 297 396 495 594 693 792 891 990
1, 2, 4, 5, 10, 20, 25, 50, 100 100 200 300 400 500 600 700 800 900 1000
Biden’s Approval Hits 33 Percent; Демократы хотят вариантов на 2024 год, опрос показывает
Реклама
Продолжить чтение основного сюжета
Страна, охваченная всепроникающим чувством пессимизма, теряет поддержку президента.
Президент Байден в Кливленде на прошлой неделе. Только 26 процентов избирателей-демократов заявили, что партия должна повторно выдвинуть его кандидатуру в 2024 году. Кредит… Хайюн Цзян/The New York Times
11 июля 2022 г.
Президент Байден сталкивается с тревожным уровнем сомнений внутри самого себя. партия, при этом 64 процента избирателей-демократов заявили, что они предпочли бы нового знаменосца в президентской кампании 2024 года, согласно опросу New York Times / Siena College, поскольку избиратели по всей стране недовольны его лидерством, что дало ему скудные 33 процента работы -Рейтинг одобрения.
Широко распространенные опасения по поводу экономики и инфляции помогли сделать настроения в стране решительно мрачными, как в отношении г-на Байдена, так и в отношении траектории нации. Более трех четвертей зарегистрированных избирателей считают, что Соединенные Штаты движутся в неправильном направлении, всепроникающее чувство пессимизма охватывает каждый уголок страны, все возрастные группы и расовые группы, города, пригороды и сельские районы, а также политические стороны.
Только 13 процентов американских избирателей заявили, что страна находится на правильном пути — это самый низкий показатель в опросе Times со времен финансового кризиса более десяти лет назад.
Для г-на Байдена мрачная национальная перспектива привела к тому, что его рейтинг одобрения работы упал до опасно низкой отметки. Республиканская оппозиция предсказуемо подавляющая, но более двух третей независимых теперь также не одобряют действия президента, и почти половина решительно не одобряет. Среди коллег-демократов его рейтинг одобрения составляет 70 процентов, что является относительно низким показателем для президента, особенно в преддверии промежуточных выборов 2022 года, когда г-ну Байдену необходимо сплотить демократов на выборах, чтобы сохранить контроль над Конгрессом.
В знак глубокой уязвимости и беспокойства среди того, что должно составлять его политическую базу, только 26 процентов избирателей-демократов заявили, что партия должна повторно выдвинуть его кандидатуру в 2024 году.
Г-н Байден неоднократно заявлял, что намерен баллотироваться переизбрание в 2024 году. В свои 79 лет он уже является самым старым президентом в американской истории, и опасения по поводу его возраста занимают первое место в списке избирателей-демократов, которые хотят, чтобы партия нашла альтернативу.
Негативная реакция на г-на Байдена и желание двигаться в новом направлении были особенно острыми среди молодых избирателей. В опросе 94 процента демократов в возрасте до 30 лет заявили, что предпочли бы другого кандидата в президенты.
Николь Фарриер, 38-летняя учительница дошкольного образования из Мичигана, разочарована ростом стоимости жизни. Фото… Элейн Кроми для The New York Times
«Я просто выйду и скажу: я хотят более молодой крови», — сказала Николь Фарриер, 38-летняя воспитательница дошкольного учреждения в Ист-Тавасе, маленьком городке на севере Мичигана. «Я так устал от всех стариков, управляющих нашей страной. Я не хочу, чтобы кто-то постучал в дверь смерти».
Приближаются промежуточные выборы, и вот на какой позиции стоит президент Байден.
Защита демократии: Стремление президента Байдена укрепить демократию внутри страны и за рубежом приобрело еще большую актуальность из-за стойкой власти Китая, России и бывшего президента Дональда Трампа.
Каверзное сообщение: Даже осуждая трампизм, г-н Байден приложил все усилия, чтобы показать, что он понимает, что не все республиканцы являются теми, кого он называет экстремистскими «республиканцами MAGA».
В предвыборной кампании: Одержав ряд побед в законодательных органах, г-н Байден вернулся к предвыборной кампании. Но его низкие рейтинги одобрения могут осложнить его усилия по оказанию помощи демократам на промежуточных выборах.
Вопросы о 2024 году: Г-н Байден сказал, что планирует баллотироваться на второй срок, но в 79 лет его возраст стал неудобной проблемой.
Г-жа Фарриер, демократ, голосовавшая за г-на Байдена в 2020 году, сказала, что надеялась, что он сможет сделать больше для преодоления разногласий в стране, но теперь, будучи матерью-одиночкой, она озабочена тем, что она описывается как калечащий рост ее стоимости жизни. «Я перешла от комфортного образа жизни к тому, что больше ничего не могу себе позволить», — сказала она.
По мнению 20 процентов избирателей, рабочие места и экономика были наиболее важными проблемами, с которыми столкнулась страна, а инфляция и стоимость жизни (15 процентов) не отставали от них, поскольку цены растут самыми быстрыми темпами за поколение. Один из 10 избирателей назвал состояние американской демократии и политического раскола самой насущной проблемой, примерно столько же назвали политику в отношении оружия после нескольких громких массовых расстрелов.
Более 75 процентов избирателей в опросе заявили, что экономика для них «чрезвычайно важна». И все же только 1 процент оценил экономические условия как отличные. Среди людей типично трудоспособного возраста — избирателей в возрасте от 18 до 64 лет — только 6 процентов считают, что экономика находится на хорошем или отличном уровне, а 93 процента оценили его плохо или удовлетворительно.
Белый дом пытался трубить о значительном росте рабочих мест, в том числе в пятницу, когда г-н Байден заявил, что наблюдал за «самым быстрым и сильным восстановлением рабочих мест в американской истории». Но опрос Times/Siena показал огромный разрыв между этим хвастовством, силой некоторых экономических показателей и финансовой реальностью, с которой, по мнению большинства американцев, они сталкиваются.
«Раньше мы тратили 200 долларов в неделю только на то, чтобы развлечься или пойти и купить дополнительные продукты, если нам это было нужно, а теперь мы не можем сделать даже этого», — сказала Келли Кинг, бывшая фабричная работница в Гринсбурге. Ind., который в настоящее время выбыл из игры из-за травмы спины. «Мы едва можем купить то, что нам нужно».
38-летняя г-жа Кинг сказала, что не знает, виноват ли г-н Байден в резком скачке цен на бензин и продукты, но считает, что он должен сделать больше, чтобы помочь. «Мне кажется, что он на самом деле мало говорил об этом», — сказала г-жа Кинг. «Он не сделал того, на что, как мне кажется, он способен как президент, чтобы помочь американскому народу. Как демократ, я полагал, что он действительно будет на нашей стороне и вернет нас на правильный путь. И я просто чувствую, что это не так».
Как репортеры Times освещают политику. Мы полагаемся на то, что наши журналисты будут независимыми наблюдателями. Таким образом, хотя сотрудники Times могут голосовать, им не разрешается поддерживать или проводить кампании в поддержку кандидатов или по политическим мотивам. Это включает в себя участие в маршах или митингах в поддержку движения или пожертвование или сбор денег для любого политического кандидата или предвыборной кампании.
Узнайте больше о нашем процессе.
Теперь, сказала она, она надеется, что республиканцы захватят Конгресс в ноябре, чтобы скорректировать курс.
Одна из хороших новостей для г-на Байдена заключается в том, что опрос показал, что он имеет небольшое преимущество в гипотетическом матче-реванше в 2024 году с бывшим президентом Дональдом Трампом: 44 процента против 41 процента.
Результат напоминает один из любимых афоризмов мистера Байдена: «Не сравнивай меня со Всевышним, сравнивай меня с альтернативой». Опрос показал, что опасения демократов в отношении г-на Байдена, казалось, в основном исчезли, когда им предложили выбирать между ним и г-ном Трампом: 92 процента демократов заявили, что они будут придерживаться г-на Байдена.
Рэндейн Райт, водитель грузовика, говорит, что часто говорит с друзьями о недостатках г-на Байдена. Кредит … Брайан Ансельм для The New York Times
Типичным представителем этих избирателей является Рэндейн Райт, 41-летний водитель грузовика из Оушен-Тауншип, штат Нью-Джерси. Он сказал, что часто говорил с друзьями о недостатках г-на Байдена. «Он просто недостаточно агрессивен в выполнении своих планов», — пожаловался мистер Райт. Напротив, по его словам, «Трамп не боялся подчинить своих людей».
Но хотя он предпочел бы другого кандидата в 2024 году, г-н Райт сказал, что он все равно не станет голосовать за республиканцев в 2024 году, если ему предстоит матч-реванш Байден-Трамп.
В целом избирателям г-н Байден нравится больше, чем его деятельность на посту президента: 39% заявили, что у них сложилось о нем благоприятное впечатление — на шесть процентных пунктов больше, чем одобрение его работы.
Заявляя, что они хотят другого кандидата в 2024 году, демократы ссылались на множество причин, большинство из которых в открытом вопросе ссылались на его возраст (33 процента), за которым следовала неудовлетворенность тем, как он выполняет свою работу. Примерно каждый восьмой демократ просто сказал, что хочет кого-то нового, а каждый десятый сказал, что он недостаточно прогрессивен. Меньшие фракции выражали сомнения в его способности побеждать и остроте ума.
Опрос Times/Siena среди 849 зарегистрированных избирателей по всей стране был проведен с 5 по 7 июля после решения Верховного суда от 24 июня об отмене дела Роу против Уэйда, отменившего конституционное право на аборт, которое было защищено полвека. Постановление отправило демократов на улицы и спровоцировало поток политических пожертвований.
Как правило, избиратели, поддерживающие правящую партию — демократы теперь владеют Палатой представителей, Сенатом и Белым домом — более оптимистичны в отношении курса страны. Но только 27 процентов демократов считали, что страна находится на правильном пути. А с падением Роу среди демократов возник заметный гендерный разрыв: только 20 процентов женщин-демократов заявили, что страна движется в правильном направлении, по сравнению с 39 процентами женщин-демократов.процентов мужчин-демократов.
В целом аборты назвали наиболее важным вопросом 5 процентов избирателей: 1 процент мужчин, 9 процентов женщин.
Политика в отношении обращения с оружием после массовых расстрелов в Буффало, техасском городе Увалде и других местах, а также постановление Верховного суда от 23 июня, отменяющее закон Нью-Йорка, который налагал строгие ограничения на ношение оружия вне дома, были названы главным вопросом 10 процентов избирателей — гораздо больше, чем было характерно для общенациональных опросов последних лет. Опрос показал, что этот вопрос имел еще большее значение для чернокожих и латиноамериканских избирателей, занимая примерно такое же место, как инфляция и стоимость жизни.
Пандемия коронавируса, которая так основательно нарушила жизнь в конце правления Трампа и в течение первого года президентства Байдена, в значительной степени ушла из памяти избирателей, показал опрос. В открытом вопросе менее одного процента избирателей назвали вирус самой важной проблемой страны.
Когда г-н Байден победил в 2020 году, он старался завоевать позиции белых избирателей из рабочего класса, которые в массовом порядке покинули Демократическую партию в эпоху Трампа. Но какой бы перекрестной привлекательностью ни обладал когда-то г-н Байден, похоже, он уменьшился. Его рейтинг одобрения работы среди белых избирателей без высшего образования составлял целых 20 процентов.
Джон Уолдрон, зарегистрированный республиканец в Скенектади, штат Нью-Йорк, сожалеет о голосовании за г-на Байдена. Кредит… Ричард Бивен для The New York Times
Джон Уолдрон, 69-летний зарегистрированный республиканец и бывший машинист в Скенектади, штат Нью-Йорк, голосовал за г-на Байдена в 2020 году. Сегодня, по его словам, он сожалеет об этом и планирует голосовать за республиканцев в 2024 году. «Я думал, что он собирается что-то сделать для этой страны, но теперь он ничего не делает», — сказал г-н Уолдрон.
Как и другие, он выразил беспокойство по поводу возраста г-на Байдена и словесных ошибок. В пятницу клип г-на Байдена на мероприятии, посвященном объявлению указа об абортах, стал вирусным, когда он наткнулся, например, на фразу «прекращение президентских полномочий» вместо «беременность».
«Вы когда-нибудь видели его по телевизору?» — сказал мистер Уолдрон, сравнив президента с зомби. — Вот как он выглядит.
Базой г-на Байдена в 2020 году и сейчас остаются чернокожие избиратели. Они дали президенту 62-процентный рейтинг одобрения работы — более высокие оценки, чем у любой другой расы или этнической принадлежности, возрастной группы или уровня образования. Но даже среди этого электората есть серьезные признаки ослабления. Что касается вопроса о повторном выдвижении г-на Байдена в 2024 году, то немногим больше темнокожих избирателей-демократов заявили, что хотят другого кандидата, чем заявили, что предпочитают г-на Байдена.
«Любой человек мог бы работать лучше, чем сейчас», — сказал Клифтон Херд, 44-летний специалист по техническому обслуживанию в Фоули, штат Алабама. в 2020 году, но разочарован состоянием экономики и стремительно растущими ценами на газ и сейчас пересматривает мнение г-на Трампа.
«Я понимаю, что у них тяжелая работа», — сказал он об администрации г-на Байдена. «Он не был готов к работе».
Общенациональный опрос The Times/Siena проводился по телефону с участием операторов. Погрешность выборки составляет плюс-минус 4,1 процентных пункта. Кросс-таблицы и методология доступны здесь .
Элис Макфадден предоставила отчет.
111 Статистика обслуживания клиентов и факты, которые нельзя игнорировать
Ваше качество обслуживания клиентов является основным отличием между вами и вашими конкурентами, и вся статистика обслуживания клиентов подтверждает это.
Ниже мы собрали 111 ключевых статистических данных, изучающих актуальность и важность хорошего обслуживания клиентов, а также раскрывая стоимость и последствия плохого обслуживания клиентов.
Вместо того, чтобы просматривать эти статистические данные в вакууме, наложите их на свой собственный опыт и услуги, которые вы предлагаете в настоящее время. В следующих главах есть кое-что для всех — независимо от того, являетесь ли вы новичком и просто пытаетесь проложить путь для своей команды или занимаетесь этим годами.
Попробуйте платформу поддержки клиентов, которая понравится вашей команде и клиентам
Команды, использующие Help Scout, настраиваются за считанные минуты, в два раза продуктивнее и экономят до 80% годовых расходов на поддержку. Начните бесплатную пробную версию, чтобы увидеть, что он может сделать для вас.
Попробуйте бесплатно
Окупаемость инвестиций в отличное обслуживание клиентов
«Мы рассматриваем наших клиентов как приглашенных гостей на вечеринку, а мы — хозяева. Наша ежедневная работа заключается в том, чтобы сделать каждый важный аспект обслуживания клиентов немного лучше». –Джефф Безос
Каждый хочет, чтобы его знали за отличное обслуживание клиентов. Быть полезным не только приятно, но и является ключевым отличием, как показывает следующая статистика обслуживания клиентов.
Обслуживание клиентов, если оно сделано хорошо, оказывает такое же влияние, как и надежная воронка продаж или отличные маркетинговые усилия. Кроме того, если ваша команда обслуживания клиентов проделает фантастическую работу, это может помочь повысить эффективность других ваших команд.
Легче совершить продажу, когда ваши клиенты чувствуют поддержку, а маркетинг из уст в уста после необычайного опыта — один из лучших предложений на рынке.
Не убежден? Вот несколько статистических данных по обслуживанию клиентов, которые подчеркивают, насколько первостепенное значение может иметь превосходное обслуживание клиентов для вашей прибыли:
68% потребителей говорят, что готовы платить больше за продукты и услуги от бренда, который предлагает хорошее обслуживание клиентов. (HubSpot)
Для 86% хорошее обслуживание клиентов превращает бывших клиентов в долгосрочных чемпионов бренда. (Хорос)
Показатель NPS Promoter имеет пожизненную ценность клиента, которая на 600%-1400% выше, чем у Detractor. (Bain & Company)
89% потребителей с большей вероятностью сделают еще одну покупку после положительного опыта обслуживания клиентов. (Исследования отдела продаж)
93% клиентов, вероятно, сделают повторные покупки в компаниях, которые предлагают отличное обслуживание клиентов. (HubSpot Research)
Если обслуживание клиентов компании отличное, 78% потребителей обратятся к ней снова после ошибки. (Salesforce Research)
Увеличение коэффициента удержания клиентов всего на 5% может увеличить прибыль на 25–95%. (Bain and Company)
Почти трое из пяти потребителей сообщают, что хорошее обслуживание клиентов жизненно важно для них, чтобы чувствовать лояльность к бренду. (Зендеск)
Хорошее обслуживание клиентов сильно влияет на рекомендации. Потребители, которые оценивают услуги компании как «хорошие», на 38% чаще рекомендуют эту компанию. (Qualtrics XM Institute)
Инвестировать в новых клиентов от 5 до 25 раз дороже, чем удерживать существующих. (Invesp)
83% клиентов согласны с тем, что они чувствуют себя более лояльными к брендам, которые реагируют на их жалобы и разрешают их. (Хорос)
Предприятия могут увеличить свои доходы на 4-8% по сравнению с рыночными показателями, уделяя приоритетное внимание повышению качества обслуживания клиентов. (Bain & Company)
80% компаний используют показатели удовлетворенности клиентов для анализа качества обслуживания клиентов и его улучшения. (Harvard Business Review)
72% компаний считают, что могут использовать аналитические отчеты для улучшения качества обслуживания клиентов. (Deloitte)
Мировой рынок управления качеством обслуживания клиентов в 2020 году оценивается в 7,6 млрд долларов. Это 16,9% по сравнению с прошлым годом по сравнению с 6,5 миллиардами долларов в 2019 году. (Grand View Research)
Как вы понимаете, отличное обслуживание клиентов имеет большое значение, независимо от того, в какой отрасли вы работаете. Это помогает увеличить доход, сохранить лояльность клиентов и улучшить общую бизнес-стратегию.
Ключевые сведения о клиентах, такие как оценка удовлетворенности клиентов и NPS, помогают вашей команде по обслуживанию клиентов улучшать и увеличивать свое влияние. Однако помимо этого они также помогают другим вашим командам, работающим с клиентами, понять, что они могут улучшить. Кто не хотел бы дать всем остальным ногу?
Рекомендуем к прочтению
Служба поддержки клиентов 10 способов обеспечить неизменно высокое качество обслуживания клиентов
Инвестиции в службу поддержки клиентов являются ключом к долгосрочному успеху в бизнесе. Вот 10 лучших способов обеспечить отличное обслуживание клиентов.
Стоимость плохого обслуживания клиентов
Теперь, когда мы знаем, насколько важным может быть хорошее обслуживание клиентов для вашего бизнеса, пришло время понять, какое влияние оно может иметь, когда дела идут плохо.
Точно так же, как хорошее обслуживание клиентов приводит к успеху вашей команды, плохое обслуживание клиентов отбрасывает их назад. Хороший опыт означает, что клиенты гораздо более склонны к прощению, если другой опыт пойдет наперекосяк. Следующая статистика обслуживания клиентов помогает проиллюстрировать это:
Требуется 12 положительных отзывов клиентов, чтобы компенсировать один отрицательный. («Понимание клиентов» Руби Ньюэлл-Легнер)
58% американских потребителей поменяют компанию из-за плохого обслуживания клиентов. (Microsoft)
65% клиентов сказали, что они перешли на другую марку из-за плохого опыта. (Хорос)
После более чем одного неудачного опыта около 80% потребителей говорят, что предпочли бы иметь дело с конкурентом. (Зендеск)
Только каждый пятый потребитель простит плохой опыт в компании, чье обслуживание клиентов они оценивают как «очень плохое». (Почти 80% простят плохой опыт, если они оценят сервисную команду на «очень хорошо». ) (Qualtrics XM Institute)
78% клиентов отказались от покупки из-за плохого обслуживания клиентов. (Взгляд)
Посмотрите на последний! Более трех четвертей опрошенных клиентов отказались от покупки, потому что обслуживание клиентов было не таким хорошим, как ожидалось. Если вы покажете эту метрику своему отделу продаж, они будут выступать за то, чтобы ваша служба поддержки клиентов получала столько ресурсов, сколько им нужно.
Кроме того, обслуживание клиентов закладывает основу для успеха всей вашей компании. Влияние вашей службы поддержки клиентов ощущается шире, чем влияние любой другой команды. Когда они терпят неудачу, это делают все — и ваши клиенты знают об этом.
Рекомендуемая литература
Обслуживание клиентов 11 Типы плохого обслуживания клиентов (и как их избежать)
Прочитайте истории о вопиющем плохом обслуживании клиентов, а также получите несколько советов о том, как предотвратить подобные ситуации в вашей компании.
Забота о том, что думают клиенты
Это необоснованное, но распространенное заблуждение, что ваши клиенты знают не так много, как вы. Хотя они, конечно, не всегда правы , но очень часто они, по крайней мере, думают в правильном направлении . Точно так же они обычно знают, когда что-то пошло не так или ведет себя не так, как должно быть.
Мысли и мнения ваших клиентов имеют значение. Они могут помочь вам создать лучший продукт, помочь улучшить ваши внутренние процессы и дать вам хорошую информацию о том, что они думают о том, чтобы сбить вас с толку.
Вот некоторые статистические данные по обслуживанию клиентов, которые помогут вам понять, что ваш средний клиент чувствует во время или после взаимодействия:
90% клиентов оценивают «немедленный» ответ как существенный или очень важный, когда у них есть обслуживание клиентов вопрос. 60% клиентов определяют «немедленно» как 10 минут или меньше. (HubSpot Research)
Более 70% потребителей считают, что компании должны сотрудничать от их имени, чтобы им не приходилось повторять информацию разным представителям. (Зендеск)
90% потребителей во всем мире считают решение проблем самой важной задачей обслуживания клиентов. (KPMG)
70 % клиентов сообщают, что технологии упрощают передачу их бизнеса конкуренту, если это необходимо. (Salesforce)
90% американцев используют обслуживание клиентов как фактор при принятии решения о сотрудничестве с компанией. (Microsoft)
71% потребителей (в возрасте 16–24 лет) считают, что быстрый ответ службы поддержки может значительно улучшить качество обслуживания их клиентов. (Комм100)
Почти 90 % клиентов доверяют компании, услуги которой они оценивают как «очень хорошие». С другой стороны, только 16% из тех, кто поставил оценку «неудовлетворительно», в той же степени доверяют компаниям. (Qualtrics XM Institute)
70% пути клиента зависит от того, как клиент чувствует, что с ним обращаются. (McKinsey)
53% покупателей считают, что их отзывы не доходят до тех, кто может на них реагировать. (Майкрософт)
Вероятность того, что клиент переключится на конкурента, в четыре раза выше, если его проблема связана с обслуживанием. (Bain and Company)
Почти 90% потребителей доверяют компании, чьи услуги они оценили как «очень хорошие», чтобы удовлетворить их потребности. (Qualtrics XM Institute)
Есть несколько показателей, которые выделяются. Во-первых, большинство клиентов указывают, что получение ответа в течение 10 минут после их запроса необходимо или очень важно — это 9 баллов.3344 чрезвычайно впечатляющий показатель.
В мире, где время первого отклика и разрешение проблемы имеют решающее значение, насколько вы близки к этой 10-минутной отметке? При таком уровне отклика 71% молодых потребителей считают, что их опыт резко улучшился — и дальше все идет как снежный ком.
Когда вы создаете превосходный опыт обслуживания клиентов, вы завоевываете доверие, защищаете себя от того, что клиенты уходят к вашим конкурентам, и уделяете первостепенное внимание тому, чтобы сделать их путешествие приятным.
Вторая захватывающая статистика заключается в том, что более 70% потребителей считают, что компании должны сотрудничать от их имени. Поэтому, если клиент сообщает о проблеме с интеграцией, которую он использует с вашим продуктом, вместо того, чтобы посоветовать ему обратиться в службу поддержки другого продукта, вы вместо этого отвечаете напрямую.
Такой уровень персонализации и внимания к деталям может значительно повлиять на ваших клиентов, как вы увидите в следующем разделе.
Рекомендуемое чтение
Рост и культура Отзывы клиентов: почему это важно + 7 способов их получения
Отзывы клиентов помогают компаниям понять опыт и потребности своего сообщества. Вот способы сбора информации о ваших клиентах
Сила личного контакта
«Если вы нравитесь покупателю — и продолжаете любить вас, — он продолжит иметь с вами дело. Если нет, то не будет». – Пол Гринберг
Каждый хочет чувствовать себя известным. Они хотят верить, что люди в их жизни думают о них, учитывают их и понимают их желания и потребности.
Это распространяется и на ваших клиентов. Если вы сделаете все возможное, чтобы ваши клиенты чувствовали, что их видят, слышат и о них заботятся, это может оказать огромное влияние на их опыт и прибыль вашей компании.
Если вы можете узнать предысторию и историю пользователя перед звонком, интегрируйте это в сеанс обслуживания клиентов. Если вы не углубляетесь и не просматриваете такие вещи, как история продаж или личная информация, по телефону минимум найдите время, чтобы узнать имя клиента.
Прочтите потрясающую статистику обслуживания клиентов, связанную с персонализацией:
70% клиентов говорят, что осведомленность агентов по обслуживанию о взаимодействиях при продажах имеет основополагающее значение для сохранения их бизнеса. (Salesforce)
80% клиентов говорят, что опыт, который предоставляет компания, так же необходим, как и ее продукты или услуги. (Salesforce)
63% потребителей ожидают, что компании будут знать их уникальные потребности и ожидания, в то время как 76% покупателей B2B ожидают того же. (Исследования отдела продаж)
59% клиентов считают, что компаниям необходимо предоставлять передовые цифровые технологии, чтобы сохранить свой бизнес. (Salesforce)
90 % людей с большей вероятностью будут доверять компании, если у них есть твердая политика конфиденциальности. (Salesforce)
Ваш коэффициент онлайн-конверсии может повыситься примерно на 8%, если вы включите персонализированный потребительский опыт. (Trust Pilot)
88% людей доверяют компаниям, которые клянутся не делиться своей личной информацией без разрешения. (Продажи)
92% клиентов ценят компании, предоставляющие им контроль над сбором информации о них. (Salesforce)
23% компаний используют социальные сети как инструмент для сбора и анализа данных. (Gartner)
79 % клиентов готовы поделиться важной информацией о себе в обмен на контекстуализированное взаимодействие, при котором их сразу узнают и понимают. (Salesforce)
56% клиентов не против поделиться своей личной информацией в обмен на лучший сервис. (Продажи)
В среднем агенты по обслуживанию клиентов запрашивают имя клиента только в 21% случаев. (Взгляд)
Как видите, дело не только в том, как вы используете личную информацию клиента, хотя это важно. Многих клиентов волнует, как вы собираете данные и , что вы делаете с ними после того, как они у вас есть.
Более половины клиентов готовы поделиться личной информацией в обмен на отличный сервис, но вам все равно нужно осторожно использовать эти данные. Ведь около 90% клиентов с большей вероятностью будут вам доверять, если у вас будет отличная политика конфиденциальности.
Персонализация помогает построить более глубокие отношения, но только если она сделана правильно. Если это не сделано правильно, вы можете ожидать, что ваши клиенты будут говорить об этом.
Рекомендуем к прочтению
Служба поддержки клиентов Осуществляйте поддержку с помощью данных
Предоставление группам поддержки легкого доступа к релевантным контекстуальным данным повышает качество обслуживания клиентов и делает их более человечными. Вот как это сделать.
Важность молвы
Клиенты любят поговорить. Они поделятся своим хорошим опытом, плохим опытом и всем, что между ними. Точно так же клиенты любят слушать .
Как вы увидите из следующей статистики обслуживания клиентов, многие пользователи доверяют отзывам других клиентов или ответам в социальных сетях больше, чем маркетингу вашей компании.
Предоставление превосходного обслуживания клиентов, особенно в социальных сетях, является огромным благом для маркетинговых усилий вашей компании.
Хотя 50% клиентов не делятся своим опытом в социальных сетях, 72% расскажут о нем лично. Это число становится еще выше, если учесть, как клиенты говорят в социальных сетях о плохих впечатлениях .
Прочтите довольно впечатляющую и шокирующую статистику обслуживания клиентов о том, когда люди делятся или не делятся:
36% потребителей будут делиться своим опытом обслуживания клиентов, хорошим или плохим. Более трети отчетов публикуются в Facebook, за ними следует Instagram. (Группа CFI)
В 2020 году 87% потребителей читают онлайн-отзывы о местных компаниях. (Bright Local)
72% клиентов поделятся своим хорошим опытом с другими. (Salesforce)
72% клиентов расскажут шести или более людям, если они остались довольны. (Эстебан Кольски)
94% американских клиентов порекомендуют компанию, услуги которой они оценивают как «очень хорошие». (Институт Qualtrics XM)
67% клиентов сообщают о том, что плохое качество обслуживания клиентов является причиной смены бизнеса. (Эстебан Кольский)
Только 13% потребителей порекомендуют компанию, обслуживание клиентов которой они оценили как «очень плохое». (Qualtrics XM Institute)
50% клиентов говорят, что они не делятся своими плохими или хорошими впечатлениями об обслуживании через социальные сети. (CFI Group)
33% потребителей порекомендовали бы бренд, который дает быстрый, но неэффективный ответ. (Нильсен-МакКинзи)
78% клиентов, которые жалуются на бренд в Twitter, ожидают ответа в течение часа. (литий)
13% клиентов рассказывают 15 или более людям, если у них есть негативный опыт. (Эстебан Кольский)
79% клиентов, которые делятся своими жалобами в Интернете, видят, что их жалобы игнорируются. (RightNow)
Только 17% потребителей порекомендовали бы бренд, который предлагает медленное, но эффективное решение. (Нильсен-МакКинзи)
Только 1 из 26 клиентов расскажет компании о своем негативном опыте; согласно фактам обслуживания клиентов, остальные просто уходят. (Эстебан Кольски)
Эта статистика о клиентах, уходящих без единого слова, каждый раз ужасает нас! Подумайте, сколько негативных ответов вы получили в опросах CSAT или NPS, а затем умножьте это на 26 — страшно, правда?
К счастью, некоторые довольно современные технологии упрощают предоставление отличной поддержки клиентов и поиск самородков ценной информации по мере того, как вы это делаете.
Рекомендуемая литература
Рост и культура10 Методы сбора данных о клиентах
Самые успешные современные компании понимают своих клиентов на более глубоком уровне. Как? Голос данных Заказчика. Вот 10 способов его собрать.
Выбор правильных каналов поддержки
И телефон, и электронная почта являются проверенными и надежными каналами обслуживания клиентов. Еще в 1960-х годах, когда впервые появились телефонные банки, клиенты привыкли к тому, что у них есть прямая линия поддержки. Затем появилась электронная почта, предоставляющая либо один адрес, либо групповую электронную почту для связи с командами обслуживания клиентов.
Теперь есть живой чат, совместный просмотр, виртуальные видеозвонки, упоминания в социальных сетях и множество новых способов связи с клиентами. Какой из них лучше всего подходит для вашей компании ? Взгляните на диаграмму ниже, чтобы увидеть различные каналы и то, как часто каждый из них используется группами поддержки и клиентами:
У каждого канала есть свои плюсы и минусы. Вот некоторые статистические данные об обслуживании клиентов, которые помогут осветить положительные и отрицательные стороны каждого из них и помогут вам принять решение.
Многоканальная поддержка
Многоканальная поддержка — это непрерывная связь для клиентов между всеми вашими каналами. Фактически это означает, что то, что кто-то делает с командой на любом канале, может беспрепятственно перемещаться на другие каналы с полным контекстом. Например, ваш клиент может начать с живого чата, а затем плавно перейти к телефонному звонку по мере необходимости.
Многоканальная поддержка обеспечивает превосходный опыт для клиентов, поскольку это означает, что им никогда не придется заново объяснять то, что они уже сказали другому члену вашей команды. Когда все сделано правильно, это может показаться волшебством:
75 % клиентов хотят постоянного взаимодействия, независимо от того, как они взаимодействуют с компанией (через социальные сети, лично, по телефону и т. д.). (Salesforce)
Эффективность ботов в решении вопросов упала до 28%. Американские потребители не считают ботов эффективными: 40% полагаются на другие каналы связи с сервисными службами. (Microsoft)
64% клиентов хотят делать покупки в компаниях, которые могут удовлетворить их потребности в режиме реального времени. (Продажи)
64 % групп обслуживания клиентов используют порталы для клиентов по сравнению с 84 % клиентов, которые используют порталы для клиентов. (Salesforce)
Как вы можете заметить, своевременность, возможность использования нескольких каналов и согласованность являются основными преимуществами многоканальности.
Рекомендуемая литература
Обслуживание клиентов13 лучших программных платформ для обслуживания клиентов на 2022 год
Если вашей команде пора внедрить программное обеспечение для обслуживания клиентов, это руководство расскажет вам, что вам нужно знать, чтобы сделать правильный выбор.
Поддержка по телефону
Поддержка по телефону — одна из старейших форм помощи. С момента изобретения дискового телефона как компании, так и клиенты зависели от этой ценной и надежной технологии. Давайте взглянем на некоторую статистику обслуживания клиентов в командах, использующих телефоны:
Исследование показало, что более 76% всех потребителей предпочитают традиционный способ телефонных звонков, чтобы связаться с представителями службы поддержки. (Группа CFI)
Более 50% клиентов всех возрастных групп обычно используют телефон для связи со службой поддержки, что делает его наиболее часто используемым каналом обслуживания клиентов. (Zendesk)
63 % групп обслуживания клиентов используют текстовые сообщения, по сравнению с 78 % клиентов, которые используют текстовые сообщения для связи с компанией. (Salesforce)
51 % групп обслуживания клиентов используют мобильные приложения по сравнению с 82 % клиентов, которые используют мобильные приложения для общения с компанией. (Продажи)
Несмотря на то, что группы поддержки широко используют традиционную поддержку по телефону, кажется, что есть некоторые инструменты, которые они могли бы использовать больше. Например, количество клиентов, предпочитающих текстовые сообщения и мобильные приложения, по сравнению с количеством групп обслуживания клиентов, которые их используют, оставляет желать лучшего.
Поддержка по телефону проверена временем, но возможности, доступные через мобильные телефоны , кажутся новыми границами.
Основы отличного обслуживания
Откройте для себя инструменты и методы, используемые высокоэффективными организациями по обслуживанию клиентов, в нашем бесплатном видеокурсе из шести частей.
Зарегистрируйтесь бесплатно
Поддержка самообслуживания
Документация полезна для помощи клиентам без необходимости вмешательства вашей службы поддержки клиентов. Например, клиент может искать в вашей базе знаний и находить ответы в течение нескольких минут, что в долгосрочной перспективе гораздо лучше, чем ждать ответа в электронной почте или в очереди в чате.
Однако, к сожалению, если документация ведется некачественно, это может принести больше вреда, чем пользы. Вот некоторые статистические данные по обслуживанию клиентов, в которых исследуются как положительные, так и отрицательные стороны ваших справочных документов:
28% потребителей говорят, что самая неприятная проблема — это информация, которая проста, но ее трудно найти. (Drift)
69% потребителей сначала пытаются решить свою проблему самостоятельно, но менее трети компаний предлагают варианты самообслуживания, такие как база знаний. (Зендеск)
Клиенты предпочитают базы знаний всем другим каналам самообслуживания. (Forrester)
Базы знаний используют 66 % групп обслуживания клиентов по сравнению с 82 % клиентов, использующих базы знаний. (Salesforce)
Как видите, большинство клиентов предпочли бы использовать базу знаний/документацию для решения своих проблем, но они не всегда могут их найти. Немногие компании приложили усилия для создания документации, баз знаний или других вариантов, с помощью которых клиенты могли бы обслуживать себя.
Рекомендуемая литература
Служба поддержки клиентов11 лучших программных платформ базы знаний на 2022 год
Узнайте, какую пользу программное обеспечение базы знаний может принести вашему бизнесу, и откройте для себя 11 различных вариантов, которые можно рассмотреть для вашей команды.
Поддержка социальных сетей
Несмотря на роль социальных сетей как места для общения с друзьями и коллегами, многие предприятия и потребители также используют их для связи.
Функциональность, такая как обмен сообщениями в Facebook и Instagram, упростила для пользователей прямую связь с брендами более осмысленным и аутентичным способом, чем раньше. Из-за этого многие компании стремятся усилить свое присутствие в этих средах.
Эти две статистические данные по обслуживанию клиентов в социальных сетях позволяют легко понять, почему:
79% американских интернет-пользователей используют Facebook, что делает его самой популярной платформой социальных сетей. (Lyfe Marketing)
95% взрослых в возрасте от 18 до 34 лет, скорее всего, следят за брендом через каналы социальных сетей. (MarketingSherpa)
Подумайте, со всеми ли людьми ваш бренд мог бы связаться, если бы вы переключились на обслуживание клиентов через каналы социальных сетей?
Рекомендуемая литература
Обслуживание клиентовУправление обслуживанием клиентов в социальных сетях: стратегии и советы
Разработайте процесс управления обслуживанием клиентов в социальных сетях, который наилучшим образом соответствует вашим бизнес-целям, бюджету, ресурсам и опыту работы с клиентами.
Поддержка в чате
Чат в первую очередь считается самым быстрым способом получения поддержки потребителями. Это кажется немедленным, часто может быть реализовано с помощью автоматизации и не всегда требует большой пропускной способности для персонала. Точно так же многие молодые потребители предпочитают его более традиционным технологиям, таким как телефоны.
Если вы еще не внедрили чат в своей команде, вот две статистические данные по обслуживанию клиентов, которые могут помочь вам понять, будет ли это хорошим шагом:
Миллениалы предпочитают живой чат для обслуживания клиентов любому другому каналу связи. (Comm100)
52% групп обслуживания клиентов используют онлайн-чат или поддержку в режиме реального времени, по сравнению с 81% клиентов, которые используют онлайн-чат или поддержку в режиме реального времени для общения с компанией. (Продажи)
Клиентов, которые предпочитают использовать чат, гораздо больше, чем компаний, которые его предлагают! Если у вас есть ресурсы для его реализации, чат может стать отличной возможностью встретиться с вашими клиентами там, где они есть. Обратите внимание: если ваши клиенты ищут онлайн-чат, а вы его не предлагаете, это может еще больше их разочаровать.
Рекомендуем к прочтению
Служба поддержки клиентов11 лучших инструментов интерактивного чата для поддержки клиентов
Если вы планируете добавить чат в свой набор каналов поддержки, начните поиск с просмотра этого списка из 11 лучших инструментов живого чата.
Работа с разгневанными клиентами
«Наше отношение к другим определяет их отношение к нам». –Эрл Найтингейл
Гнев – широко распространенная эмоция, которую чрезвычайно трудно контролировать. Например, треть людей, принявших участие в опросе о гневе, отметили, что у них или у кого-то из их знакомых были серьезные проблемы с контролем своего гнева.
Неудивительно, что многие из ваших клиентов, которые уже находятся в стрессовой ситуации и нуждаются в помощи, могут рассердиться во время взаимодействия.
Гнев может быть пугающим, но когда вы понимаете, откуда он берется и почему это происходит, с ним становится легче совладать. Например, многим членам команды обслуживания клиентов было бы полезно напомнить себе, что клиент зол на ситуацию, которая привела их к взаимодействию, а не на само взаимодействие.
Еще несколько напоминаний о гневе в контексте обслуживания клиентов и о том, как определенное поведение может привести к более глубокому гневу клиентов, ознакомьтесь со следующей статистикой обслуживания клиентов:
21% людей, ожидающих в больничной аптеке, решили получить рецепт в другом месте, потому что им пришлось ждать слишком долго. (Sage Journals)
Почти 70% клиентов раздражаются, когда их звонок переводится из одного отдела в другой. (Zendesk)
Ощущение, что вас не ценят, — основная причина, по которой клиенты переключаются на продукты и услуги. (New Voice Media)
33% клиентов больше всего недовольны тем, что им приходится ждать на линии ожидания, а 33% больше всего недовольны тем, что им приходится повторяться с несколькими представителями службы поддержки. (Исследование HubSpot)
70% недовольных клиентов, чьи проблемы были решены, готовы снова делать покупки в компании. (Взгляд)
Почти 60 % клиентов считают, что долгие ожидания и задержки являются наиболее неприятными моментами в обслуживании. (Zendesk)
62% клиентов предпочли бы «раздать парковочные талоны», чем ждать обслуживания в автоматизированном телефонном дереве или повторять свои действия несколько раз разным членам команды. (концентратор)
35% клиентов разозлились, разговаривая со службой поддержки. (American Express)
27% американцев сообщают, что неэффективное обслуживание является для них главным разочарованием в обслуживании клиентов. (Statista)
12% американцев оценивают свое разочарование в обслуживании как «отсутствие скорости». (Statista)
72% клиентов говорят, что объяснение своих проблем нескольким людям является плохим обслуживанием клиентов. (Измерительные исследования)
79% потребителей, которые использовали онлайн-отзывы, чтобы пожаловаться на плохое обслуживание клиентов, были проигнорированы. (Harris Interactive)
84% клиентов сообщают, что их ожидания не были превышены при последнем взаимодействии со службой поддержки. (Harvard Business Review)
78% клиентов отказались от транзакций из-за отрицательного клиентского опыта. (American Express)
67% клиентов разочарованно заканчивают разговор, когда не могут связаться с представителем службы поддержки клиентов. (Взгляд)
Большая часть недовольства клиентов возникает из-за ожидания или необходимости повторяться. Какими способами вы могли бы ускорить взаимодействие со службой поддержки или предоставить членам команды дополнительный контекст для работы над этими двумя распространенными проблемами?
Внедрение некоторых процессов может помочь вам в работе со статистикой обслуживания клиентов в будущем. Упреждающее решение проблем и разочарований клиентов до того, как они возникнут, является признаком действительно высокоэффективной организации обслуживания клиентов.
Рекомендуем к прочтению
Служба поддержки Как расстаться с оскорбительными клиентами
Когда оскорбительный клиент делает жизнь вашей службы поддержки невыносимой, пришло время отпустить его. Вот учебник.
Служба поддержки клиентовКак уволить клиента (правильный способ) за 5 шагов
Увольнение клиента — важное деловое решение, требующее большой вдумчивости и такта
Служба поддержки клиентовКак работать с трудными клиентами
Каждый сотрудник службы поддержки должен знать, как работать с трудными клиентами. Узнайте о типах трудных клиентов и о том, как им помочь.
Создание команды поддержки мирового класса
«В эпоху, когда компании рассматривают онлайн-поддержку как способ оградить себя от «дорогостоящих» взаимодействий со своими клиентами, пришло время рассмотреть совершенно другой подход: создание клиентоориентированного подхода. обслуживание с помощью замечательных людей и умных технологий. Итак, познакомьтесь со своими клиентами. Очеловечить их. Очеловечить себя. Это стоит того.» – Кристин Смоби
Независимо от того, сколько мы говорим о гневе, расстройстве или разочаровании, факт остается фактом: команды обслуживания клиентов делают основную тяжесть работы, чтобы ваши клиенты были счастливы и успешны.
К сожалению, обслуживание клиентов часто считается последним, когда речь идет о политике компании, обмене информацией или расширении возможностей команд. Однако, если эта статистика что-то и показала, так это то, что обслуживание клиентов важно и ценно для ваших клиентов.
Вот некоторые из лучших практик, которые применяют лучшие в своем классе специалисты по обслуживанию клиентов, и то, как это заставляет их клиентов чувствовать:
75% потребителей по-прежнему предпочтут взаимодействовать с реальным человеком, даже несмотря на совершенствование технологии автоматизированных решений. (PwC)
Треть всех потребителей считают, что наиболее важным аспектом качественного обслуживания клиентов является решение их проблемы за одно взаимодействие, независимо от количества затраченного времени. (Statista)
88% высокоэффективных лиц, принимающих решения в сфере обслуживания, вкладывают значительные средства в обучение агентов по сравнению с 57% неэффективных сотрудников. (Продажи)
83% высокоэффективных сервисных агентов говорят, что они проходят обучение, необходимое им для качественного выполнения своей работы, по сравнению с 52% неэффективных сотрудников. (Salesforce)
69% высокоэффективных агентов по обслуживанию активно ищут ситуации для использования искусственного интеллекта (ИИ) по сравнению только с 39% неэффективных сотрудников. (Salesforce)
Подавляющее число 95% потребителей говорят, что обслуживание клиентов имеет важное значение для лояльности к бренду, а 60% потребителей сообщают, что отказались от бренда и переключились на конкурирующую компанию из-за плохого обслуживания клиентов. (Майкрософт Динамика 365)
Похоже, что основным фактором, определяющим эффективность, является соответствующее обучение и доверие компании, и потребители замечают разницу. Когда вы заботитесь о своих сотрудниках и обеспечиваете их необходимыми инструментами, они могут лучше заботиться о ваших клиентах.
Рекомендуемая литература
Служба поддержки клиентов Как создать успешную группу поддержки и отдел с нуля
Выполните следующие 7 основных шагов, чтобы создать совершенно новый отдел поддержки или добиться максимального успеха существующей команды поддержки клиентов.
Забота о вашей команде поддержки
«Вот простое, но мощное правило: всегда давайте людям больше, чем они ожидают получить». – Нельсон Босуэлл
Бизнес меняется. Многие компании понимают, что их лучших сотрудников могут переманить и уволить в другое место за большей оплатой и, возможно, лучшим опытом работы. Поэтому очень важно расставить приоритеты в потребностях членов вашей команды обслуживания клиентов и учитывать их приоритеты.
Ниже приведены некоторые статистические данные по обслуживанию клиентов, которые подчеркивают, насколько важен уровень обслуживания, которое вы предоставляете:
В сфере обслуживания клиентов самая высокая текучесть кадров среди всех предприятий. По статистике колл-центров этот показатель достигает 45%! (QATC)
По оценкам Института человеческих ресурсов, текучесть кадров стоит около 10-15 тысяч долларов для рядового сотрудника. (QATC)
Большинство представителей по обслуживанию клиентов не планируют оставаться на этой работе вечно, так как часто у них мало возможностей для роста. 31% потребителей считают, что компетентный агент является наиболее важным фактором для положительного клиентского опыта. (Томаснет)
Поскольку 77% потребителей сегодня считают трудность связаться с агентом самой большой проблемой обслуживания клиентов, стоит инвестировать в ее решение. (Review42)
89% компаний с качеством обслуживания клиентов «значительно выше среднего» работают лучше в финансовом отношении, чем их конкуренты. (Qualtrics XM Institute)
Отличная поддержка клиентов также дает долгосрочные результаты. 24% потребителей продолжают иметь дело с поставщиками в течение двух или более лет после положительного знакомства. (Зендеск)
64% потребителей в США обращались в службу поддержки в 2017 году. (Аспект)
73% клиентов говорят, что они остаются лояльными к брендам благодаря дружелюбным агентам по обслуживанию клиентов. (HubSpot)
73% клиентов влюбляются в бренд из-за дружелюбных представителей службы поддержки. (RightNow)
Рассмотрим эти статистические данные и представьте, что в начале года у вас есть шесть сотрудников. К концу года двое или трое из них, скорее всего, уйдут. Это от 30 до 45 тысяч долларов на расходы на 9 человек.3344 потеряли сотрудников, которые, вероятно, отлично справлялись со своей работой.
Как мы знаем, хорошие специалисты по обслуживанию клиентов могут укреплять или разрушать отношения с клиентами, поэтому чрезвычайно важно отдавать предпочтение людям, которые хорошо работают.
Подумайте, в чем больше нуждается ваша служба поддержки клиентов, и попытайтесь найти способы предложить это. Затем поговорите непосредственно с членами вашей команды об изменениях, которые вы внесли, и о том, как они повлияли на качество их жизни. Спросите их мнение, внимательно выслушайте, а затем реализуйте то, что можете.
Создание лучшей рабочей среды для ваших агентов создаст превосходную среду для ваших клиентов.
Рекомендуемая литература
Служба поддержки клиентовКак создать сильную культуру обслуживания клиентов
Узнайте о стратегиях, которые руководители, руководители службы поддержки и агенты службы поддержки могут использовать для создания и поддержания сильной культуры обслуживания клиентов компании.
Воздействие COVID-19
Хотя говорить о COVID-19 больно, наша жизнь изменилась из-за пандемии и связанных с ней последствий. Говоря о здоровой среде для сотрудников, уместно не упомянуть о влиянии COVID-19 наимеет на индустрии обслуживания клиентов.
Основные тенденции заключаются в том, что клиентам становится все труднее угодить, они с большей готовностью переключаются на компанию, которая соответствует их потребностям, и значительно менее терпеливы. Мы не можем их винить!
Однако, учитывая эти изменения, вашей команде по обслуживанию клиентов может потребоваться изменить свои стратегии, чтобы напрямую решать проблемы, которые возникают у клиентов в этом новом мире (все следующие статистические данные взяты из HBR):
Типичный уровень сложности звонков колеблется от 10% до 20%, но пандемия ухудшила статистику клиентского опыта.
В среднем по компании процент звонков, оцененных торговыми представителями как «сложные», увеличился более чем на 100%.
Было больше неожиданных отмен поездок, просьб о продлении срока оплаты счетов, споров о страховом покрытии и других звонков, вызванных беспокойством, чем когда-либо в истории.
Статистика обслуживания клиентов за 2020 год показывает, что торговые представители считают, что их работа намного сложнее и менее приятна.
В некоторых компаниях, участвовавших в исследовании, время ожидания увеличилось на 34%, а число эскалаций увеличилось более чем на 68%, что еще раз подчеркивает влияние обслуживания клиентов на бизнес.
Одна из компаний, занимавшихся исследованием искусственного интеллекта Tethr, предоставила статистику обслуживания клиентов, которая показала, что сложные взаимодействия с вероятностью 6% приводят к дополнительным или перекрестным продажам. Шансы обычно составляют 80%, когда качество обслуживания клиентов превосходно.
Только около 4% клиентов, которые уходят или угрожают уйти, соглашаются остаться, принимая промо, по сравнению со средним показателем в 20% в прошлом.
COVID-19 повлиял не только на рабочую среду и эмоции сотрудников, но и на клиентов. Клиенту, который выгорел и измотан, гораздо сложнее установить контакт и решить проблемы, чем клиенту, который чувствует себя в безопасности и доволен.
К сожалению, COVID-19 ставит всех в стрессовое положение, делая бесконечно трудным общение на человеческом уровне и удовлетворение потребностей клиентов через поддержку.
Рекомендуемая литература
Ключевые показатели эффективности обслуживания клиентов и деловая практика во время коронавируса
Узнайте, как быть более человечным в разгар и после глобальной пандемии и как изменить свои стратегии и тактики, чтобы приспособиться к новым нормам.
Надеемся, что вся эта статистика обслуживания клиентов дала вам много информации для размышления и обработки. Есть много разных точек зрения и вариантов для оценки, но независимо от того, что вы вынесли из этого поста, мы уверены, что вы согласитесь с этим: обслуживание клиентов имеет важное значение.
Это не только важно, но и ценно для вашей прибыли и служит решающим отличием вашей компании от других.
Если вы относитесь к каждому взаимодействию как к способу узнать и полюбить своих клиентов, ваша команда в кратчайшие сроки обеспечит превосходное обслуживание клиентов.
Ответные псалмы — для вашего брака
Существует 7 вариантов ответного псалма на брачной мессе. Мы рекомендуем вам провести время в молитве со своим женихом/невестой, чтобы выбрать псалом, который лучше соответствует вашим надеждам и мечтам о вашем браке. Христианский брак.
Земля полна благости Господней (Псалом 33)
Я благословлю Господа во все времена (Псалом 34)
Господь добр и милостив (Псалом 102)
Блажен человек, весьма любящий заповеди Господни (Псалом 112)
Блаженны боящиеся Господа (Псалом 128)
Как благ Господь ко всем (Псалом 145)
Да хвалят все имя Господне (Псалом 148)
1. Псалом 33:12 и 18, 20-21, 22
Р. (5б) Земля полна благости Господней.
Благословен народ, чей Бог есть Господь,
народ, которого он избрал своим наследием.
Да, очи Господа на боящихся Его,
уповающих на Его милостивую любовь.
Р. Земля полна благости Господней.
Душа наша Господа ждет,
Он нам помощь и щит наш,
в Нем находят радость наши сердца.
Мы верим в его святое имя.
Р. Земля полна благости Господней.
Да пребудет с нами Твоя милосердная любовь,
как мы надеемся на Тебя, Господи.
Р. Земля полна благости Господней.
2. Псалтирь 33:2-3, 4-5, 6-7, 8-9
Р. (2а) Благословлю Господа во всякое время.
ИЛИ:
Р. (9а) Вкусите и увидите благость Господню.
Я буду благословлять Господа во все времена;
хвала ему всегда у меня на устах.
Господом будет хвалиться душа моя;
смиренные услышат и возрадуются.
Р. Я благословлю Господа во все времена.
ИЛИ:
R. Вкусите и увидите благость Господа.
Прославим Господа со мною,
вместе прославим имя Его.
Я искал Господа, и Он ответил мне
от всех моих ужасов он освободил меня.
Р. Я благословлю Господа во все времена.
OR:
R. Вкусите и увидите благость Господа.
Взгляни на него и сияй;
да не смущаются ваши лица.
Этот скромный звонил; Господь услышал,
и избавил его от всех его бед.
Р. Я благословлю Господа во все времена.
ИЛИ:
R. Вкусите и увидите благость Господа.
Ангел Господень расположился станом
вокруг тех, кто боится его, чтобы спасти их.
Вкусите и увидите, как благ Господь.
Благословен тот, кто ищет в нем убежища.
Р. Я благословлю Господа во все времена.
ИЛИ:
R. Вкусите и увидите благость Господа.
3. Псалом 102:1-2, 8 и 13, 17-18а
Р. (8а) Господь добр и милостив.
ИЛИ:
R. (см. 17) Милость Господа вечна к боящимся Его.
Благослови, душа моя, Господа;
и все во мне, его святое имя.
Благослови Господа, душа моя,
и никогда не забывай всех Его благ.
Р. Господь добр и милостив.
ИЛИ:
R. Милость Господа вечна к боящимся Его.
Господь сострадателен и милостив,
медлен на гнев и богат милостью.
Как отец жалеет своих детей,
так жалеет Господь боящихся Его.
Р. Господь добр и милостив.
ИЛИ:
Р. Милость Господа вечна к боящимся Его.
Но милость Господа вечна
на тех, кто боится Его,
на детей детей правды Его,
на тех, кто соблюдает завет Его.
Р. Господь добр и милостив.
ИЛИ:
R. Милость Господа вечна к боящимся Его.
4. Псалом 112:1bc-2, 3-4, 5-7a, 7b-8, 9
R. (см. 1) Благословен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя.
Блажен муж, боящийся Господа,
находящий большое удовольствие в заповедях Его.
Его потомки будут сильными на земле;
поколение праведных будет благословлено.
R. Блажен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя.
Богатство и богатство в его доме;
Его праведность будет стоять вечно.
Свет восходит во тьме для правых;
он щедрый, милосердный и праведный.
R. Блажен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя.
Хорошо идет тому, кто щедро торгует и дает взаймы,
кто ведет свои дела справедливо.
Его никогда не тронут;
навеки будут помнить праведников.
Он не боится плохих новостей.
R. Благословен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя.
С твердым сердцем он уповает на Господа.
С твердым сердцем он не убоится;
он увидит крушение своих врагов.
R. Блажен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя.
Щедрый, он дает бедным;
его праведность стоит навеки.
Его могущество возвысится во славе.
R. Блажен человек, который очень любит заповеди Господа.
ИЛИ:
Р. Аллилуйя. (см. 1а) Блаженны боящиеся Господа.
ИЛИ:
р. (4) Посмотрите, как Господь благословляет боящихся Его.
Блаженны все боящиеся Господа,
и ходящие путями Его!
Трудом рук твоих будешь есть.
Вы будете благословлены и преуспеете.
R. Блаженны боящиеся Господа.
OR:
R. Посмотрите, как Господь благословляет боящихся Его.
Твоя жена подобна плодоносной лозе
в сердце твоего дома;
Ваши дети любят побеги оливы.
вокруг вашего стола.
R. Блаженны боящиеся Господа.
OR:
R. Посмотрите, как Господь благословляет боящихся Его.
Воистину так будет благословлен
человек, который боится Господа.
Да благословит тебя Господь с Сиона:
во все дни жизни твоей!
Увидишь ли ты детей своих детей.
R. Блаженны боящиеся Господа.
OR:
R. Посмотрите, как Господь благословляет боящихся Его.
6. Псалом 145:8-9, 10 и 15, 17-18
Р. (9а) Как благ Господь ко всем.
Господь добр и сострадателен,
медлен на гнев, многомилостив.
Как благ Господь ко всем,
сострадателен ко всем созданиям Своим.
Р. Как благ Господь ко всем.
Все твои дела будут благодарны тебе, Господи,
и все твои верные благословят тебя.
Глаза всех смотрят на тебя
и ты даешь им пищу в свое время.
Р. Как благ Господь ко всем.
Господь праведен во всех путях Своих
и свят во всех делах Своих.
Близок Господь ко всем призывающим Его,
кто взывает к нему в истине.
Р. Как благ Господь ко всем.
7. Псалтирь 147:1-2, 3-4, 9-10, 11-13а, 13в-14а
Р. (13а) Да хвалят все имя Господне.
ИЛИ:
Р. Аллилуйя.
Хвалите Господа с небес,
хвалите Его в высотах;
Хвалите его, все ангелы его,
хвалите его, все воинства его.
Р. Да хвалят все имя Господне.
ИЛИ:
Р. Аллилуйя.
Хвалите его, солнце и луна;
хвалите его, все вы, сияющие звезды.
Хвалите его, вы, высочайшие небеса,
и вы, воды выше небес.
No related posts.
Навигация по записям
Предыдущая статьяОнлайн калькулятор с корнями и дробями и степенями: Калькулятор корней онлайн
Следующая статьяПрактическая работа текстовый редактор: Текстовый редактор. Практические работы. | Материал по информатике и икт (10 класс) на тему:
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта