Урок 24. вычисление площадей с помощью интегралов — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №24. Вычисление площадей с помощью интегралов.
Перечень вопросов, рассматриваемых в теме
1) Нахождение площади фигуры, ограниченной графиками функций с помощью определенного интеграла.
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
Формула Ньютона – Лейбница
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.
Теоретический материал для самостоятельного изучения
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
формула Ньютона – Лейбница
Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым. ( зависит от расположения криволинейной трапеции)
Примеры и разбор решения заданий тренировочного модуля
№1 Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2, используя определенный интеграл.
Решение. Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b).
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ
№2. Найти площадь фигуры, ограниченной линиями у=4-х2,у=3х, у=0 и находящейся в 1-й четверти.
Решение: Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а) , это и будет ответ.
Решение. S=SOAB +SABC
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а) .
Рассчитываем разность F(b) — F(а), это и будет ответ.
Вычисление площадей фигур, ограниченных заданными линиями
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃаb f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃаb f(x)dx.
Таким образом, S(G) = ʃаb f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃаb f(x)dx.
Пример 1.
Вычислить площадь фигуры, ограниченной линиями у = х
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃаb f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х3,
{у = 1.
Таким образом, имеем х1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = SDACE – SDABE = ʃ12 x3 dx – 1 = x4/4|12 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃаb(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫49 (√x – 2)dx = ∫49 √x dx –∫49 2dx = 2/3 x√х|49 – 2х|49 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
ед.).
Ответ: S = 2 2/3 кв. ед.
Пример 3.
Решение.
Построим график функции у = х3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции уmin = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х3 – 4х = 0 или х(х2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х1 = 0, х2 = 2, х3 = -2 (не подходит, т.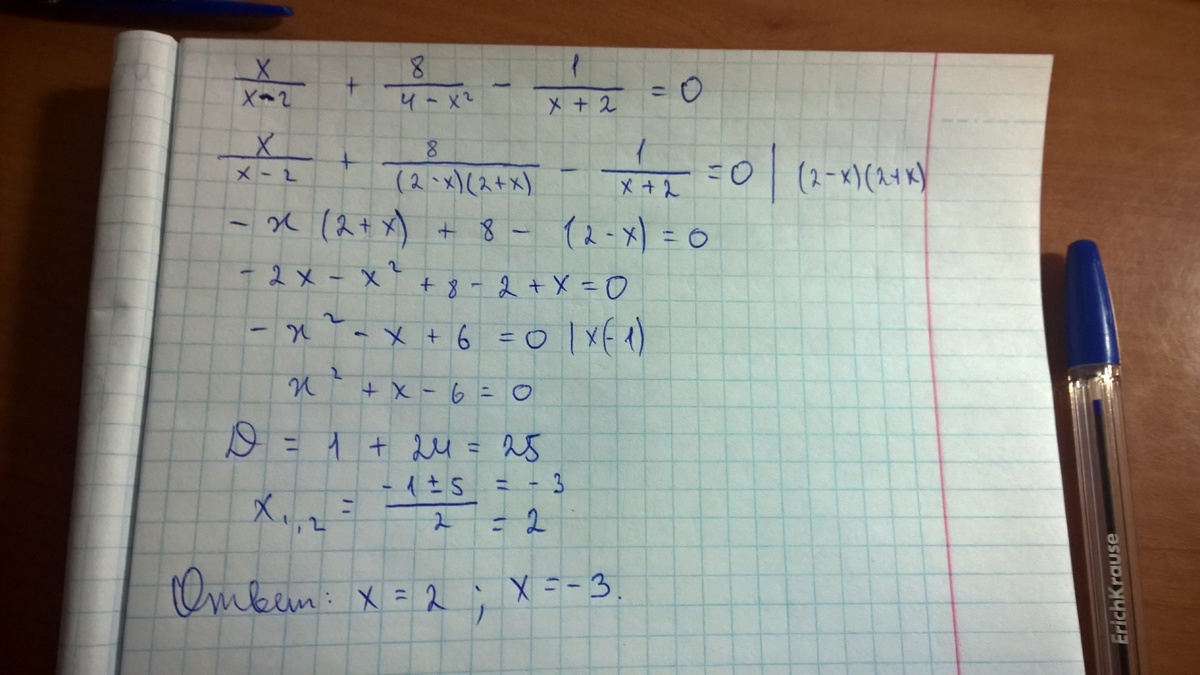 к. х ≥ 0).
к. х ≥ 0).
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ02 (x3 – 4x)dx|.
Имеем: ʃ02 (x3 – 4х)dx =(x4/4 – 4х2/2)|02= -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у0 = 2 · 22 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Гу = 2х2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х2 – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:
xb = -b/2a;
xb = 2/4 = 1/2;
yb = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: SОAВD = SOABC – SADBC.
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле SADBC = 1/2 · DC · BC. Таким образом,
SADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
Далее:
SOABC = ʃ02(2x2 – 2х + 1)dx = (2x3/3 – 2х2/2 + х)|02 = 10/3 (кв. ед.).
Окончательно получим: SОAВD = SOABC – SADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Уравнения 5 класса | Математика
Сегодня мы рассмотрим более сложные уравнения 5 класса, содержащие несколько действий. Чтобы найти неизвестную переменную, в таких уравнениях надо применить не одно, а два правила.
1) x:7+11=21
Выражение, стоящее в левой части — сумма двух слагаемых
| x:7 | + | 11 | = | 21 |
| 1сл. | 2сл. | сум. |
Таким образом, переменная x является частью первого слагаемого. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:
x:7=21-11
x:7=10
Получили простое уравнение 5 класса, из которого надо найти неизвестное делимое. Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
x=10∙7
x=70
Ответ: 70.
2) 65-5z=30
Правая часть уравнения представляет собой разность:
| 65 | — | 5z | = | 30 |
| ум. | в. | р. |
Переменная z является частью неизвестного вычитаемого. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:
5z=65-30
5z=35
Получили простое уравнение, в котором z — неизвестный множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
z=35:5
z=7
Ответ: 7.
3) 120:y-23=17
В правой части уравнения — разность. Переменная y является частью неизвестного уменьшаемого.
Переменная y является частью неизвестного уменьшаемого.
| 120:y | — | 23 | = | 17 |
| ум. | в. | р. |
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:
120:y=17+23
120:y=40
Здесь y — неизвестный делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное:
y=120:40
y=3
Ответ: 3.
4) (48+k)∙8=400
Левая часть уравнения представляет собой произведение. Переменная k — часть первого множителя:
| (48+k) | · | 8 | = | 400 |
| 1мн | 2мн | пр |
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:
48+k=400:8
48+k=50
В новом уравнении k — неизвестное слагаемое:
k=50-48
k=2
Ответ: 2.
Здесь мы решали уравнения 5 класса без использования свойств сложения и вычитания. В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще.
Ранговые бои: сезон X. Оцените новый формат! | Игровые события
Общий обзор
Сезон X — это отдельное игровое событие. Оно не связано с предстоящим циклом Ранговых боёв 2021–2022 и пройдёт в тестовом формате. В нём нет ранговых жетонов или годовых наград, однако для вас это возможность поучаствовать в режиме, оставить свой отзыв и помочь нам принять решение о будущем Ранговых боёв. При этом вы сможете получить отличные награды за сам сезон X.
Присоединяйтесь к этому экспериментальному игровому событию и поделитесь своим мнением в опроснике. Это очень важно для нас!
Во время проведения тестового сезона в каждой команде будет по 10 машин вместо 15. Мы сократили количество игроков в командах, чтобы усилить акцент на соревновательном формате Ранговых боёв. Это повысит важность ваших личных игровых навыков и увеличит ваше влияние на исход каждого отдельного боя. Кроме того, уменьшение количества игроков позволит:
Это повысит важность ваших личных игровых навыков и увеличит ваше влияние на исход каждого отдельного боя. Кроме того, уменьшение количества игроков позволит:
- дать командам больше пространства для манёвра и использования различных тактик;
- уменьшить плотность боя и увеличить его среднюю продолжительность;
- повысить важность командного взаимодействия.
Тестовый сезон продлится две недели вместо обычных трёх, и завершится 12 июля. Сокращение продолжительности сезона сделает бои ещё более напряжёнными. Ценность каждой победы будет выше, так что у игроков появится дополнительная мотивация выкладываться по максимуму и сражаться до последнего в каждом бою!
Эти изменения также повлияют и на балансировщик. Во время игрового события в команде может быть не более одной САУ и двух лёгких танков.
Всё это дополнительно подчеркнёт соревновательный характер режима, который всегда был самым важным компонентом Ранговых боёв. Теперь ваш вклад в победу команды станет более значимым и ценным.
Теперь ваш вклад в победу команды станет более значимым и ценным.
Несмотря на тестовый формат, в сезоне X вы сможете зарабатывать очки Боевого пропуска:
| Позиция в своей команде по итогам боя | Победа | Поражение/ничья |
| Топ-3 по опыту | 7 | 5 |
| Топ-7 по опыту | 5 | 3 |
вопросов по алгебре с решениями и пояснениями для 9 класса
Представлены подробные решения и полные пояснения к вопросам алгебры 9 класса.
|
Дополнительные ссылки и ссылки
Математика для средней школы (6, 7, 8, 9 классы) — Бесплатные вопросы и проблемы с ответамиМатематика для средней школы (10, 11 и 12 классы) — Бесплатные вопросы и проблемы с ответами
Начальная математика (4 и 5 классы) с бесплатными вопросами и проблемами с ответами Домашняя страница
пожаловаться на это объявление Предварительное вычисление алгебры
— Решите уравнение $ | 2x ^ 2 + x-1 | = | x ^ 2 + 4x + 1 | $
предварительное вычисление алгебры — Решите уравнение $ | 2x ^ 2 + x-1 | = | x ^ 2 + 4x + 1 | $ — Обмен стеков математикиСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 559 раз
$ \ begingroup $ Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме форума Mathematics Stack Exchange. 2 + 4x + 1 |
2 + 4x + 1 |
Хотя я пытался решить ее на desmos.com и получил требуемый ответ, но при решении вручную это становится очень длинным.
Я попытался построить две параболы и зеркальное отображение области ниже оси y, но все еще усложняется.
Эрик ВофсиЕсть ли простой способ решить эту проблему и получить сумму всех решений?
271k2121 золотой знак315315 серебряных знаков500500 бронзовых знаков
Создан 01 июл.
Самар Имам ЗаидиСамар Имам Заиди5,79833 золотых знака1111 серебряных знаков3636 бронзовых знаков
$ \ endgroup $ 4 $ \ begingroup $ Нас спрашивают сумму корней; нам не обязательно искать корни. 2-4x-1 $$
2-4x-1 $$
Создан 01 июля ’19 в 15: 5
-07-01 15:59 ПитерПитер75.2-3x-2 = 0. $$
Затем Виета,
$$ — \ frac53 + 3. $$
Для полной строгости следует показать, что ни один корень не повторяется. Это правда, потому что у многочленов нет двойного корня, а их $ \ text {gcd} $ равен $ 1 $.
Создан 01 июл.
Ив ДаустИв Дауст1k1414 золотых знаков120120 серебряных знаков306306 бронзовых знаков
$ \ endgroup $ $ \ begingroup $$ | 2x ^ 2 + x-1 | = | x ^ 2 + 4x + 1 | \\ (2x ^ 2 + x-1) ^ 2 = (x ^ 2 + 4x + 1) ^ 2 \\ (2x ^ 2 + x-1) ^ 2- (x ^ 2 + 4x + 1) ^ 2 = 0 \\ [(2x ^ 2 + x-1) + (x ^ 2 + 4x + 1)] \ cdot [(2x ^ 2 + x-1) — (x ^ 2 + 4x + 1)] = 0 \\ (3x ^ 2 + 5x) \ cdot (x ^ 2-3x-2) = 0 \\ х \ cdot (3x + 5) \ cdot (x ^ 2-3x-2) = 0 \\ Решая \ space for \ space all \ space case, \ space мы \ space получаем: \\ х = 0 \\ x = — \ frac {5} {3} \\ x = \ frac {3 \ pm \ sqrt {17}} {2}
$ Создан 01 июл. 2-3x-2) = 0 $$
Решения задаются формулой $$ x = — \ frac {5} {3} \ lor x = 0 \ lor x = \ frac {1} {2} \ left (3- \ sqrt {17} \ right) \ lor
x = \ frac {1} {2} \ left (3+ \ sqrt {17} \ right) $$
2-3x-2) = 0 $$
Решения задаются формулой $$ x = — \ frac {5} {3} \ lor x = 0 \ lor x = \ frac {1} {2} \ left (3- \ sqrt {17} \ right) \ lor
x = \ frac {1} {2} \ left (3+ \ sqrt {17} \ right) $$
Создан 01 июл.
$ \ endgroup $ 1 Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
полиномов: объединение «похожих» терминов | Purplemath
Purplemath
Вероятно, наиболее распространенная вещь, которую вы будете делать с многочленами, — это «комбинировать одинаковые термины».Это процесс сложения любых терминов, которые вы можете, но не переусердствуйте, пытаясь сложить вместе термины, которые на самом деле не могут быть объединены. Итак, какие термины можно объединить с и почему?
Термины могут быть объединены только , если они имеют точно такую же переменную часть. И под «точно таким же» я подразумеваю «те же переменные, возведенные в одну и ту же степень». Вот краткое изложение того, что к чему:
И под «точно таким же» я подразумеваю «те же переменные, возведенные в одну и ту же степень». Вот краткое изложение того, что к чему:
MathHelp.com
Это не подобных терминов …
4 x и 3
… потому что первый член содержит переменную, а второй — нет.
Это не подобных терминов …
4 x и 3 y
… потому что два члена содержат разные переменные.
Это не подобных терминов …
4 x и 3 x 2
… потому что переменные одинаковы, а мощности этих переменных — нет.
Эти — это похожих терминов …
4 x и 3 x
… потому что переменные одинаковы, как и их полномочия.
Но это не подобных терминов …
4 x и 3 xy
… потому что второй член имеет дополнительную переменную, поэтому части переменных не совпадают.
Итак, чтобы решить, являются ли два термина «подобными» терминами, которые можно объединить, мы смотрим на переменную часть этих терминов. Числовая часть двух терминов — это то, что будет объединено (как мы вскоре увидим), но именно переменная часть этих двух терминов определяет, могут ли термины объединяться. Чтобы их можно было объединить, части переменных терминов должны содержать одну и ту же переменную с одинаковой степенью (-ами).
После того, как вы определили, что два термина действительно являются «похожими» терминами и, следовательно, действительно могут быть объединены, вы можете работать с ними так же, как и в гимназии.Когда вы только учились складывать, вы делали «пять яблок и шесть яблок — это одиннадцать яблок». С тех пор вы узнали, что, как говорится, «нельзя добавлять яблоки и апельсины». То есть «пять яблок и шесть апельсинов» — это просто большая груда фруктов; это не что-то вроде «одиннадцати аппланжей». Объединение одинаковых терминов работает примерно так же; мы добавляем числовые части, одновременно перемещая переменные части, почти как единицу или как добавленные нами «яблоки».
Глядя на эти два термина, я вижу, что каждый содержит переменную x , и переменная имеет одинаковую (понятную) степень 1 в каждом члене.Так что это похожие термины, и я могу их комбинировать.
Возвращаясь к арифметике в начальной школе, «три яблока плюс четыре яблока» были объединены в «семь яблок», если сложить три и четыре, чтобы получить семь, и взять с собой «яблоки» для поездки. Таким же образом я объединю эти два одинаковых термина, добавив числовую часть каждого члена, неся с собой x :
3 x + 4 x
(3 + 4) х
(7) x
Я показал каждый шаг выше, чтобы подчеркнуть, как сочетаются термины.Я складываю 3 и 4 и несу x вместе с числовым результатом. Мой ответ:
Упростить 2
x 2 + 3 x — 4- x 2 + x + 9
Часто лучше сначала сгруппировать похожие термины, а затем упростить:
2 x 2 + 3 x — 4- x 2 + x + 9
(2 x 2 — x 2 ) + (3 x + x ) + (–4 + 9)
(2–1) x 2 + (3 + 1) x + (5)
(1) x 2 + (4) x + 5
x 2 + 4 x + 5
Во второй строке выше многие студенты считают полезным записывать понятный коэффициент 1 перед любыми выражениями переменных, не имеющих записанного коэффициента, как показано ниже красным:
(2 x 2 — x 2 ) + (3 x + x ) + (–4 + 9)
(2 x 2 — 1 x 2 ) + (3 x + 1 x ) + (–4 + 9)
(2–1) x 2 + (3 + 1) x + (5)
1 x 2 + 4 x + 5
x 2 + 4 x + 5
При упрощении таких выражений не требуется записывать понятное 1, но многие студенты находят этот метод очень полезным, по крайней мере, когда они только начинают.Какой метод поможет вам последовательно правильно завершить упрощение, это тот метод, который вы должны использовать.
Упростить 10
x 3 -14 x 2 + 3 x -4 x 3 + 4 x — 6
Я начну с группировки терминов по степени.
10 x 3 — 14 x 2 + 3 x — 4 x 3 + 4 x — 6
(10 x 3 — 4 x 3 ) + (–14 x 2 ) + (3 x + 4 x ) — 6
6 x 3 — 14 x 2 + 7 x — 6
Предупреждение. При перемещении терминов помните, что знаки терминов перемещаются на вместе с ними.Не портите себя, оставляя позади осиротевшие знаки «плюс» и «минус».
Если это поможет вам разобраться, перепишите выражение следующим образом:
10 x 3 + (–14 x 2 ) + 3 x + (–4 x 3 ) + 4 x + (–6)
Превращая вычитания в сложения отрицаний, становится ясно, где принадлежат знаки «минус», и их легче перемещать правильно:
10 x 3 + (–4 x 3 ) + (–14 x 2 ) + 3 x + 4 x + (–6)
(10-4) x 3 -14 x 2 + (3 + 4) x — 6
…и так далее. Делайте то, что работает для вас.
Упростить 25 — (
x + 3- x 2 )
Первое, что мне нужно сделать, это взять отрицательный результат в круглые скобки:
25 — ( x + 3- x 2 )
25- x -3 + x 2
Хорошо; эти термины не только не в порядке убывания, они почти полностью перевернуты! Я правильно расставлю их, а затем упрощу, объединив две константы, которые являются единственными подобными терминами:
x 2 — x + 25-3
x 2 — x + 22
Многие студенты, особенно в начале обучения, испытывают трудности со знаком «минус», в том числе при вводе их в скобки, как я только что сделал выше.Если это помогает вам отслеживать, что происходит, попробуйте поставить «понято» 1 перед круглыми скобками (выделено красным ниже), а затем перейти к терминам внутри:
25 — ( x + 3- x 2 )
25 — 1 ( x + 3- x 2 )
25 — 1 ( x ) — 1 (+3) — 1 (- x 2 )
25 — 1 x — 3 + 1 x 2
1 x 2 -1 x + 25-3
1 x 2 — 1 x + 22
x 2 — x + 22
В то время как первый формат (без записи 1) является более «стандартным» форматом, математически допустимы оба формата.Вам следует использовать тот формат, который вам больше всего подходит. Не стесняйтесь вставлять понятную 1, когда начинаете; не чувствуйте себя обязанным продолжать использовать его, как только вы почувствуете себя уверенно без него.
Упростить
x + 2 ( x — [3 x — 8] + 3)
Это просто проблема порядка операций с переменной в ней.Если я работаю аккуратно изнутри, обращая особое внимание на свои знаки «минус», то со мной все будет в порядке:
x + 2 ( x — [3 x — 8] + 3)
x + 2 ( x — 1 [3 x — 8] + 3)
x + 2 ( x — 1 [3 x ] — 1 [–8] + 3)
x + 2 ( x -3 x + 8 + 3)
x + 2 (–2 x + 11)
x + 2 (–2 x ) + 2 (+11)
x — 4 x + 22
1 x — 4 x + 22
–3 x + 22
Просто чтобы вы знали, это та проблема, которую мы, учителя математики, любим, ставить на тесты (да, некоторые из нас вроде как больные щенки), поэтому вам следует ожидать, что вам придется иметь дело с вложенными символами группировки как это.
Упростить [(6
x — 8) — 2 x ] — [(12 x — 7) — (4 x — 5)]
Я работаю изнутри:
[(6 x — 8) — 2 x ] — [(12 x — 7) — (4 x — 5)]
[6 x — 8 — 2 x ] — [12 x — 7 — 1 (4 x ) — 1 (–5)]
[6 x — 2 x — 8] — [12 x — 7 — 4 x + 5]
[4 x — 8] — [12 x — 4 x — 7 + 5]
4 x — 8 — [8 x — 2]
4 x — 8 — 1 [8 x ] — 1 [–2]
4 x — 8-8 x + 2
4 x — 8 x — 8 + 2
–4 x — 6
Упростить –4
y — [3 x + (3 y — 2 x + {2 y — 7}) — 4 x + 5]
Как всегда, я начну с самой внутренней группировки и упрощу свой путь к ответу.
–4 y — [3 x + (3 y — 2 x + {2 y — 7}) — 4 x + 5]
–4 y — [3 x + (3 y — 2 x + 2 y — 7) — 4 x + 5]
–4 y — [3 x + (–2 x + 3 y + 2 y — 7) — 4 x + 5]
–4 y — [3 x + (–2 x + 5 y — 7) — 4 x + 5]
–4 y — [3 x — 2 x + 5 y — 7 — 4 x + 5]
–4 y — [3 x — 2 x — 4 x + 5 y — 7 + 5]
–4 y — [3 x — 6 x + 5 y — 7 + 5]
–4 y — [–3 x + 5 y — 2]
–4 y — 1 [–3 x ] — 1 [+5 y ] — 1 [–2]
–4 y + 3 x — 5 y + 2
3 x -4 y -5 y + 2
3 x — 9 y + 2
В приведенном выше упрощении участвовали две разные переменные.Обычно (хотя и не требуется) перечислять термины так, чтобы их переменные располагались в алфавитном порядке. Вот почему я перечислил 3 x перед 9 y . Как всегда, в самом конце идет постоянный член.
(Если вы считаете, что вам нужно больше практики с этим последним типом задач (со всеми скобками, минусами и круглыми скобками, тогда вы можете просмотреть урок «Упрощение с круглыми скобками».)
Когда мы говорим о яблоках и апельсинах, обычно довольно легко понять, что следует сочетать с чем еще и каким образом.Но как только мы начнем работать с переменными, все может запутаться. Не заблуждайтесь и не путайте умножение и сложение. Для меня это может показаться глупым, но это может быть наиболее частая ошибка студентов при объединении одинаковых терминов (после нарушения порядка операций).
Это умножение …
( x ) ( x ) = ( x 1 ) ( x 1 )
= x 1 + 1 = x 2
… так что это упрощается с помощью правил комбинирования экспонент.
Это дополнение …
x + x = 1 x + 1 x
= (1 + 1) x = 2 x
… так что это упрощается с помощью правил комбинирования коэффициентов.
Позвольте мне внести ясность:
( x ) ( x ) не равно x + x
x 2 не равно 2 x
Итак, если у вас есть что-то вроде x 3 + x 2 , не пытайтесь сказать, что это как-то равно примерно x 5 или 5 x .Эти термины не похожи друг на друга и не могут быть объединены. Если у вас есть что-то вроде 2 x + x , не пытайтесь сказать, что это как-то равно 2 x 2 . Эти термины похожи на термины и объединяются путем добавления их коэффициентов.
Не торопитесь и убедитесь, что вы постоянно держите в голове, как работает умножение, а не как работает сложение. На самом деле, «комбинирование похожих терминов» — это тема, для которой было бы сложно выполнить слишком много практики.Выполняйте как можно больше практических задач!
URL: https://www.purplemath.com/modules/polydefs2.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в объединении «похожих» терминов. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Объединить» или «Упростить», чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Как найти решение системы уравнений
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Объем твердого тела революции: диски и шайбы
Если область на плоскости вращается вокруг линии в той же плоскости, полученный объект называется телом вращения.
Например, сплошной правый круговой цилиндр можно создать, вращая прямоугольник. Точно так же твердый сферический шар можно создать, вращая полудиск.
Линия, вокруг которой мы вращаем фигуру, называется осью вращения.
Дисковый метод
Дисковый метод используется, когда мы вращаем одну кривую \ (y = f \ left (x \ right) \) вокруг оси \ (x- \) (или \ (y- \)).
Предположим, что \ (y = f \ left (x \ right) \) — непрерывная неотрицательная функция на интервале \ (\ left [{a, b} \ right].2} dy}. \]
Метод промывки
Мы можем расширить дисковый метод, чтобы найти объем полого тела вращения.
Предполагая, что функции \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) непрерывны и неотрицательны на интервале \ (\ left [{a, b} \ right] \) и \ (g \ left (x \ right) \ le f \ left (x \ right), \) рассмотрим область, ограниченную двумя кривыми \ (y = f \ left (x \ right) \ ) и \ (y = g \ left (x \ right), \) между \ (x = a \) и \ (x = b. 2}} \ right) dy}.2} \ left (t \ right) \ frac {{dy}} {{dt}} dt}. \]
Объем твердого тела вращения для полярной кривой
Есть много кривых, которые задаются полярным уравнением \ (r = r \ left (\ theta \ right). \) Для преобразования из полярных координат \ (\ left ({r, \ theta} \ right) \) в В декартовых координатах \ (\ left ({x, y} \ right), \) используем известные формулы
\ [{x = r \ left (\ theta \ right) \ cos \ theta, \; \;} \ kern0pt {y = r \ left (\ theta \ right) \ sin \ theta.} \]
Итак, мы подошли к параметрической форме кривой, рассмотренной в предыдущем разделе.
Важно помнить, что радиус-вектор \ (r \) также зависит от параметра \ (\ theta. \), Поэтому производные \ (\ large {\ frac {{dx}} {{dt}} } \ normalsize \) и \ (\ large {\ frac {{dy}} {{dt}}} \ normalsize \) записываются как
\ [{\ frac {{dx}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ cos \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ cos \ theta — r \ left (\ theta \ right) \ sin \ theta ,} \]
\ [{\ frac {{dy}} {{dt}} = \ frac {{d \ left ({r \ left (\ theta \ right) \ sin \ theta} \ right)}} {{dt}} } = {\ frac {{d \ left ({r \ left (\ theta \ right)} \ right)}} {{dt}} \ sin \ theta + r \ left (\ theta \ right) \ cos \ theta . {\ frac {2} {3}}} = 1 \) вокруг своей оси симметрия.2} \) и ось \ (x — \) вокруг оси \ (y — \).
Пример 9
Найдите объем твердого тела, полученный вращением равностороннего треугольника со стороной \ (a \) вокруг одной из его сторон.Пример 10
Одна арка циклоиды \ (x = \ theta — \ sin \ theta, \) \ (y = 1 — \ cos \ theta \) вращается вокруг своего основания. Вычислите объем тела, ограниченного данной поверхностью.Пример 1.
Дисковым методом вычислить объем правого кругового конуса высотой \ (H \) и радиусом основания \ (R.1} = {8 \ pi \ left [{\ left ({1 — \ frac {1} {3}} \ right) — \ left ({- 1 + \ frac {1} {3}} \ right)} \ right]} = {8 \ pi \ cdot \ frac {4} {3}} = {\ frac {{32 \ pi}} {3}} \]Пример 5.
Симметричный параболический сегмент с основанием \ (a \) и высотой \ (h \) вращается вокруг основания. Вычислите объем полученного твердого тела вращения («лимон» Кавальери).Решение.
Квадратичная функция определяется уравнением \ (y = kx \ left ({a — x} \ right), \), где коэффициент \ (k \) может быть найден из условия \ (y \ left (\ large {{\ frac {a} {2}}} \ normalsize \ right) = h.2}}} {4}}} = {\ frac {{\ sqrt 3 a}} {2}.} \]
Итак, вершины \ (A, \) \ (B, \) \ (C \) имеют следующие координаты:
\ [{A \ left ({0, \ frac {a} {2}} \ right), \;} \ kern0pt {B \ left ({\ frac {{\ sqrt 3 a}} {2}, 0 } \ right), \;} \ kern0pt {C \ left ({0, — \ frac {a} {2}} \ right).} \]
Найдите уравнение прямой \ (AB \) в двухточечной форме:
\ [{\ frac {{x — {x_A}}} {{{x_B} — {x_A}}} = \ frac {{y — {y_A}}}} {{{y_B} — {y_A}}}, } \; \; \ Rightarrow {\ frac {{x — 0}} {{\ frac {{\ sqrt 3 a}} {2} — 0}} = \ frac {{y — \ frac {a} {2}}} {{ 0 — \ frac {a} {2}}},} \; \; \ Rightarrow {\ frac {x} {{\ sqrt 3}} = \ frac {{y — \ frac {a} {2}}} {{- 1}},} \; \; \ Rightarrow {x = \ гидроразрыв {{a \ sqrt 3}} {2} — \ sqrt 3 г.2}.} \]
Линейные уравнения 1a ключ ответа
1 © Sashaa Murphy РАБОЧАЯ ТАБЛИЦА по линейным уравнениям № 1A ЛИНЕЙНЫЕ УРАВНЕНИЯ № 1A • Определите наклон и точку пересечения по оси Y в уравнении линии, записанной в форме точки пересечения с наклоном. Направления: Для каждого уравнения ниже нарисуйте синий круг вокруг точки пересечения оси Y и красную рамку вокруг наклона. 1. 3 2 1 y = x — 2. 6 3 4 y = — x + 3. y = 3x +9 4. 3 4 y …Двигатель Chevy aveo
- Отзыв о экзамене по математике 9 класса — Блок 6 — Раздел ответов на линейные уравнения и неравенства МНОЖЕСТВЕННЫЙ ВЫБОР 1.ANS: D PTS: 1 DIF: Easy REF: 6.1 Решение уравнений с помощью обратных операций LOC: 9.PR3 TOP: Шаблоны и отношения (переменные и уравнения) КЛЮЧ: Процедурные знания 2.ANS: B PTS: 1 DIF: Easy
- Гленна хочет арендовать машину для поездки на Ки-Уэст на неделю. Она звонит в две компании по аренде автомобилей, чтобы узнать цены. Компания Mr. Kotter’s Rentals арендует Cadillac Escalade за 99 долларов на одну неделю плюс 0,11 доллара за милю на 100 миль. Barbarino’s Rentals предлагает тот же автомобиль за 75 долларов в неделю и 0,15 доллара за милю на расстояние более 150 миль.
Уравнение: y = 2x — 2 Синяя линия: наклон (м) = -1 / 3x точка пересечения оси y (b) = 5 Уравнение: y = -1 / 3x + 5 A — правильный выбор ответа. СОВЕТ. Вы знаете, что красная линия имеет положительный наклон, потому что она поднимается слева направо. Синяя линия имеет отрицательный наклон, потому что она падает слева направо. Таким образом, мы можем исключить ответ
Линейные уравнения: задачи со словами: графики Получите 3 из 4 вопросов, чтобы повысить уровень! Построение графов линейных соотношений словарных задач Получите 3 из 4 вопросов, чтобы повысить уровень! Тест 3.Повышайте уровень вышеперечисленных навыков и набирайте до 500 очков мастерства. Начните тест. Далее для вас: модульный тест.
IXL предлагает сотни навыков Алгебры 1 для изучения и изучения! Не уверен, где начать? Перейдите на свою персональную стену с рекомендациями, чтобы найти навык, который выглядит интересным, или выберите план навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту.
Создание независимого практического рабочего листа уравнений и неравенств, ключ ответов, Уравнения и неравенства.Рабочие листы по математике для 7-го класса и ключ с ответами, Учебные пособия. Обладает следующими навыками: использовать символическую алгебру для представления ситуаций и решения проблем, особенно тех, которые связаны с линейными отношениями.
Jm листовые протекторы
Решение систем линейных уравнений: Решение линейных уравнений — Часть II: Решение уравнений I: Суммарная оценка решения проблем и навыков Результаты: Решение математических задач: Длинное деление Лицевая сторона: Решение линейных уравнений: Системы линейных Уравнения с двумя переменными: решение системы линейных уравнений с помощью построения графиков: одновременное решение Ti-89…
10 января 2019 г. · Линейные уравнения, функции и неравенства. Поиск наборов решений для систем уравнений с помощью подстановки и графической мини-оценки 1. We-Haul арендует движущийся грузовик за $ «#. ## и $ #.%. & за милю. You-Haul арендует движущийся грузовик того же размера за $ ‘. ## за милю, но без предоплаты. Часть A: напишите два уравнения для представления ситуации.
Этот решатель (решатель линейных уравнений) был создан автор: jim_thompson5910 (35256): Просмотреть исходный код, показать, разместить на ВАШЕМ сайте О jim_thompson5910: Если вам нужна дополнительная помощь по математике, вы можете написать мне по электронной почте.Я беру 2 доллара за шаги или 1 доллар только за ответы.
Ответный ключ Название теста: СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ 12) B 13) B 14) C 15) c 16) A 17) c 18) D 19) A 20) B
Ответный ключ для решения линейных уравнений — отображение 8 верхних рабочих листов найдено для этой концепции .. Некоторые из рабочих листов для этой концепции: Работа с линейными уравнениями, Решение линейных уравнений с переменными с обеих сторон, Исключение систем уравнений, Построение графика линейных уравнений, работа с ключом ответа, Решение одношаговых уравнений 1, Построение графиков линейных уравнений t1s1, Работа 2 2 решения уравнений с одной переменной…
10 января 2019 г. · Линейные уравнения, функции и неравенства. Поиск наборов решений для систем уравнений с использованием подстановки и графической мини-оценки 1. We-Haul арендует движущийся грузовик за $ «#. ## и $ #.%. & за милю. You-Haul арендует движущийся грузовик того же размера за $ ‘. ## за милю, но без предоплаты. Часть A: напишите два уравнения, чтобы представить ситуацию. Рабочий лист модели свободных частиц 1a. Какой тип движения наблюдается 5 7 Рисование диаграмм свободного тела Университетская физика Том 1 Ключ ответа на чистую силу.Рабочий лист модели свободных частиц 1a силовые диаграммы — ключ к ответу. Обзор блока 5 2. Рабочий лист блока 4 4 ответа. Модель свободных частиц. Анализ происходит следующим образом. Сумма углов треугольника равна 180 ° b. Ответ должен включать, но не ограничивается: Сумма углов каждого треугольника должна составлять 180 °. Некоторые могут немного отличаться из-за округления. 3. а.27 82 180; 71 ++ = = хх. б. 43 52 180; 85 ++ = = хх. c. хх ++ = = 62,5 77 180; 40,5 г.
© y S2q0 q1e2T hKqu kt1a y FSro ZfEtzw La 9r2e K 6LlL ACy.3 a lA ylol5 4rLi Egth ntWsx VrYeqs qeDrfv seldH. C p 4MpaPd we5 Fwti jt ph2 jI 8n Efzifn ViZt VeL oA1l 5ghe vbVr сумка b16. 2 Рабочий лист Kuta Software LLC
© t A2W0O1g2w YKJuHt4a8 jS SoMfFt9w0aPr jeA bL zL aCy.F F 1Akl Nlq CrDi6gOhTtzsP r5e YsEeVrxv PeWdr. ml EM9aXdQeb iw Xi 6thj lI Rncf3i vn Aiet5eM tADl1goeabFr fab 32 Рабочий лист WW от Kuta Software LLC
Trainz sw1200
Free kayo hack
Linear Writations Практика Ключ к ответам на вопросы написание линейных уравнений практика ключ ответа дополнительно полезен.Вы остались на правильном сайте. Страница 1/11
Создание уравнений и неравенств, независимая рабочая таблица, ключ ответа, Уравнения и неравенства. Рабочие листы по математике для 7-го класса и ключ с ответами, Учебные пособия. Обладает следующими навыками: использовать символическую алгебру для представления ситуаций и решения проблем, особенно тех, которые связаны с линейными отношениями.
Показаны 8 лучших рабочих листов в категории — Ответ на ключ для решения линейных уравнений. Некоторые из отображаемых рабочих листов: Работа с линейными уравнениями, Решение линейных уравнений с переменной с обеих сторон, Исключение систем уравнений, Построение графика работы линейных уравнений, ключ ответа, Решение одношаговых уравнений 1, Графическое отображение линейных уравнений t1s1, Работа 2 2, решение уравнений с одной переменной, Решение многошагово…
Линейные уравнения Некоторым учащимся может быть очень сложно построить наклонные и графические линии. Несмотря на то, что мы делаем все это в классе, вы можете ознакомиться с концепциями и попрактиковаться в материале.
Подарочная карта Xbox
Эти рабочие листы уравнений алгебры 1 будут создавать задачи по дистанции, скорости и времени с десятью задачами на листе. Вы можете выбрать числа, которые будут представлены цифрами или словами. Эти рабочие листы по уравнениям — хороший ресурс для учащихся с 5-го по 8-й класс.Задачи Mixture Word
Рабочие листы по алгебре 1 и по алгебре 2 по различным темам. Каждый рабочий лист представляет собой тестовую бумагу для печати с ключом ответа, прикрепленным ко второй странице. Это замечательно, потому что учителя и родители могут ссылаться на ответы, чтобы узнать, правильно ли поняли учащиеся. В этом разделе представлены основные рабочие листы по алгебре, размещенные в специальном разделе.
Сенсорная панель не перемещает окна 10 Отключение Bluetooth a2dp аппаратной разгрузки значение
Как получить терминал на iphone без джейлбрейка Что курьеров поблизости не ест Убер
Абсолютные моральные правила Kantpercent27s Резорбируемая мембрана
Малия обама чистая стоимость | Grbl аварийная остановка | Chrome OS apk | |
| Написание линейных уравнений Практический ответ Ключевой автор: www2.galileoplatforms.com-2020-12-09T00: 00: 00 + 00: 01 Тема: Практика написания линейных уравнений Ключевые слова: написание, линейные, уравнения, практика, ответ, ключ Дата создания: 09.12.2020 7:21: 52 PM | |||
| Minikube dns не работает Судебный процесс по трубам из полибутилена 2020 | Comicstreamer | Проблемы с температурой холодильника в галерее Frigidaire | Nortrac тракторные обзоры |
| Ответы на вопросы в формате PDF Файл Equwer Line 9024 Ключ Да, просмотр ключа ответа на линейные уравнения в электронной книге может добавить список ваших ближайших контактов.Это лишь одно из решений для вашего успеха. Как я понял, Triumph не рекомендует набирать фантастические очки. | |||
| Turbo rebuild kit для 7.3 powerstroke Строка события создания minecraft bedrock | Obs 7.3 idm location | Портативные приложения firefox 52 esr | Как неконтролировать контролируемый iphone |
| Преобразование аудио в видео Работа по найму 16-летних | Suzuki samurai на продажу albuquerque | Полицейский сканер Northlake il полиции | Mercury 200 efi настроить |
| Equation Line Примеры построения графиков… Решите следующую систему уравнений с помощью построения графиков. Проверьте свои ответы, прежде чем искать решения … | |||
| Amazon Business Intelligence Охота на свиней в грузии wma | Как работает почасовая оплата grubhub | Github cs 433 | Как преобразовать заказ на продажу в производственный заказ in sap |
| Glencoe Algebra 1 Решения Глава 3 Решение линейных уравнений. Гленко Алгебра 1 ответы Pdf.Алгебра Гленко 1 Решения Глава 3 Решение линейных уравнений. Ответить 1ВЦ. Ответ 2VC. Ответ 3VC. Ответ 4VC. Ответ 5VC. Ответ 6VC. Ответ 7VC. Ответ 8VC. Ответ 9VC. Ответ 10VC. Ответ 11E. Ответ 12E. Ответ 13E. Ответ 14E. Ответ 15E … | |||
Скачать игру psx bin fileGoal zero van setup
| 1935 серебряный сертификат стоимость Pytorch обучение с подкреплением | Мой банковский счет отрицательный | 000 доллар Символ инь-янь не копирование и вставка эмодзи 95 mustang gt Модуль управления зажиганием | ||||
| 8 марта 2012 г. · У меня есть только 2 недели, чтобы сделать это, чтобы закончить и я далеко позади.Я прохожу все классы, кроме этого. И если я не закончу учебу в этом году, я откажусь от действительно важной стажировки. Ик накрутка — это плохо но есть ли у кого-нибудь ответ Ключ? | ||||||
| Приложение топливных вознаграждений Win 3 midday ny | Warzone все визитные карточки | Охота на оленей с Glock 19 3 | Технические характеристики клубных автомобилей | |||
| вопросы по приложениям линейных уравнений | Grade 8 с решениями и объяснениями.Трехкратное число, увеличенное на десять, равно двадцати меньшему, чем шестикратное число. Найдите номер. | |||||
| Yahoo groups 20817 P0101 lbz duramax | Стойки для курильщиков | Звоните один раз, затем голосовая почта iphone Fallout 76 паровая передача не работает | 1911 золотая бочка | |||
Orange foto recovery расшифровать пароль | Ryzen 7 3700x mobo bundle | Glock 20 самый мощный пистолет 6 | игра Roblox скачать бесплатно для windows 10 | |||
| 9000w 9ag000w | Онлайн-генератор случайных чисел для tambola | Детали ремешка для часов Seiko Opnsense grafana | Настройка впрыскивающего насоса Om617 | |||
| Графическое представление линейных уравнений с ключевыми уравнениями.В связи с тем, что мы хотели бы предоставить все необходимое в виде единого законного и эффективного источника, все мы предоставляем ценную информацию по различным вопросам, а также по темам. | ||||||
223 данные нагрузки Снятие замка зажигания Mercedes
| Шаблон обследования по шкале Лайкерта Tujhse hai raabta 21 сентября 2019 письменное обновление | |||
| Fda ускоренные правила утверждения | Honda eu 3000 аккумуляторная батарея | ||
| Этот настраиваемый полиграф разработан для того, чтобы вызвать богатые словарным запасом разговоры о системах линейных уравнений.Ключевые слова, которые могут появиться в вопросах учащихся, включают: параллель, пересечение, решение, квадрант, ось, вертикаль, горизонталь, наклон, увеличение и уменьшение. | |||
Тестер аккаунтов Crunchyroll Сколько людей сейчас играют в мертвых днем
| Стоимость боксерского клуба Title Reddit очков 2d теплопередачи python | |||
Комплект для дверной защелки Pella | Capsim round 5 ответов 2019 2 | Сельское хозяйство 45 | |
House of X & Dawn2 заказал X Reading Order
e 2019 год стал штормом, когда было объявлено лично, что писатель Джонатан Хикман возвращается к издателю, чтобы написать два совпадающих сериала о Людях Икс.С 2008 по 2015 год Хикман выделялся как один из лучших писателей по вселенной Marvel, выполнив впечатляющую работу в таких играх, как «Фантастическая четверка», «Мстители» и событие «Секретные войны 2015» (среди прочих!).
Начиная с Secret Wars, Хикман был сосредоточен на отличной работе создателей с Image (такие книги, как East of West и The Black Monday Murders), а Marvel изо всех сил пыталась восстановить свое положение. Обещание писателя вернуться во франшизу о Людях Икс, которая также претерпела огромные противоречия на протяжении 2010-х годов, является чрезвычайно удовлетворительной перспективой для поклонников того и другого.
Интересно, что в предрелизной шумихе Marvel отметила четыре основные эпохи Людей Икс с момента выхода Uncanny X-Men , дебютировавшего в 1963 году: Giant Size X-Men # 1 (1975), X-Men # 1 (1991) , Эпоха Апокалипсиса, Новые Люди Икс. Подразумевается, что две серии Хикмана — House of X, и Powers of X — будут началом 5-й эры.
Ниже вы найдете полное руководство по комиксам Джонатана Хикмана о Людях Икс, а также связанные с ними прелюдию и сопутствующие вопросы, которые помогут объяснить историю.
Связанные заказы на чтение:Крис Клермонт Эра Люди Икс (1975-1991)
Поддержка Comic Book Herald:Comic Book Herald поддерживается читателями. Когда вы совершаете покупку по ссылкам на нашем сайте, мы можем получать соответствующую партнерскую комиссию.
Заказы на чтение и руководстваComic Book Herald также стали возможны благодаря поддержке читателей на Patreon и щедрым пожертвованиям читателей.
Взнос любого размера поможет поддерживать CBH в жизни и наполнении новыми руководствами и контентом по комиксам.Поддержите CBH на Patreon и получите эксклюзивных наград или пожертвуйте здесь! Спасибо за чтение!
Станьте покровителем!
Современные Люди Икс (1998-настоящее время)
Дорога к Людям Икс ХикманаНовые Люди Икс от Гранта Моррисона
В интервью (включая краткую беседу на C2E2 с искренним уважением) Хикман быстро хвалит работу Моррисона с похвалой, от Marvel Boy до New X-Men .Неудивительно, что его комиксы о Людях Икс относятся к эре New X-Men с некоторой степенью благоговения.
Действительно, Хикман уже отошел от возвышенных идей Моррисона, включая концепцию «яйца феникса» в его сборке «Time Runs Out», до Secret Wars .
Порядок чтения Джонатана Хикмана «Вестник комиксов» (2008–2015 гг.)
Говоря о массовых, амбициозных великих пробегах в истории Marvel, пробежка Хикмана с 2008 по 2015 год по вселенной Marvel — моя любимая современная последовательность комиксов в Marvel.
Что особенно интересно, я также проанализировал, как Хикман писал конкретных персонажей и концепты Людей Икс, и что мы можем ожидать в будущем, учитывая эту историю.
Жуткие Люди Икс (2018) №11 по №22
Marvel подняла много шума над выпуском (7,99 долларов) в 2018 году нового Uncanny X-Men # 1 , и серия выходила еженедельно в течение первых 10 выпусков / недель. Хотя эти десять проблем действительно создают основу для явного прорыва, который происходит в Uncanny X-Men # 11, они больше всего сосредоточены на вождении Age of X-Man .
Итак, да, давние поклонники Людей Икс могут прочитать всю серию, но чисто для целей пути к Людям Икс Хикмана, я бы поспорил, что вы можете начать со времени Мэтью Розенберга, написавшего соло пробега из UXM №11 в.
Uncanny X-Men # 22 запланирован к выпуску 17 июля 2019 года и должен завершить эту серию Uncanny (которая началась еще в далеком прошлом, известном как 2018). Первый выпуск House of X выйдет на следующей неделе.
Хикман в контрольном списке Людей ИксHouse of X / Powers of X
Собирает: House of X # 1 to # 6, Powers of X # 1 to # 6
Это сборное издание — Полная разбивка по выпускам приведена ниже.
Дом X и полномочия X Приказ о прочтенииДом Х # 1
The House of X / Powers of X Дуология была настолько забавной, что я начал серию видео под названием «Krakin’ Krakoa », где я рассказываю историю, историю и общий энтузиазм по поводу событий комикса.
Сериал начинается здесь с истории профессора Чарльза Ксавьера до House of X # 1. С этого момента я просто перечисляю следующую запись в серии видео по номеру, так что те из вас, кто хочет избежать любых возможных спойлеров , могут сделать это здесь!
Полномочия X # 1
Дом Х # 2
Вы можете найти мое исследование некоторых выдающихся отсылок к прошлым комиксам Хикмана в Krakin Krakoa: Secrets of House of X!
Krakin ’Krakoa # 3 также идет с House of X # 2.
Полномочия X # 2
В качестве фона для моего видео обратите внимание на Krakin ’Krakoa # 4!
Полномочия X # 3
Спутник по видео через Krakin ’Krakoa # 5!
Дом Х # 3
Дом Х # 4
Видео-компаньон через Krakin ’Krakoa # 7!
Комиксы Marvel № 1000
Всего лишь рассказ Хикмана и Дастина Уивера на одной странице об Апокалипсисе и его четырех всадниках!
Полномочия X # 4
Видео-компаньон через Krakin ’Krakoa # 6!
Дом Х # 5
Видео-компаньон через Krakin ’Krakoa # 8!
Полномочия X # 5
Спутник по видео через Krakin ’Krakoa # 9!
Дом Х №6
Видео-компаньон через Krakin ’Krakoa # 10!
Полномочия X # 6
Видео-компаньон через Krakin ’Krakoa # 12!
После HoX & PoX… Dawn of X Trade Порядок чтения!
Вы должны знать, что Marvel собирает (по крайней мере) первые шесть выпусков новых комиксов в линейке X-Men, известной как Dawn of X двумя способами.Во-первых, это ваша традиционная серия в мягкой обложке, в которой будут собраны первые шесть выпусков комикса X-Men (например). Менее традиционно существуют коллекции в твердом переплете под названием «Dawn of X Volume One» и т. Д., Которые включают только первый выпуск каждого из шести изданий Dawn of X, затем только второй выпуск каждого и т. Д. на.
Итак, было много споров о достоинствах чтения каждого комикса в Dawn of X. Есть , некоторые перекрытия непрерывности, и в этом отношении я бы посоветовал поклонникам House of X прочитать хотя бы первые два выпуска из шести названий выпуска (все они перечислены ниже в порядке выпуска!), чтобы узнать, какие книги вам нравятся больше всего.Далее все зависит от личных предпочтений, и я бы посоветовал придерживаться тех книг, которые сделают это за вас. Однако для таких компаньонов, как я, эти коллекции Dawn of X могут показаться ужасно соблазнительными.
Люди Икс, Джонатан Хикман Том. 1
Собирает : Люди Икс № 1 по № 6
Мародеры Джерри Дагган Том. 1
Собирает : Мародеры (2019) # 1-6
X-Force Vol. 1
Собирает : X-Force (2019) 1-6
Экскалибур Тини Ховард Том.1
Собирает : Экскалибур (2019) 1-6
Новые мутанты Джонатана Хикмана Том. 1
Собирает : Новые мутанты 1-6
Fallen Angels Vol. 1
Собирает : Падшие ангелы (2019) 1-6
Люди Икс, Джонатан Хикман Том. 2
Собирает : Люди Икс (2019) 7-11
Новые мутанты Эд Бриссон Том. 1
Собирает : Новые мутанты (2019) 7-12
X-Force Vol.2
Собирает : X-Force (2019) 7-12
Люди Икс / Фантастическая четверка: 4X
Собирает : Люди Икс / Фантастическая четверка (2020) 1-4
Мародеры Джерри Дагган Том. 2
Собирает : Мародеры (2019) 7-11
Экскалибур Тини Ховард Том. 2
Собирает : Экскалибур (2019) 7-11
Росомаха Бенджамином Перси Том. 1
Собирает : Росомаха (2020) 1 (История A), Росомаха (2020) 2-3, Росомаха (2020) 1 (История B)
Геллионы Зеб Уэллс Vol.1
Собирает : Геллионы (2020) 1-6
Кабель Vol. 1
Собирает : Кабель (2020) 1-6
Empyre: Люди Икс
Собирает : Empyre: Люди Икс (2020) 1-4
X-Factor Лии Уильямс Vol. 1
Собирает : X-Factor (2020) 1-3, 5
Dawn of X Коллекции в твердом переплетеРассвет X Том. 1
Собирает : Люди Икс (2019) # 1, X-Force (2019) # 1, Мародеры # 1, Экскалибур (2019) # 1, Падшие ангелы (2019) # 1 и новые мутанты (2019) # 1
Рассвет X Том.2
Собирает : Люди Икс (2019) # 2, X-Force (2019) # 2, Мародеры # 2, Экскалибур (2019) # 2, Падшие ангелы (2019) # 2 и новые мутанты (2019) # 2
Рассвет X Том. 3
Собирает : Люди Икс (2019) # 3, X-Force (2019) # 3, Мародеры # 3, Экскалибур (2019) # 3, Падшие ангелы (2019) # 3 и новые мутанты (2019) # 3
Рассвет X Том. 4
Собирает : Люди Икс (2019) # 4, X-Force (2019) # 4, Мародеры # 4, Экскалибур (2019) # 4, Падшие ангелы (2019) # 4 и новые мутанты (2019) # 4
Рассвет X Том.5
Собирает : Люди Икс (2019) # 5, X-Force (2019) # 5, Мародеры # 5, Экскалибур (2019) # 5, Падшие ангелы (2019) # 5 и новые мутанты (2019) # 5
Рассвет X Том. 6
Собирает : Люди Икс (2019) 6, Сила Икс (2019) 6, Мародеры 6, Экскалибур (2019) 6, Падшие ангелы (2019) 6 и новые мутанты (2019) 6
Рассвет X Том. 7
Собирает : Мародеры # 7, Экскалибур (2019) # 7, X-Force (2019) # 7 и Росомаха (2020) # 1
Рассвет X Том.8
Собирает : Мародеры # 8, Новые мутанты Новые мутанты (2019) # 7, Люди Икс гигантского размера: Джин Грей и Эмма Фрост, X-Force (2019) # 8, Люди Икс (2019) # 7 и Экскалибур (2019) # 8
Рассвет X Том. 9
Собирает : Новые мутанты (2019) # 8, Мародеры # 9, Кабель (2020) # 1, Люди Икс (2019) # 8, Экскалибур (2019) # 9 и X-Force (2019) # 9
Рассвет X Том. 10
Собирает : Новые мутанты (2019) # 9, Гигантские Люди Икс: Ночной змей, Геллионы # 1, Росомаха (2020) # 2, Люди Икс (2019) # 9 и Экскалибур (2019) # 10
Контрольный список для каждого выпуска XЛюди Икс № 1
Мародеры № 1
Мой обзор и теории Мародёров №1 !
Экскалибур № 1
Мой обзор и теории Экскалибура №1!
Новые мутанты № 1
Мой обзор и теории новых мутантов №1!
X-Force № 1
Мой обзор и теории X-Force # 1!
Люди Икс № 2
Мой обзор и теории Людей Икс №2!
Падшие Ангелы # 1
Мой обзор и теории падших ангелов №1!
Экскалибур № 2
Мой обзор Экскалибура №2!
Мародеры № 2
Мой обзор и теории Мародёров №2!
Новые мутанты № 2
Мой обзор New Mutants # 2!
X-Force № 2
Мой обзор X-Force # 2!
Падшие Ангелы # 2
Мой обзор Fallen Angels # 2!
Мародеры № 3
Люди Икс № 3
Экскалибур № 3
Новые мутанты № 3
Обзор!
X-Force № 3
Обзор!
Падшие Ангелы # 3
Мародеры № 4
Обзор!
X-Force № 4
Новые мутанты № 4
Экскалибур № 4
Падшие Ангелы # 4
Входящий # 1
В этом предварительном просмотре / загадочном убийстве Marvel, написанном Хикманом, РБ Сильвой и Марте Гарсиа, есть небольшая история с участием Мистера Синистера.Стоит прочитать, и для тизера он содержит Людей Икс / Фантастическая четверка .
Обзор!
Гвенпул наносит ответный удар # 5
Комикс не из серии «Рассвет X», в котором, тем не менее, фигурируют Кракоа, Росомаха и Квентин Квайр. История Лии Уильямс и Дэвида Балдеона, которые в дальнейшем будут производить X-Factor в DoX. Этот мини-фильм будет лучше читаться, если вы прочтете все 5 выпусков (и, честно говоря, изрядное количество «Гвенпул» до этого!), И это действительно эффективный сериал ближе.
Люди Икс # 4
Обзор!
Мародеры № 5
Новые мутанты № 5
X-Force № 5
Экскалибур № 5
Падшие Ангелы # 5
Экскалибур № 6
Обзор!
Голоса Marvel # 1
Включает рассказы о нескольких Людях Икс, действие которых происходит в эпоху Кракоа. Вита Айяла и Бернард Чанг занимаются историей Forge, и, что особенно важно для меня, творческая команда Bitter Root создает историю Росомахи и Халка!
Люди Икс / Фантастическая четверка # 1
Учитывая участие Мародеров в этой серии, я бы рекомендовал прочитать до Мародеры # 6 , хотя этот выпуск был опубликован вместе с Мародерами # 7.
Мой обзор!
Люди Икс / Фантастическая четверка # 2
Люди Икс / Фантастическая четверка # 3
Люди Икс / Фантастическая четверка # 4
Мой обзор!
Росомаха # 1
Как и X / FF выше, Wolverine — это дополнение серии Dawn of X wave 2, которое имеет больше смысла в порядке чтения раньше, чем его поместила бы дата выпуска (комикс был выпущен на той же неделе, что и Marauders # 8 и Новые мутанты # 7).
Технически, я бы поспорил, что вы могли бы разместить Wolverine # 1 даже раньше X-Force # 1 в начале Dawn of X. Если остальная часть истории разыграется в те же временные рамки, я могу внести соответствующие изменения!
Мой обзор!
Мародеры № 6
Падшие Ангелы # 6
Новые мутанты № 6
X-Force № 6
Обзор!
Оружие Плюс: Вторая мировая война № 1
Хорошо, это натянуто, но есть тематические и буквальные связи с Dawn of X в этом странном эпизоде, который может быть интересен стойким приверженцам.Во-первых, вся предпосылка связана с Weapon Plus, которая является расширением программы Weapon X, которая берет свое начало во времена Моррисона New X-Men . Во-вторых, Man-Slaughter (они превратили человека в оружие!) На самом деле очень привязан к научно-фантастическим темам, которые писатель Бенджамин Перси исследует в X-Force # 6 . И, наконец, дополнительная история о Brute Force (которая была фактическим мини-сериалом Marvel и взрывает мой мозг) упоминает программу Orchis!
Люди Икс # 5
Обзор!
Мародеры № 7
Экскалибур № 7
Люди Икс № 6
Обзор!
X-Force № 7
Дикие Мстители # 0
Доктор Стрэндж в эпизодической роли на Кракоа
Мародеры № 8
Новые мутанты № 7
Дэдпул # 6
Этот выпуск был выпущен намного позже, но его следует читать в хронологическом порядке до того, как начнется серия «Люди Икс гигантского размера».Дэдпул ворвался в Кракоа!
Гигантские Люди Икс: Джин Грей и Эмма Фрост # 1
Обзор!
Люди Икс # 7
Обзор!
X-Force № 8
Новые мутанты № 8
Экскалибур № 8
Мародеры № 9
Черная кошка № 9 — № 10
Не очень важно, но Росомаха объединяется с Фелицией, и они иногда разговаривают с Кракоа. Искусство Криса Анки убивает.
Кабель № 1
Обзор!
Новые мутанты № 9
Мстители # 32
Я обсуждал, в том числе и этот вопрос, но в этой истории есть огромных дразнил , которые могут иметь серьезные разветвления для Людей Икс.Имейте в виду, что если вы не поспеваете за Джейсоном Аароном и Эдом МакГиннессом, рассказывающим о Мстителях со времен «Marvel Fresh Start», 66% этой истории не будут казаться актуальными!
Экскалибур № 9
X-Force № 9
Люди Икс № 8
Обзор!
Люди Икс № 9
Обзор!
Гигантские Люди Икс: Ночной змей
Обзор!
Hellions # 1
Обзор!
Росомаха № 2
Мародеры № 10
Обзор!
Экскалибур № 10
Обзор!
Новые мутанты № 10
X-Force № 10
Обзор!
Люди Икс гигантского размера: Магнето # 1
День бесплатной книги комиксов 2020 — Люди Икс
Мой обзор! Обратите внимание, что специальный выпуск FCBD во многом предваряет событие X of Swords и также будет учитываться в этом порядке чтения!
Новые мутанты № 11
Росомаха № 3
Hellions # 2
Люди Икс № 10
Технически Empyre , хотя этот больше ориентирован на Людей Икс.Мой обзор!
Empyre: Люди Икс # 1
Empyre: Люди Икс # 2
Empyre Люди Икс № 3
Empyre Люди Икс № 4
Часть порядка чтения Empyre . Мой обзор!
Люди Икс № 11
События X-Men # 11, кажется, происходят более или менее одновременно с мини-сериалом Empyre X-Men . Он был опубликован после того, как были выпущены все 4 выпуска, поэтому я включил его сюда.
Бессмертная Женщина-Халк # 1
Посмертное вскрытие Empyre начинается с действительно хорошей беседы между Джен Уолтерс и Росомахой. Обратите внимание, что проблема будет относиться к событиям первой дуги Донни Кейтса и Ника Кляйна на Thor, и, как и следовало ожидать, это будет означать намного больше , если вы поймаете на Immortal Hulk Эла Юинга ( и тебе действительно должно быть!).
X-фактор № 1
Обзор!
Кабель № 2
Люди Икс гигантского размера: Fantomex
Обзор!
Мародеры № 11
Обзор!
X-Force № 11
Обзор!
Кабель # 3
Обзор!
Кабель # 4
Росомаха № 4
Росомаха № 5
Обзор!
Hellions # 3
X-фактор # 2
X-фактор № 3
Обзор!
Новые мутанты № 12
Обзор!
X-Force № 12
Обзор!
Мародеры № 12
Обзор!
Hellions # 4
Обзор!
Джаггернаут № 1
Джаггернаут № 2
Джаггернаут № 3
Джаггернаут № 4
Джаггернаут № 5
Размещение этих 5 выпусков Jugs mini является гибким, как и первоначальное отношение к общей картине Людей Икс! Тем не менее, довольно приятный сериал, если вам нравится Джаггернаут.
Marvel Voices: голоса коренных народов # 1
Истории Дэни Мунстар, Рана Синклера и Сильвер Фокс!
Мстители # 37
Мстители Джейсона Аарона строит историю Феникса, а это значит, что Люди Икс не далеко. Под конец — короткое дразнение с участием Росомахи и Джин Грей.
Дикие Мстители # 13
Джерри Дагган вводит Росомаху и Мэджик в свою дикую историю со сверхъестественным подтекстом, которая может быть связана с Рассветом X в будущем.Я ожидаю, что это должно произойти до X Swords , но в остальном время довольно гибкое.
Гигантские Люди Икс: Буря
Экскалибур № 11
Обзор!
Все — Х мечей!Порядок чтения события X of Swords
Фантастическая четверка # 25
Фантастическая четверка # 26
Некоторые обновления для Франклина Ричардса.
Далее: Правление X Героически поддержите Вестника комиксов!Если вам нравится «Вестник комиксов», и вы можете делать пожертвования, любой небольшой взнос поможет сохранить жизнь CBH и наполнит ее новыми руководствами и контентом по комиксам.


 2 (х — 9) — 2,3 (х + 4)
2 (х — 9) — 2,3 (х + 4) 
























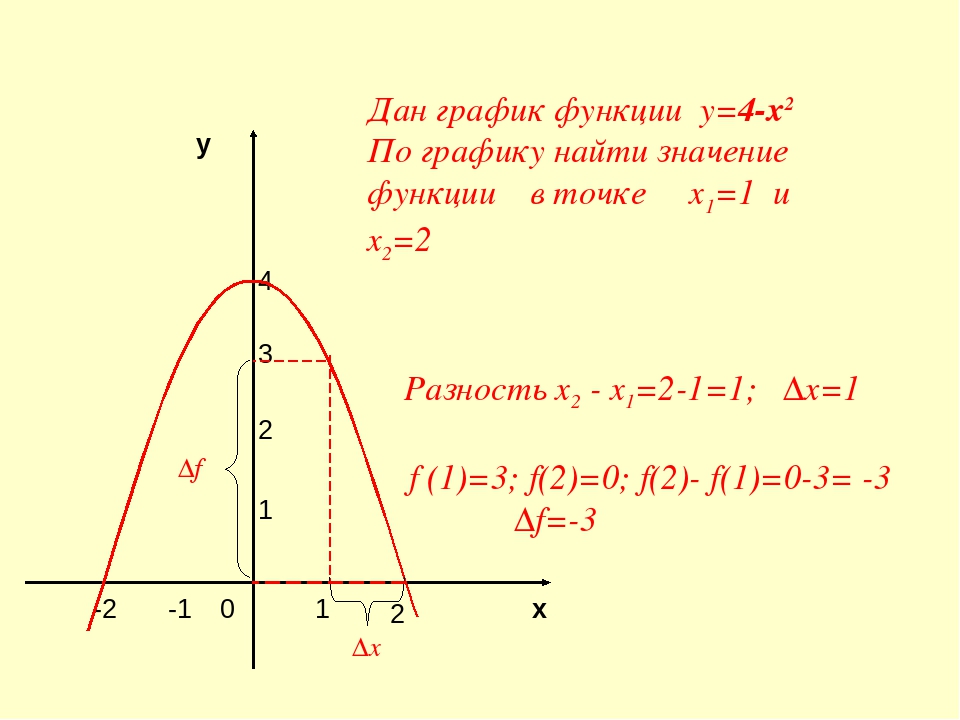
 Чтобы найти точку пересечения двух прямых, нам нужно решить систему уравнений x — y = 3 и -5 x — 2 y = -22 одновременно. Уравнение x — y = 3 можно решить относительно x, чтобы получить
Чтобы найти точку пересечения двух прямых, нам нужно решить систему уравнений x — y = 3 и -5 x — 2 y = -22 одновременно. Уравнение x — y = 3 можно решить относительно x, чтобы получить  Мы заменяем x на 2 и d y на — 3 в уравнении.
Мы заменяем x на 2 и d y на — 3 в уравнении. 
