Законы логики на уроках информатики и ИКТ
Разделы: Информатика
Урок по информатике рассчитан на учащихся 10-х классов общеобразовательной школы, в учебном плане которой входит раздел «Алгебра логики». Учащимся очень нелегко дается эта тема, поэтому мне, как учителю, захотелось заинтересовать их в изучении законов логики, упрощении логических выражений и с интересом подойти к решению логических задач. В обычной форме давать уроки по этой теме нудно и хлопотно, да и ребятам не всегда понятны некоторые определения. В связи с предоставлением информационного пространства, у меня появилась возможность выкладывать свои уроки в оболочке «learning». Учащиеся, зарегистрировавшись в ней, могут в свое свободное время посещать этот курс и перечитывать то, что было непонятно на уроке. Некоторые учащиеся, пропустив уроки по болезни, наверстывают дома или в школе пропущенную тему и всегда готовы к следующему уроку. Такая форма преподавания очень устроила многих ребят и те законы, которые им были непонятны, теперь в компьютерном виде ими усваиваются гораздо легче и быстрее. Предлагаю один из таких уроков информатики, который проводится интегративно с ИКТ.
План урока
- Объяснение нового материала, с привлечением компьютера – 25 минут.
- Основные понятия и определения, выложенные в «learning» — 10 минут.
- Материал для любознательных – 5 минут.
- Домашнее задание – 5 минут.
1. Объяснение нового материала
Законы формальной логики
Наиболее простые и необходимые истинные связи между мыслями выражаются в основных законах формальной логики. Таковыми являются законы тождества, непротиворечия, исключенного третьего, достаточного основания.
Эти законы являются основными потому, что в логике они играют особо важную роль, являются наиболее общими. Они позволяют упрощать логические выражения и строить умозаключения и доказательства. Первые три из вышеперечисленных законов были выявлены и сформулированы Аристотелем, а закон достаточного основания — Г. Лейбницем.
Закон тождества: в процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе.
Закон непротиворечия: невозможно, чтобы одно и то оке в одно то же время было и не было присуще одному и тому же в одном и том же отношении. То есть невозможно что-либо одновременно утверждать и отрицать.
Закон исключенного третьего: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано.
Закон достаточного основания: всякая истинная мысль должна быть достаточно обоснована.
Последний закон говорит о том, что доказательство чего-либо предполагает обоснование именно и только истинных мыслей. Ложные же мысли доказать нельзя. Есть хорошая латинская пословица: «Ошибаться свойственно всякому человеку, но настаивать на ошибке свойственно только глупцу». Формулы этого закона нет, так как он имеет только содержательный характер. В качестве аргументов для подтверждения истинной мысли могут быть использованы истинные суждения, фактический материал, статистические данные, законы науки, аксиомы, доказанные теоремы.
Законы алгебры высказываний
Алгебра высказываний (алгебра логики) — раздел математической логики, изучающий логические операции над высказываниями и правила преобразования сложных высказываний.
При решении многих логических задач часто приходится упрощать формулы, полученные при формализации их условий. Упрощение формул в алгебре высказываний производится на основе эквивалентных преобразований, опирающихся на основные логические законы.
Законы алгебры высказываний (алгебры логики) — это тавтологии.
Иногда эти законы называются теоремами.
В алгебре высказываний логические законы выражаются в виде равенства эквивалентных формул. Среди законов особо выделяются такие, которые содержат одну переменную.
Первые четыре из приведенных ниже законов являются основными законами алгебры высказываний.
Закон тождества:
А=А
Всякое понятие и суждение тождественно самому себе.
Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль другой, одно понятие другим. При нарушении этого закона возможны логические ошибки.
В рассуждении: Движение вечно. Хождение в школу — движение. Следовательно, хождение в школу вечно слово «движение» используется в двух разных смыслах (первое — в философском смысле — как атрибут материи, второе — в обыденном смысле — как действие по перемещению в пространстве), что приводит к ложному выводу.
Закон непротиворечия:
Не могут быть одновременно истинными суждение и его отрицание. То есть если высказывание А — истинно, то его отрицание не А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным.
Именно это равенство часто используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными. Примеры невыполнения закона непротиворечия:
1. На Марсе есть жизнь и на Марсе жизни нет.
2. Оля окончила среднюю школу и учится в X классе.
Закон исключенного третьего:
В один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А. Примеры выполнения закона исключенного третьего:
1. Число 12345 либо четное, либо нечетное, третьего не дано.
2. Предприятие работает убыточно или безубыточно.
3. Эта жидкость является или не является кислотой.
Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: «либо — либо», «истина—ложь». Там же, где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.
Рассмотрим следующее высказывание: Это предложение ложно. Оно не может быть истинным, потому что в нем утверждается, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
Парадокс (греч. paradoxos — неожиданный, странный) в этом примере возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере: В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру?
В логике из-за ее формальности нет возможности получить форму такого ссылающегося самого на себя высказывания. Это еще раз подтверждает мысль о том, что с помощью алгебры логики нельзя выразить все возможные мысли и доводы. Покажем, как на основании определения эквивалентности высказываний могут быть получены остальные законы алгебры высказываний.Например, определим, чему эквивалентно (равносильно) А (двойное отрицание А, т. е. отрицание отрицания А). Для этого построим таблицу истинности:
По определению равносильности мы должны найти тот столбец, значения которого совпадают со значениями столбца А. Таким будет столбец А.
Таким образом, мы можем сформулировать закон двойного отрицания:
Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание. Например, высказывание
Аналогичным образом можно вывести и проверить следующие законы:
Свойства констант:
Законы идемпотентности:
Сколько бы раз мы ни повторяли: телевизор включен или телевизор включен или телевизор включен … значение высказывания не изменится. Аналогично от повторения на улице тепло, на улице тепло,… ни на один градус теплее не станет.
Законы коммутативности:
A v B = B v A
А & В = В & А
Операнды А и В в операциях дизъюнкции и конъюнкции можно менять местами.
Законы ассоциативности:
A v(B v C) = (A v B) v C;
А & (В & C) = (A & В) & С.
Если в выражении используется только операция дизъюнкции или только операция конъюнкции, то можно пренебрегать скобками или произвольно их расставлять.
Законы дистрибутивности:
A v (B & C) = (A v B) &(A v C)
(дистрибутивность дизъюнкции
относительно конъюнкции)
А & (B v C) = (A & B) v (А & C)
(дистрибутивность конъюнкции
относительно дизъюнкции)
Закон дистрибутивности конъюнкции относительно дизъюнкции аналогичен дистрибутивному закону в алгебре, а закон дистрибутивности дизъюнкции относительно конъюнкции аналога не имеет, он справедлив только в логике. Поэтому необходимо его доказать. Доказательство удобнее всего провести с помощью таблицы истинности:
Законы поглощения:
A v (A & B) = A
A & (A v B) = A
Проведите доказательство законов поглощения самостоятельно.
Законы де Моргана:
Словесные формулировки законов де Моргана:
1.
2.
Мнемоническое правило: в левой части тождества операция отрицания стоит над всем высказыванием. В правой части она как бы разрывается и отрицание стоит над каждым из простых высказываний, но одновременно меняется операция: дизъюнкция на конъюнкцию и наоборот.
Примеры выполнения закона де Моргана:
1) Высказывание Неверно, что я знаю арабский или китайский язык тождественно высказыванию Я не знаю арабского языка и не знаю китайского языка.
2) Высказывание Неверно, что я выучил урок и получил по нему двойку тождественно высказыванию Или я не выучил урок, или я не получил по нему двойку.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
Для замены операции эквивалентности существует два правила:
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Знание правил замены операций импликации и эквивалентности помогает, например, правильно построить отрицание импликации.
Рассмотрим следующий пример.
Пусть дано высказывание:
Е = Неверно, что если я выиграю конкурс, то получу приз.
Пусть А = Я выиграю конкурс,
В = Я получу приз.
Тогда
Отсюда, Е = Я выиграю конкурс, но приз не получу.
Интерес представляют и следующие правила:
Доказать их справедливость можно также с помощью таблиц истинности.
Интересно их выражение на естественном языке.
Например, фраза
Если Винни-Пух съел мед, то он сыт
тождественна фразе
Если Винни-Пух не сыт, то меда он не ел.
Задание: придумайте фразы-примеры на данные правила.
2. Основные понятия и определения в Приложении 1
3. Материал для любознательных в Приложении 2
4. Домашнее задание
1) Выучить законы логики, используя курс «Алгебры логики», размещенный в информационном пространстве (www.learning.9151394.ru).
2) Проверить на ПК доказательство законов де Моргана, построив таблицу истинности.
Приложения
- Основные понятия и определения (Приложение 1).
- Материал для любознательных (Приложение 2).
3.07.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Построить таблицу истинности для логического выражения (A ^ B) -> (C v not A)
Построить таблицу истинности для логического выражения. Информатика в 8 классе.
Тема: «Основы алгебры логики».
Основы алгебры логики
Основы алгебры логики на уроках информатики изучаются в школе, начиная с 8 класса.
Прежде чем приступить к выполнению задания, разберем базовые понятия алгебры логики.

Алгебра логики (алгебра высказываний) — это формальная логическая теория, раздел математической логики. Основание алгебры логики положил Джордж Буль (1815 — 1864), развил же и усовершенствовал её Эрнст Шрёдер (1841-1902).
Высказывание — это предложение, о котором имеет смысл утверждать, истинно оно или ложно. Истина = 1, ложь =0.
Высказывание, включающее другие высказывания, называют сложным. Для образования сложных высказываний используют логические операции (связки).
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логические операции в порядке приоритета.
- Инверсия (отрицание)
- Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или A.
Читается «НЕ» (например, «не А»). - Конъюнкция (логическое умножение)
- Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б») - Дизъюнкция (логическое сложение)
- Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б») - Импликация (следование)
- Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б») - Эквивалентность (равнозначность)
- Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Для записи логических функций часто используют таблицы истинности.
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
РЕШЕНИЕ
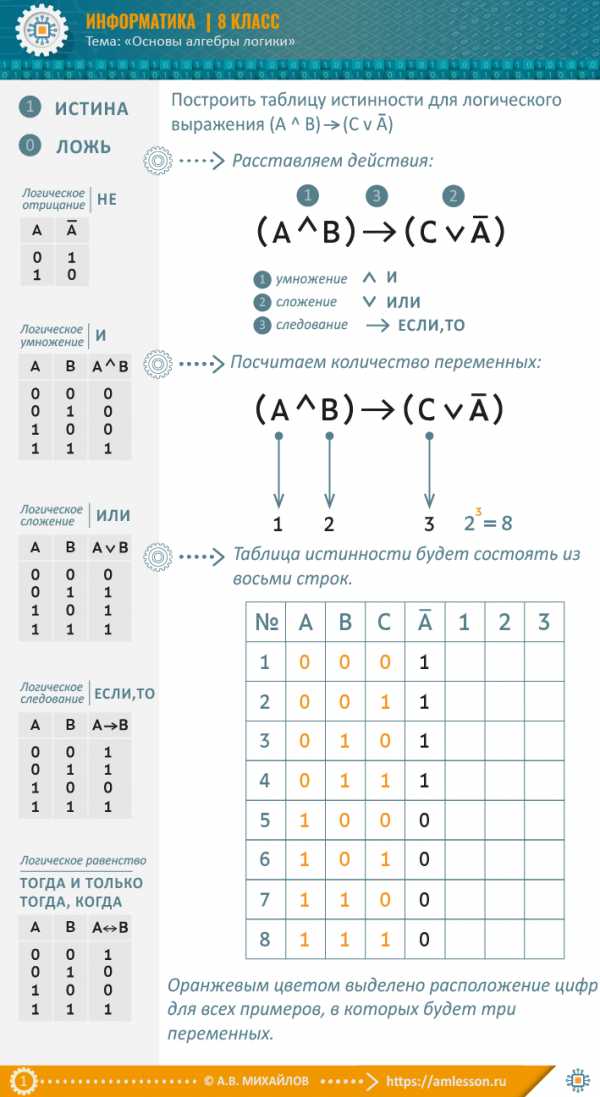
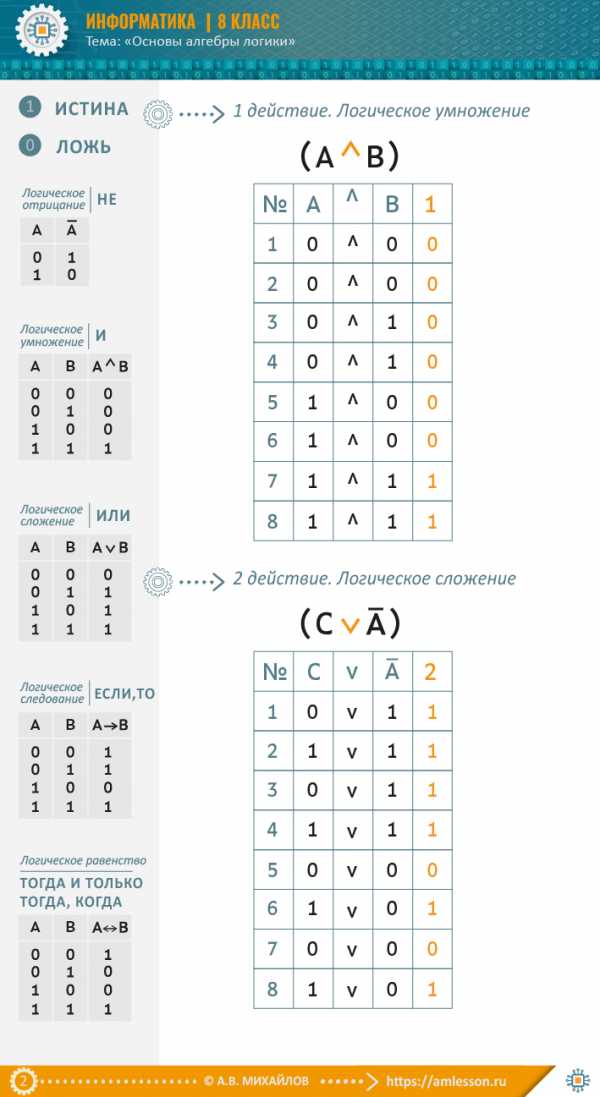
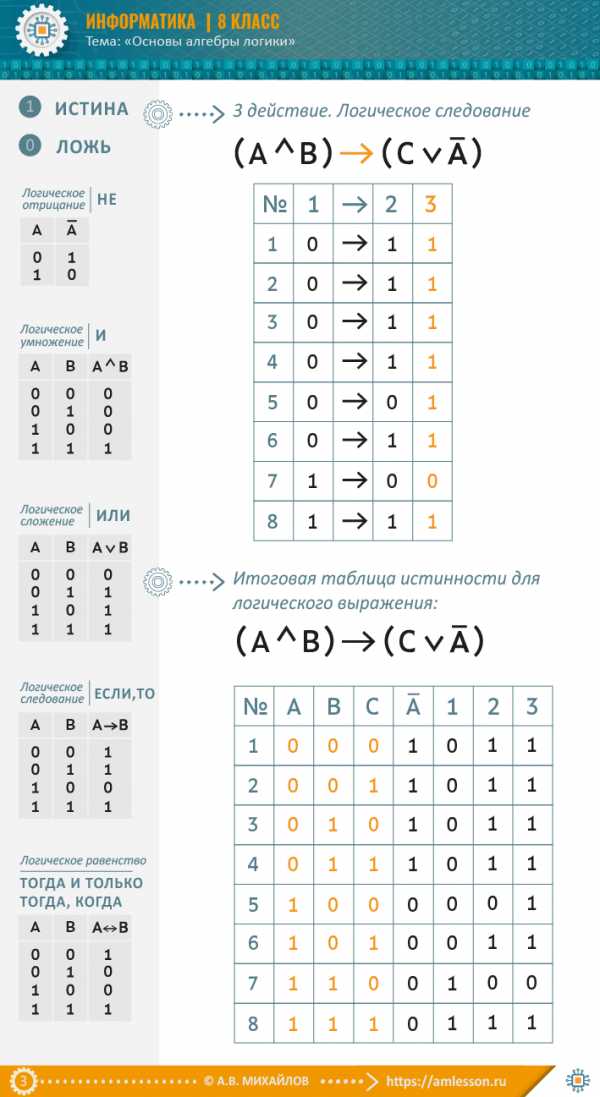
amlesson.ru
Таблица истинности онлайн с примерами
Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).
Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N — общее количество возможных комбинаций, n — число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.
Таблицы истинности для основных функций

Примеры: конъюнкция — 1&0=0, импликация — 1→0=0.
Порядок выполнения логических операций
Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.
Последовательность построения (составления) таблицы истинности:
https://uchim.org/matematika/tablica-istinnosti — uchim.org
- Определить количество N используемых переменных в логическом выражении.
- Вычислить количество всевозможных наборов значений переменных M = 2N , равное количеству строк в таблице.
- Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
- Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
- Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
- Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
- Заполнить окончательный столбец значений для функции F.
Таким образом, можно составить (построить) таблицу истинности самостоятельно.
Составить таблицу истинности онлайн
Заполните поле ввода и нажмите OK. T — истина, F — ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.
Обозначения
- Множества или выражения большими буквами латинского алфавита: A, B, C, D…
- A’ — штрих — дополнения множеств
- && — конъюнкция («и»)
- || — дизъюнкция («или»)
- ! — отрицание (например, !A)
- \cap — пересечение множеств \cap
- \cup — объединение множеств (сложение) \cup
- A&!B — разность множеств A∖B=A-B
- A=>B — импликация «Если …, то»
- AB — эквивалентность
Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами — логика
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
