Размещения, перестановки, сочетания с повторениями. Формула включения — исключения
Размещения с повторениями
Определение. Отображение множества первых натуральных чисел в данное множество , называется размещением с повторениями, составленным из данных элементов по .
Размещения с повторениями называются также конечными последовательностями.
Два размещения с повторениями одинаковы тогда и только тогда, когда на одинаковых местах находятся одни и те же элементы.
Если в размещении с повторениями некоторый элемент ставится в соответствие различным натуральным числам, т.е., иначе говоря, данный элемент занимает различных мест, то говорят, что этот элемент повторяется в размещении раз.
Пример. Всевозможные размещения с повторениями из трех элементов по 2:
Теорема. Число всевозможных размещений с повторениями из элементов по равно
Доказательство.
Предположим, что число размещений с повторениями из элементов по равно . Составим из данных элементов всевозможные размещения с повторениями по элементу. Во всяком размещении с повторениями по элементу
первые элементов
образуют некоторое размещение с повторениями из по элементов. В качестве последнего -го элемента может быть взят любой из элементов. При различных выборах получаются различные размещения. Кроме того, два различные размещения -го порядка дают два различные размещения -го порядка.
Таким образом, число всех размещений -го порядка равно
Задача. Имеется различных книг, каждая в экземплярах. Сколькими способами может быть сделан выбор книг из числа данных?
Перестановки с повторениями
Всякое размещение с повторениями, в котором элемент повторяется раз, элемент повторяется раз и т.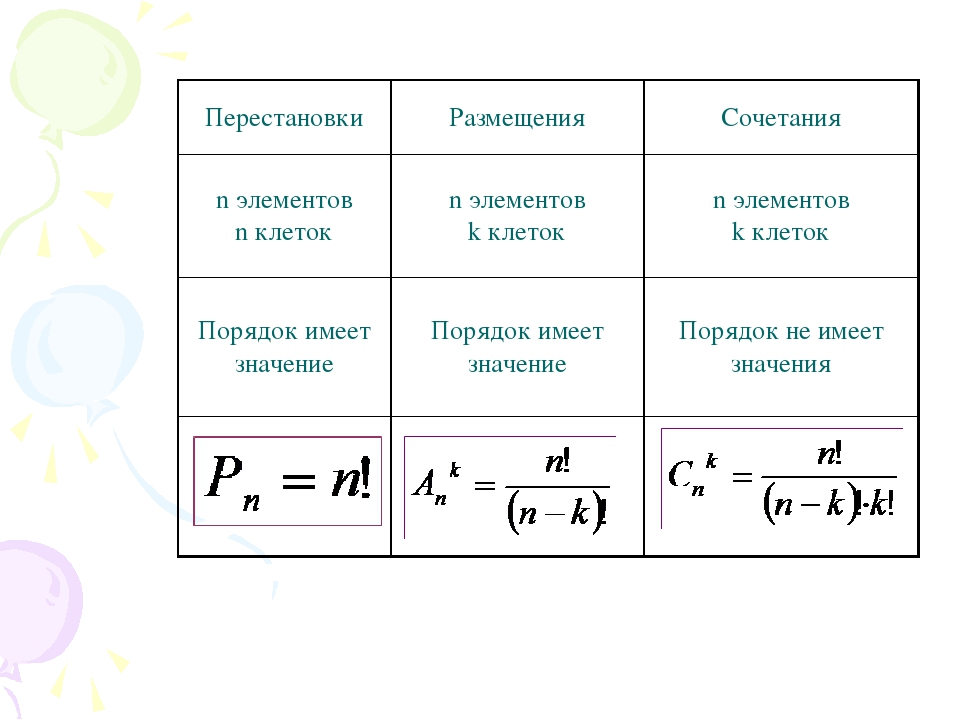 д. элемент повторяется раз, где , , , — данные числа, называется перестановкой с повторениями порядка
д. элемент повторяется раз, где , , , — данные числа, называется перестановкой с повторениями порядка
в которой данные элементы повторяются соответственно , , раз.
Теорема. Число различных перестановок с повторениями из элементов , в которых элементы повторяются соответственно раз, равно
Доказательство. Если мы будем считать все элементов перестановки с повторениями различными, то всего различных вариантов перестановок элементов — . Однако среди этих перестановок не все различны. В самом деле, все элементы мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы , , , . Таким образом, всякая перестановка может быть записана способами. Следовательно, число различных перестановок с повторениями равно
Задача. Дано различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала предметов, вторая предметов, а третья предметов?
Показать решение
Ответ.
Сочетания с повторениями
Определение. Если каждому элементу некоторого конечного множества поставлено в соответствие целое неотрицательное число — кратность данного элемента, то говорят, что задано сочетание с повторениями. Сумма кратностей всех элементов называется порядком сочетания.
Всякое сочетание с повторениями -го порядка, составленное из множества, содержащего элементов, называется также сочетанием с повторением из элементов по .
Если — кратности элементов , то по определению есть порядок сочетания
Теорема. Число сочетаний с повторениями из элементов по выражается формулой
Пример. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами можно купить 7 пирожных?
Решение. Положим пирожные в коробку, а чтобы они не перепутались, разделим их картонными разделителями. Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.
Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.
Итак два класса объектов 1 (7 штук) и 0 (3 штуки) — покупка — 10 объектов.
Два способа рассуждения:
(1) задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов.
(2) другой способ рассуждения (эквивалентный). Надо разбить 10 мест на две группы: для 7 пирожных и 3 разделителей.
В чем особенность: объекты повторяются, причем один эклер на вкус неотличим от другого. Отсюда название: сочетания с повторениями. Можно представлять себе, что пирожные непрерывно пекут, так что они не переводятся, сколько ни ешь. Это совсем другая ситуация, чем в обычных сочетаниях!!!
Пусть заданы два числа: — число выбираемых элементов, и — число типов элементов, из которых производится выбор. Число сочетаний с повторениями порядка из элементов типов равно числу способов выбора мест для собственно выбираемых элементов различных классов, или, что то же: для разделителей между ними.
Итак, основная формула:
Задача. Имеется одинаковых предметов. Сколькими способами можно распределить эти предметы между лицами?
Сочетания с повторениями с дополнительными условиями
Сколько существует сочетания с повторениями таких, что в них обязательно входят элементы фиксированных типов?
Сразу возьмем по одному элементу указанного типа, и тогда уже сразу окажутся заняты мест. Остальные мест можно заполнять элементами прежних типов.
В частности, пусть число типов — числа выбранных элементов. Сколько существует сочетаний с повторениями, так что представлены хотя бы по одному все типы элементов?
Пример. шаров размещаются по ящикам. Сколько существует способов разместить их так, что пустых ящиков нет?
Решение. Пусть нолики — шарики, а единички — стенки ящиков (потребуется единичек). Две единички сразу кладем по краям.
Теперь положим между ними шарики-нолики, а далее нужно заполнить некоторые промежутки между ними так, чтобы между любыми двумя ноликами находилась не более одной единички.
Метод координат. Подсчет числа путей
Рассмотрим координатную сетку: двигаясь по ней, помечаем каждый перекресток — производим суммирование числа возможных путей, ведущих на каждый перекресток. Получаем известный треугольник Паскаля.
Поскольку на перекресток на уровне (считая сверху и принимая верхний уровень за нулевой) ведет путей (число способов выбрать движений направо вниз из общего числа движений вниз), то свойство суммирования путей на перекрестке можно записать как
По прежнему остается справедливым свойство симметрии .
Формула включения — исключения
Определение. Число элементов множества называется мощностью множества и обозначается .
Теорема. Пусть даны множества . Тогда количество элементов в объединении этих множеств можно найти по формуле:
Доказательство проводится по индукции. Пусть . Нужно доказать формулу
Пусть . Нужно доказать формулу
Действительно, множество состоит из всех элементов множества и тех элементов множества , которые не содержатся в множестве . Тогда, сложив количества элементов во множествах и , мы два раза посчитаем количество элементов, общих для множеств и .
Предположим, что формула включения — исключения справедлива для множеств.
Докажем ее для множеств. Множество можно представить в виде
Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):
Используя формулу
и формулу включения — исключения для множеств, получаем
В эту формулу подставляем выражение, полученное ранее, и теорема доказана.
1. Есть три билета в различные театры. Сколькими способами они могут быть распределены между 25 школьниками, если каждый школьник может получить только один билет?
2. Есть три билета на КВН 1 апреля. Сколькими способами они могут быть распределены между 25 школьниками (более одного билета в руки не давать!!!)?
Есть три билета на КВН 1 апреля. Сколькими способами они могут быть распределены между 25 школьниками (более одного билета в руки не давать!!!)?
3. Телефонный номер состоит из 7 цифр. Насколько легче угадать правильный номер, если знать, что все его цифры различны?
4. В буфете продаются 5 сортов пирожков: с яблоками, с капустой, картошкой, мясом и грибами (цена всех пирожков одинакова). Скольким числом способов можно сделать покупку из 10 пирожков?
5. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы попробовать пирожков всех видов?
6. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы в нее вошло не менее двух пирожков с мясом и хотя бы один пирожок с яблоками?
7. Скольким числом способов можно вывести на арену цирка 5 львов и 4 тигра так, чтобы никакие два тигра не шли друг за другом (оказавшись рядом, они начинают драться)?
8. За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями. Для участия в спецоперации по освобождению заколдованной принцессы нужно выбрать 5 рыцарей, но при этом нельзя посылать вместе рыцарей, враждующих друг с другом. Скольким числом способов это можно сделать?
За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями. Для участия в спецоперации по освобождению заколдованной принцессы нужно выбрать 5 рыцарей, но при этом нельзя посылать вместе рыцарей, враждующих друг с другом. Скольким числом способов это можно сделать?
9. Докажите формулу
10. Докажите, что число различных решений уравнения
в неотрицательных целых числах равно .
11. Докажите, что число различных решений уравнения
в натуральных числах равно .
12. Сколькими способами можно разложить 15 одинаковых шаров по 5 различным ящикам так, чтобы оказалось не более двух пустых ящиков?
13. Сколькими способами можно разложить 20 одинаковых шаров по 5 различным ящикам так, чтобы в каждом ящике оказалось не менее двух шаров?
14. Сколькими способами можно разложить 20 одинаковых шаров по 6 различным ящикам так, чтобы в каждом ящике оказалось не более 5 шаров?
15. Докажите, что число таких перестановок чисел , которые удовлетворяют условию при всех , равно
Докажите, что число таких перестановок чисел , которые удовлетворяют условию при всех , равно
основные формулы. Перестановки, размещения, сочетания. Задачи по теории вероятностей с решением онлайн. Помощь студентам
Основные понятия и формулы
Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Правило умножения (основная формула комбинаторики)
Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:
Пример 1
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Решение
Первая монета имеет
альтернативы – либо орел, либо решка. Для
второй монеты также есть
альтернативы
и т. д., т.е.
.
д., т.е.
.
Искомое количество способов:
Правило сложения
Если любые две группы и не имеют общих элементов, то выбор одного элемента или из , или из , …или из можно осуществить способами.
Пример 2
На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.
Решение
Математическая книга может быть выбрана способами, экономическая — способами.
По правилу суммы существует способа выбора математической или экономической книги.
Размещения и перестановки
Размещения – это
упорядоченные совокупности элементов, отличающиеся друг от друга либо составом,
либо порядком элементов.
Размещения без повторений, когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .
Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:
Пример 3
Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.
Решение
Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:
Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно
Пример 4
Сколькими способами можно рассадить 4 человек за одним столом?
Решение
Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
Размещения с повторениями,
когда отобранный элемент перед отбором следующего возвращается в генеральную
совокупность. Такой выбор называется последовательным выбором с возвращением, а
его результат — размещением с
повторениями из
элементов по
.
Такой выбор называется последовательным выбором с возвращением, а
его результат — размещением с
повторениями из
элементов по
.
Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Пример 5
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Решение
Каждый из способов
распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров
по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как
один, так и несколько пассажиров, то одни и те же пассажиры могут
повторяться. Поэтому число таких комбинаций равно числу размещений с
повторениями из 7 элементов по 6:
Так как одном этаже может выйти как
один, так и несколько пассажиров, то одни и те же пассажиры могут
повторяться. Поэтому число таких комбинаций равно числу размещений с
повторениями из 7 элементов по 6:
Сочетания
Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.
Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора элементов из генеральной совокупности объема получаются комбинации, которые называются сочетаниями без повторений из элементов по .
Число сочетаний из элементов по равно:
Пример 6
В ящике 9 яблок. Сколькими
способами можно выбрать 3 яблока из ящика?
Сколькими
способами можно выбрать 3 яблока из ящика?
Решение
Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:
Количество способов, которыми можно выбрать 3 яблока из 9:
Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из элементов по .
Число сочетаний с повторениями из элементов по :
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .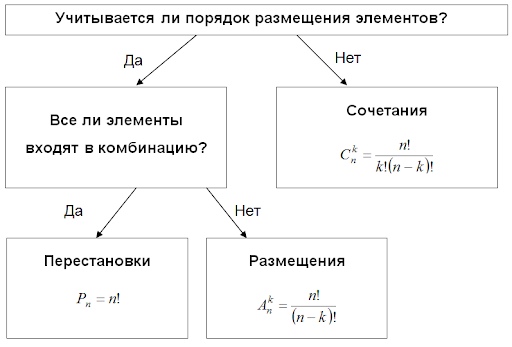
Пример 7
На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?
Решение
Это задача на отыскание числа сочетаний с повторениями из 3 по 6:
Разбиение множества на группы
Пусть множество из различных элементов разбивается на групп так, то в первую группу попадают элементов, во вторую — элементов, в -ю группу — элементов, причем . Такую ситуацию называют разбиением множества на группы.
Число разбиений на групп, когда в первую попадают элементов, во вторую — элементов, в k-ю группу — элементов, равно:
Пример 8
Группу из 16 человек
требуется разбить на три подгруппы, в первой из которых должно быть 5 человек,
во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно
сделать?
Сколькими способами это можно
сделать?
Решение
Здесь
Число разбиений на 3 подгруппы:
Задачи контрольных и самостоятельных работ
Задача 1
Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?
Задача 2
Доступ к файлу открывается, только если введен правильный пароль – определенный трехзначный номер из нечетных цифр. Какова максимальное число возможных попыток угадать пароль?
Задача 3
Группу из 10 человек требуется разбить на две непустые подгруппы и . Сколькими способами можно это сделать?
Задача 4
Два наборщика должны набрать 16 текстов. Сколькими способами они могут распределить эту работу между собой.
Задача 5
Шесть студентов-переводников нужно распределить по трем группам. Сколькими способами это можно сделать?
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Задача 6
Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?
Задача 7
В ящике 5 красных и 4 зеленых яблока. Сколькими способами можно выбрать 3 яблока из ящика?
Задача 8
Из ящика, в котором лежат 10 красных и 5 зеленых яблок, выбирают одно красное и два зеленых яблока. Сколькими способами можно это сделать.
Задача 9
В группе из 25 студентов нужно выбрать старосту и 3 членов студенческого комитета. Сколькими способами можно это сделать.
Задача 10
Акционерное собрание компании выбирает из 50 человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами это можно сделать?
Задача 11
В
телевизионной студии работают 3 режиссера, 4 звукорежиссера, 5 операторов, 7
корреспондентов и 2 музыкальных редактора. Сколькими способами можно составить съемочную
группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и
двух корреспондентов.
Сколькими способами можно составить съемочную
группу, состоящую из одного режиссера, двух операторов, одного звукорежиссера и
двух корреспондентов.
Задача 12
На группу из 25 человек выделены 3 пригласительных билета на вечер. Сколькими способами они могут быть распределены (не более одного билета в руки).
Задача 13
Имеются 7 билетов: 3 в один театр и 4 – в другой. Сколькими способами они могут быть распределены между студентами группы из 25 человек?
Задача 14
Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.
Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.
КСП урока по алгебре в 10 классе по теме «Основные элементы комбинаторики»
|
Раздел долгосрочного планирования: Основы комбинаторики Школа: КГУ«Каратальская средняя школа» Дата : класс:10 ФИО учителя: Мухамбетова Заинамгул Тлегеновна Участвовали: Не участвовали: |
|
|
Тема урока |
Основные элементы комбинаторики |
|
Цели обучения, достигаемые на этом уроке (Ссылка на учебный план) |
10. 10.3.1.2- применять формулы для вычисления перестановок, размещений и сочетаний без повторений; 10.3.1.3- применять формулы для вычисления перестановок, размещений и сочетаний без повторений и с повторениями. |
|
Цель урока |
— определять основные элементы комбинаторики; — различать понятия «перестановки», «размещения» и «сочетания» без повторений и с повторениями; — применять формулы для вычисления перестановок, размещений и сочетаний безповторений и с повторениями. |
|
Критерии оценивания |
— определяет основные элементы комбинаторики; — различает понятия «перестановки», «размещения» и «сочетания» без повторений и с повторениями; — применяет формулы для вычисления перестановок, размещений и сочетаний без повторений и с повторениями |
|
Языковые задачи |
Сочетания, используемые для диалога и письма: Факториал, элементы комбинаторики, вычисления перестановок, размещений и сочетаний без повторений и с повторениями; |
|
Воспитание ценностей |
Формировать между учащимися в классе доверие,
дружбу и уважение. |
|
Межпредметная связь |
Информатика |
|
Предыдущие знания |
На уроках информатики изучали понятие факториала. В 5-9 классах изучили приемы решения задачи по комбинаторике: метод перебора; решение с помощью дерева возможных вариантов; с помощью комбинаторного правила умножения; составление таблиц; решение с помощью графов. |
Ход урока
|
Запланированные этапы урока |
Виды упражнений, запланированных на урок: |
Ресурсы
|
||
|
1. |
1. Приветствие. Отчет дежурных о готовности класса к уроку и об отсутствующих. 1. «Размотались — замотались». Учащиеся встают в круг, на слово «размотались» широко разводят обе руки в стороны и начинают хаотично передвигаться, на слово «замотались» обнимают встречного участника , повторяется 2-3 раза. (Концентрация внимания учащихся, положительный эмоциональный настрой)
2. Мотивация к усвоению нового материала. Проблемная ситуация: «ПОПС» Вопрос: Сколько будет всего обниманий, если каждый из вас обнимется со всеми участниками? – Итак, какие будут ответы?
(Допустим нас 15.
Это комбинаторная задача. Оценивание: «Уточняющие вопросы» Итак, тема нашего урока: «Основные элементы комбинаторики». Целепологание. Каковы же цели нашего урока?
(Учащиеся высказывают свои предположения, затем четко проговаривают цели и критерии урока, используя слайд). 3. Чтобы перейти к изучению новой темы я вам предлагаю « Море вопросов»: — Что такое факториал? — На каком уроке вы изучали? (информатики). -Как обозначается факториал? (n!) -Запишите формулу факториала. (n!=1·2·3···n ) Приведите приемы решения задач по комбинато- рике, которые вы проходили в предыдуших классах? (решение методом перебора, с помощью дерева возможных вариантов, комбинаторного правила умножения, табличный способ, с помощью графов.) Форма работы: коллективная Оценивание: «Светофор» |
Слайд №1
|
||
|
Середина урока |
Деление на группы «1,2,3»
4. Группы получают конверты, в которых для каждой группы информация для индивидуального изучения и предлагается решить в группе по 2 задачи) Оценивание: «Похвальный бутерброд» Форма: групповая Дифференциация: Диалог и оказание поддержки.
5 .Стратегия «Эстафета». Форма работы: индивидуальная Дифференциация: темп и задания Оценивание: «Элективный тест»
А теперь перейдем к индивидуальной работе. «Решение комбинаторных задач» (8 минут)
3) =
5) Докажите тождество: 6) =13 б) Задания для способных учащихся: Решите уравнение: =30
Дескриптор: 1) Применяет формулу для вычисления размещений: ; 2) Применяет формулу для вычисления сочетаний: ; 3) Применяет формулу для вычисления перестановок = n! 4) Упрощает выражение , используя формулу для вычисления размещений 5) Доказывает тождество, используя формулу сочетания ; 6) Факториал разности преобразует в произведение множителей; 7)Сокращает дроби 8) Решает уравнение, используя разложение факториала суммы в произведение множителей;
Дескриптор: 1) Применяет формулу для вычисления размещений; 2) Применяет формулу для вычисления сочетаний; 3) Применяет формулу для вычисления перестановок; 4) Упрощает выражение , используя формулу для вычисления размещений; 5) Доказывает тождество, используя формулу сочетания; 6) Решает уравнение
6. Форма работы: работа в парах Оценивание: взаимооценивание по ключу.
|
Приложение 2 Конверты : информация, 2 задания.
Слайд №2
Карточки для каждой пары
Слайд №3
Приложение 2
Слайд №3
Приложение 3
У каждого ученика разноцветные стикеры A, B, C, D
Приложение 4
Приложение |
||
|
Конец урока |
Домашнее задание дифференцированное: §23, стр. Рефлексия учеников в конце урока: « Пять пальцев» На листе бумаги обведите руку. Каждый палец имеет свой смысл, согласно ему, выскажите свое мнение) |
|
||
|
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими? |
Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?
|
Охрана здоровья и соблюдение техники безопасности
|
||
|
На данном уроке использовала дифференциацию по способу «Диалог и оказание поддерж ки», в стратегии « Волонтер», «Темп» в «Решение комбинатор ных задач» с учетом потребностей учащихся, отбор заданий, в течении всего урока личную поддержку учеников. |
Ученики на данном уроке определют основные элементы комбинаторики;
— различают понятия «перестановки», «размеще- ния» и «сочетания», применяют формулы для вычисления перестановок, размещений и сочетаний. Для достижения поставленной цели на уроке, использую стратегии активного обучения и оценивание: «Море вопросов» и «Светофор», «Волонтер» и «Диалог и оказание поддержки» , Эстафету «Решение комбинаторных задач» и «Элективный тест», Для достижения поставленной цели и в целях развития навыков обсуждения применяла «Уточняющие вопросы», на каждом этапе урока имеет место оценивание, чтобы определить траекторию развития ученика, выявить пробелы и как их устранить. |
«Размотались -замотались» с целью концентрации внимания учащихся и создания положительного эмоционального настроя. Смена динамичных групп сменного состава позволяет создать благоприятную атмосферу .Чередование деятельности позволяет снять эмоциональную и физическую усталость обучающихся. |
||
|
Рефлексия по уроку Была ли реальной и доступной цель урока или учебные цели? Все ли учащиесы достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке? Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?
|
Используйте данный раздел урока для рефлексии. которые имеют важное значение в этом столбце. |
|||
|
|
||||
|
Итоговая оценка Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока
|
Приложение 1 (5-экземпляров)
«Волонтер» 1.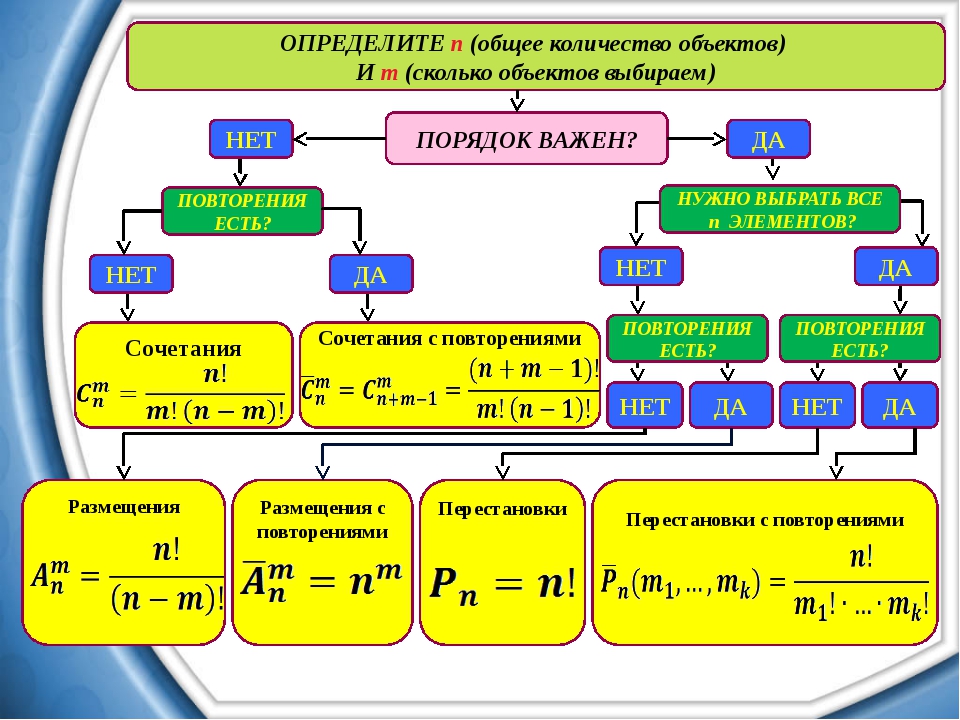 Изучить информацию индивидуально, решить задачу; 2. В группе, обсудить информацию и правильность решения задачи 3. Выбрать волонтера, который содержательно ознакомит другую группу с информацией.
Изучить информацию индивидуально, решить задачу; 2. В группе, обсудить информацию и правильность решения задачи 3. Выбрать волонтера, который содержательно ознакомит другую группу с информацией.
1. Размещения
Определение. Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.
Размещения вычисляются по формуле
Пример. При расследовании хищения установлено, что у преступника семизначный телефонный номер, в котором ни одна цифра не повторяется и нет нуля. Следователь, полагая, что перебор этих номеров потребует одного-двух часов, доложил о раскрытии преступления. Прав ли он?
Следователь, полагая, что перебор этих номеров потребует одного-двух часов, доложил о раскрытии преступления. Прав ли он?
Решение. Число номеров равно числу размещений из 9 элементов по 7, т.е. равно По формуле получаем = = =160*56*9=3024 номеров. Даже если на проверку одного номера тратить 1 минуту, то на все уйдет 3024 часа или 126 суток. Таким образом, следователь – не прав.
Ответ: следователь – не прав.
=
Дескриптор: — определяет понятие «размещения»; — записывает формулу; — определяет количество размещений, применяя формулу; -записывает ответ.
Приложение 1
2. Сочетания
Определение. Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. (Подмножества, отличающиеся друг от друга только порядком следования элементов, не считаются различными.)
Число сочетаний из n элементов по m обозначается символом и вычисляется по формуле:
Пример. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?
Решение. Можно выбрать трёх для участия в праздничном концерте из15 учеников класса способом сочетания по по формуле: 13*7 *5= 455
Ответ: 455 способами
Дискриптор: — определяет понятие «сочетания»; — записывает формулу; — определяет количество сочетаний, применяя формулу; — записывает ответ.
Приложение 1
3. Перестановки
Определение. Перестановками из n элементов называются такие соединения из n элементов, которые отличаются друг от друга лишь порядком следования элементов.
= n!
Пример. Сколькими способами могут встать в очередь в билетную кассу 5 человек?.
Решение. Cпособы, которыми могут встать в очередь в билетную кассу 5 человек, равно числу перестановок из пяти элементов, т.е. .
Ответ: 102 способами
Вычислить:
Вычислить: =
Дискриптор: — определяет понятие «перестановки»; — записывает формулу; — определяет количество перестановок применяя формулу; -записывает ответ
Стратегия «Эстафета» «Решение комбинаторных задач»
Проверка по образцу
= = =
= =
3) =17=5040
(n-3)³
4) Докажите тождество: , 495, или
5) Решите уравнение: =13, , х+1=13, х=12
Дескриптор:
1) Применяет формулу для вычисления размещений; 2) Применяет формулу для вычисления сочетаний;
3) Применяет формулу для вычисления перестановок;
4) Упрощает выражение , используя формулу для вычисления размещений; 5) Доказывает тождество, используя формулу сочетания;
6) Решает уравнение
|
№ |
Элемент комбинаторики |
|
Определение понятия |
|
Формула |
|
1 |
Сочетания |
A
|
Соединения из n элементов, которые отличаются друг от
друга лишь порядком следования элементов. |
1 |
|
|
2
|
Перестановка |
B |
Соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования |
2 |
|
|
3 |
Размещения |
C |
Соединения, которые отличаются друг от друга хотя бы одним элементом |
3 |
= n! |
Ключ : 1С2; 2А3; 3В1
2.
 3 Формулы комбинаторики — СтудИзба
3 Формулы комбинаторики — СтудИзба2.1. Формулы комбинаторики
2.1.1. Перестановки
1) Перестановки без повторений.
Перестановки — это комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком расположения этих элементов. Возьмем n различных элементов a1, a2, a3, … an; будем переставлять эти элементы всевозможными способами, оставляя без изменения число элементов и меняя только порядок их расположения. Обозначим общее число полученных таким образом перестановок P(n). P — первая буква французского слова permutation — перестановка.
Составив таблицу перестановок для n элементов и применив (n — 1) раз правило произведения, получим число всех возможных перестановок:
P(n) = n • (n -1) • (n — 2) • … • 3 • 2 • 1 = n!
Такие перестановки называются перестановками без повторений (один и тот же элемент не может повториться в комбинации, все элементы различны).
Задача: шесть человек могут в разном порядке сесть за круглый стол, сколько существует способов разместить эти шесть человек за столом?
Решение: т.к. все люди различны и их комбинации различаются только порядком следования, то мы имеем перестановки без повторений. Определим их число:
Р(6) = 6! = 1 • 2 • 3 • 4 • 5 • 6 = 720.
2) Перестановки с повторениями
Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.
Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., nk элементов к-го вида, то имеем перестановки с повторениями, их число:
, где n1+…+nk = n.
Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА.
Решение: имеем перестановки с повторениями.
А) ДЕД n=3, k=2, n1=2, n2=1
P3(2, 1) = 3!/(2! • 1!) = 6 / 2 = 3;
Б) МАТЕМАТИКА n=10, k=6, n1=2, n2=3, n3=2, n4=n5=n6=1
P10(2,3,2,1,1,1)=10!/(2! • 3! • 2!)=2•4•5•6•7•9•10 = 134 400.
2.1.2. Размещения
1) Размещения без повторений.
Размещениями называют комбинации, составленные из n данных элементов по k элементов (k<=n, k>0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения Ank . А — первая буква французского слова arrangement, что в переводе означает «размещение», «приведение в порядок». Число всех возможных размещений находится по формуле:
.
Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар.
Решение: имеем размещения без повторений из пяти элементов по два, из число: .
2) Размещения с повторениями.
Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:
.
Задача: сколько четырехзначных номеров можно составить из 10 цифр?
Решение: имеем размещения с повторениями из 10 элементов по 4, их число: .
2.1.3. Сочетания
1) Сочетания без повторений.
Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: Cnk C — первая буква французского слова combinasion — сочетание.
Сочетания обозначаются: Cnk C — первая буква французского слова combinasion — сочетание.
Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет Cnk . Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет Pk, т.к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет Cnk • Pk . Но такие комбинации называются размещениями. Таким образом, Ank = Cnk • Pk, тогда:
.
Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия?
Решение: имеем сочетания без повторений из 7 элементов по 2; их число: .
2) Сочетания с повторениями.
Если в сочетаниях некоторые элементы (или все) могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями. Их число определяется по формуле: .
Задача: сколько наборов из 7 пирожных можно составить, если в продаже имеется 4 сорта пирожных?
Решение: имеем сочетания с повторениями из четырех по 7 по, их число: .
Math.ru
Наум Яковлевич ВиленкинМ.: Наука, 1969. 328 с.
Тираж 100000 экз.
| |||||||||||
Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой .
 В данной книге о комбинаторных проблемах рассказывается в занимательной, популярной форме. Тем не менее в ней разбираются и некоторые довольно сложные задачи, дается понятие о методах рекуррентных соотношений и производящих функций.
Первая глава книги посвящена общим правилам комбинаторики — правилам суммы и произведения. Во второй главе изучаются размещения, перестановки и сочетания. В главе 3 изучаются задачи, в которых на рассматриваемые комбинации налагаются те или иные ограничения. В главе 4 рассмотрены задачи на разбиения чисел и рассказано о геометрических методах в комбинаторике. Глава 5 посвящена задачам о случайных блужданиях и различным модификациям арифметического треугольника. В главе 6 рассказано о рекуррентных соотношениях, а в главе 7 — о производящих функциях, и в частности о биномиальной формуле.
В данной книге о комбинаторных проблемах рассказывается в занимательной, популярной форме. Тем не менее в ней разбираются и некоторые довольно сложные задачи, дается понятие о методах рекуррентных соотношений и производящих функций.
Первая глава книги посвящена общим правилам комбинаторики — правилам суммы и произведения. Во второй главе изучаются размещения, перестановки и сочетания. В главе 3 изучаются задачи, в которых на рассматриваемые комбинации налагаются те или иные ограничения. В главе 4 рассмотрены задачи на разбиения чисел и рассказано о геометрических методах в комбинаторике. Глава 5 посвящена задачам о случайных блужданиях и различным модификациям арифметического треугольника. В главе 6 рассказано о рекуррентных соотношениях, а в главе 7 — о производящих функциях, и в частности о биномиальной формуле.Содержание
Предисловие
Глава I. Общие правила комбинаторики
Суеверные велосипедисты
Размещения с повторениями
Системы счисления
Секретный замок
Код Морзе
Морской семафор
Электронная цифровая вычислительная машина
Генетический код
Общие правила комбинаторики
Задача о домино
Команда космического корабля
Задача о шашках
Сколько человек не знают иностранных языков?
Формула включений и исключений
В чем ошибка?
Решето Эратосфена
Глава II. Размещения, перестановки и сочетания
Размещения, перестановки и сочетания
Футбольное первенство
Размещения без повторений
Научное общество
Перестановки
Задача о ладьях
Лингвистические проблемы
Хоровод
Перестановки с повторениями
Анаграммы
Сочетания
Генуэзская лотерея
Покупка пирожных
Сочетания с повторениями
Снова футбольное первенство
Свойства сочетаний
Частный случай формулы включений и исключений
Знакопеременные суммы сочетаний
Глава III. Комбинаторные задачи с ограничениями
Львы и тигры
Постройка лестницы
Книжная полка
Рыцари короля Артура
Девушка спешит на свидание
Сеанс телепатии
Общая задача о смещении
Субфакториалы
Караван в пустыне
Катание на карусели
Очередь в кассу
Задача о двух шеренгах
Новые свойства сочетаний
Глава IV. Комбинаторика разбиений
Комбинаторика разбиений
Игра в домино
Раскладка по ящикам
Букет цветов
Задача о числе делителей
Сбор яблок
Сбор грибов
Посылка фотографий
Флаги на мачтах
Полное число сигналов
Разные статистики
Разбиения чисел
Отправка бандероли
Общая задача о наклейке марок
Комбинаторные задачи теории информации
Проблема абитуриента
Уплата денег
Покупка конфет
Как разменять гривенник?
Разбиение чисел на слагаемые
Диаграммная техника
Двойственные диаграммы
Формула Эйлера
Глава V. Комбинаторика на шахматной доске
Человек бродит по городу
Арифметический квадрат
Фигурные числа
Арифметический треугольник
Расширенный арифметический треугольник
Шахматный король
Обобщенный арифметический треугольник
Обобщенные арифметические треугольники и m-ичная система счисления
Некоторые свойства чисел Cm(k,n)
Шашка в углу
Арифметический пятиугольник
Геометрический способ доказательства свойств сочетаний
Случайные блуждания
Броуновское движение
У Шемаханской царицы
Поглощающая стенка
Блуждания по бесконечной плоскости
Общая задача о ладьях
Симметричные расстановки
Два коня
Глава VI. Рекуррентные соотношения
Рекуррентные соотношения
Числа Фибоначчи
Другой метод доказательства
Процесс последовательных разбиений
Умножение и деление чисел
Задачи о многоугольниках
Затруднение мажордома
Счастливые троллейбусные билеты
Рекуррентные таблицы
Другое решение проблемы мажордома
Решение рекуррентных соотношений
Линейные рекуррентные соотношения с постоянными коэффициентами
Случай равных корней характеристического уравнения
Третье решение задачи мажордома
Глава VII. Комбинаторика и ряды
Деление многочленов
Алгебраические дроби и степенные ряды
Действия над степенными рядами
Применение степенных рядов для доказательства тождеств
Производящие функции
Бином Ньютона
Полиномиальная формула
Ряд Ньютона
Извлечение квадратных корней
Производящие функции и рекуррентные соотношения
Разложение на элементарные дроби
Об едином нелинейном рекуррентном соотношении
Производящие функции и разбиения чисел
Сводка результатов по комбинаторике разбиений
Задачи по комбинаторике
Решения и ответы
| |||||||||||
Задачи на подсчет числа сочетания
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников
Тема программы: Комбинаторика
Тема: «Задачи на подсчет числа размещений, перестановок, сочетаний».
– повторить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний без повторов; изучить формулы для нахождения числа различных видов комбинаций: размещений, перестановок, сочетаний с повторами, научиться распознавать задачи на нахождение размещений, перестановок, сочетаний; решить простейшие комбинаторные задачи с помощью этих формул;
– развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать умения сравнивать, систематизировать, обобщать;
– формировать научное мировоззрение у обучающихся, культуру математической речи, информационную и коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.
I . Организационный момент
Преподаватель проверяет готовность к уроку.
Я рада приветствовать всех Вас на сегодняшнем уроке.
II . Мотивация. Сообщение темы, целей урока
Определения: перестановки, размещения, сочетания.
Важен ли порядок? В каких соединениях? (размещение)
№1. Экзамен состоит из 5 задач, которые можно решать в любом порядке. Сколькими способами можно расставить задачи. (способов)
№2. В магазине продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора. (способа)
№3. Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 0, 2, 4, 6, 8. (всего чисел А, а чисел начинающихся с нуля –, тогда А–=96)
Тема сегодняшнего урока «Задачи на подсчет числа размещений, перестановок, сочетаний.». Давайте вместе попробуем сформулировать цели урока:
– научиться распознавать задачи на нахождение размещений, перестановок, сочетаний;
– решать простейшие комбинаторные задачи с помощью этих формул.
III . Изучение новой темы
Рассмотрим слово «КВАНТ», состоящее из 5 различных букв. Если менять порядок букв, получим 5!=120 перестановок
Если проделать то же самое со словом «АТАКА», то перестановок будет меньше, потому что, меняя местами 1,3 и 5-ю буквы, будем получать то же самое слово. Т.к. три буквы А можно менять местами 3!=6 способами, то перестановок будет в слове «АТАКА» в 6 раз меньше, т.е.
Вывод: Перестановками в такой выборке, где есть один элемент, называются перестановками с повторениями. Обозначается : Р(n1 , n2,…. nk)
Р ( n 1, n 2,…. nk )= , где n – количество повторений элементов
Задача: Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»
перестановки
Ответ: 151200 перестановки
Рассмотрим следующую задачу.
В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить 8 различных открыток?
Сколькими способами можно купить 8 различных открыток?
Решение. Данная задача на отыскание числа сочетаний без повторений, т.к. требуется купить 8 различных открыток
Ответ: 45 способов
Проделаем то же самое, но только определим «Сколькими способами можно купить в нем 8 открыток?
Данная задача на отыскание числа сочетаний с повторениями из n = 10 элементов по k =8. Следовательно, она решается по формуле
Ответ : 24310 способов
Вывод: Иными словами, выборки которые отличаются количеством элементов хотя бы одного типа, называются сочетаниями с повторениями, а их общее число будем обозначать .
Задача: В кондитерской имеется 3 вида пирожных. Сколькими способами можно купить 9 пирожных?
Решение. В задаче требуется найти число всевозможных групп по 9 элементов, которые можно составить из данных трех различных элементов, причем указанные элементы в каждой группе могут повторяться, а сами группы отличаются друг от друга хотя бы одним элементом. Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
Это задача на отыскание числа сочетаний с повторениями из трех элементов по девять. Следовательно,
В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими различными способами могут выйти пассажиры на каждом этаже, начиная со второго?
способов
А теперь ту же задачу, но вопрос сформулируем иначе.
В лифт восьмиэтажного дома вошли 5 пассажиров. Сколькими способами могут выйти пассажиры на каждом этаже, начиная со второго?
Задача такого вида называется «размещения с повторением», обозначается и вычисляется по принципу умножения.
Вычисляется по следующей формуле:
Решение. Задача сводится к распределению 5 пассажиров по 7 этажам (т. е. набор упорядоченный), причем возможны повторения (т. е. несколько пассажиров могут выйти на одном этаже). Таким образом, задача сводится к нахождению числа размещений с повторениями:
Задача: Сколькими способами девочка Яна может разложить 12 кукол по трём ящикам, если каждый ящик может вместить все куклы?
Ответ:
Задача №1. Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Буквы азбуки Морзе состоят из символов – точка и тире. Сколько букв получим, если потребуем, чтобы каждая буква состояла не более чем из пяти указанных символов?
Решение. Число всех букв, каждая из которых записывается одним символом, равно
Число всех букв, каждая из которых записывается двумя символами, равно .
Число всех букв, каждая из которых записывается тремя символами, равно .
Число всех букв, каждая из которых записывается четырьмя символами, равно .
Число всех букв, каждая из которых записывается пятью символами, равно .
Число всех указанных букв будет равно 62.
Задача №2. Сколько всего чисел (не больше 100000) можно составить из цифр 1, 2, 3, 4 и 5 в каждом из которых цифры расположены в неубывающем порядке?
Решение. Это задача о числе сочетаний из пяти цифр по одному, по два, по три, по четыре и по пяти с повторениями в каждом случае. Поскольку , , , , , то существует чисел, удовлетворяющих условию задачи.
V . Подведение итогов занятия. Рефлексия.
(Обобщаются новые знания, делаются выводы о достигнутых целях урока. Поощряются активные студенты, выставляются обоснованные преподавателем оценки.)
1) Подведем итоги нашего занятия.
Соединения виды перечислить?
На какие они делятся ? ( повторения и без)
Важен ли порядок? В каких соединениях? (размещение)
4) Формулы нахождения: перестановок, размещения, соединения с повторениями и без.
2) Обсуждение и выставление оценок за урок.
Достиг ли ты своих целей? ______________
Оцени степень усвоения: _______________
Продолжи одно из предложений:
VI . Домашнее задание
1. Сколькими способами можно разместить 8 пассажиров по трем вагонам?
Ответ: .
2. Сколькими способами Буратино, кот Базилио и лиса Алиса могут поделить между собой 5 одинаковых золотых монет?
Ответ: .
3. Сколько различных браслетов можно сделать из 5 одинаковых изумрудов, 6 одинаковых рубинов и 7 одинаковых сапфиров ( всего в браслет входит 18 камней)? ( =)
Определение числа сочетаний
Пусть имеется $n$ различных объектов. Чтобы найти число сочетаний из $n$ объектов по $k$, будем выбирать комбинации из $m$ объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).
Например, есть три объекта <1,2,3>, составляем сочетания по 2 объекта в каждом. Тогда выборки <1,2>и <2,1>- это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: <1,2>, <1,3>, <2,3>.
На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета). k$ онлайн, используйте калькулятор ниже.
k$ онлайн, используйте калькулятор ниже.
Видеоролик о сочетаниях
Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Полезные ссылки
Решебник по ТВ
Решебник с задачами по комбинаторике и теории вероятностей:
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*. *nk.
Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*. *nk.
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая – из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2.
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n1*n2*n3=6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=. nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов <1, 2, 3>по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается An m и вычисляется по формуле:
Замечание: n!=1*2*3*. *n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т. к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6. Для множества <1, 2, 3>сочетаниями являются <1, 2>, <1, 3>, <2, 3>.
Число сочетаний из n элементов по m
Число сочетаний обозначается Cn m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов <1, 2, 3>являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
Презентация «Основы комбинаторики.
 Размещения, перестановки, сочетания» 11 класс
Размещения, перестановки, сочетания» 11 классОсновы комбинаторики.
Размещения, перестановки,
сочетания.
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
знать:
- определения трех важнейших понятий комбинаторики:
- размещения из n элементов по m;
- сочетания из n элементов по m;
- перестановки из n элементов;
- основные комбинаторные формулы
- отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;
- применять основные комбинаторные формулы при решении простейших комбинаторных задач.

уметь:
множество
Множество характеризуется объединением некоторых однородных объектов в одно целое.
Объекты, образующие множество, называются элементами множества.
Множество будем записывать, располагая его элементы в фигурных скобка {a, b, c, … , e, f}.
Во множестве порядок элементов роли не играет, так {a, b} = {b, a}.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается символом ø.
множество
Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В.
В
А
Множество {a, b} является подмножеством множества {a, b, c, … , e, f}.
Обозначается
Пример:
Задача
Перечислите возможные варианты подмножества множества {3, 4, 5, 7, 9}.
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству.
Комбинаторика является важным разделом математики, который исследует закономерности расположения, упорядочения, выбора и распределения элементов с фиксированного множества.
ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут быть выполнены в соответствии k и m способами, тогда какое-то одно из этих действий можно выполнить k + m способами.
Пример №1
Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Сколькими способами можно добраться из города А в город В?
Решение
N=12+13+23=38
Пример № 2
В ящике имеется n разноцветных шариков. Произвольным образом вынимаем один шарик. Сколькими способами это можно сделать?
Решение. Конечно, n способами.
Конечно, n способами.
Теперь эти n шариков распределены по двум ящикам: В первом m шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами это можно сделать?
Решение.
Из первого ящика шарик можно вытянуть m различными способами, из второго k различными способами, всего N = m + k способами.
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Пусть две выполняемые одно за другим действия могут быть осуществлены в соответствии k и m способами Тогда обе они могут быть выполнены k ∙ m способами.
Пример № 3
В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места?
Решение
N=8∙7∙6=336
Пример № 4
Сколько можно записать двузначных чисел в десятичной системе счисления?
Решение. Поскольку число двузначное, то число десятков (m) может принимать одно из девяти значений: 1,2,3,4,5,6,7,8,9. Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, что m = 9, а k= 10. Всего получим двузначных чисел
Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, что m = 9, а k= 10. Всего получим двузначных чисел
N = m ·k = 9·10 =90.
Пример № 5
В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение. По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет
N =182 + 30 = 212.
Типы соединений
Множества элементов называются соединениями.
Различают три типа соединений:
- перестановки из n элементов;
- размещения из n элементов по m;
- сочетания из n элементов по m (m < n).

Определение: Перестановкой из n элементов называется любое упорядоченное множество из n элементов.
Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте.
ПЕРЕСТАНОВКИ
Перестановки – это такие соединения по n элементам из данных элементов, которые отличаются одно от другого порядком элементов.
Число перестановок из n элементов обозначают Рn.
Рn = n · (n — 1) · (n – 2) · … · 2 · 1 = n!
Определение:
Пусть n — натуральное число. Через n! (читается «эн факториал») обозначается число, равное произведению всех натуральных чисел 1 от до n:
n! = 1 · 2 · 3 · … · n.
В случае, если n = 0, по определению полагается: 0! = 1.
ФАКТОРИАЛ
Пример № 6
Найдем значения следующих выражений: 1! 2! 3!
7!
Пример № 7
Чему равно
а)Р5 ;
б) Р3.
Пример № 8
Упростите
а) 7! · 8
б) 12! · 13 ·14
в) κ! · (κ + 1)
Пример № 9
Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?
Решение.
n =8
Р8=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320
РАЗМЕЩЕНИЯ
Определение. Размещением из n элементов по m называется любое упорядоченное множество из m элементов, состоящее из элементов n элементного множества.
Число размещений из m элементов по n обозначают:
вычисляют по формуле:
Пример № 9
Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?
Решение.
Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (уроков) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре (m=9, n=4) то есть A94:
При составлении расписания мы будем выбирать 4-элементное подмножество (уроков) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре (m=9, n=4) то есть A94:
Пример № 10
Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты?
Решение.
Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A242:
СОЧЕТАНИЯ
Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества
Число сочетаний из n элементов по m обозначают
и вычисляют по формуле:
Пример № 11
Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных ?
Решение.
n =24, m=2
Учитывается ли порядок следования элементов в соединении?
Д А
НЕТ
Все ли элементы входят в соединение?
СОЧЕТАНИЯ
РАЗМЕЩЕНИЯ
ПЕРЕСТАНОВКИ
Рn = n!
Д А
НЕТ
Определить к какому типу относится соединений относится задача.
1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
2. В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
Учитывается ли порядок следования элементов в соединении?
( да)
Все ли элементы входят в соединение?
( да)
Вывод: перестановка
Учитывается ли порядок следования элементов в соединении?
Все ли элементы входят в соединение?
(нет)
(на этот вопрос ответ не нужен)
Вывод: сочетания
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
Учитывается ли порядок следования элементов в соединении?
Все ли элементы входят в соединение?
(нет)
( да)
Вывод: размещение
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Сколько различных вариантов расположения музыкантов возможно?
Решение.
Учитывается ли порядок следования элементов в соединении?
( да)
Все ли элементы входят в соединение?
(да)
Вывод: перестановка
Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1
n =4
Р4 = 4! = 4 · 3 · 2 ·1=24
«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»?
Кто автор высказывания?
Е
Е
перестановки
К
размещение
Л
сочетание
Е
А
С
Й
Н
И
О
Ы
Р
Ч
В
М
12
21
120
56
132
720
6720
5040
9
1
Результаты решения задач
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
А
Л
Е
К
С
Е
Й
Н
К
И
О
В
Л
А
Е
Л
О
Ч
И
В
Ы
Р
К
ДОМАШНЕЕ ЗАДАНИЕ
Выучить конспект и формулы.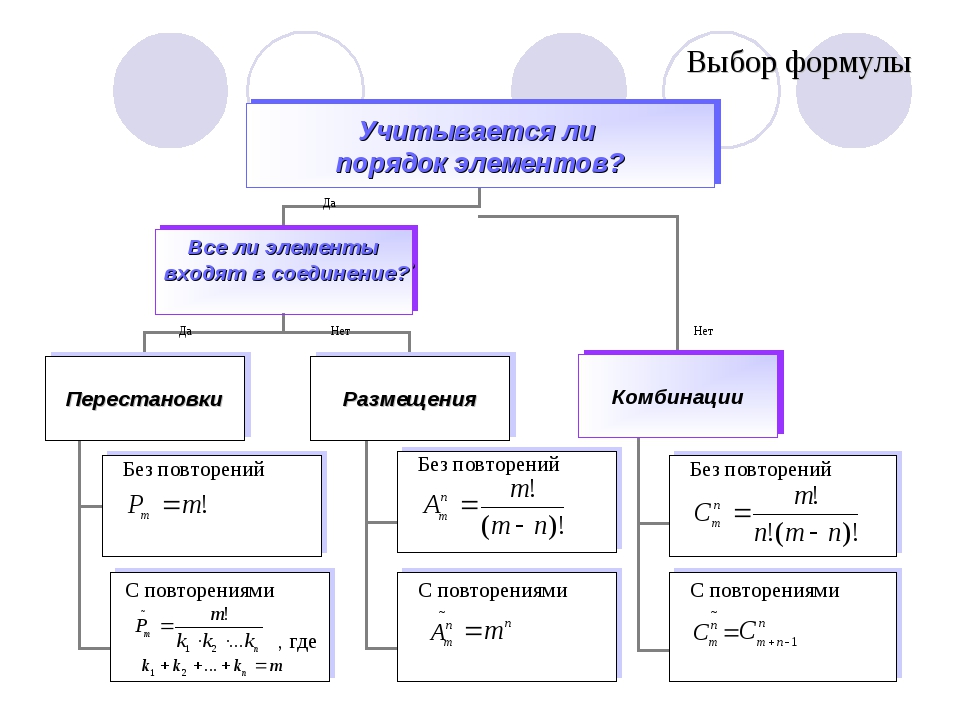
С. 321 № 1062
С. 325 №1074,1075
С. 329 №1081
Excel: объединение формул в мега-формулу
Проблема: когда мне нужно построить сложное вычисление, мне иногда нужно построить несколько промежуточных формул, чтобы помочь разобраться в проблеме. Когда все эти формулы работают, могу ли я объединить логику промежуточных формул в единую формулу?
Стратегия: Использование временных подформул — отличный способ вычислить довольно сложную формулу. Существует относительно простой способ вернуть все эти формулы в единую формулу.
Рассмотрим предыдущий пример, формула в J7 = INDEX (B2: G20, J5, J6) ссылается на две другие ячейки J5 и J6. Каждая из этих ячеек содержит формулу.
Стратегия: вы можете выбрать символы в строке формул и скопировать их в буфер обмена с помощью Ctrl + C. Когда вы копируете целую ячейку, возникает множество сложностей, в том числе проблема, связанная с невозможностью вставить эту ячейку в середину формулы или в диалоговое окно «Заменить». Вместо этого, копируя символы из строки формул, вы получаете обычный текст в буфере обмена и можете вставлять его в другую формулу или в диалоговом окне «Заменить».Вот что вы делаете:
Вместо этого, копируя символы из строки формул, вы получаете обычный текст в буфере обмена и можете вставлять его в другую формулу или в диалоговом окне «Заменить».Вот что вы делаете:
- Выберите ячейку J5. В строке формул щелкните мышью после знака равенства и перетащите в конец формулы. Нажмите Ctrl + C, чтобы скопировать эти символы в буфер обмена. Выйдите из режима редактирования, нажав клавишу Esc.
- Выберите ячейку J7. В строке формул выделите ссылку на J5 .
- Нажмите Ctrl + V, чтобы вставить формулу из J5, чтобы заменить ссылку на J5.
- Выберите ячейку J6. Нажмите F2, Ctrl + Shift + Home, Shift + стрелка вправо, Ctrl + C, Esc.Эти сочетания клавиш редактируют ячейку, а затем выделяют все, кроме знака равенства.
- Выберите ячейку J7. Выберите ссылку на J6
- Нажмите Ctrl + V, чтобы вставить формулу из J6, чтобы заменить ссылку на J6.
Результат — одна формула, заменяющая три формулы.
- Это устрашающая формула, если сложить все вместе.

Результат: ваши коллеги будут поражены вашей способностью создавать сложные формулы.
Альтернативная стратегия: вместо выполнения только что описанных шагов вы можете использовать диалоговое окно «Заменить», чтобы объединить промежуточные формулы в мега-формулы. Выполните следующие шаги:
- Выберите ячейку J5. В строке формул с помощью мыши выберите все, начиная от знака равенства и заканчивая концом формулы. Нажмите Ctrl + C, чтобы скопировать эти символы в буфер обмена. Нажмите клавишу Esc, чтобы выйти из строки формул.
- Выберите ячейки J7: J8. Попутно: убедитесь, что этот выбор содержит две ячейки, даже если вы работаете только с одной формулой! Если вы выберете две или более ячеек, команда «Заменить все» будет работать только внутри выделенного фрагмента.Если вы выберете только одну ячейку, команда «Заменить все» будет распространяться на все 17 миллиардов ячеек на листе.
- Выберите «Домой», «Найти и выделить», «Заменить» или Ctrl + H.

- В поле «Найти» введите J5.
- Вкладка в поле «Заменить на». Нажмите Ctrl + V. Excel скопирует символы из формулы J5 в диалоговое окно.
- Нажмите кнопку «Параметры».
- Убедитесь, что в раскрывающемся списке «Искать в» установлено значение «Формулы». Убедитесь, что флажок «Соответствовать содержимому всей ячейки» снят.(Если вы запустите новый сеанс Excel, оба эти параметра будут правильными. Однако в диалоговом окне запоминаются параметры из последнего поиска и замены, которые вы сделали ранее в текущем сеансе, поэтому всегда стоит потратить время, чтобы нажать кнопку Параметры чтобы убедиться, что эти настройки верны.)
- Щелкните «Заменить все». Excel удалит ссылку на J5 из выбранных ячеек и заменит ее символами из J5.
- Повторите шаг 1 для ячейки J6.
- Повторите шаги 2 «» 8.
В зависимости от того, сколько раз промежуточные формулы упоминаются в окончательной формуле, использование «Найти и заменить» может быть быстрее, чем использование метода копирования и вставки.

Попался: будьте осторожны, чтобы ваши целевые формулы не содержали ссылок, содержащих какую-либо другую форму B2 и C2, например B20 или C210909. Если ваши формулы действительно содержат такие ссылки, при замене B2 Excel вслепую поместит формулу B2, где символы B2 появляются в B20.
Дополнительные ресурсы по Microsoft Excel
Как комбинировать функции в формуле
В этом видео я покажу вам, как можно использовать несколько функций Excel для разделения, изменения и объединения значений внутри одной формулы.
Здесь у нас есть образцы данных, а в столбце B — текстовые значения с числом в конце. Что мы хотим сделать, так это увеличить эти числа, используя значение в столбце C.
Теперь, если я попытаюсь сделать это напрямую, с формулой, которая добавляет C5 к B5, я получу сообщение об ошибке, потому что значение в B является текстом, а Excel не позволит вам добавлять числа и текст.
Итак, что мне нужно сделать, это извлечь число, затем выполнить математические вычисления, а затем снова собрать все вместе. Давайте сделаем это шаг за шагом.
Давайте сделаем это шаг за шагом.
Сначала я воспользуюсь функцией ВПРАВО, чтобы извлечь 3 символа справа. Это дает нам номер. По левому краю видно, что число все еще находится в текстовом формате.
Однако теперь я могу добавить значение из столбца C.
На этот раз это работает, потому что Excel может автоматически преобразовывать текст в число как часть математической операции. Мы получаем правильный результат 2, но теряем заполнение нулями.
Итак, давайте добавим отступ обратно с помощью функции ТЕКСТ, которая позволит нам применить числовой формат внутри формулы.Мне просто нужно обернуть существующую формулу в функцию ТЕКСТ и использовать «000» в качестве числового формата.
Хорошо, теперь у нас есть увеличенное число, дополненное нулями.
Последним шагом является повторное соединение этого числа с исходной текстовой строкой с помощью простой конкатенации.
Для этого я просто жестко закодирую текст «Item» в начале формулы, а затем воспользуюсь амперсандом, чтобы присоединить текст к уже созданному нами числу с дополнениями.
Когда я нажимаю return, мы получаем окончательный результат.
Теперь я могу скопировать формулу вниз по таблице, чтобы увеличить оставшиеся значения.
Когда вы сталкиваетесь с подобной проблемой, главное — работать маленькими шагами и проверять свой прогресс в процессе. Конечный результат может показаться сложным, но в большинстве случаев каждая часть формулы делает что-то очень простое.
Использование CONCATENATE для объединения имен
Урок 18: Использование CONCATENATE для объединения имен
/ ru / excelformulas / using-the-if-function / content /
«Эй, как дела? Я знаю, что сегодня мы должны были съесть немного тайской еды, но я застрял на работе.
Мой босс хочет, чтобы я скопировал список имен из электронной таблицы в текстовый документ. Но когда я копирую и вставляю, форматирование оказывается странным. Я думаю, что было бы лучше, если бы имя и фамилия были в в том же столбце , но напечатать все это займет целую вечность ».
Наша таблица
После того, как вы загрузили нашу электронную таблицу, откройте файл в Excel или другом приложении для работы с электронными таблицами. Похоже, у нас есть список контактной информации. У каждого человека есть своя собственная строка, и есть столбцы для имени, фамилии и другой контактной информации каждого человека.
Как быстро решить эту проблему?
Мы хотим, чтобы информация из столбцов «Фамилия» и «Имя» отображалась вместе в одной и той же ячейке, но для ввода всего вручную потребуется много времени. Вместо того, чтобы объединять эти данные вручную, мы можем использовать функцию CONCATENATE , чтобы сделать это автоматически.
Как это работает
Слово конкатенация — это просто еще один способ сказать «объединить» или «соединить вместе». Функция СЦЕПИТЬ позволяет объединить текст из разных ячеек в одну ячейку.В нашем примере мы можем использовать его для объединения текста в столбце A и столбце B для создания объединенного имени в новом столбце.
Прежде чем мы начнем писать функцию, нам нужно вставить новый столбец в нашу электронную таблицу для этих данных. В нашем примере мы вставим его справа от столбца B.
Написание функции
Мы готовы ввести нашу функцию в ячейку C2 . Как обычно, мы начнем со знака равенства (=), за которым следует имя функции и открытая скобка:
= СЦЕПИТЬ (
В текущей версии Excel вы можете использовать новую функцию СЦЕПИТЬ вместо СЦЕПИТЬ.Эти две функции работают одинаково.
Теперь мы готовы ввести наши аргументы. Аргументы сообщают функции СЦЕПИТЬ , какие ячейки объединить. В нашем примере мы хотим объединить текст в ячейках A2 и B2 , поэтому мы сделаем каждую из них аргументом:
= СЦЕПИТЬ (B2, A2)
Хорошо, давайте запустим эту функцию!
Вы могли заметить, что между именем и фамилией нет пробелов. Это потому, что CONCATENATE объединит именно то, что вы ему скажете, и ничего более . Если вы хотите, чтобы в ячейке отображались знаки препинания, пробелы или другие детали, вам нужно указать СЦЕПИТЬ, чтобы они включались.
Это потому, что CONCATENATE объединит именно то, что вы ему скажете, и ничего более . Если вы хотите, чтобы в ячейке отображались знаки препинания, пробелы или другие детали, вам нужно указать СЦЕПИТЬ, чтобы они включались.
Чтобы добавить пробел, мы можем просто добавить еще один аргумент: «» (две двойные кавычки вокруг пробела) . Убедитесь, что три аргумента разделены запятыми:
= СЦЕПИТЬ (B2; «»; A2)
Отлично! Теперь мы можем использовать дескриптор заполнения , чтобы скопировать формулу в оставшиеся ячейки в этом столбце.
Вот и все! Мы готовы вернуть это нашему другу:
«Привет, это мило! Это было так просто, и теперь я могу скопировать и вставить эти имена в один столбец.
Спасибо за то, что помог мне так быстро разобраться! Ваш Pad Thai на мне сегодня вечером!»
Бонусный раздел
/ ru / excelformulas / сравнение стоимости-покупки-принтера / content /
Как быстро объединить ячейки в Excel
Посмотреть видео — Объединить ячейки в Excel (с помощью формул)
youtube.com/embed/nmvsR832GMw?feature=oembed&autoplay=1″ src=»data:text/html;https://www.youtube.com/embed/nmvsR832GMw?feature=oembed&autoplay=1;base64,PGJvZHkgc3R5bGU9J3dpZHRoOjEwMCU7aGVpZ2h0OjEwMCU7bWFyZ2luOjA7cGFkZGluZzowO2JhY2tncm91bmQ6dXJsKGh0dHBzOi8vaW1nLnlvdXR1YmUuY29tL3ZpL25tdnNSODMyR013LzAuanBnKSBjZW50ZXIvMTAwJSBuby1yZXBlYXQnPjxzdHlsZT5ib2R5ey0tYnRuQmFja2dyb3VuZDpyZ2JhKDAsMCwwLC42NSk7fWJvZHk6aG92ZXJ7LS1idG5CYWNrZ3JvdW5kOnJnYmEoMCwwLDApO2N1cnNvcjpwb2ludGVyO30jcGxheUJ0bntkaXNwbGF5OmZsZXg7YWxpZ24taXRlbXM6Y2VudGVyO2p1c3RpZnktY29udGVudDpjZW50ZXI7Y2xlYXI6Ym90aDt3aWR0aDoxMDBweDtoZWlnaHQ6NzBweDtsaW5lLWhlaWdodDo3MHB4O2ZvbnQtc2l6ZTo0NXB4O2JhY2tncm91bmQ6dmFyKC0tYnRuQmFja2dyb3VuZCk7dGV4dC1hbGlnbjpjZW50ZXI7Y29sb3I6I2ZmZjtib3JkZXItcmFkaXVzOjE4cHg7dmVydGljYWwtYWxpZ246bWlkZGxlO3Bvc2l0aW9uOmFic29sdXRlO3RvcDo1MCU7bGVmdDo1MCU7bWFyZ2luLWxlZnQ6LTUwcHg7bWFyZ2luLXRvcDotMzVweH0jcGxheUFycm93e3dpZHRoOjA7aGVpZ2h0OjA7Ym9yZGVyLXRvcDoxNXB4IHNvbGlkIHRyYW5zcGFyZW50O2JvcmRlci1ib3R0b206MTVweCBzb2xpZCB0cmFuc3BhcmVudDtib3JkZXItbGVmdDoyNXB4IHNvbGlkICNmZmY7fTwvc3R5bGU+PGRpdiBpZD0ncGxheUJ0bic+PGRpdiBpZD0ncGxheUFycm93Jz48L2Rpdj48L2Rpdj48c2NyaXB0PmRvY3VtZW50LmJvZHkuYWRkRXZlbnRMaXN0ZW5lcignY2xpY2snLCBmdW5jdGlvbigpe3dpbmRvdy5wYXJlbnQucG9zdE1lc3NhZ2Uoe2FjdGlvbjogJ3BsYXlCdG5DbGlja2VkJ30sICcqJyk7fSk7PC9zY3JpcHQ+PC9ib2R5Pg==»/>
Нам часто приходится работать с текстовыми данными в Excel. Это могут быть имена, адреса, идентификаторы электронной почты или другие текстовые строки. Часто возникает необходимость объединить в Excel ячейки, содержащие текстовые данные.
Это могут быть имена, адреса, идентификаторы электронной почты или другие текстовые строки. Часто возникает необходимость объединить в Excel ячейки, содержащие текстовые данные.
Ваши данные могут находиться в соседних ячейках (строках / столбцах), или они могут находиться далеко на том же листе или даже на другом листе.
Как объединить ячейки в Excel
В этом руководстве вы узнаете, как объединить ячейки в Excel в различных сценариях:
- Как объединить ячейки без пробела / разделителя между ними.
- Как объединить ячейки с пробелом / разделителем между ними.
- Как объединить ячейки с разрывом строки между ними.
- Как сочетать ячейки с текстом и числами.
Как объединить ячейки без пробела / разделителя
Это самый простой и, вероятно, наиболее часто используемый способ объединения ячеек в Excel. Например, предположим, что у вас есть набор данных, показанный ниже:
Вы можете легко объединить ячейки в столбцах A и B, чтобы получить строку, такую как A11, A12 и т. Д..
Д..
Вот как это можно сделать:
- Введите следующую формулу в ячейку, где вы хотите объединить строку:
= A2 & B2
- Скопируйте и вставьте это во все ячейки.
Это даст вам что-то, как показано ниже:
Вы также можете сделать то же самое, используя функцию СЦЕПИТЬ вместо амперсанда (&). Приведенная ниже формула даст тот же результат:
= СЦЕПИТЬ (A2, B2)
Как объединить ячейки с пробелом / разделителем между
Вы также можете объединить ячейки и задать разделитель между ними.Это может быть пробел, запятая или любой другой разделитель.
Предположим, у нас есть набор данных, как показано ниже:
Вот шаги, чтобы объединить имя и фамилию с пробелом между ними:
- Введите следующую формулу в ячейку:
= A2 & "" & B2
- Скопируйте и вставьте это во все ячейки.
Это объединит имя и фамилию с пробелом между ними.
Если вам нужен другой разделитель (например, запятая или точка), вы можете использовать его в формуле.
Как объединить ячейки с разрывами строк между ними
Помимо разделителей, вы также можете добавлять разрывы строк при объединении ячеек в Excel.
Предположим, у вас есть набор данных, как показано ниже:
В приведенном выше примере разные части адреса находятся в разных ячейках (имя, номер дома, улица, город и страна).
Для объединения этих ячеек можно использовать функцию СЦЕПИТЬ или знак & (амперсанд).
Однако простое объединение этих ячеек даст вам что-то, как показано ниже:
Это неправильный формат адреса.Вы можете попробовать использовать перенос текста, но это тоже не сработает.
Здесь необходимо, чтобы каждый элемент адреса располагался в отдельной строке одной и той же ячейки. Вы можете добиться этого, используя функцию CHAR (10) вместе со знаком &.
CHAR (10) — это перевод строки в Windows, что означает, что он заставляет все, что находится после него, перейти на новую строку.
Используйте следующую формулу, чтобы получить содержимое каждой ячейки в отдельной строке внутри той же ячейки:
= A2 & CHAR (10) & B2 & CHAR (10) & C2 & CHAR (10) & D2 & CHAR (10) & E2
В этой формуле используется CHAR (10) ) между каждой ссылкой на ячейку и вставляет разрыв строки после каждой ячейки. Получив результат, примените обтекание текстом в ячейках с результатами, и вы получите что-то, как показано ниже:
Получив результат, примените обтекание текстом в ячейках с результатами, и вы получите что-то, как показано ниже:
Как объединить ячейки с текстом и числами
Вы также можете комбинировать ячейки, содержащие разные типы данных. Например, вы можете комбинировать ячейки, содержащие текст и числа.
Давайте сначала рассмотрим простой пример.
Предположим, у вас есть набор данных, показанный ниже:
В приведенном выше наборе данных есть текстовые данные в одной ячейке, а число — в другой ячейке.Вы можете легко объединить эти два значения, используя следующую формулу:
= A2 & "-" & B2
Здесь я использовал тире в качестве разделителя.
Вы также можете добавить к нему текст. Таким образом, вы можете использовать следующую формулу для создания предложения:
= A2 & "регион имеет" & B2 & "офисы"
Здесь мы использовали комбинацию ссылки на ячейку и текста для построения предложений.
Теперь давайте рассмотрим этот пример и посмотрим, что произойдет, если вы попытаетесь использовать числа с примененным к ним некоторым форматированием.
Предположим, у вас есть набор данных, показанный ниже, где у нас есть значения продаж.
Теперь давайте объединим ячейки в столбцах A и B, чтобы составить предложение.
Вот формула, которую я буду использовать:
= A2 & "объем продаж в регионе" & B2
Вот как выглядят результаты:
Видите ли вы здесь проблему? Посмотрите внимательно на формат продажной стоимости в результате.
Вы можете видеть, что форматирование продажной стоимости исчезает, и результат имеет простое числовое значение.Это происходит, когда мы объединяем ячейки с числами, к которым применено форматирование.
Вот как это исправить. Используйте следующую формулу:
= A2 & "продажи в регионе" & ТЕКСТ (B2, "$ ###, 0.0")
В приведенной выше формуле вместо использования B2 мы использовали функцию ТЕКСТ. Функция ТЕКСТ позволяет отображать число в указанном формате и в виде текста. В приведенном выше случае формат: $ ###, 0,0. В этом формате Excel показывает число со знаком доллара, разделителем тысяч и одной десятичной запятой.
Точно так же вы можете использовать функцию «Текст» для отображения в любом формате, разрешенном в Excel.
Вот еще один пример. Есть имена и дата рождения, и если вы попытаетесь объединить эти ячейки, вы получите что-то, как показано ниже:
Вы можете видеть, что Excel полностью испортил формат даты. Причина в том, что дата и время хранятся в Excel как числа, и при объединении ячеек с числами, как показано выше, отображается числовое значение, но не используется исходный формат.
Вот формула, которая исправит это:
= A2 & "родился" & ТЕКСТ (B2, "дд ммм ггг")
Здесь мы снова использовали функцию ТЕКСТ и указали формат, в котором мы хотим Дата рождения отображается в результате.
Вот как работает этот формат даты:
- дд — показывает номер дня даты. (попробуйте использовать ddd и посмотрите, что произойдет).
- ммм — показывает трехбуквенный код месяца.
- ггг — показывает номер года.
Круто… Не правда ли?
Сообщите мне свои мысли в разделе комментариев.
Вам также могут понравиться следующие руководства по Excel:
Как объединить формулу и текст в Google Таблицах (2 простых способа)
Комбинирование текста и чисел является обычным явлением в электронных таблицах, например, когда вы хотите добавить некоторый контекст
Есть ряд случаев, когда вам может потребоваться объединить текстовые значения с результатами формул в Google Таблицах.Вот несколько случаев:
- Вам может потребоваться агрегировать значения из электронной таблицы и объединить результат с некоторым текстом, чтобы его было легче понять.
- Вы можете добавить блок с числом, полученным из формулы, например, 15 кВтч или 5 м / с
- Вы можете объединить текст и значения формулы из двух или более отдельных ячеек в одну ячейку.
Процесс объединения текста с формулой в Google Таблицах просто требует, чтобы вы использовали оператор или функцию конкатенации.
В этом уроке мы рассмотрим два разных способа комбинирования формулы и текста:
- Использование оператора конкатенации (амперсанд)
- Использование функции СЦЕПИТЬ
Использование амперсанда (&) для объединения формулы и текста
Оператор конкатенации обозначается символом амперсанда (&). Он используется для объединения заданных значений вместе и возвращает строку, содержащую значения, добавленные друг к другу.
Таким образом, этот оператор предоставляет отличный способ объединить формулу и текст в одно значение ячейки. Предположим, у вас есть следующий набор данных и вы хотите отобразить среднюю скорость в м / с для каждой строки.
Вот как можно использовать оператор конкатенации, чтобы объединить результат функции СРЕДНИЙ с текстом « м / с »:
- Щелкните первую ячейку, в которой должны отображаться комбинированные значения (E2).

- Введите формулу:
= СРЕДНИЙ (B2: D2) & «м / с».
- Нажмите клавишу возврата.
- Вы найдете результат функции СРЕДНИЙ в сочетании с текстом « м / с » в ячейке E2.
- Дважды щелкните маркер заполнения в правом нижнем углу ячейки E2. Это скопирует формулу во все остальные ячейки столбца E, поэтому вы получите индивидуальные средней скорости для каждой строки в сочетании с текстом «м / с».
Объяснение формулы
Оператор конкатенации (&) добавляет значение справа от значения слева.В этом случае он добавил строку « м / с » к результату формулы СРЕДНИЙ для каждой строки.
А что, если вам нужен текст перед , и результат формулы СРЕДНИЙ тоже? Например, что, если вы хотите сказать: «Средняя скорость 24,5 м / с»?
В этом случае вам просто понадобится еще один оператор конкатенации перед функцией AVERAGE, например:
= «Средняя скорость -« & СРЕДНЯЯ (B2: D2) & »м / с».
Не забудьте заключить любую строку или текстовое значение в двойные кавычки.
Вы можете использовать оператор конкатенации, чтобы объединить несколько подстрок и значений в одну. Все, что вам нужно сделать, это соединить каждую пару подстрок с оператором амперсанда (&) между ними.
Использование функции СЦЕПИТЬ для объединения формулы и текста
Функция CONCATENATE () обеспечивает те же функции, что и оператор конкатенации (&). Единственная разница в том, как они используются.
Общий синтаксис функции СЦЕПИТЬ:
= СЦЕПИТЬ (текст1, [текст2],…)
Где текст1 , текст2 и т. Д.- это подстроки, которые вы хотите объединить.
Эту функцию можно использовать для объединения нескольких подстрок и значений в одну, где каждая подстрока является параметром функции.
Давайте применим функцию СЦЕПИТЬ к тому же набору данных, который показан в методе 1 :
Ниже приведены шаги для этого:
- Щелкните первую ячейку, в которой должны отображаться комбинированные значения (E2).

- Введите формулу: = СЦЕПИТЬ (СРЕДНИЙ (B2: D2), ”м / с”).
- Нажмите клавишу возврата.
- Вы найдете результат функции СРЕДНИЙ в сочетании с текстом « м / с » в ячейке E2.
- Дважды щелкните маркер заполнения в правом нижнем углу ячейки E2. Это скопирует формулу во все остальные ячейки столбца E, поэтому вы получите индивидуальные СРЕДНЕЕ скорости для каждой строки в сочетании с текстом « м / с ».
Объяснение формулы
Функция СЦЕПИТЬ в этом примере принимает первый параметр и присоединяет второй параметр к его концу.В этом случае он взял результат функции СРЕДНИЙ и присоединил к нему текст « м / с » в конце каждой строки.
Если вы также хотите добавить текст перед , результат формулы СРЕДНИЙ, как в « Средняя скорость 24,5 м / с », тогда просто добавьте текст « Средняя скорость » в качестве первого параметра. формулы, использованной выше. Итак, ваша формула будет:
формулы, использованной выше. Итак, ваша формула будет:
= СЦЕПИТЬ («Средняя скорость», СРЕДНЯЯ (B2: D2), «м / с»)
Как форматировать числовые результаты в сочетании с текстом
По результатам обоих вышеупомянутых методов вы заметите, что результаты средних функций не выглядят очень привлекательными.Результаты, возможно, было бы легче прочитать, если бы они были отформатированы и округлены до двух знаков после запятой.
Обычно вы можете просто использовать функцию Custom Formatting для преобразования результата формулы в требуемый формат. Однако это не так просто, если у вас есть ячейка, содержащая комбинацию формулы и текста.
К счастью, есть способ отформатировать результаты, полученные в столбце E. Это можно сделать с помощью функции ТЕКСТ.
Функция ТЕКСТ используется для преобразования числа в текст в соответствии с заданным форматом.Синтаксис функции:
= ТЕКСТ (число, формат)
Здесь,
- число — это число, дата или время, которое вы хотите отформатировать
- формат — это строка, определяющая способ форматирования числа.

Обратите внимание, что параметр формата всегда следует заключать в двойные кавычки, поскольку это строка.
Например, если вы хотите отформатировать число 13,5431 до 2 десятичных разряда, вы передаете его через функцию ТЕКСТ следующим образом:
= ТЕКСТ (13.5431, ”#. ##”)
Второй параметр « #. ## » означает, что мы хотим, чтобы формат числа был ограничен только 2 десятичными знаками.
Незначительный 0 не появится в результате. Символ «#» в этой формуле называется синтаксическим знаком и довольно часто используется при форматировании чисел. Вот некоторые другие часто используемые синтаксические символы:
| Персонаж | Описание |
| 0 | представляет собой цифру в числе.В результатах появится незначащий 0. |
| # | представляет собой цифру в числе. Незначительный 0 не будет отображаться в результатах. |
| ? | представляет собой цифру в числе. Незначительный 0 появится в результатах как пробел. |
| $ | Форматирует число как значение в долларах. |
| . (Период) | Форматирует число с десятичной точкой. |
| , (запятая) | Форматирует число с разделителем тысяч. |
| / | Форматирует число как дробь. |
| % | Форматирует число в процентах |
| «текст» | Добавляет текст в формулу. Вставьте желаемый текст в кавычки, чтобы он появился. |
| @ | Показывает текст, введенный в ячейку. |
| * | Повторяет следующий символ для заполнения оставшегося места в ячейке. |
| _ (подчеркивание) | Добавляет пробел по ширине к следующему символу. |
Чтобы применить форматирование к числам, которые отображаются с текстом в столбце E нашего примера, вы можете включить функцию ТЕКСТ в формулу следующим образом:
- = ТЕКСТ (СРЕДНИЙ (B2: D2), «#.
 ##») & «м / с», если используется оператор конкатенации
##») & «м / с», если используется оператор конкатенации - = СЦЕПИТЬ (ТЕКСТ (СРЕДНИЙ (B2: D2), ”#. ##”), ”м / с”) при использовании функции СЦЕПИТЬ
В этом руководстве я показал вам два простых способа комбинировать формулу с текстом в Google Таблицах .
Я также показал вам, как можно отформатировать числа, полученные в результате формул, так, чтобы объединенный текст был легко читаемым и понятным.
Надеюсь, вы нашли это руководство полезным.
Другие руководства по Google Таблицам, которые могут вам также понравиться:
расширенных формул Excel — 10 формул, которые вы должны знать!
10 расширенных формул Excel, которые вы должны знать
Каждый финансовый аналитик Руководство для аналитиков Trifecta® Окончательное руководство о том, как стать финансовым аналитиком мирового уровня.Вы хотите быть финансовым аналитиком мирового уровня? Вы хотите следовать передовым отраслевым практикам и выделиться из толпы? Наш процесс, получивший название The Analyst Trifecta®, состоит из аналитики, презентаций и мягких навыков, он проводит в Excel больше времени, чем они могут себе представить. Основываясь на многолетнем опыте, мы составили самые важные и продвинутые формулы Excel, которые должен знать каждый финансовый аналитик мирового уровня.
Основываясь на многолетнем опыте, мы составили самые важные и продвинутые формулы Excel, которые должен знать каждый финансовый аналитик мирового уровня.
Хотите загрузить эти и другие формулы Excel?
Электронная книга Excel
Загрузите бесплатную электронную книгу, содержащую более 200 страниц важных уроков по сочетаниям клавиш, формулам и функциям Excel.1. ИНДЕКС СООТВЕТСТВИЕ
Формула: = ИНДЕКС (C3: E9, MATCH (B13, C3: C9,0), MATCH (B14, C3: E3,0))
Это расширенная альтернатива VLOOKUP или Формулы HLOOKUP (которые имеют ряд недостатков и ограничений). ИНДЕКС ПОИСКПОЗ Формула соответствия индекса Объединение функций ИНДЕКС и ПОИСКПОЗ является более мощной формулой поиска, чем ВПР. Узнайте, как использовать ИНДЕКС ПОИСКПОЗ в этом руководстве по Excel. — это мощное сочетание формул Excel, которое выведет ваш финансовый анализ и финансовое моделирование на новый уровень.
ИНДЕКС возвращает значение ячейки в таблице на основе номера столбца и строки.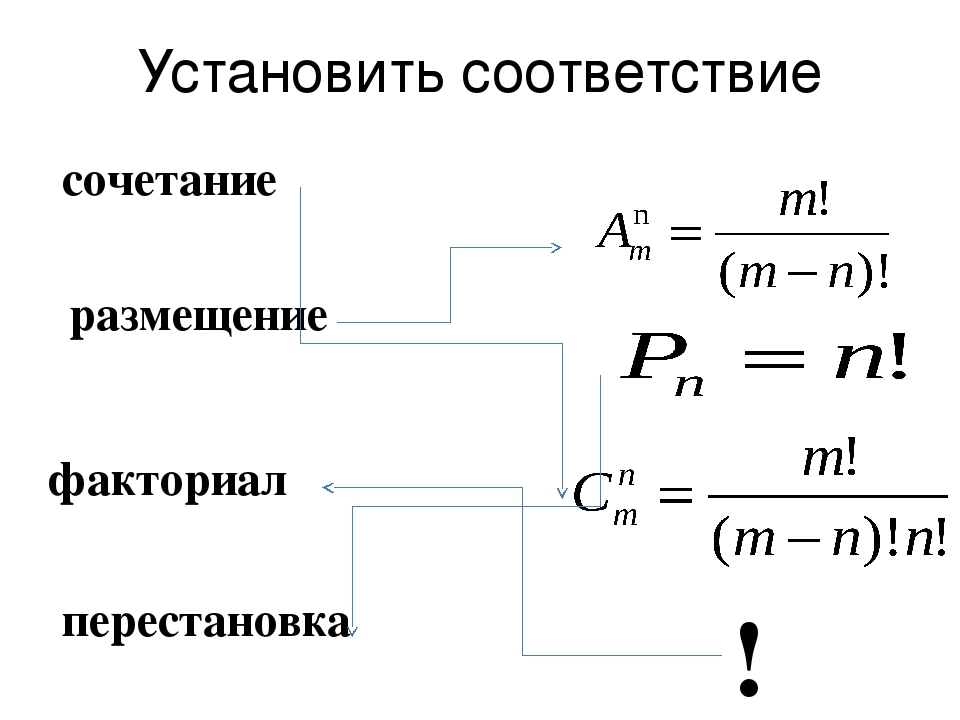
ПОИСКПОЗ возвращает положение ячейки в строке или столбце.
Вот пример сочетания формул ИНДЕКС и ПОИСКПОЗ. В этом примере мы ищем и возвращаем рост человека на основе его имени. Поскольку имя и высота являются переменными в формуле, мы можем изменить их обе!
Формула сопоставления индекса Объединение функций ИНДЕКС и ПОИСКПОЗ — более эффективная формула поиска, чем ВПР.Узнайте, как использовать ИНДЕКС ПОИСКПОЗ в этом руководстве по Excel.
Для получения пошагового объяснения или того, как использовать эту формулу, обратитесь к нашему бесплатному руководству о том, как использовать ИНДЕКС ПОИСКПОЗ в формуле совпадения индекса Индекс Комбинация функций ИНДЕКС и ПОИСКПОЗ — более эффективная формула поиска, чем ВПР. Узнайте, как использовать ПОИСКПОЗ в этом руководстве по Excel.
2.
 ЕСЛИ в сочетании с И / ИЛИ
ЕСЛИ в сочетании с И / ИЛИФормула: = ЕСЛИ (И (C2> = C4, C2 <= C5), C6, C7)
Любой, кто потратил много времени на создание различных типов финансовых моделей Типы финансовых моделей Наиболее распространенные типы финансовых моделей включают: модель с тремя отчетами, модель DCF, модель M&A, модель LBO, модель бюджета.Откройте для себя 10 основных типов и знает, что вложенные формулы ЕСЛИ могут быть кошмаром. Объединение IF с функцией AND или OR может быть отличным способом упростить аудит формул и облегчить понимание другими пользователями. В приведенном ниже примере вы увидите, как мы использовали комбинацию отдельных функций для создания более сложной формулы.
Подробное описание выполнения этой функции в Excel см. В нашем бесплатном руководстве по использованию оператора IF с оператором AND / ORIF между двумя числами. Загрузите этот бесплатный шаблон для оператора IF между двумя числами в Excel.В этом руководстве мы покажем вам шаг за шагом, как вычислить IF с помощью оператора AND. .IF Statement между двумя числамиЗагрузите этот бесплатный шаблон для оператора IF между двумя числами в Excel. В этом руководстве мы покажем вам шаг за шагом, как вычислить IF с помощью оператора AND.
.IF Statement между двумя числамиЗагрузите этот бесплатный шаблон для оператора IF между двумя числами в Excel. В этом руководстве мы покажем вам шаг за шагом, как вычислить IF с помощью оператора AND.
3. СМЕЩЕНИЕ в сочетании с СУММ или СРЕДНИМ
Формула: = СУММ (B4: СМЕЩЕНИЕ (B4,0, E2-1))
Функция СМЕЩЕНИЕ Функция СМЕЩЕНИЕ Функция СМЕЩЕНИЕ относится к функциям поиска и справочника Excel.СМЕЩЕНИЕ вернет диапазон ячеек. То есть он вернет указанное количество строк и столбцов из указанного начального диапазона. сам по себе не особенно продвинут, но когда мы объединяем его с другими функциями, такими как SUM или AVERAGE, мы можем создать довольно сложную формулу. Предположим, вы хотите создать динамическую функцию, которая может суммировать переменное количество ячеек. С помощью обычной формулы СУММ вы ограничены статическим вычислением, но добавив СМЕЩЕНИЕ, вы можете перемещать ссылку на ячейку.
Как это работает: Чтобы эта формула работала, мы заменяем конечную ссылочную ячейку функции СУММ на функцию СМЕЩЕНИЕ. Это делает формулу динамической, и в ячейке, обозначенной как E2, вы можете указать Excel, сколько последовательных ячеек вы хотите добавить. Теперь у нас есть несколько сложных формул Excel!
Это делает формулу динамической, и в ячейке, обозначенной как E2, вы можете указать Excel, сколько последовательных ячеек вы хотите добавить. Теперь у нас есть несколько сложных формул Excel!
Ниже приведен снимок экрана с более сложной формулой в действии.
Как видите, формула СУММ начинается с ячейки B4, но заканчивается переменной, которая представляет собой формулу СМЕЩЕНИЯ, начинающуюся с B4 и продолжающуюся значением в E2 («3») минус один.Это перемещает конец формулы суммы на 2 ячейки, суммируя данные за 3 года (включая начальную точку). Как вы можете видеть в ячейке F7, сумма ячеек B4: D4 равна 15, что дает нам формула смещения и суммы.
Узнайте, как построить эту формулу шаг за шагом в нашем расширенном курсе Excel.
4. ВЫБРАТЬ
Формула: = ВЫБРАТЬ (вариант, вариант1, вариант2, вариант3)
Функция ВЫБРАТЬ Функция ВЫБРАТЬ Функция ВЫБРАТЬ относится к функциям поиска и справочника Excel. Он вернет значение из массива, соответствующее указанному номеру индекса. Функция вернет n-ю запись в данном списке. Как финансовый аналитик, функция ВЫБОР полезна при выборе из заданного набора данных. Например, мы отлично подходят для сценарного анализа в финансовом моделировании. Он позволяет вам выбирать между определенным количеством вариантов и возвращать тот «выбор», который вы выбрали. Например, представьте, что у вас есть три разных предположения относительно роста доходов в следующем году: 5%, 12% и 18%.Используя формулу ВЫБРАТЬ, вы можете вернуть 12%, если скажете Excel, что хотите выбрать вариант №2.
Он вернет значение из массива, соответствующее указанному номеру индекса. Функция вернет n-ю запись в данном списке. Как финансовый аналитик, функция ВЫБОР полезна при выборе из заданного набора данных. Например, мы отлично подходят для сценарного анализа в финансовом моделировании. Он позволяет вам выбирать между определенным количеством вариантов и возвращать тот «выбор», который вы выбрали. Например, представьте, что у вас есть три разных предположения относительно роста доходов в следующем году: 5%, 12% и 18%.Используя формулу ВЫБРАТЬ, вы можете вернуть 12%, если скажете Excel, что хотите выбрать вариант №2.
Подробнее об анализе сценария в Excel Анализ сценария Анализ сценария — это процесс изучения и оценки возможных событий или сценариев, которые могут произойти в будущем, и прогнозирования.
Чтобы увидеть демонстрацию видео, посетите наш расширенный курс формул Excel.
5. XNPV и XIRR
Формула: = XNPV (ставка дисконтирования, денежные потоки, даты)
Если вы аналитик, работающий в инвестиционно-банковской сфере. Карьерный путь в инвестиционном банке.Узнайте о зарплатах в инвестиционном банке, о том, как устроиться на работу и что делать после карьеры в IB. Подразделение инвестиционного банкинга (IBD) помогает правительствам, корпорациям и учреждениям привлекать капитал и завершать слияния и поглощения (M&A)., Исследование капитала, финансовое планирование и анализ (FP & AFP & A Analyst Стать аналитиком FP&A в корпорации. Мы описываем зарплату, навыки, личность и обучение, необходимое для работы FP&A и успешной финансовой карьеры. Аналитики FP&A, менеджеры и директора несут ответственность за предоставление руководителям анализа и информации, которые им необходимы) или любой другой области корпоративных финансов, которая требует дисконтирования денежных потоков, затем эти формулы — палочка-выручалочка!
Карьерный путь в инвестиционном банке.Узнайте о зарплатах в инвестиционном банке, о том, как устроиться на работу и что делать после карьеры в IB. Подразделение инвестиционного банкинга (IBD) помогает правительствам, корпорациям и учреждениям привлекать капитал и завершать слияния и поглощения (M&A)., Исследование капитала, финансовое планирование и анализ (FP & AFP & A Analyst Стать аналитиком FP&A в корпорации. Мы описываем зарплату, навыки, личность и обучение, необходимое для работы FP&A и успешной финансовой карьеры. Аналитики FP&A, менеджеры и директора несут ответственность за предоставление руководителям анализа и информации, которые им необходимы) или любой другой области корпоративных финансов, которая требует дисконтирования денежных потоков, затем эти формулы — палочка-выручалочка!
Проще говоря, XNPV и XIRR позволяют применять определенные даты к каждому отдельному дисконтированному денежному потоку.Проблема с основными формулами NPV и IRR в Excel заключается в том, что они предполагают, что периоды времени между денежными потоками равны. Как аналитик, вы обычно будете сталкиваться с ситуациями, когда денежные потоки распределяются неравномерно, и эта формула поможет вам это исправить.
Как аналитик, вы обычно будете сталкиваться с ситуациями, когда денежные потоки распределяются неравномерно, и эта формула поможет вам это исправить.
Для получения более подробной информации см. Наше бесплатное руководство по формулам IRR и XIRR. XIRR назначает конкретные даты каждому отдельному денежному потоку, что делает его более точным, чем IRR, при построении финансовой модели в Excel.а также наше руководство по XNPV.
6. СУММЕСЛИ и СЧЁТЕСЛИ
Формула: = СЧЁТЕСЛИ (D5: D12, ”> = 21 ″)
Эти две расширенные формулы отлично подходят для условных функций. СУММЕСЛИ добавляет все ячейки, соответствующие определенным критериям, а СЧЁТЕСЛИ подсчитывает все ячейки, соответствующие определенным критериям. Например, представьте, что вы хотите подсчитать все ячейки, которые больше или равны 21 (законный возраст употребления алкоголя в США), чтобы узнать, сколько бутылок шампанского вам нужно для клиентского мероприятия.Вы можете использовать СЧЁТЕСЛИ в качестве расширенного решения, как показано на скриншоте ниже.
В нашем продвинутом курсе Excel мы разбиваем эти формулы на еще более подробную информацию.
7. PMT и IPMT
Формула: = PMT (процентная ставка, количество периодов, приведенная стоимость)
Если вы работаете в коммерческом банковском бизнесе Профиль карьеры в коммерческом банковском бизнесе Карьерный профиль в коммерческом банке предусматривает предоставление клиентам кредитных продуктов, таких как срочные займы, возобновляемые кредитные линии, синдицированные кредиты, недвижимость, FP, AFP и AF Финансовое планирование и анализ (FP&A) — важная функция в корпорации.Специалисты FP&A поддерживают принятие управленческих решений или занимают любую должность финансового аналитика, занимающегося графиками долга. Вам необходимо понять эти две подробные формулы.
Формула PMT дает значение равных платежей в течение срока ссуды. Вы можете использовать его вместе с IPMT (который сообщает вам процентные платежи по одному и тому же типу ссуды), а затем разделить основную сумму и процентные платежи.
Вот пример того, как использовать функцию PMT, чтобы получить ежемесячный платеж по ипотеке для ипотечного кредита в размере 1 миллиона долларов под 5% на 30 лет.
8. LEN и TRIM
Формулы: = LEN (текст) и = TRIM (текст)
Приведенные выше формулы немного реже, но, безусловно, очень сложные. Они отлично подходят для финансовых аналитиков. Руководство для аналитиков Trifecta® — полное руководство о том, как стать финансовым аналитиком мирового уровня. Вы хотите быть финансовым аналитиком мирового уровня? Вы хотите следовать передовым отраслевым практикам и выделиться из толпы? Наш процесс, называемый аналитиком Trifecta®, состоит из аналитики, презентаций и навыков межличностного общения, которым необходимо систематизировать большие объемы данных и манипулировать ими.К сожалению, данные, которые мы получаем, не всегда идеально организованы, и иногда могут возникать проблемы, такие как лишние пробелы в начале или конце ячеек.
Формула LEN возвращает заданную текстовую строку как количество символов, что полезно, когда вы хотите подсчитать, сколько символов содержится в некотором тексте.
В приведенном ниже примере вы можете увидеть, как формула TRIM очищает данные Excel.
9. CONCATENATE
Формула: = A1 & «больше текста»
Concatenate не является самостоятельной функцией — это просто инновационный способ объединения информации из разных ячеек и придания большей динамичности рабочим листам.Это очень мощный инструмент для финансовых аналитиков, выполняющих финансовое моделирование (см. Наше бесплатное руководство по финансовому моделированиюБесплатное руководство по финансовому моделированиюЭто руководство по финансовому моделированию содержит советы и передовые методы работы с Excel в отношении предположений, драйверов, прогнозирования, связывания трех отчетов, анализа DCF, чтобы узнать больше ).
В приведенном ниже примере вы можете увидеть, как текст «Нью-Йорк» плюс «,» соединяется с «Нью-Йорк» для создания «Нью-Йорк, Нью-Йорк». Это позволяет создавать динамические заголовки и метки на листах.Теперь вместо прямого обновления ячейки B8 вы можете обновлять ячейки B2 и D2 независимо. Имея большой набор данных, это ценный навык, который нужно иметь в вашем распоряжении.
Имея большой набор данных, это ценный навык, который нужно иметь в вашем распоряжении.
10. Функции ЯЧЕЙКА, LEFT, MID и RIGHT
Эти расширенные функции Excel можно комбинировать для создания очень сложных и сложных формул. Функция ЯЧЕЙКА может возвращать различную информацию о содержимом ячейки (например, ее имя, расположение, строку, столбец и т. Д.).Функция LEFT может возвращать текст из начала ячейки (слева направо), MID возвращает текст из любой начальной точки ячейки (слева направо), а RIGHT возвращает текст из конца ячейки (справа налево).
Ниже представлена иллюстрация трех формул в действии.
Чтобы увидеть, как их можно эффективно комбинировать с функцией CELL, мы шаг за шагом разберем ее для вас в нашем расширенном классе формул Excel.
Обучение работе с другими формулами Excel
Мы надеемся, что эти 10 лучших расширенных формул Excel были для вас полезны.Они должны пройти долгий путь к совершенствованию ваших навыков финансового анализа и финансового моделирования Навыки финансового моделирования Изучите 10 наиболее важных навыков финансового моделирования и то, что требуется для хорошего финансового моделирования в Excel. Самые важные навыки: бухгалтерский учет.
Самые важные навыки: бухгалтерский учет.
Ниже приведены дополнительные ресурсы CFI, которые помогут вам стать опытным пользователем Excel:
- Шпаргалка по формулам Excel Шпаргалка по формулам Excel Шпаргалка по формулам Excel от CFI предоставит вам все наиболее важные формулы для выполнения финансового анализа и моделирования в таблицах Excel.Если вы хотите стать мастером финансового анализа Excel и экспертом по построению финансовых моделей, вы попали в нужное место.
- Сочетания клавиш Excel Сочетания клавиш Excel Сочетания клавиш MacExcel для ПК — Список наиболее важных и распространенных сочетаний клавиш MS Excel для пользователей ПК и Mac, специалистов в области финансов и бухгалтерского учета. Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, манипулирование данными, редактирование формул и ячеек и другие краткие статьи
- Бесплатный ускоренный курс Excel
- Расширенный курс Excel
- Excel для финансового моделирования
Как внести изменения
Как правило, разные бренды одного и того же типа формулы содержат одни и те же основные ингредиенты. Переключение между брендами смеси не является проблемой, хотя многие родители задаются вопросом, может ли это вызвать суетливость или изменения стула у их ребенка.
Переключение между брендами смеси не является проблемой, хотя многие родители задаются вопросом, может ли это вызвать суетливость или изменения стула у их ребенка.
Фактически, вы даже можете смешивать смеси разных марок одного и того же типа вместе, если чувствуете, что ваш ребенок лучше реагирует на смесь одной марки с другой.
Какие бренды вы решите смешивать, зависит от личных предпочтений. Вам просто нужно знать об основных ингредиентах, содержащихся в одной и той же формуле.Если вы следуете стандартным инструкциям по смешиванию, смешивать смеси разных производителей безопасно.
Почему меняют формулы
Возможно, вы подумываете об изменении смеси вашего ребенка по разным причинам. Если у вашего ребенка газы, он плохо спит или нервничает, вы можете задаться вопросом, виновата ли смесь. Цена, доступность и простота приготовления также могут побудить вас попробовать что-то новое.
Какова бы ни была причина, прежде чем переходить на другую формулу, следует помнить о нескольких основных формулах.
Все смеси на основе молока, обогащенные железом (тип, рекомендуемый для большинства младенцев) содержат коровье молоко в качестве источника белка и лактозу в качестве углеводов. Между смесями на основе молока существуют небольшие вариации, в том числе различные комбинации белков сыворотки и казеина. Источниками жира в этих формулах являются различные типы масел.
Типы белка в формуле
В детских смесях содержатся три основных типа протеина.
- Белок коровьего молока является наиболее распространенным.
- Соевый белок иногда подходит для младенцев с определенными заболеваниями или аллергией на казеин или сыворотку, два белка, которые содержатся в коровьем молоке.
- Гипоаллергенные формулы (также известные как элементарные) содержат белок, который был разбит на более мелкие части. Эти смеси дорогие, у большинства из них не очень приятный вкус, и они обычно используются для младенцев, которые не могут переваривать неповрежденный белок.

При переходе на новую марку смеси обязательно придерживайтесь того же типа протеина.Если вы хотите перейти на смесь с другим источником белка, сначала проконсультируйтесь с врачом.
Вопреки распространенному мнению, рвота или избыток газов у ребенка обычно не связаны с типом белка в смеси. Тем не менее, переключение между брендами может помочь родителям увидеть, как их ребенок отреагирует на конкретный бренд.
Самая большая разница между формулами обычно заключается во вкусе. Некоторые дети очень разборчивы в том, что они едят, и могут предпочесть одну смесь другой.
Однако, учитывая, что вкус грудного молока меняется в зависимости от того, что ест кормящая мать, вкус обычно не является важным фактором для большинства детей, вскармливаемых смесью.
Ниже приведены некоторые признаки того, что у вашего ребенка настоящая аллергия на смесь:
- Диарея
- Спазмы в животе
- Кровь в стуле или рвоте у ребенка
- Крапивница или другие кожные высыпания
Если вы заметили какой-либо из этих признаков, немедленно позвоните своему педиатру.
Эксперименты со смесями для вашего ребенка могут помочь облегчить беспокойство по поводу пищевой непереносимости, отрыжки, запора, избытка газов или срыгивания, но в большинстве случаев в этом нет необходимости. Пока ваш ребенок здоров и не проявляет признаков истинной непереносимости смеси или аллергии, смесь, которую вы используете, действительно зависит от личных предпочтений.
Формула безопасности
Все марки детских смесей, представленные на рынке, безопасны в использовании и должны соответствовать требованиям к питательным веществам, установленным U.S. Управление по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA). Хотя фирменные и универсальные формулы могут иметь немного разные ингредиенты, они должны соответствовать одним и тем же федеральным требованиям в отношении питания и безопасности.
В магазине не забудьте проверить срок годности перед покупкой любого нового контейнера со смесью. Если вы заказываете онлайн, проверьте дату, прежде чем открывать его, чтобы вы могли вернуть все, что просрочено. Также обратите внимание на любые посторонние запахи, цвета или вкусы при открытии и смешивании формулы.
Также обратите внимание на любые посторонние запахи, цвета или вкусы при открытии и смешивании формулы.
Покупайте смесь только у надежных розничных продавцов, так как формулы с истекшим сроком годности иногда переупаковываются и продаются с измененной информацией о питании. Кормление вашего младенца устаревшей смесью или смесью, содержащей другие ингредиенты, может иметь серьезные последствия, особенно если у вашего ребенка уже есть проблемы со здоровьем.
FDA рекомендует позвонить по бесплатному телефону производителя смеси (указан на упаковке), если вы заметили что-то не так с детской смесью.
Важно следовать инструкциям по смешиванию, напечатанным на каждой емкости с формулой. Не думайте, что, поскольку в вашей стандартной формуле указано использование определенного соотношения воды и порошка, новая формула будет такой же.
Хотя может возникнуть соблазн сэкономить деньги или изменить вкус смеси вашего ребенка, разбавив ее водой, это никогда не будет хорошей идеей. Смесь (особенно готовая к употреблению) стоит дорого, но это единственный источник питания для большинства младенцев (в зависимости от их возраста).)
Смесь (особенно готовая к употреблению) стоит дорого, но это единственный источник питания для большинства младенцев (в зависимости от их возраста).)
Добавление слишком большого количества воды снизит количество потребляемых вашим ребенком калорий и питательных веществ и может повлиять на его рост и общее состояние здоровья.
Если вы смешиваете смеси двух марок, приготовьте каждую марку отдельно, следуя инструкциям для каждой из них. Таким образом, вы можете быть уверены, что концентрация каждого из них правильная. Затем смешайте две приготовленные смеси в детской бутылочке.
Как сделать переключатель
Если вы меняете формулы по рекомендации вашего педиатра (например, на гипоаллергенную формулу из-за аллергии), вам, вероятно, посоветуют отказаться от старой формулы и сразу перейти на новую.
Если, однако, вы переходите на новую смесь по другим причинам, например из-за цены или удобства, вы можете попробовать новую смесь и посмотреть, понравится ли она вашему ребенку.
Имейте в виду, что может потребоваться несколько кормлений, прежде чем ваш ребенок привыкнет к вкусу новой смеси.
Попробуйте внести изменения постепенно, если вашему ребенку не нравится новая смесь. Вы можете начать с комбинации трех старых частей и одной новой, а когда ваш ребенок примет это, переходите к половинчатым.
Продолжайте постепенно менять соотношение, пока вы не будете кормить только новой смесью. Вы можете купить небольшую емкость с новой формулой, пока не будете уверены, что хотите ее использовать.
Если вас беспокоит газообразование, придерживайтесь одной марки в течение как минимум недели или двух, чтобы увидеть, нет ли изменений в газах, стуле, срыгивании или отрыжке. Пищеварительной системе вашего ребенка нужно столько времени, чтобы приспособиться к новой диете.
При небольшом планировании, даже если вы выбираете формулу за счет стоимости и удобства, в долгосрочной перспективе вы сможете придерживаться одного бренда.

 3.1.1 -различать понятия «перестановки», «размещения», «сочетания» без повторений и с повторениями;
3.1.1 -различать понятия «перестановки», «размещения», «сочетания» без повторений и с повторениями;

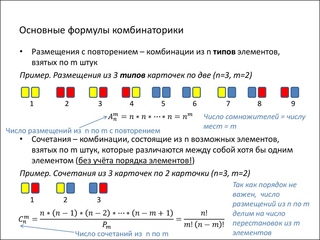 Начало урока
Начало урока
 Каждый из 15-и человек обнимался бы с 14-ю. Произведение 15 * 14 = 210 дает удвоенное число обниманий (так как первый обнял второго, а затем второй первого, на самом же деле было одно обнимание). Итак, число обниманий равно: (15 * 14): 2 = 105
Каждый из 15-и человек обнимался бы с 14-ю. Произведение 15 * 14 = 210 дает удвоенное число обниманий (так как первый обнял второго, а затем второй первого, на самом же деле было одно обнимание). Итак, число обниманий равно: (15 * 14): 2 = 105
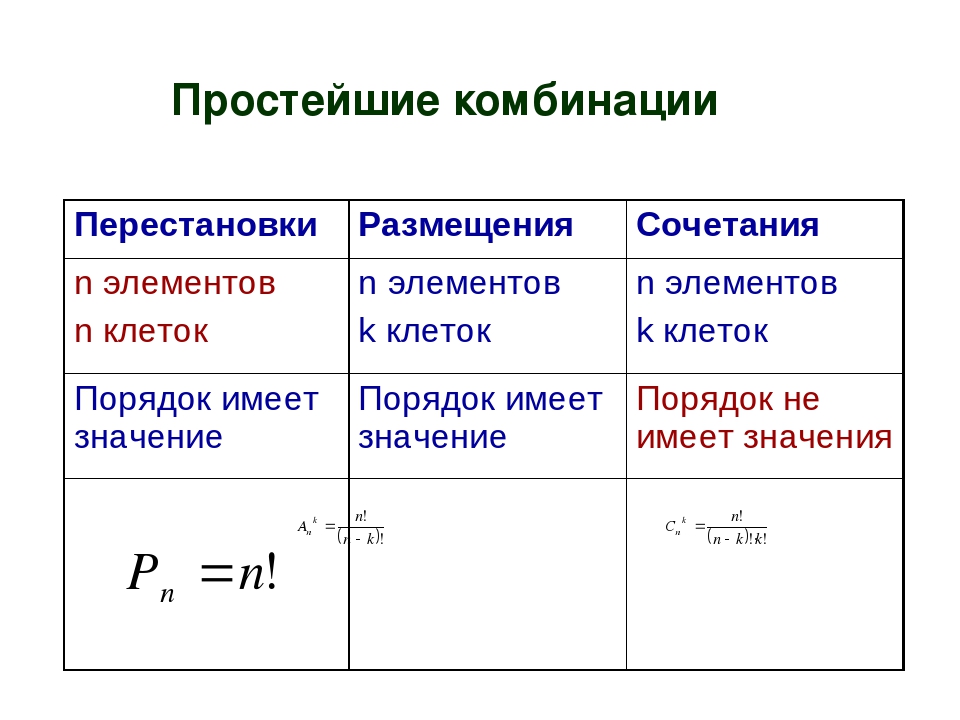
 Стратегия «Волонтер» с целью развития мыслительной деятельности учащихся на уровне знания , понимания и применения.
Стратегия «Волонтер» с целью развития мыслительной деятельности учащихся на уровне знания , понимания и применения.
 Ваша задача: решить задачи, оформить их в своих тетрадях. Задания высвечиваются на экране.
Ваша задача: решить задачи, оформить их в своих тетрадях. Задания высвечиваются на экране.
 «Установи соответствие»
«Установи соответствие»
 135-140 разобрать предложенные примеры, №271, №274, №277
135-140 разобрать предложенные примеры, №271, №274, №277

 Использовать оценивание по ключу, самооценивание по образцу,взаимооценива- ние в сочетании с индивидуальной, групповой, парной, коллективной формами урока.
Использовать оценивание по ключу, самооценивание по образцу,взаимооценива- ние в сочетании с индивидуальной, групповой, парной, коллективной формами урока.
 Ответьте на вопросы,
Ответьте на вопросы,

 58)
58)








 ##») & «м / с», если используется оператор конкатенации
##») & «м / с», если используется оператор конкатенации