Комплексные числа
Комплексное число это пара двух действительных чисел (x, y).
Мы можем представить комплексные числа, как точки в системе координат.
Пусть z — комплексное число.
z = (x,y)
x — это вещественная часть z, а y — это мнимая часть z.
Комплексные числа образуют C поле комплексных чисел.
Поле действительных чисел является его частью.
Если у нас есть два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) то:
z1 = z2 <=> x1 = x2
z1 ± z2 = (x1, y1) ± (x2, y2) = (x1 ± x2, y1 ± y2)
z1z2 = (x1, y1)(x2, y2) = (x1x2 — y1y2, x1
$\frac{z_1}{z_2}=\frac{(x_1, y_1)}{(x_2, y_2)} = \left( \frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}, \frac{x_2y_1-x_1y_2}{x_2^2+y_2^2} \right) $
Другой способ записи z это: z = x + iy,
x
— вещественная часть z,
y — мнимая часть, а
i
— мнимая единица. i2 = -1, i = √-1.
Каждое комплексное число z = x + iy имеет сопряженное число z = x — iy.
- z + z = 2x — действительное число;
- z — z = i2y — мнимое число;
- z.z = x2 + y2 = |z|2 — действительное число
Каждое комплексное число (x, y) имеет соответствующую точку в системе координат. Мы не можем сказать точка A > B, потому что мы не можем сказать так о двух комплексных числах (x1, y1) > (x2, y2) Это значит что комплексные числа не имеют порядка.
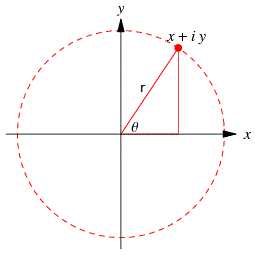
Векторная форма комплексного числа это:
z = |z|(cosθ + isinθ) = |z|eiθ
или
z = r(cos(θ) + i.sin(θ)) = r.ei.θ
Здесь |z| — это модуль комплесного числа (совпадает с величиной OM), θ -это аргумент комплесного числа или фаза. Заштрихованный круг наверху означает модуль |z| комплексного числа z, а угол θ — аргумент комплексного числа.
Действия над комплексными числами
Сложение комплексных чисел:
(a + bi) + (c + di) = (a + c) + i(b + d)
Вычитание комплексных чисел:
(a + bi) — (c + di) = (a — c) + i(b — d)
Умножение комплексных чисел:
(a + bi)(c + di) = (ac — bd) + i(ad + bc)
Деление комплексных чисел:
(a + bi)/(c + di) = ((ac + bd) + i(bc — ad))/(c2 + d2)
Формулы Муавра
zn = rn[cos(n.θ) + i.sin(n.θ)]
$\sqrt[n]{z}=\sqrt[n]{r}(cos(\frac{\theta+2k\pi}{n})+i.sin(\frac{\theta+2k\pi}{n}))$
k = 0, 1, 2,…, n-1
Пишите на нашем форуме касательно комплексных чисел.
www.math10.com
Основные темы математики : Комплексные числа
Комплексные или мнимые числа впервые появились в известном сочинении Кардано «Великое искусство, или об алгебраических правилах» 1545 года. По мнению автора, эти числа не были пригодны к употреблению. Однако это утверждение было позднее опровергнуто. В частности, Бомбелли в 1572 году при решении кубического уравнения обосновал пользу мнимых чисел. Он составил основные правила действий с комплексными числами.
И все же долгое время в математическом мире не было единого представления о сущности комплексных чисел.
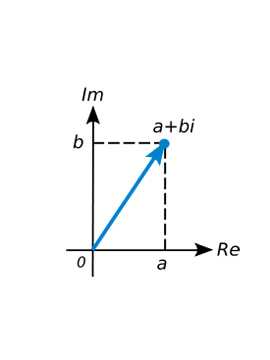
Геометрическое представление комплексного числа
Впервые символ мнимых чисел был предложен выдающимся математиком Эйлером. Предложенная символика выглядела следующим образом: i = sqr -1, где i — imaginarius, что означает фиктивный. В заслугу Эйлера также входит идея об алгебраической замкнутости поля комплексных чисел.
Итак, необходимость в числах нового типа появилась при решении квадратных уравнений для случая D < 0 (где D — дискриминант квадратного уравнения). В настоящее время комплексные числа нашли широкое применение в физике и технике, гидро- и аэродинамике, теории упругости и т.п.
Графическая запись комплексных чисел имеет вид: a + bi, где a и b — действительные числа, а i — мнимая единица, т.e. i2 = -1. Число a называется абсциссой, a b — ординатой комплексного числа a + bi. Два комплексных числа a + bi и a — bi называются сопряжёнными комплексными числами.
Существует ряд правил, связанных с комплексными числами:
- Во-первых, действительное число а может быть записано в форме комплексного числа: a+ 0 i или a — 0 i. К примеру, 5 + 0 i и 5 — 0 i означают одно и то же число 5.
- Во-вторых, комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi.
- В третьих, два комплексных числа a + bi и c + di считаются равными, если a = c и b = d. В ином случае комплексные числа не равны.
К основным действиям над комплексными числами относятся:
- Сложение. Комплексное число ( a + c ) + ( b + d ) i называется суммой комплексных чисел a + bi и c + di. Следовательно, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.
Это правило справедливо к действиям с обычными многочленами.
- Вычитание. Комплексное число ( a — c ) + ( b — d ) i называется разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое). Отсюда следует, что при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
-
Умножение. Произведением комплексных чисел a + bi и c + di является комплексное число ( ac — bd ) + ( ad + bc ) i. Это определение справедливо при соблюдении двух требований:
- числа a + bi и c + di должны перемножаться, как алгебраические двучлены,
- число i обладает основным свойством: i2 = -1.
К примеру, (a + bi)(a — bi) = a2 + b2. Отсюда следует, что произведение двух сопряжённых комплексных чисел равно действительному положительному числу.
- Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) — значит отыскать третье число e + f i (частное), умножение которого на делитель c + di даёт в результате делимое a + bi. Деление возможно только в случае, если делитель не равен нулю.
К примеру, (8 + i) : (2 — 3i) = 1 + 2i.
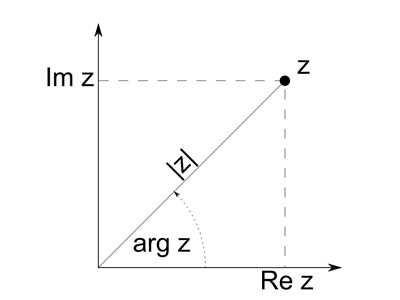
Модуль, аргумент, вещественная и мнимая части
В геометрическом представлении комплексные числа в отличие от действительных, которые изображаются на числовой прямой точками, отмечаются точками на координатной плоскости. Возьмем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на осях. В этом случае комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b. Такая система координат называется комплексной плоскостью.
Модулем комплексного числа является длина вектора OP, изображающего комплексное число комплексной плоскости. Модуль комплексного числа a + bi записывается в виде |a + bi| или буквой r и равен: r = |a + ib| = sqr a2 + b2.У сопряженных комплексных чисел имеется одинаковый модуль.
Аргументом комплексного числа является угол φ между осью OX и вектором OP, изображающим комплексное число. Отсюда получаем, tan φ = b/a.Тригонометрическая форма комплексного числа выражается через модуль r и аргумент φ абсциссы a и ординаты b комплексного числа a + bi.
a = r cosφ, b = r sinφ. a + bi = r ( cosφ + i sinφ).sitekid.ru
Комплексные числа
Теорема (правило Лопиталя раскрытия неопределенностей вида
$\frac{0}{0}$ или $\frac{\infty}{\infty}$).
Пусть функции $f(x)$ и $g(x)$ :
а) дифференцируемы в окрестности точки $a,$ за исключением, быть
может, самой точки $a,$ причем $g'(x)\neq 0$ в этой окрестности;
б) функции $f(x)$ и $g(x)$ являются одновременно либо бесконечно
малыми либо бесконечно большими при $x\rightarrow a;$
в) существует конечный $\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$
Тогда существует $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}$ и
выполняется равенство $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim\limits_{x\rightarrow a}\frac{f'(x)}{g'(x)}.$
Если функции $f(x)$ и $g(x)$ дифференцируемы в точке $a,$
$g(a)=f(a)=0,$ $ g'(a)\neq ,0$ то $\lim\limits_{x\rightarrow a}\frac{f(x)}{g(x)}=\frac{f'(a)}{g'(a)}.$
Примеры:
1. $\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$\lim\limits_{x\rightarrow 1}\frac{x^5-1}{2x^3-x-1}=\lim\limits_{x\rightarrow 1}\frac{5x^4}{6x^2-1}=1.$
2. $\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$$\lim\limits_{x\rightarrow 0}\frac{x-arctg x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{1-\frac{1}{1+x^2}}{3x^2}=\lim\limits_{x\rightarrow 0}\frac{x^2}{3x^2(1+x^2)=\frac{1}{3}.}$$
3. $\lim\limits_{x\rightarrow 1}\frac{\ln x}{\sqrt{x}}$
Имеем неопределенность вида $\frac{\infty}{\infty}.$ Применяя правило Лопиталя, получим:
$$\lim\limits_{x\rightarrow +\infty}\frac{\ln x}{\sqrt{x}}=\lim\limits_{x\rightarrow +\infty}\frac{1/x}{1/(2\sqrt{x})}=\lim\limits_{x\rightarrow +\infty}\frac{2}{\sqrt{x}}=0.$$
4. $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}.$
Имеем неопределенность вида $\frac{0}{0}.$ Замечая, что $\sin x\sim x$ при $x\rightarrow 0,$ по правилу Лопиталя находим
$\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{\sin^3 x}=\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{\cos x-\cos x+x\sin x}{3x^2}=$ $\frac{1}{3}\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}=\frac{1}{3}.$
5. $\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}.$
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
$\lim\limits_{x\rightarrow 1}\frac{x^10-10x+9}{x^5-5x+4}=\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}.$
Пользуясь еще раз правилом Лопиталя, находим
$\lim\limits_{x\rightarrow 1}\frac{10x^9-10}{5x^4-5}=2\lim\limits_{x\rightarrow 1}\frac{x^9-1}{x^4-1}=2\lim\limits_{x\rightarrow 1}\frac{9x^8}{4x^3}=\frac{9}{2}.$
6. $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}},$ где $\alpha>0,$ $\beta>0.$
Пусть $k=[\alpha]+1;$ тогда $\alpha-k<0.$
Применяя правило Лопиталя $k$ раз, получаем $\lim\limits_{x\rightarrow+\infty}\frac{x^{\alpha}}{e^{\beta x}}=\lim\limits_{x\rightarrow+\infty}\frac{\alpha x^{\alpha-1}}{\beta e^{\beta x}}=…=\lim\limits_{x\rightarrow+\infty}\frac{\alpha(\alpha-1)…(\alpha-k+1)x^{\alpha-k}}{\beta^k e^{\beta x}}=0.$
7. $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}},$ где $\alpha>0,$ $\beta>0.$
Пусть $\ln x =t;$ тогда $x=e^t$ и $\lim\limits_{x\rightarrow+\infty}\frac{\ln^{\alpha}x}{x^{\beta}}=\lim\limits_{t\rightarrow+\infty}\frac{t^{\alpha}}{e^{\beta t}}=0$ (пример 6).
Имеем неопределенность вида $\frac{0}{0}.$ Применяя правило Лопиталя, получим:
8. $\lim\limits_{x\rightarrow +0}x\ln x$
Преобразуя неопределенность вида $0\cdot\infty$ к виду $\frac{\infty}{\infty}$ и применяя правило Лопиталя имеем
$$\lim\limits_{x\rightarrow +0}x\ln x=\lim\limits_{x\rightarrow +0}\frac{\ln x}{1/x}=\lim\limits_{x\rightarrow +0}\frac{1/x}{-1/x^2}=\lim\limits_{x\rightarrow +0}(-x)=0.$$
9. $\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}.$
Имеем неопределенность вида $\frac{0}{0}.$ Полагая $1/x^2=t,$ получаем
$$\lim\limits_{x\rightarrow 1}\frac{1}{x^{50}}e^{-1/x^2}=\lim\limits_{x\rightarrow 1}\frac{t^{25}}{e^t}=0.$$
10. $\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right).$
Преобразуя неопредленность вида $\infty-\infty$ к виду $\frac{0}{0}$ и используя асимптотическую формулу $\sin x \sim x$ при $x\rightarrow 0,$ получаем
$$\lim\limits_{x\rightarrow 0}\left(\frac{1}{x^2}-ctg^2 x\right)=\lim\limits_{x\rightarrow 0}\frac{\sin^2 x-x^2\cos^2 x}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{(\sin x+x\cos x)(\sin x-x\cos x)}{x^2\sin^2 x}=$$ $$=\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}\cdot\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}.$$
Так как
$$\lim\limits_{x\rightarrow 0}\frac{\sin x+x\cos x}{x}=\lim\limits_{x\rightarrow 0}\frac{\sin x}{x}+\lim\limits_{x\rightarrow 0}\cos x=2,$$
а $\lim\limits_{x\rightarrow 0}\frac{\sin x-x\cos x}{x^3}=\frac{1}{3}$ (см. пример 4), то искомый предел равен $2/3.$
mathportal.net
Лекция по математике на тему «Комплексные числа»
Лекция 9
Тема 9. Комплексные числа.
Время: 2 часа
Цель лекции: Познакомить с понятием комплексного числа, алгебраической, тригонометрической и показательной формами комплексных чисел. Теоретически обосновать действия над комплексными числами. Показать возможность решения алгебраических уравнений в комплексной области.
План лекции:
Понятие комплексного числа.
Формы записи комплексных чисел.
Действия над комплексными числами.
Операции над комплексными числами, заданными в показательной форме.
Основная теорема алгебры.
Понятие комплексного числа.
Комплексным числом z называется выражение вида z = x +iy, где х и у – действительные числа, а i – так называемая мнимая единица, i2= –1.
Если х = 0, то число 0+iy = iy называется чисто мнимым; если у = 0, то число x +i0 = х отождествляется с действительным числом х, а это означает, что множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т.е. RС.
Число х – действительная часть комплексного числа z и обозначается х=Rе z, а у – мнимой частью z, у=Im z.
Два комплексных числа z1 = x1 +iy1 z2 = x2 +iy2 называются равными тогда и только тогда, когда равны их действительные и мнимые части. Понятия больше и меньше для комплексных чисел не вводятся. Два комплексных числа, отличающиеся лишь знаком мнимой части, называются сопряжёнными.
В
О х х
М
у
у

сякое комплексное число можно изобразить точкой М(х,у) плоскости Оху такой, что х=Rе z, у=Im z. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс – действительная ось, ось ординат – мнимая. Комплексное число можно задать в виде радиус вектора  =
= . Длина вектора
. Длина вектора  называется модулем этого числа и обозначается
называется модулем этого числа и обозначается  или r.
или r.
Величина угла между положительным направлением действительной оси и вектором  , изображающим комплексное число – аргумент этого числа, обозначается Arg z или
, изображающим комплексное число – аргумент этого числа, обозначается Arg z или  . Аргумент комплексного числа z=0 не определён. Аргумент комплексного числа z
. Аргумент комплексного числа z=0 не определён. Аргумент комплексного числа z 0 – величина многозначная и определяется с точностью до слагаемого
0 – величина многозначная и определяется с точностью до слагаемого  (k =0,–1,1,–2,2,…): Arg z= аrg z +
(k =0,–1,1,–2,2,…): Arg z= аrg z +  , где аrg z – главное значение аргумента, заключённое в промежутке
, где аrg z – главное значение аргумента, заключённое в промежутке 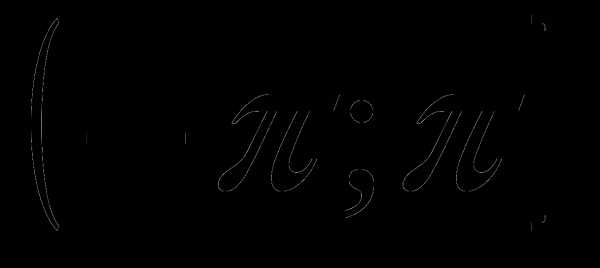 , т.е.
, т.е. 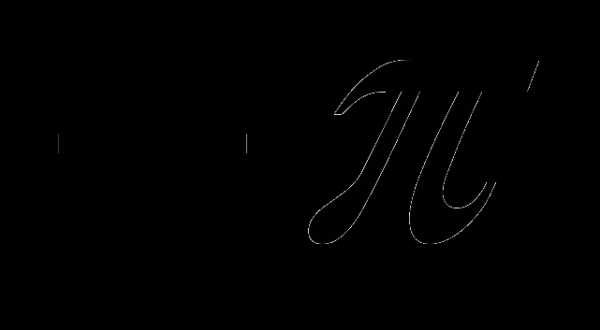 аrg z
аrg z  (иногда в качестве главного аргумента берут величину из промежутка
(иногда в качестве главного аргумента берут величину из промежутка 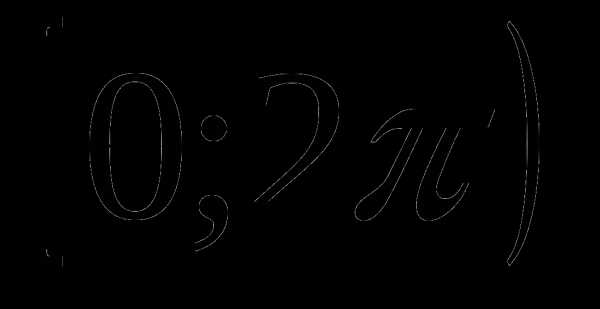 ).
).
Формы записи комплексных чисел.
Запись числа в виде называют алгебраической формой комплексного числа. Модуль r и аргумент  можно рассматривать как полярные координаты вектора
можно рассматривать как полярные координаты вектора  =
=  , изображающего комплексное число . Тогда получаем , . Следовательно, комплексное число можно записать в виде или . Такая запись называется тригонометрической формой.
, изображающего комплексное число . Тогда получаем , . Следовательно, комплексное число можно записать в виде или . Такая запись называется тригонометрической формой.
Модуль  однозначно определяется по формуле . Например, . Аргумент
однозначно определяется по формуле . Например, . Аргумент  определяется из формул
определяется из формул
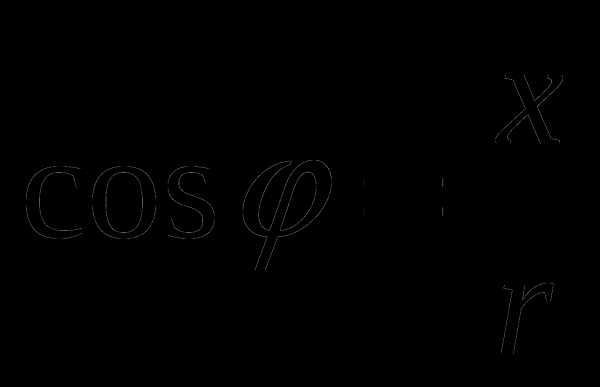 ,
, 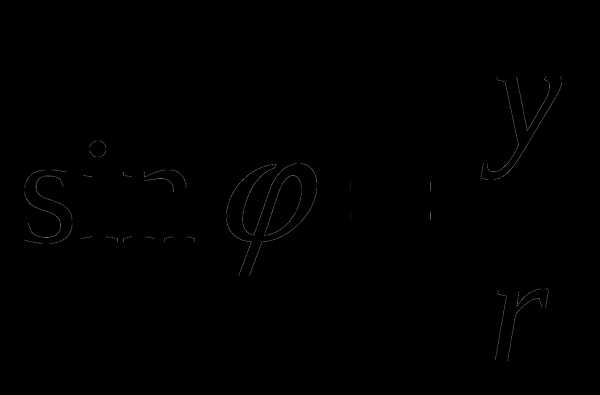 ,
, 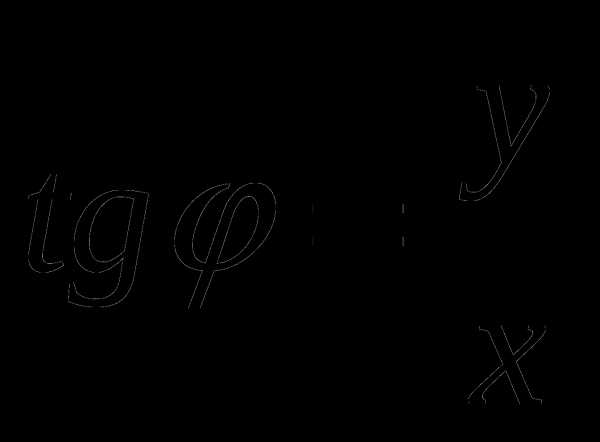
Так как , то , .
Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента z, т.е. считать .
Так как  аrg z
аrg z  , то из формулы
, то из формулы 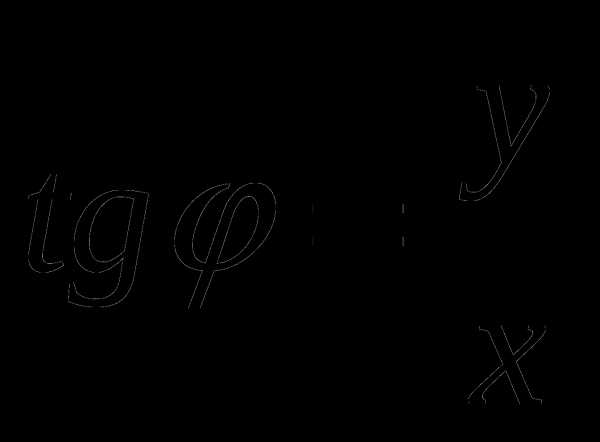 получаем, что
получаем, что
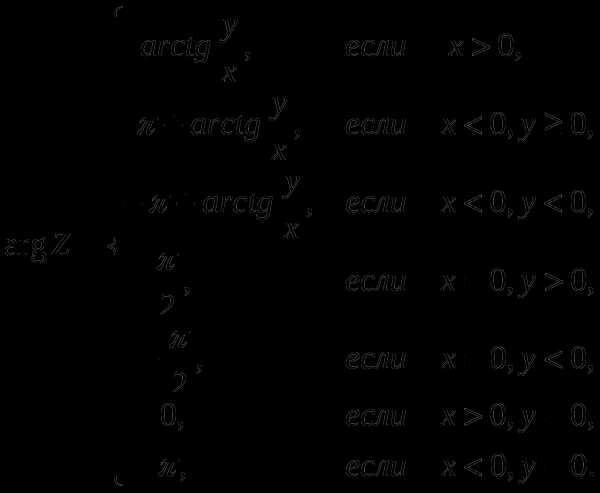
Используя формулу Эйлера , комплексное число можно записать в показательной (или экспотенциальной) форме 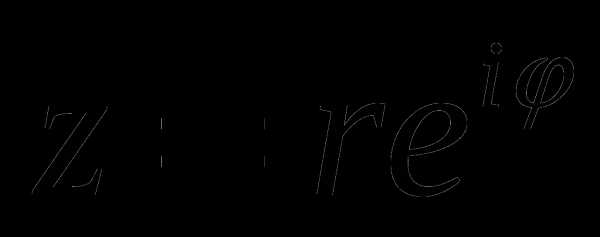 , где
, где 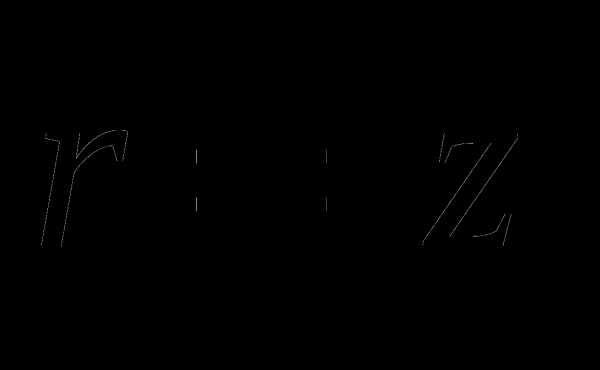 – модуль комплексного числа, а угол .
– модуль комплексного числа, а угол .
В силу формулы Эйлера функция 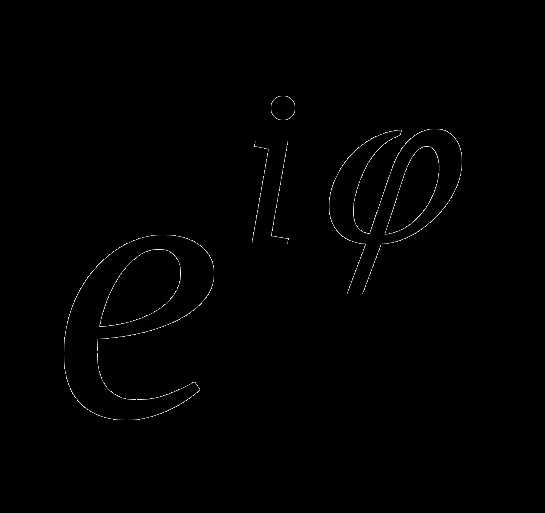 – периодическая с основным периодом 2. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать .
– периодическая с основным периодом 2. Для записи комплексного числа z в показательной форме, достаточно найти главное значение аргумента комплексного числа, т.е. считать .
Пример 1: Записать комплексные числа z1 = –1+i и z2 = –1 в тригонометрической и показательной формах.
Решение: Для числа z1 имеем:
, т.е. 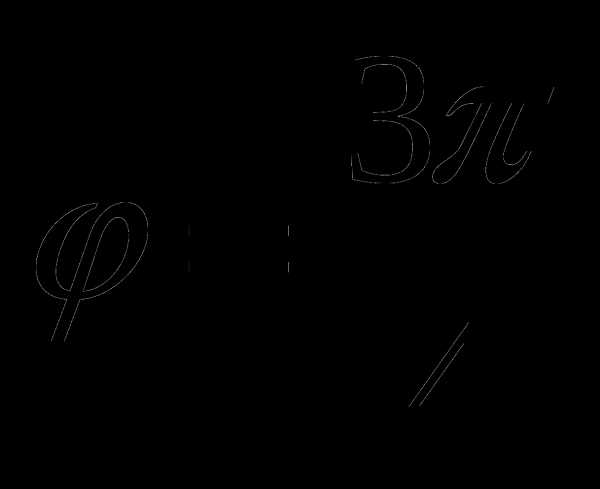 .
.
Поэтому
Для z2 имеем т.е.  .
.
Поэтому .
Действия над комплексными числами.
Суммой двух комплексных чисел z1 и z2 у z1+z2
называется комплексное число, определяемое z2
равенством . z1
O x
С
у
ложение комплексных чисел обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойствами. Из определения следует, что комплексные числа складываются как векторы. Из рисунка видно, что . Это соответствие называют неравенством треугольника.О х
z2
.
Из равенства следует, что геометрически комплексные числа вычитаются как векторы. Из рисунка видно, что .
Отметим, что, т.е. модуль разности двух комплексных чисел равен расстоянию d между точками, изображающими эти числа на плоскости.
Поэтому, например, равенство 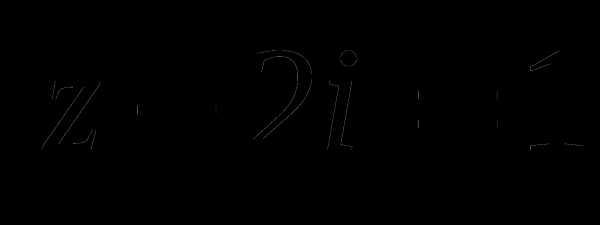 определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки
определяет на комплексной плоскости множество точек z, находящихся на расстоянии 1 от точки 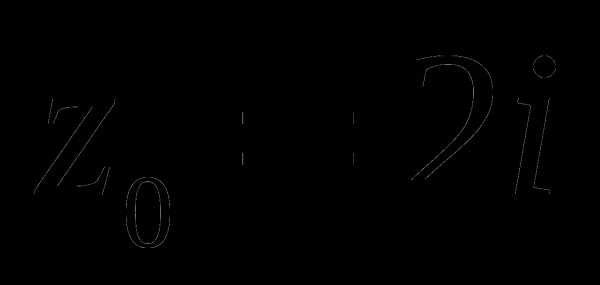 , т.е. окружность с центром в
, т.е. окружность с центром в 
Произведением комплексных чисел z1 = x1+iy1 и z2 = x2+iy2 называется комплексное число, определяемое равенством:
Произведение комплексных чисел можно находить путём формального перемножения двучленов x1 +iy1 и x2 +iy2, учитывая, что i2= –1.
Например, (2–3i)(–5+4i)= –10+8i+15i–12i2 = –10+23i+12=2+23i.
Заметим, что – действительное число.
Умножение комплексных чисел обладает переместительным, сочетательным и распределительным свойствами.
Найдём произведение комплексных чисел, заданных в тригонометрической форме:
Мы показали, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. В частности
– формула Муавра.
Пример 2: Найти 
Решение: Запишем сначала число в тригонометрической форме:
;
По формуле Муавра имеем
Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z, которое, будучи умноженным на z2, даёт число z1, т.е. 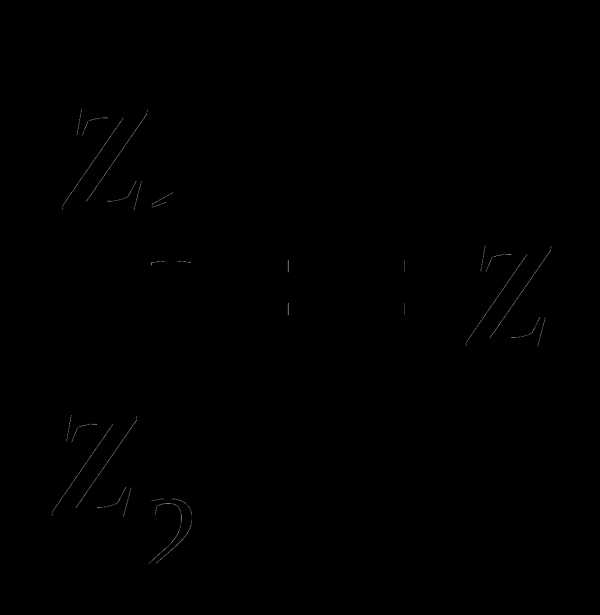 , если
, если 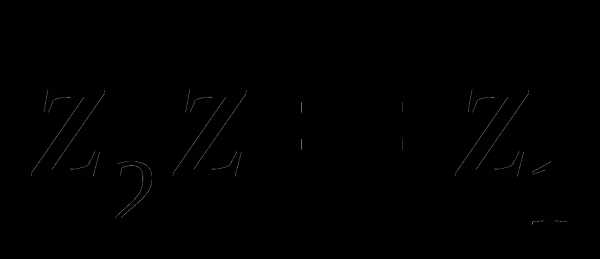 .
.
Если положить , , , то из равенства следует
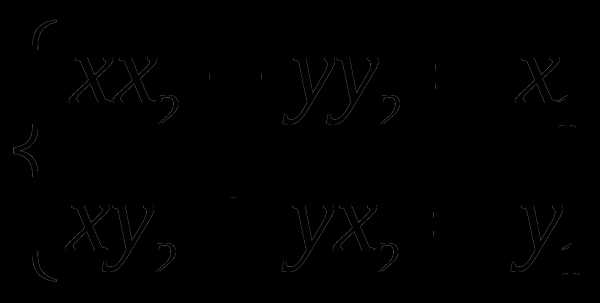
Решая систему, найдём значения х и у:
.
На практике частное двух комплексных чисел находят путём умножения числителя и знаменателя на число, сопряжённое знаменателю.
Пример 3: Выполнить деление 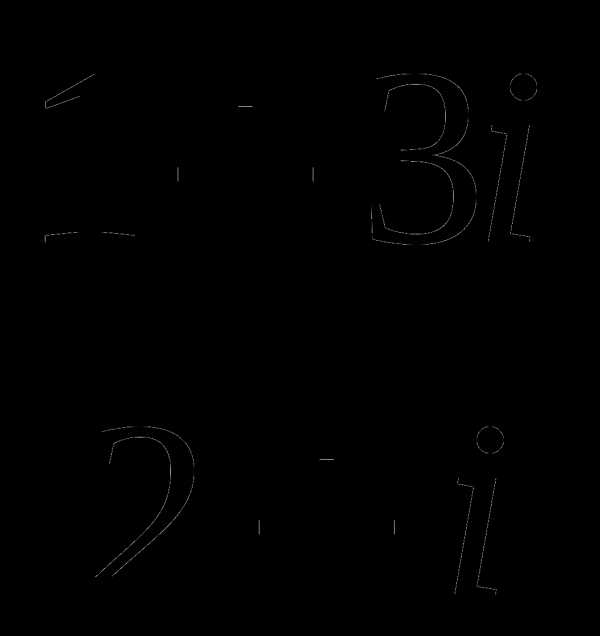
Решение:
Для тригонометрической формы комплексного числа деление имеет вид: ,
т.е. 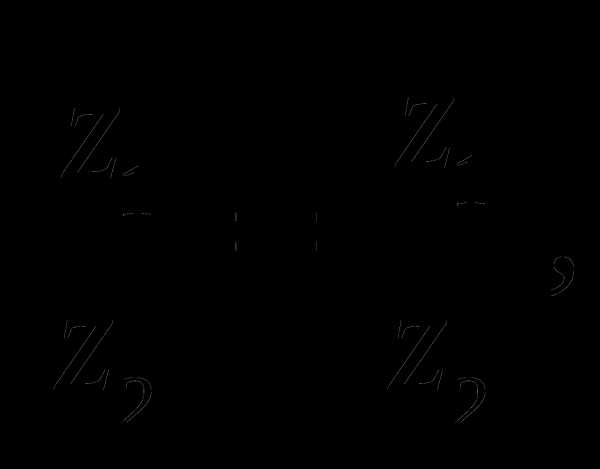 .
.
Корнем п-ой степени из комплексного числа z называется комплексное число 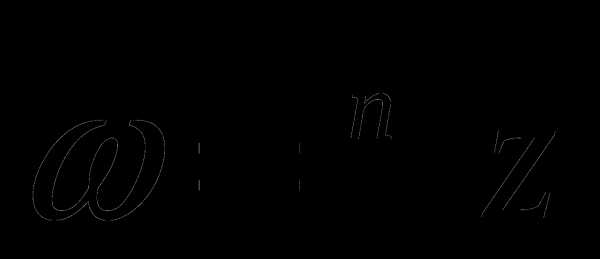 , удовлетворяющее равенству
, удовлетворяющее равенству 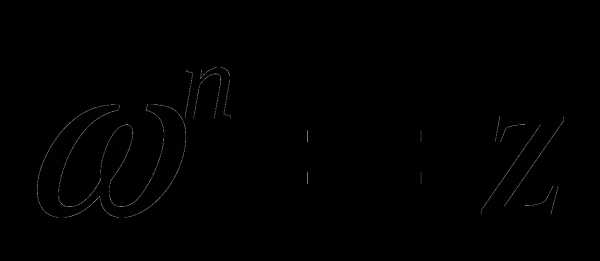 .
.
Если положить , а , то по определению корня и формуле Муавра, получаем
.
Отсюда имеем
Т.е. (арифметический корень).
Поэтому корень п-ой степени из комплексного числа имеет п различных значений, которые находятся по формуле:
,
Точки, соответствующие значениям 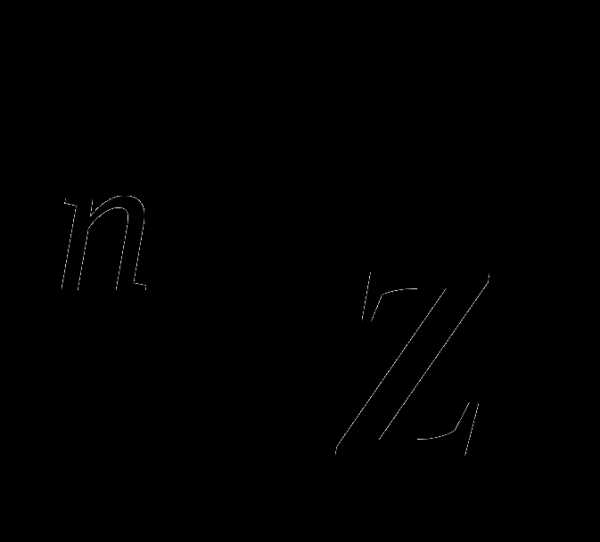 , являются вершинами правильного п-угольника, вписанного в окружность радиуса
, являются вершинами правильного п-угольника, вписанного в окружность радиуса 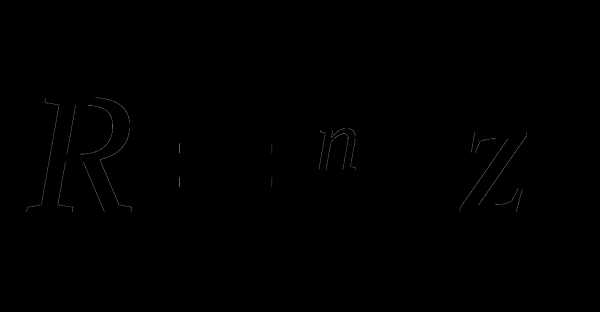 с центром в начале координат.
с центром в начале координат.
Пример 4: Найти все значения  .
.
Решение: Запишем комплексное число  в тригонометрической форме.
в тригонометрической форме.
.
.
Пример 5: Какое множество точек на комплексной плоскости определяется условием ?
Р
y
ешение: Комплексное число изображается вектором, началом которого является точка , а концом ‒ точка z. Угол между этим вектором и осью ОХ есть , и он меняется в пределах от
, а концом ‒ точка z. Угол между этим вектором и осью ОХ есть , и он меняется в пределах от  до
до  .
.С
-1 О х
‒1+i i
ледовательно, данное неравенство определяет угол между прямыми, выходящими из точки и образующими с осью ОХ углы в
и образующими с осью ОХ углы в 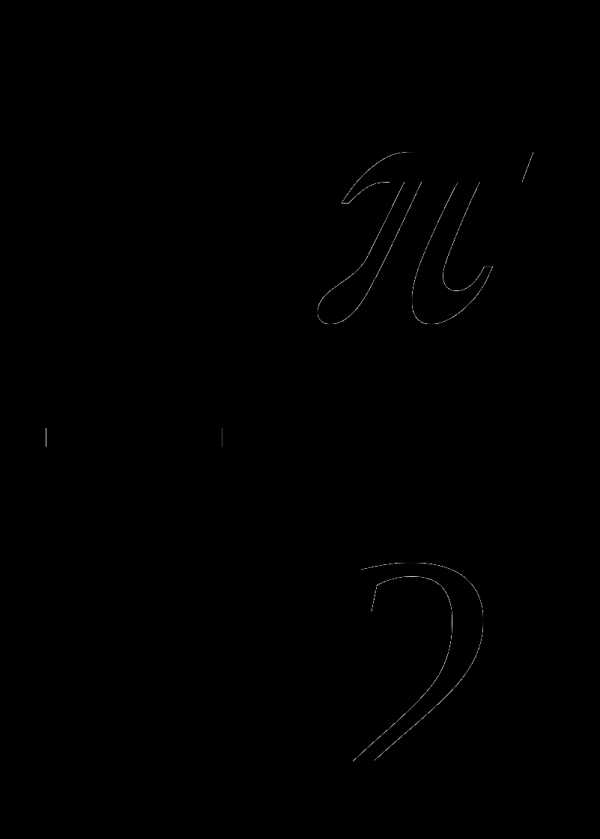 и
и 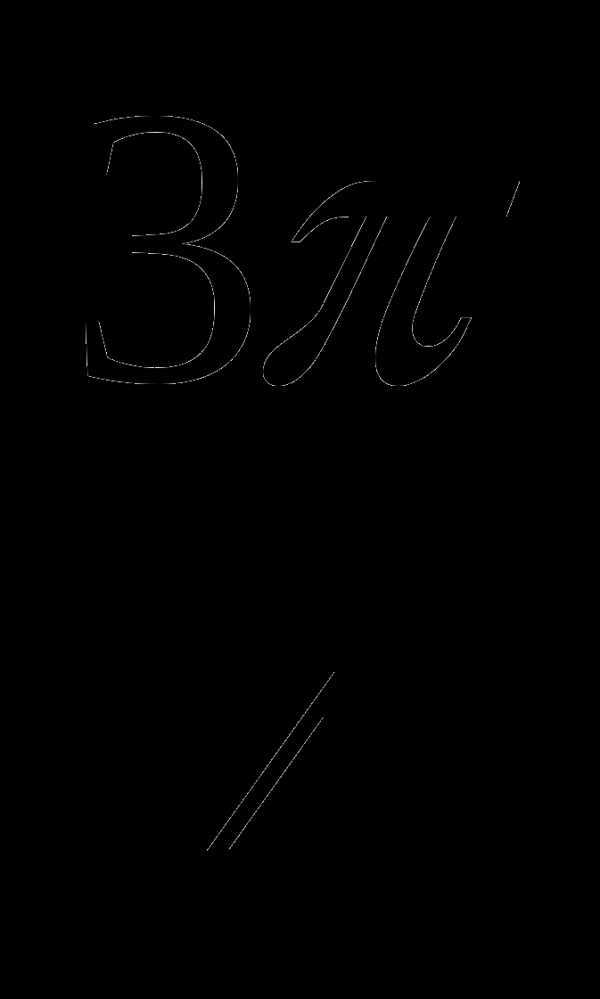 рад.
рад.Операции над комплексными числами, заданными в показательной форме
Пусть 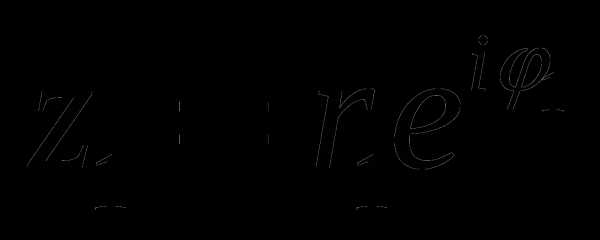 и
и 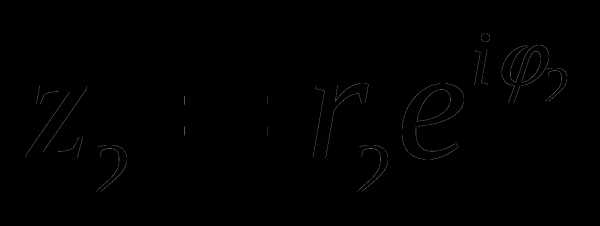 , тогда:
, тогда:
Произведение ;
Частное
 ;
;Возведение в n – ю степень ;
Извлечение корня n – й степени , .
Формулы Эйлера.
Рассмотрим разложение функции 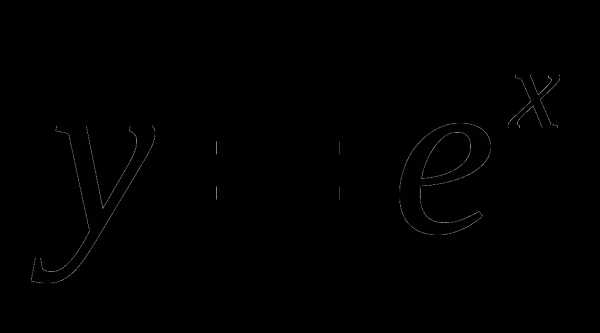 по формуле Маклорена.
по формуле Маклорена.
Если действительную переменную х заменить комплексной переменной z, то получим ряд по степеням z:
(1)
Аналогично определяются тригонометрические функции 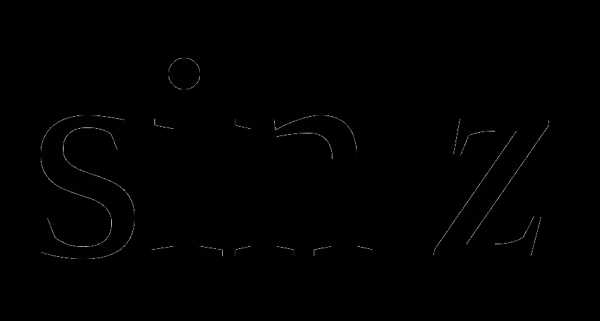 и
и  комплексной переменной z:
комплексной переменной z:
(2)
(3)
Подставим в (1) 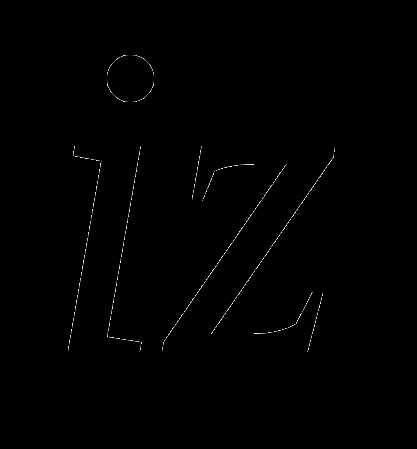 вместо z и сгруппируем в правой части все слагаемые, содержащие множитель i и не содержащие этот множитель.
вместо z и сгруппируем в правой части все слагаемые, содержащие множитель i и не содержащие этот множитель.
Сравнивая полученный результат с формулами (2) и (3), получаем
и
Таким образом, с помощью понятия комплексного числа устанавливается связь между тригонометрическими и показательной функциями:
Складывая и вычитая эти два выражения, получим
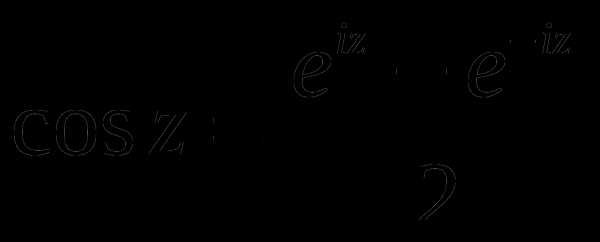 ;
; 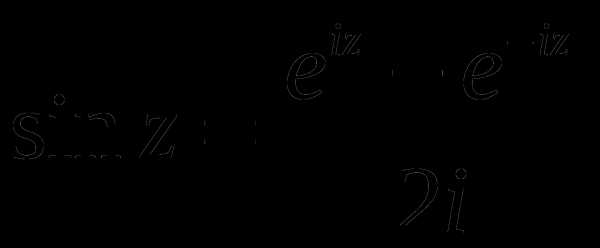 .
.
Используя понятие комплексных чисел, вводится понятие гиперболических синуса и косинуса:
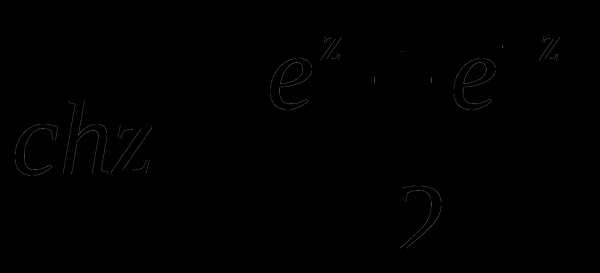 ;
; 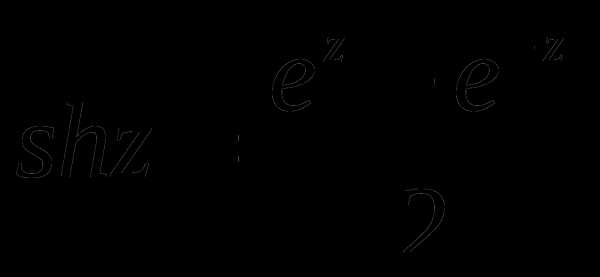 .
.
Из формулы Эйлера следует, что
; .
Приведенные известные из элементарной математики формулы:
, 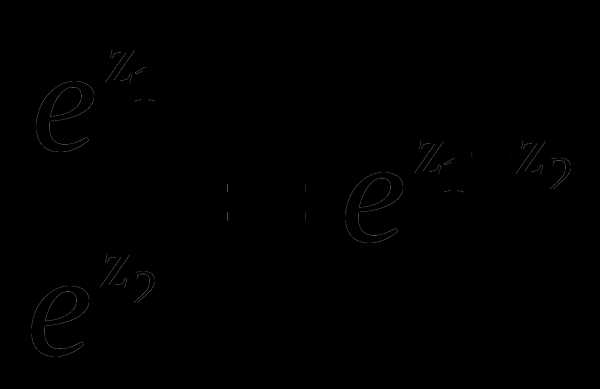 ;
;
; ,
справедливы и для комплексных значений аргументов  и
и  .
.
Основная теорема алгебры:
Функция вида , где п – натуральное число,  – постоянные коэффициенты, называется многочленом п-ой степени с действительными коэффициентами (или целой рациональной функцией).
– постоянные коэффициенты, называется многочленом п-ой степени с действительными коэффициентами (или целой рациональной функцией).
Корнем многочлена называется такое значение х0 (вообще говоря комплексное) переменной х, при котором многочлен обращается в нуль.
Теорема: Если х1 есть корень многочлена 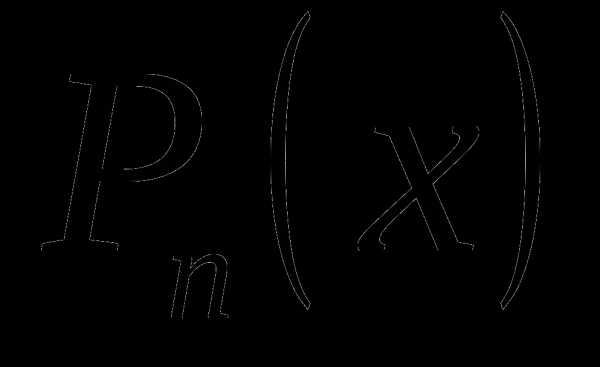 , то многочлен делится без остатка на х–х1, т.е. , где
, то многочлен делится без остатка на х–х1, т.е. , где 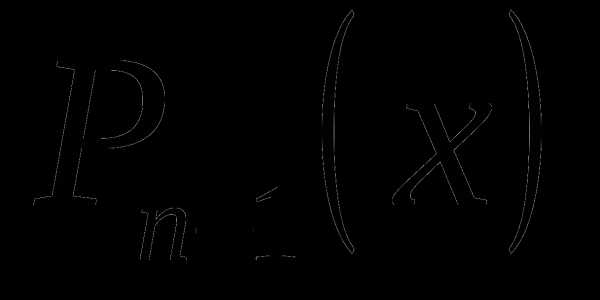 – многочлен степени (п–1).
– многочлен степени (п–1).
Теорема: (основная теорема алгебры) Всякий многочлен п-ой степени (n>0) имеет по крайней мере один корень, действительный или комплексный.
Теорема: Всякий многочлен 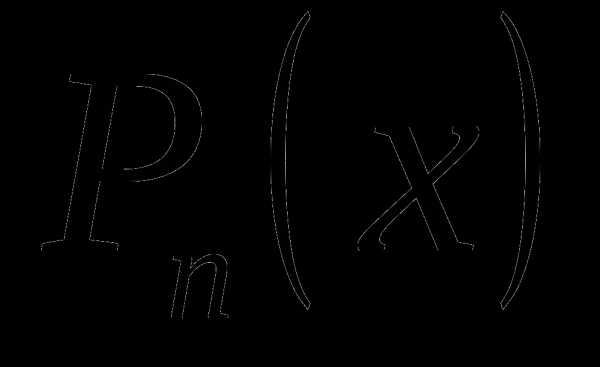 можно представить в виде
можно представить в виде
,
где – корни многочлена, 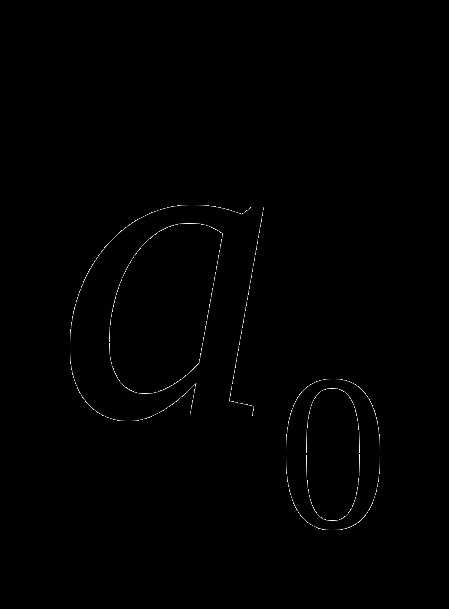 – коэффициент многочлена при хп.
– коэффициент многочлена при хп.
Множители 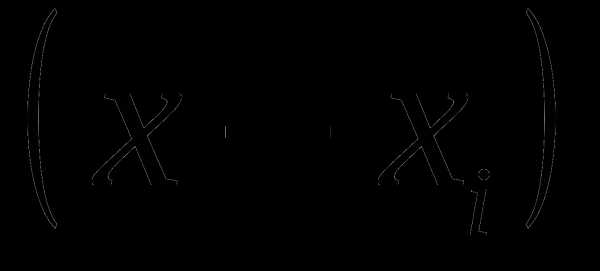 называются линейными множителями.
называются линейными множителями.
Пример 1: Разложить многочлен на множители.
Решение: Многочлен обращается в нуль при Следовательно .
Пример 2: Представить выражение в виде произведения линейных множителей.
Решение: Легко проверить, что  является корнем данного многочлена.
является корнем данного многочлена.
=
Уравнение имеет два комплексных корня  и
и  .
.
Следовательно, .
Если в разложении многочлена какой-либо корень встретился k раз, то он называется корнем кратности k. Тогда разложение многочлена можно записать в виде: , где ‒ кратности соответственно корней .
Теорема: Если многочлен 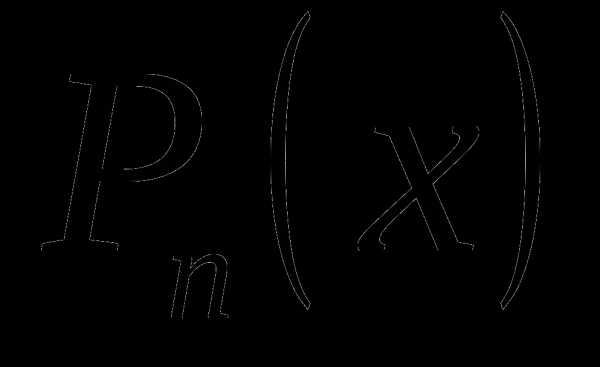 с действительными коэффициентами имеет комплексный корень
с действительными коэффициентами имеет комплексный корень 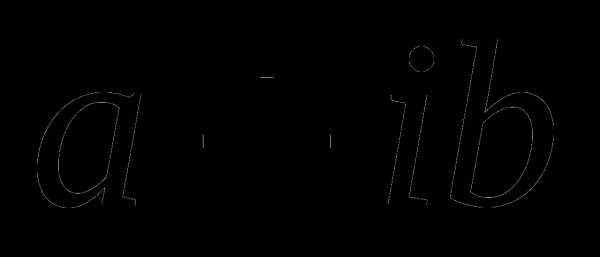 , то он имеет сопряжённый корень
, то он имеет сопряжённый корень 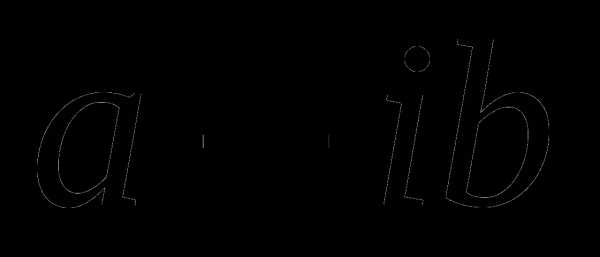 .
.
Перемножив линейные множители,
,
получили трёхчлен второй степени с действительными коэффициентами
=, где
Таким образом, произведение линейных множителей, соответствующих сопряжённым корням, можно заменить квадратным трёхчленом с действительными коэффициентами. Поэтому справедлива следующая теорема:
Теорема: Всякий многочлен п-ой степени с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:
где ,
х1, х2, … , хr – корни многочлена, а все квадратные трехчлены не имеют действительных корней.
Пример: этот многочлен имеет корни: х1= ‒2 и х2=3, других действительных корней нет. Тогда .
infourok.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).
Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y), записывается в виде
где использован символ i , называемый мнимой единицей.
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z.
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z.
Комплексные числа, у которых Im z = 0 , являются вещественными числами.
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами.
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Сложение и вычитание комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 осуществляется по правилам сложения и вычитания двучленов (многочленов) x1 + i y1 и x2 + i y2 , т.е. в соответствии с формулами
z1 + z2 == x1 + i y1 + x2 + i y2 =
= x1 + x2 + i (y1 + y2) ,
z1 – z2 =
= x1 + i y1– (x2 + i y2) =
= x1– x2 + i (y1– y2) .
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
По этой причине
z1z2 = (x1 + i y1) (x2 + i y2) =
= x1x2 + i x1 y2 +
+ i y1x2 + i 2y1 y2 =
= x1x2 + i x1y2 +
+ i y1x2 – y1 y2 =
= x1x2 – y1 y2 +
+ i (x1 y2 + i x2 y1) .
Комплексно сопряженные числа
Два комплексных числа z = x + iy и у которых вещественные части одинаковые, а мнимые части отличаются знаком, называются комплексно сопряжёнными числами.
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения, обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
Замечание. Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле


Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
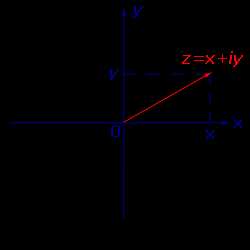
Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z.
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
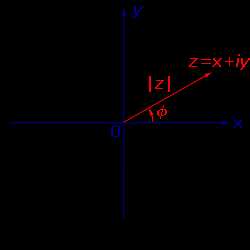
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
| (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
| (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
Расположение числа z : Положительная вещественная полуось Знаки x и y : x > 0 , y = 0 Главное значение аргумента: 0 Аргумент: φ = 2kπ Примеры: |
Расположение числа z : Первый квадрант Знаки x и y : x > 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Положительная мнимая полуось Знаки x и y : x = 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Второй квадрант Знаки x и y : x < 0 , y > 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Отрицательная вещественная полуось Знаки x и y : x < 0 , y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры: |
Расположение числа z : Третий квадрант Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Отрицательная мнимая полуось Знаки x и y : x = 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Расположение числа z : Четвёртый квадрант Знаки x и y : x < 0 , y < 0 Главное значение аргумента: Аргумент: Примеры: |
Тригонометрическая форма записи комплексного числа
Из формулы (3) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа.
Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.
Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа
cos φ + i sin φ,
или, что то же самое, числа e iφ, при любом значении φ равен 1.
Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел и записанных в экспоненциальной форме, осуществляется по формулам

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Извлечение корня натуральной степени из комплексного числа
Пусть — произвольное комплексное число, отличное от нуля.
Корнем n — ой степени из числа z0 , где называют такое комплексное число z = r e iφ , которое является решением уравнения
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
| (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
| (10) |
где
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , … , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса с центром в начале координат.
Замечание. В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
z2 = – z1 .
Пример 1. Найти все корни уравнения
z3 = – 8i .
Решение. Поскольку
то по формуле (10) получаем:
Следовательно,

Пример 2. Решить уравнение
z2 + 2z + 2 = 0 .
Решение. Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Так как
то решения уравнения имеют вид
z1 = – 1 + i , z2 = – 1 – i .
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Комплексные числа — Викиучебник
Материал из Викиучебника — открытых книг для открытого мира
Перейти к навигации Перейти к поискуЖурнал Потенциал
Содержание
- 1 Какие числа бывают
- 1.1 Задача 1[8] Задача Архимеда
- 1.2 Задача 2[8]
- 1.3 Задача 3[9]
- 2 Что такое комплексные числа?
- 2.1 Знакомство с мнимой единицей i=−1{\displaystyle \,\!i={\sqrt {-1}}}
- 2.1.1 Задача 4[8]
- 2.1.2 Задача 5[8]
- 2.1.3 Задача 6[9]
- 2.1.4 Задача 7[9]
- 2.1.5 Задача 8[8]
- 2.1.6 Задача 9[8]
- 2.1.7 Задача 10[9]
- 2.1.8 Задача 11[9]
- 2.1.9 Задача 12[9]
- 2.1.10 Задача 13[9]
- 2.1.11 Задача 14[8]
- 2.1.12 Задача 15[8]
- 2.1.13 Задача 16[8]
- 2.1.14 Задача 17[9]
- 2.1.15 Задача 18[10]
- 2.1 Знакомство с мнимой единицей i=−1{\displaystyle \,\!i={\sqrt {-1}}}
- 3 Cопряженные числа. Модуль. Деление
- 3.1 Cопряженные числа
- 3.1.1 Задача 19[7]
- 3.1.2 Задача 20[8]
- 3.1.3 Задача 21[9]
- 3.1.4 Задача 22[9]
- 3.1.5 Задача 23[9]
- 3.1.6 Задача 24[8]
- 3.1.7 Задача 25[9]
- 3.1.8 Задача 26[9]
- 3.1.9 Задача 27[9]
- 3.1.10 Задача 28[9]
- 3.1.11 Задача 29[9]
- 3.1.12 Задача 30[9]
- 3.1.13 Задача 31[9]
- 3.1.14 Задача 32[9]
- 3.1.15 Задача 33[9]
- 3.1.16 Задача 34[9]
- 3.1.1
- 3.1 Cопряженные числа
ru.wikibooks.org

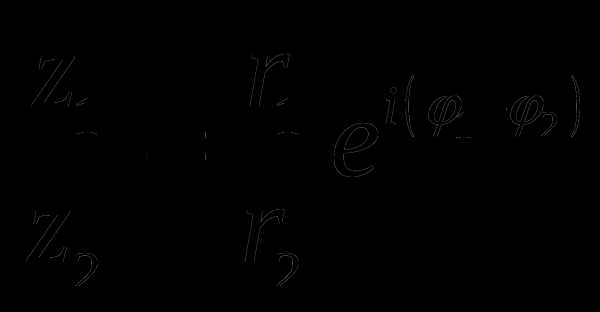 ;
;