5 факториал 6: Как решить Факториал числа. Таблица, Свойства, Примеры

alexxlab / / Разное

Содержание

Как решить Факториал числа. Таблица, Свойства, Примеры

Факториал: определение

Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».

Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:

  • -3,75! 2,23! -2!

Число должно быть целое и положительное:

  • 3! 56! 12!

Формула факториала
n!=1⋅2⋅3⋅…⋅(n−2)⋅(n−1)⋅n

Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.

Например:

  • 3! = 1*2*3 = 6
  • 4! = 1*2*3*4 = 24
  • 5! = 1*2*3*4*5 = 120
  • 6! = 1*2*3*4*5*6 = 720

Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой.

Запишитесь и участвуйте в розыгрыше 8 уроков

Формулы и свойства факториала

Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.

Запоминаем

0! = 1

1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000
16! = 20922789888000
17! = 355687428096000
18! = 6402373705728000
19! = 121645100408832000
20! = 2432902008176640000
21! = 51090942171709440000
22! = 1124000727777607680000
23! = 25852016738884976640000
24! = 620448401733239439360000
25! = 15511210043330985984000000

Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:

  • (n — 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)
  • n! = 1*2*3*4*5*…*(n — 2)(n — 1)n
  • (n + 1)! = 1*2*3*4*5*…*(n — 2)(n — 1)n(n + 1)

С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.

Такая формула дает результат с небольшой погрешностью.

Пример:

Рекуррентная формула

Примеры:

  • 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
  • 6! = 6*(6-1)! = 6*5! = 6*120 = 720

Для решения примеров обращайтесь к таблице.

Примеры умножения факториалов:

 

  1. Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800

  2. Или раскладывайте факториалы отдельно, если хотите потренироваться:
    5! = 1*2*3*4*5 = 4! * 5 =120
    7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
    120 * 5040 = 604800

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Примеры решений

Давайте поупражняемся и решим пару примеров.

1. Сократите дробь:


Как решаем:


При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100

Далее сокращаем по принципу сокращения обыкновенных дробей.

2. Вычислите значение выражения с факториалом: 8! + 5!

Как решаем:

Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.

А можно потренироваться и разложить их:

8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440

3. Вычислите значение выражения:


Как решаем:


7! = 1*2*3*4*5*6*7 = 5! * 6 *7

Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.

4. Вычислите значение выражение:


Как решаем:


Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*…..*69 = 69! * 70
49! = 1*2*3*. …49! * 48

Далее сокращаем все одинаковые множители.

5. Сократите дробь:


Как решаем:


Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.

Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.

Чему равен Факториал числа 5? — Спрашивалка

АН

Алла Неведомская

Чему равен Факториал числа 5? число факториал

2658

226

0

Ответы

НГ

Наталия Грач

Факториалом числа n (обозначается n!, произносится эн факториал) называют произведение всех натуральных чисел до n включительно. К примеру, факториал числа 5 будет выглядеть так: 5! = 1 * 2 * 3 * 4 * 5 и будет равен 120.

0

Игорь Малицкий

Это для кого вопрос, для школьников или для тех, кому пофик Ваш факториал, которые не знают, что или кто это. А так все могут ответить даже двоечники посмотрев в ГУГЛ

0

Nikas Juozaitis

А зачем вам это? Я изучал математику, в том числе и высшую, и мне в жизни факториал ни разу не пригодился, поэтому я благополучно забыл, что это такое.

0

Роберт Джемангулов

Оно мне надо?..влияет на моё самочувствие или стремительно расширяет круг моих знаний? Ну никак не прожить. .или для Вас это критерий?

0

GE

Grigory Elkin

он равен факториалу числа 6 деленному на модуль разности чисел 9,15 умноженному на единицу в первой степени.

0

АН

Алла Неведомская

Проверила — неверно!!!

1

GE

Grigory Elkin

!

1

Михаил Киранов

А почему в первой, а не в пятой степени?

1

. .

…

ФАКТОР-(днк) И-( продвижение по времени) АЛ-(начало людскаго) а что вы понимаете под этим словом (факториал)

0

Glаdiator (Woodland, Са)

Если я правильно помню подсчёт факториала из школьной программы, то это должно быть 120.

0

ВД

Владимир Дорошенко

Гораздо важнее знать , почему не может быть вулканов в других солнечных системах …!!!

0

Леонид Писанов

да какая разница- когда вокруг симпатичные девчонки в коротких сарафанчиках)

0

Маргарита Столбенникова

Предположим, что переменная n была связана с числом 5.

Т. е надо найти 5!.

0

Олег Бойко

Так… корень квадратный из (-1), вроде прошли… 5! = 5*4*3*2*1 = 120. Подхожу?

0

125

( нутром чувствую ..литр будет…а математически … выразить не могу)))

0

Виктор Быков, Ранее Неоднократно Не Судимый

120. А какое единственное число равно сумме факториалов своих цифр?

0

Артем

корень квадратный по параболе Гвоздикова!)))))))

0

Хмырь

Ух, ты! А зачем такой вопрос? Ответ известен любому школьнику.

0

БК

Бейбут Калыков

Я из числа ботаников,а не из чисел 5 Факов,пардон,Факториалов.

0

ГЗ

Галина Золотарева

И от знания факториала дети станут вундеркиндерами?

0

Виктор Посесор

120 а чему равна первая производная от скорости по времени?

0

Чудная Брунгильда,Баронесса

Четвертичному корню не состоявшейся действительности

0

Виктор

Извините я сейчас занят- вот-вот докажу теорему Ферма.

0

АН

Алла Неведомская

фермИ

1

Товарищ Товарищасухова

да какая разница, лишь бы этот Ферма (Ферми) сумел на ферме, почти кубические, корни поизвлекать, (коровы ноги ломают ((((( )

1

Следующая страница

Другие вопросы

Почему никто не доверяет мне, как дизайнеру без портфолио?!

Забыла графический ключ (андроид huawei).Что делать?

можно ли настроить вай-фай роутер с помощью планшета? кабель интернетный у меня есть. будет ли работать?

Хочу сделать Soft Reset на Nokia 5228. Это удалит мои смски, календарь, приложения? ? Помогите!

Какой фильм произвел на вас наибольшее впечатление в этом году ?

при загрузке компьютера выдает ошибку «не удалось прочитать правила транслитерации» и далее только нажмите ок

Посоветуйте фильм психиатрические, что то на подобии «Остров проклятых» или «Пролетая над гнездом кукушки»?

Какая сейчас последняя прошивка для андроида

Подскажите хороший аудио конвертер (wav->mp3), без потери качества, битрейта,

Помогите найти песню для дуэта

Как изменить жесткий димк, на который будут по умолчанию скачиваться и сохраняться файлы?

Asus k52n нет звука на колонках (встроенных)

хочу собрать комп недорогой, как сборка??? внутри, может чё посоветуете.

Не пойму что с фотошопом

Что произойдет если заменить батарею на ноуnбуке Asus A52j 10.8V 4400mAh на 11.1V 5200mAh

Перестановки и факториал — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Перестановки и
факториал
Лавлинский М.В., [email protected]
I. Факториал
Факториал числа n (n!) — произведение всех натуральных
чисел от 1 до n включительно
1800 г. – Л. Арбогаст (1759 — 1803) ввёл термин факториал
1808 г. — К. Крамп (1760 — 1826) придумал обозначение n!
Если n=0 то n!=1
Если n>0 то n!=1 2 3 … n
#:
2! = 1 2 = 2
3! = 1 2 3 = 6
4! = 1 2 3 4 = 24
5! = 1 2 3 4 5 = 120
Рекуррентная формула:
n 0
1
n!
n (n 1)! n 0
Таблица факториалов
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000
16! = 20922789888000
100! ≈ 9,33×10157
17! = 355687428096000
1000! ≈ 4,02×102567
18! = 6402373705728000
10000! ≈ 2,85×1035 659
19! = 121645100408832000
20! = 2432902008176640000
21! = 51090942171709440000
22! = 1124000727777607680000
23! = 25852016738884976640000
24! = 620448401733239439360000
25! = 15511210043330985984000000
26! = 403291461126605635584000000
27! = 10888869450418352160768000000
28! = 304888344611713860501504000000
29! = 8841761993739701954543616000000
30! = 265252859812191058636308480000000
II. Решение задач
#1. Вычислить:
5! 4! 5
4! 1 2 3 4 24
5
5
#2.
14!
7! 8 9 10 11 12 13 14 5 11 12 13 14
7! 3! 4!
7! 1 2 3 1 2 3 4
1
120120
#3. Делится ли 11! на 49?
1 2 3 4 5 6 7 8 9 10 11
7 7
Ответ: нет
#4. Сколькими нулями оканчивается число 26!
26!
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26
Ответ: 6
#5. Сократить дробь
(4m 1)! (4m 3)!(4m 2)( 4m 1)
(4m 3)!
(4m 3)!
(4m 2)( 4m 1)
#6. Упростить выражение
(3k 3)! k! (k 3)!(3k 1)
:
18 (3k 2)
2
(3k )!
3!(k 5k 6)
2
(3k )! (3k 1) (3k 2) (3k 3) k! 3!(k 5k 6)
(3k )!
(k 3)!(3k 1)
2
(3k 2) (3k 3) k!
3!(k 5k 6)
1
k!(k 1)(k 2)(k 3)
(3k 2) (3k 3) 3!(k 2)( k 3)
1
(k 1)( k 2)( k 3)
(3k 2) (3k 3) 3! (3k 2) 3 (k 1) 6
(k 1)
(k 1)
#7. Решить уравнение
(k 10)! 77(k 11)!
(k 10)! 77(k 11)!
(k 11)!
(k 11)!
(k 11)! (k 10) 77(k 11)!
(k 11)!
(k 11)!
(k 10) 77
k 87
III. Перестановки
Перестановки из n элементов
— это комбинации из n элементов, отличающиеся друг от
друга только порядком расположения в них элементов.
Pn – обозначение
#1. Найдите все возможные перестановки цифр: 1, 2, 3.
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
P3 = 3! = 6
Формула нахождение количества перестановок:
Pn = n!
IV. Решение задач
Задача №1.
«Проказница-Мартышка, Осел, Козел
Да косолапый Мишка
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки
И сели на лужок под липки,Пленять своим искусством свет.
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! — кричит Мартышка. Погодите!
Как музыке идти? Ведь вы не так сидите.
*** *** *** *** ***
Послушались Осла: уселись чинно в ряд;
А все-таки Квартет нейдет на лад.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…»
Сколькими
различными
способами могут сесть
музыканты?
Решение:
n=4
P4 = 4! =24
Ответ: 24
Задача 2.
Сколькими способами можно развесить 5
цветных шаров на гирлянде?
Решение:
Р5 = 5! = 1·2·3·4·5= 120
Ответ: 24
Задача №3. В расписании 9 класса на четверг должно быть 6
предметов: русский язык, литература, алгебра, география,
физика, физкультура. Сколькими способами можно
составить расписание на этот день?
P6 = 6! = 720
Задача №4. Сколькими способами можно составить
расписание из тех же 6 предметов, если требуется, чтобы
урок физкультуры был последним?
P5=5!= 120
Задача №5.
Сколькими способами из тех же 6 предметов можно
составить такое расписание, в котором русский язык и
литература стоят рядом?
P5= 5!*2 = 240
(1. РЛ 2. ЛР)
Задача 6.
Сколько различных 5-значных чисел, все цифры которых
различны можно записать с помощью цифр 4, 5, 6, 7, 8?
P5 = 5! = 120
Задача 7.
Сколькими способами можно расставить на полке 8 книг,
если среди них 2 книги одного автора, которые при любых
перестановках должны стоять рядом?
P7 = 7! = 5040
5040 * 2 = 10080
V. Обобщения факториала
1. Двойной факториал числа n
— обозначается n!!
— произведение всех натуральных чисел в отрезке [1,n],
имеющих ту же чётность что и n.
Для чётного n:
n!! = 2 · 4 · 6 · … · n
Для нечётного n:
n!! = 1 · 3 · 5 · … · n
#: Вычислить:
10!! = 2 · 4 · 6 · 8 · 10 = 3840
9!! = 1 · 3 · 5 · 7 · 9 = 945
0!! = 1
!!
2. Праймориал (примориал) числа n
— обозначается n#
— произведение простых чисел, не превышающих n.
11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310
#: Вычислить:
7# = 8# = 9# = 10# = 2 · 3 · 5 · 7 = 210
5# = 6# = 2 · 3 · 5 = 30
3# = 4# = 2 · 3 = 6
2# = = 2
#
3. Суперфакториал числа n
— обозначается sf(n)
— произведение первых n факториалов
— определили в 1995 г. – Н.Слоан и С.Плоуф
sf(4) = 1! · 2! · 3! · 4! = 288
#: Вычислить:
sf(3) = 1! · 2! · 3! = 12
sf(2) = 1! · 2! = 2
sf(1) = 1! = 1
sf(0) = 1
sf

English     Русский Правила

Мат-2019, результаты 7-6-5-4-3-2-1.

2))  + 1 = 2019 (Skarbovoy)

А вот для 5-ки и ниже уже требуются супер-суб-факториалы и праймориалы, а также разные хорошо известные числовые ряды.

===== 5 4 3 2 1 =====

Для решения этой задачки и ниже разрешается использовать ещё более расширенные возможности:

!n = субфакториал.
# n = праймориал.
sf(n) = суперфакториал.

и стандартные числовые последовательности вроде таких:

F() = числа Фибоначчи,
Fm() = числа Ферма,
C() = числа Каталана,
L() = числа Леонардо,
M() = числа Мерсена

и разные прочие общеизвестные, обозначенные в интернетах.

Итак, какие варианты есть для пятёрки? Вот такой сразу, адаптированный из «2018»:

( 5! — 4! ) * F( F( 3! )) + 2 + 1 = 96 * 21 + 3 = 2019

А также:

5 * C (( M ( F( 4 ))) — M ( M( 3 )) + 2 — 1 = 2019 (Яна Барсукова)

А также моё без каких-либо именных числовых рядов:

5# — ( 4! * sf( 3 ) ) — 2 — 1 = 2310 — 24*12 — 3 = 2019

Опаньки! Праймориал-факториал-суперфакториал — и готово! Что означает, что ещё есть место для манёвров. Не все ещё возможности математических операций до конца проверены, проинвентаризированы и использованы.

Немного читерства со склейкой цифр:

-5! + F( 4 ) * ( 3! )! — 21 = 2019  (Skarbovoy)

===== 4 3 2 1 =====

Упражнения становятся всё интереснее и интереснее, чем меньше цифр – тем сложнее задачка, всё как мы любим 🙂

C( 4 ) * F( (3!)!!!! ) + 2 + 1 = 14 * 144 + 3 = 2019 (адаптация решения для 2018).

От Яны Барсуковой:

C( 4 ) * F ( sf( 3 )) + 2 + 1 = 2019
sf( 4 ) * M( 3 ) + 2 + 1 = 2019

Как всем хорошо известно, кратными факториалами можно чёрта лысого из любой цифры сотворить. Посему их применение надо как-то ограничить. Попробую договориться, что кратные факториалы могут использоваться либо однократно, либо же их значение не может превышать половины кратно-факториализуемого (о как задвинул). То есть, либо один раз, либо 32!!! Изволь умножать через каждую тройку. Я понятно рассказываю?

Ну, если так, то можно ещё раз подойти и к вот такому упражнению: 4 3 2 1 = 2019. Что из этого получается:

4!*sf(3) = 4*3*2 * 3!*2! = 24*12 = 288

288!!!…281-кратный-факториал…!!! = 288*7 = 2016 // как же удобно и приятно, когда такие хорошие и правильные числа лежат в шаговой доступности 🙂

( 4! * sf( 3 ) )!!!…281-кратный-факториал…!!! + 2 + 1 = 2019

А если приглядеться… Умножение на семёрку можно же было и раньше сделать, вот эта кучка восклицательных знаков — это оно и есть ->

( 4! ) !!!!!!!!!!!!!!!!!  * sf( 3 ) + 2 + 1 = 2019

===== 3 2 1 =====

Можно, конечно, вот так извернуться, но это тоже по мотивам русских народных сказок успешных прошлогодних опытов ->

L(L( 3 )!!) + !L(M( 2 )) + F( Fm( !1 )) = L(15) + !L(3) + F(3) = 1973 + 44 + 2 = 2019

А вот ещё:

3 + (( M( 2 ))! )!! * C(Fm(1)) = 2019  (Яна Барсукова</a>)

===== 2 1 =====

Едем дальше. .. и видим двойку. Как получить 2019 всего из двух цифр? Что-то как-то только вот так получается… через числа Mian-Chiwla… слышали о таких? Я пока тоже нет. Но в Википедии есть описание (ссылка выше). Нашёл я их вот здесь: Online Encyclopedia of Integer Sequences.

2019 = 2584 — 565
2584 = F(18) = F(6*3) = F(6!!!) = F( (3!)!!! ) = F( ( M(2)! )!!! )
565 = MC(21) = MC( MC( 3! )) = MC( MC( Fm(!1)! ))

Итого:

F( ( M(2)! )!!! ) — MC( MC( Fm( !1 )! )) = 2019

Вроде нигде не ошибся.

Ещё один подход к задачке 2 1 = 2019. Как я уже когда-то говорил, кратным факториалом можно чёрта лысого слепить. Ну, пробуем лепить этого чёрта лысого номер года нашего нынешнего…

2019 = 673*3 = 673!!!…!!! // 670-кратный факториал.

673 = 672 + 1 // единицу использовали и выбрасываем, осталась двойка.

А, пойду самым простым и проверенным путём. Из двойки делаем 0 (например, субфакториалом) и потом Ферма превращает брюки в шорты ноль в тройку.

!2 = 1
!1 = 0
Fm( !(!2) ) = 3.

Тройка! А это уже не двойка какая-то поганая. Это уже тройка! Начинаем удобрять её кратными и просто факториалами…

3! = 6
6!! = 6*4*2 = 48
48!!!…!!! (46-кратный он же) = 96.
96!!!….!!! (89-кратный) = 96*7 = (берём в руки калькулятор…) = искомое 672, которое = 25 * 3 * 7

Ура, товарищи!

((((( Fm( !(!2) )! )!! )!!!…46-кратный…!!!)!!!…89-кратный...!!!) + 1 )!!!…670-кратный…!!! = 2019

Проверяйте 🙂

Чуть позже меня осенило:

Двойка мне, неразумному! Я же про праймориалы забыл! Получается ещё проще, Ферма и факториал 3! убираем…

2#  = 2*3 = 6, исходя из этого…

((((( 2# )!! )!!!…46-кратный…!!!)!!!…89-кратный...!!!) + 1 )!!!…670-кратный…!!! = 2019

Из чего следует, что нет предела нашему интегралу! совершенству и упражнениям для саморазвития.

===== 1 =====

Ну и напоследок, наше традиционное и самое любимое упражнение. Лепим «2019» из единственной цифры один: «1 = 2019«. Ага, а тут есть вот такая штукенция: числа Тетраначчи (Tetranacci numbers), далее Tcci (это я придумал). Поехали…

Tcci(12) = 673

12 = 6!!!!

6=3! — а тройку уже давно умеем получать из единицы ловкостью чисел Ферма: !1=0, Fm(0)=3. Итого:

Tcci(( Fm( !1 )! )!!!! ) !!!…!!! (670-кратный факториал) = 673*3 = 2019

Вуаля.

Всем спасибо за внимание!

Задачка решена, но увидеть более красивые решения всё равно очень хочется!

Метки: chtogdekogda, math

Что такое факториал числа 5? – Обзоры Вики

Факториалы чисел от 1 до 10 Таблица

n Факториал числа n! Значение
5 5! 120
6 6! 720
7 7! 5,040
8 8! 40,320

Отсюда, как вы делаете факториалы? Чтобы найти факториал числа, умножьте число на факториал предыдущего числа. Например, чтобы узнать значение 6! умножьте 120 (факториал 5) на 6 и получите 720.

Как читать пять факториалов? Функция факториала (символ: !) предлагает умножить все целые числа из выбранного нами числа на 1.
…
Небольшой список.

n n!
4 24
5 120
6 720
7 5,040

Дополнительно Что такое факториал 1? Это по-прежнему считается способом организации, поэтому по определению нулевой факториал равен единице, как 1! равно единице, потому что существует только одно возможное расположение этого набора данных.

Что такое пять как число? 5 (число)

← 4 5 6 →
Кардинальный 5
порядковый 5 (пятый)
Система счисления пятеричный
факторизация простое число

Как вам найти 5?

Как написать 5-й? 5 = пятый (Это пятый раз, когда я сдавал экзамен по вождению.)

Что означает 5?

5 представляет любопытство и приключения; важность числа 5 присутствует во всех культурах и религиях мира; и вещи, связанные с числом 5, варьируются от приземленных до причудливых! Люди даже используют нумерологию 5, чтобы определить свое будущее.

Как получить 5% от числа?

5 процентов — это половина от 10 процентов. Чтобы вычислить 5 процентов числа, просто разделите 10 процентов числа на 2. Например, 5 процентов от 230 — это 23, разделенное на 2, или 11.5.

Как написать 5 предложений?

Абзац из пяти предложений состоит из предложения с основной идеей, трех предложений, которые объясняют основную идею с причинами, подробностями или фактами, и заключительного предложения.

  1. Мозговой штурм. Для начала ученица начальной школы излагает свои идеи на бумаге в виде паутины, сосредоточенной вокруг основной идеи. …
  2. Контур. …
  3. Напишите абзац. …
  4. Просмотрите его.

Как правильно 21 или 21?

в английском нет такой позиции, как «21th»; «21-е» правильно. оно произносится как «двадцать первый», а не как «двадцать один», и поэтому «ст» в «21-м». первые несколько позиций: 1-я, 2-я, 3-я и 4-я. это краткие формы первого, второго, третьего и четвертого.

Какие пять предложений? 5 предложений:

  • Мы продолжали слышать звук мусоровоза.
  • Я знал, что забыл сделать домашнее задание.
  • Мама тоже хотела записаться на прием к педиатру.
  • Синоптики предсказывали, что день будет солнечным.
  • Новый ведущий продолжал говорить о выборах.

Есть ли дислексия в математике?

Исследования показывают, что это так же распространено, как дислексия — расстройство чтения, но не так хорошо изучено. На самом деле, дети и родители иногда называют это «математической дислексией», но это может сбивать с толку, потому что дискалькулия — это совсем другое состояние.

Как написать 5 римскими цифрами? Цифры 1–10:

  1. 1 = Я.
  2. 2 = II.
  3. 3 = III.
  4. 4 = IV.
  5. 5 = В.
  6. 6 = VI.
  7. 7 = VII.
  8. 8 = VIII.

Что означает 6 год?

Определение шести

1: число, которое на единицу больше пяти — см. Таблицу чисел. 2: шестой в наборе или серии.

Какое число Имя 7?

Что такое имя числа?

Цифры: Номер Имя:
5 Пять
6 Шесть
7 Семь
8 Восемь

Можно ли умножать факториалы? Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.

Как решать факториальные уравнения?

Можно ли умножать факториалы? Факториалы, обозначаемые a. … Вы также можете умножить факториалы вручную. Самый простой способ сделать это — вычислить каждый факториал по отдельности, а затем перемножить их произведения вместе. Вы также можете использовать определенные правила факториалов для извлечения общих множителей, что может упростить процесс умножения.

Насколько велик факториал 52?

52! является приблизительно 8.0658e67. Чтобы получить точное представление, просмотрите факториальную таблицу или попробуйте калькулятор «новой школы», который понимает длинные целые числа.

Что такое факториал 9?

Ответ: Факториал числа 9 равен 362,880.

Калькулятор — факториал(6) — Solumaths

Факториал, интерактивный расчет

Резюме:

Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.

факториал онлайн

Описание:

Онлайн-калькулятор факториала имеет функцию факториала . что позволяет вычислить онлайн факториал целого числа.

Восклицательный знак обычно используется как обозначение факториала, калькулятор позволяет использовать это обозначение.

Например, для , вычисляющего факториал 5 , используйте следующий синтаксис факториал(`5`), после вычисления возвращается результат 120. Следующий синтаксис также можно использовать для вычисления факториала 5!

Для небольших чисел калькулятор может выдать детали расчетов факториала.

Синтаксис:

factorial(n), где n — целое число.

Можно использовать восклицательный знак для вычисления факториала n!

Примеры:

factorial(`5`), возвращает 120

Расчет онлайн с факториалом (факторный калькулятор)

См. также

Список связанных калькуляторов:

  • Номер расстановки комплекта калькулятора : расстановка. Вычислить онлайн количество расположения p элементов множества из n элементов.
  • Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел.
  • Для подсчета комбинаций: комбинация. Вычислить количество k элементов части множества из n элементов.
  • Преобразователь base-n : base_converter. Калькулятор позволяет выполнять десятичные, двоичные, шестнадцатеричные преобразования и, в более общем случае, преобразование в любое основание n от 2 до 36.
  • Калькулятор простой факторизации : prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители.
  • Калькулятор частного и остатка: euclidean_division. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел.
  • Четность числа: is_odd. Функция Is_odd возвращает true, если переданное число нечетное, иначе false.
  • Четность числа: is_even. Функция Is_even возвращает 1, если число четное, иначе 0.
  • Калькулятор факториала: факториал. Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число.
  • Калькулятор перестановок: перестановка. Подсчитать онлайн количество перестановок набора из n элементов.
  • Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД.
  • Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК).
  • Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника.
  • Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.

Напоминания о курсах, калькуляторы, упражнения и игры: Числа

 

Калькулятор факториала

Найдите факториал любого целого числа от 0 до 10 000. За помощью в использовании калькулятор, ознакомьтесь с часто задаваемыми вопросами или просмотрите образец задачи.

  • Введите неотрицательное целое число (n) в незатененное текстовое поле.
  • Нажмите Кнопка Calculate для отображения значения факториала этого числа (n!).
Целое число (n)
Научное обозначение
Обозначение E
Факториал n

(n!)

Объявление

Часто задаваемые вопросы

Факторный калькулятор | Пример задачи

Инструкции: Чтобы найти ответ на часто задаваемый вопрос, просто нажмите на вопрос.

Что такое факториал?

Факториал — это произведение целого числа и каждого меньшего положительного целого числа. Этот продукт представлен символ n !, который называется n факториалом . По соглашению 0! = 1. Таким образом,

0! = 1

2! = (2)(1) = 2

3! = (3)(2)(1) = 6

4! = (4)(3)(2)(1) = 24

5! = (5)(4)(3)(2)(1) = 120

и т. д. …

Факториалы могут стать очень большими и очень быстрыми. Срок 10000! это наибольший факториал, который может вычислить факториал. Срок 10000! является равно примерно 2,846 x 10 35659 .

Пример вычисления факториала см. Пример задачи 1.

Что такое научная нотация?

Факторный калькулятор использует научную запись для выражения очень больших чисел. Научная нотация — это способ записи слишком больших или слишком мал, чтобы быть кратко записанным в десятичном формате.

В экспоненциальном представлении любое положительное целое число может быть выражено числом от 1 до 10. умноженное на степень 10. Вот пример числа, записанного с использованием экспоненциальной записи:

3,02 * 10 12 = 3 020 000 000 000

Что такое нотация Е?

Факторный калькулятор использует нотацию E для выражения очень большие числа. Нотация E — это способ записи слишком больших или слишком мал, чтобы быть кратко записанным в десятичном формате.

В обозначении Е буква Е представляет «умноженное на десять, возведенное в степень ». Вот пример числа, записанного с использованием нотации E:

3,02E12 = 3,02 * 10 12 = 3 020 000 000 000

Насколько точен факториальный калькулятор?

Калькулятор факториала отображает результаты в трех форматах: экспоненциальное представление, Нотация E и обычные целые числа.

Целочисленные результаты являются точными для всех вычислений до 10 000 факториалов (10 000!). Полученные результаты представленные в экспоненциальной записи и записи E, также точны до 21 факториала (21!). После факториала 21 результаты, представленные в экспоненциальной записи и в записи E, очень хорошие. приближения, с точностью до 14 значащих цифр.

Какой самый большой факториал может обрабатывать этот калькулятор?

Калькулятор факториала может вычислить факториал для любого числа до 10 000.

Свыше 10 000 калькулятор выдает оценку по нижней границе. Вот логика. Значение из 10000! составляет примерно 2,846 x 10 35659 . Итак, мы знаем факториал любого целого числа больше 10 000 будет как минимум 10 35663 . Итак, для любого целое число больше 10 000, калькулятор сообщит, что значение факториала будет более 10 35663 .

Пример задачи

Факторный калькулятор | Часто задаваемые вопросы


  1. Стандартная колода игральных карт состоит из 13 пик. Как много как можно расположить эти 13 пик?

    Решение:

    Решение этой задачи включает вычисление факториала. Первая карта выбранной может быть любая из 13 пик; вторая — любая из оставшихся 12 пик; третий, любая из оставшихся 11 пик; и так далее. Так как мы хотим знаем, как можно расположить 13 карт, мы вычисляем значение для 13 факториал.

    13! = (13)(12)(11)(10)(9)(8)(7)(6)(5)(4)(3)(2)(1) = 6 227 020 800


    Обратите внимание, что приведенный выше расчет немного громоздкий для выполнения вручную, но его можно легко вычислить с помощью факториального калькулятора. Чтобы использовать Факторный калькулятор, выполните следующие действия:
    • Введите «13» вместо n.
    • Нажмите кнопку «Рассчитать».

    Ответ, 6 227 020 800, отображается в «Факториале n». текстовое поле, как показано ниже.

Факторный калькулятор | Определение | Формула

Создано Альваро Диесом и Богной Шик

Отредактировано Стивеном Вудингом и Джеком Боуотером

Последнее обновление: 11 марта 2022 г.

Содержание:
  • Восклицательный знак в математике: что такое факториал?
  • Получение математики: определение факториала и формула факториала
  • Основные значения факториалов
  • 0-факториал и почему он такой особенный
  • Гамма-функция: факториалы нецелочисленных значений
  • Реальные приложения
  • Как вычислить факториал в языках программирования?

Добро пожаловать в калькулятор факториала: инструмент, который вычисляет факториал любого числа от 0 до 170 . Помимо вычисления, например, 0-факториала или 5-факториала… мы также покажем вам, как использовать восклицательный знак в математике, предоставим информацию о формуле n-факториала и возможностях ее применения. К концу этого у нас будет ответ на вопрос «что такое факториал?» используя факториальное определение. И, наконец, мы углубимся в математику, стоящую за этим, чтобы выяснить, как мы можем включить больше, чем просто положительные целые числа, с помощью гамма-функции.

Восклицательный знак в математике: что такое факториал?

Когда вы впервые увидели восклицательный знак в математике , вы наверняка были шокированы или даже подумали, что это какая-то ошибка или опечатка. Но реальность другая: этот восклицательный знак в математике называется факториалом или n-факториалом. Факториал — достаточно неизвестный оператор, который на самом деле можно рассматривать скорее как аббревиатуру, чем реальный оператор, по крайней мере, вначале.

Когда вы видите восклицательный знак в математике.

Важно не путать факториал с простой факторизацией числа, которая представляет собой способ получения простых чисел, которые при умножении дают ваше число. Факторизация простых чисел используется в математике и, возможно, более известна, чем n-факториал. Одной из причин популярности простой факторизации является ее полезность при вычислении наибольшего общего множителя (GCM) и наименьшего общего множителя (LCM), но мы отвлеклись.

Чтобы понять, что делает или означает факториал, мы должны начать с примера. Мы могли бы выбрать любое число n и вычислить его значение n-факториала, но лучше выбрать относительно небольшое число, поэтому воспользуемся 5-факториалом.

5! = 5 * 4 * 3 * 2 * 1 = 120

Из этого примера видно, что это не высшая математика, и вы даже можете угадать формулу факториала. Вы также можете понять, почему этот восклицательный знак в математике можно рассматривать как аббревиатуру, поскольку это не новая операция, а скорее набор умножений. Короче говоря, и несколько неформально, мы можем определить факториал как произведение всех положительных целых чисел, меньших и равных заданному числу.

Немного поигравшись с этим, мы можем увидеть, что для 5-факториала мы можем напрямую связать его с 4-факториалом:

5! = 5 * (4 * 3 * 2 * 1) = 5 * 4!

Такая связь между n-факториалами с разными n лежит в основе математической формулы, определяющей операцию факториала, как мы увидим в следующем разделе.

Операция факториала не везде используется в математике, но она необходима в статистике и вероятностных задачах. В этих случаях, особенно когда приходится иметь дело с перестановками или комбинаторикой, почти всегда появляется n-факториал. В следующих разделах нашего калькулятора факториала мы увидим реальные примеры задач, которые требуют использования факториалов и формулы факториала.

Знакомство с математикой: определение факториала и формула факториала

До сих пор мы видели несколько расплывчатый ответ на вопрос «что такое факториал?», но мы не дали правильного определения факториала . Что ж, именно в этом и заключается цель этого раздела: увидеть и объяснить формулу факториала и то, как мы можем найти из нее определение факториала более математическим способом.

Для более математического описания формулы факториала давайте посмотрим на n-factorial и его связь с другими факториалами . В этом случае n может быть любым числом. Если мы посмотрим на предыдущие примеры с 5-факториалом, то увидим, что:

5! = 5 * 4! = 5*(5-1)!

Если мы теперь экстраполируем это на n-факториал:

n! = п * (п-1)!

Вышеприведенная общая формула факториала является неотъемлемой частью определения факториала. Однако мы уверены, что это число не отвечает на все вопросы о факториалах 9.0017 у вас может быть. Например, что произойдет, если мы возьмем отрицательное число? Когда я перестану вычитать числа? Это правильные вопросы, на которые приведенная выше формула факториала не отвечает, но они имеют основополагающее значение для правильного определения факториала.

На эти два вопроса можно легко ответить, заявив, что формула факториала определена только для положительных целых чисел , что означает, что мы не можем опуститься ниже n = 1 . Но это также поднимает другой вопрос: что такое 0-факториал? Поскольку мы не можем использовать эту формулу, простите вас за то, что вы думаете, что на этот вопрос нет ответа, а все факториалы — это «фейковые новости». Однако есть «уловка», чтобы обойти это: установка значения нулевого факториала на число по определению.

И, следовательно, приходим к условности:

0! = 1

Здесь требуется небольшой отказ от ответственности, поскольку в математике никогда не бывает так просто, как «выбери число и сверни его». Существует много сложных причин того, почему было установлено значение нулевого факториала на один и ни на какой другой номер. Однако подробное объяснение этих причин выходит далеко за рамки этого факторного калькулятора.

Базовые значения факториалов

Теперь проверим некоторые значения n-факториала нескольких малых n , таких как нулевой факториал, 3 факториал, 5 факториал. Обратите особое внимание на значение факториала 0, потому что оно самое важное, и мы поговорим о нем позже .

  • 0! = 1
  • 1! = 1
  • 2! = 2
  • 3! = 6
  • 4! = 24
  • 5! = 120
  • 6! = 720
  • 7! = 5040
  • 8! = 40 320
  • 9! = 362 880
  • 10! = 3 628 800

Мы можем видеть, как быстро увеличивается факториал числа, когда мы используем большие числа. Это еще одна ситуация, когда научная запись может спасти день (если мы знаем, как правильно усекать до необходимых значащих цифр), если вам нужно работать с такими большими числами. Для факториалов чисел больше 10, не стесняйтесь используйте калькулятор факториала выше . Кроме того, вы можете использовать логарифмы для вычисления факториалов больших чисел. Чтобы узнать, как это сделать, вы можете воспользоваться нашим калькулятором логарифмов, где мы объясним, как можно применить логарифм к такой арифметике.

💡 А вы знали, что…

факториалы следуют известному закону Бенфорда ?

0-факториал и почему он такой особенный

0-факториал является ключевой частью определения факториала. Чтобы понять, почему это так важно, мы можем показать проблемы, с которыми мы сталкиваемся, когда пытаемся вычислить его, используя приведенную выше формулу факториала:

0! = 0 * (0-1)!

Похоже неважно какое значение (0-1)! получается, результат всегда должен быть 0! = 0 , но в математике все сложнее. В предыдущем разделе мы видели, что n-факториал определен только для n > 0, поэтому здесь у нас есть проблема. Срок (0-1)! — это то, что математики называют: неопределенное выражение , что означает, что выражение неверно, и, следовательно, не имеет математического смысла. Эта проблема такая же, как и при делении на ноль. Дело не в том, что мы не можем это вычислить. Проблема в том, что выражение не имеет смысла , оно не имеет смысла.

Вот почему 0! важно определить как условное значение. Установка его значения на 0! = 0 не было бы хорошей идеей, так как это означало бы, что n! = 0 для любого значения n . Вы можете понять, почему на применив формулу факториала . С другой стороны, если мы установим нулевой факториал равным 1 , мы теперь сохраним ожидаемые значения для n-факториала при простом соглашении о значении 0! .

В следующем разделе мы увидим еще одну причину для установки нулевого факториала равным 1 , за которой стоит немного больше математической логики. При этом мы также введем Гамма-функцию , которая представляет собой расширенную формулу факториала , которая включает все положительные числа и 0-факториал.

Гамма-функция: факториалы нецелых значений

Можно определить факториал нецелых чисел — фактически можно для всех вещественных и комплексных чисел, кроме целых отрицательных. Это требует использования сложных математических инструментов, поэтому мы постараемся дать здесь более простую версию, сохранив как можно большую точность. Было несколько подходов к расширению формулы факториала для включения всех положительных чисел , каждое из которых имеет небольшие отличия, и все они в основном совместимы друг с другом.

Гамма-функция построена

Начнем с функции Гамма. Гамма-функция — это функция, которая расширяет понятие n-факториала за пределы целых чисел . Очевидно, что формула не может быть такой же, как мы использовали раньше, потому что мы зашли бы в тупик. На самом деле, эта функция расширяет n-факториал до комплексных чисел, а также до , где интуитивное понятие факториала понять гораздо труднее. Единственными числами, для которых не определена гамма-функция, являются отрицательные целые числа:

𝚪(z) = ∫tᶻ⁻¹ e⁻ᵗ dt

Это определения Гамма-функции, где t — переменная интегрирования от нуля до бесконечности, а z — (неотрицательная целое число) комплексное число . Эта формула сводится к формуле n-факториала при применении к любому положительному целому числу n .

н! = 𝚪(n+1)

Из этой формулы видно две вещи:

  1. Гамма-функцию гораздо сложнее использовать, чем формулу n-факториала для целых чисел.
  2. Это не точная копия n-факториала, так как вам нужно вычислить значение Гамма-функции для n+1 , чтобы получить n! .

Чтобы решить вторую «проблему », мы можем ввести функцию Пи .

𝚷(z) = ∫tᶻ e⁻ᵗ dt

Функция Pi очень похожа на функцию Gamma, но сдвинута ровно настолько, чтобы факториал и функция соответствовали .

𝚷(n) = n!, n ∈ 𝗡

Вы можете быть сбиты с толку сложностью математики этой формулы факториала, но не волнуйтесь! . В качестве простого трюка мы можем сказать вам, что (-0,5)! = √π и (0,5)! = 0,5√π .

Интересно, что первая формула факториала здесь все еще действует. Так, например,

(2,5)! = 2,5 * (1,5)! = 2,5*1,5*(0,5)! = 1,875√π

Реальные приложения

Мы уже обсуждали, что факториал обычно используется в вероятностных вычислениях или перестановках, но это еще не все. давайте посмотрим других мест , в которых появляется n-факториал. Оставаясь в рамках чистой математики, мы приходим к биномиальному распределению, которое помогает вычислять вероятности, например, независимых экспериментов, дающих схожие результаты.

Увеличение энтропии в статистической физике

Помимо математики, n-факториал появляется во многих других расчетах, особенно в статистической физике и физике элементарных частиц , которые являются частями физики, которые, среди прочего, имеют дело с перестановками частиц. В частности, статистическая физика представляет собой полезную область физики, которую можно рассматривать как «9».0514 микроскопическая «версия термодинамики. Это связано с тем, что статистическая физика имеет дело с проблемами термодинамики (такими как расчет скрытой теплоты или теплопроводности), но она делает это на основе анализа частиц .

Есть и другие области (в основном в физике), которые используют факториалы в вычислениях, и мы могли бы очень глубоко погрузиться в то, как и почему они используют формулу факториала в своих вычислениях.Тем не менее, для простого калькулятора, такого как этот, это было бы далеко за пределами его досягаемости.

Как вычислить факториал в языках программирования?

В нашем современном мире утомительные расчеты обычно возлагаются на компьютеры (точно так же, как вы делаете, используя этот калькулятор факториала). Использование языков кодирования для создает небольшие программы , которые сделают эти вычисления для нас все более распространенными. N-факториал является идеальным кандидатом, так как он не очень сложен концептуально. Однако людям требуется слишком много времени, чтобы вычислить огромные числа. Для тех, кто использует языки программирования, мы оставим несколько примеров для некоторых из наиболее распространенных языков программирования.

  • Факториал Python (после 2.6): используйте math.factorial(x) , чтобы получить значения факториала Python,
  • Факториал Java : В стандартных пакетах Java нет метода факториала Java,
  • Факториал Matlab : Для вычисления факториала Matlab использует factorial(x) . Дополнительную информацию о факториальной функции Matlab можно найти в официальной документации,
    • .
  • Факториал в Excel : Используйте ФАКТ для расчета факториала в Excel. Обратите внимание, что факториал в Excel работает только с целыми числами,
  • Factorial C++ : В стандартные библиотеки не включена функция factorial C++. См. здесь пример факториальной функции С++,
  • Факториал Javascript : В стандартные библиотеки не включена функция факториала javascript.

Альваро Диес и Богна Шик

факториал

Посмотреть 61 похожий арифметический калькулятор ➗

Абсолютное значениеДобавление Ассоциативное свойство… Еще 58

Биномиальное расширение — с примерами для A Level, IB и IIT JEE

Биномиальное расширение

Это руководство разработано таким образом, что даже студент со скромным математическим образованием может его понять отдельные темы по математике. Обычно он входит в базовый математический модуль 2 на уровне AS.

На протяжении всего урока и после него учащимся не рекомендуется использовать калькулятор для того, чтобы найти значений nCr . Вместо этого рекомендуется использовать треугольник Паскаля , что намного быстрее, чем нажатие ряда кнопок калькулятора.

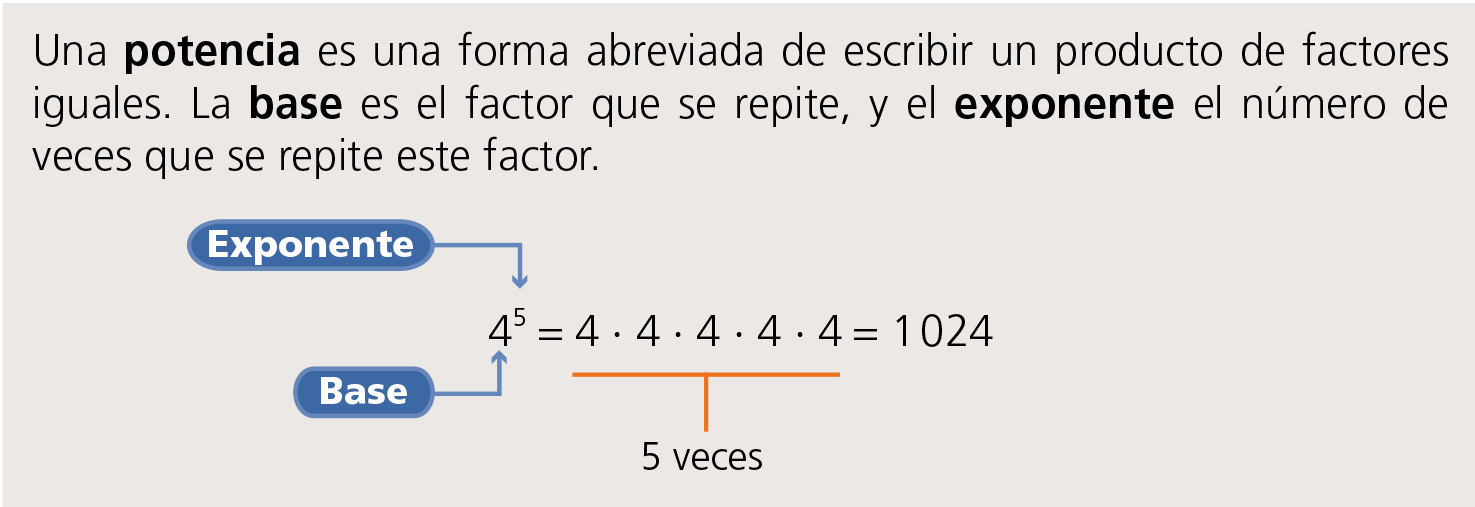
Факториал — н!

Факториал числа определяется следующим образом:

n! = n(n-1)n-2)(n-3)…….1

3! = 3 х 2 х 1 = 6

4! = 4 х 3 х 2 х 1 = 24

5! = 5 X 4 X 3 X 2 X 1 = 120

Факториал обоих 0 и 1 определяются как 1 — 0! = 1; 1! = 1.

Факторный калькулятор — n!

n  

Теперь давайте займемся простыми вычислениями с использованием факториалов чисел:

Например, 1

Найдите 5!/3!

5!/3! = 5 х 4 х 3!/3!
= 5 х 4
= 20
Мы останавливаем разложение верхнего факториала на 3, чтобы факториал 3 внизу можно было сократить.

Например, 2

Найти 6!/4!

6!/4! = 6 х 5 х 4!/4!
= 6 х 5
= 30
Мы останавливаем разложение верхнего факториала на 4, чтобы факториал 4 внизу можно было сократить.

Пример 3

Найти 6!/5!

6!/5! = 6 Х 5!/5!
= 6
= 6
Мы останавливаем разложение верхнего факториала на 5, чтобы факториал 5 внизу можно было сократить.

Например, 4

Найти 6!/(4! 2!)

6!/(4! 2!) = 6 X 5 X 4!/(4! 2!)
= 6 х 5 х 4!/ 4! 2!
= 30/2!
= 30/2
= 15 Мы останавливаем разложение верхнего факториала на 4, большем факториале знаменателя, так что факториал 4 внизу можно сократить.

Например, 5

Найти 6!/(5! 1!)

6!/(5! 1!) = 6 X 5!/(5! 1!)
= 6 х 5!/ 5! 1!
= 6 / 1!
= 6 / 1
= 6 Мы останавливаем разложение верхнего факториала на 5, большем факториале знаменателя, так что факториал 5 внизу можно сократить.

Например, 6

Найти 6!/(6! 0!)

6!/(6! 0!) = 6!/(6! 0!)
= 6!/ 6! 0!
= 1 / 0!
= 1/1
= 1 Мы останавливаем разложение верхнего факториала на 6, большем факториале знаменателя, так что факториал 6 внизу можно сократить.

Комбинации — nCr

nCr = n!/(n-r)!r!

Например, 1

Найдите 6C2.

6C2 = 6!/(6-2)!2!
= 6! / 4! 2!
= 6 х 5 х 4!/4! 2!
= 30/2!
= 30/2
= 15

Пример 2

Найти 6C2.

7C5 = 7!/(7-5)!5!
= 7! / 2! 5!
= 7 х 6 х 5!/2! 5!
= 42/2!
= 30/2
= 21

Например, 3

Найти 8C1.

8C1 = 8!/(8-1)!1!
= 8! / 7! 1!
= 8 х 7!/7! 1!
= 8 / 1!
= 8 / 1
= 8

Например, 4

Найти 8C0.

8C0 = 8!/(8-0)!0!
= 8! / 8! 0!
= 8!/8! 0!
= 1 / 0!
= 1/1
= 1

Треугольник Паскаля

Треугольник Паскаля дает все nCr значения n th ряд треугольника.


Например, возьмем 6 -й ряд:
6C0 = 1
6С1 = 6
6С2 = 15
6С3 = 20
6С4 = 15
6С5 = 6
6С6 = 1

Теперь вы можете поэкспериментировать с ним, используя приведенный ниже калькулятор:

Калькулятор для нахождения nCr

n:    r:  

 

Формула биномиального разложения

(1 + x) n =Σ nCr x r

Легче получить значений nCr из Треугольника Паскаля , чем из калькулятора; написание занимает время!

Пример 1

Расширение (1 + x) 5

(1 + x) 5 = Σ 5Cr x r
= 5C0 x 0 + 5C1 x 1 + 5C2 x 2 + 5C3 x 3 + 5C4 x 4 + 5C5 x 5
= 1 + 5х + 10х 2 + 10х 3 + 5x 4 + x 5

Например,

Расширение (1 + x) 3

(1 + x) 3 9016 = ° 3CR 3CR 3CR 3CR 3CR (1 + x) 3 9016 = ° 3CR 3CR 3CR 3CR (1 + x) 3 9016 = ° 3CR 3CR 3CR 3CR 3CR 3CR

(1 + x) 3 9016 = ° 3CL = 3C0 x 0 + 3C1 x 1 + 3C2 x 2 + 3C3 x 3
= 1 + 3x + 3x 2 + x 3

Например.
= 5C0 (2x) 0 + 5C1 (2x) 1 + 5C2 (2x) 2 + 5C3 (2x) 3 + 5C4 (2x) 4 + 5C5 (2x) 5

= 1 + 10x + 40x 2 + 80x 3 + 80x 4 + 32x 5

Например. 2) 5 = Σ 5Cr (x/2) r
= 5C0 (x/2) 0 + 5C1 (x/2) 1 + 5C2 (x/2) 2 + 5C3 (x/2) 3 + 5C4 (x/2) 4 + 5C5 (x/2) 5
= 1 + 5/2x + 5/2x 2 + 5/4x 3 + 5/16x 4 + x 5 /32

Например, 5

Расширить (1 — x) 5

(1 + (-x)) 5 = Σ 5Cr (-x) r
= 5C0 (-x) 0 + 5C1 (-x) 1 + 5C2 (-x) 2 + 5C3 (-x) 3 + 5C4 (-x) 4 + 5C5 (-x) ) 5
= 1 — 5х + 10х 2 — 10x 3 + 5x 4 — x 5

Например. [2(1 + x/2)] 5 =2 5 [ Σ 5Cr (x/2) ] r
= 2 5 [5C0 (x/2) 0 + 5C1 (x/2) 1 + 5C2 (x/2) 2 + 5C3 (x/2) 3 + 5C4 (x/ 2) 4 + 5C5 (x/2) 5 ]
= 2 5 [1 ​​+ 5/2 x + 5/2 x 2 + 5/4 x 3 + 5/16 x 4 + x 5 /32]
= 32 + 80x + 80x 2 + 40x 3 + 10x 4 + x 5

Например,

. Найти коэффициент из

. 5

[3(1 + 2x/3)] 5 =3 5 [ Σ 5Cr (2x/3) ] r
Третий член равен 3 5 X 5C2 X (2x/3) 2
3 5 X 10 X 4x 2 /3 2
3 3 Х 10 Х 4х 2
1080x 2
Итак, коэффициент при сроке 3 rd равен 1080.

Например, 8

Показать, что nCr = nC(n-r)
nCr = n!/(n-r)! р! = n(n-1)(n-2). ..(n-r+1)(n-r)!/(n-r)! р! = n(n-1)(n-2)…(n-r+1)/r!
нС(н-р)! = n!/(n-r)! р! = n(n-1)(n-2)…(n-r+1)(n-r)!/(n-(n-r))!(n-r)! = n(n-1)(n-2)…(n-r+1)(n-r)!/r!(n-r)!= n(n-1)(n-2)…(n -г+1)/р!
nCr = nC(n-r)

Биномиальное разложение — отрицательные индексы и дроби

(1 + x) n = Σ nCr
nC0 x 0 + nC1 x + nC2 x 2 + nC3 x 3 + ……+ nCn x n
1 + nx + n(n-1)!/2!(n-2)! x 2 + n(n-1)(n-2)(n-3)!/3! х 3 + ……
1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3 + ……
если x очень мал — |x| Итак, расширение можно остановить следующим образом:

(1 + x) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3

Обратите внимание на знак почти равно вместо знака равенства.

Например, 1

Расширьте (1 + x) 1/2 до четвертого члена.
(1 + x) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3
(1 + х) 1/2 ≈ 1 + (1/2)х + (1/2)(-1/2)/2 х 2 + (1/2)(-1/2)( 1/2-2)/6 х 3
(1 + х) 1/2 ≈ 1 + (1/2)х — (1/4)/2 х 2 + (3/16)/6 х 3
(1 + x) 1/2 ≈ 1 + (1/2)x — (1/8) x 2 — (1/16) x 3

Например, 2

(1 + х) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3
(1+x) −3 ≈ 1+(−3)x + (−3)(−4)/2! + x 2 + (−3)(−4)(−5)/3! х 3
(1+x) −3 ≈ 1 −3x + 6x 2 − 10x 3

Например, 3

Разверните (1 + 2x) -3 и укажите значение x, для которого справедливо расширение.
(1 + x) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3
(1 + 2x) -3 ≈ 1 + (−3)(2x) + (−3)(−4)(2x ) 2 /2! +(−3)(−4)(−5)(2x) 3 /3!
≈ 1 − 6x + 24x 2 − 80x 3
Расширение допустимо, если |2x| |х|

Например, 4

Разверните (1 — x) -5 и укажите значение/с x, для которых расширение действительно.
(1 — x) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3
(1 — x) -5 ≈ 1 + (−5)(-x) + (−5)(−6)(-x ) 2 /2! +(−5)(−6)(−7)(-x) 3 /3!
≈ 1 + 5x + 15x 2 + 35x 3
Расширение допустимо, если |-x| |х|

Например, 5

Расширьте (1 + 3x) 1/2 и, следовательно, найдите приближение для √103.
(1 + x) n ≈ 1 + nx + n(n-1)/2 x 2 + n(n-1)(n-2)/6 x 3
(1 + 3x) 1/2 ≈ 1 + (1/2)(3x) + (1/2)(1/2-1)(3x) 2 /2! +(1/2)(1/2-1)(1/2-2)(3x) 3 /3!
≈ 1 + (3/2)x + (-9/8)x 2 — (27/16)x 3
Пусть х = 0,01
Тогда (1 + 3 х 0,01) 1/2 ≈ 1 + (3/2)0,01 + (-9/8)0,01 2 − (27/16)0,01 3
(1 + 3 х 0,01) 1/2 ≈ 1 + (0,03/2) + (-0,0009/8) — (0,000027/16)
(1 + 0,03) 1/2 ≈ 1 + 0,015 -0,0001125 — 0,0000017
(1 + 0,03) 1/2 ≈ 1,0148858
(1 + 3/100) 1/2 ≈ 1,0148858
(103/100) 1/2 ≈ 1,0148858
103 1/2 /10 ≈ 1,0148858
√103 ≈ 10,148858
√103 ≈ 10,149 (3 д. п.)

Вам нужен учебник с большим количеством проработанных примеров в качестве Разжечь книгу ? Вот ссылка для Amazon:

Рекомендуемая литература


 

Математика сложная; так найти правильную книгу. К.А. Страуд в этой книге умело изложил все основные темы с помощью большого количества примеров; Популярность книги говорит сама за себя — 7 -й -й тираж в печати.

Рекомендуется — GCSE и iGCSE


 

Это лучшая книга, доступная для новой спецификации GCSE(9-1) и iGCSE: есть много рабочих примеров; действительно хороший сборник задач для тренировки; каждая отдельная тема адекватно освещена; темы расположены в логическом порядке.

Рекомендуется для уровня A


 

Это лучшая книга, которую можно порекомендовать для нового уровня A — доска Edexcel: она подробно описывает каждую тему; множество проработанных примеров; достаточно задач для отработки; красиво и понятно изложено.

100 Таблица факториалов Таблица и калькулятор

126605635584000000253607267086228733750385214863546777600000000008104739
  • 55367672371710738018221445712183296000000000000000
    •  710100 = 85047858856786231752116764423992601028858460812079623588643076338858868037807

    972800000000000000000

    9 2010! = 612344583768860868615240703852746727407780697328983823014963978384987221689274204160000000000000000 7! = 2480 тр>05 80103 ! = 1132428117820629783145752115873204622873174957948825199628256688353252342007662450862131773440000000000000000090 90! = 894618213078297528685144171539831652069808216779571

    386806322783795018605333618108410101760000000000000000000    130071318084719360000000000000000000641298857222н. = 2817104114380550276949479442260611594800566343305742064051012560026159795933451040286452340924018275123200000000000000000000
    1! = 1
    2! = 2
    3! = 6
    4! = 24
    5! = 120
    6! = 720
    7! = 5040
    8! = 40320
    9! = 362880
    10! = 3628800
    11! = 390
    12! = 4700
    13! = 6227020800
    14! = 871782
    15! = 1307674368000
    16! = 20922789888000
    17! = 355687428096000
    18! = 6402373705728000
    19! = 121645100408832000
    20! = 2432

    8176640000

    21! = 510

    171709440000

    22! = 1124000727777607680000
    23! = 25852016738884976640000
    24! = 620448401733239439360000
    25! = 15511210043330985984000000
    26! = 4032
    27! = 10888869450418352160768000000
    28! = 304888344611713860501504000000
    29! = 8841761993739701954543616000000
    30! = 2652528598121

    636308480000000

    31! = 8222838654177922817725562880000000
    32! = 263130836933693530167218012160000000
    33! = 8683317618811886495518194401280000000
    34! = 29523279
  • 04140847618609643520000000
    • 35! = 10333147966386144929666651337523200000000
    36! = 3719933267897467999448150835200000000
    37! = 137637530345046315979581580

    0000000
    38! = 5230226174666011117600072241000742000000
    39! = 20397882081197443358640281739

    7356800000000

    40! = 8153247897734345611269596115894272000000000
    41! = 33452526613163807108170062053440751665152000000000
    42! = 1405006117752879898543142606244511569936384000000000
    43! = 60415263063373835637355132068513997507264512000000000
    44! = 26582715747884487680436258110146158

    638528000000000

    45! = 119622220865480194561963161495657715064383733760000000000
    46! = 5502622159812088949850305428800254892961651752960000000000
    47! = 25862324151116818064296435515361197996323800000000
    48! = 12413
    49! = 60828186403426756087225216332129537688755283137

    40000000000

    50! = 304140932017133780436126081660647688443776415689605120000000000000
    51! = 1551118753287382280224243016469303211063259720016986112000000000000
    52! = 80658175170943878571660636856403766975289505440883277824000000000000
    53! = 42748832840600255642980137533893996496

    788366813724672000000000000

    54! = 230843697339241380472092742683027581083278564571807941132288000000000000
    55! = 12696403353658275925965100847566516959580321051449436762275840000000000000
    56! = 7109985878048634518540456474637249497364979788811684586874470400000000000000
    57! = 4052648772167556806012322134980384796226602145184481280000000000000
    58! = 235056133128287857182947450746838288623181811429244206990000000000000
    59! = 13868311854568983573793203894063456772687432540821294940160000000000000
    60! = 83209871127413

    2763411832233643807541726063612459524492776964096000000000000000

    61! = 5075802138772247988008568121766252272260045289880360030994059394809856000000000000000
    62! = 31469973260387937525653122354950764088012280797258232192163168247821107200000000000000
    63! = 19826083154044400641161467083618981375447736
  • 268628106279599612729753600000000000000
    • 64! = 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000
    65! = 824765054706667231703067854962521862585513454374929221231343889557749760000000000000000
    66! = 54434493

    430640037292402478427526442930643887988745328601268696710811484160000000000000000
    67! = 36471110

    868528824985

    054644271676353140495245937016285002679624369438720000000000000000
    68! = 24800355424368305996009 56
    69! = 17112245242814131137246833888127283705448935203693936480409232572797541406474240000000000000000
    70! = 11978571669969807278372168364589381425464258575553628646280095827898453196800000000000000000
    73! = 44701154615126843408138125051110076800700282

    58192370422104067183317016

  • 00000000000000000
    • 99 ! = 3307885441519386412259530282212537821456832518209349711706119268354112357009715654592508723200000000000000000
    11395398047711659403366092624388657012283779589451265584267757286740944381542400000000000000000000
    76! = 188549470166605025498793226086114655823039453537932933567248798296184404349553792311772997222400000000000000000007 5555 = 1451830

    2858696340707840863082849837403792242083588467815746880619

    1564200800652078612480000000000000000000
    80! = 71569457046263802294811533723186532165584657342365752577109445058227039254801488426689448680814085800000000000000000000000000000000000000000008н = 579712602074736798587973423157810123572447316259587458650497163

    69388

    25618453424974594000000000000000000000000000000000000000000000000000000000000000000000008н 9787979745940488

    256184534249745940488

    25618453424974594000000000000000000000000000000000000865661845342н. = 47536433370128417484213820698940494664381329406799332861716093407674399473489

    83! = 39455239697206586511897471180120610571436503407643446275224357528369751562966293348795
      1X37708706887348795
        10377087096883487959
          1037708706883487995
            1037708707883487995
              1X3770870688! = 3314240134565353266999387573128800066628624204948711884603238305
    86! = 2422709538367273238176552320344125971528487055242938175X838764496720162249742450276789464634
    96557450276789464634965574202767889646349тели = 2107757298379527717213600518699389595229783738061356212322925112146541572759317408068342326414757тели75931740806834232364147575744740806834232364147757594740806834232364147575944740806834232тели. = 1854826422573984396845645546284380220968949399346684421580986889562184028199314124480450182841663351685000

    0000000103

    89! = 16507955160    10812162453619309839666236496541854907078317103437853999907876662англей. = 14857159644817614973095227336208257388555699612846887669421686370498539306587654599921377088453930658765459999213770884539Х55876545499921370884539306587654545992131370885393065876545459921377088453930588765454599213770884539305887654545992137708845393058876545459921377088453930658765454599тели = 135200152767840296255166568759495142147586866476
    77734597153670771559994765685283954750449427751168336760000081
      000000103
    875414356840239582938137753519518444430461238370413475351951844443ter6388370англи = 115677250708164157475
  • 623062404362147532295764135351861422812132468071214673152152ть. = 1087366156656743080273652852567866010041868035801828723074973744340451998694179276302214583415458560865651202385340530688000000000000000000000
    • 934870949687140154189380115818364865126779544437605483849222280999876894760370007489820750947389657543056398745600000000000000000000007615810447731933374561248187549880587
    92! = 1243844140546413072554753243258755530777779
    95! = 1032997848823
  • 62599702099394727095397746340117372869212250571234293987594703124871765375385424468563282236864226607350415360000000000000000000000
    • 96! = 9
    97! = 9619275968248211985332842594956369871234381391
    8
    51261284189679678167647067832320000000000000000000000 98! = 9426888324774562618574305724247380969376407895166349423877729470707002322379888297615
  • 223605850588608460429412647567360000000000000000000000 99! = 933262154439441526816992388562667004

    9682643816214685929638952175999932298941463976156518286253697722375825118521040000000000000000000000 100! = 9,33262154439441e+157

    TOP 10 что такое 6 factorial ЛУЧШИЙ и НОВЕЙШИЙ

    Вы задаетесь вопросом что такое 6 factorial но в настоящее время нет ответа, поэтому давайте kienthuctudonghoa. com подведем итоги и перечислим лучшие статьи с вопросом. ответьте на вопрос, что такое факториал 6, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать более правильный выбор и получить больше полезной информации. – Факторная функция в математике – Byju’s

  • 2 2.Что такое факториал числа 6? – CoolConversion
  • 3 3.Калькулятор – факториал(6) – Solumaths
  • 4 4.Факториальная функция ! – Math is Fun
  • 5 5. Определение, расчет | Факториал сотен и 0 – Cuemath
  • 6 6.Факториальный калькулятор n!
  • 7 7.6! Факториал 6 – The Learning Point
  • 8 8. Таблица множителей. – OnlineMSchool
  • 9 9.Что такое факториал 6? 6! = 720 – Visual Fractions
  • 10 10. Объяснение факториалов – Purplemath

    • 1.Что такое факториал? - Факторная функция в математике -

      • Автор: Byjus.com
      • Дата после: 5 Вчера
      • Оценка: 3 (660 Отзывы)
      • . : 2
      • Резюме: Следовательно, факториал числа 6 равен 720. Пример 2. Чему равен факториал числа 0? Решение: факториал 0 равен 1, т. е. 0 ! = 1.

      См. подробности

      2.Что такое факториал числа 6? - CoolConversion

      • Автор: CoolConversion.com
      • Дата поста: 28 вчера
      • Оценка: 1 (1511 Обзоры)
      • Высокий рейтинг: 4
      • . Резюме: 6! точно: 720; Количество конечных нулей в 6! равно 1. Количество цифр в факториале 6 равно 3. Факториал 6 вычисляется, …

      См. Подробности

      3. Калкулятор - Фактор (6) - Solumaths

      • Автор: www.solumaths.com
      • Пост Дата: 12 вчера
      • . Самый высокий рейтинг: 3
      • Низкий рейтинг: 2
      • Итог: 6!=6*5*4*3*2*1=720 · Факториал 6 равен 720.

      Подробнее

      4. Факториальная функция ! – Математика – это весело

      • Автор: www.mathsisfun.com
      • Дата поста: 26 вчера
      • Оценка: 1 (1560 Обзоры)
      • Высокий рейтинг: 3
      • . Итог: Функция факториала (символ: !) предлагает умножить все целые числа из выбранного числа на 1. Примеры: 4! = 4 × 3 × 2 × 1 = 24; 7! = 7 × 6 × 5 …

      Подробнее

      5. Определение, расчет | Факториал сотен и 0 – Cuemath

      • Автор: www.cuemath.com
      • Дата поста: 5 Вчера
      • Оценка: 3 (1477 Обзоры)
      • Высокий уровень: 3
      • . Резюме: Факториал. Факториал целого числа «n» определяется как произведение этого числа на каждое целое число, меньшее или равное «n» до 1.

      Подробнее

      6.

      Калькулятор множителей n!
      • Автор: www.calculatorsoup.com
      • Пост Дата: 29 Вчера
      • Рейтинг: 5 (1462 Обзоры)
      • Высокий уровень: 5
      • . Описание: Факториал — это функция, которая умножает число на каждое число под ним. Например, 5!= 5*4*3*2*1=120. Функция используется, в том числе, для поиска …

      Подробнее

      7.6! Факториал 6 – Пункт обучения

      • Автор: www.TheLearningPoint.NET
      • Дата поста: 13 вчера
      • Оценка: 3 (351 Обзоры)
      • Высокая. Сводка: Точка обучения > Математика > Факториал > . 6! Факториал 6. Значение 6!, то есть факториал 6 = 720. Учебник по факториалам. Комментарии …

      Подробнее

      8.Таблица коэффициентов. – Онлайн-школа

      • Автор: onlinemschool. com
      • Дата поста: 29 вчера
      • Рейтинг: 2 (1888 Обзоры)
      • Высокий рейтинг: 4
      • . : Лучшая таблица факториалов и калькулятор, которые помогут вам найти факториал числа. … Калькулятор для нахождения факториала! = 6 …

      Подробнее

      9.Что такое факториал числа 6? 6! = 720 – визуальные фракции

      • Автор: VisualFractions.com
      • Пост Дата: 12 вчера
      • Рейтинг: 3 (877 Обзоры)
      • Высокий рейтинг: 3
      • . : При описании факториала обычно говорят 6! например, «6 факториал», «6 визг» или «6 ударов». Лично я предпочитаю визг! Надеюсь, эта статья помогла …

      Подробнее

      10. Объяснение факториалов — Purplemath

      • Автор: www.purplemath.com
      • Дата поста: 17 вчера
      • Рейтинг: 5 (672 Обзоры)
      • Высокий рейтинг: 3
      • .

        No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *