примеры с дробями для тренировок
Тренажёр для 5 класса: примеры с дробями для тренировок1 2 3 4 5 6 7 8 9 0 . C
Ответить
<table> <tr> <td> <p>7</p> <p>5</p> </td> <td> + </td> <td> <p>5</p> <p>8</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>1</p> <p>3</p> </td> <td> + </td> <td> <p>7</p> <p>9</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>5</p> <p>2</p> </td> <td> + </td> <td> <p>4</p> <p>7</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>7</p> <p>3</p> </td> <td> + </td> <td> <p>3</p> <p>10</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>4</p> <p>1</p> </td> <td> + </td> <td> <p>5</p> <p>9</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>8</p> <p>1</p> </td> <td> + </td> <td> <p>2</p> <p>8</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>5</p> <p>3</p> </td> <td> + </td> <td> <p>8</p> <p>5</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>6</p> <p>5</p> </td> <td> + </td> <td> <p>9</p> <p>10</p> </td> <td> = </td> </tr> </table>
<table> <tr> <td> <p>6</p> <p>5</p> </td> <td> + </td> <td> <p>8</p> <p>8</p> </td> <td> = </td> </tr> </table>
Попробуй другие онлайн тренажеры с дробями
Сложение и вычитание дробей 5 класс
Обыкновенные дроби 5 класс примеры для тренировки
Умножение дробей.
Тренажер 5 классЧто такое часть от целого?
Тема «дроби» в 5 классе в математике одна из самых сложных для
восприятия школьниками. А упражнения с дробями в 5 класс вызывают страх и неприязнь. Без тренировки по этим темам никак!
Также эта тема очень большая, поскольку охватывает сразу несколько разделов.
При изучении дробей в математике очень важно не упустить момент если ребенок
что-то хоть немного недопонял или сомневается или не уверен.Главное сразу приступить к
тренировкам и решению заданий и примеров на тему ДРОБИ для 5 класса. Чем раньше — тем лучше.
В данном случае главное объяснить где применяется «дробная часть числа»,
а также наглядность примеров дробей для 5 класса по математике.
Само слово «Дробь» уже подразумевает дробление, деление, часть от чего-то.
В школьной программе 5 класса к примерам по математике для тренировки с дробями
приступают только после изучения всех операций
над целыми числами. Вначале дети тренируются на
примерах с простыми дробями для 5 класса по математике
.
Затем, приступают к примерам сложнее на умножение дробей. Их
также легко можно отработать на тренажёре умножения дробей
Но объяснить ребенку что такое обыкновенные дроби и решать задания,
и познакомиться с примерами решения дробей лучше гораздо раньше.
Это сформирует пространственное представление и логическое мышление. Наш тренажер сложения дробей в этом, конечно, поможет.
А в 5 классе изучение дробей со сверстниками не составит труда!
Но если надо решить уже имеющуюся дробь, ту придет на помощь
калькулятор решающий дроби. Вы также можете
распечатать примеры на дроби для 5 класса с ответами
для тренировки
Как рассказать про часть, чтобы ребенок понял?
Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы. Правильные дроби – это дроби, в которых числитель меньше знаменателя Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя
Дробь — число не целое, оно обозначает количество долей целого
Обыкновенная дробь состоит из двух частей: числитель и знаменатель
Дроби бывают правильные и неправильные. У правильных дробей числитель меньше знаменателя.
У неправильных дробей наоборот, числитель больше знаменателя,
а значит любую неправильную дробь можно перевести в смешанную,
выделив у нее целую часть и отняв ее из числителя
Познакомься с другими тренажерами курса
Меры измерения
Мер величин много и в них легко запутаться. Изучайте меры длины, времени и массы на тренажере
Скорей заниматься
Римские цифры
Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры
Скорей заниматься
Задачи на объем, площадь, периметр
Решение задач на применение формул объем, площадь, периметр
Скорей заниматься
Контрольная работа Обыкновенные дроби Математика 5 класс
Контрольная работа по теме Обыкновенные дроби, которая изучается в 5 классе. С помощью этого теста вы сможете проверить свои знания обыкновенных дробей и показать, чему вы научились во время урока.
Этот тест поможет вам увидеть, что, возможно, понадобится еще немного повторить. Не спешите, внимательно читайте каждый вопрос и выбирайте правильные ответы!
Ваша фамилия и имя:
Контрольная работа на тему Обыкновенные дроби. Проверьте свои знания с помощью онлайн заданий по математике за 5 класс
1. Запиши число пять девятнадцатых в виде дроби
1). 1 \frac{5}{19}
2). \frac{5}{19}
3). \frac{19}{5}
4). \frac{5}{9}
Номер ответа:
2. Укажи дробь, которая больше дроби \frac{7}{11}
1). \frac{5}{11}
2). \frac{3}{11}
3). \frac{6}{11}
4). \frac{8}{11}
Номер ответа:
3. Из дробей выбери все правильные
1). \frac{6}{6} ; 2). \frac{3}{11} ; 3). \frac{7}{1} ; 4). \frac{2}{9} ; 5). \frac{5}{4} ; 6). \frac{1}{3} .
Ответ в виде 1234:
4.
Подай неправильную дробь \frac{31}{7} в виде смешанного числа
Целая часть:
Числитель:
Знаменатель:
5. У Даниила было 42 рубля, \frac{5}{6} из которых он потратил на покупку блокнота. Сколько стоил блокнот?
Ответ
6. Реши пример: \frac{7}{13} + \frac{2}{13} — \frac{4}{13}
Числитель:
Знаменатель:
7. Реши пример: 1 — \frac{4}{11}
Целая часть:
Числитель:
Знаменатель:
8. В кружок авиаконструкторов зачислили 36 учеников, что составляет \frac{4}{9} количества детей, которые хотели в нем учиться.
Сколько детей желали учиться в этом кружке?
Ответ
9. Реши уравнение: 1 \frac{7}{15} + (x — \frac{11}{15}) = 5 \frac{3}{15}
Целая часть:
Числитель:
Знаменатель:
10. При каких натуральных значениях x дроби \frac{x+3}{8} и \frac{6}{x} оба неправильные? Перемножь эти числа и введи ответ.
Ответ:
Контрольная работа по теме Обыкновенные дроби 5 класс
Проектное обучение математике: сложение дробей в отличие от знаменателей
- Описание
- Стандарты и уровень
- Отзывы (0)
Описание
В этом 5-дневном учебном пособии по математике математические концепции применяются в реальном сценарии, чтобы научить учащихся сложению дробей с разными знаменателями .
В этом 5-дневном блоке учащиеся будут складывать дроби с разными знаменателями, чтобы открыть магазин смузи. Этот математический проект дробей привлекателен и аутентичен. Кроме того, он доступен как в цифровом, так и в печатном виде.
Этот ресурс по математике на основе проекта охватывает концепции измерения времени и приведен в соответствие со следующими общими базовыми стандартами штата по математике для 5-го класса:
CCSS.MATH.CONTENT.5.NF.A.1
Сложение и вычитание дроби с разными знаменателями (включая смешанные числа) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (В общем, a/b + c/d = (ad + bc)/bd.)
CCSS.MATH.CONTENT.5.NF.A.2
Решение задач со словами на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи с разными знаменателями, например, с помощью визуальных моделей дробей или уравнений для представлять проблему.
Используйте эталонные дроби и численный смысл дробей для мысленной оценки и оценки обоснованности ответов. Например, распознайте неправильный результат 2/5 + 1/2 = 3/7, заметив, что 3/7 < 1/2 .
Этот ресурс доступен как в печатной, так и в цифровой версии Google Slides.
Что включено в этот ресурс:
- Базовые знания: Используя KWL, учащиеся получат базовые знания о магазинах смузи и о том, как они работают.
- Сложение дробей: С помощью прилагаемых страниц с инструкциями учащиеся узнают, как складывать дроби, находя наименьший общий знаменатель.
- Выберите пункты меню: Учащиеся будут применять концепцию сложения фракций, чтобы определить общее количество необходимого каждого ингредиента, используемого в меню.
- Добавление смешанных чисел: С помощью прилагаемых страниц с инструкциями учащиеся узнают, как складывать смешанные числа и упрощать их до минимума.
- План открытия: Учащиеся подсчитывают общее количество каждого смузи, чтобы подготовиться к открытию магазина.
- Рассчитать Всего: Используя понятия сложения дробей, учащиеся определят общее количество, необходимое для приготовления 10 смузи.
- Сравнение дробей: С помощью прилагаемых страниц с инструкциями учащиеся узнают, как сравнивать дроби.
- Составление списка покупок: Учащиеся будут применять принципы сравнения дробей, чтобы сравнить необходимое количество каждого ингредиента с количеством в одной упаковке и определить, сколько упаковок каждого ингредиента нужно купить.
- Окончательное меню: Студенты разработают окончательное меню и придумают броские названия для каждого типа смузи.
- Подведение итогов: Учащиеся составляют свой окончательный план магазина смузи и объясняют свои решения.
************************************************* ****************************
Стандарты и уровни
Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставлять отзывы.
Математика 5-го класса — Интерпретация дробей
Пряди
Числа и операции: дроби, геометрия
Обзор
В этом уроке особое внимание уделяется концепции эквивалентности, которая связана со стандартом пятого класса 5.NF «Использование эквивалентных дробей в качестве стратегии сложения и вычитания дробей». Чтобы использовать концепцию сложения и вычитания, учащиеся должны понимать эквивалентные дроби. Это основано на стандартах третьего и четвертого классов, связанных с этой концепцией: 3.G.2 «Разделите формы на части с равными площадями. Выразите площадь каждой части в виде доли единицы целого»; 3.NF.2 «Представить дробь 1/b на числовой линейной диаграмме, определив интервал от 0 до 1 как целое и разбив его на b равных частей»; 4.NF.1 «Объясните, почему дробь a/b эквивалентна дроби (n x a)(n x b), используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби одинаковы.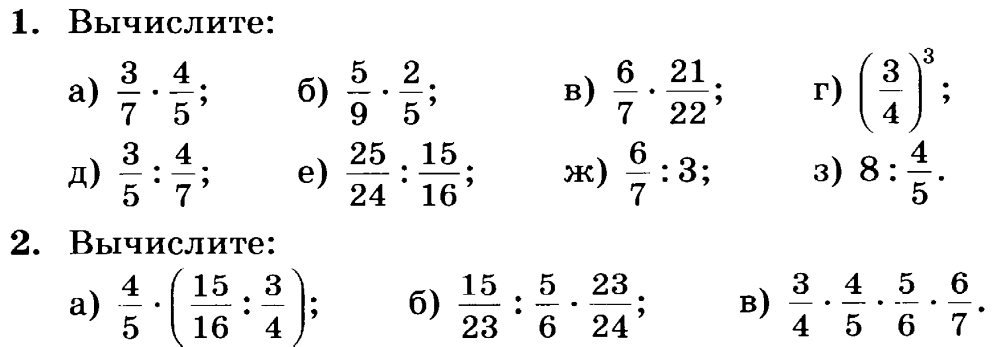
размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби».
Этот формирующий урок повторного вовлечения под названием «Интерпретация дробей» начался с предварительной оценки «Дробей», которая включала размещение дробей на числовой прямой и предоставление обоснования размещения с использованием ½ и 1 в качестве ориентиров. Введение в класс включало использование доски для представления дробей с использованием символических обозначений, моделей площадей, измерений (числовых линий), наборов и дробных ситуаций (задачи со словами). Совместное задание началось с того, что учащиеся сопоставили дроби, представленные числами (набор карточек A), с моделями площадей (набор карточек B). В этом видеоролике показана следующая часть задания, в котором учащиеся сопоставляют набор карточек C, показывая модель измерения (числовую строку), с предыдущими наборами. На следующих уроках учащиеся будут сопоставлять дробные наборы и ситуации (наборы карточек D и E). После этого учащиеся совершат прогулку по галерее, чтобы сравнить свое мышление с мнением других групп и использовать обоснование для критики совпадений, с которыми они не согласны.