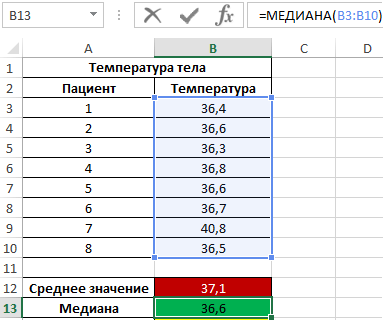
Как вычислить среднюю, моду и медиану интервального ряда?
Начнём опять с ситуации, когда нам даны первичные статические данные:
Пример 10
По результатам выборочного исследования цен на ботинки в магазинах города получены следующие данные (ден. ед.):
– это в точности числа из Примера 6. Но теперь нам нужно найти среднюю, моду и медиану.
Решение: чтобы найти среднюю по первичным данным, нужно
просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.
Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то,
конечно, забиваем в любую свободную ячейку:
=СУММ(, выделяем мышкой все числа, закрываем скобку ), ставим знак деления /, вводим число 30 и жмём Enter. Готово.
Что касается моды, то её оценка по исходным данным, становится непригодна.
Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter: . Причём, здесь даже ничего не нужно сортировать.
Но в Примере 6 я проводил сортировку совокупности по возрастанию (вспоминаем и сортируем), и это хорошая возможность повторить формальный алгоритм отыскания медианы.
Делим объём выборки пополам:
, и поскольку она состоит из чётного
количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного
ряда:
ден. ед.
Ситуация вторая. Когда даны не первичные данные, а готовый интервальный ряд (что в учебных задачах бывает чаще).
Продолжаем анализировать этот же пример с ботинками, где по исходным данным был составлен ИВР. Для вычисления средней потребуются середины интервалов:
– чтобы воспользоваться знакомой формулой дискретного случая:
– и это отличный результат! Расхождение с
более точным значением (), вычисленным по
первичным данным, составило всего 0,04!
Здесь мы использовали упомянутый ранее приём – приблизили интервальный ряд дискретным, и это приближение оказалось весьма эффективным. Впрочем, с современными программами не составляет особого труда вычислить точное значение даже по очень большому массиву первичных данных. Если они нам известны 😉
С другими центральными показателями всё занятнее.
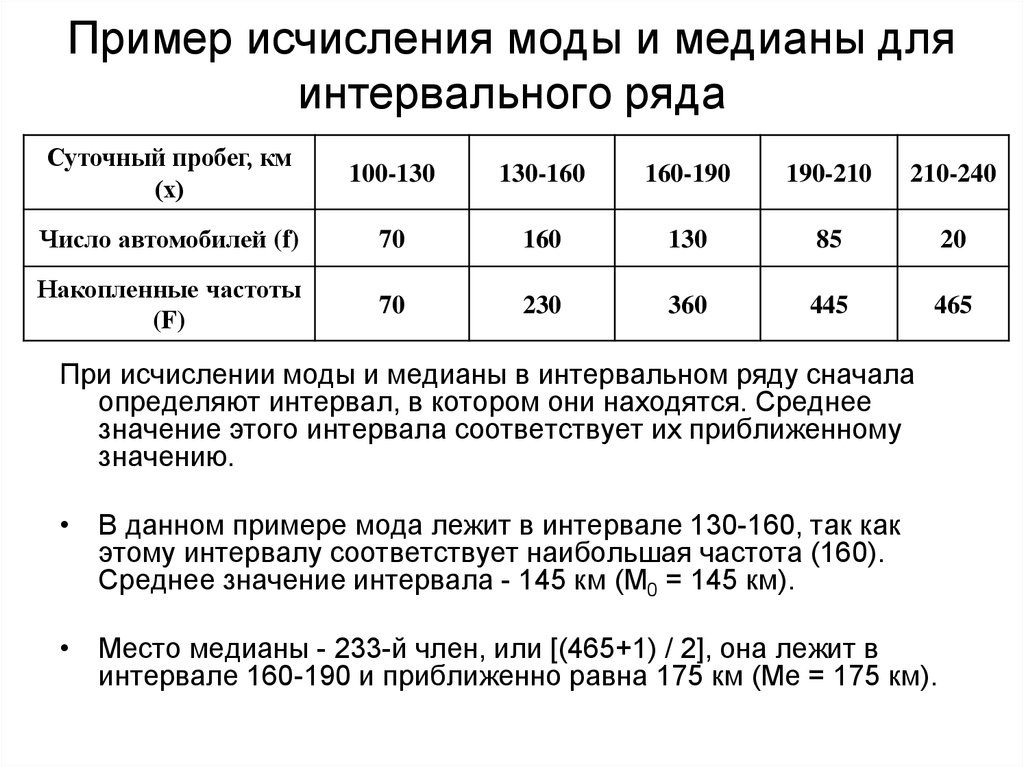
Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в нашей задаче это интервал с частотой 11, и воспользоваться следующей страшненькой формулой:
, где:
– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.
Таким образом:
ден. ед. – как видите, «модная» цена на
ботинки заметно отличается от среднего арифметического значения .
Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот
и отмечу :
откуда хорошо видно, что мода смещена относительно центра модального интервала
Справочно остановлюсь на редких случаях:
– если модальный интервал крайний, то либо ;
– если обнаружатся два смежных модальных интервала, например, и ,
то рассматриваем модальный интервал , при этом
близлежащие интервалы (слева и справа) по возможности тоже укрупняем в два раза;
– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым две
или бОльшее количество мод.
Вот такой вот депеш мод 🙂
И медиана. Она рассчитывается чуть по менее страшной формуле. Для её применения нужно найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две равные части.
Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты
, здесь же сподручнее рассчитать
«обычные» накопленные частоты . Вычислительный
алгоритм такой же – первое значение сносим слева (красная стрелка), а каждое следующее получается как сумма
предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера):
Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопится» на всех «пройденных»
интервалах, включая текущий.
Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит -ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .
И ориентируясь по накопленным частотам, легко
прийти к выводу, что эти варианты содержатся в интервале .
Формула медианы:
, где:
– объём статистической совокупности;
– нижняя граница медианного
интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота
предыдущего интервала.
Таким образом:
ден. ед. – заметим, что медианное
значение, в отличие от моды, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:
Справочно особые случаи:
– если медианным является крайний левый интервал, то ;
– если вариационный ряд содержит чётное количество вариант и две средние варианты попали в разные интервалы, то
объединяем эти интервалы, и по возможности удваиваем предыдущий интервал.
Ответ
 ед.
ед.
По сравнению с предыдущей задачей , центральные показатели оказались заметно отличны друг от друга. Это говорит об асимметрии («скошенности») распределения цен, что хорошо видно по гистограмме и совершенно логично – ботинок низкого и среднего ценового сегмента много, а премиального – мало.
Задание для тренировки:
Пример 11
Для изучения затрат времени на изготовление одной детали рабочими завода проведена выборка, в результате которой получено
следующее статистическое распределение:
…да, тот самый завод Петровского 🙂 Найти среднюю, моду и медиану.
Решаем эту задачу в Экселе – все числа и инструкции уже там. Если нет Экселя, считаем на
калькуляторе, что в данном случае может оказаться даже удобнее. Образец решения, как обычно, в конце книги. Это, кстати, уже
каноничная «интервальная» задача, в которой исследуется непрерывная величина – время.
Что ещё можно сказать по теме?
Несмотря на разнообразия рассмотренных показателей, их всё равно бывает не достаточно. Существуют крайне неоднородные совокупности, у которых варианты «кучкуются» во многих местах, и по этой причине средняя, мода и медиана плохо характеризуют положение дел.
В таких случаях вариационный ряд дробят с помощью квартилей, децилей, а в упоротых специализированных исследованиях – и с помощью перцентилей.
Квартили упорядоченного вариационного ряда – это варианты , которые делят его на 4 равные (по количеству вариант) части. Из чего автоматически следует, что 2-я квартиль – есть в точности медиана: .
В тяжёлых случаях проводится разбиение на 10 частей – децилями – это варианты, который делят упорядоченный вариационный ряд на 10 равных (по
количеству вариант) частей.
И в очень тяжелых случаях в ход пускается 99 перцентилей .
После разбиения вариационного ряда каждый участок исследуется по отдельности – рассчитываются локальные средние и другие показатели.
В учебном курсе квартили, децили, перцентили встречаются редко, и посему я оставляю этот материал (их нахождение) для самостоятельного изучения.
Ну а сейчас мы переходим к изучению второй группы статистических показателей:
3.2. Показатели вариации
3.1.3. Медиана| Оглавление |
Структурные средние: мода, медиана —
Теория
Модой называется значение изучаемого признака, имеющего наибольшую частоту и обозначают Мо.
В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в вариационном ряду, он считается соответственно бимодальным («верблюдообразным») либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой сумму нескольких совокупностей с разными модами.
Это говорит о неоднородности совокупности, возможно, представляющей собой сумму нескольких совокупностей с разными модами.
В интервальном вариационном ряду и при непрерывной вариации признака, предполагается, что каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается
, (9)
— нижняя граница модального интервала;
– частота в модальном интервале;
— частота интервала предшествующего модальному;
— частота интервала следующего за модальным;
i — величина интервала.
Пример. Рассчитать моду по данным представленным в таблице.
Таблица 4
Распределение хозяйств области по урожайности зерновых культур
Урожайность, ц/га, хi | Число хозяйств, fi | Середина интервала, ц/га, хi | хi fi
| Накопленная частота, fi |
1 | 2 | 3 | 4 | 5 |
10-15 | 6 | 12,5 | 75,0 | 6 |
15-20 | 9 | 17. | 157,5 | 15 |
20-25 | 20 | 22,5 | 450,0 | 35 |
25-30 | 41 | 27,5 | 1127,5 | 76 |
30-35 | 26 | 32,5 | 845,0 | 102 |
35-40 | 21 | 37,5 | 787,5 | 123 |
40-45 | 14 | 42,5 | 595,0 | 137 |
45-50 | 5 | 47,5 | 237,5 | 142 |
50-55 | 1 | 52,5 | 52,5 | 143 |
Итого | 143 |
| 4327,5 |
|
При изучении вариации применяются такие характеристики вариационного ряда, которые описывают количественно его структуру, строение. Такова, например, медиана — величина варьирующего признака, делящая совокупность на две равные части по числу единиц совокупности.
Такова, например, медиана — величина варьирующего признака, делящая совокупность на две равные части по числу единиц совокупности.
Медиана не зависит от значений признака на краях ранжированного ряда. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая средняя, если ряд значений неоднороден, включает резкие отклонения от средней.
При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при 10 значениях признака — среднюю из пятого и шестого значений в ранжированном ряду.
В интервальном вариационном ряду для нахождения медианы применяется формула
(10)
где Me — медиана;
хе — нижняя граница интервала, в котором находится медиана;
п — число наблюдений;
— накопленная частота в интервале, предшествующем медианному;
— частота в медианном интервале;
i — величина медианного интервала.
Пример. Рассчитать значение медианы по условиям предшествующей задачи.
Решение. В нашем примере имеется нечетное число значений (143+1)/2 = 72, т.е. в середине ряда находится 72-е от начала ряда значение урожайности. Как видно из ряда накопленных частот (табл. 5.4), оно находится в четвертом интервале. Тогда
В равноинтервальном ряду медиана — это середина среднего интервала при их нечетном числе или средняя арифметическая из границ двух средних интервалов при их четном числе.
Как найти среднее значение, медиану и моду за 3 простых шага | Prodigy
Мы все помним, как изучали эти термины на уроках математики. Но что именно они собой представляют и как их найти, вспомнить сложно.
Поверьте мне, вы не одиноки, если думаете так!
Математика — это непросто, и если ваш ребенок испытывает затруднения на уроках математики или испытывает математическую тревогу, он не одинок.
Эта статья даст вам краткий обзор того, как быстро найти среднее значение, медиану и моду в наборе данных, а также примеры того, когда вам может понадобиться найти эти средние арифметические значения.
Если к концу статьи вы не чувствуете себя экспертом, у нас также есть отличные ресурсы, к которым вы можете обратиться за дополнительной помощью.
Меры центральной тенденции
Среднее значение, медиана и мода — все это «меры центральной тенденции». Звучит сложно, но это всего лишь разные средние точки набора данных.
Хотя каждый указывает нам среднюю точку, все они разные.
Итак, в чем разница между средним, медианой и модой? Среднее значение вычисляется, чтобы найти среднее значение данных. Медиана — это число в середине набора данных. И режим находит самый распространенный номер в списке номеров.
На некоторые расчеты могут повлиять выбросы или диапазон набора данных. Таким образом, во многих случаях одно значение намного полезнее, чем два других.
Как найти среднее значение
Среднее значение, также называемое средним, рассчитывается путем сложения всех чисел и последующего деления на количество значений в наборе.
Как именно вы это делаете? Продолжайте читать, и мы дадим вам пошаговый пример.
1. Что означает?
Важно сначала понять, что на самом деле означает среднее значение. Когда есть определенный набор данных, наиболее распространенным значением, которое люди хотят знать о нем, является среднее или среднее. Среднее значение набора данных использует все точки данных, чтобы определить, к чему усредняются все значения.
2. Пошаговые инструкции
Теперь, как найти среднее значение? Вот пошаговые инструкции, которые можно использовать для нахождения среднего значения любой группы чисел.
Начнем с набора данных. Нашими числами будут 2, 7, 9, 12, 13, 13 и 21.
Сначала мы найдем общее число, когда все эти значения будут сложены вместе.
2+7+9+12+13+13+21= 77
Затем мы подсчитываем количество значений в нашем наборе данных. В этом примере есть 7 значений. Итак, делим общее число на 7.
77/7= 11
И все. Вы нашли середину!
Вы нашли середину!
Как найти медиану
Медиана находится путем перечисления значений от наименьшего к наибольшему, а затем нахождения числа в середине.
1. Что такое медиана?
Медиана — это число в середине набора значений. Иногда его называют средней точкой данных.
2. Пошаговые инструкции
Поиск среднего значения набора данных всегда начинается с упорядочивания чисел от меньшего к большему. Хотя можно найти медиану в неорганизованном наборе данных, это гораздо сложнее.
Для начала мы будем использовать тот же набор данных, что и выше: 2, 7, 9, 12, 13, 13 и 21. это среднее число. Медиана 12 .
Этот набор данных также был проще, потому что в нем было нечетное количество переменных. Что произойдет, если будет четное количество значений?
Допустим, набор данных — это 5, 9, 11, 11, 17, 19, 22 и 25. Когда мы считаем до середины, мы обнаруживаем, что 11 и 17 — это два числа в середине. Затем мы складываем эти два числа вместе.
Затем мы складываем эти два числа вместе.
11+17=28
Затем мы делим на 2, чтобы найти середину этих двух чисел.
28/2= 14
Таким образом, для этого набора данных 14 является медианой.
Как найти моду
Мода — это наиболее часто встречающееся значение в наборе данных.
1. Какой режим?
Многие наборы данных имеют значения, которые повторяются несколько раз. Мода — это значение, которое повторяется с наибольшей частотой.
2. Пошаговые инструкции
Самый простой способ найти режим — упорядочить значения данных в порядке возрастания или убывания. Такая организация данных также поможет вам увидеть выбросы.
В нашем наборе данных 2, 7, 9, 12, 13, 13 и 21 есть только одно значение, которое повторяется более одного раза. Поскольку 13 встречается дважды, это режим.
Во втором наборе данных, который мы рассмотрели, нахождение режима очень похоже.
5, 9, 11, 11, 17, 19, 22 и 25
11 встречаются с наибольшей частотой, так что это мода.
Применение среднего, медианы и моды
Хотя среднее, медиана и мода могут показаться абстрактными математическими понятиями, на самом деле они имеют множество применений в реальном мире.
Эти значения используются исследователями для понимания собранных ими данных. Он используется маркетологами, чтобы понять, какая реклама работает хорошо, а какая нет. Его используют те, кто занимается недвижимостью, и они определяют среднюю цену дома на конкретном рынке.
Вполне вероятно, что вы даже используете расчеты среднего, медианы и моды в своей повседневной жизни, даже не осознавая этого.
Вы можете подсчитать, сколько миль вы проезжаете в среднем в день и средний расход бензина в вашем автомобиле, чтобы знать, нужно ли вам ехать на заправку сегодня или завтра. В этом случае вы найдете среднее значение миль, которые вы проезжаете в день, и среднее значение расхода бензина, который обычно получает ваш автомобиль.
Совет учителя!
Превратите отработку среднего, медианы и моды в увлекательное адаптивное занятие для ваших учеников с помощью Prodigy Math. Вот как это работает:
- Вы устанавливаете материалы, которые учащиеся должны практиковать, на панели управления учителя
- Ваши ученики играют в Prodigy Math, отвечая на стандартизированные вопросы
- Вы просматриваете данные об успеваемости и отчеты в режиме реального времени, без необходимости оценивания!
Prodigy может не только помочь вам сэкономить время и поддержать ваших учеников, но и бесплатно предоставляется учителям и школам!
Посмотрите, как это работает
Пример задачи 1: Куриные наггетсы
Вы можете вспомнить среднее количество куриных наггетсов, которые съедает каждый из ваших детей, прежде чем решить, сколько приготовить сегодня на обед. В некоторые дни они могут съесть два, а в другие дни они могут съесть шесть. Таким образом, вы, скорее всего, решите использовать этот режим и сделать количество, которое они чаще всего едят.
В некоторых случаях легко определить, следует ли искать среднее значение, медиану или моду. В других случаях полезно спросить: «Есть ли какие-то выбросы?»
Как и в примере с куриными наггетсами, Сюзи, возможно, вчера съела 6 куриных наггетсов, но вы знаете, что это нетипично, поэтому вы используете режим или число вместо этого она ела чаще всего.
Также может быть полезно спросить: «Есть ли большой разброс в числах?» Это вопрос о том, есть ли большая разница между наибольшим и наименьшим числом в наборе данных. Если есть большой диапазон с большим количеством чисел, заполняющих пространство между ними, это может изменить используемую вами формулу среднего значения.
Пример задачи 2: Заработная плата
Еще одно распространенное место использования этих формул — это когда речь идет о заработной плате. Давайте вместе проанализируем набор данных, чтобы понять, когда вы будете использовать среднее значение, медиану и моду.
В одной компании годовая заработная плата исчисляется тысячами, но для этого примера мы удалим нули.
Наши номера: 28, 29, 30, 30, 30, 31, 33, 35, 42, 45, 45, 47, 54, 88, 97 и 185.
Этот набор данных представляет новых сотрудников компании, вплоть до тех, кто занимает высшие руководящие должности.
Чтобы вычислить среднее, складываем все числа, равные 849. Затем делим на количество значений в наборе. 849/16= 53
Наши числа уже расположены в порядке возрастания для расчета медианы и моды. Медиана находится путем перехода к числу в середине. В этом наборе это числа 35 и 42. Итак, мы складываем эти два числа вместе, а затем делим на 2.
Режим находится путем поиска числа с наибольшей частотой. В этом наборе данных это 30 , которое встречается три раза.
Поскольку в этом наборе данных очень широкий диапазон чисел, разные значения позволяют увидеть различия. Среднее значение показывает средний доход работника, но оно сильно искажено из-за высоких зарплат тех, кто находится наверху.
Медиана ближе к опыту большинства сотрудников в компании. Он убирает действительно высокие и низкие цифры, чтобы вы могли лучше понять, что делает большинство людей в этой компании.
Он убирает действительно высокие и низкие цифры, чтобы вы могли лучше понять, что делает большинство людей в этой компании.
Этот режим полезен для понимания того, какая зарплата обычно используется в компании. Если бы вы рассматривали возможность подачи заявки на эту работу, вы могли бы знать, что вам, вероятно, предложат именно эту зарплату.
Нахождение среднего, медианы и моды с использованием отрицательных чисел и десятичных дробей
Когда набор данных содержит отрицательные числа и десятичные дроби, это может показаться очень сложным. Однако процесс остается прежним. И особенно если вы пользуетесь калькулятором, сделать это ненамного сложнее.
Дополнительные ресурсы, которые помогут вам
Существует множество ресурсов, которые помогут вам помочь вашему ребенку или учащимся в расчете среднего значения, медианы и моды. Посмотрите на эти примеры:
- Попробуйте использовать калькулятор средней медианы и моды.
- Используйте Excel или Google Таблицы, где ваши учащиеся могут ввести формулу для нахождения среднего значения, медианы или моды, и программное обеспечение сделает всю работу за них.

- Используйте статистический калькулятор, чтобы найти среднее значение, медиану и моду.
- Поищите онлайн-таблицы с примерами, изображениями и подробными инструкциями по выполнению этих формул.
- Блог Prodigy охватывает множество других математических тем, включая все, от бесплатных математических ресурсов до лучших математических головоломок.
Если вы ищете увлекательный способ помочь вашему ученику или ребенку освоить математические понятия, такие как среднее значение, медиана или мода, попробуйте Prodigy Math! Игровая обучающая платформа охватывает тысячи математических навыков с 1-го по 8-й класс, включая контент Common Core. А благодаря интеграции учителей и родителей это отличный способ привлечь учащихся к математике как в классе, так и дома.
Посмотрите ниже, что учителя говорят о Prodigy Math!
Среднее значение, медиана и мода – определение, формулы и примеры решений
Среднее значение, медиана и мода являются показателями центральной тенденции . Эти значения используются для определения различных параметров данного набора данных. Мера центральной тенденции (среднее значение, медиана и мода) дает полезную информацию об изучаемых данных, они используются для изучения любого типа данных, таких как средняя заработная плата сотрудников в организации, средний возраст любого класса, количество людей. кто играет в крикет в спортивном клубе и т. д. Три показателя центральной тенденции:
Эти значения используются для определения различных параметров данного набора данных. Мера центральной тенденции (среднее значение, медиана и мода) дает полезную информацию об изучаемых данных, они используются для изучения любого типа данных, таких как средняя заработная плата сотрудников в организации, средний возраст любого класса, количество людей. кто играет в крикет в спортивном клубе и т. д. Три показателя центральной тенденции:
- Среднее (x̅ или μ)
- Медиана(M)
- Мода(Z)
Эти параметры подробно обсуждаются в статье.
СреднееСреднее — это сумма всех значений в наборе данных, деленная на количество значений в наборе данных. Его также называют средним арифметическим. Среднее значение обозначается как x̅ и читается как x bar
Среднее (x̅) = сумма значений / количество значений
Если x 1, x 2, x 3 ,……, x n являются значениями набора данных, то среднее значение рассчитывается как:
x̅ 902 + x 2 + x 3 + …… + x n ) / n
Среднее значение данных 10, 30, 40, 20, 50 равно
Среднее = (сумма всех значений) / (количество значений)
Среднее = (10 + 30 + 40 + 20+ 50) / 5
= 30
Также, проверьте Среднее
Медиана А является средним значением для сортированных данных. Сортировка данных может производиться как по возрастанию, так и по убыванию. Медиана делит данные на две равные половины. Формула для медианы:
Сортировка данных может производиться как по возрастанию, так и по убыванию. Медиана делит данные на две равные половины. Формула для медианы:
Если количество значений (значение n) в наборе данных нечетное, то формула для расчета медианы:
Медиана = [(n + 1)/2] число термин
Если количество значений (значение n) в наборе данных четное, то формула для расчета медианы:
Медиана = [(n/2) -й -й термин + {(n/2) + 1} -й -й термин] / 2
Пример. Найдите медиану заданного набора данных 30, 40, 10, 20 и 50
Решение:
РежимМедиана данных 30, 40, 10, 20, 50:
Шаг 1: Упорядочить данные в порядке возрастания:
10, 20, 30, 40, 50
Шаг 2: Проверить, является ли n (количество членов набора данных) четным или нечетным, и найти медиана данных с соответствующим значением «n».
Шаг 3: Здесь n = 5 (нечетное)
Медиана = [(n + 1)/2] число термин
Медиана = [(5 + 1)/2] число член
= 30
Режим — это наиболее часто встречающееся значение или элемент набора данных. Набор данных обычно может иметь одно или несколько значений режима. Если набор данных имеет одну моду, то он называется «унимодальным». Точно так же, если набор данных содержит 2 режима, он называется «бимодальным», а если набор данных содержит 3 режима, то он называется «тримодальным». Если набор данных состоит из более чем одного режима, то он известен как «мультимодальный» (может быть бимодальным или трехмодальным). Для набора данных нет режима, если каждое число появляется только один раз.
Пример: найти режим заданного набора данных 1, 2, 2, 3, 3, 4, 5
Решение:
Данный набор равен {1, 2, 2, 2, 3, 3, 4, 5}
Поскольку приведенный выше набор данных расположен в порядке возрастания.
Наблюдая за приведенным выше набором данных, мы можем сказать, что
Мода = 2
Так как он имеет самую высокую частоту (3)0002 Для любой группы данных отношение между тремя центральными тенденциями, средним, медианой и модой определяется формулой:
Мода = 3 Медиана – 2 Среднее самое высокое значение и самое низкое значение. Это способ понять, как числа распределяются в наборе данных. Формула для нахождения диапазона:
Диапазон = наибольшее значение – наименьшее значение
Пример: найти диапазон заданного набора данных 12, 19, 6, 2, 15, 4
Решение:
Данный набор равен {12, 19, 6, 2, 15, 4}
Здесь
Наименьшее значение = 2 0 902 9091 Максимальное значение Диапазон = 19 − 2
= 17Разница между средним и медианой
Среднее математическое значение известно как среднее значение набора данных, тогда как среднее позиционное считается медианой.
Различие между средним и медианным можно понять на следующем примере. В школе есть 8 учителей с зарплатой 20000 рупий, директор с зарплатой 35000, найдите их среднюю зарплату и медианную зарплату.
Среднее = (20000 + 20000 + 20000 + 20000 + 20000 + 20000 + 20000 + 20000 + 35000)/9
= 195000/9
= 21666,67С. Средняя заработная плата составляет 21 666,67.
Для медианы в порядке возрастания: 20000, 20000, 20000, 20000, 20000, 20000, 20000, 20000, 35000. медиана — 5 th наблюдений.
Медиана = 20000
Следовательно, медиана составляет 20 000 вон.
После сравнения среднего и медианы для приведенного выше набора данных. Очевидно, что средняя заработная плата составляет 21 666,67 рупий, а медиана — 20 000 рупий.
Также проверьте
- Центральная тенденция
- Статистические формулы
Решенные примеры для среднего, медианы и моды заданный набор данных.
Решение:
Среднее значение = (сумма всех значений данных) / (количество значений)
= 6,75
Упорядочить данные в порядке возрастания: 5, 6, 7, 9
Здесь n = 4 (четное)
Медиана = [(n/2) th член + {( n/2) + 1} -й срок] / 2
Медиана = (6 + 7) / 2
= 6,5Режим = наиболее частые значения
= 9 (самое высокое значение)Диапазон = самое высокое значение — самое низкое значение
Диапазон = 9 — 5
= 4Пример 2: Найдите среднее, Медиан, Медиан, Медиан, Median, Median, Median, режим и диапазон для заданных данных
190, 153, 168, 179, 194, 153, 165, 187, 190, 170, 165, 189, 185, 153, 147, 161, 127, 180
Решение:
Среднее значение:
190, 153, 168, 179, 194, 153, 165, 187, 190, 170, 165, 189, 185, 153, 147, 161, 127, 180 наблюдений) / (Количество наблюдений)
= (190 + 153 + 168 + 179 + 194 + 153 + 165 + 187 + 190 + 170 + 165 + 189 + 185 + 153 + 147 + 161 + 127 + 180) / 18
= 2871/18
= 159,5
Следовательно, среднее значение равно 159,5
Для медианы:
В порядке возрастания данных наблюдений:
127, 147, 153, 153, 153, 161, 165, 165, 168, 170, 179, 180, 185, 187, 189, 190, 190, 194 Здесь
n = 18
Медиана = 1/2 [(n/2) + (n/2 + 1)]-е наблюдение
= 1/2 [9 + 10]-е наблюдение
= 1/2 (168 + 170)
= 338/2
= 169Таким образом, медиана равна 169
Для режима:
Число с наибольшей частотой = 153
Таким образом, Mode = 53
для диапазона:
Диапазон = самое высокое значение — самое низкое значение
= 194 — 127
= 67Пример 3: Найдите средний из данных 25, 12, 5, 5, 5, 5, 5, 5, 5, 24, 15, 22, 23, 25
Решение:
25, 12, 5, 24, 15, 22, 23, 25
Порядок данных в порядке возрастания:
5, 12, 15, 22, 23, 24, 25, 25
Шаг 2: Проверьте, является ли n (количество членов набора данных) четным или нечетным, и найдите медиану данных с соответствующим значением «n».
Шаг 3: Здесь n = 8 (четное), тогда
Медиана = [(n/2) th term + {(n/2) + 1) th term] / 2
Медиана = [(8/2) TH Термин + {(8/2) + 1} TH Термин] / 2
= (22 + 23) / 2
= 22,5
Пример 4: Найдите моду заданных данных 15, 42, 65, 65, 95.
Решение:
Данный набор данных 15, 42, 65, 65, 95
Число с наибольшей частотой = 65
Мода = 65
Среднее значение Вопрос 1: Что такое средняя медиана и мода?Ответ:
Вопрос 2: Какая связь между средним значением, медианой и модой?Среднее, медиана и мода являются мерами центральной тенденции. Эти три меры центральной тенденции используются для получения обзора данных. Они представляют собой истинную сущность данного набора данных.
Ответ:
Вопрос 3: Как найти медиану и моду?Связь между средней медианой и модой:
Мода = 3 Медиана – 2 Среднее
Ответ:
Среднее значение, медиана и мода любого заданного набора данных вычисляются с использованием подходящих формул, которые обсуждались выше в статьях.

 5
5