Факультативное занятие по математике в 3-м классе: «Магические квадраты»
Задачи:
1. Научить заполнять магические квадраты.
2. Развивать наблюдательность, умение обобщать.
3. Прививать стремление к познанию нового, интерес к математике.
Оборудование: компьютер, мультимедиа проектор с экраном, презентация PowerPoint (Приложение 1).
В давние времена, научившись
считать и выполнять арифметические действия, люди с удивление обнаружили, что
числа имеют самостоятельную жизнь, удивительную и таинственную. Складывая различные
числа, располагая их друг за другом или одно под другим, они иногда получали
одинаковую сумму. Наконец, разделив числа линиями так, чтобы каждое оказалось в
отдельной клетке, увидели квадрат, любое из чисел которого принимало участие в
двух суммах, а те, что расположены вдоль диагоналей – даже в трех, и все суммы
равны между собой! Недаром древние китайцы, индусы, а вслед за ними и арабы
приписывали таким конструкциям таинственные и магические свойства.
Магические квадраты появились на Древнем Востоке еще до нашей эры. Одна из сохранившихся легенд повествует о том, что когда император Ю из династии Шан (2000 г до н.э.) стоял на берегу Ло, притоке Желтой реки, вдруг появилась большая рыба (в других вариантах – огромная черепаха), у которой на спине был рисунок из двух мистических символов – черных и белых кружочков (слайд 2), который был осознан затем как изображение магического квадрата порядка 3. (слайд 3)
Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман. Их можно встретить на палубах больших пассажирских судов как площадку для игры.
Итак, под
магическими будем понимать квадраты, в которых суммы чисел, стоящих в любом
столбце или в любой строке, а также по диагоналям, одинаковы.
До сих пор вы использовали магические квадраты чаще всего для устного счета. При этом несколько чисел, в том числе и центральное, уже расставлены по клеткам квадрата. Требуется расставить остальные числа так, чтобы в любом направлении получилась определенная сумма.
Задача 1. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Часть из них расставлена по клеткам Требуется расставить остальные числа, чтобы в сумме получалось 15. (слайд 4)
|
|
1 |
|
|
|
5 |
|
|
4 |
|
|
Находим необходимое число,
вычитая из 15 сумму двух известных чисел, стоящих в одной строке, диагонали или
столбце. Получаем следующий квадрат. (слайд 5)
Получаем следующий квадрат. (слайд 5)
|
8 |
1 |
6 |
|
3 |
5 |
7 |
|
4 |
9 |
2 |
Оказывается, все другие магические квадраты, составленные из этих же чисел, можно получить из данного симметрией относительно строки, столбца или диагонали, поэтому во всех квадратах числа расставлены по одним и тем же правилам. (слайд 6)
Можно заметить ряд закономерностей, облегчающих заполнение клеток квадрата или дающих возможность решить задачу при меньшем числе данных в условии.
Например, в условиях задач, подобных предыдущей, не
обязательно указывать, какая сумма должна получиться в любом направлении.
Задача 2. Найдите способ, как сосчитать сумму по строчкам, столбцам и диагоналям из предыдущей задачи.
Можно рассуждать следующим образом: сумма чисел в каждой строке одинакова, таких строк 3, значит сумма чисел в каждой строке в три раза меньше суммы всех чисел. Следовательно, в нашем примере, сумма в каждой строке равна 15 (45 : 3). Но это число можно найти и другими способами: сложить три центральных числа 4, 5 и 6 или умножить центральное число 5 на 3.
Задача 3. Даны числа: 2, 3, 4, 5, 6, 7, 8, 9, 10. Требуется вписать их в клетки квадрата так, чтобы в любом направлении в сумме получилось одно и то же число. Часть чисел уже вписана в квадрат. (слайд 7)
|
|
|
9 |
|
|
6 |
|
|
|
|
5 |
Найдем вначале сумму чисел,
которая будет получаться в строках и столбцах.
Получаем следующий квадрат: (слайд 8)
|
7 |
2 |
9 |
|
8 |
6 |
4 |
|
3 |
10 |
5 |
Задача 4. Даны числа 5, 6, 7, 8, 9, 10, 11, 12, 13. Два их них вписаны в клетки квадрата. Впишите остальные так, чтобы в любом направлении получилось в сумме одно и то же число. (слайд 9)
Найдем сумму: 9 × 3 = 27. Заполняем квадрат: (слайд 10)
|
6 |
11 |
10 |
|
13 |
9 |
5 |
|
8 |
7 |
12 |
Посмотрим на все три заполненных
квадрата и попробуем найти еще ряд закономерностей, которые помогут заполнить
квадрат еще с меньшим чисел, вписанных в квадрат. (слайд 11)
(слайд 11)
|
8 |
1 |
6 |
|
3 |
5 |
7 |
|
4 |
9 |
2 |
1, 2, 3, 4, 5, 6, 7, 8, 9
|
7 |
2 |
9 |
|
8 |
6 |
4 |
|
3 |
10 |
5 |
2, 3, 4, 5, 6, 7, 8, 9, 10
|
6 |
11 |
10 |
|
13 |
9 |
|
|
8 |
7 |
12 |
5, 6, 7, 8, 9, 10, 11, 12, 13
Посмотрите, какое число стоит в
центре квадрата? Как оно расположено в ряду данных чисел? (слайд 12) (В
центре квадрата всегда записывается число, стоящее на пятом месте нашей
последовательности, т. е. одинаково удаленное с левого и правого ее краев.)
е. одинаково удаленное с левого и правого ее краев.)
Можно заметить еще ряд особенностей: в квадрате по разные стороны от центрального числа стоят числа, одинаково удаленные от левого и правого краев последовательности. Покажем пары соответствующих чисел на примере заполнения квадрата числами от 1 до 9: (слайд 13)
Зная это, можно заполнить квадрат, почти не считая.
Посмотрите, как расположены в квадрате числа, стоящие рядом с центральным, а также числа, записанные от них через одно число. Они соединены линиями сверху. (Они расположены по диагоналям квадрата.) А где расположены остальные числа, которые соединены линиями снизу? (Они расположены по вертикали и по горизонтали.)
Давайте проверим, выполняются ли такие закономерности в других квадратах. (слайд 14)
(Да, такие закономерности выполняются.)
Итак, давайте подведем итог. Какие свойства магических квадратов мы выяснили?
1) Чтобы найти сумму чисел в
каждом столбце или строке, можно центральное число умножить на 3.
2) В центре квадрата стоит число, записанное в ряду пятым.
3) В квадрате по разные стороны от центрального числа стоят числа, одинаково удаленные от левого и правого краев последовательности.
4) Числа, стоящие рядом с центральным и через одно от него, расположены по диагоналям квадрата. Числа, стоящие с краю и через одно от него, расположены в квадрате по вертикали и по горизонтали.
Задача 5. Даны числа: 3, 4, 5, 6, 7, 8, 9, 10, 11. Впишите их в клетки квадрата так, чтобы в любом направлении получилось одно и то же число. (слайд 15)
(Найдем, какая сумма должна
получаться в каждом направлении. Для этого умножим центральное число 7 на 3. В
результате получим 21. В центр квадрата поставим число 7, по одной диагонали
числа 6 и 8, по другой – 4 и 10. Осталось расставить недостающие числа: сумма
записанных в первой строке чисел равна 10, до 21 недостает 11, значит, в пустой
клетке верхней строки запишем число 11 (первое справа). Тогда в нижней строке
запишем число 3 (первое слева). В левый столбик запишем число 5 (21 – (6 +
10)), тогда в правом столбике останется записать число 9. Таким образом, мы
расставили все 9 чисел в клетки магического квадрата, при этом ни одно число по
условию задачи в квадрате не было поставлено.)
Тогда в нижней строке
запишем число 3 (первое слева). В левый столбик запишем число 5 (21 – (6 +
10)), тогда в правом столбике останется записать число 9. Таким образом, мы
расставили все 9 чисел в клетки магического квадрата, при этом ни одно число по
условию задачи в квадрате не было поставлено.)
Задача имеет несколько решений, но все квадраты получаются из других симметрией относительно средних линий или диагонали. (слайд 16)
Задача 6. Даны числа 2, 4, 6, 8, 10, 12, 14, 16, 18. Впишите их в клетки квадрата так, чтобы в любом направлении получилось в сумме одно и то же число.
Один из вариантов решения на слайде. (слайд 17)
Задача 7. Сравните условие задач 1 и 6 и подумайте, как можно было решить задачу, зная решение задачи 1.
(Числа из задачи 6 в два раза
больше соответствующих чисел задачи 1. Поэтому можно каждое число квадрата из
задачи 1 просто удвоить и получить искомый квадрат. )
)
Существуют различные способы построения магических квадратов. Рассмотрим метод террас, который придумали древние китайцы. Следуя этому методу надо «естественный» числовой квадрат повернуть относительно центра на половину прямого угла (слайд 19) и отделить квадратной рамкой таблицу 3´3. (слайд 20) Числами, записанными вне рамки, и образующими выступы («террасы»), заполняем пустые клетки у противоположной стороны таблицы. (слайд 21)
Аналогично можно построить любой квадрат нечетного порядка. Заполним клетки магического квадрата 5´5 числами от 1 до 25. (слайды 22, 23, 24)
Для построения магического квадрата 4´4 наиболее простым и доступным является следующий метод: в «естественном» квадрате меняются местами дополнительные числа на главных диагоналях, а остальные остаются без изменения. (слайды 25, 26)
Подведение итогов занятия
Какую тайну магических квадратов вы открыли сегодня на занятии? Что вам в этом помогло?
3-8Различия в квадратных числах | NZ Maths
Цель
Это задание по алгебре 5-го уровня из серии «Разберись».
Прилагается PDF-файл с заданиями для учащихся.
Цели достижения
NA5-9: связывать таблицы, графики и уравнения с линейными и простыми квадратичными отношениями, встречающимися в числовых и пространственных закономерностях.
Разработка АО и другие учебные ресурсы
Деятельность учащихся
Нажмите на изображение, чтобы увеличить его. Нажмите еще раз, чтобы закрыть. Скачать PDF (246 КБ)
Конкретные результаты обучения
найти закономерность в квадратных числовых последовательностях
использовать закономерность для предсказания
Необходимые материалы
FIO, уровень 4+, алгебра, книга четвертая, разница в квадратных числах, стр. 1
квадратные плитки или лист бумаги с квадратной сеткой
Упражнение
В этом упражнении учащиеся ищут закономерности в расположении квадратных плиток. Показ различий с помощью плиток, многозвенных кубов или рисунков на бумаге в клетку, вероятно, поможет учащимся увидеть различные закономерности.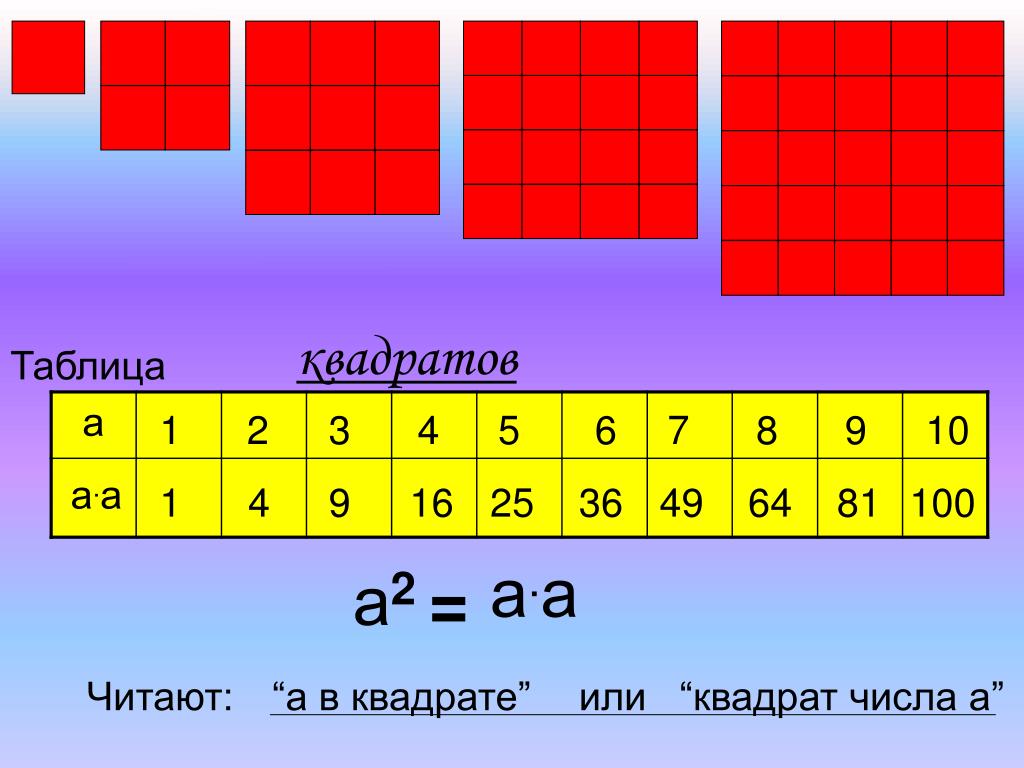
: В вопросе 1 расположение плиток связано с различиями между последовательными квадратными числами. Когда 32, представленный квадратом 3 на 3, сравнивают с 2 2 (квадрат 2 на 2), разница составляет 5 квадратов, представленных в виде буквы L.
Разность между двумя последовательными квадратными числами, например, 2 2 – 1 2 , 3 2 – 2 2 или 4 2 – 3 2 , , может быть представлена следующим образом:
Рассматривая уравнения или диаграммы, учащиеся могут увидеть простое правило для этих вычислений, в котором разница между числами, возводимыми в квадрат, равна 1. Правило таково: сложите два числа, которые возводятся в квадрат. Например, 7 2 – 6 2 можно представить как 7 + 6 = 13, а 19 2 – 18 2 как 19 + 18 = 37. Это правило
также можно выразить алгебраически так: Если b = a + 1 (где a и b — последовательные числа), то b 2 — a 2 = а + б».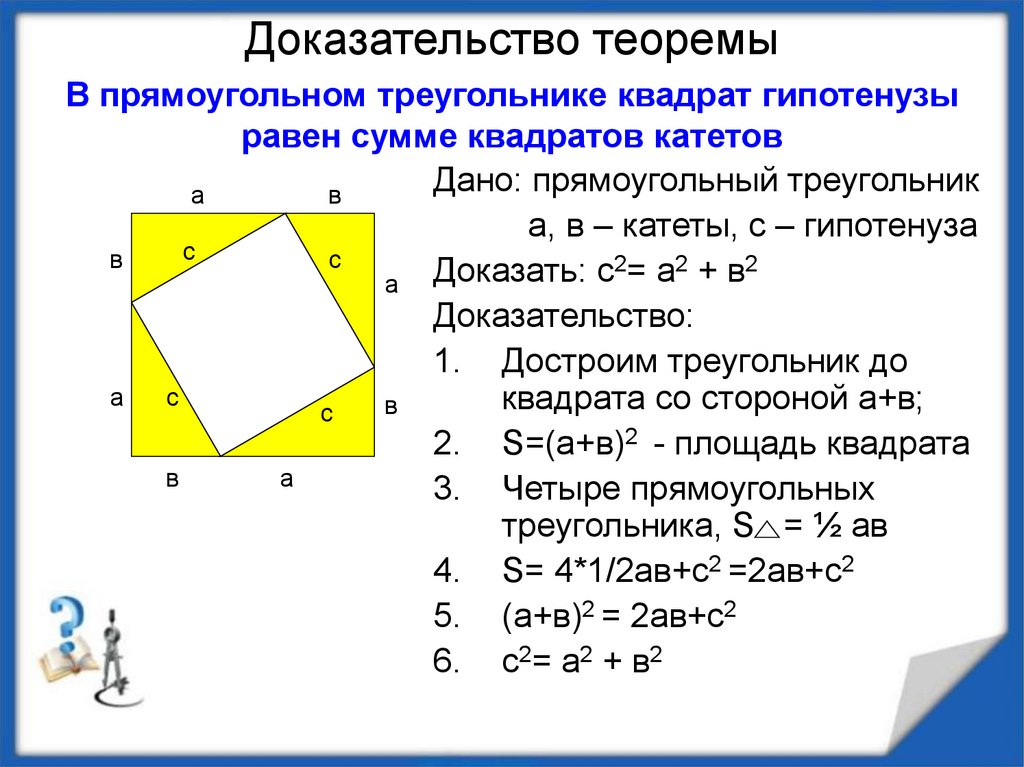 Приведенные выше диаграммы должны помочь учащимся геометрически понять, почему правило работает. Например, 20 2 – 19 2 = 20 + 19 (что равно b 2 – a 2 = a + b для значений a = 19, b = 20)
Приведенные выше диаграммы должны помочь учащимся геометрически понять, почему правило работает. Например, 20 2 – 19 2 = 20 + 19 (что равно b 2 – a 2 = a + b для значений a = 19, b = 20)
= 39
В вопросе 2 , закономерность различий между альтернативными квадратными числами может быть показана следующим образом:
Учащиеся могут увидеть простое правило для этих вычислений, согласно которому разница между числами, возведенными в квадрат, равна 2. Правило таково: удвойте сумму из двух чисел, возведенных в квадрат. Так, например, 27 2 – 25 2 = 2 х (27 + 25).
Еще раз, приведенные выше диаграммы помогут учащимся геометрически понять, почему правило работает.
Алгебраически правило здесь такое: если b = a + 2, то b 2 – a 2 = 2(a + b).
В вопросе 3 образец разницы между любым квадратным числом и третьим следующим квадратным числом может быть показан следующим образом:
Учащиеся могут увидеть простое правило для этих вычислений, в котором разница между числами, возведенными в квадрат равно 3. Правило таково: утроите сумму двух чисел, возведенных в квадрат. Так, например, 27 2 – 24 2 = 3 х (27 + 24). Алгебраически правило здесь такое: если b = a + 3, то b 2 – a 2 = 3(a + b).
Правило таково: утроите сумму двух чисел, возведенных в квадрат. Так, например, 27 2 – 24 2 = 3 х (27 + 24). Алгебраически правило здесь такое: если b = a + 3, то b 2 – a 2 = 3(a + b).
Эти правила могут быть дополнительно обобщены. В следующих таблицах обобщаются расчеты для вопросов с 1 по 3. Для каждой из этих таблиц кратчайший расчет всегда представляет собой разницу, умноженную на сумму двух возведенных в квадрат чисел. Обратите внимание, что в первой таблице ниже разница равна 1, поэтому мы можем написать 4 + 3 вместо 1 x (4 + 3) и так далее.
В общем случае действует правило: b в квадрате минус a в квадрате равно разнице между b и a, умноженной на сумму b и a. Алгебраически мы можем записать это как:
b 2 – a 2 = (b – a) x (b + a)
= (b – a)(b + a).
Это правило будет работать для всех значений a и b. В следующей таблице показано, как можно использовать это правило:
Ответы на задание
1.
