Прямоугольный и обычный параллелепипед, как находить полную площадь поверхности и какие формулы при этом нужны
При изучении школьной математики часто встречаются задания, в которых требуется определить полную или боковую площадь поверхности прямоугольного или обычного параллелепипеда. Научимся это делать.
Для того, чтобы научиться вычислять площадь поверхности параллелепипеда необходимо представлять, что это такое.
Содержание:
- Общие понятия
- Нахождение площадей фигур
- Площадь поверхности параллелепипеда
- Площадь поверхности куба
- Площадь поверхности прямоугольного параллелепипеда
- Поверхность параллелепипеда
- Заключение
- Видео
Общие понятия
Изучим основные понятия. В дальнейших наших рассуждениях площадь будем обозначать латинской буквой S, угол между сторонами a и b будем обозначать как (ab).
Параллелепипедом в математике именуется четырехугольная призма, у которой все грани являются параллелограммами.
- Грань — одна из поверхностей пространственного тела.
- Параллелограмм — четырёхугольник с попарно параллельными противоположными сторонами.
- Поверхности параллелепипеда это сумма поверхностей всех его граней.
- Прямоугольный параллелепипед — пространственное тело у которого гранями являются прямоугольники.
- Прямоугольник — четырёхугольник у которого все углы прямые.
- Куб — пространственное тело у которого гранями являются квадраты.
- Квадрат — прямоугольник у которого все стороны равны между собой.
- Равными называются фигуры, совмещающиеся при наложении.
Нахождение площадей фигур
Рассмотрим, как находятся площади, могущие составлять грани параллелепипеда.
- Площадь квадрата равна произведению его стороны самой на себя.
2. - Прямоугольника — вычисляется с помощью умножения большей его стороны (длины) на меньшую его сторону (ширину). Формула площади прямоугольника имеет вид S = a*b.
- Параллелограмма — найти сложнее и имеется несколько различных способов. Наиболее часто в математике применяются формулы для нахождения с помощью стороны и опущенной на неё высоты или двух сторон и синуса угла между ними. Записываются они следующим образом: S = a*h, S = a*b*sin (ab).
2.Рассмотрим на примерах как найти площадь каждой из рассматриваемых нами фигур
.1. Длина стороны квадрата равна 1600 метров. Определим его площадь.
- S = a*a, отсюда в искомом случае S = 1600*1600 = 2 560 000 метров квадратных.
2. Стороны прямоугольника равны 90 и 200 метров соответственно. Определим его S.
- S = a*b, следовательно в нашем варианте получится S = 90*200 = 18 000 метров квадратных.
3. С параллелограммом рассмотрим два случая нахождения.
Сторона равна 300 метров, а опущенная на неё высота 250 метров. Тогда получится:
- S = a*h = 300*250 = 75 000 метров квадратных.
Второй вариант — стороны равны 550 и 200 метров соответственно. Угол между ними 30 градусов. Имеем:
- S = a*b*sin (ab) = 550*200*sin 30 = 110 000*0.5 = 55 000 квадратных метров.
Как видно из примеров, приведённых выше, никаких сложностей нет.
Площадь поверхности параллелепипеда
Так как наши тела имеют три принципиально различных варианта, то каждый из них мы рассмотрим в отдельности. Учтём, что полной поверхностью является сумма площадей всех граней тела, а боковой — только боковых граней.
Площадь поверхности куба
Здесь все крайне просто — грани этой фигуры равны между собой, так что S = a*a*6.
На примере это выглядит следующим образом:
Сторона равна 88 сантиметров.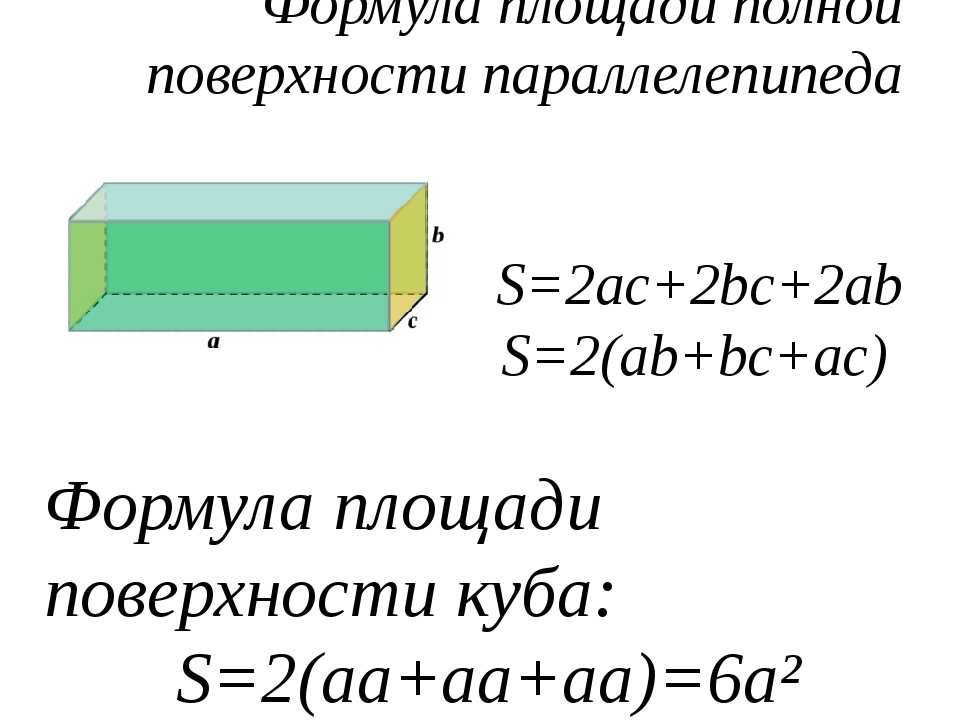
Площадь полной поверхности?
При данных условиях имеем:
S = a*a*6 = 88*88*6 = 46 464 сантиметра квадратного.
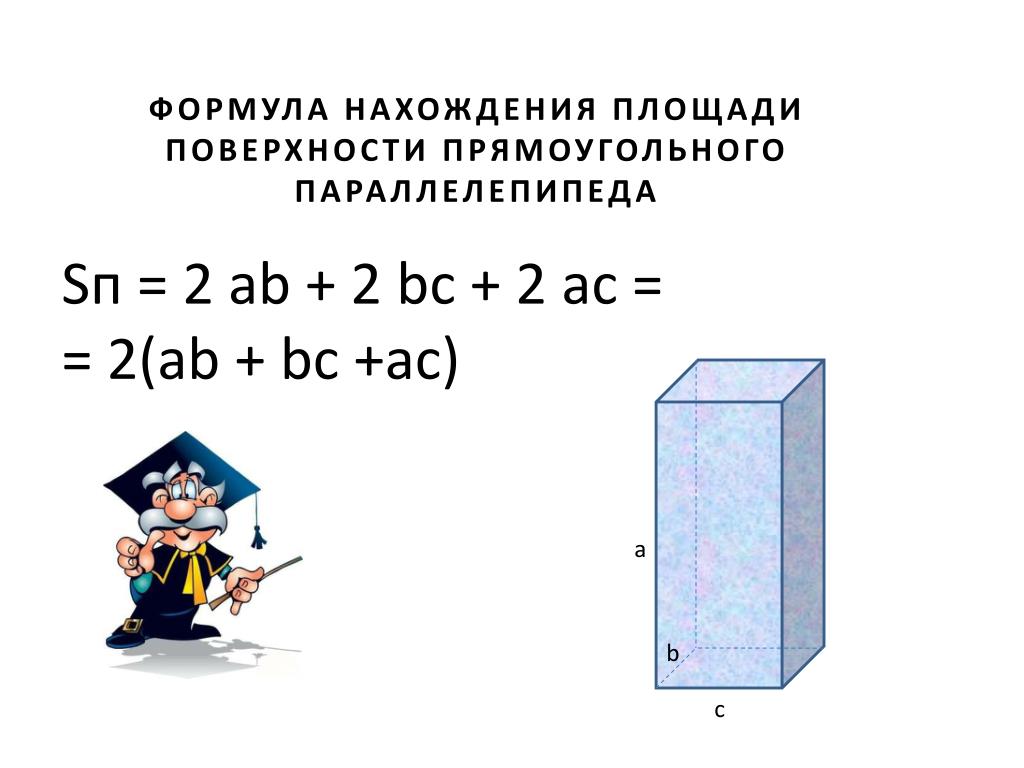
Площадь поверхности прямоугольного параллелепипеда
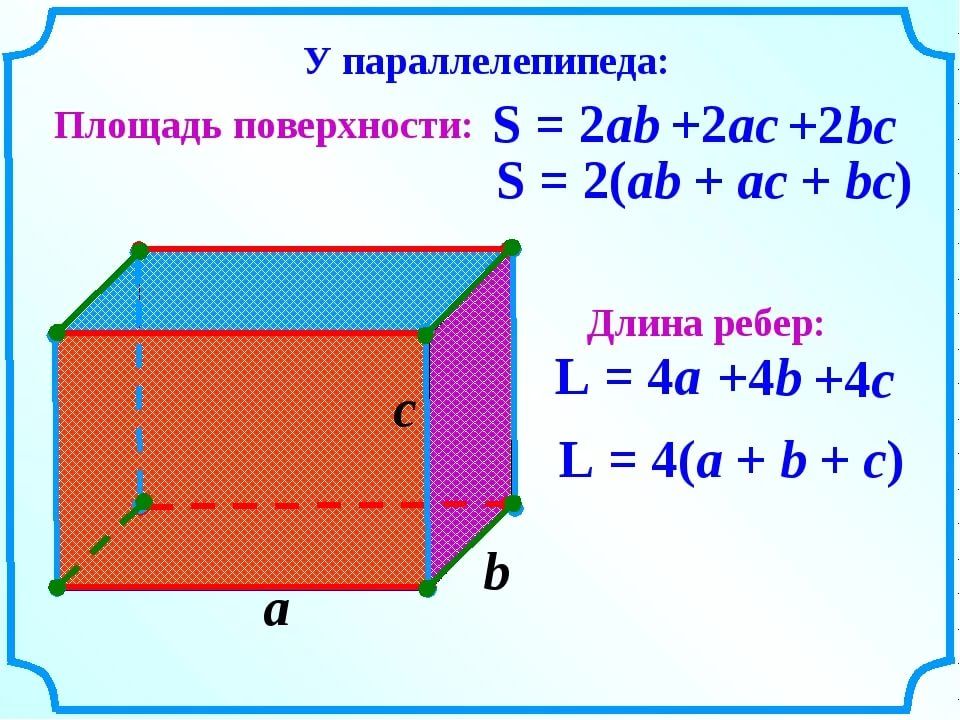
Здесь все так же довольно легко — нужно помнить, что противоположные грани равны. Таким образом, находим поверхность трёх различных граней, и каждую удваиваем. Формулы нахождения будут выглядеть следующим образом:
S = 2*(S1 + S2 + S3), где S1, S2, S3 площади всех граней соответственно.
Второй вариант S = 2*(a*b + a*c + b*c), где a, b, c соответствующие рёбра прямоугольного параллелепипеда.
Снова рассмотрим пример. Пусть рёбра прямоугольного параллелепипеда равняются 20, 30 и 40 метров. Площадь полной поверхности?
Имеем, S = 2*(a*b + a*c + b*c) = 2*(20*30 + 20*40 + 30*40) = 2*(600 + 800 + 1200) = 2*2600 = 5 200 квадратных метров.
Как видно, находить площадь прямоугольного параллелепипеда также совершенно несложно.
Поверхность параллелепипеда
Теперь рассмотрим случай когда заданное нам тело имеет вид простого параллелепипеда, его гранями являются обычные параллелограммы.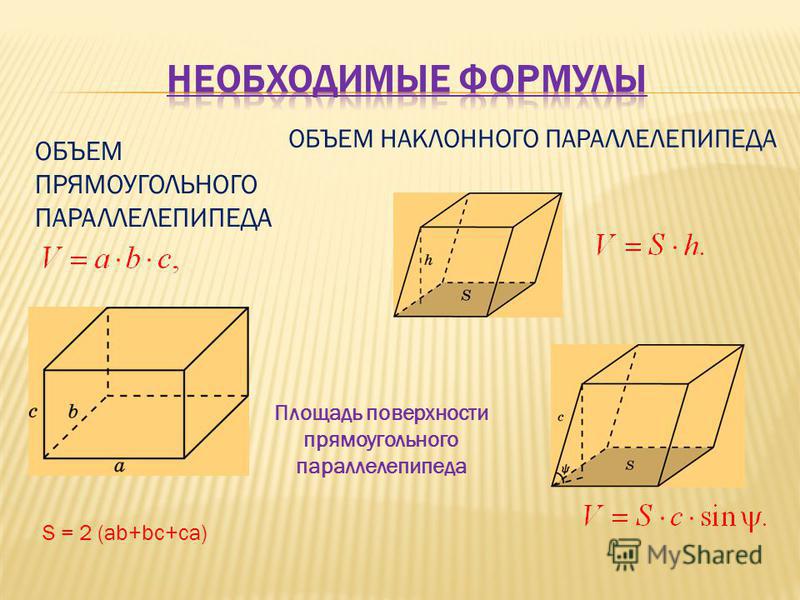
Здесь, как и в предыдущем случае противоположные грани равны. Следовательно, определив поверхность трёх различных граней, мы сможем определить и полную поверхность. Значит, одна из формул опять-таки будет иметь вид:
- S = 2*(S1 + S2 + S3), где S1, S2, S3 площади трёх различных граней соответственно. Запишем исходя из наших рассуждений, ещё две формулы:
- S = 2*(a*h2 + b*h3 + c*h4), где a, b, c соответствующие рёбра параллелепипеда, а h2, h3, h4 опущенные на них высоты.
- S = 2*(a*b*sin (ab) + a*c*sin (ac) + b*c*sin (bc)), где a, b, c соответствующие рёбра, а (ab), (ac), (bc) углы между ними.
- a = 15, b = 25, c = 25, h2 = 10, h3 = 20, h4 = 15. Пл. полной поверхности? Согласно формуле получим:
- S = 2*(a*h2 + b*h3 + c*h4) = 2*(15*10 + 25*20 + 25*15) = 2*(150 + 500 + 375) = 2*1025 = 2 050 миллиметров квадратных.
В некоторых заданиях требуется определение только площади боковой поверхности параллелепипеда.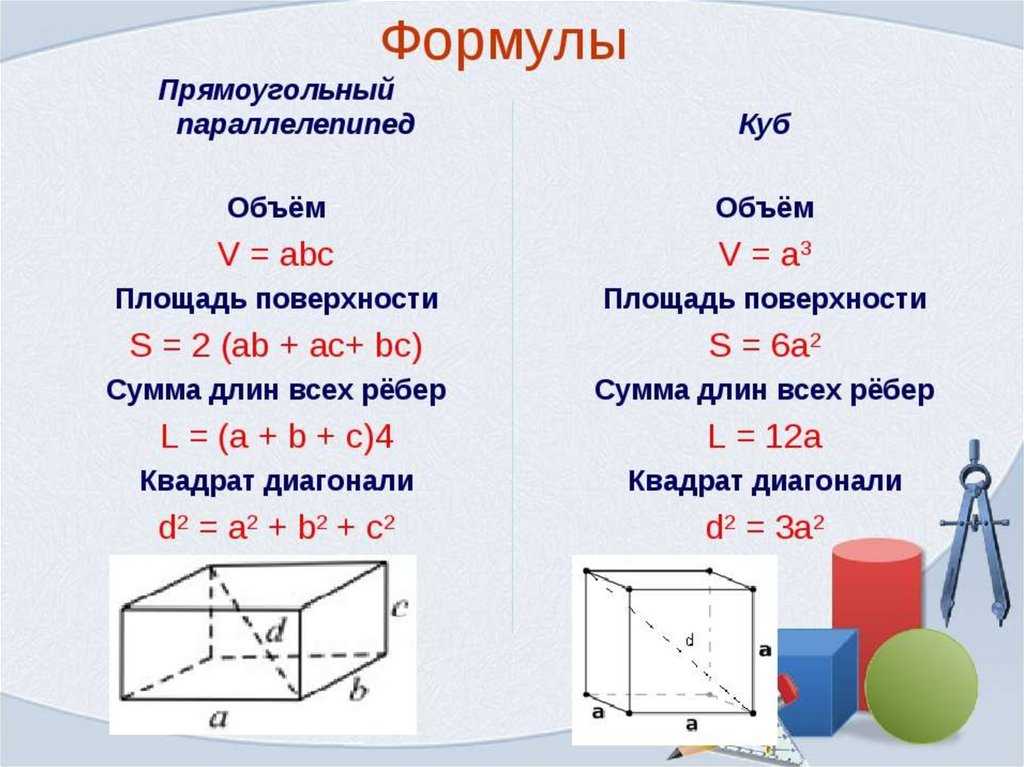
В таком случае чётко указывается, что является основанием и находится только суммарная пл. четырёх боковых граней. Все приведённые выше рассуждения остаются верными.
Заключение
Тщательно изучив все сказанное выше, можно отметить, что никакой особой сложности задача по определению площади параллелепипеда не вызывает. Нужно всего-навсего чётко представлять все данные в материале математические понятия, абсолютно точно выучить формулы, ну и, разумеется, уметь хорошо проводить арифметические действия.
Видео
Из видео вы узнаете, как находить площать прямоугольного параллелепипеда.
Применение формул объема и площади поверхности прямоугольного параллелепипеда для решения практических задач и математического моделирования
Применение формул объема и площади поверхности прямоугольного параллелепипеда для решения практических задач и математического моделирования
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (181 кБ)
Цель урока: На практике научиться применять формулы объёма и площади поверхности прямоугольного параллелепипеда.
Инструменты: мультимедийная установка, мел, доска, макеты параллелепипедов.
I. Проверка домашнего задания.
II. Устный опрос.
- Сколько ребер у прямоугольного параллелепипеда? Какой фигурой они являются?
- Сколько граней у прямоугольного параллелепипеда? Какой фигурой они являются?
- Сколько вершин у прямоугольного параллелепипеда? Какой фигурой они являются?
III.
Работа по готовым чертежам.- Что такое a, b и c?
- Как найти площадь боковой грани? Есть ли еще грани с такой же площадью?
- Как найти площадь верхней грани?
- Как найти площадь передней грани?
- Записать на доске формулу для нахождения площади поверхности параллелепипеда.
- Записать формулу для нахождения объёма параллелепипеда.
- В каких единицах измеряется площадь поверхности параллелепипеда, а в каких объём.
IV. Решить задачу по чертежу, изображенному на рисунке.
Найти площадь поверхности и объём прямоугольного параллелепипеда.
Решение.
- 3*4 = 12 (кв. см) – площадь передней поверхности.
- 3*5 = 15 (кв. см) – площадь боковой поверхности.
- 4*5 = 20 (кв. см) – площадь верхней поверхности.
- 2*(12+15+20) = 94 (кв. см) – площадь боковой поверхности параллелепипеда.
Ответ: 94 кв.см.
V. Практическая часть. Раздать параллелепипеды
- Измерить ребра параллелепипеда (длину, высоту и ширину). Записать результаты в тетрадь.
- Найти площадь боковой поверхности параллелепипеда.
- Найти объем параллелепипеда.
- Подписать грань параллелепипеда площадь, которой равна
- Вариант 1 – 14 кв. см
- Вариант 2 – 18 кв. см
- Вариант 3 – 48 кв. см
VI. Письменная работа на доске с фронтальным обсуждением.
Задача.
Найти площадь поверхности и объём прямоугольного параллелепипеда с вырезом.
Решение.
- 2*(4*5+5*5+5*4) = 130 кв. см – площадь поверхности.
- 5*5*4 = 100 куб. см – объём параллелепипеда.
Ответ: 130 кв. см и 100 куб. см.
VII. Задача с практическим содержанием.
Сколько ведер воды по 8 литров каждое, налито в аквариум, изображенный на рисунке.
Мы знаем, что 1 литр = 10 куб.дм.
- 25-5 = 20 (см) – высота налитой воды.
- 20*40*60 = 48000 (куб. см) – объём воды в аквариуме.
48000 куб. см = 48 куб. дм = 48 литров - 48:8 = 6 (вед.) – воды потребуется.
Ответ: 6 ведер.
VIII. Выставление оценок.
IX. Домашнее задание.
Формулы объема и поверхности
Объем выражает количество чего-то (например, воды), которое нам нужно, чтобы заполнить форму.
Космические фигуры имеют только объем. Плоские фигуры (треугольники, квадраты) не имеют объема.
Стандартное обозначение для тома — V.
Прямоугольный параллелепипед
Прямоугольный параллелепипед имеет 6 граней, которые являются прямоугольниками.
Если стороны прямоугольника внизу равны а и
b, а высота параллелепипеда c
(третье ребро прямоугольного параллелепипеда).
92$
Параллелепипед
Параллелепипед образован 6 параллелограммами.
Если площадь дна равна А, а высота
параллелепипед h.
Формула объема:
$V = A \cdot h$
Пирамида
Пирамида — это фигура с многоугольным основанием (треугольник, квадрат, прямоугольник), соединенным с одной точкой, называемой вершиной.
Площадь боковой поверхности = $\pi\cdot r \cdot l$
Полная площадь поверхности прямого круглого конуса равна площади боковой поверхности + площади основания.Общая площадь поверхности = $\pi\cdot r(r + l)$
Сфера
Сфера — это поверхность полностью круглого шара.
Каждая сфера имеет центральную точку, называемую «центром» сферы.
Радиус — это длина от центра до любой точки на поверхности сферы.
Объем сферы радиусом r:
92 \cdot ч$
Площадь криволинейной поверхности цилиндра:
Площадь изогнутой (боковой) поверхности = $2\cdot\pi\cdot r \cdot h$
Общая площадь поверхности = площадь изогнутой (боковой) поверхности + площадь двух круглых концов:
Общая площадь поверхности = $2\cdot\pi\cdot r(h + r)$
Викторина: Объем и площадь поверхности
Вот все, что вам нужно знать о прямоугольном параллелепипеде
Как называются коробки для обуви, книги и кирпичи? Это прямоугольник или параллелограмм? Это прямоугольный параллелепипед.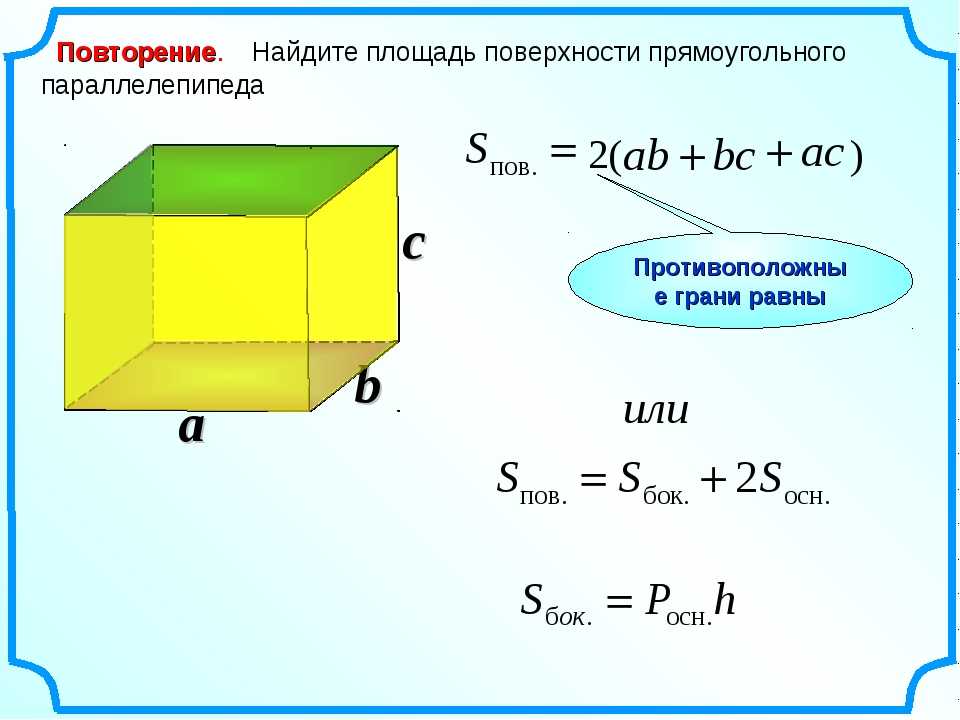
Разберемся, что такое параллелепипед. Параллелепипед — это трехмерная фигура, состоящая из шести параллелограммов. Прямоугольный параллелепипед – это вид параллелепипеда, составленный из параллелограммов прямоугольной формы. Все противоположные грани прямоугольного параллелепипеда равны и параллельны, а параллельные ребра имеют одинаковую длину. В этой статье рассматриваются определение прямоугольного параллелепипеда, характеристики прямоугольного параллелепипеда и формула прямоугольного параллелепипеда.
Параллелепипед состоит из шести параллелограммов. Это трехмерная форма. Слово «параллелепипед» восходит к параллелепипеду , греческому слову, означающему тело, имеющее параллельные тела. Параллелепипед состоит из 6 граней, похожих на параллелограмм, 12 ребер и восьми вершин. Некоторые специальные виды параллелепипедов куб, ромб и прямоугольный параллелепипед.
Что такое прямоугольный параллелепипед? Прямоугольный параллелепипед, более известный как параллелепипед, представляет собой параллелепипед с прямоугольными гранями.
Следовательно, прямоугольный параллелепипед можно определить как трехмерную фигуру, состоящую из шести параллелограммов прямоугольной формы. Следовательно, он состоит из шести граней, в которых все противоположные грани параллельны и равны. Это также шестигранник, многогранник, состоящий из шести граней. Некоторыми распространенными примерами прямоугольного параллелепипеда являются обувная коробка, кирпичи, книги, картонные коробки и т. д.
Прямоугольный параллелепипед имеет следующие характеристики: –
- Прямоугольный параллелепипед представляет собой трехмерную форму.
- Состоит из шести параллелограммов прямоугольной формы.
- Он также известен как прямоугольный параллелепипед.
- Все противоположные грани равны и параллельны.
- Параллельные ребра имеют одинаковую длину.
- Диагональ, проходящая вдоль каждой грани, называется диагональю грани.
- Три грани прямоугольного параллелепипеда видны одновременно.
- Шестигранник означает многогранник, состоящий из шести граней.
Прямоугольный параллелепипед — трехмерная фигура. Три измерения — это длина, высота и ширина, далее обозначаемые как l, h и b соответственно. Формулы прямоугольного параллелепипеда, которые используются для расчета площади его боковой поверхности, площади поверхности, диагонали и объема, следующие:0006
Рассмотрим коробку из-под обуви. У коробки для обуви есть шесть сторон. Допустим, A и B — две противоположные боковые грани, C и D — две другие противоположные боковые грани, а E и F — верхняя и нижняя грани.
- Общая площадь поверхности или TSA-
Общая площадь поверхности прямоугольного параллелепипеда – это площадь поверхности всех его граней. Это означает, что это общая площадь шести прямоугольных граней.
Таким образом, общая площадь поверхности прямоугольного параллелепипеда = 2 × площадь A + 2 × площадь C + 2 × площадь D.
(Поскольку B, D и F равны A, C и E)
TSA = 2 × площадь параллелограмма + 2 × площадь параллелограмма C + 2 × площадь параллелограмма.
TSA = 2× L × B + 2 × B × H+ 2 × H × L.
TSA = 2( LB + BH + HL).
- Площадь боковой поверхности или LSA-
Площадь боковой поверхности прямоугольного параллелепипеда означает площадь всех сторон прямоугольного параллелепипеда. Это произведение высоты и периметра основания.
Площадь боковой поверхности прямоугольного параллелепипеда = периметр основания × высота.
(Основой прямоугольного параллелепипеда является прямоугольник. Следовательно, его периметр будет равен периметру прямоугольника)
LSA = 2 (длина + ширина) × высота.
LSA = 2 (lh+bh).
Кроме того, общую площадь поверхности можно рассчитать как
TSA = LSA + 2LW.
- Объем или V-
Объем прямоугольного параллелепипеда относится к пространству, занимаемому прямоугольным параллелепипедом.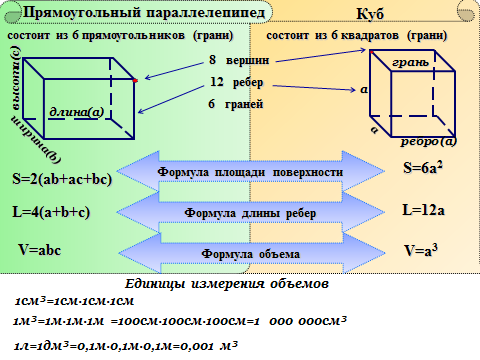
Это произведение площади грани на высоту прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда = площадь основания × высота.
(Так как основание прямоугольного параллелепипеда — прямоугольник. Следовательно, его объем будет равен объему прямоугольника)
V = L×b×h.
V = LBH
- Формула диагонали –
Диагональ прямоугольного параллелепипеда может быть определена как прямая, соединяющая два противоположных угла прямоугольного параллелепипеда своей вершиной.
Длина диагонали прямоугольного параллелепипеда = √ l2 + b2 + h3
Заключение Определение прямоугольного параллелепипеда — это трехмерная фигура, состоящая из шести параллелограммов прямоугольной формы. Это особый вид параллелепипеда, в котором все параллелограммы прямоугольной формы. Он широко известен как кубоид. Это многогранник с шестью прямоугольными гранями, известный как шестигранник.