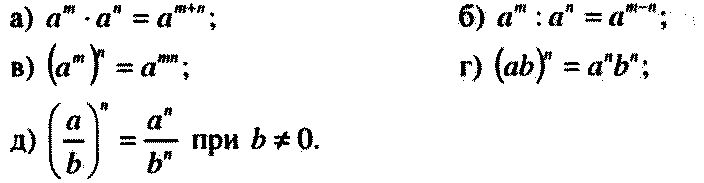Порядок выполнения действий в формулах Excel
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
-
Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула в Excel всегда начинается со знака равно (=). Excel интерпретирует символы после знака равно как формулу. После знака равно вычисляются элементы (операнды), например константы или ссылки на ячейки. Они разделены операторами вычислений. Excel вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

-
Приоритет операторов в формулах Excel
Если в одной формуле используется несколько операторов, Microsoft Excel выполняет операции в порядке, указанном в приведенной ниже таблице. Если формула содержит операторы с одинаковым приоритетом ( например, если формула содержит операторы умножения и деления), Excel оценивает операторы слева направо.
Оператор
Описание
: (двоеточие)
(один пробел)
, (запятая)
Операторы ссылок
–
Знак «минус»
%
Процент
^
Возведение в степень
* и /
Умножение и деление
+ и —
Сложение и вычитание
&
Объединение двух текстовых строк в одну
=
< >
<=
>=
<>Операторы сравнения
org/ListItem»>
Использование скобок в Excel формулах
Чтобы изменить порядок выполнения формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, результатом приведенной ниже формулы будет число 11, поскольку в Microsoft Excel умножение выполняется раньше сложения. В данной формуле число 2 умножается на 3, а затем к результату добавляется число 5.
=5+2*3
Если же с помощью скобок изменить синтаксис, Microsoft Excel сложит 5 и 2, а затем умножит результат на 3; результатом этих действий будет число 21.
=(5+2)*3
В приведенном ниже примере скобки, в которые заключена первая часть формулы, задают следующий порядок вычислений: определяется значение B4+25, после чего полученный результат делится на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Значение символа | Пример |
|---|---|---|---|
| + | плюс | дополнение | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 |
| × | знак умножения | умножение | 2 /3 × 5/6 |
| : | знак деления | деление | 1/2 : 3 |
| / | деление косая черта | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
другие математические задачи »
Видео: Решение простых уравнений с помощью Неизвестно в показателеСтенограмма видео Это вопросы типа экспоненты семейства, которые требуют от вас вспомнить и применить правила экспоненты. 𝑥 в 𝑎 умножить 𝑥 на 𝑏 равно 𝑥 на 𝑎 плюс 𝑏; это правило сложения. 𝑥 на 𝑎 разделить на 𝑥 на 𝑏 равно 𝑥 на 𝑎 минус 𝑏; это правило вычитания. Теперь у нас есть другие видеоролики, в которых более подробно рассказывается об этих правилах, если вы в них не уверены. Но в этом видео мы собираемся использовать эти правила в сочетании с нашими знаниями о различных степенях двойки, тройки, пятерки и десятки для решения некоторых задач. Итак, первый вопрос: найдите значение 𝑥, если два в степени 𝑥 равно восьми в степени 𝑥 плюс три. Ну, на первый взгляд это выглядит сложно. Но, надеюсь, мы сможем вспомнить, что дважды два раза два, два в кубе, равно восьми. Так что я могу повторно выразить восемь как степень двойки. Итак, переписав это уравнение с двумя в кубе вместо восьми, мы получили два в степени 𝑥 равно двум в кубе все в степени 𝑥 плюс три. Теперь у нас есть нечто в степени чего-то в степени чего-то еще, поэтому мы можем использовать правило умножения. Таким образом, два в степени трех, все в степени 𝑥 плюс три просто означает, что два в степени три, умноженные на 𝑥 плюс три, в скобках. Теперь я могу использовать распределительный закон, чтобы перемножить скобки так, чтобы я знал, что 𝑥 равно трем 𝑥 плюс девять. Теперь, если я уберу 𝑥 из обеих частей моего уравнения, у меня будут все 𝑥 с одной стороны. Итак, в левой части 𝑥 убери 𝑥 ничего. А в правой части три 𝑥 отнять 𝑥 будет два 𝑥, а у меня еще останется плюс девять. Так что теперь я пытаюсь получить 𝑥 самостоятельно; уберите девять с обеих сторон. И в левой части ноль за вычетом девяти будет минус девять. А справа у меня есть два 𝑥 плюс девять минус девять, так что эти два сокращаются, поэтому у меня только два 𝑥. Теперь мы все еще хотим знать, что такое единица 𝑥, поэтому мне нужно разделить обе части на два. А два разделить на два — это всего лишь один, поэтому один 𝑥 равен минус девять больше двух. Итак, при решении этого уравнения было несколько ключевых приемов. Во-первых, мы должны были знать, что восемь — это то же самое, что два в кубе, поэтому вам нужно знать свои показатели степени простых чисел, таких как два, три, четыре, пять, десять, те немногие. А затем нам нужно было знать правило умножения, поэтому нам нужно было знать, что два в степени трех все в степени 𝑥 плюс три равно двум в степени трех лотов или трижды 𝑥 плюс три. Затем мы заметили, что это два в степени 𝑥 и два в степени, умноженной на три 𝑥 плюс три, поэтому эти два показателя степени должны быть равны. Остальное было просто, решение линейной алгебры. И мы пришли к нашему окончательному ответу, 𝑥 минус четыре с половиной. Следующий вопрос, решите для 𝑥: девять в степени 𝑥 плюс пять равно двадцати семи в степени 𝑥 минус один. Итак, девять и двадцать семь кратны трем, поэтому трижды три дают нам девять, а трижды трижды три дают двадцать семь. Итак, первая строка равна трем в квадрате в степени 𝑥 плюс пять равно трем в кубе в степени 𝑥 минус один. А теперь снова воспользуемся правилом умножения. Таким образом, мы можем переписать это как три в степени умноженной на два 𝑥 плюс пять равно трем в степени умноженной на три 𝑥 минус один. Итак, теперь у нас есть то же самое основание для наших показателей, три в степени чего-то равно трем в степени чего-то. Теперь, если это так, эти вещи должны быть равны, поэтому два раза 𝑥 плюс пять должны равняться трем умноженным на 𝑥 минус один. И теперь мы можем использовать распределительный закон умножения, чтобы умножить скобки. И мы видим, что два 𝑥 плюс десять равно трем 𝑥 минус пять. Теперь у меня две 𝑥 слева и три 𝑥 справа. Если я уберу две 𝑥 с обеих сторон, у меня все еще будет положительное число 𝑥 с правой стороны, а у меня не будет ни одной 𝑥 с левой стороны. Итак, в левой части у меня есть два 𝑥 плюс десять, уберите два 𝑥, так что два 𝑥 сократятся, и у меня останется только десять. А в правой части у меня три 𝑥 убери два 𝑥 всего один 𝑥 и тогда у меня все еще есть минус три. Итак, теперь я могу добавить три к обеим частям уравнения, что даст мне тринадцать в левой части. А справа у меня три минус три, и у меня есть 𝑥, так что у меня останется 𝑥. Итак, мой ответ: 𝑥 равно тринадцати. Итак, снова в этом вопросе мы должны были подумать об основаниях наших показателей. И в первом случае мы смогли определить, что это три в квадрате. А во втором случае было три в кубе. Таким образом, если мы сможем использовать правило умножения для получения одинаковых оснований в каждом случае, мы сможем просто сравнить показатели напрямую, и это превратит его в часть простой линейной алгебры. Теперь для числа три найдите значение 𝑥, если единица больше ста двадцати пяти в степени 𝑥 равна пяти в степени двойки 𝑥 минус три. Итак, наша первая подсказка здесь заключается в том, что сто двадцать пять — это просто пять в кубе, поэтому я собираюсь повторно выразить сто двадцать пять как пять в кубе. А теперь я воспользуюсь тем фактом, что я знаю об отрицательных показателях, так что пять в отрицательной степени три 𝑥 будет таким же, как один больше пяти в тройке 𝑥, поэтому я собираюсь переформулировать это слева- сторона руки. Так что вместо того, чтобы писать как один на пять в степени три 𝑥, я буду писать как пять в степени минус три 𝑥, так что мы действительно проверяем здесь ваше знание показателей степени. А это равно пяти в степени двойки 𝑥 минус три. Итак, мы пришли к ситуации, когда у нас есть одно и то же основание, пять в каждом случае, и пять в степени минус три 𝑥 равно пяти в степени двойки 𝑥 плюс два 𝑥 минус три. Таким образом, эти два показателя степени должны быть равны; минус три 𝑥 должен быть равен двум 𝑥 минус три. Теперь нам нужно решить линейную алгебру, поэтому я добавлю три 𝑥 к обеим частям, чтобы получить положительное число 𝑥 с одной стороны уравнения. А у меня еще минус три, так что пять 𝑥 минус три. Итак, теперь, если я добавлю три к обеим частям уравнения, в левой части у меня будет ноль плюс три, что равно трем, а в правой части у меня будет минус три плюс три. Таким образом, эти два сокращаются, что оставляет мне пять 𝑥, поэтому три равно пяти 𝑥. Итак, теперь просто разделите обе части моего уравнения на пять. А справа у меня 𝑥 умножить на пять, разделить на пять, так что эти две пятерки сокращаются, поэтому я только что получил 𝑥. А это равно трем пятым. Поэтому я делаю свой ответ красивым и ясным: 𝑥 равно трем пятым. Таким образом, ключевым шагом к решению этой задачи было определение того факта, что сто двадцать пять — это пять в степени три, чтобы мы могли получить тот же базовый показатель степени, с которым мы работаем. Затем мы используем правило умножения, и нам нужно было немного знать об отрицательных показателях, чтобы получить это в том же формате. Теперь для нашего последнего примера, номер четыре, найдите значение 𝑥, если тысяча в степени двух третей равна сотне в степени два 𝑥 плюс пять. Теперь у нас есть несколько основных подходов, которые мы могли бы использовать здесь. Мы могли бы заметить тот факт, что тысяча — это десять в кубе, а сотня — это десять в квадрате, чтобы мы могли произвести эти замены, а затем использовать наши степенные правила и попытаться приравнять показатели степени, или мы могли бы использовать наше знание показателей степени, чтобы сказать, что это означает, что кубический корень из чего-то возведенного в квадрат, поэтому кубический корень из тысячи равен десяти, а затем возводим его в квадрат, и мы получаем сотню. И тогда мы видим, что у нас будут одинаковые базы с каждой стороны, так что на самом деле я думаю, что это будет более быстрый способ добраться сюда; так я и пойду. Итак, я проверю левую сторону. Итак, мы просто повторно выражаем, что вместо сотни в степени двух третей мы знаем, что это кубический корень из тысячи, а затем все это возводится в квадрат. Итак, кубический корень из тысячи равен десяти, поэтому левая часть равна десяти в квадрате, то есть всего лишь сотне. Итак, у нас есть сотня равна сотне в степени два 𝑥 плюс пять. Ну, сто это то же самое, что сто в степени один. Итак, теперь у меня есть сотня в степени один равна сотне в степени два 𝑥 плюс пять. Итак, у меня есть та же самая база для моих показателей, поэтому я могу приравнять эти показатели. Ну, это просто оставляет меня с одним равным двум 𝑥 плюс пять, так что просто вычтите пять с обеих сторон. А справа у меня пять минус пять — это ничто, так что отрицательное число четыре равно двум 𝑥. Теперь я могу разделить обе части на два, что означает, что двойки будут сокращаться слева и справа, а минус четыре на два будет просто минус два. Последний пример очень похож на предыдущие. |


 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая десятичная дробь представляет долю выстрелов, которые делает Деа?
Какая десятичная дробь представляет долю выстрелов, которые делает Деа?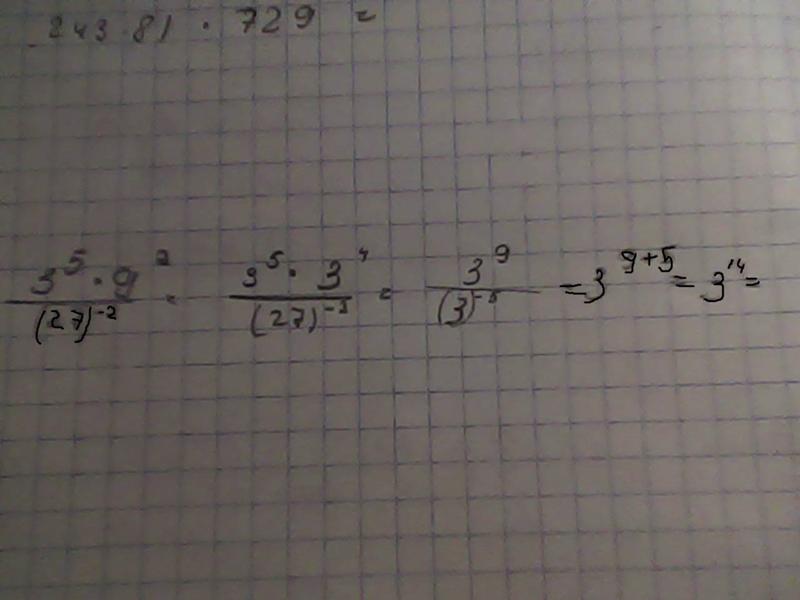 Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения.
И 𝑥 в степени 𝑎 все в степени 𝑏 равно 𝑥 в степени 𝑎 умножить на 𝑏; это правило умножения.

 Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.
Итак, три в кубе — это двадцать семь. Таким образом, мы можем заменить девять и двадцать семь числами, у которых одинаковые основания для их степеней, то есть три в квадрате и три в кубе.