9 в 16 степени: сколько будет 9 в 16 степени

Содержание

Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней

Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!

n	1	2	3	4	5	6	7	8	9	10
1ⁿ	1	1	1	1	1	1	1	1	1	1
2ⁿ	2	4	8	16	32	64	128	256	512	1024
3ⁿ	3	9	27	81	243	729	2187	6561	19683	59049
4ⁿ	4	16	64	256	1024	4096	16384	65536	262144	1048576
5ⁿ	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6ⁿ	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7ⁿ	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8ⁿ	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9ⁿ	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10ⁿ	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

Таблица степеней от 1 до 10

1¹=1

1²=1

1³=1

1⁴=1

1⁵=1

1⁶=1

1⁷=1

1⁸=1

1⁹=1

1¹⁰=1

2¹=2

2²=4

2³=8

2⁴=16

2⁵=32

2⁶=64

2⁷=128

2⁸=256

2⁹=512

2¹⁰=1024

3¹=3

3²=9

3=27

3⁴=81

3⁵=243

3⁶=729

3⁷=2187

3⁸=6561

3⁹=19683

3¹⁰=59049

4¹=4

4²=16

4³=64

4⁴=256

4⁵=1024

4⁶=4096

4⁷=16384

4⁸=65536

4⁹=262144

4¹⁰=1048576

5¹=5

5²=25

5³=125

5⁴=625

5⁵=3125

5⁶=15625

5⁷=78125

5⁸=390625

5⁹=1953125

5¹⁰=9765625

6¹=6

6²=36

6³=216

6⁴=1296

6⁵=7776

6⁶=46656

6⁷=279936

6⁸=1679616

6⁹=10077696

6¹⁰=60466176

7¹=7

7²=49

7³=343

7⁴=2401

7⁵=16807

7⁶=117649

7⁷=823543

7⁸=5764801

7⁹=40353607

7¹⁰=282475249

8¹=8

8²=64

8³=512

8⁴=4096

8⁵=32768

8⁶=262144

8⁷=2097152

8⁸=16777216

8⁹=134217728

8¹⁰=1073741824

9¹=9

9²=81

9³=729

9⁴=6561

9⁵=59049

9⁶=531441

9⁷=4782969

9⁸=43046721

9⁹=387420489

9¹⁰=3486784401

10¹=10

10²=100

10³=1000

10⁴=10000

10⁵=100000

10⁶=1000000

10⁷=10000000

10⁸=100000000

10⁹=1000000000

10¹⁰=10000000000

Остались вопросы?

Здесь вы найдете ответы. x=3 log2(3)=x

90 в 10 степени

90 в 10 =34867844009999998976.00000

12 в степени 1/3

Сложная формула но в кратце ответ — 6

Слишком сложно?

Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!

1.2. Корень n-й степени

В 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).

Перейдем к изучению корней степени n для произвольного натурального числа n≥2.

Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .

Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.

Корень 3-й степени называется также кубическим.

Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.

Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.

Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается

Например, 1253=5,−1287=−2,07=0.

Стр. 11

Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.

Согласно определению, когда n нечетное, то при любом значении а верно равенство

Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.

Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому

при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.

Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.

Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны.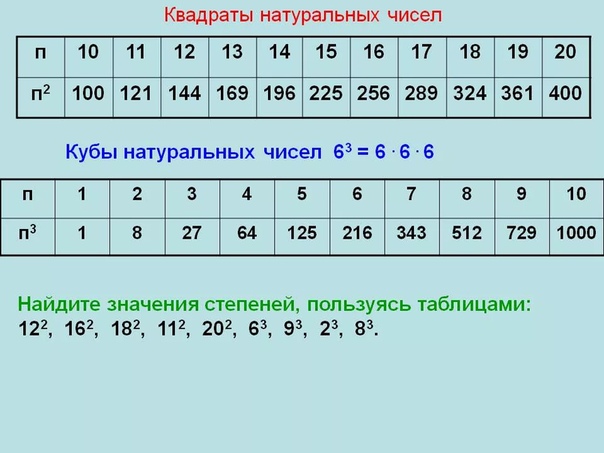 Положительный корень обозначается

Например, 814=3,646=2.

Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда n четное, то при любом положительном значении а верно равенство

Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.

Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то

Стр. 12

не существует корня четной степени из отрицательного числа.

Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .

При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении записи an слово «арифметический» обычно пропускают).

Выражение, стоящее под знаком корня, называется подкоренным выражением.

Извлечь корень n-й степени из числа a — это значит найти значение выражения an.

Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.

Например, не имеют смысла выражения −814 и −646.

Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство

Поэтому равенство (1) является тождеством.

В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так, выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.

Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.

Знак еще называют радикалом.

Стр. 13

Пример 1. Верно ли, что:

а) (−2)44=−2;

б) (−2)77=−2?

Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.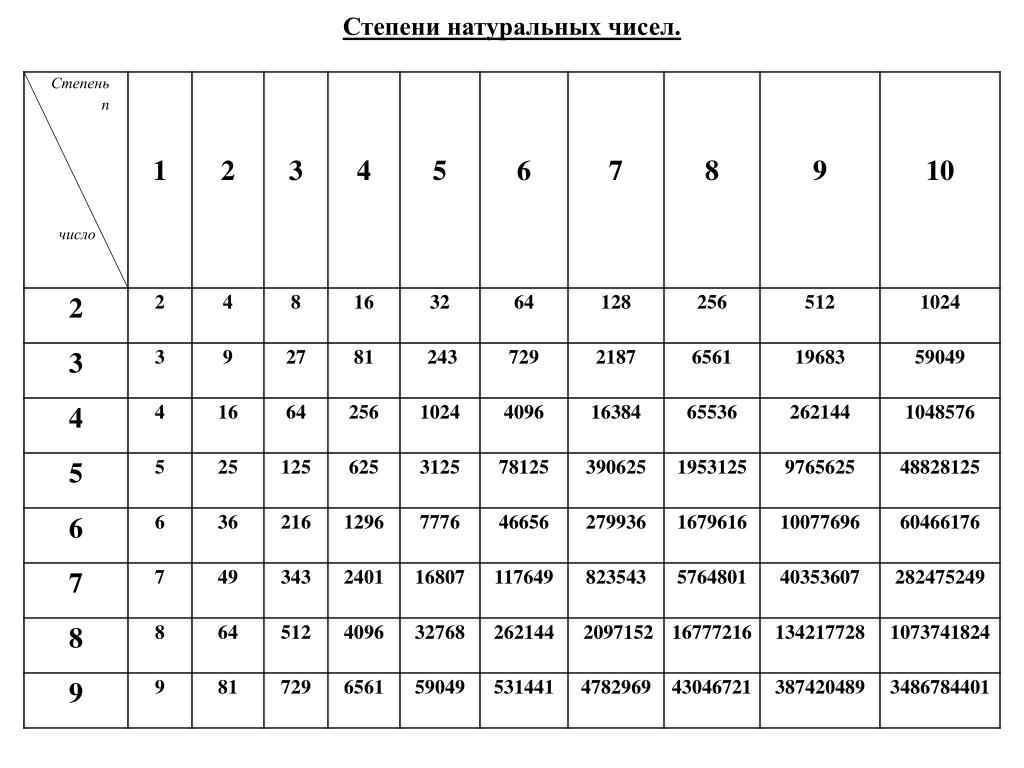

Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.

б) По определению корень n-й степени из числа а (n — нечетное число) является числом, n-я степень которого равна подкоренному выражению а.

Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.

Пример 2. Решить уравнение:

а) x3=7;

б) x4=5.

Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:

б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т. е. x=±54.

Ответ: а) 73; б) ±54.

В тетради решение уравнения б) (аналогично и а)) можно записать так:

Решение: x4=5 ⇔ x=±54.

Ответ: ±54.

Пример 3. Решить уравнение:

а) (x8)8=x;

б) (x13)13=x.

Стр. 14

Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.

б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.

Ответ: а) [0;+∞); б) R.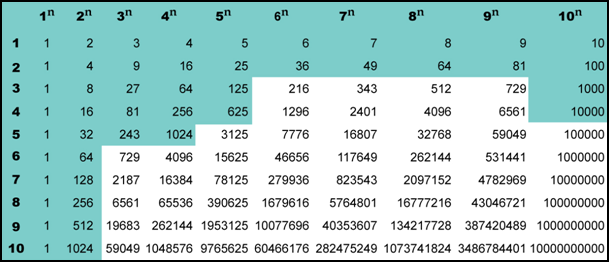

Пример 4. Решить уравнение

Решение. Обозначим x6=t, тогда получим уравнение

Корни этого уравнения

Таким образом, имеем

откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).

Ответ: ±2.

1Какое число называется корнем n-й степени из числа а?

2Сколько существует корней четной степени n из положительного числа а?

3Корень какой степени существует из любого числа а?

4Какой корень n-й степени из числа а называется арифметическим?

5При каких значениях а верно равенство (an)n=a, если:

а) n — нечетное число;

б) n — четное число?

Упражнения

1. 24°

1.24°Используя определение арифметического корня n-й степени, докажите, что:

1) 2564=4;

2) 102410=2;

3) 7296=3;

4) 65618=3;

5) 409612=2;

6) 14 6414=11.

1.24°

Стр. 15

1.25°

1.25°Верно ли, что:

1) число −4 является корнем четвертой степени из числа 256;

2) число −0,3 является корнем четвертой степени из числа −0,0081?

1.25°

1.26°

1.26°Верно ли, что:

1) −17283=−12;

2) −33753=15;

3) −16 8075=7;

4) −77765=−6?

1.26°

1.27°

1.27°Найдите арифметический квадратный корень из числа:

1) 16;

2) 49;

3) 0;

4) 1;

5) 0,81;

6) 0,25;

7) 2,25;

8) 1,21;

9) 36169;

10) 144289;

11) 169100;

12) 81256.

1.27°

1.28°

1.28°Найдите кубический корень из числа:

1) 1;

2) 0;

3) 343;

4) 8;

5) 127;

6) 0,027;

7) 0,001;

8) 64125.

1.28°

1.29°

1.29°Найдите арифметический корень четвертой степени из числа:

1) 0;

2) 1;

3) 16;

4) 0,0016;

5) 1681;

6) 256625;

7) 0,0001;

8) 0,1296.

1.29°

Вычислите (1.30—1.42).

1.30°

1.30°1) 9,16,25,49,81,100;

2) 0,16,0,09,0,01,0,04,0,0025,0,0001;

3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;

4) 164,6254,10 0004,0,00814,0,000000164,24014;

5) 325,10245,2435,0,031255,100 0005,0,000015;

6) 646,7296,15 6256,40966,0,0466566,1 000 0006.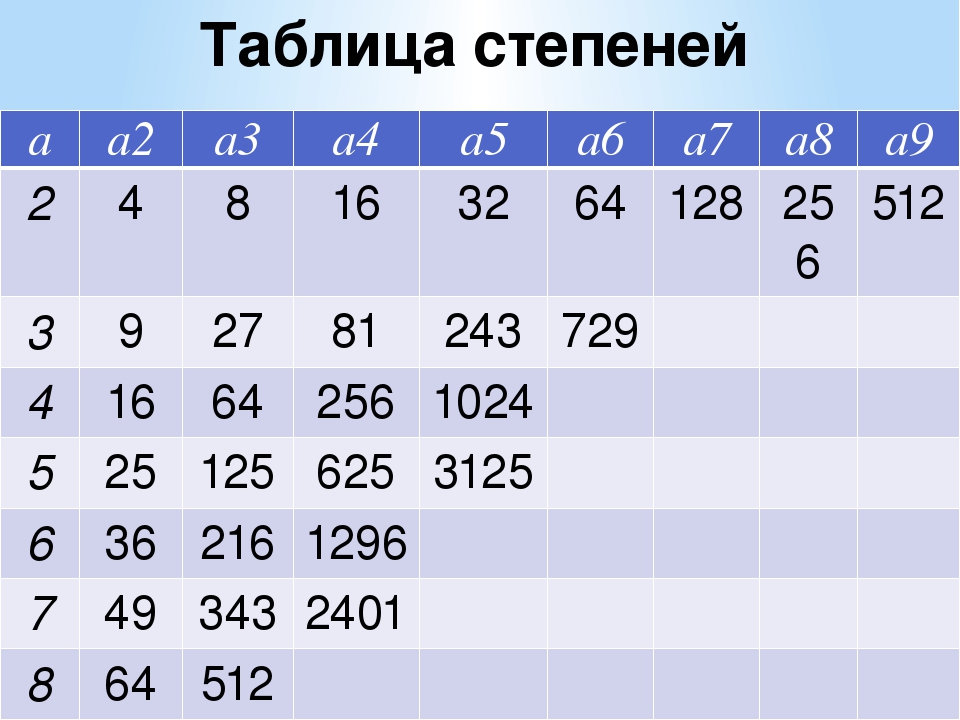

1.30°

1.31°

1.31°1) −10003;

2) −115;

3) −643;

4) −10245;

5) −1273;

6) −3433;

7) −272163;

8) −31255;

9) −0,000325.

1.31°

Стр. 16

1.32

1.321) ⎛⎝−33⎞⎠3;

2) ⎛⎝−145⎞⎠5;

3) ⎛⎝−307⎞⎠7;

4) ⎛⎝−1511⎞⎠11;

5) ⎛⎝−69⎞⎠9;

6) ⎛⎝−9915⎞⎠15.

1.32

1.33

1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;

2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.

1.33

1.34

1.341) ⎛⎝53⎞⎠6;

2) ⎛⎝0,14⎞⎠12;

3) ⎛⎝1125⎞⎠10;

4) ⎛⎝2136⎞⎠18;

5) ⎛⎝567⎞⎠21;

6) ⎛⎝239⎞⎠36.

1.34

1.35

1.351) ⎛⎝35⎞⎠10;

2) ⎛⎝534⎞⎠48;

3) ⎛⎝7610⎞⎠120;

4) ⎛⎝643⎞⎠12;

5) ⎛⎝108⎞⎠16;

6) ⎛⎝1294⎞⎠36.

1.35

1.36°

1.36°1) ⎛⎝10⎞⎠2;

2) ⎛⎝53⎞⎠3;

3) ⎛⎝−124⎞⎠4;

4) −1244;

5) ⎛⎝−35⎞⎠5;

6) ⎛⎝323⎞⎠3;

7) ⎛⎝−444⎞⎠4;

8) ⎛⎝−157⎞⎠7;

9) −5555;

10) ⎛⎝−36⎞⎠6;

11) ⎛⎝−229⎞⎠9;

12) −488.

1.36°

1.37°

1.37°1) 325+−83;

2) 6254−−1253;

3) 12−60,1253;

4) 1+100,00814;

5) 3164−4273;

6) −3383+2,25;

7) 83−643;

8) 164−643.

1. 37°

1.38°

1.38°1) 9+4;

2) 36−164;

3) 0,81+0,0013;

4) 0,0273−0,04;

5) 5−2564;

6) 7+83;

7) −325+164;

8) −273+814.

1.38°

1.39°

1.39°1) (1−2)⎛⎝1+2⎞⎠;

2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;

3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;

4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;

5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;

6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.

1.39°

Стр. 17

1.40

1.401) 1225244⋅15−1382−2323;

2) 58+442−26235;

3) 90+31⎛⎝572−262⎞⎠83;

4) 2364+⎛⎝482−3225⎞⎠−13.

1.40

1.41

1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;

2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;

3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;

4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).

1.41

1.42

1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;

2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;

3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;

4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.

1.42

Найдите естественную область определения выражения (1.43—1.44).

1.43

1.431) x+4;

2) −9+2×4;

3) 5×2−6×10;

4) 8x−4×212;

5) x+33;

6) x−75;

7) x2−47;

8) 2×2−329.

1.43

1.44

1.441) 34x−112;

2) −48x−314;

3) 2−59−5×8;

4) 3−1016−7×6;

5) 2+x4−2(8−6x)3;

6) 12−6×2−7x+(3x−1)·25;

7) −x22(x−2)−5⎛⎝1−3x)−24;

8) 3(x+4)−6(2−x)+9×428.

1.44

Стр. 18

1.45

1.45Найдите длину ребра куба, если его объем равен:

1) 27 см³;

2) 64 мм³;

3) 0,125 дм³;

4) 0,216 м³.

1.45

Решите уравнение (1.46—1.54).

1.46°

1.46°1) x2=0,49;

2) x2=121;

3) x3=0,008;

4) x3=1000;

5) x3=−64 000;

6) x3=216;

7) x4=0,0625;

8) x4=−16.

1.46°

1.47

1.471) x3=−27;

2) x5=−132;

3) x7=−1;

4) x9=−512;

5) x3=−0,027;

6) x11=0.

1.47

1.48°

1.48°1) x2=11;

2) x4=19;

3) x8=27;

4) x3=25;

5) x7=38;

6) x9=−2;

7) x15=−6;

8) x17=4;

9) x13=−13.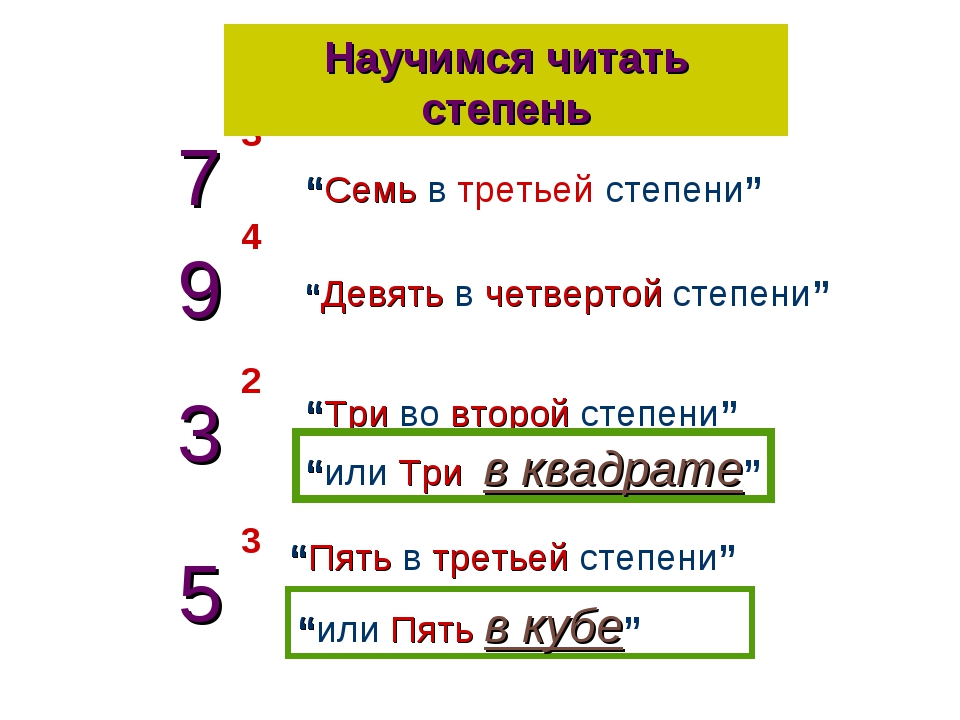

1.48°

1.49

1.491) x2=25 600;

2) x2=0,0196;

3) x2+1=1,0016;

4) 5×2−20=0;

5) x2+25=0;

6) x2+179=0;

7) x2·4=0;

8) −6×2=0;

9) 113×2−12=0;

10) 13×2−1=0.

1.49

1.50

1.501) 4×3+4125=0;

2) 8×3+27=0;

3) −0,1×4=−0,00001;

4) 16×4−81=0;

5) 12×5+16=0;

6) 132×6−2=0.

1.50

1.51

1.511) x4+2=7;

2) x5−3=30;

3) x6−7=19;

4) x3+5=5.

1.51

1.52

1.521) (x+1)4=16;

2) (x−2)6=64;

3) (2x+1)3=27;

4) (3x−1)5=32.

1.52

1. 53

1.531) x10−31×5−32=0;

2) x8−15×4−16=0;

3) x4−12×2+27=0;

4) x6−7×3−8=0;

5) x8−82×4+81=0;

6) x4+2×2−15=0.

1.53

Стр. 19

1.54

1.541)° (x6)6=x;

2)° (x10)10=x;

3)° (x3)3=x;

4)° (x5)5=x;

5) ⎛⎝x−14⎞⎠4=x−1;

6) ⎛⎝x+212⎞⎠12=x+2;

7) ⎛⎝1×7⎞⎠7=1x;

8) ⎛⎝1x−211⎞⎠11=1x−2.

1.54

Квадратный корень

Предварительные навыки

Основные сведения

Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.

Найдём площадь квадрата, длина стороны которого 3 см

S = 3² = 9 см²

Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.

Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.

Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.

Введём для работы с корнями новые обозначения.

Символ кóрня выглядит как . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня .

Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)

Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)

Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.

Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:

Значит квадрат площадью 9 см² имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.

Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9

Получается, что выражение имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.

Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.

Например, извлечём квадратный корень из числа 4

Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4

Поэтому ответ к выражению вида записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.

Запишем ответ к выражению с плюсом и минусом:

Определения

Дадим определение квадратному корню.

Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.

То есть число b должно быть таким, чтобы выполнялось равенство b²= a. Число b (оно же корень) обозначается через радикал так, что . На практике левая и правая часть поменяны местами и мы видим привычное выражение

Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16

4² = 16

Корень 4 можно обозначить через радикал так, что .

Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16

(−4)² = 16

Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.

Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b²= a.

В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.

В разговорном языке можно использовать сокращение. К примеру, выражение полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».

Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.

Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.

Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи можно использовать запись. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.

Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:

Это по причине того, что единица во второй степени равна единице:

1² = 1

и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:

Квадратный корень из нуля равен нулю. То есть справедливо равенство , поскольку 0²= 0.

Выражение вида смысла не имеет. Например, не имеет смысла выражение , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.

Если выражение вида возвести во вторую степень, то есть если записать , то это выражение будет равно подкореннóму выражению a

Например, выражение равно 4

Это потому что выражение равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.

Еще примеры:

Корень из квадрата числá равен модулю этого числá:

Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5

Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5

Действительно, если не пользуясь правилом , вычислять выражение обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5

Не следует путать правило с правилом . Правило верно при любом a, тогда как правило верно в том случае, если выражение имеет смысл.

В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:

Примеры: √4, √9, √16.

Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.

Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.

49 < 64

Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,

√49 < √64

Отсюда:

7 < 8

Примеры извлечения квадратных корней

Рассмотрим несколько простых примеров на извлечение квадратных корней.

Пример 1. Извлечь квадратный корень √36

Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 6²= 36

√36 = 6

Пример 2. Извлечь квадратный корень √49

Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 7²= 49

√49 = 7

В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:

7 × 7 = 49

Но 7 × 7 это 7²

7²= 49

Отсюда, √49 = 7.

Пример 3. Извлечь квадратный корень √100

Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 10² = 100

√100 = 10

Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.

Пример 3. Извлечь квадратный корень √256

Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.

Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.

Видим, что это число 16. Значит √256 = 16.

Пример 4. Найти значение выражения 2√16

В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2

Пример 7. Решить уравнение

В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.

Значение переменной x равно 16, поскольку . Значит корень уравнения равен 16.

Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом .

Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.

Из определения мы знаем, что квадратный корень равен числу b, при котором выполняется равенство b²= a.

Применим равенство b²= a к нашему примеру . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем , а именно переменная x

В выражении 4²= x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.

Пример 8. Решить уравнение

Перенесем −8 в правую часть, изменив знак:

Возведем правую часть во вторую степень и приравняем её к переменной x

Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения равен 64

Пример 9. Решить уравнение

Воспользуемся определением квадратного корня:

Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x

В выражении 7² = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:

Корень уравнения равен . Выполним проверку, подставив его в исходное уравнение:

Пример 10. Найти значение выражения

В этом выражении число 2 умножается на квадратный корень из числа 49.

Сначала нужно извлечь квадратный корень и перемножить его с числом 2

Приближённое значение квадратного корня

Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.

Например, извлечь квадратный корень можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 8²= 64. То есть

А извлечь квадратный корень нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.

Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.

Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.

Найдём значение корня приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня будет представлять собой десятичную дробь, у которой после запятой одна цифра.

Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:

√1 = 1

Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2

√4 = 2

√1 меньше, чем √4

√1 < √4

А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:

√1 < √3 < √4

Точные значения корней √1 и √4 известны. Это числа 1 и 2

1 < √3 < 2

Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.

Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1

1,1² = 1,21

Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.

Проверим тогда дробь 1,8

1,8² = 3,24

Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.

Проверим тогда дробь 1,7

1,7² = 2,89

Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈

√3 ≈ 1,7

Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.

В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.

Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8

1,7 < √3 < 1,8

Проверим дробь 1,74

1,74² = 3,0276

Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.

Проверим тогда дробь 1,73

1,73² = 2,9929

Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.

Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:

√3 = 1,732 (вычислено с точностью до тысячных)

√3 = 1,7320 (вычислено с точностью до десятитысячных)

√3 = 1,73205 (вычислено с точностью до ста тысячных).

Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:

√3 ≈ 1

Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.

В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.

Приближенное значение квадратного корня с недостатком или избытком

Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.

В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.

С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.

Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:

√3 ≈ 1

Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.

Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2

√3 ≈ 2

Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:

√3 ≈ 2 (с избытком)

Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.

Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.

Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:

√5 ≈ 2,23

Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1

√51 ≈ 7

Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1

√51 ≈ 7,1

Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01

√51 ≈ 7,14

Границы, в пределах которых располагаются корни

Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].

Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 8²= 64. Значит квадратный корень из числа 64 есть 8

Пример 2. Извлечь квадратный корень из числа 49

Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 7²= 49

√49 = 7

Пример 2. Извлечь квадратный корень из числа 1

Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 1²= 1

√1 = 1

Пример 3. Извлечь квадратный корень из числа 100

Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 10²= 100

√100 = 10

Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].

Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:

√37 ≈ 6,08

Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.

Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:

1² = 1
2² = 4
3²= 9
4²= 16
5²= 25
6²= 36
7²= 49
8²= 64
9²= 81
10²= 100

И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.

Например, 6²= 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600

60²= 3600

А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:

600² = 360000

Тогда можно сделать следующий вывод:

Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.

Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3

Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3

Пример 2. Извлечём квадратный корень из числа 90000

Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:

Пример 3. Извлечем квадратный корень из числа 36000000

Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:

Пример 4. Извлечем квадратный корень из числа 2500

Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:

Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.

Например, . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:

И наоборот, если в равенстве уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:

Пример 2. Увеличим в равенстве подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз

Пример 3. Уменьшим в равенстве подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз

Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.

Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.

Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:

Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:

Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.

В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.

Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, .

Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.

Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.

Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:

Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз

Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.

Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225

Теперь в равенстве уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз

Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].

В этом случае применяется таблица квадратов:

Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576

Видим, что это число 24. Значит .

Пример 2. Извлечь квадратный корень из числа 432.

Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.

Извлечем квадратный корень из числа 432 с точностью до десятых.

В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.

Проверим, например, число 20,8. Для этого возведём его в квадрат:

20,8² = 432,64

Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7

20,7²= 428,49

Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.

Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.

Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900

3600 < 4225 < 4900

Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:

Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)

Корень 64 не годится. Проверим корень 65

Получается 4225. Значит 65 является корнем числа 4225

Тождественные преобразования с квадратными корнями

Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.

Квадратный корень из произведения

Квадратный корень из произведения это выражение вида , где a и b некоторые числа.

Например, выражение является квадратным корнем из произведения чисел 4 и 9.

Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение в виде произведения корней . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6

Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36

Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.

Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12

Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.

Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:

В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.

Тогда четыре двойки можно заменить на запись 2²× 2², а две тройки заменить на 3²

В результате будем иметь следующее разложение:

Теперь можно извлекáть квадратный корень из разложения числа 144

Применим правило извлечения квадратного корня из произведения:

Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.

Тогда получится произведение 2 × 2 × 3, которое равно 12

Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.

Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:

затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:

Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:

С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.

Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.

Итак, разложим число 13456 на простые множители:

В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 2². А два числа 29 предстáвим как 29². В результате полýчим следующее разложение числа 13456

Теперь будем извлекать квадратный корень из разложения числа 13456

Итак, если a ≥ 0 и b ≥ 0, то . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

Докажем равенство . Для этого воспользуемся определением квадратного корня.

Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b²= a.

В нашем случае нужно удостовериться, что правая часть равенства при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.

Итак, выпишем правую часть равенства и возведём ее во вторую степень:

Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:

Ранее было сказано, что если выражение вида возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня

Значит равенство справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.

Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:

, при a ≥ 0 и b ≥ 0, c ≥ 0.

Пример 1. Найти значение квадратного корня

Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

Пример 2. Найти значение квадратного корня

Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:

Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100

Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:

Пример 3. Найти значение квадратного корня

Воспользуемся правилом возведения степени в степень. Степень 11⁴ предстáвим как (11²)².

Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:

В нашем случае квадратный корень из числа (11²)² будет равен 11². Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:

Далее возводим число 11 во вторую степень и получаем окончательный ответ:

Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 11⁴ нужно записать в виде произведения 11²× 11². Затем извлечь квадратный корень из этого произведения:

Пример 4. Найти значение квадратного корня

Перепишем степень 3⁴ в виде (3²)², а степень 5⁶ в виде (5³)²

Далее используем правило извлечения квадратного кóрня из произведения:

Далее используем правило извлечения квадратного кóрня из квадрата числа:

Вычислим произведение получившихся степеней и полýчим окончательный ответ:

Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения

Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:

Пример 6. Найти значение квадратного корня

Пример 7. Найти значение квадратного корня

Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.

Например, произведение 8 × 4 равно 32

8 × 4 = 32

Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.

(8 × 2) × (4 : 2) = 32

Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.

Например, извлечём квадратный корень из произведения . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.

Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.

Запишем полное решение данного примера:

Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:

Пример 9. Найти значение квадратного корня

Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:

Если в равенстве поменять местами левую и правую часть, то полýчим равенство . Это преобразовáние позволяет упрощáть вычисление некоторых корней.

Например, узнáем чему равно значение выражения .

Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом , то есть заменим выражение из двух корней на выражение с одним корнем, под которым будет произведение из чисел 10 и 40

Теперь найдём значение произведения, находящегося под корнем:

А квадратный корень из числа 400 извлекается. Он равен 20

Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.

Например, найдём значение выражения .

Воспользуемся правилом

Сомножитель 32 это 2⁵. Предстáвим этот сомножитель как 2 × 2⁴

Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 2⁴ предстáвим в виде степени с показателем 2

Теперь воспóльзуемся правилом и вычислим окончательный ответ:

Пример 12. Найти значение выражения

Воспользуемся правилом

Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7

Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 2²× 2², а две семёрки как 7²

Теперь воспользуемся правилом и вычислим окончательный ответ:

Квадратный корень из дроби

Квадратный корень вида равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b

Например, квадратный корень из дроби равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9

Вычислим квадратные корни в числителе и знаменателе:

Значит, квадратный корень из дроби равен .

Докáжем, что равенство является верным.

Возведём правую часть во вторую степень. Если в результате полýчим дробь , то это будет означать, что равенство верно:

Пример 1. Извлечь квадратный корень

Воспользуемся правилом извлечения квадратного корня из дроби:

Пример 2. Извлечь квадратный корень

Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:

Пример 3. Извлечь квадратный корень

Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.

Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:

Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:

Пример 4. Найти значение выражения

Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:

Также можно воспользоваться правилом извлечения квадратного корня из дроби:

В данном примере первый способ оказался проще и удобнее.

Пример 5. Найти значение выражения

Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4

Пример 6. Найти значение выражения

Сначала найдём значение квадратного корня . Он равен 0,6 поскольку 0,6²= 0,36

Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:

Вынесение множителя из-под знака корня

В некоторых задачах может быть полезным вынесение множителя из-под знака корня.

Рассмотрим квадратный корень из произведения . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:

В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение оставим без изменений:

Это и есть вынесение множителя из-под знака корня.

На практике подкореннóе выражение чаще всего требуется разложить на множители.

Пример 2. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:

Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:

Пример 3. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:

Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:

Пример 4. Вынести множитель из-под знака корня в выражении

Воспользуемся правилом извлечения квадратного корня из произведения:

Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:

Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:

Пример 5. Вынести множитель из-под знака корня в выражении

Разлóжим подкореннóе выражение на множители 4 и 3

Воспользуемся правилом извлечения квадратного корня из произведения:

Извлечём корень из числа 4, а выражение √3 остáвим без изменений:

Пример 6. Упростить выражение

Предстáвим второе слагаемое в виде . А третье слагаемое предстáвим в виде

Теперь в выражениях и вынесем множитель из-под знака корня:

Во втором слагаемом перемнóжим числа −4 и 4. Остальное перепишем без изменений:

Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:

Вычислим содержимое скобок, полýчим −1

Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3

Внесение множителя под знак корня

Рассмотрим следующее выражение:

В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.

Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.

Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15

Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.

Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:

Итак, если данó выражение , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:

Пример 1. Внести множитель под знак корня в выражении

Возведём число 7 во вторую степень и внесём его под знак корня:

Пример 2. Внести множитель под знак корня в выражении

Возведём число 10 во вторую степень и внесем его под знак корня:

Пример 3. Внести множитель под знак корня в выражении

Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида не имеет смысла.

Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.

Пример 4. Внести множитель по знак корня в выражении

В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:

Пример 5. Выполнить возведéние в степень в следующем выражении:

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)² = a²+ 2ab + b²

Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:

Теперь необходимо упростить получившееся выражение.

Для выражений и применим правило . Ранее мы говорили, что если выражение вида возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.

А в выражении для множителей и применим правило . То есть заменим произведение корней на один общий корень:

Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом вычислить произведение, которое под кóрнем:

Задания для самостоятельного решения

Задание 1. Найдите значение квадратного корня:

Решение:

Задание 2. Найдите значение квадратного корня:

Решение:

Задание 3. Найдите значение квадратного корня:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение квадратного корня:

Решение:

Задание 6. Найдите значение квадратного корня:

Решение:

Задание 7. Найдите значение квадратного корня:

Решение:

Задание 8. Найдите значения следующих выражений:

Решение:

Задание 9. Извлеките квадратный корень из числа 4624

Решение:

Задание 10. Извлеките квадратный корень из числа 11025

Решение:

Задание 11. Найдите значение квадратного корня:

Решение:

Задание 12. Найдите значение квадратного корня:

Решение:

Задание 13. Найдите значение квадратного корня:

Решение:

Задание 14. Найдите значение квадратного корня:

Решение:

Задание 15. Найдите значение квадратного корня:

Решение:

Задание 16. Найдите значение выражения:

Решение:

Задание 17. Найдите значение выражения:

Решение:

Задание 18. Найдите значение выражения:

Решение:

Задание 19. Найдите значение выражения:

Решение:

Задание 20. Найдите значение выражения:

Решение:

Задание 21. Найдите значение выражения:

Решение:

Задание 22. Найдите значение выражения:

Решение:

Задание 23. Найдите значение выражения:

Решение:

Задание 24. Найдите значение выражения:

Решение:

Задание 25. Найдите значение выражения:

Решение:

Задание 26. Найдите значение выражения:

Решение:

Задание 27. Найдите значение выражения:

Решение:

Задание 28. Найдите значение выражения:

Решение:

Задание 29. Найдите значение выражения:

Решение:

Задание 30. Найдите значение выражения:

Решение:

Задание 31. Найдите значение выражения:

Решение:

Задание 32. Найдите значение выражения:

Решение:

Задание 33. Найдите значение выражения:

Решение:

Задание 34. Вынести множитель из-под знака корня:

Решение:

Задание 35. Вынести множитель из-под знака корня:

Решение:

Задание 36. Вынести множитель из-под знака корня:

Решение:

Задание 37. Вынести множитель из-под знака корня:

Решение:

Задание 38. Вынести множитель из-под знака корня:

Решение:

Задание 39. Вынести множитель из-под знака корня:

Решение:

Задание 40. Вынести множитель из-под знака корня:

Решение:

Задание 41. Вынести множитель из-под знака корня:

Решение:

Задание 42. Вынести множитель из-под знака корня:

Решение:

Задание 43. Вынести множитель из-под знака корня:

Решение:

Задание 44. Вынести множитель из-под знака корня в следующих выражениях:

Решение:

Задание 45. Внести множитель под знак корня:

Решение:

Задание 46. Внести множитель под знак корня:

Решение:

Задание 47. Внести множитель под знак корня:

Решение:

Задание 48. Внести множитель под знак корня:

Решение:

Задание 49. Внести множитель под знак корня:

Решение:

Задание 50. Внести множитель под знак корня в следующих выражениях:

Решение:

Задание 51. Упростить выражение:

Решение:

Задание 52. Упростить выражение:

Решение:

Задание 53. Упростить выражение:

Решение:

Задание 54. Упростить выражение:

Решение:

Задание 55. Упростить выражение:

Решение:

Задание 56. Упростить выражение:

Решение:

Задание 57. Упростить выражение:

Решение:

Задание 58. Упростить выражение:

Решение:

Задание 59. Упростить выражение:

Решение:

Задание 60. Упростить выражение:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Untitled-1

%PDF-1.5 % 1 0 obj >/OCGs[8 0 R 878 0 R]>>/Pages 3 0 R/Type/Catalog>> endobj 2 0 obj >stream 2018-02-07T10:13:32+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:13:49+03:002018-02-07T10:13:49+03:00

256176JPEG/9j/4AAQSkZJRgABAgEBLAEsAAD/7QAsUGhvdG9zaG9wIDMuMAA4QklNA+0AAAAAABABLAAAAAEA AQEsAAAAAQAB/+4ADkFkb2JlAGTAAAAAAf/bAIQABgQEBAUEBgUFBgkGBQYJCwgGBggLDAoKCwoK DBAMDAwMDAwQDA4PEA8ODBMTFBQTExwbGxscHx8fHx8fHx8fHwEHBwcNDA0YEBAYGhURFRofHx8f Hx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8f/8AAEQgAsAEAAwER AAIRAQMRAf/EAaIAAAAHAQEBAQEAAAAAAAAAAAQFAwIGAQAHCAkKCwEAAgIDAQEBAQEAAAAAAAAA AQACAwQFBgcICQoLEAACAQMDAgQCBgcDBAIGAnMBAgMRBAAFIRIxQVEGE2EicYEUMpGhBxWxQiPB UtHhMxZi8CRygvElQzRTkqKyY3PCNUQnk6OzNhdUZHTD0uIIJoMJChgZhJRFRqS0VtNVKBry4/PE 1OT0ZXWFlaW1xdXl9WZ2hpamtsbW5vY3R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo+Ck5SVlpeYmZ qbnJ2en5KjpKWmp6ipqqusra6voRAAICAQIDBQUEBQYECAMDbQEAAhEDBCESMUEFURNhIgZxgZEy obHwFMHR4SNCFVJicvEzJDRDghaSUyWiY7LCB3PSNeJEgxdUkwgJChgZJjZFGidkdFU38qOzwygp 0+PzhJSktMTU5PRldYWVpbXF1eX1RlZmdoaWprbG1ub2R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo +DlJWWl5iZmpucnZ6fkqOkpaanqKmqq6ytrq+v/aAAwDAQACEQMRAD8AuyiuZ7qOxspJluZ2CRaf eIZA5P7KP1P0Mc58RvpfueqmBXFIAgfxRNfMfsCYyflV5gvXKzeXri0l/wB/27J6Z/2LFT/wuXjF lHIJj2n4Y9OQSHdLn+PilN7+TPnqIk22nS3C9hx4N+J4/jlsYz6xLm4u2sJ+o8P2ob/lT/5k/wDV jm/4OL/mvJ+HLub/AOVtN/Ph3u/5U/8AmT/1Y5v+Di/5rx8OXcv8rab+ePtd/wAqf/Mn/qxzf8HF /wA14+HLuX+VtN/Ph3u/5U/+ZP8A1Y5v+Di/5rx8OXcv8rab+ePtd/yp/wDMn/qxzf8ABxf814+H LuX+VtN/Ph3o/Qvyp8/2uqQ3FzosyxR8jWsbb8SB9liepyGTFMxoBxdZ2ngniMYyFlOB+XnnY24i fSJifQihfZaEu9bjv2X7+2Ufl59xcA6vFxWJD6pH5D0q3+AvOfr+qdInP76SYg8dyqenCOvQjf27 4Py+Tua/zOOq4h9Ih32Vg/L3zqsQVdLn5rEsSyUFQ0rVuJOvXww/l59zL83iJuxzv5fSF3/Kv/On KselTwmvoxOFU+jAo6oKn4np9Hfpg/Lz7kfmsVbkHqf6UvPyh55qB/LnzWSX/wAOM/E9ZWJnanfm AwB8Pi+7D4GTuLP87Dl4ny+n5fsav/J/mrTbN7y5sJ0gs1EsVxNTkvIgNA7AnkGrQHf8BkZYZAWR QYx1GORqx6tjXLykPx+llP5JGMeaL2JPsJZNJB7RTSRMB9DBgMyND9Z9zi9pX4YJ6nf3i/0U3+d7 KvmOxcyXENLMUmgHNV/ev/eLRqj/AGOHXfWPcnswXAionfkf0H9rEIfJnmPWLKK8TSF1ixnBMN5A BFIQDQ05EDqP5hmPDDM7xBc0amOOVCRxyHQ7j8fBD3n5J+aSvqWljPEx39GUK1PbkhNPxy4QyDnF ycXbkRtOj5j9qVf8qc/MmpC6JKwH7XOIA/8ABODloxy7nNHa+m/n/e7/AJU3+Zf/AFY5P+RkH/VT Hwpdyf5X038/7/1O/wCVN/mX/wBWOT/kZB/1Ux8KXcv8r6b+f9/6nf8AKm/zL/6scn/IyD/qpj4U u5f5X038/wC/9Tv+VN/mX/1Y5P8AkZB/1Ux8KXcv8r6b+f8Af+p3/Km/zL/6scn/ACMg/wCqmPhS 7l/lfTfz/v8A1Mkg/LXzqlhHbnSZgy2voGhTZpWBl3DdgOvftmMcGS7rq6eeuxGZlxD67+XJFf8A KvvOZuPUOlTcDceqR8h3Ei4Rjr/Nvkfy+TuafzWPhriH018zZ+xRH5d+ePQC/oqYSCAR8gU2kmet ww+L9nqPHth/Lz7mZ1eK+Yriv4RHpVG/LvzkzOv6JmSKRhEQCvw20a/Ci/F+2evgDvj+XydzEavG P4hY3/zj1+CnJ+XXnOVUM2iSTFtlgkKiCBR0Xipbk3vSnuMfy+QdCyGsxx5Trzh2S/UHR/l35ziV 2h0SSFk6wxlTBOp6rxYrxb3pT3OP5fIehWWrxyq535n6o/rCT3dnNp17JZ3KFZLN1ieNtz6E54GN vHg4+4ZSQRsW2MuMWP4v91He/iEx8kTgeb9HhF1KK3cVbO7T97s4+w5oWp/ststwD1jbqw1MP3cj wjkfVE7fEf2PUvzA/MLWPL+rw2NpaK0brFIJXV29Tm5VgCopRabjr7jNpqM4x1ZA/V+P7Hn8Gnnk J4Ryh5/h3oHzB+c11oj6ZBNoPrXF/p66hKrXkFsYwzOpX05fjIqg36fFmS0pTD/zkbBOImh0WKRZ 15xU1KAVVVLSE8kUKEEcnxMaEoQDUqCqi7T/AJyD0t70R3ljb2dmskaT3b6lbkpG7hDJ6dAzBAQx A332rjSvSf01by6XJqdk6XNmbNb21lU/DIjozqQfBlApkJyoE9yYizTH5fO+o29ysdxZQ+mFR5DH KxbiyLJ8IZBU8XzDOqkDuA3+CCNiil85TcipsCSpKkhpACQT0rF4DJ/mj3fj5I8HzVrTzY8syrPa GKh5vUmX1XpTsAI996DDHU2dx+Pkg4vNHHzJpPDmHkYEFl4wTGoG23wZZ48fwCw8Mrm8waWrFWaU EHif3E3XwqEw+NH8Ar4ZRYuVdbeSLeOc7Egg8ShYbGhHTvlgNi2BDz7UPzRu4vOUujQw28VtZsyT i4YrLLw3LJXjT2oreJ2IzH7RyT0+OOQASB6fj72/ST00hKOSRhMfT3E7/PlysFZq/wCbV3YahPAL S0aKGRkXnclJWALD7BTY/DQjt92ZEDYB72gph5k1s6r+Vtzq0yRxiZUdljf1ECpcqv2iFrsu+2Y+ s/uz8PvcjSgnIAGFfkbG6eaJ1YUMejQRt/rLKCR+OYuiPrPx/Q7btWQOP35JFX/O+UR+YrFjPLbU tB+9jTnGP3r7SCjbeH68Gu+se5h3ZG4EUJb8jsfgyvyxq93pv5T2+p2qLfXEEcjqI1JV63LAsFU1 oAa7HM3R14Yv8but14IySAFe/wByWaR+bWrTaVq+pXGmCaDTY/VjCsYObNOIhGZZQsY6mg60Hfrj psvHCyQTfT8H9vPZhqMMsc6IrZKf+hjoPgB0WFGdPWAbU7eghAFZWYKVC8mCjff9mtDTIppXN/zk XEVHoaJFM7EcUGp2yko6LIjUZQRyRmahHRcaVm/k38xtJ80WNwbd4Y9UtY2luLCOdbkIn7D+pGAp VsCozWfMWo2V7LBbW0MscP1YO0kjI3K6dkWgVG2BXfMXLnlE0B3fa2wxgjdAxeerpkirp4eV1DFI 5HI+OOOVKERn9mYA++QGrPd+Nv1szhHeqt51ugyEaaSjg8aPISSADtSLwrh/NHu/HyR4I700h8y6 f6SfWPUiuQnKaIQzsFYEK4B9P4grGlcuGeNb8/cWBxlUHmHSz0aWhNAfQm67/wCR7YfHj+AUeGUR aanZ3cjRwMxdBVuUciCm3dlUd8lHIJckGJDHfPnnWTyz5dh2FYkee5IRWk5CKMmMuXag6Dj05D8D l8MZlddAw8SMZDiuieiSP+Z2qQ6Ha3b29i928irdlrn04UDHfiwEikp3+Km32hmu0eqllMoyFGJc vVxwif7mXHD9SM8lfmFqWva02nXVtYxoIWlWWzumuCeDBSKGNAB8Qpvv+vOcV5X5/dW83a2BsRII 6j+aSchR94zQ5/rPvL0mkH7uPx+yO6Rflnr+pXHnXRLO4cTRvdx/Gw+McTXYinh4y/HiAmCO92Xa OhxxwynHYgPqK+0yyvvS+tIX9FucVHdKN4/AVzbPEq0ltbysGkiR2XZWZQSPkTiq1LKyQ1S3jU0p UIo2pSmwxVYul6Yq8VtIVWvLiI0Ar49OuKqrW0DRvG0amN09N0p8JTccaeG+Ai1CidK00kFrWJiG RxVQaNEOKHfuo2GR8OPcy4io/wCHtD58/qMPM1+LgK/Fscj4MO5PiS71kfljy/G7OlhEGY1b4aiv IN0O3UYBggOi+JLvaPlfy6xq2nwH5oDj+Xh4BfEl3pplzBoqrFSRUqar7GhH6jiqQ3/kTyrfawdX ubFWv24erIGZRJ6e6+ooIVqe4yM4iQotc8UZcwuufI/lW5unuprBWnkdpHYPIoLuArHirAbgeGSb En/MTTdN078tdQsoVMFjF6P7sFnJDXSMyVYsx5liKe+2Y+r/ALs/jq5egvxo1z3+7n8ObC/yUZv8 U3wkFJ3s3lnHZC0sQjSviqLv9/fMLQ/Wfc5/aIHhiuV0PPnZ+aXf85C6rfaf5m0p7V+POzPNSAQ1 JWpWvzy3VwEpb9zm9h6aGXFLiHX9D0z8prhrn8vdHndQrSJKzBdhUzv0zJ0wqAh55um7SxiGeUR0 /UySx0qwsbdre2i4wu3NlYs9WNBuXLHsMvcFebCxNa20Rr1+Bd/wxVptO09nR2tYmeP7DFFJX5Gm 2KobVJ9L0bR9Q1KW3C2tnbzXNysCLzaONDI4UDjUkA9+uKsE/wCV6/k1MVmn1Mx3EnotJHJZXhkV 0YmNX4wsOSPXoTvkTAHdlZWj82/yNljZBfwlIizFPqN2tC7DmQvoA9QK0yBxQ7gnil3qL/m3+Qsk YJ1CLgD2s70bseO9Ie9MBwQ7k8cu9DH84vyPkuWRuX1e3AAvvqc/pcaFyQAvq0DfCap19t8Tgh4L xy72QeWPzV/K/UdYtNC8uXfq3+pM5jhjtbiEUjheZnZpo4lpxjptvUjbLIwEeQYyJPNnuSYpfrGg aTrGnHTtRtxPafCRGSQQV2BVhuDTvigi0vi8geUo7SO0FgGt4md41Z5CQ0goTyLcjt0qdu2RjER5 MYY4wFAK2j+TfLWjTrPplkttKqGIMryN8LUJFGYg/ZGSZvC/PTRp5w1h2jPCK7aSUd5J6BYo1r9D fdmjz/WXpNMCccR3xr3R6n9DEPys/wDJh6D/AMxafqOZUPqHvd92p/i8/c+vc2T567FUi85eddC8 n6ZDqetyPFZTXMdr6saGTg0taMwXfioUk0BPtirGR/zkF+UB6eYB14/7y3nX/kTimmH+a/z9tpry C58n+YtOht4hLHNp+rWV+TPIhYBlaCElVK0K1dfenTFaSx/z882JNJC2veU0cBDFystdPMPGswYc Ubbi/fevbFaVJPz/APMBgieHzF5TLEFZS1nrpXnzbjxIi6FKde/LsMVpRuvz382vZPTzN5Ut2mWS OO4js9bLo4Aqyh5XWqBqjkpBPbFaXJ+fnmQGTh5j8sGN3me1+s2WtCT0mmb0q+lEF48CtO9PtVNc VplflH88vL8OkSz+cdfsmu572ZLN9PtL9YfRSKFwvGSh2Kj1a1bqCN+uK0nJ/wCcgPyiDBTr4Bat K2t52of98++K0znTNRstT0201Kxk9ayvoY7m1loy84pVDo3FgrCqsDQiuKETirFfzRdk8iaoyukZ X0T6kv2V/wBIjqx+WY+r/uz+OrlaIXlAon3e5gH5Jcv8SXXEFYTZSMjP/eSkzRcpWHYHt/tZhaH6 z7nYdpfQO+x7hsdkj/5yW/5SPSP+YNv+TpzI1h2fB2ns5/dy/rfoepfk5/5LTQ/+MUn/ACfky/B9 AdF2v/jM/f8AoDM8udc7FXnt9+T3r6jcXlr5x8yafHd3U91PaWt8EhU3DNIyQoI/gCuwpXltt13C m0DrH5OyR2kl/D5r8239/ZQytZ28eqRJK7lfsI7xBVL0A60xW3nSaR+Y8qJDJpfnWAzzRSzXP6Zh mcCHktFb6tGU2lr/ALEbHFKhcw/mNa3jq9h5/mgeGKRRFqvNldlLSjmtoymgKqFABBB3JNFCoyHS /wA0bJUW4tfOt7KZJUleHV4o41TiyKyK8Vw7Vpy3bbY9cKu0jQfPOoaxYvdWPnuGBzH6dxNq9vzt jLUTPWWGPbhQcTxPXxoFVTR9C8/XWqaGNTtPOdvaXkq0vX1tZ2s+QaMySxGwjMZ4SGtSDTbxGKvS f+VOvxI/x15t3Na/pNainh+5xRadeU/IbeXb2a6PmPW9ZE0fp/V9WuxcxJ8QbmiiNOLbU69MUMpx V2KvnLzyzt511X05PUmjuJPTDCkduD9qSTfdv5R4fSc0ef6z73o9MB4QsUCPjLyHl3/2Bh/5Wf8A kw9B/wCYtP1HMqh2D3u/7U/xefufXubJ89dirsVU4be3hMhhiSMyuZJSiheTkAFmp1Y064qxfzl+ XyeZ76zvG17VdKksaejHp06Qx15VZyDGzcyhKV5bDtim0nk/J6T9HXltD5y8wrPd+qzXEl1G/KSR I0RpQscbSBFhVacxUVFRXZW0Lof5M6pZXlu+o+ddV1KzsnjmsbR+AWGWCVXiZfV9dKKimMgIKgnc dMVtcn5MalHch5vP/mVYHPO5Q3gaR3AUAq/Gi7LSnE9vDdW3H8kIJLa3sbnzVrl5pkPqg2c9yvFV aF4ofR9JYhG0PNWWoZar9mm2K2ynyL5Obynpl1p36Vu9WhmunuYJr5zJNGjxonpF60YBkLbBevTu VDI8VdirsVYp+aZC+Q9TYtGvH0Dzm/u1pcRnkfl1HvmPq/7s/jq5ehF5Rz68ufJgH5JUbzPeSgO/ Oyet1L8JkpLF9hP2UHb/ADOYWh+s+52HaW2MDYb8h058z3pJ/wA5Lf8AKR6R/wAwbf8AJ05kaj6v g7P2c/u5f1v0PUvyc/8AJaaH/wAYpP8Ak/Jl+D6A6Ltf/GZ+/wDQGZ5c652KuxVKvMWs3uk2tvNa aXcas806wvb2vh2ERlZjKeVF4qVFasOu29AVUki89a9LzC+TdVVkkMREhtlBoAeQPqkFSD1+jrti qW+YfMfmW+02KaHy/runyW07u8VqbdpZkRGHCiy04ty5ruN1p34kqxy50HzxLG3ozeZ7WSJz8KXM To4Zifh9S5dgBxC/Ex2p7nFDJ9D1vzXocTaZqGk6trj/AF144NRP1dv3DM3F3asPwrQdRX4qDYYp TZvNPmSOnqeV7p+UjRqYJoXAVeNHfmYiA3M0oD9k1ptUKnWiXl/e6VbXd/Z/o+6nX1Hs+ZkMasSU DsUiPPhTkvh5WqKmlSqjsVdirsVfOPntvU85avDU3BFyxFog4iv8077/AA+A8OxzR5/rPvek0wrF E/Tt9R/3o/HwYh+Vn/kw9B/5i0/UcyofUPe77tT/ABefufVMvmvyvDK0MusWMcqO0bxtcwqyuhIZ CC1QylTUZsnz1r/FvlX/AKvNj/0kw/8ANWKu/wAW+Vf+rzY/9JMP/NWKu/xb5V/6vNj/ANJMP/NW KsU1Pzx5ginuDp995altvUZbRbjUDHK4JolQvJfs7tvXwGFWn85eaxCCmo+U2nKVZG1CZUVx2DBG LKfHiKeBxVi2uaXb6nqeoV/w1JbXMssnrTapKgYXCxl3VU9QrJyhSuw7kh5iMUKUPlTTbUG80698 uWWpxejLahNUuTEJ44lqWZfTPD1l6calOtCTirMpfN+uzi5SLVvLtmFlK2srXnrM0XCUB2X4QDz9 I0r05DbY4pVbHzfqz6mBqGreXYNN9V97W8M0phG6cvUMIV26GgIHX2xVkf8Ai3yr/wBXmx/6SYf+ asCu/wAW+Vf+rzY/9JMP/NWKu/xb5V/6vNj/ANJMP/NWKsd/MXW9IvvImrmw1G0nMP1YyskiTrHz uUCFlRu/E8fE5j6sfuz+Orl6EXlGxPPl7iw38kwW8z3kpErcrJ/383wlv3sWyR7cV+gZhaH6z7nP 7S2xgbc+Q+PM9Skf/OS3/KR6R/zBt/ydOZGo+r4O09nP7uX9b9DMvy8TQW8leVW1tLVrNLK+Ia9E fpq/1qOlPV+GtK5kYPoDou1/8Zn7/wBAZL5N8r+WpfKGhyzaRZPLJp9q0jtbxMxZoEJJJXck5a65 Of8ACXlX/qzWP/SND/zTirv8JeVf+rNY/wDSND/zTirv8JeVf+rNY/8ASND/AM04qxzTtHsFinVP J9rcxrd3apNxsxyVbmQCgbcCmFUV+iLP/qSbX7rHFWKWnn38trqOKSHy9Z8ZiQgkhgjaoJBqskas N1PUY0hkOp+XYrzT7i1g8pQWU0yFI7uJbAvGT+0vLao98UsVbyb5kS8jsGiUTTwTSRMtholFWFo1 r8SN8X75evXFDJND8tXFjYiDUvLcGrXIav1uSHTIGI4gU4QqidQT074pSW489flvb31xYz+X7KO7 tZHhnhaK3BV4iVf9jcAjqNsUJ5o8vl7WbVrvTPKFnc26uY2kVbMAOoBI+IA9xilXu9NtojayJ5Tt 7JlvLOl2gtOUf+lR/EOHxfdiryfz2TL5x1eCslwBcvW0jHBd6f30p7eAr07HNFn+s+96TTCscTtH bmd/9KPx7wxf8t9PvrP8xdBW5heL/S0AJHwnY9GGxzIxSBkK73c6/PDJpp8Jv0voPy/qNjLJa2Ud zC97BreqtcWyyKZY1aa+KlkHxCtR1GbR4JmWKuxV2KpF5qa4U6QbdEkl/SMVFkcxr/dyftBZD+GK o719f/5Y7X/pKk/7J8VSnX/NGuaMsDNoUl+s5YE2DTXJj4gGsirb8gDXagOKqWhecdX1m6mtotCu LNoEV2kv0u7WNudNkeW1VWYV3A6Yq1r3l7zFq1zDcx3k+mPFwBSy1F0jdVfkQ8b2jqSwPEnrTCqV 6V5e8xXUAuE1TUB6VzPGwfUw3P6vcPEQwNjTi3p9gNvffFU+8w+Y9a0TTWv5NI+uhXjj+rWMk1xO fUcKWEa2/wBlAS7nsoPywKktv+Zeoz3K26eWdQDGRImdre8CIzkj43+q0AXq3gDvhVlnr6//AMsd r/0lSf8AZPgVgP5g3V1FY+apr0xWXDTtHpJEzXAAN/citGjj37dDmPqheM/jq5mggZZogDi57fAs Y/IjUbO7826gtv6sjJYsXuJju1Zo9go2UfIDMXRwIlv3O27W084YgZUPVyHuKE/5yPsru41/THgi aVYrM+pwFacpWpsN+2T1MgJ79zkez+aEYSEjVn9DIPKfly517yH5Qs4ZraAxQXk0n1y0W9jZUuko BE7IoYOVYMa9Kd6jK0/0B03a3+Mz/HQM98qWhuvy80ezM0sJn0i2hNxA3pypztlXnG2/FxWqnsct dchx5EuQpUeatcpQcK3FuSpGxIJgq3LvyqPCmKuXyNdgQhvNGtMIVUFvXhDSUDA+pSEKa8h9lQdu uKpxoOjz6VaywTaldao0krSrPesjSqpVVEYKLGvFeO3w/OpqcVYprYj0zQrjULeK9u72a+vFitor 27hjZzcykD4Zo4oht3oPAE7GM5UzjAkEgXQ5WB96nobR6zo9ldzC/sbxb6O0vrcajqBUSBQZEVml XmoLU5LUGmDHPiDLLiMKvmQDzBq+myCbWwvm2PSzZagdIkn+qLqH6Rv+f1hpOIT0Vmd1UAMS7hR9 B5ZYa4bve+VFrjCRkRQoRu+KPy57ny5+TesXF1pmkI9hFfanqE97qEUUMmpX0a8ILuRFBlM4VeKA AdSfDqwwtXqTjrcC75uXpNMMp9R4Rtv+zmjooNLup7DVUbUAn6N1KQobzUeXKGe2U0UyepQlTsBv 77ZZgz+JiE2vJpzHLwWOnUdfPkkmh67c6hfT2N/a39i8yzyWh/SV659FIS0cvOOd4lJaJ6xly29a 02yyGSzTDwZcHGRw+quYv30DaK8y340RNPSys77UHaKK5v5G1G9j9OJgRLMtZw0rcQfhRTvsSNq3 RrezVNRjL00L4jXMCvM2dh5/qRs720TahqEcmovAulabd21p9e1A0kupbkNs00ZBIVAeRUbb8d8x tRl4MZkPtbseEynwe/qOnny/X0W+X5zqmniS/t7uy1OzvLFpbc397cQgPeL6e7yGKSqpUjeld8q0 mq8UyG3p/T5N2r0oxUQeIH9l7c+vx6PKvzL1ewtvOGsQ3DzTMtw3+hL8EYr8XxsACwatab/LMLLj Jmfe9B2fpZzxxMQI7fVzPwV/JEwXzfo8IuZkrdw1s7pauaOPsSHrTr9pshhHrHvadTG8cjwg7h2R /SP2B6Z5W8u3Nr5i/TPrWv1a91jVFe3js447gyJNeKkkl2D6knFQ60YdCKU47715lleu+Tth2q8i vLtrqO4hjMSPbXM1uOBbkQyxMqtv4jAqXr+WegK8bi61TlHIk2+o3h5MnTl+8+JT3U7HvircH5a6 BAYWjnvwYGRkBvJip9MggFCeHGo+zxoO1MNqjfNtnaXg0iC7gjuIG1GLlFKquhpHJ1VgRgV55rGo ppfm24t5NA0mTS4FJ+oG3txe8WeiXDDiqrAeJUMC5LEf6uU8Z4q83IjiBJuUBEQv+Kye6q947rHN NvMWn6RpNlr9zY6PponS/VEluYIVt4VGnwSM0rcHZUFCTRfmV+0MiO5AcaX0k2Nh2/HxUPLMWmav aQQapoOnx39ndWqTzxW0CxzGQPV41Ab923Dktd6Hp3IPWuTIxoDcEkb1ex7twP1ebljVfPb6a2h6 Y2nlgi2AtYDeBGlCC6K0UCAKG3BY/wDERqTqpjKI7/VXLp9/LrydmNJiOEyveufTluP610O7zQvm SGx0jQK6VpmkW91JfagDd6hBCtsii/kjXkeBY7sFUCgqR8XQNsckiHW8J4CRw8W31Ej8ftTWzstD uotP1SXy/axT/ozU5JLT6tbhucE9ugqu6ctj+193TDCRMbLblxRjk4RIEd+9fde3uSTy5dw3l3d6 fquh6RNHcC6Frc2cEJSEQxtWGRmRHaZGjPMemKVHSlDdMAHa+Tj4wTAyJjd1Qu67+VeXO/JHeara DTDokenaTpUNvMkPrS3VtB++J3aC3+h5p2RTQMw+Tfs6rW6mWOWxPLu2+bstFpseQEy8+XTuJ8rW ecNM08aD5jWPSVtRdaVoktzYQIkDCQ3twSGClV5J/rdsvyzJw2djQ/Qx0Z8PUDhkNial06+XX3JF +Q+n2Fr5svzbetG72Lc4J1IK0mjpQ0ofvOUaKRMt+52fa2fJPEOKiOLmPcUZ+d7hPMdixlngpaCk sK80H71/7xaNt9GR131D3NHZguBFRO/I7h5J55Um1A+XPLUllfiJ2tr/AJXEdnJeBx9aj6RxNVfn XMzSD92Px1ddrRWUiq8vgidDv7u30WxtrHzMk1lbW8UVvL+iLg8o44wFJIf+WhzJcVMG1LW0+1r4 Xau+jXI2rT+fxxVpdU1lioXzCpLfZA0a5Na+Hx4q46prQIB8wKCdgP0Nc/8ANeKsV1C8/MCZL3Sb e3j1fQbp543uHsZ4xIszMZ1eJhUcZHdNidhWvbEgFChLrH5oRxWlt+jorO3t54haRx2kqpUEhVCq gAFOwxAATapaXn5kLqI1I6NDb6hPF6U1ytjIzgJ6kiqWCjYvI248d8KK6oOTUPzEutLa0TSodWsG uZJriGazcr9YNw006AMvEmC45Lv145CUIyFEWzhklE3E0WUWFx5mmuNPub/UjYaotrcIunrpFxKF jaSHnR1KhuPCPp44QABQY2vg0e40+C9a1v0tBdGaa6lj0K5BLT0Mz15ftFQTiAByVc2mXl3HYyT6 gl0bPhJaTSaDcsQVjZFYVb+WVqfPDaCF8f6W/Td5KNdZr2S1to7iA6JdECFZLgxNTl+0zyD6MBAO xSths77TbSxsba8SLTo7yyUWcOjT2qU+tRbcy3FK/wAxyMICPIUynklM3I2Xkv5maVplx501eW5j uIHac/6Wg5xGigbgcqU6bgZqc0yJmnqtBqckcURExkK5cj+Pmr+SJ/8Anb9IhF45h2uKtrdJSbZx 9hjxrT6dsrwD1jbq0amH7uR4enOJ2+P4D0X9ONpNk13fR6pFZxa1qS291E2lLbiSS9ukG87rIFoz D4x1zevNIyTz3Agr6+pPQorCOfQZCpkT1E5BJW4hkHIE9sVRVp5ouby6NraDVbi4VDI0UUuhOQgI Ut8Mp25GmKo7655i/wCWHXP+C0T/AKq4FY350uvPbDSv0Xa6gkwvVp9dGlMpf034cfRmHv8Aa2wq kl1efmqdZtku7GzfVmIFtHJ+jPrHAK0iFKyltjFKRt2J8cVXtqH5oR2utSXNmqos4OqG4Om/VxS2 i3bnLSno+n7dcUKMFx+ayWtm1vpsSWck0bQi2GnoDciqGvGTfdaVP04qjn1r84DeTWVvHG2pBaiB m0wShF4mrATMfhEqnp+0PHBQ5pTiS+gGlMbvT9WbTxd3JpdfoNl+srPK01A8h/bElPb2wqi0u70a jYiLT9bWcWk31JUOiBBb8oPUAAk4jf06YqhrS8t5Ev5rDTtTLKsiX0lsNBDgNXmGZZK7lT9OKolt euLOCzWeHV4EkRTaes+hqSPgjBHKXrWVV/2WClSPzc99Np3mz65bX6v9Q0fjFcPaLMQL65NY2s34 UH+U1cx9X/dn8dXL0JrMNwOfPlySr8kZQ3me8jFxLLxsn/c3CcZE/ex96LyH+dcw9CPWfc7DtONY weEDfmDsea/875RF5jsWNxJa0sxSRU5xf3r/AN5sae24x1w9Y9y9mRuBFCW/fR+CfeVr5YfKvl5z q9rpkslvd+nfShDCwW+hd1VXdAfUjVl+1UVr2zM0n92Px1ddrRWUiiPe8q0O8sDHYho9OKyi3Sdn tFBdQAv7yf6uxOx3kqada5kuIqx31mdIZWt7WNIikkMc0cHNC7BmoscG5rI3Pfuewwq9G0+z8k+j a3TaZ5XN0EjczPfpHJzHF6lPqvwHmoPHscCVWTTvIshBfTfLJoKUGqkCm4IoLem/L4vHviqLh8zQ N5furJrnSILcyXYJh2Wkqp68h/dqLWQ9Ps0FT23xVUuvNaRWel28d1ozpbzQKrNq3JyEUgF/9GX6 Tiq6LzHbJ5hm1H6/pbXMkAjMJ1hvqoQsu6gWgQyVj7ktQ+FMVS208xw3Plm8s7i80yCKS/vpGeDV mScf7kpZRwC2sjcT4gbrvtXFUwfzfw8wacRc6KwisbuPkdWqN5LX7TfVvtHjsKb7+GBVkH5hre2W rKE061aJ5YmF1qrD1CIh+8twYGBjPQUpuDtvUlW5PzCjs7LSw/6Nn5tBEv1bVHbgzgRhp1S32jXn VuVVFKnpirdt5xp5s1GX6xovx2FitTqtE+Ga8OzfV9z8W4ptt44FWaX58XWrC0RIrS0V7+1QW8+o NJeH/SomqsTxcn67fH+rCrzb8wJRD501d/XuLQmc/vWX1LZqAdQahfD9nNHqN5nq9JpY8WKIqMtu XKX7ftSH8tPMGo3PnXRLO5ZZka7jpIy/GvE12Ip4ZbjxATBHe7LtHQ444pTjtt8HrWvM8XlpHufQ axGu3xiEz3cY9Vr2/DiVrVXk40K+nQfaoDm3eJSNtT0o3SrzsGR4vsm41/1OUQpGo+A1QL3/AGel N6hQrQa1pcFxczCe2S/9FDbiKfXhJwaJnPNyFLI0oj49BxqetMVZXoGpeX9Q01JpZtTnuVZkuDZS a5JCHBqFDVO/EqSDilS18eXzLpPE62KX8Zbl+munpydOXf5b4qgb670MecbKNY7lrVUCyTzSa2L+ NikoZYk8C0kIHsze1VVt9NoMNn5lcDUXLXcaRx3rayluwe0tl4zEfzVNOW/TtTFVaGby7PpOlOn6 TXhdJGyWray8K+k7xmNDuKoV4kLuCCMVUre88vt51uYglyIljEZmSTWjqJZkDJG6jen7qU0P7K7d DiqC1GfQodAVTHdzepql2pj1FtYWJh9dmICbhTLToOteu9cVTa0m0W41TRric6t6kumXDz+g2tOn qO9oT6Th52j60I26V7YqlXl2/wBEubbVo547iK4+rrI502TWXLM6MecoqaAgjjy9+uKFXW7nyzDH oayJcSABHkbUX1lGRUMbM8Fe4RXNR0IU4qp+dZtKg0jzbNG1+LZbHRhIbk3izBjf3ABQ3ZEnHcdN vxzh2QJxmnO7NhKWeIjV78+XIpb+Rl5Fc+ZLsw3v1uNbJ6K6hZU/fR/aI41+7MLRRqZ2rZ2HauIw gLjwm/hyP45oP/nIXVr3TvM2lNbOFD2Z9RCAQ1JWpX78s1cBKW/c5PYemhlxS4h2/Qy/yBrJg8se Wb6WB3jksr31IraMuwaXULeMMFr9lfULN4DftmTphWMB03aWPgzyjzr9TCvL95qqaPYUsL3iotjG 8U9xThwP7xV+sRqFpuyU6kUG22S4KKtdQ1G31NZ5LPU4IQsStPNcztFUUUKI/rjVNTSpoW2+hVfe 6jqEpiQ2d40yJO3BJ7kOFeFFDToLj95yYFF2fjSvfFV1nNfSxRwTWFz6TTozW2pvdXMBAR/jkYTX bmhNKU3rXFWVnzfqdrpTfUHiv5pLu7VohaXUHFGmmbn6hk8aDbcV9sCqcXnLV76wsJtU9HTLtbyO tr9UuLiigfa9RJKHcnbriq/S/PvmO5vY1vrNbCJxSScwTSqgClh+7Sbc8qLsPwGNKgovOuuWlm0O nwJqMUl1qLySLbzwFGN5MUX4pQfir26DxxpUdD5qu7vU9KnvbiKyuZNOuxcW31G5l9J3ktapyWSj 0p9obYqgrKx0vSori4t9WlkmjgliT17S8YFXDMdhLSlZD1+7piq67tdN1VLa5utWkEjW0NuyQ2d2 iKiESVIEgqeSjfc+GKqv1+3n1nUbF9TUW7abp0Qk+oXZYiGe7I+1Ixr0qT1xVdp4stNjSOzv2la9 vtPEkM1pdA0W7jHwu0jImx/zOKvNvP2o2sfnvWYVv2tblZzyjmHOBqqCKV+zt1owzSaiB4zs9Tps EjhieDijXT6vx8CxT8rP/Jh6D/zFp+o5kQ+oe93Xan+Lz9z2TVZdRk0p7ezjubqeLXb1o7a5tRLZ SB7y9LcGS2uHZo1jY7g8W45s3zxD3Mmtu88Vlp0Amh9FAX06ST91IrPOrqumoyUbjw68gSTTFWl1 G6d47c29tcamU9KWFbJlNYhtFxOmu4VAo7GlOgpiqfeWNQmtLa5F2L3SbcFZKWli7o0tOM7O31BO jIBuOnXfYKonX9RjaXSqX+rnjfxk8tOdf91ydK2YqfbFLV5c+WZtWhuLi4u5LyBl/wBIl03/AEiO Q/3IWtgW+LgSPih3dq9lVKG802WXXob271GaCa8Q+jPprMjlLK3Yc1aycCnCvToK074q19d0lLDT o9OvNQjgS7iLR22nn01c1ZuJFkvI716VPWmKFdbny22tm+W4vDfr8h2waafrPqgcCppYVqEaleVd yKUO6lJbm4ubjSfq0MV/qcTXmpM6T6bzRHN3KI2q1qOJPM8uNSNxtihF22oX8VxpnqS6hb30Om3y R2sGnyekhWW2ESIPqS/BxUVoNvbFKhp9zqEEl/6lre6bZy2cgeaHTOLtIhpEnwWh/diMsd6UP3lQ t10XN7a6b6Nrc6qIIEMUl5pjM0UlBXixsvsslQePXodicVQH5mziby15xdZ7qcfUNFWt5AbZxTUZ zsjRW5I360+nKc/0F2vYv+NQ+P8AuSxf/nGv/lLNT/5gD/yejzH0/wBXwd57Rf3Uf636Cq/85Lf8 pHpH/MG3/J046j6vgx9nP7uX9b9D0P8AKL/lE/K//MBff9RcWZGD6A6Ltf8Axmf46B5NbafeS2Fu 6aciI0Vr+8FlcOWYooU+oISrcmodtm6b13vdamFjp+txtbFbJGZZ2ZT9TkjPE3Kn0ORh5qFNF/mp 4mtVVOy07VjLClvpCBAruEewmUeiTLWLi8QIJ+M8mU8uorirO/LcH5spo9sthJZrYrGBbQPGsRjj 40VTG0aOpHg2/jgVN9M13zPY6DFHqFla85p7i3N6b8Q+pO80nIoBAQpLA8cUqk3mXXtStrGez0y0 uIVvIlEkeocwXUE8T+4FDviqqvnPVDfhPqVp68kjWa251Kg9aNviQKbf7dWAOKoOw8x67aaY8Vxp tvAJ7zUOD/pDg3IX0nML+4PRm4++Kqya/wCYtQ1rTbu00q2milsb4QvFqFVZfWtgzBxB2IpiqCt9 M81WTXdwourwwwyxzWtzrXrxKZFZ6tH9XB5Uk+Gp6Uptihu907zVqCWU7Lc6f6lvFbRw2ms/V45C KSghDbt+8IQj4d+NcUqi/wCLZtb1GyGnGOQabpiNPHqXGcLFPdlX9X0DyZyCG2/XiqpYQeY7WJXl iku7S6vLESXFxqYuxH6d0gJiQQRipJ+IA9sVeC/m7/5MjXf+M6/8m1zW5PqL6B2T/i0Pd+lS/Kz/ AMmHoP8AzFp+o4IfUPey7U/xefue0+Zra3/wiZr+4D2J12/DWlzHE9ty+vXYSv7iWT7dCDvQ75s3 zxi9vqun3Ymh2Kya4k4W8kA4sGjDq1OQ0/jRSitX6fmVbXU9HMM93dwWPMiRZ/iMgINYnRlbTdxx Z6ilPo3wKi9JsdO1y/ubbT7KxuLuSMyQSxyqrTRrKAfUkNgnT1HKjke1MVei63p+pEaIZ9SuVma+ h9RALZgrGKSvFvQWtD7YpU73yV5dn1tWvL2eTVbxWnVX9AmRbfijHj6XGi+sBT3xtVN9As7xtfGr X88lnb3yyuXW2K7afAC5/c9lcjb9eKqn+HbWws7AaZf3CW1zexTigtzyaQf3m8NakAdcVah8qeWW 11lj1CR9Ztne54kWzSxNIUkd1DQniGLoTTY7eGyqvo2nctHnN1qky2/16+DiRbThUX8oBPOEipbf 59MVVbjTrz/FGnr+lLok2N6Q/G2qKS2m39zTevhgVWutNIsdRMGqzFgsn1kItpUyemP7zjBXlx49 d6UxV1rppOn2BuNVmFVi9AOtptJw+Hhyg+1StO+FWB/m1byw+X/OCyXMlyTp+ikNKIwR/uSuNh6a RjKc/wBBdp2L/jUPj/uSw/8A5xr/AOUs1P8A5gD/AMno8x9P9Xwd57Rf3Uf636Cq/wDOS3/KR6R/ zBt/ydOOo+r4MfZz+7l/W/QyHyzc6vbeQPKUulSXS3P1W+BSziWZmU3KfaDQXVACB+yPnmRp/oDo u1/8Zn7/ANAYVpWmpc2lg01jc31u8MInu1dYggEQWno/o24DGhIJ57/ibnWp1FodgvotaWN2kBkk uI7kKjoCUE0UwQaWgf1J6qfiFKcqnpiqHbRI4xb+np13PKJTLcBCsSq5CMX30t/22k+DcfDXkOmK p1oXlTypJBcNqEmr6bIsv7uJLcTH0uC7l1sBT4yy8em3huVU5hg9Hy0lpY3es6hDb3E0cFm+nRMg iE8icg0unOOQQ71PiPbFVWN7iPTtO9a/1rT5mvVL2sWmRcFo7BWBTTVBZkCn8MUuj+v/AOIF/wCO vHZK7s2pHTLf1a0Yh2Uaby3IANd98UIN21BtMQ2k2ramwvtRDpLp0NEBuZmVlL6cwq0ipzFdvDam KUdYSXCajo/q6lrVlN+j7oy20WmxUidpbUsiBdOCkV6kA9t991Vseq+Z7j67FqF1rlpZC2kKTfUY nLS8R8PFdO2U1b4iR0xV15q3ma1sbRNIuddv6wRks1lDEitxoRVtOJp03FcVXy3d9Fr2sy2mra5P dLptmYIzpyK0jrLeFUaun0Va9GoOp322Cqmn6jrt2qfpW61iBl1K0W3t57OIQyxC5iIaSRLGLhvX 9tcKvD/zd/8AJka7/wAZ1/5NrmtyfUX0Dsn/ABaHu/SmH5daA1j540OW5uYluBdx8LVTyc1ND4dB vlOLLchQ6uHrtb4mGYjE8Nc3rPmmTj5JR/VSKMa/fiR5H9IU+vXY/vPVt+B5U35+w3IzcPFsMvdb FnaqrXkDpaCR5B+kpnPKMNWI/wC5BjIa7U364oXHUUiEtu2oQfWtNAjNp+kWZjJGWJR+Wo8qmg5c /b6VWUzfmr5gCSyWz6XdxxtIEaJoSXjjqQ4X69WhCNt2pvjSt2/m3zbr+sWlsjactpbX0Dx3cSiY lZYpDE0kK3fqR8+LUB8OtajFWeNB5hFzGh2LTRclX9IGxl5lKrz4/wCl1pXjyp7YEpXp9n5gkufM CT32ntCbxROJbGRkI+o21ag3VOPHxxVfqFp5gS30xbe/04W31mH0BFYyBAtDx40u6caeGFUetrrw unCahpguyoeQCxk9Ti3whm/0vlQ8KfR7YFSrSJtbsdHnubrVtPtrdb6/DSS2coUH69NXf62OpxVX uLfzR/ijTwdQsef1G9ofqU1KetaV2+t/Lviq+4uNbu7HUEt9Y06ZreOVJ1SzlJVl5owP+l9QyMPm MVdFda1Y6dp/1vWdNtxcLBDAJLOUcpJOKIg/0vcszAD3OKsJ/NePUU8vecBfzwzyHT9F4NBC0Chf 0lcbEPLNU+9cqz/QXadi/wCNQ+P+5LEv+ca/+Us1P/mAP/J6PMfT/V8Hee0X91H+t+gpp/zkDpEm oeY9Nb1o4IYbM+rJIaAcpWpT/gcr1eThl8HD7F1QxY5CiSZdGdflfDFB5c8tRRSieNLG+CygUDf6 VF065l6Y3jDqO0pmWeRIo93weXaTJZNFY8reyuy1tbQvH6ultOrlt/8AR3Pr83Si0I3BDE16XuCi Fs0SSqR2E2lmQ+kwfQIRNFzd1f8AvfsSSByR9oEnrSuKtWFlptxNFcldLAM1x6iiXQKuVhrBIfTd w3N2CgVBHEchSmKs40n8ufLWqRXc+narZXypKIjcQWVpJHHIqK5UFQUOzqTx+Xjjasx0JZNN8uen DF9Ze1luY1jjUR8wlzIvwqo4rt0AFO2BKrfTTT2ekzTQm2mluLd5bdiGaNmUlkJGxKnbbFUTDfai +sXFo+ntHYxIGi1AyKVkchSUEf2hTkd/bFUrsL29s9CmmsrJtQm/SN+v1dHCGhvp6nk222Ko65/5 SrTv+YG+/wCT1pirTXt9cWWqpc2TWiwrMkMhcOJUHMBxQAiqqGp79euKrEv9Rt49HgtdPa7guY1F 1crIqCBQEAYhh8VeRNB4Yqsidk83aw6LzddM08qnSpE19Qd+uKty3l5eaFbXF5ZtYXL3drztHYOy cb1FHxLseQAb6cVfMX5u/wDkyNd/4zr/AMm1zXZPqL6B2T/i0Pd+lk/khGh82aMohhso5LuIiFjy uJfiBqTX6T9rMTDvMdd3Sak8WOW8pkDn/CPx8GdeZYNVHlaWRL1ktpdcuxDHEiiWIi9vRIVcyRA8 qr1Owr16ZvXmWKtcasltGz3uoARr/fkgM/I1qW+uAMQ223Q7dtiqrYnXl1uArc3k9zE6uiXCRtFc 0JZUbjclpKEsoXr2xV6Noa+cry3d/qOnabwYL6dxZSRliVDEoFuGqBypUgb1wJW61aecYpdKpLpS cr+Lj6dtOvxCOSnL99uKYqjZtU81Q6nDpcmoaUt/cDlDB9VuiWFHatRLx6RN3/WMCoK0n832c3mC 6mvNMihgu1e5ka3uCBxsrckgLNWnGmFXS3vmvU9O0nUbS+0yazu54JrWVba6TkrglWKvKGAp2Iri qKh2jzRNrE2jR6hpZ1K3j9WaD6pdiiHia8jLwP8AeL0OBUNo1t5uk0mdZZ9Ja3N7fc1nt5mUt9dl r1mpTl0wqq3EXnj/ABNYVudM9X6lecT6Fxx4+ra8qj1q1rSmBVa6tPN6WV+0U2jqWjk+sGO2nDE8 SfiIm6/FXfxwq61tfOD2Fj6s+kMFSIwerbTkhgoK0rN9rbtirC/zRXV18t+cRqklvJP9Q0XgbVHj Th+kZ+okeQ1rXvlOf6C7TsX/ABqHx/3JYr/zjX/ylmp/8wB/5PR5j6f6vg7z2i/uo/1v0Fkf52xM /mSxZbeKVkswRNOf3cX719yO5P8Amco1x9Q9zquzZVjNyI35DmWSeUbfUL7y55dFjqS28/1O+Juo 4hIjD1414hSw2BIINe2Zul/uw63WxrKRVe9gOnQL/hezEmqSW6qkUikQ6eCr0Q8kMl6v2T+0yBvh 3FRmQ4qLuZLhYILdr24azVAy3Ri04ISHcLIxOoDlzLHdR9HXFUNcXdxFyiOoXNyhO4dNLCGSTkgZ qahtx5D4uu42JrirL9A8naveWUZ0vz05RFR54bVIm4uwH956MxWp40228MVZT5esfNEWmekup2kg jnuUMktnKzsVuJAWYi6UVY79MCXa1beaf9ArqFif9MipSymG+/8Ay94qmX1bzV/1cbH/AKQZv+yv FUr8uW/mc6fNw1CyUfXb+oaylJr9dm5Ha6HU9MVdcW/mf/E+ng6hZep9SveLfUpaAera1Bh2r5d8 VReo23mn9h4XLULEr6MlQLKYGnE9/rZxV2m23mn9HWtNQsQPRjoDZTE04j/l7xVAWtv5m/xfqYF/ Zep+j7Dk31KXiV9a84gL9a2I3qa/2qozU4PMSwwG5vrOSAXdn6iR2ksbkfWo+jtcyAf8CcVfNH5u /wDkyNd/4zr/AMm1zXZPqL6B2T/i0Pd+lkvkVUPmzSZbeINC13DzvZyTLMeY+x/k/hToMxMP1i+9 0uqJ4CJHej6Ryj7/AMe8vSPMEPqeT4EPGQN5hvwYpQjI/O/vF4sHgugRVqgen1AqQKnN68yxB7qJ 7dPqcenGS2X1TE1rb0WMrv6f+4pacxsP44odZXaJDFeW1tZxahBI7WixwwoY5kMbHi36JRk/dM7t QdRsGJOKso0zV/zI1iJptGvY7qONVEqvNFDR3BYfE+m9ONOinFKJu7Pz/LqulxardSW1iL2LhcRS 2crmQwsfhT6mmwbkKt7bb7Ksolili1KHTX8wah9bnUvGohtGXiKn4nFoVX7J+0RgVAWtpcWUvmO7 udfvo7e1uhJM6xWbnitjbMTxW1ZiabUUfRXFV15Z3V7ZaTeW+vX7wXNxbywlorNTxdSykqbUEGh6 HCqLh5S6rPpSeYdQN7boJJUMNmAFIU15G14n7Y7/AKjgVAaVa3Nlolxdz67qCQx318H9OG0kPxX8 qV4rasx3NTT9WKoi40fUf8Uaev6cviTY3pDcLKopNabf7zU3rirmSS/sdTS21/UGa0E0M6vDZp8a clNOVqvIVU7jbFXBW07T9M+t+Yb+P636FvABDZtWSXiiL8Nq1PiYdcVYz5+06RLDzXBdTT6sr6fo 5KS+ij0F/c7KYkgXald8x9Uaxn8dXM7PkY5okHhO+/wLGvyHsNPtfNuoG1MqM1iweCdSrLSaPoSB UffmLo5Ey37nbdr58k8UeKvq5j3FGfnekT+ZdPQwNcym0BigrSKolerSdqL7/QMjrvqHuaOzCRjJ vhF8+vuDKPKOr2mmaF5cmv3+FrS9jrbRSyry+sxGgWJZGAFKVOZmk/uw63WV4pq/i8x0qW7n0uzE dncS2hhiPD0LcxuDClah7GVySw7t33r1zJcVlsekeWL/AMvwWup313Zz8WWThpqvJGrDj6aSrZIo X9ocVqGJ36UVVbjy75Rnm9V9d1FuSp6qPpMTB5EUKZCfqAarFeR369MUoqxsdD09XXTvMup2CSf3 iWmlrCpNKL0s6/DXapxQn+n+avLUukTWk891R57oM4tLrnQ3MjBqiGgOKVlx5o8r2Wn6RYW0t20F lNbRRmS1vHfhEvAFmaKrNQbnqcVRcPmPyjFqs+ppNefWLhAki/Vb306KFAPD0qV+Ab/1OKpVBrnl PVfL9zp19NeLBLfXzv6NteIxBvZmX41iqOor9xxVh4HnXy8fM1hKJLjgtleKT9Tu61aW1I29Kv7J wKs/T/lGyt9VltprwyXyySSq9tesoY82+ENFRd3OFV0fmLyndQ6XcTTXYmsY1MXC1vAKlVqGpFuP hGKqUXnDy8/mnVWaW4EU2nWMYYWl1yqs15y29IkbOOowKvt9Y8sWumWej6bLdOPrtt6XrwXdaveI 55SSRqOp7nCrxv8AM7StLuPOery3KzWzmc/6Yo5xNRQPipy406b0zS5pkTNPWdn6nJHFERMZCvp6 /j5pT5D1afUfzM0KRiVhW7UQxdlWh7eOWYIcJHvc3VaaOLSTHXh4L1PzIusP5blVLuxltU1u/b6i 8TpKoN7eU5zi9tgASppTj4DfrtnhmMW5nmtVjW0t3jhAMEbSSPzR3CO2+vMWVWJJ5d+m+KFlteX9 pew3aRQxmwEd1YyNJI4d3kYMhSTW+DKPtjmTWu3QYqye5/NDzrFLNHD9QuWRykXpW9sfVUb81rrA oKb/ABUxpKKtfM3mzXbuwikvtNt5Ib+L0o/qgZnJjkqwEWpT7ICvKoh3hvirNnPmhLhLZ9b0pbiU ExwmxmDsACSVX69U9DgVLtNi81RXmvSvq2mxJHeK08kljMFFLK2PKpvRxAWnU4q1qH+KLy00y6tN a0q4t7i4gktriKxleN1YEq6st8Q6keBxVErN5qa9NgvmPRGvlXm1qNPmMoX+Yp+keVPoxVB6M3mW z0W4ubrW9KtbaK8vzNPPZSogP12YMxZr5QoLdK9OlT1xVWntvNx8zaeRqmnFjY3hRxYTcePq2tdv ru9dqGv9iqrcy+Y7m01CKDXNJne2jdLqKKylZ424n4XAvm4nY9Riq2G58wWdjYrda/pFqZokECTW ciM1EBIXlfLyoOtMVY354h2NbDzUupSpeSmw0cqbGJ7Uhfr9z0DzTHkDvXkPCmY+r/uz+Orl6E1m G4HPny5FI/yRmD+Z7xBcvNxsn/czpwlSssfXZaj6Mw9CPWfc7DtOFYweEDfmDseaA/5yL1O5tNZs IIDw+s2dHcdQqyvsPnyyzVQuYJ7nL7B08Zgyl/CWQeSYtal8ieVE0hOVx9Tv+R9c25Cm4QV5BXrQ kbZl6f6A6rtf/GZ+/wDQGDaFDI9nYfXZNHKKtu81rJc3FvdeiFWRkryABZSTyWPoa/5WXOtZU03k EQzrJpGliBRE07vrU3Ac5GaKrslK87ckCtRT3GKt3CeRXRbifS9NMD+nCpbXJuFVHCMV4bHjHT6M VT6z/M7SdNt7bTLVdJRI1SK2t11cSPTYKB+5Z264pTGE+b77T/TTTfq4jvLmT1LbUvSYkXMhKN/o 7VWu3viq+3svOdtbRQLp/wBa9O6W6Mt5qZmfYU4K31cUXwGKrYtN84R3kF19VuHNu7yei+sExP6l KrIn1ejKOPwjtU0xVRbSPOcqw8rSS1MM97Nxs9V9FJFvJnk4yr9XblwEnwnqDuMVVbfT/OcBtU/R 5nS3tbu1a4n1QtdN9akik5esIFNU9Kg+jwxVZFpHnGKVpRbXE7GGSEQ3GrmSE+oWPJk+rirLzoD4 U8MVbuNJ84XBRmtJ7dlhjhMdtq7RRfuypqEFvsTwoT4EjFXXWm+dLme8ZrD0EurSztfXt9T9K5Bt JZpC/qi3/b9YA0Hj44q3Fa+aLOTndW0skF1d6eJXuNS+siER3SfFFF6EdC/L4t99vDFXln5gTCHz pqz/AFma0JuD+8kXnbNsPoX71zR6jeZ6vSaWPFiiOGMtum0v2/aw/wDKz/yYeg/8xafqOZMPqHvd 92p/i8/c9zk8ua5rmk3NvbWdlDEdW1BzfC6aK6dY766AFDZzqpBfapYZs3z1C/8AKr/MHw+mY7bg WCfV76Jf3Z6IeelSE+J33O+NoXXH5Y67NcXM3wobhuQUX8BWPYgLHz0hthXataY2lMbfyRrMGtDV BpmnOOPBrNrtBBTjQUVNMQ7deuNqqa7aa1plpBqlv5b0yIaZMtw0djPM87pupREjsQxqXrQeGKoK X8yLlrqO4k8tI91CD6U5F+XQMp6OdNqvIVFPoPXFULa/mLqMb30smgetDqki3IiZdRBC+ktrweNt O5CptS3xKAQdq4qrN52v2srGOz0CG1s7RkmghiN8EEcTtEEVE0/4On2aVA6jFVTSPPst/rsCW/lm 3t9VvjJFFcz/AF2B3WIM3xTPpwopVSy8j+OKshs7PzZFYS2d1pOlXUUtxcTsj30xUi4uHnClWsSD x9SmBVSWPzo+rW1/+jtNAt7eeAx/pCff13hetfqXb0PxxVuSHzT6N0kGjaVBJdqwmkS+mBZmBHJq WI5Hfviqm9h5huLS3t7/AEDR7wW6BEM15JIBReJID2LUrirFPP8Ad3qaZ5rm1mFLThYaMB9RuHnP E6hcANzeK3IPI7ih3+7KNULxmnN7OhKWeIjV78+XIpN+Rt3HceZLsxXovIxZPTkoWVayx/apSv8A wOYWijUztWzn9qYjCAuPCb+HX8c0m/5yW/5SPSP+YNv+Tpy/UfV8HZezn93L+t+hlPkwaa3kPypH f3lxZQvZ3wEtry5km5ReJKpJt8Xh2pmRp/oDou1/8Zn7/wBAY3oWn66tihczwE20AAa4u4nJROIj 4rbSFOIUftUHQeAvdajILTzI1i8NxdTRuxLfury7oApYxqtbIfzUY+1R4YFTaxkuNHuWltx+konD AwajPcPHyHpyLIFFio5hlYcuw7b7Kp1p3mu7bUbT69o+n21q9frlxCLmSRX+Pj6YNtHUU47netRS nxYqnujebNCWzkDTSA/Wrs/7zz9DcyEf7rxSjH85+XU487iReRCrW3uNyeg/u8FKu/xfoH+/pP8A pHuP+qeNKtj86eXJVLR3LuoZkJEFwfiRirD+77MCMaVBLr/lmPWze/pG7M80LKtkyXJg4qY+TrEY 9iKLuP5j44VRzecfL6qWaeQKoqSbe4oAP+eeClcvnHy+yhlnkKsKgi3uKEH/AJ540q0edfLZmaEX LmZFV3j9C4qFcsFJHp9CUb7saVD6n5m0a5ht4IZZGlkvLNUBgmUV+tRd2QAfThV4l5+1C3j89azA uofVrgTnlDOoaA1UEU6U2P8ANmk1ETxk09PpsEjhjIw4o1zh2fj4MT/Kz/yYeg/8xafqOZEPqHvd 32p/i8/c9c1LTZY7a6vna0itpNXvuMwVGuIWF3fVlYGCWqv0YGuy7Zs3zxL472GSZoU8yWRuApHD 9HwBQYwzyEj9G1rxHTl28cVdbvYFbi1h8wWssnpRlH+rCQo8AUySq31Cj8hC/JN13Pw4q219p6OL RNXtS6j94/1N5EDLxrV/qNfiDbDl4nrvhVkV3qmhanqmm2FhpWmyXMd9WRQJFWkXONhza0VT8RHQ nAqJuYLWPzxBatp9okjwhBp68jbMxDEOz/VSqmh9ug+lVbf2EdvZeZppdL0+1SK8i/0iMs7RVtbW nFVtqkVO/wBOKr7C1hvfL+h4EGlafdIZ4Yjdy1jkmaItE7uhtQRzZCcVWaXDbP5yv7IwWNxPxYpp bxvHFEAEDFZfqnF6cdv9Y9dsVQWrWKQeVnd7Wx0vlqd8gu4Q0z/71XNU4rbVpQbHtQYqnVvp8dzr GjzxaLprxXGm3MqFm48lZ7Qhmh2UUajeHfFKU+XEstRttcmtrWzvzwaX0Z1kh+rxzNNJGih7UAkA lKjsq133KhvWo7W2fy9bSWNpZTSmF1WBZJFnUFC0crLbcUVuNCzdicVS380LT6t5d84r9StrLlp+ inhankrf7kbjc/u4d/oynP8AQXa9i/41D4/7ksW/5xr/AOUs1P8A5gD/AMno8x9P9Xwd57Rf3Uf6 36Cq/wDOS3/KR6R/zBt/ydOOo+r4MfZz+7l/W/QmlrfWNp+U/lr6/btPZSwSichVZUCanbyVYGa2 YV4UVg3wtQnYHMjT/QHRdr/4zP8AHQMft9R0uNlW4SGSYMzXDxxoCV2V6IdTkpQDqSd/DL3WouW/ 0/0ovUjVvTBay5CJESpeR9/0kzEuwbq1ew8CFRuhav5GgA/S+lvfXRaZrRrP0Y/T9RHEwMZv5qEi RvDrQDFU70vXPyzfU7CTTvL96b5Z0NiVnt95iTwA5XnFtz36YqyyDUdXu9Hnto9E1W3Zru4cTwS6 erjjeO5Wv1tTvTi304pX6jrGqxW+mRNoOpuYrmBfVkk04u5UEVJF19psVV0vdbXV31A6Pq7RNEYx ZGXTvRBJT46fW/tD09vmcCpXa3Wsah5fubOHSdXs3e9vyLu0msEkQm9mJAJuxuK0O1PDscVR1xru qf4n09v8O6gCLK9AT1NPqQZbXcf6XTanj3xVabzWbS01R30fV7hblZXVJ5tPZYgxd+Kf6WSAOdPk BhVwvNZurXS3j0fV7cWyxOywTaeqygcG4uDd7qeFOnQnFVOHWdTfzXqo/wAP6iGk06xQqslgHUet e0aoux1rtRq7dtsCr4rnVrXSrOwudM1SWl7bc9QvZbFyA96j/H6Vy7UXlxHFTsBhV88fm7/5MjXf +M6/8m1zW5PqL6B2T/i0Pd+lNvIuj2w8+6LqFg4Fut5GJrZvhkiZjTiV+ZyjBk9QB73X6rVy8CWP J9XDsehegeZbDTpfL8xj08reS61qHqXbkQQv6d5fMtZSsig/GwDFD1I75uXjkil8smUCSSyWKH0w qGC9iq7orDYvagV50DdOn0YVWWvlxZLGNLi0WGVENeF9C5Zg/KrObWpHCSvbbiDiq5vLySWqxpaR epE4bml5H8UCliJJCbc8allVqBh0xVl6eXdA07S9AtrnQJJrr67G1w89rFM/N45GeMScQWVW2WvY YFTS40WBtbglg0G3j0dAfrFsdNhaVyQKUbj8IBB+dfamKoeLS9GkfX0sfLsaXP16L0WexhKqBaWp Zd1alRy7d8UufStKisNNXU/LsMt99dX1ZIdPiVCrO5RQKDonEHxxQq22hxrr808+h3z6IyEQ2g02 h2g9diXCLtT54qhLfSbKbRWGk6BbxXQ1C+5yXGnxyL6Yu7gBRt1B4/dilEwaXoaaxo8d75cjlul0 25F0yWESo8yvaBnVadK1p4VxVTtdEggsL86vocFzyth6PpabCnCRVf1DUKtQ3wkeh5lQ1caKk0ej vpWh31vaIsbais2mxO8icOkZ47Gu9TiqRfmXBpsPlvzkthpw06M2Gil4hCsHI/pG4+Ki7HKc/wBB dr2L/jUPj/uSxn/nGv8A5SzU/wDmAP8AyejzH0/1fB3ntF/dR/rfoKcfn9p9pfa/p8Msohufqg+r O32SfVeqn5/flWskYzHucDsbPPHAkC43v+tG20WpWP5Z+X7aJJjc/V54ZDbPcq6o9/CGcGzpMQFO 9CNuvhmZpjcAXWdpZBPPKQ5H9SFXU9chuVktZL2VYx6pVxrsi8mH75dyFbjJz48m+EUG2XuApxnV 3urqZZNRgmW2WRpEOubSRsZKHmGjKiINsP2vDFW47jUriBofrF+sgdKGV/MJasCsCfjYMU5Tb0qG 29sVTjygkms6g2najc6h6Kl5lkt59aj43DCjD1pm9PgvNqDls1Dtir0XT7gW2j3dyY3lEE99IYox yduFzK3FASKsabb4ErtZJK6eSCpN5CSppUddtq4qiV1CNtTl070pRJFBHcGYoRCVkd0CrJ0Lj06s vYEeOKpXpN6tlodzctFLOE1C+HpQIZJDz1GVBRR1pyqfbFUTc/8AKVad/wAwN9/yetMVVru59ax1 NPSeP6uskXJwAHrCH5JQmq/HT5g4qpw6hFaWWkRvHLIb0x26NEhcI3otJykI+ylIyOR7kDviqhaf 8pnqn/bO07/k/fYquvL1b3SIbhYpIQ15bL6cy8HBjvUQ1G+xK1HiN8VfL/5u/wDkyNd/4zr/AMm1 zXZPqL6B2T/i0Pd+llHktXk83aLO6RXQF1EE1CFgppyGzqOv0E79hmJg+se90eoIGOUQTHY+k/oZ vrV3bR6LcQW2pQnUJNYvlk06aa2IRfrl5yJju+USiRJaNyXcUpvvm9eaY5b6bIqNEZdMW3loy25/ w5whfiWZkpE1W9Q1+IHFV1tp3G6imM+nRxPGWubVToHpCZEMZogULynVF5P2B41ooGKrbjRrS3hj FkdJQtD6c4hj8ugMnMyek4aLdQ3E0UdRXFXpmteYfLTLoifpizmNvfQtJItxCNlikUuwRqAVPyxS i5dc0F9Zhv180WsdrHHwk08XEBjdvio5POoPxj7sCoODzB5enPmOBPMFtYvd3PG3vI7iDmnKxt0E sfMspKsDSoIqMVX3HmDy/DZaZBJr9peyw3MRluGuIeTAE/EwVtqYVRNvrmgR6vc3z+aLWS2nULHY G4g9OMgKOSnnWp4k/TgVLIdX0K88u3NlF5jttMuJL68dLmO4jEiqb+WQEfGmzp+BwqjZPM/loeY9 Nb9MWTpHY3iPL9YipyMtrSp5dW4k4FU4NY0Oz0/VUn80W2oG6aea3SS4hrCsimkKUcsVXtU4VVE1 zy/PBpcieZ7ezW2RDNbR3Frxm2Q8ZOfJhTiR8JHU4FYV+at/Y3+iec7ixuY7q3Gm6HGZYXWRA66l ckrVSRyAYE/RlWf6C7TsX/GofH/cliv/ADjX/wApZqf/ADAH/k9HmPp/q+DvPaL+6j/W/QWSfnYJ H8xWcSCGUPZDnazbGQCV/snehX5ZRrvrHudT2bQgSbHq+odETW0i8heX0uYnihaGdWtyqzvT67CW VQZEB+GpBqaeFMzdJ/dh22tN5Zb2xvS7WF1e4mtY/RsgDBaT21ukrBpVSb03S9avOEsAKAqKGh6Z kuKo/VYUitllV515M8n+460DBm/dqSF1IABUUU3JoBXfFWT2fknS5rKO8XzBYWV7PHHM0foQIDKx MjiaNpZG57hT8W1OmBWa2OlflvYXtvfWjWEV3a1+ryi4UlOSGM0q5/YYjFKN0bXtDSzkDajaqfrV 2aGaMbG5kIPXuDgVbrOvaG31HjqNs3G7iZqTRmgFdzvhVMf8Q6B/1crX/kfH/wA1YFSvy5ruiR6f Kr6hbIxvb9gGmjBo17Mync9CDUYq6413RD5n0+QahbGNbK9Vn9aOgLS2pAJr1PE4qi9S1/Qm066V dStSxhkAAmjqTxP+VirtN1/Ql061VtStQwhjBBmjqDxH+ViqAtdc0Ueb9TlOoWwibT7BVf1o+JZZ rwsAa0qAwr88VReq61o89vDFBf28sr3dmEjSVGYn61H0ANcVfMf5u/8AkyNd/wCM6/8AJtc12T6i +gdk/wCLQ936WR+UwIfNOl3k1vDHxuY3a/hkCQEBq1lBIoPf4qZh5ZVIb9erpc8rxyiJHl9Mhv8A D8B6rB518wywosOp+WJrpa+vG2oMpUiRunpiX9jj9ObMZjW5j83Wy0uIbkZQOnp/XS8+eNdRVNze eWbVnqFjl1RuVakDpFQ/RhGYnrH5oGkxH6Rll7oftbfzl5mVo2Nx5d9EENOy6gzVQULemWVPiblR eW2xqRUZHxz3x+aBp8PL95f9VMNE86peW15LeahoscgJ+ow29+ktNjQXDD4Qa0+xXLBmHUxHxas+ lECABPzuNfJLYPPerwC2S+vvLrTyQ1mj/SKwsJeYpQh2aj0zvT9rvTIDMa5x+bedHjlZiMlX/Nvb 7FG88/8AmNFLRSeXVUl+LPqilQoB4sTSP7RI6dKe+w8c9DH5pho8RNfvP9ImWj+eJ7zRru5urvRY b/gTYxRX8c0XLhULM6najbHicmM+xsxv3tOfSxhMAcddbjR+CATz3rscKTPd+XbiF44h6g1ERASk ASAn94pHLZQPxyHjnvj8246TETVZAd/4b2d/j3zGt6quNCNui854o9TjM/HlxHHkUUfZLVbahHcG r+YP9H5o/KYeG7nf9XZXtvzGhk0CWa41TQbbW+X7m2XUoZouFR9puUfxUrtWnvlniHh6WsuzyMgA jkMO/gIKFu/zJvo5pFttQ8tTxcz6Uh2VEITsGXepHjXfwGROWX9H5tkezgRvHKP8xpvzNvT6YW58 tqWqJSdZjYKa0Uj4FLCm5w+LLy+a/wAmx7sv/KsoWD80NdMwWWbyyIySfU/TEQoKkAEDn8QFD4fw iMsvL5sz2bCthl/0hSP8xPPE2q+RNbsry60X95HbG1i0/UUup3kW7iZh6YCmnAE7dKYJ5CYm6crs /RDHnhKIydb4o0PpKQf841/8pZqf/MAf+T0eR0/1fBy/aL+6j/W/QWR/ndC0vmGyX6tFdL9TUmJ2 4PtK+8Zp1H0ZRrj6x7nU9my4YE2Y78+nxTrRJtPm/L7SLFNZi0i6iLvxuLoxXC0kkotVlXvT7XIc fvzK02SIgLIcPV4pzyyIHF/VGyCSXzhHFxOpQsiyfDMddQMYmopZq2zAcVBZRVt+pPa/xod4cTwp dxXQv5i4OLfXo7rkDEf9zUVFGziTl6DMGqvA9dj074+LDvCZYJx5xI+Chdr5lVri3XzDHVmkFuW1 5I3ZKgodrYlSR1G9PHHxYd4SMGQixE17kRe/4lgtpkt9YRgEHCSfXETkxKlgZPq7FR4HjXbwOPjQ 7wxGKZNAFqyuPMPO4D61BIt3KCJE1tGW3gMyM4i5QmrhQ3EsvT4duuPiw7wyODIOcT8kPFceaRGw j1mB7uRWRrd9fjIH7wfGrC2Y14ICvw9yNsfFh4hTp8gF8Mq9yvbz+aY5XE+o280kSQy20Ta6vJng HpmPisEdUkSRi7s1WYDp1x8WHeEeDOro17lL615uSN4l1S2MUBdRdnX0LMZAgYTVtaLwK/BQV3Pt j4sO8L4E+XCd/JueXzIn1aOXX4IT6f70trsYZWB+HrbDmDvUkD5Hs+LDvCY6fJLlGR+BTLSPOGvW drKklzo9y7EyI11rSO/IoPgJSEBVqO1cfEj3hl+Vy/zJfIss07zloUljC9/qmm296ygzwx3kMiK3 cK9VqPox8SPeF/K5f5kvkUT/AIu8qf8AV6sP+kmH/mrHxI94X8rl/mS+Rd/i7yp/1erD/pJh/wCa sfEj3hfyuX+ZL5F8s/mpc211+YOtT20qTwSTAxyxsHRh6a7hlqDmBM3IvddlxMdPAEUaT20/Jf8A Ni0blbWixHqQtzDQ/Mc6HGWnkeYcPL2ro5/Vv8Cm8f5X/mRPxGp6HBcFek8dxAko+RD/AKiMrOjm OTgy1emj/d5DHyIJh5+aKP5Wef0QrDa+rEetvdy28gp4cxJy++uQ/KZO77XH/O4Sd9j3xsfZX6ls P5T+dVFYdOewk7rDc27wk/6jvT7lGE6XJ3Wynr8Z5kTHmCD8/wBq1vyp88yS1utIikYdLuC4ihm+ 71P+N8fymToPuSNdiA9MiPIix936FR/ys/MILwW0S5i/31dtbsR/s0kh5g4PymTu+1gNbgu/pPfG /uIQ6flP59VuS+X9Pjbs4lhYj6Kr+vJHS5PP7P1tp7Qwkf3mQ/j4oh/yp89SJW7sjdAfZtkmt4Yf kw9QsR8yflkRpMnQNcddiB9J4fPcn7mv+VW+fzS4k01JLlNraATwLBF2r9urh4p8qY/lMnd9y/nc P0iVR6nfiKG1H8p/zGNm9vZ2Aaa53vLmS4gVm/yVAc0XtTwyUNLO7IbtPr9Px8UzQj9IopB/yoj8 y/8Aq3R/9JEH/NeX+DPudp/Lmm/nH5F3/KiPzL/6t0f/AEkQf814+DPuX+XNN/OPyLv+VEfmX/1b o/8ApIg/5rx8Gfcv8uab+cfkXf8AKiPzL/6t0f8A0kQf814+DPuX+XNN/OPyLv8AlRH5l/8AVuj/ AOkiD/mvHwZ9y/y5pv5x+Reifkp+XHm3yt5gvrzWrVILee0MMbLLHJV/URqURieinLsOOQlZDp+2 e0MWfGBA2Qe5U/Or8vfN3mfW9OvNDt1ljtrcxyOZY4iHLltuTKemOfGZHYMex9fhwwlHIeZ7rYda flf+b0K+nNYQ3UPQxzTwNUfPnX78xJaMnpTl5NXoZGwTE+QKPg/Kjzsq8odNfT5epSG5t3hr/qM9 PuAyB0mTutxZ6/h2kJjzBB+f7XN+VPnmSWt1pEUjDpd29xFDN93qf8b4/lMnQfcka7EB6ZEf0ZCx 936F0v5WfmD6fD6il5AesF3Jb1/5GK5/FTgGkyd1fFjHW4Lu+A98b+4/rdF+VPniNa2tnJZt/vk3 FvND9CtJUD5UxOkydRay1+I/URPzog/d+tRl/Kjz87Vk0KwnbvI0kSE/Ryf9eEaXJ5/MfrZx1+Ec p5B+PgrRflZ+YYXgLGGziputq1vy+hmkp/wuA6TJ3X8QwlrcHOzI/wBK/wBH63L+VXnlWaODTvq8 T7z3JuIHuJPapkNPnX5Y/lMnd9ynXYucjxHoKIiGh+VXnYFR+igtrbb2toJ4Picbh5GL+Pz8cfym TuSddj/neqXOVHl3D8eSQX35K/mle3T3M1hGXc9PrMFAOwHx9BmRHTyAqnaYe1tJjiIgn5FD/wDK iPzL/wCrdH/0kQf814fBn3Nv8uab+cfkXf8AKiPzL/6t0f8A0kQf814+DPuX+XNN/OPyLv8AlRH5 l/8AVuj/AOkiD/mvHwZ9y/y5pv5x+Rd/yoj8y/8Aq3R/9JEH/NePgz7l/lzTfzj8i7/lRH5l/wDV uj/6SIP+a8fBn3L/AC5pv5x+Rf/Z

Corel PDF Engine Version 16.3.0.1114application/pdf

Alik Sayfutdinov

Untitled-1

1TrueTrue104.999997148.000010Millimeters

Cyan

Magenta

Yellow

Black

PANTONE 872 C

Группа образцов по умолчанию0

PANTONE 285 CSPOT100.000000CMYK89.99999847.9999990.0000000.000000

PANTONE 286 CSPOT100.000000CMYK100.00000072.0000030.0000000.000000

PANTONE 368 CSPOT100.000000CMYK63.0000000.00000097.0000030.000000

PANTONE 661 CSPOT100.000000CMYK100.00000075.0000000.0000005.000000

PANTONE 872 CSPOT100.000000CMYK20.00000030.00000169.99999915.000001

xmp.did:4f0ac00a-8dc4-40d4-a8bb-4406cb66fc31uuid:7c085fee-ed39-3b4c-8796-c19e27d531a1xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdfuuid:c1a45d90-2395-3648-9968-205825bbdf0bxmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdf

savedxmp.iid:7522bfa4-97e0-4cd5-a60f-e84474223c632017-06-30T17:21:45+03:00Adobe Illustrator CC (Macintosh)/

savedxmp.iid:4f0ac00a-8dc4-40d4-a8bb-4406cb66fc312018-02-07T10:13:32+03:00Adobe Illustrator CC (Macintosh)/

endstream endobj 3 0 obj > endobj 10 0 obj >/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 896 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>> endobj 11 0 obj >/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 905 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>> endobj 897 0 obj >stream H|n$ z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXC

Новости за 7 дней.

Сколько предметов домашнего обихода должно быть под рукой в ванной комнате? Их десятки. И что с ними делать? Как правило, они не отличаются выдающимся дизайном. Основой набора мебели для ванной комнаты Step стали популярные накладные раковины, устанавливаемые на столешницу, для которых предусмот….

Ассортимент гофрированных труб из нержавеющей стали торговой марки Stahlmann пополнился новыми диаметрами: 40А и 50А. Компания «Электросистемы и технологии» (входит в ГК «ССТ), официальный дистрибьютор бренда Stahlmann, по многочисленным просьбам клиентов расширила ассортимент гибких гофрированны….

Компания группы PORCELANOSA Grupo представляет свои новые коллекции напольного покрытия для наружного применения и самые инновационные технические решения для ванных комнат и систем гидроизоляции в официальных магазинах Испании и Португалии. Butech расширяет свой каталог продукции и технических реш….

В ассортименте EKF появилась эргономичная розетка для кухни со встраиваемой техникой. Новинка c разъёмами типа РШ-ВШ позволяет удобно и эстетично подключить сразу два прибора – варочную панель и духовку. Преимущества нового изделия: привлекательная цена – можно сэкономить до 20 % бюджета; ла….

Серия MPT включает четыре модели носимых видеорегистраторов Dahua со встроенными видеокамерами для ведения аудио- и видеозаписи непосредственно на месте события и формирования в случае происшествия доказательной базы. Эти мобильные устройства предназначены для использования в сфере обеспечения обще….

Одноабонентская вызывная панель IP-видеодомофона VTO2211G-WP обладает элегантным дизайном и тонкой легкой конструкцией. При этом она оснащена всем необходимым для быстрой установки и удобства эксплуатации. Помимо проводного интерфейса Ethernet, который также поддерживает подачу питания PoE, вызывн….

Стремительное развитие технологий и рост современных городов значительно влияют на наш образ жизни, дизайн и архитектуру. В интерьерах стиль лофт лучше всего отражает урбанистический дух, предоставляя простор для творчества и самовыражения. Новая коллекция мебели AQUATON ЛОФТ Урбан объединяет ос….

Решить проблему размещения на плоских кровлях дополнительного оборудования призваны два инновационных технических решения, разработанных Группой компаний fischer, мировым лидером в разработке и производстве современных крепежных изделий. Новые кровельные опоры — FFRB и FFRBH — призваны сделать эксп….

За изысканным интерьером всегда стоит качественный крепёж, который позволяет надёжно фиксировать полки, картины, люстры и другие аксессуары. Именно эту задачу решает серия пластиковых дюбелей с крюком EasyHook — новинка компании fischer, мирового лидера в сфере инновационных крепёжных решений. В с….

Качественная краска для деревянного пола – эффективное решение при реставрации старого или обустройстве нового напольного покрытия. Правильно подобранный ЛКМ защитит дерево от истирания, исцарапывания, влаги, ультрафиолета, сохранит красивую фактуру дерева, придаст нужный оттенок, а также продлит с….

Представляем НОВИНКУ – клей SUPERFLEX K77 Белый для керамической плитки и керамогранита. SUPERFLEX K77 Белый – высокоэластичный плиточный клей на основе белого цемента для укладки любого типа плитки из керамогранита, клинкера, керамики и натурального камня, в том числе крупного формата. Свойства….

Динамики подавляющего большинства телевизоров хорошо справляются лишь с воспроизведением голосов дикторов новостей, а вот для музыки и спецэффектов в кино требуется более серьезное решение. Вот только большие колонки полноформатного домашнего кинотеатра — далеко не самый удобный и комфортный выход ….

Устройства ввода — это та часть компьютера, с которой мы напрямую контактируем каждый день. И именно от них часто зависит, насколько удобно нам будет работать, учиться или играть. Поэтому компания SVEN постоянно расширяет ассортимент компьютерных мышей и клавиатур, предлагая все новые решения. Ко….

Выбирайте паровую станцию, чтобы почувствовать себя обладателем профессиональной техники для домашнего использования. По сравнению с классическими паровыми утюгами, паровая станция VT-2430 позволит Вам гладить белье в несколько раз быстрее и качественнее. Отгладить костюм, брюки, платье, плащ или ….

Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.

Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.

Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10.

Таблица квадратов
Таблица кубов
Таблица логарифмов Таблица синусов/косинусов Таблица тангенсов/котангенсов и другие таблицы численных значений

6⁷=279 936

	В степени:
Число	2	3	4	5	6	7	8	9	10
2	4	8	16	32	64	128	256	512	1 024
3	9	27	81	243	729	2 187	6 561	19 683	59 049
4	16	64	256	1 024	4 096	16 384	65 536	262 144	1 048 576
5	25	125	625	3 125	15 625	78 125	390 625	1 953 125	9 765 625
6	36	216	1 296	7 776	46 656	279 936(пример)	1 679 616	10 077 696	60 466 176
7	49	343	2 401	16 807	117 649	823 543	5 764 801	40 353 607	282 475 249
8	64	512	4 096	32 768	262 144	2 097 152	16 777 216	134 217 728	1 073 741 824
9	81	729	6 561	59 049	531 441	4 782 969	43 046 721	387 420 489	3 486 784 401
10	100	1 000	10 000	100 000	1 000 000	10 000 000	100 000 000	1 000 000 000	10 000 000 000
11	121	1 331	14 641	161 051	1 771 561	19 487 171	214 358 881	2 357 947 691	25 937 424 601
12	144	1 728	20 736	248 832	2 985 984	35 831 808	429 981 696	5 159 780 352	61 917 364 224
13	169	2 197	28 561	371 293	4 826 809	62 748 517	815 730 721	10 604 499 373	137 858 491 849
14	196	2 744	38 416	537 824	7 529 536	105 413 504	1 475 789 056	20 661 046 784	289 254 654 976
15	225	3 375	50 625	759 375	11 390 625	170 859 375	2 562 890 625	38 443 359 375	576 650 390 625
16	256	4 096	65 536	1 048 576	16 777 216	268 435 456	4 294 967 296	68 719 476 736	1 099 511 627 776
17	289	4 913	83 521	1 419 857	24 137 569	410 338 673	6 975 757 441	118 587 876 497	2 015 993 900 449
18	324	5 832	104 976	1 889 568	34 012 224	612 220 032	11 019 960 576	198 359 290 368	3 570 467 226 624
19	361	6 859	130 321	2 476 099	47 045 881	893 871 739	16 983 563 041	322 687 697 779	6 131 066 257 801
20	400	8 000	160 000	3 200 000	64 000 000	1 280 000 000	25 600 000 000	512 000 000 000	10 240 000 000 000
21	441	9 261	194 481	4 084 101	85 766 121	1 801 088 541	37 822 859 361	794 280 046 581	16 679 880 978 201
22	484	10 648	234 256	5 153 632	113 379 904	2 494 357 888	54 875 873 536	1 207 269 217 792	26 559 922 791 424
23	529	12 167	279 841	6 436 343	148 035 889	3 404 825 447	78 310 985 281	1 801 152 661 463	41 426 511 213 649
24	576	13 824	331 776	7 962 624	191 102 976	4 586 471 424	110 075 314 176	2 641 807 540 224	63 403 380 965 376
25	625	15 625	390 625	9 765 625	244 140 625	6 103 515 625	152 587 890 625	3 814 697 265 625	95 367 431 640 625

Раздел: Таблицы численных значений + Таблицы Брадиса:

Таблица умножения — традиционная 10×10, 12х12 и 20х20
Таблица деления — традиционная 10×10 и 12х12
Таблицы квадратов. Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
Таблица квадратов натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ).
Таблицы кубов. Натуральных чисел от 1 до 20 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99.
Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней.
Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.
Таблица 4-ой и 5-ой степени чисел от 1 до 100.
Точная и приблизительная таблицы факториалов (1-255)
Таблицы логарифмов и основные формулы
Таблица. Длина окружности диаметра D.
Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.
Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты.
Таблица и формулы соотношений между стороной, радиусами вписанной и описанной окружности и площадью для правильных многоугольников
Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан.
Таблица синусов, она-же косинусов (см.примечание внутри). Углы в угловых градусах. Таблица значений синусов.
Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов.
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
Таблица тангенсов, она же котангенсов (см.примечание внутри). Углы в угловых градусах.
Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.
Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее
Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)², π², π³, π⁴ и др.
Численные значения числа e, 1/e, e², log₁₀ e и др.
Постоянная Эйлера γ, золотое сечение (золотая пропорция) φ, ln γ, e^γ, 1/φ и др.
Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000
Таблица случайных чисел.
Таблицы : 100 случайных двузначных чисел и генератор случайных последовательностей.

Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.

TehTab.ru

Реклама, сотрудничество: [email protected]

Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

5 ступень — Нормы ГТО для школьников 16-17 лет

№ п/п	Виды испытаний (тесты)	Возраст 16-17 лет
		Юноши			Девушки
		БЗ	СЗ	ЗЗ	БЗ	СЗ	ЗЗ
Обязательные испытания (тесты)
1.	Бег на 100 м (сек.)	14,6	14,3	13,8	18,0	17,6	16,3
2.	Бег на 2 км (мин., сек.)	9.20	8.50	7.50	11.50	11.20	9.50
2.	или на 3 км (мин., сек.)	15.10	14.40	13.10	—	—	—
3.	Прыжок в длину с разбега (см)	360	380	440	310	320	360
3.	или прыжок в длину с места толчком двумя ногами (см)	200	210	230	160	170	185
4.	Подтягивание из виса на высокой перекладине (кол-во раз)	8	10	13
	или рывок гири (кол-во раз)	15	25	35
	или подтягивание из виса лежа на низкой перекладине (кол-во раз)	—	—	—	11	13	19
	или сгибание и разгибание рук упоре лежа на полу (кол-во раз)	—	—	—	9	10	16
5.	Поднимание туловища из положения лежа на спине (кол-во раз 1 мин.)	30	40	50	20	30	40
6.	Наклон вперед из положения стоя с прямыми ногами на гимнастической скамье (см)	+6	+8	+13	+7	+9	+16
Испытания (тесты) по выбору
7.	Метание спортивного снаряда весом 700 г (м)	27	32	38	—	—	—
7.	или весом 500 г (м)	—	—	—	13	17	21
8.	Бег на лыжах на 3 км (мин., сек.)	—	—	—	19.15	18.45	17.30
	или на 5 км (мин., сек.)	25.40	25.00	23.40	—	—	—
	или кросс на 3 км по пересеченной местности*	—	—	—	Без учета времени
	или кросс на 5 км по пересеченной местности*	Без учета времени			—	—	—
9.	Плавание на 50 м (мин., сек.)	Без учета		0.41	Без учета		1.10
10.	Стрельба из пневматической винтовки из положения сидя или стоя с опорой локтей о стол или стойку, дистанция — 10 м (очки)	15	20	25	15	20	25
10.	или из электронного оружия из положения сидя или стоя с опорой локтей о стол или стойку, дистанция — 10 м (очки)	18	25	30	18	25	30
11.	Туристический поход с проверкой туристических навыков	В соответствии с возрастными требованиями
Кол-во видов испытаний видов (тестов) в возрастной группе		11	11	11	11	11	11
Кол-во испытаний (тестов), которые необходимо выполнить для получения знака отличия Комплекса**		6	7	8	6	7	8
* Для бесснежных районов страны
** При выполнении нормативов для получения знаков отличия Комплекса обязательны испытания (тесты) на силу, быстроту, гибкость и выносливость.

градусов Цельсия в градусы Фаренгейта преобразование

Использование Цельсия и Цельсия

Термин Цельсия часто неправильно используется для обозначения Цельсия.

Преобразователь градусов

Конвертер градусов C в F и наоборот прост в использовании.
Просто введите температуру в градусах Цельсия или Фаренгейта для преобразования.

Формула для преобразования градусов Цельсия и Фаренгейта

Преобразуйте градусы Цельсия в Фаренгейты по следующей формуле: Цельсия * 9/5 + 32 .

Чтобы преобразовать градусы Фаренгейта в Цельсия, просто выполните: (по Фаренгейту — 32) * 5/9 ;

История градуса Фаренгейта

Эта единица измерения была создана специалистом по физике Даниэлем Габриэлем Фаренгейтом. Шкала Фаренгейта была изобретена в 1724 году, когда температура замерзала до 32 градусов, а температура кипения составляла 212 градусов.

История градусов Цельсия

Единица градус Цельсия была принята в 1948 году, до тех пор она использовалась в качестве шкалы температур по шкале Цельсия с 1742 года.Физик и астроном из Швеции Андерс Цельсий был изобретателем шкалы, в которой 0 считался точкой замерзания, а 100 — температурой кипящей воды.

Лихорадка и температура

Средняя температура тела человека, измеренная с помощью термометра во рту (или базальная температура тела), составляет 37 ° C или 98,6 F.
Эта же средняя температура в прямой кишке выше, чем во рту, примерно на 0,5 градуса Цельсия или +/- 1 градус Фаренгейта (0.9 градус, если быть точным).

Когда температура во рту поднимается выше 37,5 градусов Цельсия (или 99,5 F), 38 градусов по Цельсию (100,4 F) в прямой кишке, это можно рассматривать как лихорадку.

Когда температура достигает 40 C или 104 F, это считается серьезной проблемой для здоровья

График изменения нормальной температуры тела человека

От самой низкой температуры человеческого тела до самой высокой.

Часть тела	Нормальные колебания температуры (Цельсия и Фаренгейта)
Температура во рту (или во рту)	от 35,5 ° C до 37,5 ° C (от 95,9 ° F до 99,5 ° F)
Температура подмышкой (или подмышечной впадиной)	36.От 5 до 37,5 ° C (от 97,8 до 99,5 F)
Температура в ухе (барабанная)	от 35,8 ° C до 38,0 ° C (от 96,4 ° F до 100,4 ° F)
Температура в прямой (или ректальной) кишке	от 36,6 до 38,0 ° C (от 97,9 до 100,4 F)

Таблица преобразования температуры

9005 3

Цельсия (C)	по Фаренгейту (F)
35	95
35,1	95,18
35,2	95,36
35,3	95,54
35 , 4	95,72
35,5	95,9
35,6	96,08
35,7	96,26
35,8	96,44
35,9	96,62
36	96,8
36,1	96,98
36,2	97, 16
36,3	97,34
36,4	97,52
36,5	97,7
36,6	97,88
36,7	98,06
36,8	98,24
36,9 90 058	98,42
37	98,6
37,1	98,78
37,2	98,96
37,3	99, 14
37,4	99,32
37,5	99,5
37,6	99,68
37,7	99,86
37,8	100,04
37,9	100,22
38	100,4
38,1	100,58
38 , 2	100,76
38,3	100,94
38,4	101,12
38,5	101,3
38,6	101,48
38,7	101,66
38,8	101,84
38,9	102,02
39	102,2
39,1	102,38
39,2	102,56
39 , 3	102,74
39,4	102,92
39,5	103,1
39,6	103,28
39,7	103,46
39,8	103,64
39,9	103,82
40	104
40,1	104,18
40,2	104,36
40,3	104,54
40,4	104,72
40,5	104,9

Преобразование температуры, формула Excel

градусов по Фаренгейту

У вас есть градус Цельсия (например, 35) в формате A1 в Excel.Вы хотите получить градус Фаренгейта B1 с округлением до 2 десятичных знаков.

Ячейка B1: = ОКРУГЛ (A1 * 9/5 + 32, 2)
Ячейка B1: = 95

Фаренгейта в Цельсия

У вас есть степень по Фаренгейту (например, 100) в формате A1 в Excel. Вы хотите округлить B1 до 2 десятичных знаков.

Ячейка B1: = ОКРУГЛ ((A1 — 32) * 5/9, 2)
Ячейка B1: = 37.78

Как правильно писать по Фаренгейту

Как бы то ни было, довольно легко запутаться в том, как писать по Фаренгейту, например, ошибка, ранее отображавшаяся на сайте calcconversion: по Фаренгейту или по Фаренгейту , остается, что правильная терминология — по Фаренгейту.

Преобразователь температуры

К сожалению, здесь не удалось отобразить график, потому что ваш браузер не поддерживает холст HTML5.

Руководство пользователя

Этот инструмент преобразования преобразует значение температуры из и в единицы измерения градус Цельсия, градуса Фаренгейта или Кельвина.

Этот инструмент также отображает шкалу преобразования, применимую к каждой преобразованной температуре.

Самая низкая возможная температура — ноль Кельвина (K), -273,15 ° C или -459,67 ° F, и это называется абсолютным нулем. Этот преобразователь не будет преобразовывать значения ниже абсолютного нуля.

Введите значение температуры, которое вы хотите преобразовать, в верхнее поле ввода.
Выберите соответствующие единицы из верхнего списка выбора для введенной выше температуры.
Выберите единицы температуры из нижнего списка выбора, которые вы хотите использовать для преобразования.
Преобразованная температура будет отображаться в нижнем текстовом поле.

Формулы преобразования

Этот инструмент для преобразования температуры использует следующие формулы:

по Цельсию

 ° C = (° F - 32) x 5/9

 ° С = К - 273.15

по Фаренгейту

 ° F = (° C x 9/5) + 32

 ° F = ((K - 273,15) x 9/5) + 32

Кельвин

 К = ° С + 273,15

 К = ((° F - 32) x 5/9) + 273,15

Таблицы преобразования температуры

Справка по преобразованию температуры

градусов по Фаренгейту

Градус Цельсия равен тому, сколько градусов Фаренгейта?

Преобразование между градусами Цельсия и градусами Фаренгейта не является прямо пропорциональным, поэтому каждое преобразование должно вычисляться независимо, например.грамм. 1 ° C = 33,8 ° F, но 2 ° C не равны 67,6 ° F.

Преобразование можно легко выполнить с помощью калькулятора, умножив значение Цельсия на 9/5, а затем прибавив 32, чтобы преобразовать в единицы температуры по Фаренгейту.

 по Фаренгейту = (Цельсия x 9/5) + 32

от 0-600 ° K до ° C

Как выглядит диапазон температур 0–600 К в градусах Цельсия?

Эта шкала преобразования температуры от 0 до 600 градусов Кельвина в градусы Цельсия показывает соотношение:

от 0 до 350 ° F в ° C

Как показания по Цельсию изменятся в диапазоне 0–350 градусов по Фаренгейту?

На этом графике показана взаимосвязь между 0–350 градусами Фаренгейта и

градусами Цельсия.

от 0 до 400 ° F до ° C

Как значения по Цельсию меняются от 0 до 400 ° F?

На этом графике показаны эквивалентные значения в градусах Цельсия для диапазона от 0 до 400 градусов Фаренгейта:

Преобразование температуры из Цельсия в Фаренгейт

Быстрый градус Цельсия (

° C, ) / Фаренгейт ( ° F, ) Преобразование:

Измерьте / изображения / термометр.js? mode = коробки

Введите значение в любое поле

Или используйте бегунок

или интерактивный термометр

Или этот метод:

° C до ° F	Разделите на 5, затем умножьте на 9 и прибавьте 32
° F до ° C	Вычтите 32, затем умножьте на 5, затем разделите на 9

(объяснение ниже…)

Типичные температуры

(только полужирным, точно такие же)

° С	° F	Описание
220	430	Горячая печь
180	360	Духовка среднего размера
100	212	Вода закипает
40	104	Горячая ванна
37	98.6	Температура тела
30	86	Погода на пляже
21	70	Комнатная температура
10	50	Прохладный день
0	32	Температура замерзания воды
−18	0	Очень холодный день
−40	−40	Extremely Cold Day (и столько же!)

16 около 61
28 около 82

Пояснение

Существуют две основные температурные шкалы:

° C , шкала Цельсия (часть метрической Система, используемая в большинстве стран)
° F , шкала Фаренгейта (используется в США) и

Они оба измеряют одно и то же (температуру!), Но используют разные номера:

Кипящая вода (при нормальном давлении) измеряет 100 ° по Цельсию, но 212 ° по Фаренгейту
И замерзание воды измеряет 0 ° по Цельсию, но 32 ° по Фаренгейту

Как это:

Глядя на схему, обратите внимание:

Шкалы начинаются с другого числа (0 против 32), поэтому мы будем нужно добавить или вычесть 32
Шкала увеличивается с разной скоростью (100 против 180), поэтому мы также нужно умножить

И так, преобразовать:

от Цельсия до Фаренгейта: сначала умножьте на 180 100 , затем добавьте 32

от Фаренгейта до Цельсия: сначала вычтите 32, затем умножьте по 100 180

180 100 можно упростить до 9 5 ,
и 100 180 можно упростить до 5 9 , поэтому мы получаем

от ° C до ° F: Разделите на 5, затем умножьте на 9, затем добавьте 32

от ° F до ° C: Вычтите 32, затем умножьте на 5, затем разделите на 9

Пример: преобразовать 25 ° Цельсия

(хороший теплый день) в Фаренгейта.

Сначала: 25 ° / 5 = 5
Затем: 5 × 9 = 45
Затем: 45 + 32 = 77 ° F

Пример: преобразовать 98.6 ° по Фаренгейту

(нормальная температура тела) от до по Цельсию

Сначала: 98,6 ° — 32 = 66,6
Затем: 66,6 × 5 = 333
Затем: 333/9 = 37 ° C

Мы можем поменять местами порядок деления и умножения, если захотим, но не меняем сложение или вычитание. Так что это тоже нормально:

Пример: преобразовать 98,6 ° Фаренгейта в Цельсий (снова)

Первый: 98,6 ° — 32 = 66,6
Затем: 66.6/9 = 7,4
Тогда: 7,4 × 5 = 37 ° C

(Тот же ответ, что и раньше, было легче или сложнее?)

Мы можем записать их в виде формул:

Цельсия в Фаренгейта: (° C × 9 5 ) + 32 = ° F
Фаренгейта в Цельсию: (° F — 32) × 5 9 = ° C

Другие эффективные методы

Используйте 1.8 вместо 9/5

9/5 равно 1,8, поэтому мы также можем использовать этот метод:

градусов Цельсия в Фаренгейта: ° C × 1.8 + 32 = ° F
по Фаренгейту в Цельсию: (° F — 32) / 1,8 = ° C

Чтобы упростить «× 1,8», мы можем умножить на 2 и вычесть 10% , но это работает только от ° C до ° F:

Цельсия в Фаренгейта: (° C × 2) минус 10% + 32 = ° F

Пример: преобразовать 20 ° Цельсия

(хороший день) в градусы Фаренгейта

20 x2 = 40
минус 10% составляет 40−4 = 36
36 + 32 = 68 ° F

Сложить 40, умножить, вычесть 40

Поскольку обе шкалы пересекаются при −40 ° (−40 ° C равно −40 ° F), мы можем:

доб 40,
умножить на 5/9 (для ° F – ° C) или 9/5 (для ° C – ° F)
вычесть 40

Как это:

градусов Цельсия в градусы Фаренгейта: прибавьте 40, умножьте на 9/5, затем вычтите 40
градусов по Фаренгейту в градусы Цельсия: прибавьте 40, умножьте на 5/9, затем вычтите 40

Пример: преобразовать 10 ° Цельсия

(прохладный день) в градусы Фаренгейта

10 +40 = 50
50 × 9/5 = 90
90-40 = 50 ° F

Чтобы запомнить 9/5 для ° C — ° F, подумайте, что «F больше, чем C, поэтому существует больше ° F, чем ° C»

Быстро, но

Неточно

по Цельсию по Фаренгейту: удвоить, затем прибавить 30
по Фаренгейту к Цельсию: вычтите 30, затем уменьшите вдвое

Примеры ° C → ° F:

0 ° C → 0 + 30 → 30 ° F (меньше на 2 °)
10 ° C → 20 + 30 → 50 ° F (точно!)
30 ° C → 60 + 30 → 90 ° F (выше на 4 °)
180 ° C → 360 + 30 → 390 ° F (высокий на 34 °, плохо)

Примеры ° F → ° C:

40 ° F → 10/2 → 5 ° C (почти справа)
80 ° F → 50/2 → 25 ° C (меньше примерно на 2 °)
120 ° F → 90/2 → 45 ° C (низкая примерно на 4 °)
450 ° F → 420/2 → 210 ° C (ниже примерно на 22 °, плохо)

Сноска: Температура — это мера того, насколько быстро движутся частицы объекта.

1041, 1042, 1043, 1044, 3724, 3725, 3726, 3727, 3728, 3729

Преобразовать часовые углы в градусы

1 Часовые углы = 15 градусы	10 Часовые углы = 150 Градусов	2500 Часовые углы = 37500 Градусов
2 Часовые углы = 30 Градусов	20 Часовые углы = 300 Градусов	5000 Часовые углы = 75000 Градусов
3 Часовые углы = 45 Градусов	30 Часовые углы = 450 Градусов	10000 Часовые углы = 150000 Градусов
4 Часовые углы = 60 Градусов	40 Часовые углы = 600 Градусов	25000 Часовые углы = 375000 Градусов
5 Часовые углы = 75 Градусов	50 Часовые углы = 750 Градусов	50000 Часовые углы = 750000 Градусов
6 Часовые углы = 90 Градусов	100 Часовые углы = 1500 Градусы	100000 Часовые углы = 1500000 Градусов
7 Часовые углы = 105 Градусов	250 Часовые углы = 3750 Градусов	250000 Часовые углы = 3750000 Градусов
8 Часовые углы = 120 Градусов	500 Часовые углы = 7500 Градусов	500000 Часовые углы = 7500000 Градусов
9 Часовые углы = 135 Градусов	1000 Часовые углы = 15000 Градусов	1000000 Часовые углы = 15000000 Градусов

Градус (°) Преобразование единиц угла

Градус — это единица измерения угла.Используйте один из приведенных ниже калькуляторов преобразования, чтобы преобразовать в другую единицу измерения, или читайте дальше, чтобы узнать больше о градусах.

Калькуляторы перевода в градусы

Выберите единицу угла, в которую нужно преобразовать.

Связанные калькуляторы

Определение и использование степени

Градус — это угол, равный 1/360 оборота или окружности. ^[1] Число 360 имеет 24 делителя, поэтому с ним довольно легко работать.В персидском календарном году также 360 дней, и многие предполагают, что ранние астрономы использовали 1 градус в день.

Градус — это единица измерения угла в системе СИ, используемая в метрической системе. Градус иногда также называют градусом дуги, градусом дуги или градусом дуги. Градусы могут быть сокращены как ° , а также иногда сокращаются как ° . Например, 1 градус можно записать как 1 ° или 1 градус.

В качестве альтернативы десятичной форме градусы также можно выразить с помощью минут и секунд.Минуты и секунды выражаются с помощью штрихов (‘) и двойных штрихов (″), хотя для удобства часто используются одинарные и двойные кавычки.

Одна минута равна 1/60 градуса, а одна секунда равна 1/60 минуты.

Транспортиры обычно используются для измерения углов в градусах. Это полукруглые или полукруглые устройства со степенью маркировка, позволяющая пользователю измерить угол в градусах. Узнайте больше о том, как использовать транспортир или загрузите транспортир для печати.

Предпосылки и происхождение

Хотя истинное происхождение степени неизвестно, вероятно, она возникла в вавилонской астрономии. Вавилонские, а затем и греческие астрономы наблюдали, что каждую ночь звезды продвигаются по небу примерно на 1/360 своей круговой траектории. Они также разделили эклиптику, или круг, представляющий путь Солнца, на 360 частей.

Другая распространенная теория состоит в том, что градусы произошли из персидского календаря, который состоит из 360 дней в году.360 также очень близко к 365 фактическим дням в году и 354 среднему количеству дней в лунно-солнечном году.

Независимо от происхождения, число 360 легко использовать математически, что делает его привлекательным для использования. Привлекательность исходит от того, что у числа 360 24 делителя.

использует

Градусы — это очень широко используемая единица измерения угла, которая используется в управляемых полях. Хотя градус не является единицей СИ, он принят для использования в качестве меры угла.

A Температурный справочник — Общество открытого плавания Общество открытого плавания

0-6 ГРАДУСОВ: Балтийский

Прыжки в воду могут ухудшить дыхание у непосвященных, так как дыхание сопровождается сильными прерывистыми вздохами и создается ощущение, что кто-то зажал ледяной шейный бандаж. Вода вызывает укусы, кожные раздражения и ожоги. Это зимнее плавание. Конечности вскоре становятся слабыми — 25 метров может быть достижением — и всего через минуту или две при низких температурах кожа становится мрачно-пурпурно-оранжево-красной (для тех, у кого более светлая кожа), когда вы выходите.

Тем не менее, радость плавания без гидрокостюма в этом конце температурного диапазона — это пик холодной воды: чистое возбуждение и прилив эндорфинов, которые вы получаете от входа в воду. Зимние пловцы часто становятся зависимыми от этого, и этого достаточно мощно, что 1-2-минутное плавание может подарить вам хорошее самочувствие на весь день. По неофициальным данным, клубы зимнего плавания, такие как Serpentine Swimming Club и Tooting Bec Swimming Clubs, сообщают о повышении иммунитета и меньшем количестве простудных заболеваний.

6-11 ГРАДУСОВ: замерзание

Очень похоже на балтийский, но не настолько болезненный и захватывающий.

12-16 ГРАДУСОВ: Свежий

При такой температуре начинают работу триатлоны. В гидрокостюме вы можете какое-то время комфортно плавать, за его пределами вода пресная, доступная для смельчаков и не проблема для закаленных любителей открытой воды.

17-20 ГРАДУСОВ: Летнее плавание

Озера и более зрелые реки достигают этой температуры летом, в жаркие периоды. Еще свежий при входе, но удобный пикник, ленивое летнее купание.

21 ГРАДУС ПЛЮС: теплый

Можно подумать, что это хорошо, но в тех редких случаях, когда речные бассейны и мелкие озера достигают такой температуры во время жарких периодов, возникает странное ощущение, что чего-то не хватает …волнующее чувство, когда выходишь из дома, этот холодный запах воды. С другой стороны, некоторые из вас смогут часами плавать без гидрокостюма.

30 ГРАДУСОВ: Температура бассейна

Возможно неприятно. К тому же, как комментирует Роб Фрайер, «солнце не приглашено».

Чикаго, Иллинойс. Рекорды температуры

Рекорды температуры Чикаго

Чикаго 100-е годы

Ежедневные высокие температуры в 100 градусов и выше, зарегистрированные в Чикаго — с самых ранних до самых последних.

Дата	Температура
16 июля 1887 г.	100
17 июля 1887 г.	100
10 июля 1901	102
21 июля 1901 г.	103
* 3 июля 1911 г.	100
* 4 июля 1911 г.	102
* 5 июля 1911 г.	102
27 июля 1916 г.	100
30 июля 1916 г.	102
5 августа 1918 г.	102
6 августа 1918 г.	101
12 августа 1918 г.	101
19 июля 1930	101
7 июня 1933	100
27 июня 1933	100
1 июня 1934 г.	102
22 июля 1934 г.	101
24 июля 1934 г.	105
8 августа 1934 г.	100
10 июля 1936 г.	102
7 сентября 1939	100
24 июля 1940	101
25 июля 1940	101
17 июля 1942 г.	100
27 июня 1944 г.	100
18 июля 1946 г.	100
* 4 августа 1947 г.	100
* 5 августа 1947 г.	100
* 6 августа 1947 г.	101
24 августа 1947 г.	100
3 июля 1949 г.	102
28 июня 1952 г.	101
19 июня 1953 г.	102
20 июня 1953 г.	104
1 сентября 1953 г.	101
2 сентября 1953 г.	101
25 июня 1954 г.	100
27 июля 1955 г.	100
1 июля 1956 г.	103
7 сентября 1960	100
27 июня 1971 г.	101
28 июня 1971 г.	101
10 июля 1976 г.	100
7 июля 1980 г.	102
20 июля 1980 г.	101
22 июля 1983 г.	100
28 июля 1983 г.	100
** 20 июня 1988 г.	104
** 21 июня 1988 г.	101
** 25 июня 1988 г.	103
** 14 июля 1988 г.	100
** 15 июля 1988 г.	102
** 1 августа 1988 г.	100
** 2 августа 1988 г.	100
10 июля 1989 г.	101
22 июля 1991 г.	101
2 августа 1991 г.	101
13 июля 1995 г.	104
14 июля 1995 г.	100
30 июля 1999 г.	101
24 июля 2005 г.	102
28 июня 2012 г.	100
* 4 июля 2012 г.	102
* 5 июля 2012 г.	103
* 6 июля 2012 г.	103

* Наибольшее количество последовательных 100-градусных дней (3)

** Наибольшее количество 100-градусных дней в году (7)

Число дней 100 градусов или более по декадам

1872–1879	0
1880–1889	2
1890-1899	0
1900–1909	2
1910-1919	8
1920-1929	0
1930-1939	9
1940-1949	10
1950–1959	8
1960-1969	1
1970–1979	3
1980–1989	12
1990–1999	5
2000-2009	1
2010-2019	4

Наибольшее последовательное количество дней в каждом

Год при максимальной температуре 90 градусов или выше

1871… 0	1872… 4	1873… 2	1874…3	1875… 0	1876… 4
1877… 1	1878… 2	1879… 3	1880… 4	1881… 3	1882… 1
1883… 3	1884… 1	1885… 2	1886… 1	1887… 3	1888… 2
1889… 2	1890… 3	1891… 3	1892… 5	1893… 3	1894… 3
1895… 4	1896… 4	1897… 3	1898… 5	1899… 1	1900… 8
1901… 2	1902… 1	1903… 5	1904… 3	1905… 3	1906… 3
1907… 1	1908… 3	1909… 2	1910… 3	1911… 6	1912… 2
1913… 3	1914… 3	1915… 1	1916… 5	1917… 4	1918… 4
1919… 3	1920… 5	1921… 5	1922… 4	1923… 8	1924… 1
1925… 3	1926… 3	1927… 4	1928… 2	1929… 2	1930… 5
1931… 6	1932… 5	1933… 3	1934… 8	1935… 2	1936… 5
1937… 2	1938… 2	1939… 4	1940… 7	1941… 3	1942… 3
1943… 4	1944… 7	1945… 3	1946… 3	1947… 8	1948… 8
1949… 6	1950… 2	1951… 2	1952… 5	1953… 11	1954… 11
1955… 11	1956… 5	1957… 3	1958… 2	1959… 11	1960… 5
1961… 3	1962… 6	1963… 3	1964… 7	1965… 2	1966… 4
1967… 2	1968… 5	1969… 5	1970… 7	1971… 4	1972… 4
1973… 10	1974… 3	1975… 4	1976… 3	1977… 9	1978… 6
1979… 1	1980… 9	1981… 2	1982… 2	1983… 9	1984… 4
1985… 4	1986… 5	1987… 10	1988… 9	1989… 2	1990… 2
1991… 5	1992… 2	1993… 2	1994… 6	1995… 5	1996… 3
1997… 5	1998… 3	1999… 5	2000… 3	2001… 5	2002… 5
2003… 2	2004… 1	2005… 8	2006… 6	2007… 4	2008…3
2009 … 3	2010 … 5	2011 … 5	2012 … 7	2013 … 4	2014 … 1
2015 … 2	2016 … 4	2017 … 7	2018 … 3	2019 … 3	2020 …?

Наибольшее количество дней подряд с

Максимальная температура 90 градусов или выше

11 дней:	10 дней:
24 августа — 3 сентября 1953 г.	25 августа — 3 сентября 1973 г.
11–21 июня 1954 г.	17-26 июля 1987 г.
26 июля — 5 августа 1955 г.
19-29 августа 1959 г.

Наибольшее количество дней с максимумом

Температура 90 градусов или выше в любой год *

1) 47 (1988)	6) 39 (1959)
2) 46 (2012)	7) 38 (1952)
46 (1955)	8) 36 (1954)
4) 42 (1983)	9) 35 (1971)
42 (1953)	35 (1964)

* Нормальное количество дней, когда максимальная температура достигает не менее 90 градусов:

О’Хара… 14

Мидуэй… 15

Север Остров … 8

Наибольшее количество дней с максимумом

Температура 90 градусов или выше по месяцам

2 (апрель 1930)	18 (август 1947 г.)
10 (май 1977 г.)	8 (сентябрь 1959 и 1971)
16 (июнь 1954 г.)	2 (октябрь 1971)
19 (июль 1955 и 1987)

Наименьшее количество дней с максимальным

Температура 90 градусов или выше в любой год

0 (1871 и 1875)	3 (2014, 2004 и 1902 годы)
1 (1882 и 1915)	4 (1904, 1907, 1917, 1967, 2000 и 2009)
2 (1889 и 1979)	5 (1909)

Самые низкие зарегистрированные температуры

в Чикаго (-16 градусов и ниже)

-16	2 января 1879 г.	-19	16 января 1977 г.
	15 января 1893		14 января 1979 г.
	26 января 1897 г.		9 января 1982 г.
	7 января 1912 г.		19 января 1994
	18 января 1930 г.
	29 января 1966	-20	9 января 1875 г.
	16 января 1994		25 января 1879 г.
	6 января 2014 г.		20 января 1984 г.

-17	8 февраля 1899 г.	-21	22 декабря 1872 г.
	12 февраля 1899 г.		9 февраля 1899 г.
	22 января 1936 г.		23 декабря 1983 г.
	5 февраля 1979 г.		18 января 1994 г.
	25 декабря 1983 г.		31 января 2019 г.
	15 января 1994	-22	21 января 1984 г.

-18	23 декабря 1872 г.	-23	24 декабря 1872 г.
	23 февраля 1873 г.		17 января 1982 г.
	3 января 1876 г.		19 января 1985 г.
	5 января 1884 г.		30 января 2019 г.
	10 февраля 1899 г.	-25	16 января 1982 г.
	13 февраля 1905 г.		24 декабря 1983 г.
	23 января 1963 г.
	22 декабря 1983 г.	-26	10 января 1982 г.

-27 20 января 1985 г. * (охлаждение ветром достигало –60 при продолжительном ветре около 25 миль в час)

Зарегистрированные минимальные среднесуточные температуры

в Чикаго (-10 градусов и ниже)

-10	4 января 1884 г.	-13	16 января 1977 г.
	15 января 1893
	26 января 1897 г.	-14	9 февраля 1899 г.
	10 февраля 1899 г.		23 декабря 1983 г.
	20 января 1984 г.
	30 января 2019 г.	-15	25 января 1879 г.
			10 января 1982 г.
-11	5 января 1885 г.
	8 февраля 1888 г.
	13 февраля 1905 г.	-16	20 января 1985 г.
	23 января 1963 г.		18 января 1994 г.
	25 декабря 1983 г.
	15 января 1994	-18	24 декабря 1983 г.
	2 февраля 1996 г.

-12	9 февраля 1933 г.
	3 февраля 1996 г.

Наибольшее последовательное количество дней в каждом

Год с нулевой минимальной температурой в градусах или ниже

1872… 4	1873… 5	1874…. 2	1875… 8	1876… 3	1877… 2
1878… 2	1879… 5	1880… 5	1881… 1	1882… 2	1883… 6
1884… 5	1885… 6	1886… 3	1887… 3	1888… 6	1889… 3
1890… 2	1891… 2	1892… 3	1893… 5	1894… 2	1895… 4
1896… 3	1897… 3	1898… 3	1899… 7	1900… 5	1901… 4
1902… 4	1903… 4	1904… 3	1905… 5	1906… 0	1907… 3
1908… 1	1909… 2	1910… 2	1911… 1	1912… 10	1913… 1
1914… 2	1915… 3	1916… 3	1917… 5	1918… 3	1919… 3
1920… 2	1921… 0	1922… 2	1923… 2	1924… 3	1925… 2
1926… 2	1927… 3	1928… 3	1929… 3	1930… 3	1931… 0
1932… 2	1933… 3	1934… 3	1935… 4	1936… 7	1937… 0
1938… 1	1939… 0	1940… 3	1941… 2	1942… 7	1943… 2
1944… 2	1945… 6	1946… 2	1947… 2	1948… 3	1949… 2
1950… 2	1951… 3	1952… 1	1953… 1	1954… 1	1955… 4
1956… 0	1957… 3	1958… 3	1959… 2	1960… 3	1961… 2
1962… 4	1963… 9	1964… 0	1965… 8	1966… 4	1967… 2
1968… 6	1969… 1	1970… 5	1971… 4	1972… 3	1973… 1
1974… 2	1975… 2	1976… 3	1977… 5	1978… 4	1979… 7
1980… 2	1981… 3	1982… 6	1983… 5	1984… 4	1985… 5
1986… 4	1987… 3	1988… 7	1989… 5	1990… 2	1991… 1
1992… 2	1993… 2	1994… 8	1995… 2	1996… 6	1997… 4
1998… 1	1999… 3	2000… 6	2001… 1	2002… 2	2003… 1
2004… 3	2005… 1	2006… 1	2007… 6	2008 г…2	2009 … 4
2010… 1	2011… 2	2012… 0	2013… 2	2014… 5	2015… 6
2016… 3	2017… 3	2018… 3	2019…3	2020 … 1

Наибольшее количество дней подряд

с минимальной температурой 0 или ниже

10 дней:	9 дней:
4 января — 13 января 1912 г.	13-21 декабря 1963 г.

Наибольшее количество дней в месяце

с минимумом ноль или меньше

17	Январь 1977 г.	13	Январь 1887 г.
			Январь 1888 г.
15	Январь 1963 г.		Январь 1912 г.
			Февраль 1936 г.
14	Февраль 1875 г.		Январь 1982 г.
	Январь 1979 г.
		12	Январь 1885 г.

Наибольшее количество дней в течение

Зима с температурами ниже нуля

1884-85… 25

1935-36… 24

1962-63… 24

1981-82… 22

1874-75… 21

1978-79… 21

1872-73… 19

Зимы без нулевой или более низкой температуры *

Самая низкая температура той зимой в скобках

1881-82 (1)	1938-39 (2)
1905-06 (6)	1955-56 (2)
1930-31 (6)	1959-60 (6)
1931-32 (1)	1982-83 (3)
1936-37 (1)	2011-12 (5)

* (Обычно бывает 13 дней минусовых низких температур)

лет без нулевой или более низкой температуры

Самая низкая температура в этом году в скобках

1906 (6)	1939 (3)
1921 (8)	1956 (2)
1931 (6)	1964 (2)
1937 (1)	2012 (5)

Самый продолжительный непрерывный период ниже точки замерзания

43 дня	28 декабря 1976 г. — 8 февраля 1977 г.

33 дня	15 января 1985 г. — 16 февраля 1985 г.

29 дней	18 декабря 1878 г. — 15 января 1879 г.
	22 января 1895-19 февраля 1895

28 дней	22 января 1905 г. — 18 февраля 1905 г.
	28 декабря 1917 — 24 января 1918

Максимальное количество часов подряд ниже нуля

100 часов

22 декабря ^-е — 25 декабря 1983

Первая остановка сезона

Средняя дата:	15 октября ^-е
Самая ранняя дата:	22 сентября 1995 г. (32)
Последняя дата:	24 ноября 1931 (30)

Последняя весенняя заморозка сезона

Средняя дата:	23 апреля ^рд
Самая ранняя дата:	19 марта 1925 (28)
Последняя дата:	25 мая 1992 г. (32)

Первый смертельный мороз (28 градусов и ниже)

Средняя дата:	27 октября ^-е
Самая ранняя дата:	2 октября 1974 г. (28)
Последняя дата:	3 декабря 1899 (27)

Самое большое изменение температуры от одного дня к следующему

Высокие и Низкие температуры для дней в скобках

Падение на 61 градус:	11-12 ноября 1911 г.	(74/32; 32/13)

Падение 58 градусов:	8-9 февраля 1900 г.	(62/10; 19/4)
	13-14 декабря 1901	(49/8; 8 / -9)

Падение 57 градусов:	18-19 января 1996 г.	(61/13; 13/4)

Повышение на 58 градусов:	13-14 февраля 1887 г.	(30/0; 58/18)
	10-11 марта 1972 г.	(40/15; 73/30)

Повышение на 56 градусов:	9-10 апреля 1977 г.	(62/29; 85/48)
	23-24 апреля 1986 г.	(63/25; 81/47)

Самый большой диапазон за один календарный день

Высокая и низкая температура в скобках

52 градуса:	8 февраля 1900 г.	(62/10)

51 градус:	21 февраля 1873 г.	(40 / -11)
	13 января 1888 г.	(42 / -9)

49 градусов:	29 марта 1895 г.	(80/31)

Наибольшее падение температуры за один час

30 градусов 26 марта 1908 г.

71 градус в 14:00 и упал до 41 градуса в 15:00.

Прочие значительные изменения температуры

20 апреля 1936 г. — Температура упала с 82 градусов до 55 за 10 минут.

Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней

Таблица степеней от 1 до 10

Остались вопросы?

1.2. Ко­рень n-й сте­пе­ни

1.2. Ко­рень n-й сте­пе­ни

Упраж­не­ния

Квадратный корень

Основные сведения

Определения

Примеры извлечения квадратных корней

Приближённое значение квадратного корня

Приближенное значение квадратного корня с недостатком или избытком

Границы, в пределах которых располагаются корни

Тождественные преобразования с квадратными корнями

Квадратный корень из произведения

Квадратный корень из дроби

Вынесение множителя из-под знака корня

Внесение множителя под знак корня

Задания для самостоятельного решения

Навигация по записям

Untitled-1

Новости за 7 дней.

Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.

5 ступень — Нормы ГТО для школьников 16-17 лет

градусов Цельсия в градусы Фаренгейта преобразование

Использование Цельсия и Цельсия

Преобразователь градусов

Формула для преобразования градусов Цельсия и Фаренгейта

История градуса Фаренгейта

История градусов Цельсия

Лихорадка и температура

График изменения нормальной температуры тела человека

Таблица преобразования температуры

Преобразование температуры, формула Excel

градусов по Фаренгейту

Фаренгейта в Цельсия

Как правильно писать по Фаренгейту

Руководство пользователя

Формулы преобразования

по Цельсию

по Фаренгейту

Кельвин

Таблицы преобразования температуры

Справка по преобразованию температуры

градусов по Фаренгейту

от 0-600 ° K до ° C

от 0 до 350 ° F в ° C

от 0 до 400 ° F до ° C

Преобразование температуры из Цельсия в Фаренгейт

Быстрый градус Цельсия (

Типичные температуры

Пояснение

Пример: преобразовать 25 ° Цельсия

Пример: преобразовать 98.6 ° по Фаренгейту

Пример: преобразовать 98,6 ° Фаренгейта в Цельсий (снова)

Другие эффективные методы

Используйте 1.8 вместо 9/5

Пример: преобразовать 20 ° Цельсия

Сложить 40, умножить, вычесть 40

Пример: преобразовать 10 ° Цельсия

Быстро, но

Преобразовать часовые углы в градусы

Градус (°) Преобразование единиц угла

Калькуляторы перевода в градусы

Определение и использование степени

Предпосылки и происхождение

использует

A Температурный справочник — Общество открытого плавания Общество открытого плавания

0-6 ГРАДУСОВ: Балтийский

6-11 ГРАДУСОВ: замерзание

12-16 ГРАДУСОВ: Свежий

17-20 ГРАДУСОВ: Летнее плавание

21 ГРАДУС ПЛЮС: теплый

30 ГРАДУСОВ: Температура бассейна

Чикаго, Иллинойс. Рекорды температуры

Добавить комментарий Отменить ответ

1.2. Корень n-й степени

1.2. Корень n-й степени

Упражнения