A b c матрица – Виды матриц и операции над матрицами

Содержание

Основные сведения о матрицах

В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.

Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….

Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: a_ij_,где i — номер строки, j — номер столбца.

Например, матрица:

В сокращенной записи обозначаем A=(a_ij); i=1,2,…m; j=1,2,…,n

Приведем пример матрицы 2 на 2:

Вы видите, что a₁₁ = 1, a₁₂ = 0, a₂₁ = 2, a₂₂=5

Наряду с круглыми скобками используются и другие обозначения матрицы:

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij= b_ijдля любых i=1,2,…m; j=1,2,…n

Виды матриц

Матрица, состоящая из одной строки, называется матрицей (вектором) — строкой, а из одного столбца — матрицей (вектором)- столбцом:

A=(a₁₁,a₁₂,…,a_1n) — матрица — строка

Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Например,

Элементы матрицы a_ij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a₁₁, a₂₂,…,a_nn.

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется

диагональной.

Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые — специфические.

1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой b_ij=a_ij для i=1,2,…m; j=1,2,…n

Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_ij_{для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).}

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.

4. Умножение матриц.

Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m∙B _kназывается такая матрица C_m, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

i=1,2,…,m; j=1,2,…,n

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):

A+B=B+A

(A+B)+C=A+(B+C)

λ (A+B)= λA+ λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ (AB)=( λA)B=A(λB)

A(BC)=(AB)C

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.

b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.

5. Транспонирование матрицы — переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:

Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n

В литературе встречаются и другие обозначения транспонированной матрицы, например, А^Т

Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица

В начало

Содержание портала

statistica.ru

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ. — КиберПедия

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ.

Матрицей называется прямоугольная таблица чисел, содержащая m-строк одинаковой длины и n-столбцов одинаковой длины. Матрица записывается в виде:

где a_ijÎR 1 £ i £ m 1 £ j £ n

Обозначают матрицу А, В, С, или сокращают. A_3×2B_mxnA = (a_ij)_3×4

Числа, составляющие матрицу, называют элементами матрицы и обозначают . a_ij, где i – номер строки, j – номер столбца.

Матрицы называются равными, если они одинаковых размеров, и на одинаковыъ позициях стоят одинаковые элементы.

Матрица, все элементы которой равны 0, называется нулевой и обозначается 0_mxn.

Матрица, у которой число строк m равно числу столбцов n, называется квадратной. Квадратную матрицу размера mxn называют матрицей n-ого порядка. A_n

Элементы квадратной матрицы, у которой номер столбца равен номеру строки, называются диагональными и образуют главную диагональ.

Квадратная матрица, у которой все элементы кроме элементов главной диагонали равны нулю, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны, называется скалярной. Скалярная матрица, у которой на диагонали стоят единицы, называется единичной матрицей. E = E

Если в квадратной матрице все элементы, лежащие ниже или выше главной диагонали равны нулю, то такая матрица называется треугольной. a_ij=0, i>j верхняя треугольная

a_ij=0, i<j нижняя треугольная

Линейные операции над матрицами – сложение, умножение на число.

Сложение матриц. Вводится только для матриц одинаковых размеров. Определение. Пусть A = (a_ij)_mxn B = (b_ij)_mxn – 2 матрицы одинаковых размеров. Суммой двух матриц А и В одинакового размера называется матрица, обозначаемая A+B такая, что (A+B)_mxn = (a_ij+b_ij)_mxn

. таким образом, сложение матриц осуществляется покомпонентно.

Умножение матрицы на число. Определение. Пусть A = (a_ij)_mxn и αÎR. Произведением матрицы A на число называется матрица, обозначаемая αА, такая, что (αА)_mxn = (αa_ij)_mxn_.. т.е. каждый элемент которой получен умножением соответствующего элемента матрицы А на число. Следствие: общий множитель всех элементов матрицы можно вынести за знак матрицы.

Матрица равная – А = (-1)А называется противоположной матрице А. Разность матрицы можно определить как А-В=А+(-В)

Свойства:

1. А+В=В+А

2. (А+В)+С=А+(В+С)

3. А-А=А+(-А)=О

4. 0А=О

5. 1А=А

6. α(А+В)=αА+αВ

7. (α+β)А=αА+βА

8. α(βА)=(αβ)А

УМНОЖЕНИЕ МАТРИЦ.

Упорядоченная пара (А, В) двух матриц называется согласованно, если число столбцов первой матрицы А равно числу строк второй матрицы В. В частности, согласованы в любом порядке 2 квадратные матрицы одного размера. Умножать можно только согласованные пары в порядке их согласования.

Произведением двух согласованных матриц называется матрица, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующий элемент j-ого столбца матрицы В.

Произведение n-экземпляров квадратной матрицы А АхА……А = Аⁿ^{называется n-ной степенью.}

Свойства произведения матриц:

1. А(ВС)=(АВ)С

2. (А+В)С=АС+ВС

3. С(А+В)=СА+СВ

4. α(АВ)=(αА)В=А(αВ)

5.ЕА = АЕ = А

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

Каждой квадратной матрице можно поставить в соответствие число, которое называется определителем, которое обозначается d(A) или = detA

1. Для матрицы A₁ = (a)

Det(a) = |a| = a

2. A₂ =

= a₁₁a

22 – a₁₂a₂₁

3. detA₃= a₁₁a₂₂a₃₃+ a₁₂a₂₃a₃₁ + a₂₁a₃₂a₁₃ – a₁₃a₂₂a₃₁ – a₁₂a₂₁a₃₃ – a₂₃a₃₂a₁₁

свойства определителей.

1. Det(AB) = det(A)det(B)

2. detA = detA^T Определитель матрицы равен определителю транспонированной матрицы, т.е. любое верное утверждение относительно строк определителя остается верным и для столбцов

3. общий множитель любой строки (столбца) определителя можно вынести за знак определителя, т.о. если у определителя имеется нулевая строка (столбец), то он равен нулю.

4. Если у определителля поменять местами любые две строки (столбца), то он изменит знак на противоположный, т.е. если у определителя 2 одинаковых (пропорциональные) строки (столбца), то он равен нулю.

5. Если каждый элемент строки/столбца представлен в виде суммы 2ух слагаемых, то этот определитель равен сумме 2ух определителей.

6. Если к одной троке определителся прибавить любую другую строку, умноженную на любое число, то он не изменится.

ОБРАТНАЯ МАТРИЦА.

Понятние обратной матрицы существует только для квадратных матриц.

Определение. Пусть а – квадратная матрица. Матрицей, обратной А, называется матрица, обозначаемая А^-1, такая что АА^-1 = А^-1А = Е, где Е – единичная матрица.

Квадаратная матрица называется невырожденной, если ее определитель отличен от нуля, и вырожденной – в противном случае.

Теорема: для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Доказательство. Есть А^-1 Û detA¹0

Необходимость. У А есть А^-1

Надо доказать что detA¹0

Т.к. АА^-1 = Е => det(AA^-1) = detE => detAdetA^-1 = detE. Т.е. detAdetA^-1=1 =>detA¹0

Достаточность. Дано: detA¹0. Надо доказать что существует А^-1

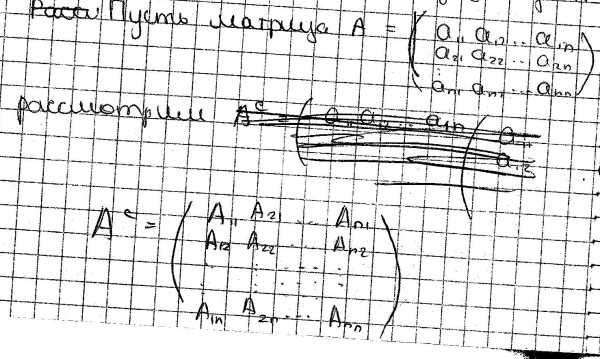
Схема построения обратной матрицы.

1. Находим detA=d¹0

2. Находим все алгебраические дополнения A_ij

3. Строим матрицу А^с = (A_ij)^T

4. A^-1 = (1/detA)A^c

Если обратная матрица существует, то она единственная. Действительно. A, detA¹0 и пусть B, C – две обратные к А.

Рассмотрим. BAC = (BA)C = EC = C => B=C

B(AC) = BE = B

Понятие обратной матрицы позволяет решать т.н. матричные ур-я вида АХ = В, где А, В – заданные матрицы, Х – неизвестная матрица.

Действительно. Если |A|¹0 , то есть A^-1 умножим: A^-1(AX) = A^-1B => X=A^-1B

Аналогично: XA = B, X=BA^-1

Или: AXB = C => X = A^-1CB^-1

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. КОМПЛАНАРНОСТЬ ТРЕХ ВЕКТОРОВ.

Смешанным произведением 3х векторов a,b,c называется число [a,b]c , полученное скалярным умножением векторного произведения [a,b] на третий вектор с. обозначается abc = (a,b,c) = [a,b]c

Пусть {a,b,c} – правая тройка.

Тогда abc = [a,b]c = |[a,b]||c|cosq q — угол между [a,b] и c

abc = Sпараллелограмма|c|cosq = Sпараллелограмма H = V паралелипипеда, построенного на этиъ векторах.

Если {a,b,c} – левая тройка, то abc = -V

Свойства:

1. a[b,c] = [a,b]c

2. abc = cab = bca = -bac = -cab = -acb

3. (a₁ + a₂)bc = a₁bc + a₂bc

4. (aa)bc = a(ab)c = ab(ac) = aabc

Вычисление смешанного произведения

Пусть a(a_x, a_y, a_z) b(b_x, b_y, b_z) c(c_x, c_y, c_z) abc — ?

abc = [a,b]c = ( , — , )(c_x, c_y, c_z) = c_x — c_y + c_z =

Т.е. abc = [a,b]c =

Формулировка: для того, чтобы 3 вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Необходимость: дано: 3 вектора компланарны, доказать: abc = 0

Если a,b,c компланарны, то [a,b]^c => abc = [a,b]c = 0

Достаточность. Дано: abc = 0, доказать: a,b,c – компланарны.

0 = abc = [a,b]c = |[a,b]||c|cosq = |a||b|sinj|c|socq = 0

1. |a| или |b| или |c| равны 0 => среди векторов есть нулевой вектор => a,b,c компланарны

2. sinj = 0 => a||b => a,b,c компланарны

3. cosq=0 => c^[a,b] = p/2 => с принадлежит плоскости ab

применение смешанного произведения

1. вычисление объемов параллелипипедов ( V = |abc|), трегольных призм ( V = |abc|/2), пирамид ( V = |abc|/6)

2. определение компланарности трех векторов

ЧИСЛО Е.

Неравенство Бермули (1+a)ⁿ>= 1+na, a>-1

Теорема. Последовательность x_n = (1+1/n)ⁿсходится, т.е. имеет предел.

Доказательство:

Рассмотрим

Ясно также, что y_n>0 при всех nÎN, т.к. y_n ограничена.

По предыдущей теореме

Пределом x_n = (1+1/n)ⁿ^{называется число е = 2,718281828459045}

е играет огромную роль в анализе, а сам предел называется вторым замечательным пределом. Логарифм по основанию числа е называют натуральным логарифмом.

ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИИ.

Теорема1. Для существования предела ф-ии f(x) в точке x₀ необходимо и достаточно существование обоих односторонних пределов в этой точке и их равенство.

Теорема2. Если функция f(x) и g(x) определены в некоторой окрестности точки x₀ и для всех xÎO(x₀) имеет место неравенство f(x)<=g(x), то lim_x->x0f(x)<= lim_x->x0g(x) если они существуют.

Теорема3. Пусть в окрестности точки x₀ – O(x₀) определены ф-ии f(x), j(x), y(x) и f(x)£ j(x)£ y(x)

Предположим, что существует = =A

Тогда существует = A

Теорема4. Пусть = A и = B

Тогда:

1. ± = A ± B

2. g(x) = AB

3. /g(x) = A/B, B¹0

lim сf(x) = c lim f(х), если с – const, постоянную величину можно вынести за знак предела;
lim хⁿ = (lim x)ⁿ:
lim ⁿÖx = ⁿÖlim x.

ДИФФЕРЕНЦИАЛ. ИНВАРИАНТНОСТЬ ФОРМЫ.

limy=A, y=A+a

limDy/Dx=y`, Dy/Dx=y`+a, Dy=y`Dx+aDx

Dx®0

Dy=y`Dx+e, где e-б.м.в., величина более высокого порядка малости,, чем Dx(a), и ее можно отбросить.

dy=y`Dx

Дифференциалом ф-ции наз. величина, пропорциональная б.м. приращению аргумента Dх и отличающаяся от соответствующего приращения ф-ции на б.м.в. более высокого порядка малости, чем Dх.

Если y=x, то dy=dx=x`Dx=Dx, dx=Dx

Если y¹x, то dy=y`dx, y`=dy,dx

Геометрический смысл: дифференциал — изменение ординаты касательной, проведенной к графику ф-ции в точке (x₀,f(x₀)) при изменении x₀на величину Dx

Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)

2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV

3.d(c)=c`dx=0*dx=0

4. d(U/V)`=(V`dU-U`dV)/V².

ИНВАРИАНТНОСТЬ:

Дифференциал ф-ии всегда равен произведению производной и дифференциала аргумента и не зависит от то, является ли аргумент независимой переменной или промежуточной функцией.

АССИМПТОТЫ ГРАФИКА ФУНКЦИИ.

ассимптоты бывают 2х видов – вертикальные и наклонные.

Определение. Прямая x=x₀ называется вертикальной ассимптотой графика ф-ии y=f(x) если хотя бы один из односторонних пределов ф-ии f(x) в точке x₀ равен +(-) бесконечность.

Ясно, что непрерывная на всей оси ф-я вертикальных ассимптот не имеет.

Определение. Прямая y=kx+b называется наклонной ассимптотой (при к=0 – горизонтальной) графика ф-ии y=f(x) при x стремящемся к +(-) бесконечности, если ф-ию f(x) можно представить в виде:

F(x) = kx + b + a(x), где a(x) стремится к 0 при х стремящемся к +(-) бесконечности.

Если такое представление возможно только при х стремящемся к +бесконечности, то соответствующая наклонная ассимптота называется правой (-бесконечности – левой).

Теорема.

Для того, чтобы график ф-ии y=f(x) имел наклонную ассимптоту y=kx+b необходимо и достаточно чтобы существовали конечные пределы.

= k

И = b

ФОРМУЛА ТЕЙЛОРА.

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ.

где a_ijÎR 1 £ i £ m 1 £ j £ n

Обозначают матрицу А, В, С, или сокращают. A_3×2B_mxnA = (a_ij)_3×4

Матрица, все элементы которой равны 0, называется нулевой и обозначается 0_mxn.

a_ij=0, i<j нижняя треугольная

cyberpedia.su

Матрицы и операции над ними.

Краткий конспект лекций

Определение.Матрицей называется множество чисел, которое составляет прямоугольную таблицу, состоящее изmстрок иnстолбцов

коротко матрицу обозначают так:

где элементы данной матрицы,i– номер строки,j– номер столбца.

Если в матрице число строк равно числу столбцов (m = n), то матрица называетсяквадратнойn-го порядка, а в противном случае –прямоугольной.

Если m=1 и n >1, то получаем однострочную матрицу

которая называется вектор-строкой, если, жеm>1 иn=1, то получаем одностолбцовую матрицу

которая называется вектор-столбцом.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой элементы главной диагонали равны единице, называется единично, обозначаетсяE.

Матрица, полученная из данной заменой ее строки столбцом с тем же номером, называется транспонированнойк данной. Обозначается.

Две матрицы иравны, если равны между собой элементы, стоящие на одинаковых местах, то есть если

при всех i иj(при этом число строк (столбцов) матрицAиBдолжно быть одинаковым).

1°. Суммой двух матрицA=(a_ij) иB=(b_ij) с одинаковым количествомm строк иnстолбцов называется матрицаC=(c_ij), элементы которой определяются равенством

Сумму матриц обозначают C=A+B.

Пример.

2⁰. Произведением матрицыA=(a_ij) на числоλназывается матрица, у которой каждый элемент равен произведению соответствующего элемента матрицыAна числоλ:

λA=λ(a_ij)=(λa_ij), (i =1,2…,m ; j=1,2…,n ).

Пример.

3⁰. Произведением матрицыA=(a_ij), имеющейmстрок иkстолбцов, на матрицуB=(b_ij), имеющейk строк иnстолбцов, называется матрицаC=(c_ij), имеющаяmстрок иnстолбцов, у которой элементc_ijравен сумме произведений элементовi-ой строки матрицыA иj-го столбца матрицыB, то есть

При этом число столбцов матрицы Aдолжно быть равно числу строк матрицыB. В противном случае произведение не определено. Произведение матриц обозначается A*B=C.

Пример.

Для произведения матриц не выполняется равенство между матрицами A*B иB* A, в общем случае одна из них может быть не определена.

Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Пример.Пусть,, тогда согласно правилу умножения матриц имеем

откуда заключаем, что

Определители и их свойства.

Пусть дана квадратная матрица третьего порядка:

(1)

Определение. Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом

и определяемое равенством

.(2)

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «-«, полезно использовать следующее правило треугольников.

+ —

Пример.

Сформулируем основные свойства для определителей третьего порядка, хотя они присущи определителям любого порядка.

1. Величина определителя не изменится, если его строки и столбцы поменять местами, т. е.

2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.

3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

4. Умножение всех элементов одного столбца или одной строки определителя на любое числоλравносильно умножению определителя на это числоλ.

= λ

5. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю.

6. Если элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

7. Если каждый элементn-го столбца (n-ой строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один вn-ом столбце (n-ой строке) содержит первые из упомянутых слагаемых, а другой — вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же.

Например,

8⁰. Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель, то величина определителя не изменится.

Например,

Миноромнекоторого элемента определителя называется определитель, получаемый из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Например, минором элемента а₁определителяΔявляется определитель 2-го порядка

Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1)^p, гдер— сумма номеров строки и столбца, на пересечении которых расположен этот элемент.

Если, например, элемент а₂находятся на пересечении 1-го столбца и 2-ой строки, то для негор=1+2=3 и алгебраическим дополнением является

9⁰. Определитель равен сумме произведений элементов какого–либо столбца или строки на их алгебраические дополнения.

10⁰. Сумма произведений элементов какого–либо столбца или какой–либо строки определителя на алгебраические дополнения соответствующих элементов другого столбца или другой строки равны нулю.

Возникает вопрос, можно ли для квадратной матрицы А подобрать некоторую матрицу, такую что умножив на нее матрицу А в результате получить единичную матрицу Е, такую матрицу называют обратной к матрице А.

Определение. Матрицаназывается обратной квадратной матрицеA, если.

Определение. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.

Всякая невырожденная матрица имеет обратную.

Элементарными преобразованиями матрицявляются:

перестановка местами двух параллельных рядов матрицы;
умножение всех элементов матрицы на число, отличное от нуля;
прибавление ко всем элементами ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Матрица В, полученная из матрицыАс помощью элементарных преобразований, называетсяэквивалентнойматрицей.

Для невырожденной квадратной матрицы

третьего порядка обратная матрица А^-1может быть вычислена по следующей формуле

здесь Δ — определитель матрицы А,A_ij– алгебраические дополнения элементовa_ij матрицыА.

Элемент строки матрицы называется крайним, если он отличен от нуля, а все элементы строки, находящиеся левее него, равны нулю. Матрица называетсяступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. Например:

— не ступенчатая; — ступенчатая.

studfiles.net

Матрица

Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения операций над матрицами сделаны такими,

чтобы было удобно записывать системы линейных уравнений. Обычно матрицу обозначают Заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также

выделение квадратными скобками «[…]», двойными прямыми линиями «||…||») А числа, составляющие матрицу (элементы матрицы), обозначают той же буквой, что и саму матрицу, но маленькой. у каждого элемента матрицы есть 2 нижних индекса (aij) — первый «i» обозначает

номер строки, в которой находится элемент, а второй «j» — номер столбца.

Операции над матрицами

Пусть aij элементы матрицы A, а bij — матрицы B.

•Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы

B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

bij = λaij

•Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны по парной сумме всех соответствующих элементов матриц A и B, то есть каждый

элемент матрица C равен

cij = aij + bij

•Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

cij = aij — bij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

•Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

cij = ∑ aikbkj

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C

есть . Умножение матриц не коммутативно. Это видно хотя бы из того, что если матрицы не квадратные, то можно умножать только одну на другую, но не наоборот. Для

квадратных матриц результат умножения зависит от порядка сомножителей.

Возводить в степень можно только квадратные матрицы.

Единичная матрица

Для квадратных матриц существует единичная матрица E такая, что умножение любой

матрицы на неё не влияет на результат, а именно

EA = AE = A

У единичной матрицы единицы стоят только по

диагонали, остальные элементы равны нулю

•Для некоторых квадратных матриц можно найти так называемую обратную матрицу.

Обратная матрица A — 1 такова, что если умножить матрицу на неё, то получится единичная матрица

AA − 1 = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются

невырожденными, а для которых нет — вырожденными. Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк

(столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется нормированный кососимметрический линейный функционал на строках матрицы. Матрица

вырождена тогда и только тогда, когда ее определитель равен нулю.

Свойства матриц

1.A + (B + C) = (A + B) + C

2.A + B = B + A

3.A(BC) = (AB)C

4.A(B + C) = AB + AC

5.(B + C)A = BA + CA

9.Симметричная матрица A положительно определена (A > 0), если значения у всех ее главных угловых миноров Ak > 0

10.Симметричная матрица A отрицательно определена (A < 0), если матрица ( − A)

положительно определена, то есть если для любого k главный минор k-го порядка Ak имеет знак ( − 1)k

Системы линейных уравнений

Cистему из m уравнений с n неизвестными

a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nxn=b2

amx1+amx2+…+amxn=bm

можно представить в матричном виде

и тогда всю систему можно записать так: AX = B

Операции над матрицами

Пусть aij элементы матрицы A, а bij — матрицы B.

•Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы

B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен bij = λaij

Пример

2*А

Запишем матрицу А

Умножим первый элемент матрицы А на 2

Растянем значения, сначала по горизонтали, а затем по вертикали (можно наоборот)

элемент матрица C равен

cij = aij + bij

Пример

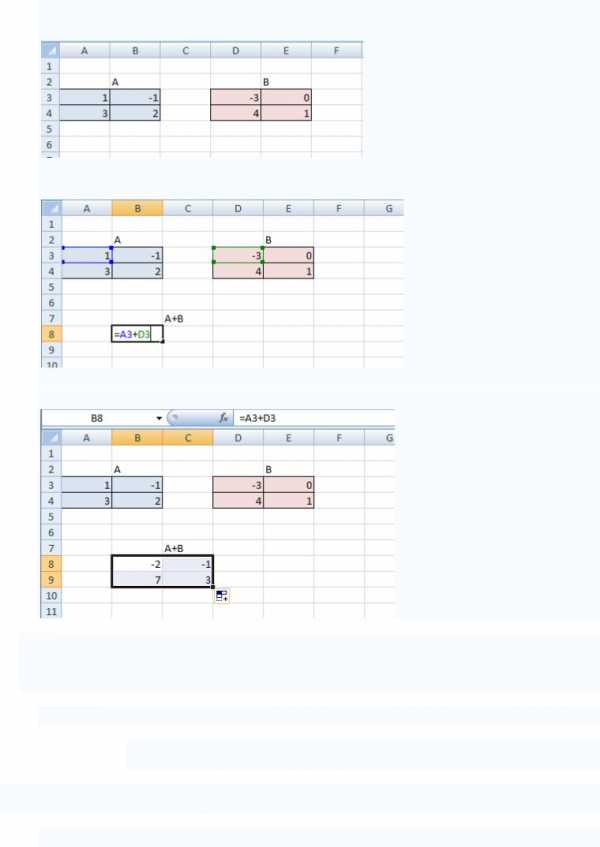
А+В Запишем матрицы А и В

Выполним сложение первых элементов матриц

Растянем значения, сначала по горизонтали, а затем по вертикали (можно наоборот)

cij = aij — bij

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A

Все элементы нулевой матрицы равны нулю.

•Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция

вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

cij = ∑ aikbkj

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно. Это видно хотя бы из того, что если матрицы не квадратные,

то можно умножать только одну на другую, но не наоборот. Для квадратных матриц результат умножения зависит от порядка сомножителей.

Возводить в степень можно только квадратные матрицы.

В текстовом процессоре Excel имеется функция умножения матриц – МУМНОЖ

Пример: А*В

Запишем матрицы А и В

Выделяем область, в которую поместим произведение матриц.

вызываем математическую функцию МУМНОЖ и выделяем сначала матрицу А, а затем В

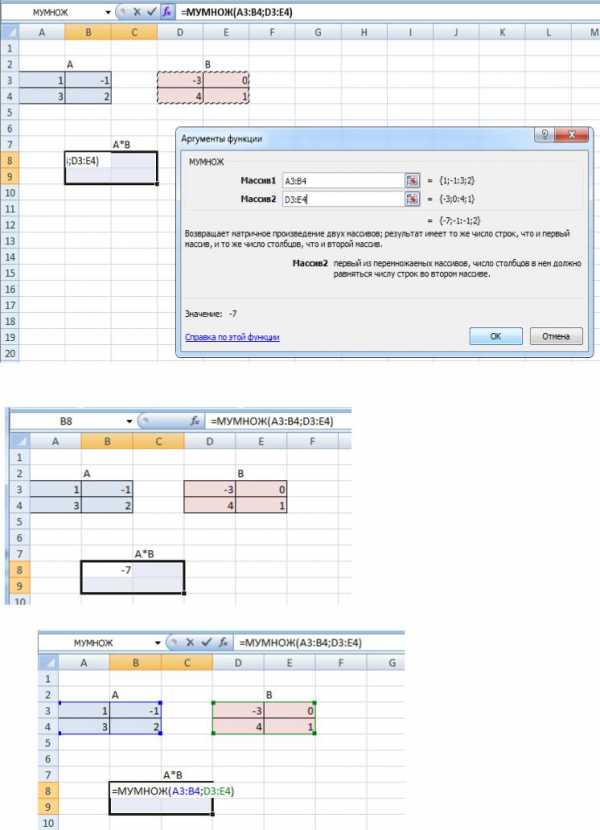
Значение появится только в одной ячейке.

Для заполнения выделенного диапазона нажать кнопку F2 (в ячейке появится формула)

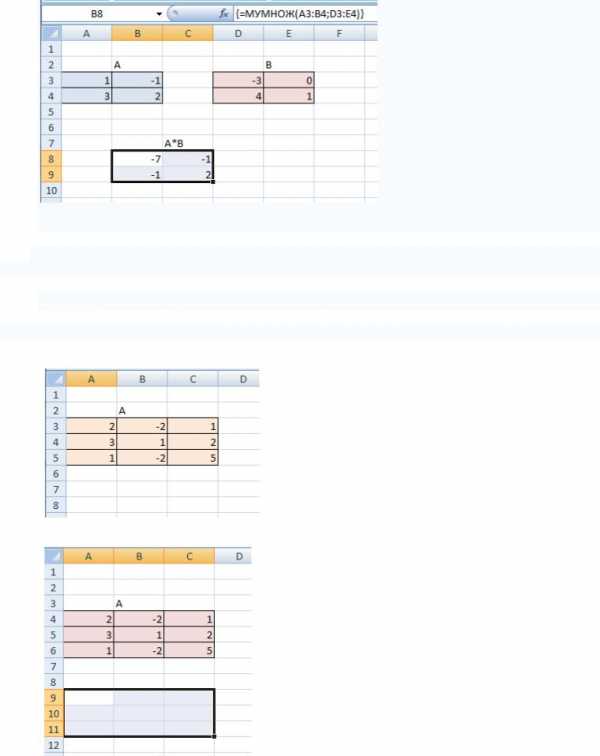
И комбинацию клавиш Ctrl+Shift+Enter

• Нахождение обратной матрицы

Обратная матрица A — 1 такова, что если умножить матрицу на неё, то получится единичная матрица

AA − 1 = E

Пример: найти обратную матрицу А

Записываем матрицу А

Находим обратную матрицу А-1 для этого, выделяем область, в которую поместим обратную

матрицу,

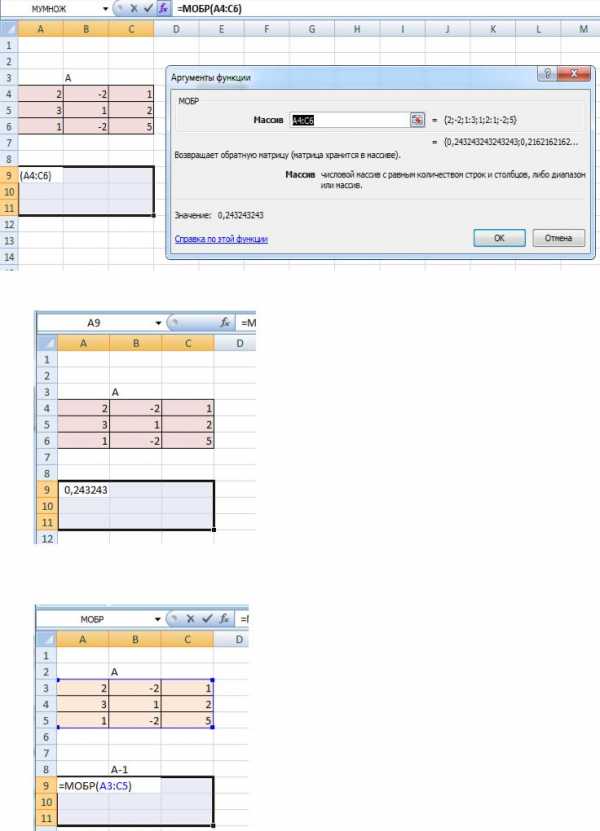
вызываем математическую функцию МОБР и выделяем матрицу А.

Значение появится только в одной ячейке.

Для заполнения выделенного диапазона нажать кнопку F2 (в ячейке появится формула)

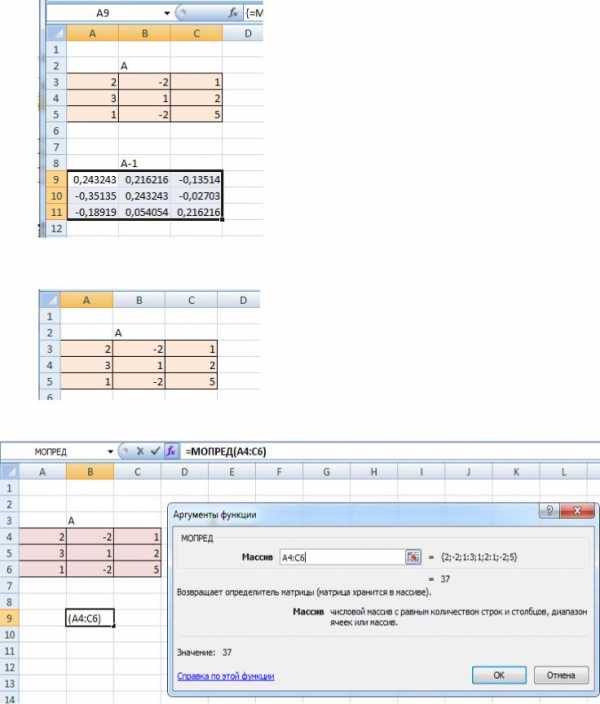
И комбинацию клавиш Ctrl+Shift+Enter

• Нахождение определителя матрицы А

Записываем матрицу А

Выделяем ячейку куда рассчитаем значение определителя и вызываем математическую функцию

МОПРЕД, выделяем матрицу А

studfiles.net

Определение матрицы. Виды матриц.

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки.

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядкомматрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевойи обозначается (0), или просто 0.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольнойматрицей.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональнойматрицей. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичнойматрицей и обозначается буквой E.

Действия над матрицами

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если

, то .

Эту матрицу B называют транспонированнойматрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде .

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по

Правилу

или .

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы. Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Обратная матрица

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратнойдля неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)

Справедлива следующая теорема:

Теорема.Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Итак, чтобы найти обратную матрицу нужно:

1. Найти определитель матрицы A.

2. Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу , элементами которой являются числа A_ij.

3. Найти матрицу, транспонированную полученной матрице , и умножить её на — это и будет обратная матрица .

Аналогично для матриц второго порядка, обратной будет следующая матрица .

Лекция 3

Рекомендуемые страницы:

lektsia.com

Понятие матрицы. Виды Матриц. — КиберПедия

Определение.Матрицей размера m n называется прямоугольная таблица чисел, содержащая mстрок и n столбцов.

= или = , =1,2,…, , 1,2,…, .

– элемент матрицы, стоящий на пересечении -й строки и -го столбца.

Определение. Если , то матрица называется квадратнойn-го порядка, в противном случае – прямоугольной.

Элементы , = 1, 2, …, n квадратной матрицыА образуют ее главную диагональ.

Матрица размера 1хn называется матрицей-строкой, а матрица размера – матрицей-столбцом.

Определение. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.

Определение. Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть

На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой .

Определение. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.

Действия над матрицами

Сложение и вычитание матриц

Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.

Определение.Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

сij = aij + bij

Определение.Вычитание матриц (разность матриц) A — B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицыC равен:

с_ij = a_ij — b_ij

Примеры задач на сложение и вычитание матриц

Умножение матриц

Определение.Результатомумножения матрицA_m×_nиB_n×_kбудет матрицаC_m×_kтакая, что элементматрицыC, стоящий вi-той строке иj-том столбце (c_ij), равен сумме произведений элементов i-той строки матрицыAна соответствующие элементыj-того столбца матрицыB:

c_ij = a_i₁ · b₁_j + a_i₂ · b₂_j + … + a_in · b_nj

Замечание.Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Свойства умножения матриц

(A · B) · C= A · (B · C) — произведение матриц ассоциативно;
(z · A) · B=z · (A · B), гдеz — число;
A · (B + C) = A · B + A · C — произведение матриц дистрибутивно;
E_n· A_nm= A_nm· E_m= A_nm— умножение наединичную матрицу;
A · B ≠ B · A — в общем случае произведение матриц не коммутативно.
Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.

Примеры на умножение матриц
Пример 1.
Найти матрицу C равную произведению матриц A = и B = .
-3
Решение:
Элементы матрицы C вычисляются следующим образом:
c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ = 4·3 + 2·(-3) = 12 — 6 = 6
c₁₂ = a₁₁·b₁₂ + a₁₂·b₂₂ = 4·1 + 2·4 = 4 + 8 = 12
c₂₁ = a₂₁·b₁₁ + a₂₂·b₂₁ = 9·3 + 0·(-3) = 27 + 0 = 27
c₂₂ = a₂₁·b₁₂ + a₂₂·b₂₂ = 9·1 + 0·4 = 9 + 0 = 9
Пример 2.
Найти матрицу C равную произведению матриц A =

-3
-1

и B =
-1
-3

.
Решение:

Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 2·5 + 1·(-3) = 10 — 3 = 7
c12 = a11·b12 + a12·b22 = 2·(-1) + 1·0 = -2 + 0 = -2
c13 = a11·b13 + a12·b23 = 2·6 + 1·7 = 12 + 7 = 19
c21 = a21·b11 + a22·b21 = (-3)·5 + 0·(-3) = -15 + 0 = -15
c22 = a21·b12 + a22·b22 = (-3)·(-1) + 0·0 = 3 + 0 = 3
c23 = a21·b13 + a22·b23 = (-3)·6 + 0·7 = -18 + 0 = -18
c31 = a31·b11 + a32·b21 = 4·5 + (-1)·(-3) = 20 + 3 = 23
c32 = a31·b12 + a32·b22 = (4)·(-1) + (-1)·0 = -4 + 0 = -4
c33 = a31·b13 + a32·b23 = 4·6 + (-1)·7 = 24 — 7 = 17

Определение.Транспонирование матрицы — это операция над матрицей, при которой ее строки и столбцы меняются местами:

(a_ij) ^T= a_ji

Определение. Обратная матрица A⁻¹ — матрица, произведение которой на исходную матрицу A равно единичной матрице E:
A·A^-1 = A^-1·A = E
Обратная матрица для матрицы — го порядка имеет вид:
.
Замечание.Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.
Теорема. Всякая невырожденная матрица имеет обратную, причем одну.
Определение. Квадратная матрица называется невырожденной, если . Если , то называется вырожденной.
Пример. по свойству 6 определителей, то есть – вырожденная.

, значит, – невырожденная.
Пример. Найти матрицу, обратную для .
=3 существует.
Проверка:

cyberpedia.su
Тема 1.1. Матрицы и действия с ними.

Определение и виды матриц.

Действия с матрицами.

Определитель и его свойства.

Алгебраические дополнения и миноры.

Обратная матрица.

Пункт 1. Определение и виды матриц.

Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевойи обозначается (0), или просто 0. Например,

.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольнойматрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

Пункт 2. Действия с матрицами.

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде .

Пример 1. Найти матрицу транспонированную данной.

1.

2.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

Или

Пример 2. Найти сумму матриц:

1. .

2. — нельзя, т.к. размеры матриц различны.

3. .

Сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

1.

2.

3. .

Пример 3.

1. .

2. Найти 2A-B, если , .

.

3. Найти C=–3A+4B.

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

Пример 4.

1. Пусть

Найти элементы c₁₂, c₂₃ и c₂₁ матрицы C.

2. Найти произведение матриц.

.

3. .

4. — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.

5. Пусть

Найти АВ и ВА.

6.

Найти АВ и ВА.

, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.

Умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

При умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

.

infopedia.su
No related posts.

Основные сведения о матрицах

Виды матриц

Операции над матрицами

МАТРИЦЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ. — КиберПедия

Матрицы и операции над ними.

Определители и их свойства.

Матрица

Операции над матрицами

Единичная матрица

Свойства матриц

Системы линейных уравнений

Операции над матрицами

Определение матрицы. Виды матриц.

Понятие матрицы. Виды Матриц. — КиберПедия

Тема 1.1. Матрицы и действия с ними.

Добавить комментарий Отменить ответ