5. Последовательность независимых испытаний (схема Бернулли). Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа
Вероятность появления событияраз внезависимых испытаниях (опытах), в каждом из которых вероятность появления события равна, определяетсяформулой Бернулли: , где.
Вероятность появления события не менее раз виспытаниях вычисляется по формуле
или .
Вероятность появления события хотя бы один раз в испытаниях будет.
Наивероятнейшее число появлений события внезависимых испытаниях.
Теорема Пуассона. Вероятность того, что в независимых испытаниях в
каждом из которых вероятность появления события равна , событие наступит ровнораз при достаточно большоми малом
приближенно равна ,
где .
Локальная теорема Муавра-Лапласа.
,
где .
Интегральная теорема Муавра-Лапласа. Вероятность того, что в независимых испытаниях, в каждом из которых вероятность появления события равна, событие наступит не менеераз и не болеераз при достаточно большомприближенно равна
,
где — функция Лапласа,
.
Типовые задачи для решения в аудитории
1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен) : а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми?
Решение. Так как противники равносильны, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны .
а) Вероятность выиграть три партии из четырех
.
Вероятность выиграть пять партий из восьми
.
Так как , то вероятнее выиграть три партии из четырех.
б) Вероятность выиграть не менее трех партий из четырех
,
а вероятность выиграть не менее пяти партий из восьми
Так как , вероятнее выиграть не менее пяти партий из восьми.
2. Из таблицы случайных чисел наудачу выписаны 200 двузначных случайных чисел (от 0 до 99). Определить вероятность того, что среди них число 33 встретиться: а) три раза; б) четыре раза.
Решение. Вероятность того, что наудачу выбранное двузначное число равно 33, равна , поскольку выбирается одно из 100 возможных. Число испытаний. Так как числовелико, а вероятностьмала, воспользуемся формулой Пуассона:
,
где .
а) ; б).
3. Вероятность появления события при одном опыте равна 0,3. С какой вероятностью можно утверждать, что частота этого события при 100 опытах будет лежать в пределах от 0,2 до 0,4?
Решение. Для того чтобы частота лежала в пределах от 0,2 до 0,4 в серии из 100 опытов, число появлений события должно быть не менее 20 и не более 40.
Воспользуемся интегральной теоремой Муавра-Лапласа:
.
По условию , следовательно:
,
.
studfiles.net
14. Локальной и интегральной формуле Муавра – Лапласа
Локальная теорема Муавра-Лапласа.
Вычисление вероятности по формуле Бернулли становится затруднительным при больших, поскольку. Поэтому на практике применяют приближенные формулы. Одна из них формула Муавра-Лапласа.
где
Функция — четная:; достигает максимумав точке. При этомбыстро стремится к нулю с увеличением абсолютной величины:
Интегральная формула Муавра-Лапласа.
Если нас интересует вероятность того, что в серии из испытаний событиепоявится не менееи не болеераз, то
где
Здесь — функция Лапласа. Функциянечетная. При возрастанииот 0 дофункциябыстро возрастает почти до 0,5.,. Можно считатьпри всех.
3 Частота и вероятность
Относительной частотой события называют отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний.
Вероятность вычисляют до опыта, а относительную частоту — после.
В различных опытах относительная частота изменяется мало (тем меньше, чем больше произвели испытаний) и колеблется возле некоторого постоянного числа — вероятности.
35. Корреляционный момент и коэфф.Корреляции.
Корреляционным моментом случайных величин X и Y называют математическое ожидание произведения их отклонений.
Для дискретных величин
Для непрерывных величин
Теорема. Корреляционный момент двух независимых случайных величин равен 0
Коэффициентом корреляции независимых случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
34 Зависимые и независимые случайные величина.
Случайные события называются независимыми, если появление одного из них никак не влияет на вероятность появления других событий.
Для независимых событий справедлива теорема умножения вероятностей: вероятность совместного (одновременного) появления нескольких независимых случайных событий равна произведению их вероятностей:
Р(А1и А2 и А3 … и Аk) = Р(А1) ∙Р(А2) ∙…∙Р(Аk). (7)
Совместное (одновременное) появление событий означает, что происходят события и А1, и А2 ,и А3 … и Аk .
Если А и В зависимые события, то вероятность наступления события В первым (т.е. до события А) называется безусловной вероятностью этого события и обозначается Р(В). Вероятность наступления события В при условии, что событие А уже произошло, называется условной вероятностью события В и обозначается Р(В/А) или РА (В).
Аналогичный смысл имеют безусловная – Р(А) и условная – Р(А/В) вероятности для события А.
Теорема умножения вероятностей для двух зависимых событий: вероятность одновременного наступления двух зависимых событий А и В равна произведению безусловной вероятности первого события на условную вероятность второго:
Р(А и В) = Р(А) ∙Р(В/А) , если первым наступает событие А, или
Р(А и В) = Р(В) ∙Р(А/В), если первым наступает событие В.
studfiles.net
5.9. Интегральная формула Муавра – Лапласа
Для того, чтобы определить вероятность попадания числа m (появления события A в схеме Бернулли при большом числе испытаний n) в заданный промежуток [а,в]: , можно использовать интегральную формулу Муавра – Лапласа:
где
– функция Лапласа, значения которой находятся по таблицам.
Для относительной частоты (частости) m/n появления события A в n испытаниях Бернулли справедлива приближенная формула
Для числа m появлений события A справедлива приближенная формула
Примеры:
______________________________________________________
1. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью q = 0,25. Найти вероятность того, что количество спелых арбузов будет находиться в пределах от 560 до 600.
Из условия задачи имеем n=768 испытаний Бернулли с вероятностью найти зрелый арбуз, равной р=0,75. Если m – число удачных выборов, то требуется найти вероятность , где a = 560, b = 600.
Поскольку
то по интегральной формуле Муавра – Лапласа получим:
2. Сколько нужно произвести бросаний монеты, чтобы с вероятностью 0,99 можно было утверждать, что относительная частота выпадения герба отличается от 0,5 по модулю не более чем на ?
По формуле , в которой , имеем:
По таблицам значений функции Лапласа находим, что
Откуда выражаем п и, подставляя p=0,5; q=0,5, получим:
________________________________________________________________
5.10. Случайные величины. Закон распределения случайной величины
Случайной величиной называется величина, которая в результате опыта может принять определенное, но заранее не известное, значение. Дискретной называют случайную величину, возможные значения которой есть отдельные числа, которые можно пронумеровать. Например, число участников испытания, количество положительных тестов в психодиагностике.
Непрерывной называется случайная величина, которая может принимать значения из некоторого бесконечного или конечного промежутка, т.е. возможные значения заполняют непрерывно некоторый промежуток. Например, скорость некоторого объекта, ошибка взвешивания на точных весах и т.д.
Случайные величины обозначаются большими буквами X, Y, Z, а их возможные значения – малыми буквами x, y, z. Запись X= x означает, что случайная величина Х приняла значение х, запись Р(Х=х) означает вероятность того, что Х приняла значение х.
Каждое значение дискретной случайной величины появляется с некоторой вероятностью. Законом распределения случайной величины называется соответствие между значениями случайной величины и их вероятностями. О случайной величине говорят, что она имеет данный закон распределения. Простейшей формой задания закона распределения является таблица, называемая рядом распределения, в которой перечислены возможные значения случайной величины и соответствующие им вероятности (таблица 5.1).
Таблица 5.1
хi | x1 | x2 | … | xn |
pi | p1 | p2 | … | pn |
В этой таблице – это вероятность события . Так как в каждом испытании случайная величина Х принимает одно и только одно возможное значение, события Х = х1, Х = х2, … Х = хп образуют полную группу, а, значит, сумма вероятностей равна единице:
=1.
Пример:
_________________________________________________________
Всхожесть семян данного растения определяется вероятностью 0,6. Пусть X – случайная величина – число появившихся растений из 5 семян. Найти закон распределения X.
Случайная величина X может принимать значения 0, 1, 2, 3, 4 ,5. Вероятности, соответствующие этим значениям случайной величины – . Вычислим эти вероятности. Можно считать, что имеется схема n = 5 испытаний Бернулли с вероятностью успешного результата p = 0,6. Тогда по формуле Бернулли . При n = 5, p = 0,6, q = 0,4 находим: ;.
Таким образом, получаем закон распределения случайной величины X:
хi | 0 | 1 | 2 | 3 | 4 | 5 |
pi | 0,01024 | 0,0768 | 0,2304 | 0,3456 | 0,2592 | 0,07776 |
Можно проверить, что =1.
_____________________________________________________________
studfiles.net
Локальная теорема Муавра –Лапласа.
Лапласом
была получена важная приближенная
формула для вероятности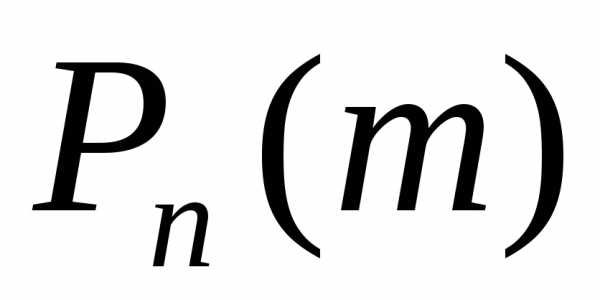 
появления события
точно
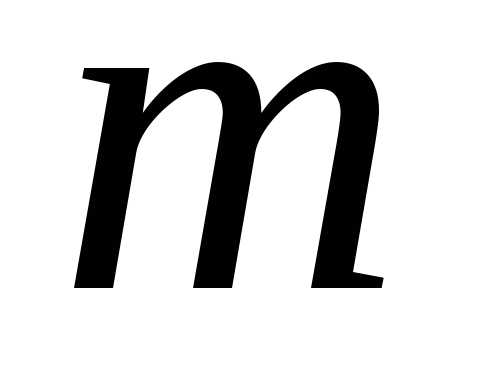раз, при условии, что
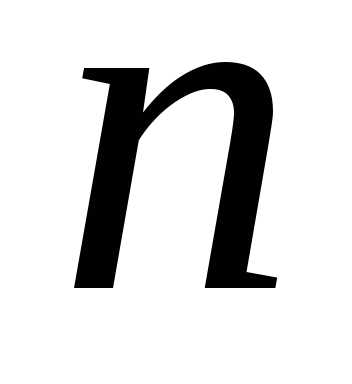достаточно велико. В отличие от формулы
Пуассона здесь нет ограничения на
малость величины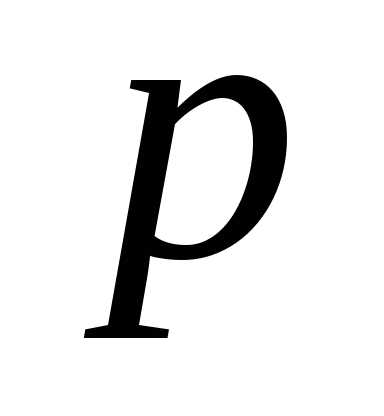
в отдельном испытании, т.е. область
применимости формулы Лапласа шире.
Теорема.
Вероятность того, что в условиях схемы
Бернулли событие
при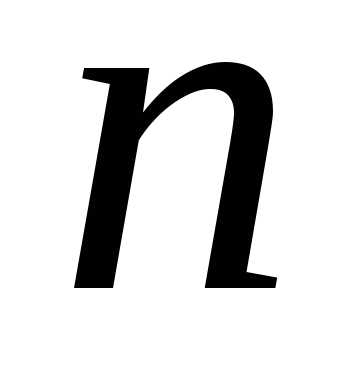
испытаниях появится точно
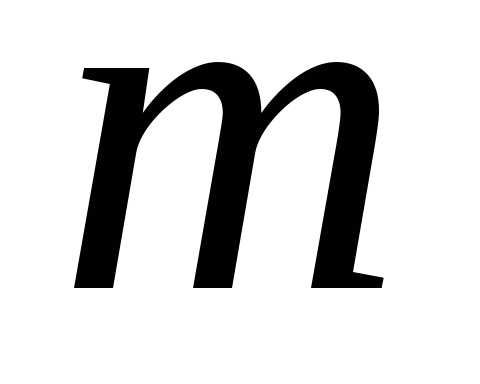раз, выражается приближенной формулой
Лапласа
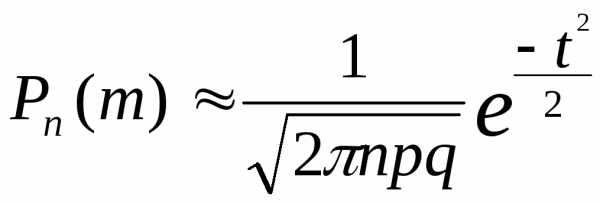
где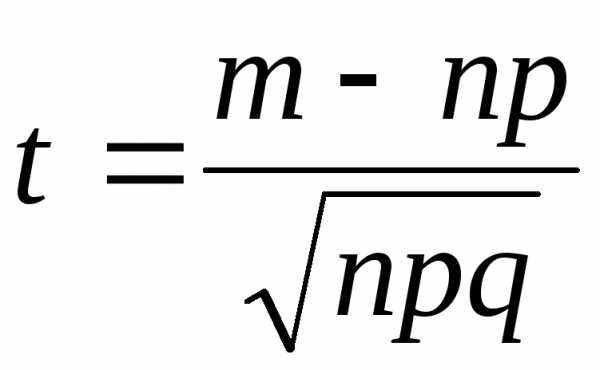 
.
Формулу Лапласа иногда называют асимптотической формулой, поскольку доказано, что относительная ошибка формулы Лапласа стремится к нулю при .
Интегральная (глобальная) теорема Муавра – Лапласа.
Интегральная
теорема Муавра-Лапласа содержит
приближенную формулу для вероятности
того, что событие
появится не менее
раз и не более
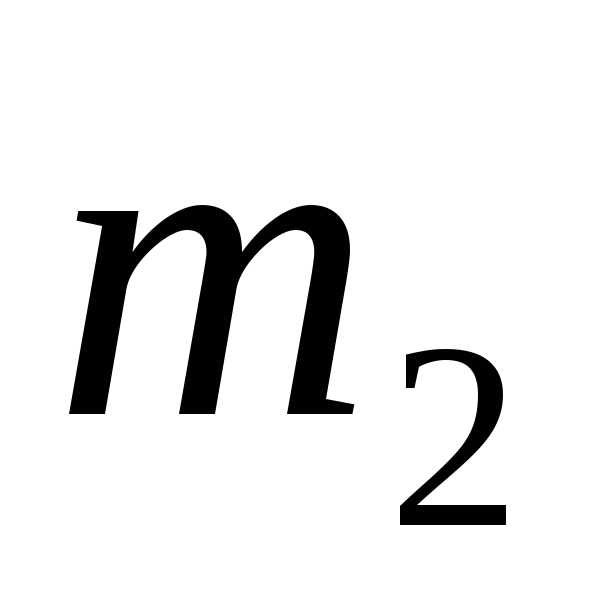раз.
Теорема. Вероятность того, что событие
появится в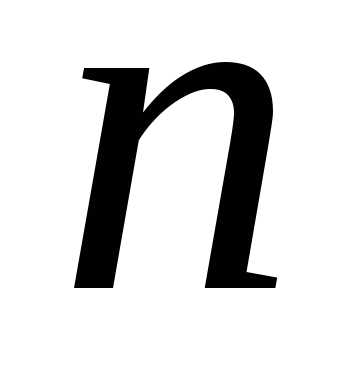
испытаниях от
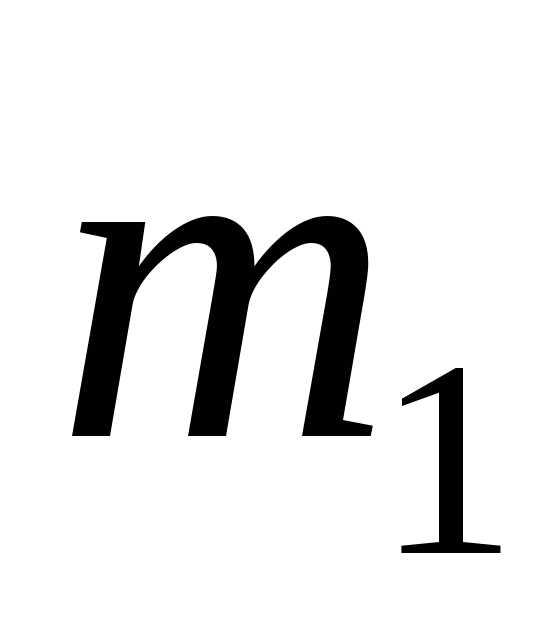до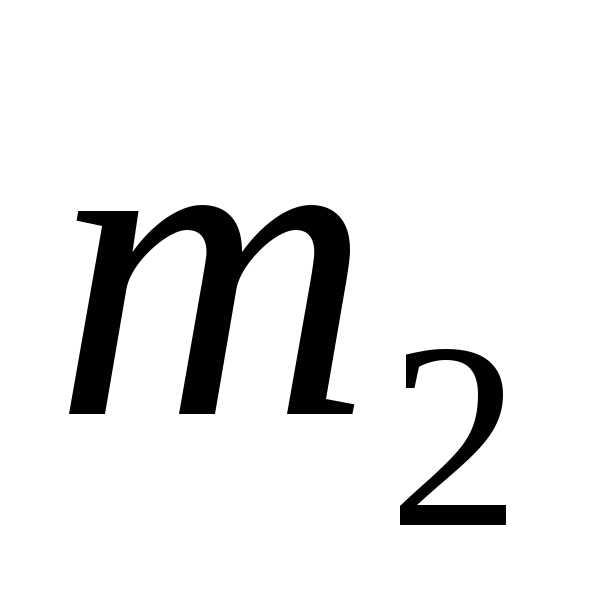
раз, приближенно равна определенному
интегралу
,
где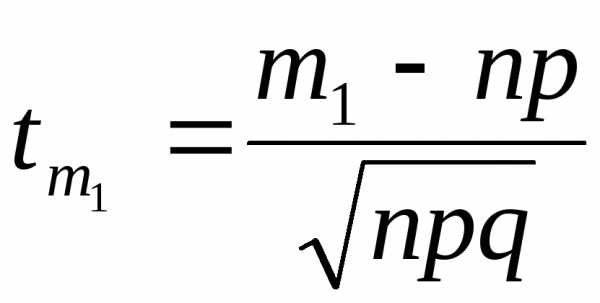 
;
.
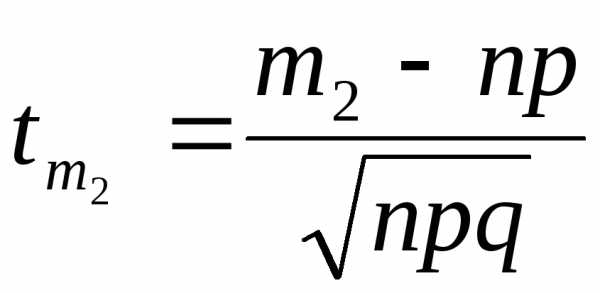
Доказательство. На основании теоремы сложения вероятностей несовместных событий
.
Или, используя локальную теорему Лапласа,
,
Введем обозначение ,
И
запишем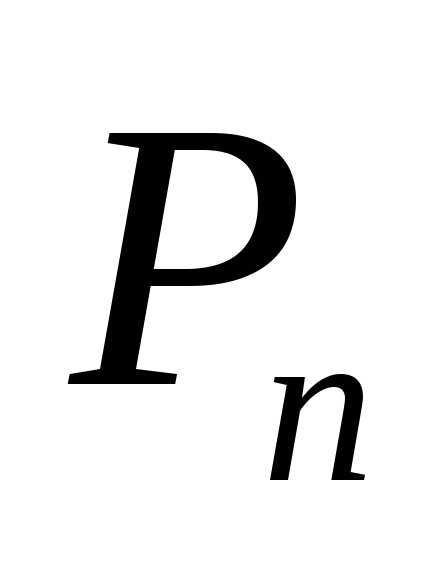 
в виде.
Очевидно,
при
величина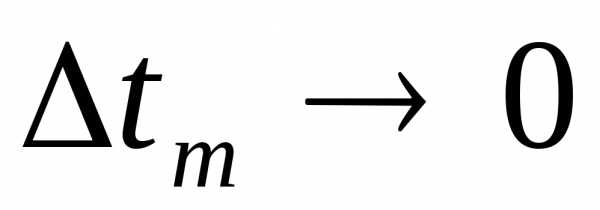
и
последняя сумма стремится к определенному
интегралу:
,
что и требовалось доказать.
Введем стандартный интеграл Лапласа (функцию Лапласа):
,
который, очевидно, является первообразной функции Гаусса
.
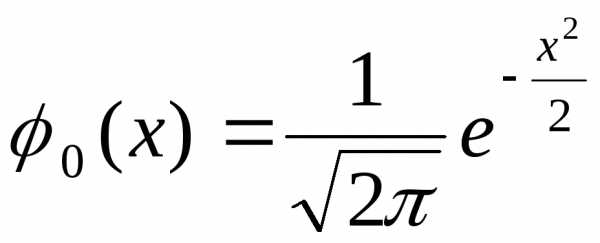Тогда на основании формулы Ньютона – Лейбница можно записать
.
Значения
функци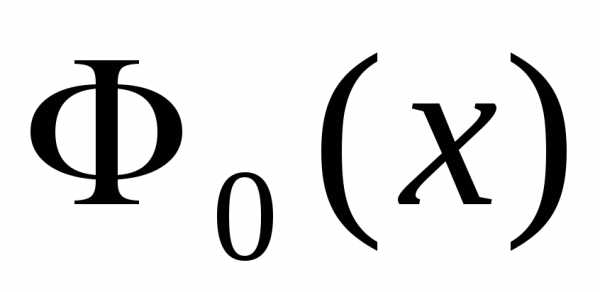й 
и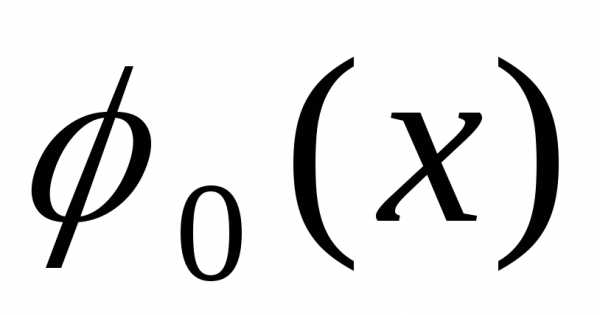
обычно находятся из таблиц, причем
таблицы обычно даны лишь для неотрицательных
значений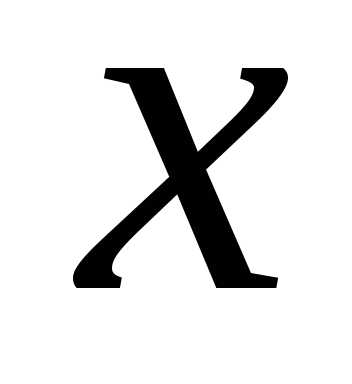
,
поскольку
– четная функция, а
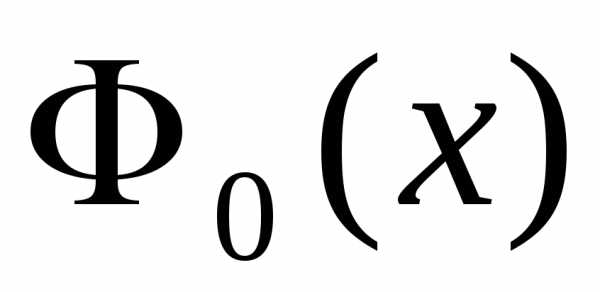– нечетная.
Лекция 6. Случайная величина и ее функция распределения. Свойства функции распределения.
Одним из важнейших понятий теории вероятностей является понятие случайной величины.
Случайнойназывают величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Пример 1. Число родившихся мальчиков среди ста новорожденных – случайная величина, имеющая следующие возможные значения: 0, 1,… 100.
Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, является случайной величиной, которая зависит не только от установки прицела, но и от силы и направления ветра, температуры, влажности и т.д. Возможные значения этой случайной величины принадлежат некоторому промежутку (a,b).
Случайная величина обычно обозначается прописной латинской буквой (), ее конкретные значения – строчными буквами ().
Более
строгое формально-математическое
определение случайной величины: случайной
величиной называется функция
,
определенная на множестве элементарных
событий
,
.
Случайные величины делятся на дискретныеинепрерывные.
Дискретной(прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетное множество значений).
Непрерывнойназывают случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
studfiles.net
7.4. Интегральная и локальная теоремы Муавра – Лапласа. Следствия.
Интегральная теорема Муавра—Лапласа. Если
вероятность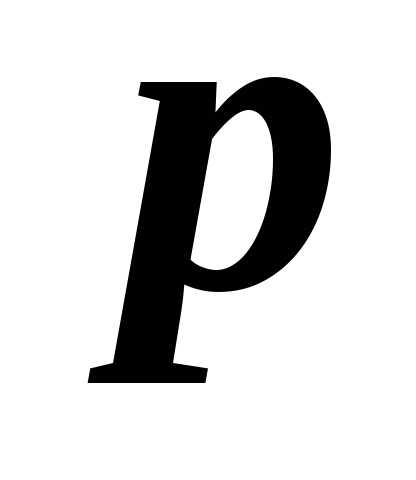 
наступления
события 
в каждом испытании постоянна и отличнаот 
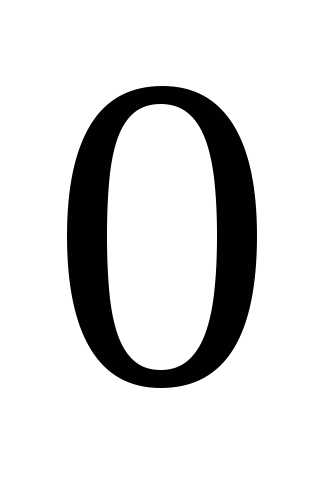и
,
то вероятность того, что число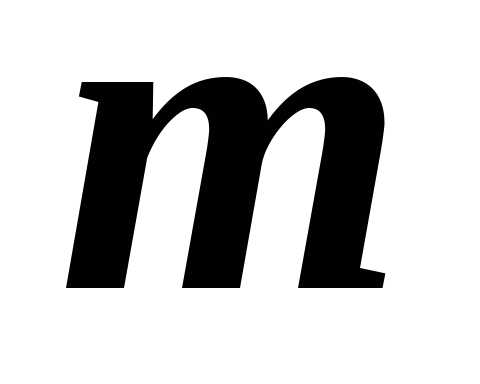
наступления события
в 
независимых испытаниях заключено в
пределах от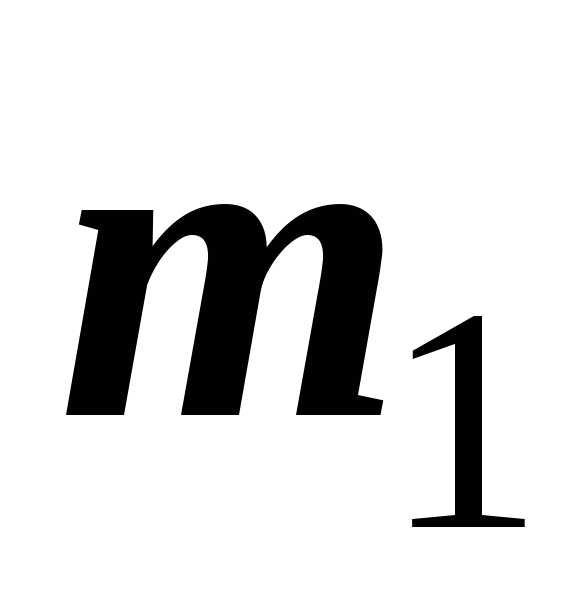
до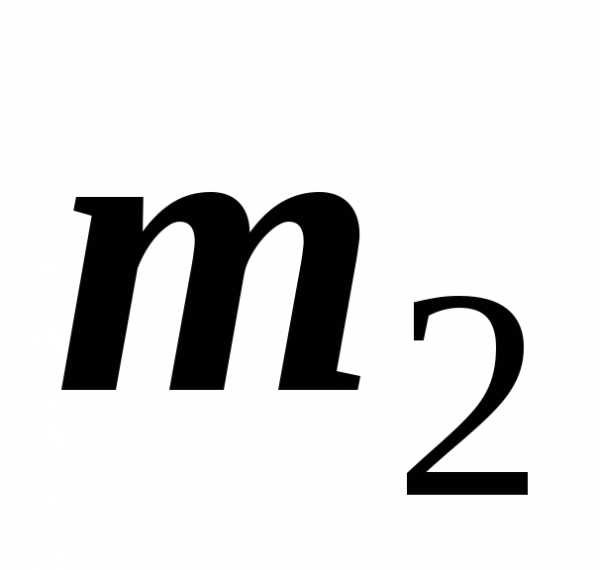
(включительно),
при достаточно большом числе 
приближенноравна
, (1)
где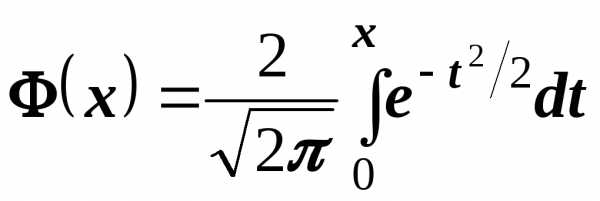 
-функция
Лапласа.
Формула (1) называется интегральной формулой Муавра— Лапласа.
Чем больше 
, тем точнее
эта формула. При выполнении
условия интегральная
формула (1) дает незначительную погрешность
вычисления вероятностей.
Следствия
Следствие 1. Если вероятность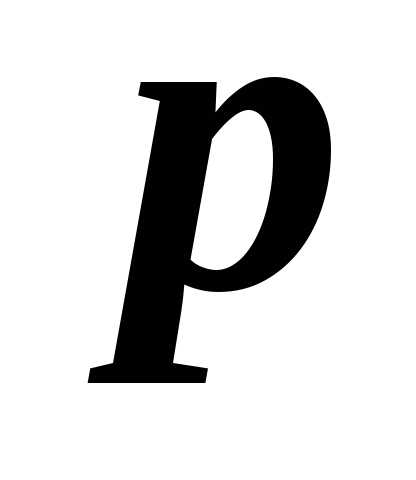 
наступления
события 
в каждом испытании постоянна и отличнаот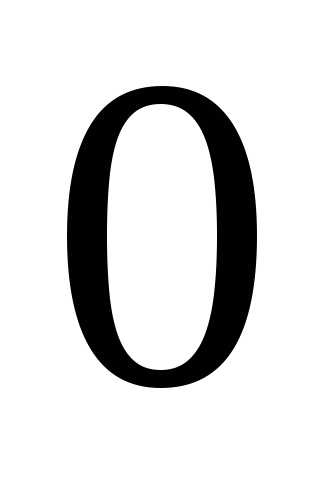 
и
,
топри
достаточно большом
числе 
независимых испытаний вероятность
того, что частота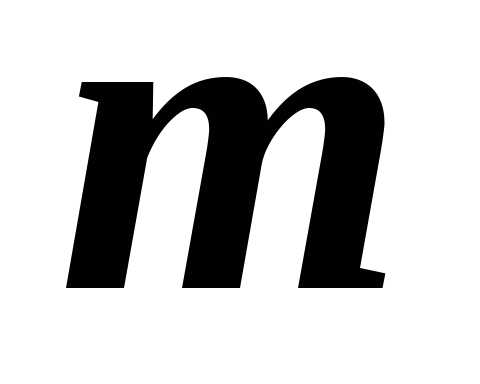
наступления события
отличается от произведения
по
абсолютной величине не более, чем на
величину 
,
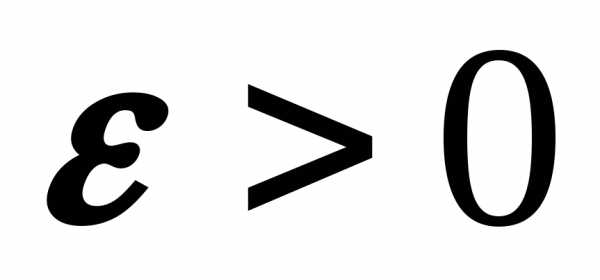определяется по формуле
. (2)
Доказательство.
Следствие 2. Если вероятность наступления
события 
в каждом испытании постоянна и отличнаот 
и
,
топри
достаточно большом
числе 
независимых испытаний вероятность
того, что частость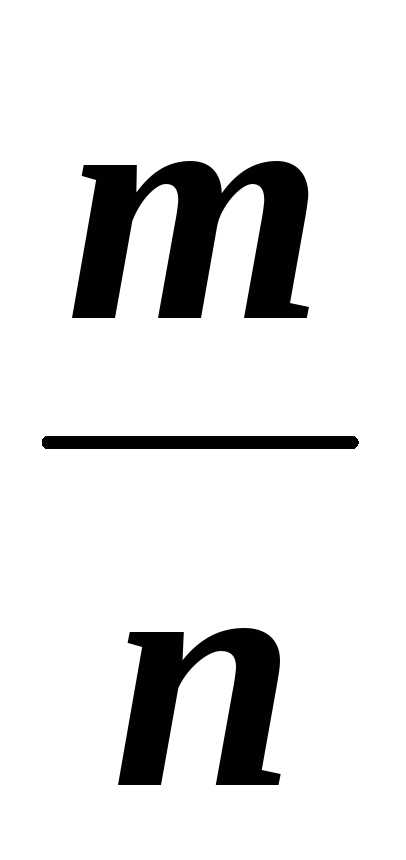
наступления события
отличается от вероятности этого события
в отдельном испытании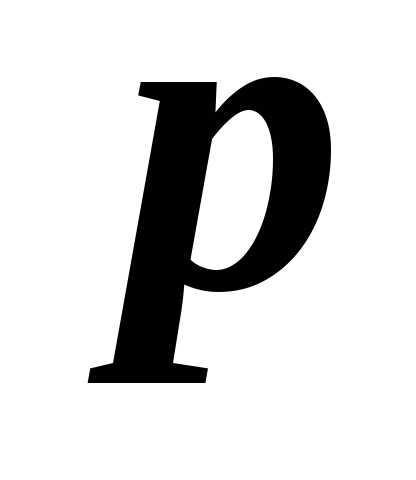
по абсолютной величине не более,
чем на величину 
,
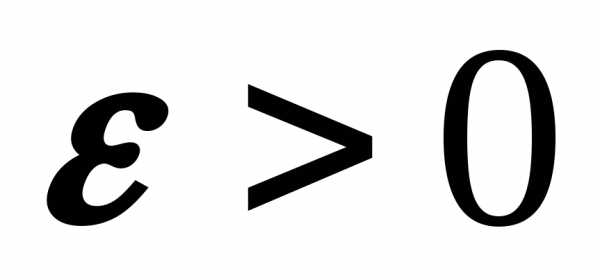определяется по формуле
.(3)
Доказательство.
Локальная теорема Муавра-Лапласа. Если вероятность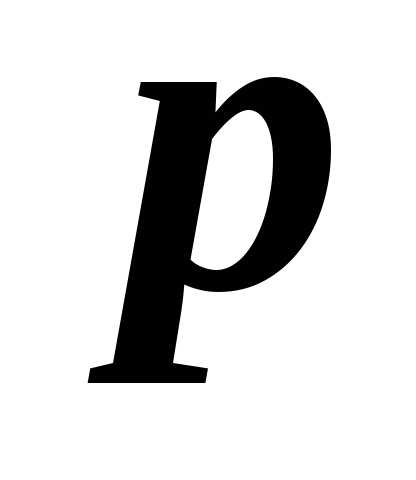 
наступления
события 
в каждом испытании постоянна и отличнаот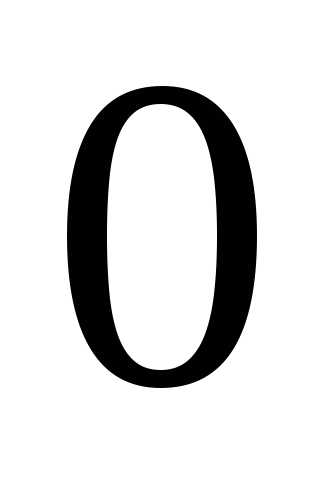 
и
,
топри
достаточно большом
числе 
независимых испытаний вероятность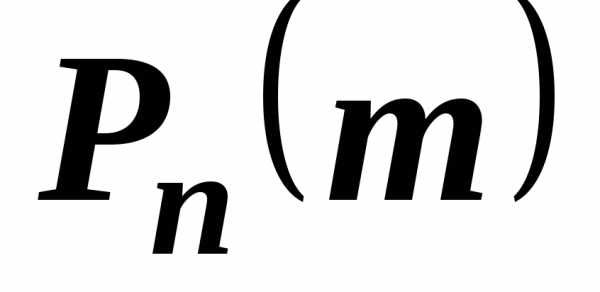
того, чтособытие 
произойдет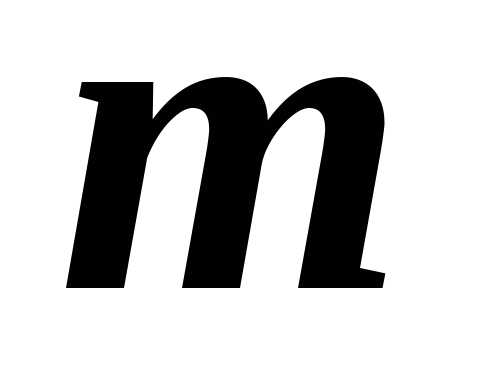
раз в
независимых испытаниях определяется по
формуле
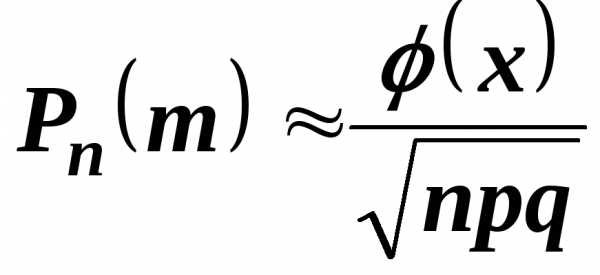, (4)
где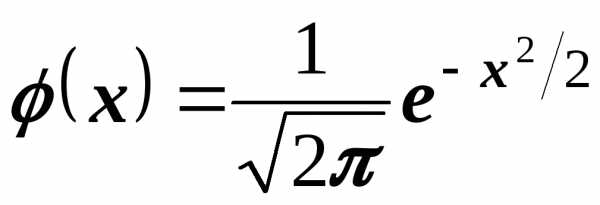 
,
.
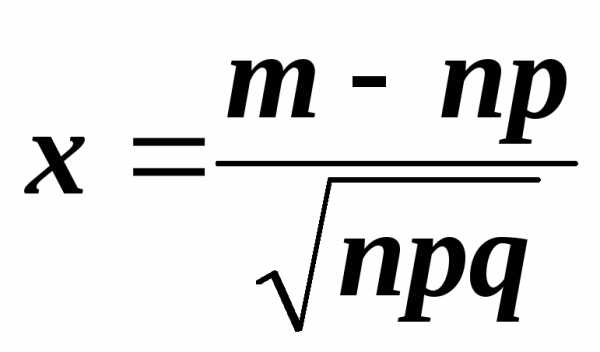Формула (4) называется локальной формулой Муавра—Лапласа.
Чем больше 
, тем точнее
эта формула. При выполнении
условия локальная
формула (4) дает незначительную погрешность
вычисления вероятностей.
Таблица значений функции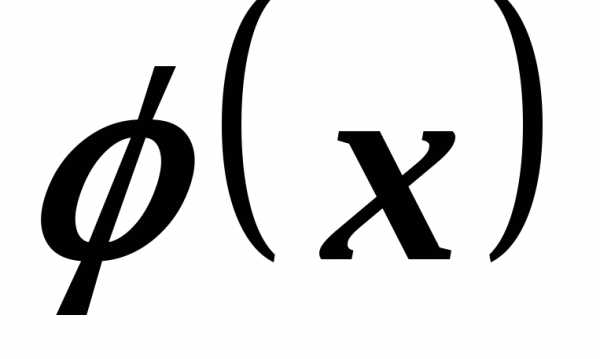 
приведена в
приложении 1.
109
studfiles.net
Интегральная теорема Муавра – Лапласа — МегаЛекции
Формула Бернулли.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас интересует не результат каждого выстрела, а общее число попаданий. Такие задачи решаются достаточно просто, если опыты являются независимыми.
Определение. Независимыми относительно события А испытаниями называются такие, в которых вероятность события А в каждом испытании не зависит от исходов других испытаний.
Пример. Несколько последовательных выниманий карты из колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются; в противном случае это – зависимые опыты.
Пример. Несколько выстрелов представляют собой независимые опыты только в случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы (стрельба очередью, бомбометание серией), выстрелы представляют собой зависимые опыты.
Независимые испытания могут производиться в одинаковых или различных условиях. В первом случае вероятность события А во всех опытах одна и та же, во втором случае вероятность события А меняется от опыта к опыту. Первый случай связан со многими задачами теории надежности, теории стрельбы и приводит к так называемой схеме Бернулли, которая состоит в следующем:
1) проводится последовательность n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться;
2) вероятность появления события А в каждом испытании постоянна и равна , как и вероятность его не появления .
Формула Бернулли, с помощью которой находится вероятность появления события А k раз в n независимых испытаниях, в каждом из которых событие А появляется с вероятностью p:
. (1)
Замечание 1. С возрастанием n и k применение формулы Бернулли связано с вычислительными трудностями, поэтому формула (1) применяется, в основном, если k не превосходит 5 и n не велико.
Замечание 2. В связи с тем, что вероятности по форме представляют собой члены разложения бинома , распределение вероятностей вида (1) называется биномиальным распределением.
Пример. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность пяти попаданий при шести выстрелах.
Решение. Так как , то , кроме того и . Пользуясь формулой Бернулли, получим:
Пример. Производится четыре независимых выстрела по одной и той же цели с различных расстояний. Вероятности попадания при этих выстрелах равны соответственно:
.
Найти вероятности ни одного, одного, двух, трех и четырех попаданий:
Решение. Составляем производящую функцию:
откуда
Пример. Производится пять независимых выстрелов по цели, вероятность попадания в которую равна 0,2. Для разрушения цели достаточно трех попаданий. Найти вероятность того, что цель будет разрушена.
Решение. Вероятность разрушения цели вычисляем по формуле:
.
Пример. Производится десять независимых выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0,1. Для поражения цели достаточно одного попадания. Найти вероятность поражения цели.
Решение. Вероятность хотя бы одного попадания вычисляем по формуле:
3. Локальная теорема Муавра-Лапласа
В приложениях часто приходится вычислять вероятности различных событий, связанных с числом появлений события в n испытаниях схемы Бернулли при больших значениях n. В этом случае вычисления по формуле (1) становятся затруднительными. Трудности возрастают, когда приходится ещё суммировать эти вероятности. Затруднения при вычислениях возникают также при малых значениях p или q.
Лаплас получил важную приближенную формулу для вероятности появления события А точно m раз, если — достаточно большое число, то есть при .
Локальная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы , , величина ограничена равномерно по m и n, то вероятность появления события А ровно m раз в n независимых испытаниях приближенно равна
(4)
где — функция, значения которой определяются таблично.
Замечание. Формулу (4) часто используют при и , хорошие приближения эта формула дает также при . Указания о границах применимости формулы (4) являются очень приближенными и носят скорее качественный характер: к ним следует относиться с осторожностью. Отметим также, что из того, что следует стремление к бесконечности m. Это значит, что m и n должны отличаться друг от друга не очень сильно, так, для локальная теорема дает плохое приближение.
Пример. Вероятность поражения цели при одном выстреле равна 0,3. Найти вероятность того, что при 100 выстрелах цель будет поражена 30 раз.
Решение. Так как , , , , то получим:
.
Отсюда по формуле (4) имеем:
.
Интегральная теорема Муавра – Лапласа
Зададимся вопросом: какова вероятность того, что в условиях схемы Бернулли событие А, имеющее вероятность , при испытаниях появляется не менее раз и не более раза?
Введем функцию Лапласа:
, (11)
Интеграл не выражается через элементарные функции, для его вычисления используются специальные таблицы. Функция обладает следующими свойствами:
1) ;
2) ;
3) , то есть функция нечетна;
4) — монотонно возрастающая функция;
5) при , с точностью до тысячных, можно принять .
Интегральная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы , то при вероятность появления события А ровно в n независимых испытаниях не менее раз и не более раз приближенно равна
(12)
где — функция Лапласа, значения которой определяются таблично, .
Замечание 1. Для того, чтобы можно было пользоваться таблицей функции Лапласа, соотношение (12) преобразуют к виду:
.
Замечание 2. Функция Лапласа является нечетной функцией . При можно принять .
Пример. Вероятность того, что деталь не прошла проверку ОТК, равна . Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию , , , , . Воспользуемся интегральной теоремой Лапласа:
Найдем
,
.
Таким образом, получим:
.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru