Формулы сокращенного умножения
Формулы сокращенного умножения| Номер | Название формулы | Короткая запись | Раскрытие скобок/разложение на множители |
| (1) | Разность квадратов | a2-b2 | (a-b)(a+b) |
| (2) | Квадрат суммы/разности | (a±b)2 | a2±2ab+b2 |
| (3) | Квадрат суммы для n переменных | (a1+a2+…+an)2 | a12+a22+…+an2+2∑i,jaiaj |
| (4) | Сумма/разность кубов | a3±b3 | (a±b)(a2∓ab+b2) |
| (5) | Куб суммы/разности | (a±b)3 | a3±3a2b+3ab2±b3 |
| (6) | Куб суммы для n переменных | (a1+a2+. ..+an)3 ..+an)3 | a13+a23+…+an3+3∑i,jai2aj+6∑i,j,kaiajak |
| (7) | Разность четвертых степеней | a4-b4 | (a-b)(a+b)(a2+b2) |
| (8) | Четвертая степень суммы/разности | (a±b)4 | a4±4a3b+6a2b2±4ab3+b4 |
| (9) | Сумма/разность nх степеней | an-bn | (a±b)(an-1+an-2b+an-3b2+…+b n-3a2+bn-2a+bn-1) |
| (10) | Сумма (2n+1)х степеней | a2n+1+b2n+1 | (a+b)(a2n-a2n-1b+a2n-2b2+.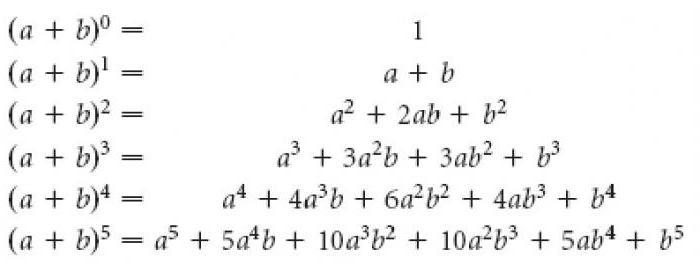 ..+b2n-2a2-b2n-1a+b2n) ..+b2n-2a2-b2n-1a+b2n) |
| (11) | Nая степень суммы/разности | (a±b)n | an±(n1)an-1b+(n2)an-2b2±..+(nn-2)a2bn-2±(nn-1)abn-1+bn |
— версия для печати
- Определение
- Nая степень числа — результат умножения числа на себя n раз. Также квадратом числа называется результат возведения числа в степень
- Пример:
- (4a—3b)3 = 64a3 — 144a2b + 108ab2 — 27b3
- Пояснение
- Под (nk) подразумевается биномиальный коэффициент, равный
(nk) = n!
(n-k)!k!
Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см.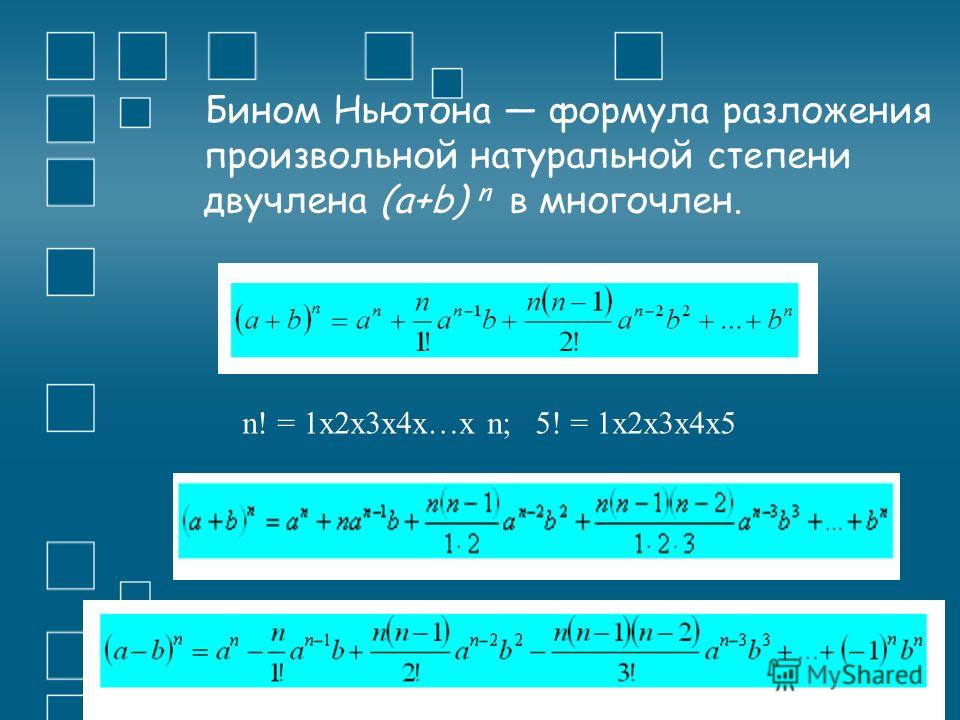 раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
Формулы сокращенного умножения
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 — b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 — ab + b2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 — b3 = (a — b) (a2 + ab + b2)
8. Разность чисел в четвертой степени
(a — b)4 = a4 — 4a3b + 6a2b2 — 4ab3 + b4
9. Сумма чисел в четвертой степени
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
10. Разность чисел в пятой степени
(a — b)5 = a5 — 5a4b + 10a3b2 — 10a2b3 + 5ab4 — b5
11. Сумма чисел в пятой степени
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
12. Квадрат трехчлена
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
13. Квадрат линейной формы
Квадрат линейной формы
(a + b + c + … + u + v)2 = a2 + b2 + c2 + … + u2 + v2 + 2(ab + ac + … + au + av + bc + … + bu + bv + … + uv)
14. Куб трехчлена
(a + b + c)3 = a3 + b3 + c3 + 3a2b + 3ab2 + 3a2c + 3ac2 + 3b2c + 3bc2 + 6abc
Формулы факторинга
Ниже приведены некоторые формулы факторинга, которые используются для факторизации некоторых общих математических выражений.
a 2 — b 2 = (a — b) × (a + b)
a 4 — b 4 = (a — b) × (a + b) × (a 2 + b 2 )
a 6 — b 6 = ( a — b ) × ( a + b ) × ( a 2 — ab + b 2 ) × ( a 6 + 6 +
6 аб + б 2 )
а 8 — b 8 = ( a — b ) × ( a + b ) × ( a 2 + b 2 ) × ( a 4 + b 4 )
a +
3 b
3 = (a + b) × (a 2 — ab + b 2 )a 3 — b 3 = (a — b) × (a + 2 ab 2 )
A 5 — B 5 = (A — B) × (A 4 + A 3 B + A 2 B 2 + AB 3 + B . 0005 4 )
0005 4 )
A 5 + B 5 = (A + B) × (A 4 — A 3 B + A 2 B 2 — AB 3 + B . 4 )
A 6 — B 6 = (A — B) × (A 5 + A 4 B + A 3 B 2 + A 2 B 3 B 2 + A 2 B 3 6. + ab 4 + b 5 )
a 6 + b 6 = ( a 2 + b 2 ) × ( a 4 — A 2 B 2 + B 4 )
A 7 — B 7 = (A — B) × (A 6 + A 5 B + A 4 B 2 + A 3 B 3 + A 2 B 4 + AB 5 + B 6 )
A 4 + A 2 B 2 6. + b 4 = (a 2 + ab + b 2 ) × (a 2 — ab + b 2 )
A 4 + 4B 4 = (A 2 + 2AB + 2B 2 ) × (A 2 — 2AB + 2B 2 )
Формитории Формии
Уловка, чтобы разложить a n — b n , когда n нечетное число. Вы не можете использовать этот прием, если n четно или разложить на множители a n + b n
Вы не можете использовать этот прием, если n четно или разложить на множители a n + b n
Сначала начните с записи ( a — b ) × ( ………… . …………………………… )
Затем заполните скобки справа.
Для этого следуйте этой инструкции.
Вычесть 1 из n. Например, если n = 7, как в a 7 — b 7 , вычтите 1 из 7, чтобы получить 6.
Первым членом всегда будет первая переменная, возведенная в степень 6.
Последним членом всегда будет вторая переменная, возведенная в степень 6.
Операция внутри всегда полезна.
Таким образом, это будет выглядеть как (a — b) × (a 6 + ………………………………………………………. .. + b 6 )
Теперь самое сложное!
Чтобы получить следующий член, это 5 b. Это делается путем вычитания 1 из 6 и включения другой переменной.
Теперь все, что вам нужно сделать, это продолжать вычитать 1 из показателя степени a и прибавлять 1 к показателю степени b, как показано ниже.
Следующим членом будет a 4 b 2 .
Делайте это до тех пор, пока переменная a не исчезнет, и вы не получите ответ, уже показанный выше. 92 Формула?
Формула а 2 — b 2 задается следующим образом: умножьте (a — b) (a + b) и посмотрите, получится ли 2 — b 2 .
Проверка a
2 — b 2 ФормулаДавайте посмотрим на доказательство формулы квадрат минус b квадрат. Чтобы убедиться, что a 2 — b 2 = (a — b) (a + b), нам нужно доказать, что LHS = RHS. Попробуем решить уравнение:
а 2 — б 2 = (а — б) (а + б)
Умножаем (a — b) и (a + b) получаем
=а(а+б) -б(а+б)
=а 2 + аб — ба — б 2
=а 2 + 0 + б 2
=а 2 — б 2
Следовательно, проверено
a 2 — b 2 = (a — b) (a + b)
Вы можете понять формулу a 2 — b 2 геометрически, используя следующий рисунок: 92 Формула
Доказательство того, что значение a 2 — b 2 равно (a + b)(a — b). Рассмотрим приведенный выше рисунок. Возьмите два квадрата со сторонами a единиц и b единиц соответственно. Это также может быть представлено как сумма площадей двух прямоугольников, как показано на рисунке ниже.
Рассмотрим приведенный выше рисунок. Возьмите два квадрата со сторонами a единиц и b единиц соответственно. Это также может быть представлено как сумма площадей двух прямоугольников, как показано на рисунке ниже.
Один прямоугольник имеет длину в единицу и ширину в (a – b) единиц, с другой стороны второй прямоугольник имеет длину в (a – b) и ширину в b единиц. Теперь сложите площади двух прямоугольников, чтобы получить результирующие значения. Соответствующие площади двух прямоугольников равны (a – b) × a = a(a – b) и (a – b) × b = b(a – b). Сумма площадей прямоугольников представляет собой фактическое полученное результирующее выражение, т. е. a(a + b) + b(a — b) = (a + b)(a — b). Снова переставляя отдельные прямоугольники и квадраты, мы получаем: (a+b)(a−b)=a 92 формула.
Пример 1: Используя формулу 2 — b 2 , найдите значение 106 2 — 6 2 .
Решение: Чтобы найти: 100 2 — 6 2 .
Предположим, что a = 100 и b = 6.
Мы заменим их в формуле a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
106 2 — 6 2 = (106 — 6) (106 + 6)
= (100) (112)
= 11200
Ответ: 106 2 — 6 2 = 11200.
Пример 2: Фактор. — 64.
Мы будем использовать формулу a 2 — b 2 , чтобы разложить это на множители.
Мы можем записать данное выражение как
25x 2 — 64 = (5x) 2 — 8 2
Подставим a = 5x и b = 8 в формулу a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
: Упрощение 10 2 — 5 2 с использованием a 2 — b 2 формула
92 Формула
Что такое расширение формулы
2 — b 2 ? a 2 — b 2 формула читается как квадрат минус b квадрат. Его разложение выражается как а 2 — b 2 = (a — b) (a + b)
Его разложение выражается как а 2 — b 2 = (a — b) (a + b)
Что такое а
2 — b 2 Формула в алгебре?Формула a 2 — b 2 также известна как одна из важных алгебраических тождеств. Это читается как квадрат минус b квадрат. это 2 — b 2 формула выражается как a 2 — b 2 = (a — b) (a + b)
?
Давайте разберемся в использовании формулы a 2 — b 2 на следующем примере.
Пример: Найдите значение 10 2 – 2 2 , используя формулу a 2 – b 2 .
Найти: 10 2 — 2 2
Предположим, что a = 10 и b = 2,
Мы подставим их в формулу a 2 — b 2 .
а 2 — б 2 = (а — б) (а + б)
10 2 -2 2 = (10-2)(10 + 2)
= 10 (10 + 2) — 2 (10 + 2)
= 10(12) — 2(12)
=120 — 24 = 96
Ответ: 10 2 — 2 2 = 96.
