А в степени х а в степени у: Показательная функция, её график и свойства — урок. Алгебра, 11 класс.

Степенные или показательные уравнения.

Для начала вспомним основные формулы степеней и их свойства.

Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=aⁿ

1. a⁰ = 1 (a ≠ 0)

2. a¹ = a

3. aⁿ • a^m = a^{n + m}

4. (aⁿ)^m = a^nm

5. aⁿbⁿ = (ab)ⁿ

6. a^-n= 1/aⁿ

7. aⁿ/a^m= a^{n — m}

Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.

Примеры показательных уравнений:

6^x=36

В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.

Приведем еще примеры показательных уравнений.
2^x*5=10
16^x — 4^x — 6=0

Теперь разберем как решаются показательные уравнения?

Возьмем простое уравнение:

2^х = 2³

Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:

2^х = 2³
х = 3

Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.

Теперь подведем итоги нашего решения.

Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем

степени и решаем полученное новое уравнение.

Теперь прорешаем несколько примеров:

Начнем с простого.

2^х+2 = 2⁴

Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.

x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2

В следующем примере видно, что основания разные это 3 и 9.

3^3х — 9^х+8 = 0

Для начала переносим девятку в правую сторону, получаем:

3^3х = 9^х+8

Теперь нужно сделать одинаковые основания. Мы знаем что 9=3² . Воспользуемся формулой степеней (aⁿ)^m = a^nm.

3^3х = (3²)^х+8

Получим 9^х+8 =(3²)^х+8 =3 ^2х+16

3^3х

= 3 ^2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.

3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.

Смотрим следующий пример:

2^2х+4 — 10•4^х = 2⁴

В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (aⁿ)^m = a^nm.

4^х = (2²)^х = 2^2х

И еще используем одну формулу aⁿ • a^m = a^{n + m}:

2^2х+4 = 2^2х•2⁴

Добавляем в уравнение:

2^2х•2⁴ — 10•2^2х = 24

Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2

2х ,вот и ответ — 2^2х мы можем вынести за скобки:

2^2х(2⁴ — 10) = 24

Посчитаем выражение в скобках:

2⁴ — 10 = 16 — 10 = 6

6•2^2х = 24

Все уравнение делим на 6:

2^2х = 4

Представим 4=2²:

2^2х = 2² основания одинаковые, отбрасываем их и приравниваем степени.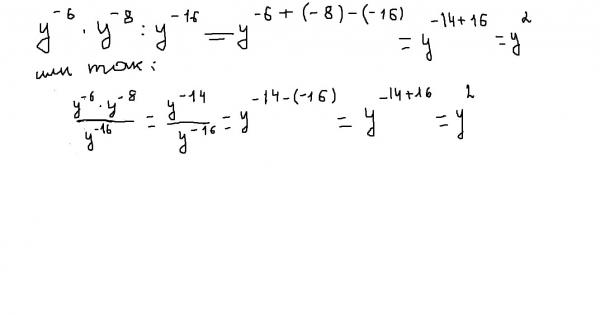
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.

Решим уравнение:

9^х – 12*3^х +27= 0

Преобразуем:
9^х = (3²)^х = 3^2х

Получаем уравнение:
3^2х — 12•3^х +27 = 0

Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить

методом замены. Число с наименьшей степенью заменяем:

3^х = t

Тогда 3^2х = (3^х)² = t²

Заменяем в уравнении все степени с иксами на t:

t² — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t₁ = 9
t₂ = 3

Возвращаемся к переменной x.

Берем t₁:
t₁ = 9 = 3^х

Стало быть,

3^х = 9
3^х = 3²
х₁ = 2

Один корень нашли. 2Формула экспонентов

 – Что такое формула экспонентов? Примеры

Показатель степени числа означает, сколько раз любое число умножается само на себя. Существуют различные формулы показателей степени, используемые для решения уравнений. Показатели важны, потому что они помогают в представлении продуктов, где число повторяется само по себе много раз. Давайте узнаем о формулах экспонент с несколькими решенными примерами в конце.

Что такое формулы экспоненты?

Формулы экспоненты относятся к формулам, которые помогают вычислять экспоненты. Показатель степени числа представлен в виде: x

n , что означает, что x умножается сам на себя n раз.   Здесь

• x называется «основой»
.
• n называется «показатель степени» или «степень»
• x ⁿ читается как «x в степени n» (или) «x в степени n»

Формулы степени

Формулы степени выражены как:

• a ⁰  = 1
• а ¹  = а
• a ^м  × a ⁿ  = a ^m+n
• a ^m  / a ⁿ  = a ^m−n
• а ^{− м} = 1/а ^м
• (a ^м ) ⁿ  = a ^mn
• (ab) ^м  = a ^м b ^м
• (a/b) ^м  = a ^м /b ^м

Давайте лучше разберемся в формулах экспонент на нескольких решенных примерах.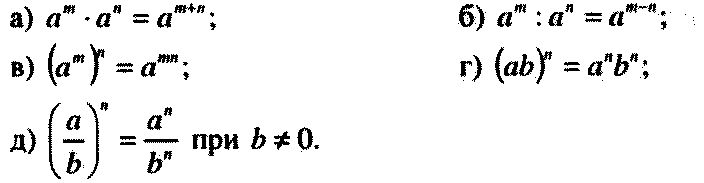

 

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Примеры с использованием экспонентных формул

Пример 1: В лесу на каждом дереве около 5 ⁷ листьев, а в лесу около 5 ³ деревьев. Используя формулу показателей, найдите общее количество листьев.

Решение: 

Найти: Общее количество листьев.

Количество деревьев в лесу = 5 ³

Количество листьев на каждом дереве = 5 ⁷ (дано)

Используя формулу показателей, ^x+y

Подстановка значений 0008  = 5 ¹⁰

Ответ: общее количество листьев 5 ¹⁰ .

Пример 2: Размеры шкафа: x ⁵ дюймов, y ³ дюймов и x ⁸ дюймов. Найдите его объем.

Решение: 

Найти: объем гардероба.

Размеры шкафа: длина (д) = x ⁵ дюймов, ширина (ш) = y ³ дюймов, высота (h) = x ⁸ дюймов (данные)

Использование формулы показателей ,

a ^x  x a ^y  = a ^x+y

Подстановка значений,

Volume = x ⁵ × 7 × x

0 8   = x ¹³  × y ³

Объем = x ¹³  × y ³

Ответ: Объем гардероба равен x ¹³  × y ³ .

Пример 3: Определите значение x ^-5/2  при x = 3.

Решение:

Чтобы найти: значение x ^-5/2  

Дано: x = 3

Используя формулу экспонент,

x ^-5/2 = (3) ^-803

= (1/3) ^5/2

= (1/3 × 1/3 × 1/3 × 1/3 × 1/3) ^1/2

= (1/243) ^1/2

= √(1/243) = 1/9√3.

Ответ: Значение x ^-5/2  при x = 3 равно 1/9√3.

Часто задаваемые вопросы о формулах экспоненты

Что такое формулы экспоненты в математике?

Мы знаем, что показатель степени числа представлен в виде: x ⁿ  (n — показатель степени). Другими словами, вы можете сказать, что показатели степени — это надстрочные числа. Формулы экспонент – это формулы, которые помогают решать задачи, связанные с экспонентами. Некоторые важные формулы показателей представлены в виде

• a ⁰ = 1
.
• а ¹  = а
• a ^м  × a ⁿ  = a ^m+n
• а ^м / а ⁿ  = а ^m−n
• а ^{− м} = 1/а ^м
• (a ^м ) ⁿ  = a ^mn
• (ab) ^м  = a ^м b ^м
• (a/b) ^м  = a ^м /b ^м

Каковы применения формул экспоненты?

Формулы экспонентов имеют широкий спектр применения:

• научные шкалы, такие как шкала pH или шкала Рихтера.
• расчет площади, объема и другие подобные задачи.
• сокращает то, что в противном случае было бы очень утомительно писать.
• используется в компьютерных играх, мерных весах.
• Наука, инженерия, экономика, бухгалтерский учет, финансы.
• Экспоненты часто используются для описания памяти компьютера.
• Изготовление лекарств в лаборатории.

Как использовать формулы экспоненты?

Формулы степени просты в использовании

• Шаг 1: Проверьте заданные параметры.
• Шаг 2: Найдите подходящую формулу экспоненты.
• Шаг 3: Подставьте заданные значения (основание и степень) в формулу.

Какие компоненты формул экспоненты?

Формулы экспонент включают основания, степени и математические символы. Показатель степени числа представлен как x ⁿ , где «x» — основание, а «n» — степень.

Экспоненциальные функции и их графики

4.1 — Экспоненциальные функции и их графики

Экспоненциальные функции

До сих пор мы имели дело с алгебраическими функциями. Алгебраические функции — это функции, которые могут быть выражены с помощью арифметических операций и значения которых либо рациональны, либо являются корнем Рациональное число. Теперь мы будем иметь дело с трансцендентными функциями. трансцендентный функции возвращают значения, которые не могут быть выражены в виде рациональных чисел или корней рациональных чисел. числа.

Алгебраические уравнения в большинстве случаев можно решить вручную. Трансцендентальные функции часто могут решить вручную с помощью калькулятора необходимо, если вы хотите десятичной аппроксимации. Однако когда трансцендентные и алгебраические функции смешиваются в уравнении, графическом или числовом методы иногда являются единственным способом найти решение.

Простейшая экспоненциальная функция: f(x) = a ^x , a>0, а≠1

Причины ограничений просты. Если a≤0, то при возведении в рациональную степень вы не можете получить реальный номер. Пример: Если a=-2, то (-2) ^0,5 = sqrt(-2), что не реально. Если а=1, то независимо от того, что такое x, значение f(x) равно 1. Это довольно скучная функция, и она определенно не один в один.

Вспомните, что у функций «один к одному» есть несколько свойств, которые делают их желательными. У них есть обратные, которые также являются функциями. Их можно применять к обеим частям уравнения.

Графики экспоненциальных функций

График y=2 ^x показан справа. Вот некоторые свойства экспоненциальной функции, когда основание больше 1.

• График проходит через точку (0,1)
• Домен состоит из всех действительных чисел
• Диапазон: y>0.
• График увеличивается
• График асимптотичен относительно оси x при приближении x отрицательная бесконечность
• График неограниченно увеличивается по мере приближения x положительная бесконечность
• График непрерывный
• График гладкий

Каким будет перевод, если заменить каждый x на -Икс? Это будет отражение относительно оси Y. Мы также известно, что когда мы возводим основание в отрицательную степень, один результат состоит в том, что берется обратное число. Так, если бы мы построили график y=2 ^-x , график будет отражение относительно оси Y y = 2 ^x , и функция будет быть эквивалентным y=(1/2) ^x .

График y=2 ^-x показан справа. Свойства экспоненциальная функция и ее график при основании даются от 0 до 1.

• График проходит через точку (0,1)
• Домен состоит из всех действительных чисел
• Диапазон: y>0.
• График уменьшается
• График асимптотичен относительно оси x, когда x приближается к положительной бесконечности
• График неограниченно увеличивается, когда x приближается к отрицательной бесконечности
• График непрерывный
• График гладкий

Обратите внимание, что разница только в том, является ли функция возрастающей или убывающей, и поведение на левом и правом концах.

Переводы экспоненциальных графиков

Вы можете применить свои знания о переводах (из раздела 1.5), чтобы помочь вам нарисовать график показательных функций.

Горизонтальный перевод может влиять на увеличение/уменьшение (при умножении на минус) левое/правое поведение графика и y-перехват, но это не изменит местоположение горизонтальной асимптоты.

Вертикальное смещение может повлиять на увеличение/уменьшение (при умножении на отрицательное значение), точку пересечения по оси Y и положение горизонтальной асимптоты. Это не изменится, если график пойдет без границ или асимптотически (хотя может меняться там, где оно асимптотично) влево или верно. 9Икс приблизится к трансцендентному числу и .

Представленное предельное обозначение взято из исчисления. Предельное обозначение — это способ задать вопрос, что происходит с выражением, когда x приближается к показанному значению. Предел — это разделительная линия между исчислением и алгеброй. Исчисление — это алгебра с понятием предела. Люди всегда есть этот страх исчисления, что я не могу понять. Сам расчет несложный. Причина люди не преуспевают в вычислениях не из-за вычислений, а потому что они плохие по алгебре.

Значение для e приблизительно равно 2,718281828. Вот чуть точнее, но не более полезный, приблизительный.

2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45716 82178 52516 64274 27466 39193 20030 59921 81741 35966 29043 57290 03342 95260 59563 07381 32328 62794 34907 63233 82988 07531 95251 01901 15738 34187 93070 21540 89149 93488 41675 09244 76146 06680 82264 80016 84774 11853 74234 54424 37107 539Икс. На калькуляторах TI-8x он находится слева, как a [2 ^nd ] [Ln]. экспоненциальная функция с основанием e иногда обозначается аббревиатурой exp(). Одно общее место это Аббревиатура появляется именно при написании компьютерных программ. Я упоминаю об этом, когда пишу exp(x), ты знаешь о чем я говорю.

Сложные проценты

Сумма на вашем сберегательном счете может быть вычислена с помощью экспоненциальной функции. Каждый период (я предполагается ежемесячно), вы получаете 1/12 годовой процентной ставки (r), применяемой к вашему счету. Новый сумма на счету составляет 100% от того, с чего вы начали, плюс r%/12 от того, с чего вы начали. Это означает, что теперь у вас есть (100%+r%/12) того, с чего вы начали. В следующем месяце вы будет то же самое, за исключением того, что оно будет основано на том, что у вас было в конце первого месяца.

Запутанно, я знаю. На странице 304 текста есть пояснение, но результирующая формула для сложные проценты равны A = P (1+i) ⁿ .

A — Сумма на счете. P — это принципал, с которого вы начали. я — периодическая ставка, которая представляет собой годовой процент (записанный в виде десятичной дроби) r, разделенный по количеству периодов в году, млн. n — количество периодов начисления процентов, что равно число периодов в году, m, умноженное на время в годах, t. Формула Показанная мной выше формула немного отличается от формулы в книге, но согласуется с формулой, которую вы будете использовать, если пойдете к конечной математике (Math 160). В конечной математике есть целую главу о финансах и соответствующих формулах.

Непрерывное соединение и рост/распад

Раньше проценты начислялись непрерывно. Вы не найти его больше, потому что он дает наибольшую отдачу от инвестиций, и банки находятся в бизнесе, чтобы сделать деньги, как и любое другое коммерческое учреждение.

Модель для непрерывного компаундирование: A = P e ^rt .

A — Сумма, P — Основная сумма, r — годовая процентная ставка (записывается в виде десятичной дроби), а t — время в годах. e — основание натуральных логарифмов.

Однако непрерывная модель имеет смысл для роста населения и радиоактивного распада. Радиоактивность изотопа меняется не раз в месяц в конце месяца, а постоянно меняется.

No related posts.