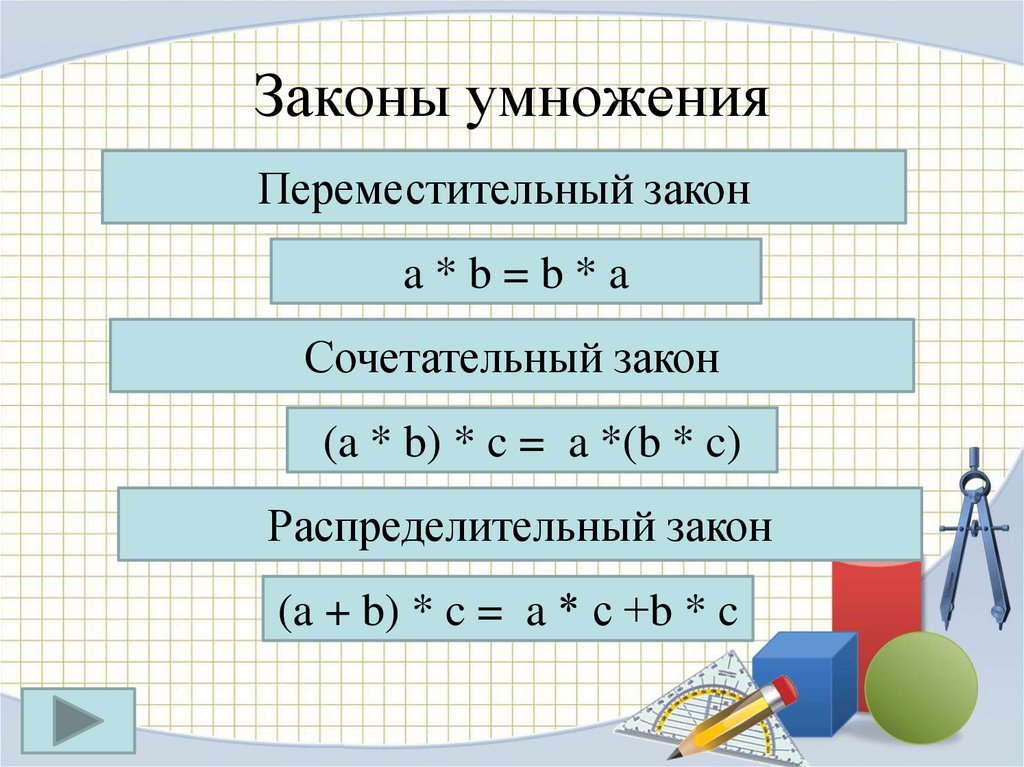
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае — к тому что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку.
И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если на одну чашу весов положить пакет, в котором 10 килограмм яблок, и на другую чашу так же положить пакет, в котором 10 килограмм яблок, то весы выровнятся, и не важно что яблоки в пакетах лежат вразброс.
Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел.
Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b.
Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2.
Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения.
Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3.
Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Показать решение
Задание 2.
Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Показать решение
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
Показать решение
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Показать решение
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Законы математики — intmag24.
ruЗаконы математики — это те правила, которые помогают правильно и быстро выполнять любые арифметические действия. Их использование значительно упрощают даже самые сложные процессы вычислений. А их несоблюдение может привести к тому, что будет больше времени затрачиваться на вычисления, будут появляться ошибки и т.д.
В статье рассмотрим следующие законы:
- Переместительный закон сложения,
- Сочетательный закон сложения,
- Переместительный закон умножения,
- Сочетательный закон умножения,
- Распределительный закон умножения.
от перемены мест слагаемых сумма не изменяется.Формула: a + b = b + a
Пример: 2+3=5 и 3+2=5 ⇒ 2+3=3+2
Действительно,
➜ если мы в пакет положим сначала два яблока, а потом три — получим пять яблок;
➜ если мы в пакет положим сначала три яблока, а потом два — также получим пять яблок.
✅ Сочетательный закон сложения
если в примере есть несколько слагаемых, то можно сложить два из них между собой, а потом к результату прибавить оставшееся слагаемое.Формула: (a + b) + c = a + (b + c)
Пример: (2+3)+5=10 и 2+(3+5)=10 ⇒ (2 + 3) + 5 = 2 + (3 + 5)
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Таким образом, можно значительно ускорить выполнение вычислений и складывать сколько угодно большие выражения.
Рассмотрим, как можно применять сочетательный закон на практике:
Так как проще складывать десятки, то при сложении чисел нужно в первую очередь группировать слагаемые, которые в сумме дадут десятки без единиц, то есть 10, 20, 30 и так далее.
Например: 13+28+15+17+2=(13+17)+(28+2)+15=30+30+15=60+15=75
✅ Переместительный закон умножения
от перемены мест множителей произведение не меняется.
То есть, если множимое и множитель поменять местами — их произведение не изменится.
Формула: a × b = b × aПример: 5×2=10 и 2×5=10 ⇒ 5×2 = 2×5
Действительно,
➜ если мы возьмем 2 пакет яблок по 5 штук — получим 10 яблок;
➜ если мы возьмем 5 паков яблок по 2 штуки — также получим 10 яблок.
✅ Сочетательный закон умножения
если выражение состоит из нескольких множителей, то их произведение не зависит от порядка действий.
Таким образом, чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Формула: a × b × с = (a × b) × с = a × (b × с)Пример: 2×3×4=24 и (2×3)×4=24 и 2×(3×4)=24 ⇒ 2×3×4 = (2×3)×4 = 2×(3×4)=24
Любой пример, в котором присутствует только умножение, можно вычислять в любом порядке.
В нашем примере:
➜ сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4;
➜ сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
✅ Распределительный закон умножения
- Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
- Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.
где: выражение в скобках (a + b) — это множимое; переменная с — множитель.
Пример: (2+3)×4=5×4=20 и 4×(2+3)=4×5=20 и 2×4+3×4=8+12=20
⇒ (2+3)×4 = 4×(2+3) = 2×4+3×4
Из переместительного закона умножения: от перемены мест множимого и множителя произведение не изменится.
Таким образом, если множимое (a + b) и множитель c поменять местами, то получим выражение c×(a+b).
Чтобы применять законы математики, необходимо также знать темы: раскрытие скобок и порядок действий в примерах.
Основные законы математики
В нашей жизни есть правила, которым мы должны подчиняться. Соблюдение правил гарантирует мирную и беззаботную жизнь. Когда вы не соблюдаете законы, это приводит к печальным последствиям.
В математике есть свои законы, которым тоже нужно следовать. Несоблюдение законов математики в лучшем случае приведет к снижению оценок, а в худшем к падению самолетов, зависанию компьютеров, сносу крыш из-за сильного ветра, плохой связи и тому подобным плохим вещам.
Законы математики состоят из простых свойств. Эти свойства знакомы нам со школы. Но не помешает вспомнить их еще раз, а еще лучше записать и выучить наизусть.
В этом уроке мы рассмотрим лишь небольшую часть законов математики.
Их нам хватит для дальнейшего изучения математики.
Определение. Переместительный закон сложения гласит, что не имеет значения, в каком порядке вы складываете числа.
Действительно, прибавь пятерку к двойке и получишь семерку. И наоборот, к пятерке прибавляем двойку и снова получаем семерку:
5 + 2 = 7
2 + 5 = 7
Если в один мешок положить 10 кг яблок, а в другого мешка, мешков будет поровну, и неважно, что яблоки в мешках перемешаны случайным образом. Если взять мешок с весов и смешать в нем яблоки, как шарики в лотерейном мешке, мешок все равно будет весить 10 килограммов. Сумма не изменится от перестановки слагаемых. Слагаемые в данном случае — яблоки, а сумма — общий вес.
Таким образом, выражения 5+2 и 2+5 можно приравнять. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Предположим, что вы усвоили один из предыдущих уроков, который назывался выражениями, поэтому запишем закон перестановки сложения с использованием переменных:
a + b = b + a
Этот коммутативный закон сложения будет работать для любых чисел.
Например, возьмем любые два числа. Пусть a = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3. Эти значения войдут в основное выражение a + b = b + a и подставят там, где это необходимо. Номер 2 будет заменен на a, номер 3 будет заменен на b
Ассоциативный закон сложения
Определение. Ассоциативный закон сложения гласит, что изменение группировки складываемых чисел не меняет их результирующей суммы. Этот закон позволяет группировать слагаемые вместе для облегчения вычислений.
Рассмотрим сумму трех слагаемых:
2 + 3 + 5
Для вычисления этого выражения можно сначала сложить числа 2 и 3 и прибавить результат к числу 5. Для удобства сумма чисел 2 и 3 можно поставить в круглые скобки, указывая, что эта сумма будет рассчитана первой:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Или можно сложить числа 3 и 5, затем прибавить результат к числу 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Как видите, в обоих случаях вы получаете одинаковый результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, так как они равны одному значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем ассоциативный закон сложения по переменным:
(a + b) + c = a + (b + c)
Ассоциативный закон умножения
Определение. Ассоциативный закон умножения гласит, что независимо от того, как вы группируете числа, вы умножаете их вместе.
Рассмотрим следующее выражение:
2 × 3 × 4
Это выражение можно вычислять в любом порядке. Сначала можно умножить числа 2 и 3, а результат умножить на 4:
Или можно сначала перемножить числа 3 и 4, а результат умножить на число 2
Таким образом, между выражениями (2×3)×4 и 2×(3×4) можно положить знак равенства, потому что они равны одному и тому же значению:
Запишем комбинаторный закон умножения с использованием переменных:
a × b × c = (a × b) × c = a × (b × в)
Пример 2 .
Найдите значение выражения 1 × 2 × 3 × 4
Это выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке действий:
Распределительный закон умножения
Определение. Распределительный закон умножения гласит, что любое число, умноженное на сумму двух или более чисел, равно сумме этого числа, умноженного на каждое из чисел в отдельности.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала нужно выполнить действие в скобках. Делаем так:
(3 + 5) = 8
В основном выражении (3 + 5) × 2 замените выражение в скобках на полученную восьмерку:
8 × 2 = 16
Ответ равно 16. Тот же пример можно решить, используя распределительный закон умножения.
Для этого умножьте каждое слагаемое в скобках на 2, затем сложите результаты:
Мы слишком подробно рассмотрели распределительный закон умножения. В школе этот пример записали бы очень кратко. Вам тоже нужно привыкнуть к этому типу обозначений. Выглядит так:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или еще короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с использованием переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Его начало выглядит так: (a+b)×c.
Если рассматривать выражение в скобках (a + b) в целом, то оно будет множителем, а переменная c будет множителем, потому что они связаны знаком умножения ×
Из коммутативного закона умножения мы узнали, что если поменять местами первый множитель и второй, произведение не изменится.
Если поменять местами множитель (a + b) и множитель c, мы получим выражение c × (a + b).
Затем мы умножаем переменную c на сумму (a + b). Чтобы сделать это умножение, мы применяем распределительный закон умножения. В этом случае переменная c должна быть умножена на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2 . Найдите значение выражения 5 × (3 + 2)
Умножьте число 5 на каждое слагаемое в скобках и сложите результаты:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3 . Вычислите 6 × (5 + 2)
Умножьте 6 на каждое слагаемое в скобках и сложите результаты:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если скобки являются не суммой, а разницей, необходимо сначала умножить множитель на каждое число, указанное в скобках. Затем из первого числа вычтите второе число. В принципе, ничего нового.
Пример 4 . Найдите значение выражения 5 × (6 — 2)
Умножьте 5 на каждое число в скобках. Затем из первого числа вычтите второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5 .
Вычислите 7 × (3 — 2)
Умножьте 7 на каждое число в скобках. Затем из первого числа вычтите второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Упражнения
Задача 1. Найдите значение выражения с помощью распределительного закона умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Показать решение
Задание 2. Найдите значение выражения по дистрибутивному закону умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Показать решение
Задача 3. Найдите значение выражения, используя порядок действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
Показать решение
Задача 4.
Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Показать решение
Задача 5. Найдите значение выражения с помощью распределительного закона умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Показать решение
Коммутативные, ассоциативные и дистрибутивные законы
Вау! Какой набор слов! Но идеи простые.
h2zsWdHC_V8
Коммутативные законы
«Законы коммутации» говорят, что мы можем поменять местами числа и все равно получить тот же ответ…
… когда мы добавляем :
а + б = б + а
Пример:
… или когда мы умножаем :
а × б = б × а
Пример:
Проценты тоже!
Потому что a × b = b × a также верно, что:
а% от б = б% от
Пример: чему равно 8% от 50?
8% от 50 = 50% от 8
= 4
Почему «коммутативный » .
.. ?
Потому что номера могут перемещаться туда-сюда, как пассажир .
4591, 4599, 4615, 4639, 4647, 4592, 4600, 4616
КБфнкУГЭМВИ
Ассоциативные законы
«Ассоциативные законы» говорят, что не имеет значения, как мы группируем числа (т.е. какие мы вычисляем первыми)…
… когда мы добавляем :
(а + б) + в = а + (б + в)
… или когда мы умножаем :
(а × б) × в = а × (б × в)
Примеры:
| Это: | (2 + 4) + 5 = 6 + 5 = 11 |
| Имеет тот же ответ, что и этот: | 2 + (4 + 5) = 2 + 9 = 11 |
| Это: | (3 × 4) × 5 = 12 × 5 = 60 |
| Имеет тот же ответ, что и этот: | 3 × (4 × 5) = 3 × 20 = 60 |
Использование:
Иногда проще складывать или умножать в другом порядке:
Сколько будет 19+36+4?
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
Или немного переставить:
Что такое 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
4603, 4610, 4627, 4631, 4643, 4654, 4606, 4612
0v-G6OwcKmU
Распределительный закон
«Распределительный закон» — САМЫЙ ЛУЧШИЙ из всех, но требует особого внимания.
Вот что он позволяет нам делать:
3 партии (2+4) идентичен 3 партии 2 плюс 3 партии 4
Итак, 3× можно «распределить» по 2+4 , на 3×2 и 3×4
И пишем так:
a × (b + c) = a × b + a × c
Попробуйте посчитать сами:
- 3 × ( 2 + 4 ) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
В любом случае ответ один.
По-английски мы можем сказать:
Мы получим тот же ответ, если:
- умножим число на группу чисел, сложенных вместе или
- сделать каждый умножить отдельно, затем добавить их
Использование:
Иногда бывает проще разбить сложное умножение:
Пример: Что такое 6 × 204?
6 × 204 = 6 × 200 + 6 × 4
= 1200 + 24
= 1224
Или комбинировать:
Пример. Сколько будет 16 × 6 + 16 × 4?
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
Мы также можем использовать это в вычитании:
Пример: 26×3 — 24×3
26×3 — 24×3 = (26 — 24) × 3
= 2 × 3
= 6
Мы могли бы использовать его и для длинного списка дополнений:
Пример: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6 ×7 + 2 ×7 + 3 ×7 + 5 ×7 + 4 × 7
= (6+2+3+5+4) × 7
= 20 × 7
= 140
5656, 5657, 5658, 5659, 5660, 5661, 3172
Таковы Законы.
