Онлайн объем трапеции: Расчет объема трапеции онлайн калькулятор

Онлайн калькулятор: Объем геометрических фигур

УчебаМатематикаГеометрия

Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

Формула:

Объем куба

Сторона (H)

Длина ребра куба (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем прямоугольной призмы

Размеры прямоугольной призмы

Формула:

Объем прямоугольной призмы

Ширина (W)

Высота (H)

Высота (H)

Длина (L)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем пирамиды

Размеры пирамиды

Формула:

Объем пирамиды

Площадь основания (Sb)

Площадь основания

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем усеченной пирамиды

Размеры усеченной пирамиды

Формула:

Объем усеченной пирамиды

Площадь первого основания (Sb1)

Площадь второго основания (Sb2)

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем конуса

Размеры конуса

Формула:

Объем конуса

Радиус (R)

Высота (H)

Высота (H)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем цилиндра

Размеры цилиндра

Formula:

Объем цилиндра

Высота (H)

Высота (H)

Радиус (R)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем сферы

Размеры сферы

Формула:

Объем сферы

Радиус (R)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем эллипсоида

Размеры эллипсоида

Формула:

Объем эллипсоида

Радиус 1 (R1)

Радиус 2 (R2)

Радиус (R3)

Точность вычисления

Знаков после запятой: 5

Объем

 

Объем тороида

Размеры тороида

Формула:

Объем тора

Радиус 1 (R1)

Радиус 2 (R2)

Точность вычисления

Знаков после запятой: 5

Объем

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Куб
• • Конус
• • Тор
• • Объем сегмента цилиндра
• • Объем жидкости в прямоугольном баке под наклоном
• • Раздел: Геометрия ( 97 калькуляторов )

 #геометрия #объем Геометрия Инженерные конус куб Математика объем пирамида прямоугольная призма сфера тор тороид усеченная пирамида цилиндр эллипсоид

 PLANETCALC, Объем геометрических фигур

Anton2020-11-03 14:19:26

по 4 сторонам и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В публикации представлены онлайн-калькуляторы и формулы для расчета площади трапеции по разным исходным данным: через длины оснований и высоту, по всем сторонам, через диагонали и угол между ними.

• Расчет площади
  • 1. Через основания и высоту
  • 2. По 4 сторонам (формула Герона)
  • 3. Через диагонали и угол между ними

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через основания и высоту

Формула расчета

2. По 4 сторонам (формула Герона)

Формула расчета

p – полупериметр трапеции, считается так:

3. Через диагонали и угол между ними

Формулы расчета

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор объема трапециевидной призмы

Создано Wei Bin Loo

Отредактировано Анна Щепанек, доктор философии и Стивен Вудинг

Последнее обновление: 09 февраля 2023 г.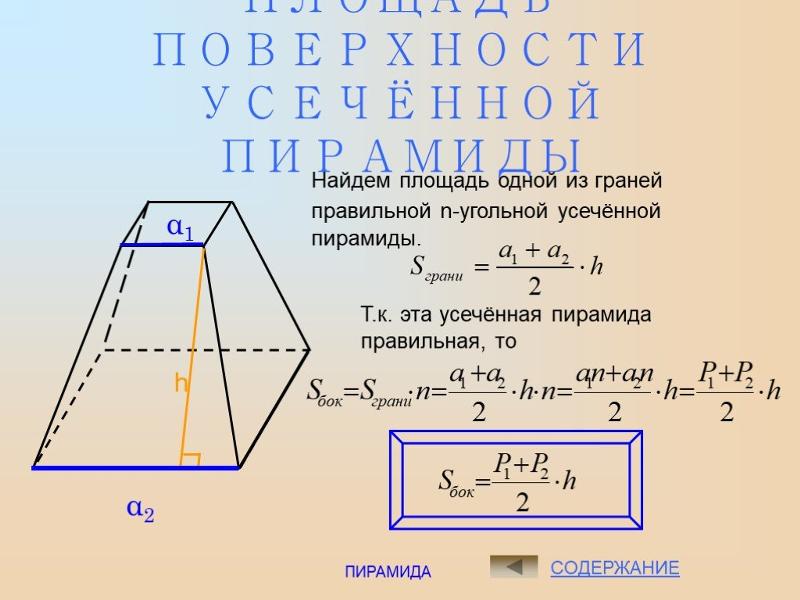

Содержание:

• Что такое объем трехмерного объекта?
• Как найти объем трапециевидной призмы?
• Часто задаваемые вопросы

С помощью этого калькулятора объема трапециевидной призмы мы стремимся помочь вам рассчитать объем трапециевидной призмы . Вы можете проверить наш калькулятор трапеции и калькулятор площади трапеции, чтобы понять больше по этой теме.

Мы написали эту статью, чтобы помочь вам понять что такое объем трапециевидной призмы и как найти объем трапециевидной призмы . Мы также продемонстрируем несколько примеров, которые помогут вам понять формулу объема трапециевидной призмы.

Что такое объем трехмерного объекта?

Объем 3D-объекта – это объем пространства, занимаемый  3D-объектом. Чем больше объем, тем больше места занимает объект. Одним из способов измерения объема является измерение количества воды, которое вытесняет объект, когда его опускают в воду.

Пожалуйста, ознакомьтесь с нашим калькулятором объема, чтобы лучше понять эту тему.

Как найти объем трапециевидной призмы?

Трапециевидная призма

Чтобы понять формулу объема трапециевидной призмы, рассмотрим пример ниже:

• Длина короткого основания (b): 5 м
• Длина длинной базы (B): 5 м
• Длина (ℓ): 5 м
• Высота (в): 3 м

1. Определите длину короткой базы (b).

   Первым шагом является определение длины короткого основания b трапециевидной призмы. Для нашего примера b равно 5 м .

2. Определите длину длинной базы (B).

   Следующим шагом является определение длины длинного основания B трапециевидной призмы. Для нашего примера b равно 5 м .

3. Рассчитать длину (ℓ).

   Теперь вам нужно вычислить длину ℓ трапециевидной призмы. л этой трапециевидной призмы составляет 5 м .

4. Определить высоту (h).

   Кроме того, высота h трапециевидной призмы равна 3 м .

5. Вычислите объем трапециевидной призмы.

   Последним шагом является расчет объема трапециевидной призмы по формуле:

   ((б + В) / 2) × ч × л

   Таким образом, объем трапециевидной призмы равен ((5 м + 5 м)/2) × 5 м × 3 м = 75 м³ .

Часто задаваемые вопросы

Может ли громкость быть отрицательной?

Нет , объем не может быть отрицательным. Это потому, что нулевого и отрицательного объема просто не существует. Объект не может иметь нулевой или отрицательный объем.

Каков объем трапециевидной призмы со всеми сторонами 1 м?

Объем этой трапециевидной призмы будет 1 м³ . Вы можете рассчитать его по следующей формуле:

объем = ((длина короткого основания + длина длинного основания) / 2) × высота × длина .

Как рассчитать объем трапециевидной призмы?

Объем трапециевидной призмы можно рассчитать за пять шагов:

1. Определить длину короткой базы (b)

2. Определить длину длинной базы (B)

3. Рассчитать длину (ℓ)

4. Определить высоту (h)

5. Примените формулу объема трапециевидной призмы :

   ((б + В) / 2) × ч × л

Что такое боковая область для трехмерного объекта?

Боковая площадь трехмерного объекта представляет собой сумму площадей всех сторон трехмерного объекта, кроме основания и вершины .

Вэй Бин Лоо

Высота

Длина

Длинная база (B)

Короткая база (b)

Объем

Посмотреть 23 похожих калькулятора 3d геометрии

Объем трапециевидной призмы

LearnPracticeDownload

Объем трапециевидной призмы — это емкость призмы. Его также можно определить как пространство внутри трапециевидной призмы. Призма имеет конгруэнтные многоугольники на верхней и нижней гранях, а основания одинаковы. Боковые грани призмы представляют собой параллелограммы, которые называются боковыми гранями. Призму можно назвать по форме двух одинаковых граней на ее конце. Трапециевидная призма представляет собой трехмерное тело, имеющее два основания трапеции/трапеции внизу и вверху. Форма боковых граней/боковых граней трапециевидной призмы – параллелограмм.

1.	Каков объем трапециевидной призмы?
2.	Объем трапециевидной призмы Формула
3.	Как рассчитать объем трапециевидной призмы?
4.	Часто задаваемые вопросы об объеме трапециевидной призмы

Каков объем трапециевидной призмы?

Объем трапециевидной призмы – это пространство внутри нее. Трапециевидная призма представляет собой трехмерную фигуру с двумя трапециевидными основаниями и четырьмя гранями в виде параллелограмма. Призма представляет собой многогранник с равными многоугольниками на верхней и нижней гранях и имеет одинаковые основания. Трапециевидные призмы бывают двух видов: косые и прямые. У косой трапециевидной призмы боковые грани — параллелограммы, а у правильной трапециевидной призмы — прямоугольники. В общем случае трапециевидная призма означает правильную трапециевидную призму. Следовательно, боковые грани прямоугольники. Таким образом, у трапециевидной призмы всего 6 граней, 12 ребер и 8 вершин. Два основания имеют форму трапеции или трапеции, которые конгруэнтны друг другу. Он имеет

• 6 сторон
• 12 кромок
• 8 вершин
• 4 стороны: прямоугольник
• Трапеция/трапеция в качестве основания снизу и сверху

Объем трапециевидной призмы Формула

Объем трапециевидной призмы — вместимость призмы (или) объем трапециевидной призмы — пространство внутри нее.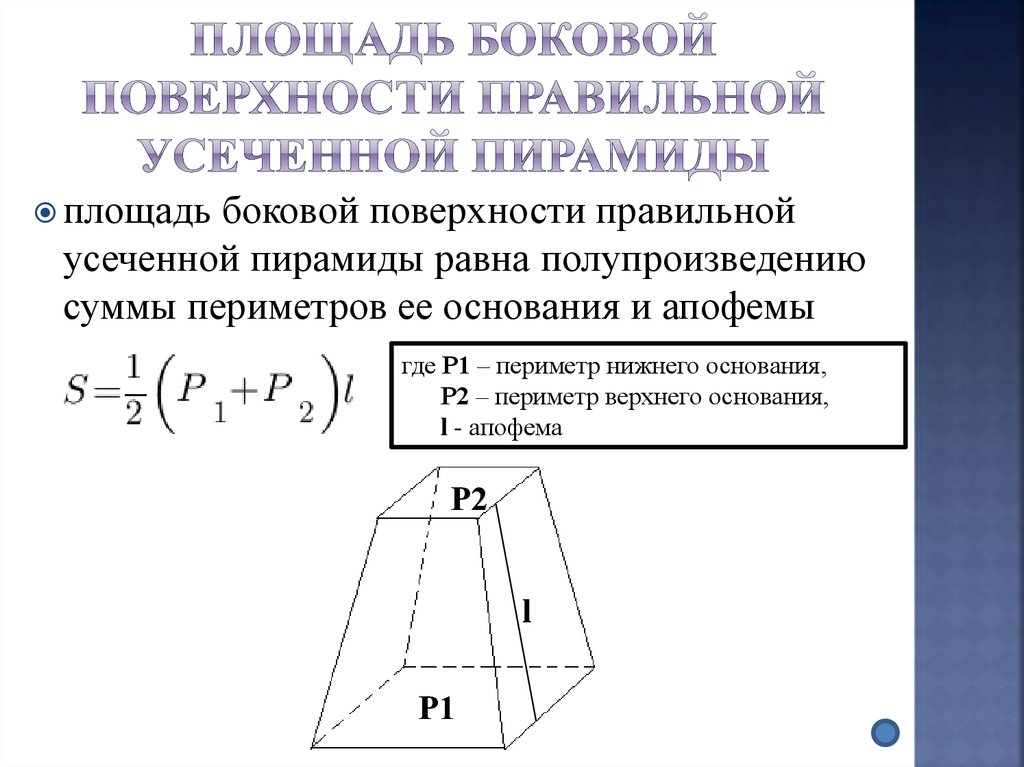 Измеряется в кубических единицах, таких как мм ³ , см ³ , ³ и т. д. Мы увидим формулы для расчета объема трапециевидной призмы. Объем призмы можно получить, умножив площадь ее основания на общую высоту призмы. т. е. объем призмы = площадь основания × высота призмы. Мы также будем использовать эту формулу для расчета объема трапециевидной призмы. Рассмотрим трапециевидную призму, две параллельные стороны основания которой равны \(b_1\) и \(b_2\), высота равна ‘h’, а длина призмы равна L. Мы знаем, что основание трапециевидная призма — это трапеция/трапеция. Таким образом,

Площадь основания (площадь трапеции) = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)

Теперь, используя объем призмы формула (как указано выше),

Объем трапециевидной призмы = площадь основания × длина = \(\dfrac{1}{2}{(b_{1} + b_{2})×h}×L\)

Как рассчитать объем трапециевидной призмы?

Ниже приведены шаги для расчета объема трапециевидной призмы. Убедитесь, что все измерения выполнены в одних и тех же единицах. Обратитесь к следующему примеру.

• Шаг 1: Определите, что параллельные стороны основания (трапеции) равны \(b_1\) и \(b_2\), а перпендикулярное расстояние между ними равно \(h\), и найдите площадь трапеции, используя формула:
  Площадь трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\)
• Шаг 2: Определите его высоту/длину призмы (расстояние по вертикали между двумя основаниями).
• Шаг 3: Умножьте площадь основания, полученную на шаге 1, и высоту, полученную на шаге 2, чтобы найти объем.

 

Примеры объема трапециевидной призмы

1. Пример 1: Найдите объем трапециевидной призмы заданных размеров.

   Решение:

   На приведенном выше рисунке, Учитывая, что

   Основание 1 (\(b_1\)) = 6 дюймов, основание (\(b_2\)) = 20 дюймов

   Высота основания трапеции = 12 в

   Длина трапеции = 17 в

   Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h}\)

   ⇒ A = \(\dfrac{1}{2}\) (6 + 20) × 12
   ⇒ А = 13 × 12
   ⇒ a = 156 в ²

   Как мы знаем, объем трапециевидной призмы = область × общая длина трапеции

   ⇒ 156 ^{× 17}

   ⇒ 2652 в ³

   . трапецеидальная призма равна 2652 в

   3 .

2. Пример 2: Рассчитайте объем трапециевидной призмы, учитывая, что высота основания трапеции 5 см, а длины ее параллельных сторон 14 см и 10 см, длина призмы 6 см.

   Решение:

   На приведенном выше рисунке Учитывая, что

   Основание 1 (\(b_1\)) = 14 см, основание (\(b_2\)) = 10 см

   Высота основания трапеции (h ) = 5 см

   Общая длина трапеции = 6 см

   Площадь трапеции/трапеции = \(\dfrac{1}{2}{(b_{1} + b_{2})× h }\)

   ⇒ А = (1/2) (14 + 10 ) × 5
   ⇒ А = 12 × 5
   ⇒ A = 60 см ²

   Как мы знаем, объем трапециевидной призмы = площадь × длина трапеции

   объем = 60 ^{× 6 = 360 см 3}

   Ответ : Объем трапециевидной призмы равен 360 см ³ .

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Запись на бесплатный пробный урок

Практические вопросы по объему трапециевидной призмы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об объеме трапециевидной призмы

Имеет ли трапециевидная призма объем?

Призма представляет собой трехмерное твердое тело. Трехмерное твердое тело имеет внутри себя пространство. Объем объясняется как пространство внутри объекта. Таким образом, трапециевидная призма имеет объем, поскольку представляет собой трехмерную форму и измеряется в кубических единицах.

Что вы подразумеваете под объемом трапециевидной призмы?

Объем трапециевидной призмы — вместимость призмы. Формула объема трапециевидной призмы представляет собой площадь основания × высоту призмы в кубических единицах.

По какой формуле найти объем трапециевидной призмы?

Объем трапециевидной призмы равен произведению площади основания на высоту призмы в кубических единицах.