Алгебра буля для чайников: Булева алгебра для чайников: логика буля

Булева алгебра (алгебра логики)

• Понятие алгебры логики
• Логические функции
• Булев базис (логический базис)
• Аналитическое представление логических функций
• Способы описания логических функций
• Аксиомы алгебры логики
• Теоремы алгебры логики
• Законы алгебры логики

На этом уроке знакомимся с алгеброй логики (булевой алгеброй). Одним из её основателей стал английский математик Джордж Буль (1815-1864), который был из довольно бедной семьи, а в юности зарабатывал переводами сочинений древнегреческих философов. За этим занятием его и посетила мысль о том, что высказываниям можно присваивать значения 1 («истина») и 0 «ложь».

Итак, алгебра логики (булева алгебра) — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать, а затем манипулировать ими подобно обычным числам в математике.

Создание алгебры логики в середине ХIХ века в трудах Джорджа Буля представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Пусть функция от n переменных и любой из её аргументов могут принимать значения только из множества {0, 1}. Тогда эта функция называется логической, или булевой, или переключательной, или функцией алгебры логики. Описанную функцию часто называют также булевым вектором. Количество функций от n переменных равно 2 в степени n. То же самое можно сказать и иначе: число различных n-мерных булевых векторов равно 2 в степени n. А число различных функций алгебры логики от этих векторов равно уже .

Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая «1») или сигнал отсутствует (логический «0»).

На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.

Законы булевой алгебры применяются и в программировании — при написании сложных логических условий и сложных запросов к базе данных. Один пример со скриптом на PHP приведён здесь (это статья о системе многокритериального поиска по сайту с базой данных). Ещё один пример — применение алгебры логики в создании многоуровневого меню сайта, в котором были бы открыты все пункты всех уровней, по которому пролегает путь к конечному открытому пункту меню.

Часто оказывается, что изначально построенное логическое выражение можно упростить, используя аксиомы, теоремы и законы алгебры логики.

Способам и приёмам минимизации логических функций посвящены отдельные материалы сайта — минимизация логических функций: общие сведения, минимизация логических функций: метод непосредственных преобразований и минимизация логических функций: метод Квайна.

Логические функции одной переменной

Функция	Название	Обозначение
	Константа нуля
	Повторение x
	Логическое отрицание, инверсия, «НЕ»
	Константа единицы

 

Переменная	Логические функции
x
0	0	0	1	1
1	0	1	0	1

 

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Логические функции двух переменных

Функция	Название	Обозначение
	Константа нуля	или False
	Логическое умножение, конъюнкция, «И»	или или или
	Запрет по	или
	Переменная
	Запрет по	или
	Переменная
	Сложение по модулю 2, отрицание эквивалентности, исключающее «ИЛИ»	или или
	Логическое сложение, дизъюнкция, «ИЛИ»	или или или
	Функция Пирса (Вебба), «ИЛИ-НЕ»	или или
	Логическая равнозначность, эквиваленция	или или или
	Отрицание
	Правая импликация	или
	Отрицание
	Левая импликация	или
	Функция Шеффера, «И-НЕ»	или или
	Константа единицы	или True

Ниже дана таблица истинности для логических функций от двух переменных.

X1	0	0	1	1
X2	0	1	0	1
	0	0	0	0
	0	0	0	1
	0	0	1	0
	0	0	1	1
	0	1	0	0
	0	1	0	1
	0	1	1	0
	0	1	1	1
	1	0	0	0
	1	0	0	1
	1	0	1	0
	1	0	1	1
	1	1	0	0
	1	1	0	1
	1	1	1	0
	1	1	1	1

В логических схемах функции могут быть реализованы с произвольных количеством входных переменных, примеры — в материале Логические схемы и таблицы истинности.

Ответить на контрольные вопросы, а затем посмотреть ответы

Контрольный вопрос 1. Даны две переменные x1 и x2. Число различных булевых векторов и различных ФАЛ от полученных векторов равны соответственно:

• 8 и 16
• 8 и 32
• 4 и 8
• 4 и 16

Контрольный вопрос 2. Какие из функций не являются ФАЛ одной переменной (и одна, и вторая в варианте ответа):

• отрицание и сложение по модулю два
• эквивалентность и повторение x
• отрицание и импликация
• функция Шеффера и эквивалентность
• запрет по x2 и отрицание

Правильные ответы на вопрос 1 и вопрос 2.

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Математическая логика

Любую булеву функцию с произвольным количеством аргументов можно построить через подстановку элементарных функции вместо аргументов (суперпозицию). Набор простейших функций, с помощью которого можно выразить любые другие, сколь угодно сложные логические функции, называется функционально полным набором, или логическим базисом.

Инверсия (логическое отрицание, «НЕ»)

.

0	1
1	0

Конъюнкция (логическое умножение, «И»)

.

0	0	0
0	1	0
1	0	0
1	1	1

Дизъюнкция (логическое сложение, «ИЛИ»)

.

0	0	0
0	1	1
1	0	1
1	1	1

В булевом базисе обычно строятся логические схемы, которые реализуют сколь угодно сложные логические функции, примеры — в материале Логические схемы и таблицы истинности.

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований
• Пригодится: минимизация логических функций методом Квайна

В качестве исходного описания сложных логических функций обычно используется таблица истинности, однако упрощение функций удобнее производить в аналитической форме. При аналитической записи функция алгебры логики представляется либо в виде логической суммы элементарных логических произведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элементарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи имеет название дизъюнктивной нормальной формы (ДНФ), вторая — конъюнктивной нормальной формы (КНФ). В этих названиях термин «нормальная» означает отсутствие общей инверсии (отрицания) над несколькими перемнными сразу.

Дизъюнктивная нормальная форма

.

X1	X2	f
0	0	1
0	1	1
1	0	1
1	1	0

Конъюнктивная нормальная форма

.

X1	X2	f
0	0	0
0	1	0
1	0	1
1	1	0

Применяются следующие способы описания логических функций:

• словесный;
• табличный;
• числовой;
• аналитический;
• координатный;
• графический.

Пример табличного описания функций алгебры логики. В верхней таблице под набором подразумевается набор значений логических переменных (1 или 0), а f — это значение функции алгебры логики, заданной определённой формулой. Нижняя таблица несёт в себе более подробную информацию о наборах, поскольку в ней указаны значения переменных.

Номер набора	f
0	0
1	1
2	0
3	0
4	1
5	1
6	0
7	1

 

X1	X2	X3	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

Приведённые выше таблицы имеют название таблиц истинности. Такие таблицы в практике необходимо строить для любой, сколь либо сложной булевой функции. Примеры таблиц истинности для булевых функций, реализованных в логических схемах — в материале Логические схемы и таблицы истинности.

Пример числового описания логических функций

или .

Пример аналитического описания логических функций

Пример координатного описания логических функций

Карта Карно

Пример графического описания логических функций

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований
• Пригодится: минимизация логических функций методом Квайна

Аксиомы конъюнкции

.

Аксиомы дизъюнкции

.

Аксиомы отрицания

если , то ; если , то .

Теоремы исключения констант

.

Теоремы идемпотентности (тавтологии, повторения)

.

для n переменных

.

Теорема противоречия

.

Теорема «исключённого третьего»

.

Теорема двойного отрицания (инволюции)

.

Ассоциативный (сочетательный) закон

.

Коммутативный (переместительный) закон

.

Дистибутивный (распределительный) закон

.

.

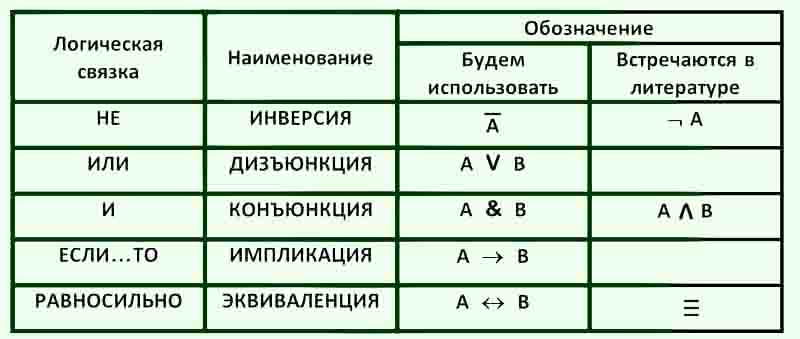
Законы де Моргана (законы общей инверсии или дуальности)

.

.

Закон поглощения (элиминации)

.

Закон склеивания (исключения)

.

• Пригодится: минимизация логических функций — общие сведения
• Пригодится: минимизация логических функций методом непосредственных преобразований
• Пригодится: минимизация логических функций методом Квайна

Пройти тест по теме Математическая логика

К началу страницы

Логика высказываний

Логические схемы и таблицы истинности

Алгебра логики и логические основы компьютера

Алгебра логики

Алгебра логики, или булева алгебра, – это раздел математики, возникший в XIX веке благодаря работам английского математика Джорджа Буля. Поначалу булева алгебра не имела практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем.

Законы и аппарат алгебры логики стали применяться при проектировании различных частей компьютеров, в частности памяти и процессора. Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы определения истинности или ложности сложных логических высказываний с помощью алгебраических методов.

Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь. Истине сопоставляется 1, лжи – 0. При этом аргументами функций выступают простые высказывания, которые также могут иметь только два значения – 0 или 1.

Фразы «два больше одного», «5.8 является целым числом» будем считать примерами простых логических высказываний. Анализируя эти высказывания, мы делаем вывод, что первая фраза правдивая, вторая – ложная. Это и есть результат выполнения простого логического выражения.

Алгебра логики не касается сути высказываний. Она занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.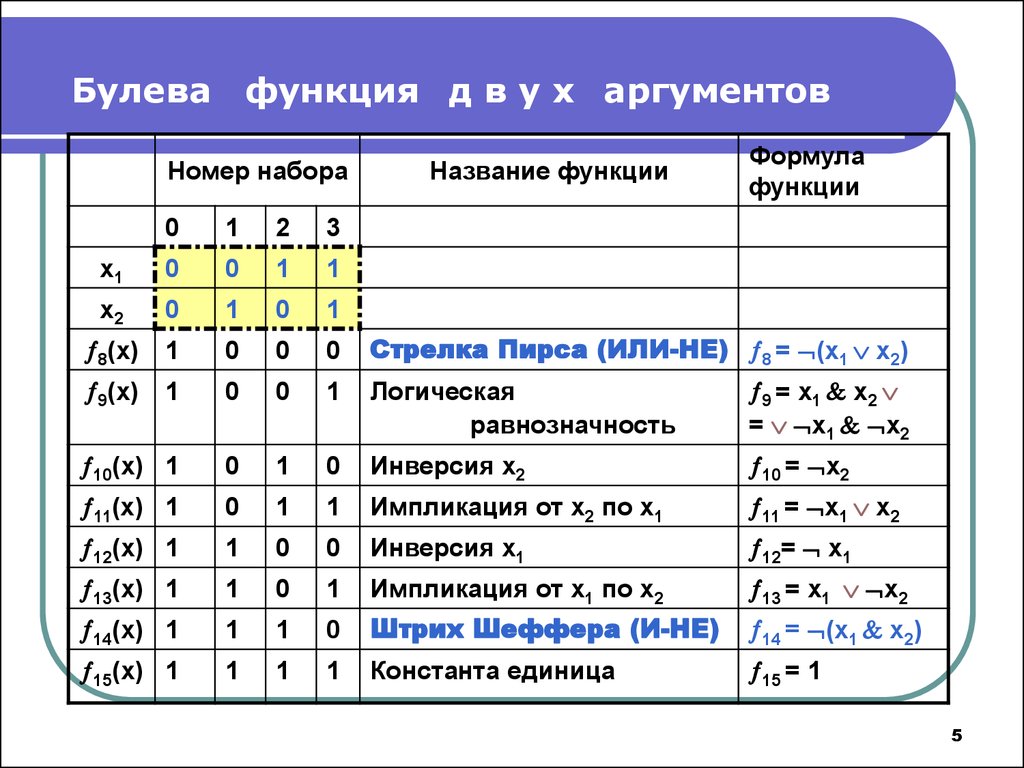

Логические операции. Дизъюнкция, конъюнкция и отрицание

Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи: и, или, либо, не, если, то, тогда. С их помощью создаем сложные высказывания: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду смотреть телевизор, когда наступит вечер», «5 не равно 6″.

Как мы решаем, что нам сказали правду или нет? Логически, где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае истинности обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет таковым. А вот при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, так как с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем.

Базовыми операциями являются конъюнкция И, дизъюнкция ИЛИ и отрицание НЕ. Часто конъюнкцию обозначают &, дизъюнкцию — ||, а отрицание — чертой над переменной, обозначающей высказывание.

При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, так как выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.

Таблицы истинности

Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными, например, A и B.

Логические основы компьютера

В ЭВМ используются различные устройства, работу которых описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно, она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

Переключательные схемы

В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Один переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

Вентили, триггеры и сумматоры

Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.

Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.

Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.

Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Булева алгебра Учебник

Булева алгебра!

Это действительно логично.

Введение

Следующие страницы предназначены для того, чтобы дать вам прочную основу для работы с булевой алгеброй. Булеву алгебру также иногда называют булевой логикой или просто логикой. Это метод представления выражений с использованием только двух значений (обычно True и False), впервые предложенный Джорджем Булем в 1847 году. порядок, но если вы пришли сюда только для того, чтобы узнать о конкретной теме, то кто я такой, чтобы вас тормозить, просто идите прямо дальше.

Продолжайте читать ниже, чтобы начать работу с булевой алгеброй, или перейдите к одному из следующих разделов.

1. Основы булевой алгебры — что такое булевая алгебра и обзор основных операторов.
2. Законы булевой алгебры — основной набор приложений и следствий операторов.
3. Выражения логической алгебры. Использование правил для управления и упрощения выражений логической алгебры.

Так зачем мне учить булевую алгебру?

Булева алгебра лежит в основе работы программного и аппаратного обеспечения, которое мы используем каждый день. Если вы занимаетесь информационными технологиями, то понимание булевой алгебры полезно во многих отношениях.

Если вы не занимаетесь информационными технологиями, понимание булевой алгебры может оказаться очень полезным. Даже если вы никогда не используете его формально, его изучение повлияет на то, как вы смотрите на мир и как вы видите и решаете проблемы. Это улучшит ваше мышление и сделает вас более способным решать проблемы. Это также позволит вам представлять и думать о процессах альтернативными способами, чтобы лучше понять их, а затем потенциально упростить их.

Я считаю, что изучение булевой алгебры может быть полезным практически для всех и, что более важно, доставляет удовольствие.

Изучение булевой алгебры

Основы булевой алгебры, как правило, довольно легко освоить. Затем кривая обучения становится немного крутой. Большая часть этого заключается в том, что это довольно абстрактно. Лучше всего решить, какие стратегии и подходы лучше всего помогут вам лучше визуализировать и понять, что происходит. Вот несколько идей для начала, но все люди разные. Вам нужно выяснить, что работает лучше всего для вас.

• Пройдитесь по предметам несколько раз с хорошими перерывами между ними. Вы будете удивлены, как что-то может иметь мало смысла при первом прочтении, но если вы оставите это на некоторое время, чтобы оно поварилось в вашей голове, а затем вернетесь к нему, оно обретет больше смысла при втором прочтении.
• Нарисуйте на бумаге. Я встречаю много студентов, которые ленивы и говорят: «Нет, все в порядке, я просто проработаю это в уме». Для абстрактных вещей, таких как булева алгебра, это не работает, когда вы достигаете определенного уровня сложности. Немного времени и усилий, чтобы нарисовать это на бумаге, сэкономит вам много часов разочарования. Это также позволит очень легко вернуться к своим шагам, когда что-то пойдет не так.
• Произнесите это вслух , а не просто мысленно. Это может показаться глупым, но когда вы произносите это, а не просто думаете, вы увидите это с другой точки зрения, и это может помочь лучше понять, что происходит.
• Практика!! Чем больше вы будете практиковаться, тем больше ваш разум будет собирать кусочки головоломки на основе этих абстрактных понятий. Чем больше вещей начнет иметь смысл.

Если вы выберете этот подход, то обнаружите, что это довольно приятный путь к мастерству в булевой алгебре. Вы также можете найти наш Учебник по решению проблем, который стоит быстро прочитать.

Определение булевой алгебры

Рассмотрено

Питер Вестфолл

Рассмотрено Питер Вестфолл

Полная биография

Питер Вестфолл — выдающийся профессор информационных систем и количественных наук Техасского технологического университета.

Узнайте о нашем Совет по финансовому обзору

Что такое булева алгебра?

Булева алгебра — это раздел математики, который имеет дело с операциями над логическими значениями и включает двоичные переменные. Булева алгебра берет свое начало в книге 1854 года математика Джорджа Буля.

Отличительной чертой булевой алгебры является то, что она занимается только изучением бинарных переменных. Чаще всего логические переменные представлены возможными значениями 1 («истина») или 0 («ложь»). Переменные также могут иметь более сложные интерпретации, например, в теории множеств. Булева алгебра также известна как бинарная алгебра.

Ключевые выводы

• Булева алгебра — это раздел математики, который занимается операциями над логическими значениями с двоичными переменными.
• Логические переменные представлены в виде двоичных чисел для представления истин: 1 = истина и 0 = ложь.
• Элементарная алгебра имеет дело с числовыми операциями, тогда как булева алгебра имеет дело с логическими операциями.
• Булева алгебра в настоящее время в основном используется в языках компьютерного программирования.
• В финансах булева алгебра используется в биномиальных моделях ценообразования опционов, что помогает определить, когда опцион должен быть исполнен.

Понимание булевой алгебры

Булева алгебра отличается от элементарной алгебры тем, что последняя имеет дело с числовыми операциями, а первая — с логическими операциями. Элементарная алгебра выражается с использованием основных математических функций, таких как сложение, вычитание, умножение и деление, тогда как булева алгебра имеет дело с соединением, дизъюнкцией и отрицанием.

Понятие булевой алгебры было впервые введено Джорджем Булем в его книге «Математический анализ логики» и далее расширено в его книге «Исследование законов мышления». Поскольку ее концепция была детализирована, булевская алгебра в основном использовалась в языках компьютерного программирования. Его математические цели используются в теории множеств и статистике.

Булева алгебра в финансах

Булева алгебра имеет приложения в финансах посредством математического моделирования рыночной деятельности. Например, исследованиям ценообразования опционов на акции может помочь использование бинарного дерева для представления диапазона возможных результатов в базовой ценной бумаге. В этой биномиальной модели ценообразования опционов, где есть только два возможных результата, логическая переменная представляет увеличение или уменьшение цены ценной бумаги.

Этот тип моделирования необходим, потому что в американских опционах, которые могут быть исполнены в любое время, траектория цены ценной бумаги так же важна, как и ее окончательная цена. Биномиальная модель ценообразования опционов требует, чтобы путь цены ценной бумаги был разбит на ряд дискретных временных диапазонов.

Таким образом, модель ценообразования биномиальных опционов позволяет инвестору или трейдеру отслеживать изменение цены актива от одного периода к другому. Это позволяет им оценить вариант на основе решений, принятых в разных точках.

Поскольку опцион в США может быть исполнен в любое время, это позволяет трейдеру определить, следует ли ему исполнить опцион или удерживать его в течение более длительного периода. Анализ биномиального дерева позволит трейдеру заранее увидеть, следует ли исполнять опцион. Если значение положительное, то опцион должен быть исполнен, если значение отрицательное, то трейдер должен удерживать позицию.

Источники статей

Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами.