Алгебра формула: Формулы сокращённого умножения — урок. Алгебра, 7 класс.

существуют ли законы хита // Смотрим

Физики и лирики. Формула успеха. Алгебра и гармония: существуют ли законы хита // Смотрим

• Профиль

• Избранное

25 ноября 2022, 11:00 25 ноября 2022, 12:00 25 ноября 2022, 13:00 25 ноября 2022, 14:00 25 ноября 2022, 15:00 25 ноября 2022, 16:00 25 ноября 2022, 17:00 25 ноября 2022, 18:00 25 ноября 2022, 19:00 25 ноября 2022, 20:00 25 ноября 2022, 21:00

Как работают законы и «лекала» шоу-бизнеса: например, почему из двадцати бойз-бэндов, созданных по всем канонам, выстрелят три, а помнить будут вообще один.

О формуле успеха рассуждал музыкальный критик, журналист Илья Легостаев.

• музыка
• шоу
• Александр Пушной
• лирика
• Рита Митрофанова
• эволюция
• радио
• мода
• природа
• физика
• медицина
• искусство
• история
• наука
• культура
• общество
• Популярные радиопрограммы
• История (Радио Маяк)
• Популярные шоу (Радио Маяк)
• Жизнь (Радио «Маяк»)
• Научпоп (Радио «Маяк»)
• В эфире (Радио «Маяк»)

Авто-геолокация

Math.

ru

Израиль Моисеевич Гельфанд, Александр Шень

ФАЗИС, 1998. 192 с.
ISBN 5-7036-0047-2

Загрузить (Mb) djvu (1.35) pdf (-) ps (-) html (-) tex (-)

Эта книга ? про алгебру. Алгебра ? наука древняя, и от повседневного употребления ее сокровища поблекли. Авторы старались вернуть им первоначальный блеск. Основную часть книги составляют задачи, большинство которых приводится с решениями. Начав с элементарной арифметики, читатель постепенно знакомится с основными темами школьного курса алгебры, а также с некоторыми вопросами, выходящими за рамки школьной программы, так что школьники разных классов (6 — 11) могут найти в книге темы для размышлений.

---

Содержание

l. Предисловие

2. Перемена, мест слагаемых

3. Перемена мест сомножителей

4. Сложение столбиком

5. Таблица умножении. Умножение столбиком

6. Деление ?уголком?

7. Двоичная система счисления

8. Коммутативность

9. Ассоциативность

10. Расстановки скобок

11. Дистрибутивность

12. Буквы в алгебре

1З. Сложение отрицательных чисел

14. Умножение отрицательных чисел

15. Действия с дробями

16. Степени

17. Отрицательные степени

18. Как умножать а^m на ⁿ, или почему наше определение удобно

19. Правило умножения степеней

20. Формулы сокращенного умножения. Квадрат суммы.

21. Как объяснить формулу (a+b)&sup2=a&sup2+2ab+b&sup2 младшему брату или сестре

22. Квадрат разности

23. Разность квадратов

24. Куб суммы

25. Четвертая степень суммы

26. (a+b)⁵, (a+b)⁶ и треугольник Паскаля

27. Многочлены

28. Отступление: какие многочлены считать равными?

29. Сколько одночленов останется?

30. Коэффициенты и значения

31. Разложение на множители

32. Рациональные выражения

33. Преобразование рационального выражения в частное двух многочленов

34. Многочлены и рациональные дроби с одной переменной

35. Деление многочленов с остатком

36. Остаток при делении на x-a

37. Многочлены, эначения, интерполяция

38. Арифметические прогрессии

З9. Сумма арифметической прогрессии

40. Геометрические прогрессии

41. Сумма геометрической прогрессии.

42. Разные задачи о прогрессиях

43. Хорошо темперированный клавир

44. Сумма бесконечной прогрессии

45. Уравнения

46. Квадратное уравнение.

47. Случай р=0 . Квадратный корень

48. Свойства квадратных корней

49. Уравнение x&sup2+px+q=0

50. Теорема Виета

51. Разложение квадратного трехчлена на множители

52. Формула для корней уравнения ax&sup2+bx+c=0 (a≠ 0)

53. Еще одна формула корней квадратного уравнения

54. Квадратное уравнение становится линейным

55. График квадратного трехчлена

56. Квадратные неравенства

57. Максимум и минимум квадратного трехчлена

58. Биквадратные уравнения

59. Возвратные уравнения

60. Как завалить на экзамене. Советы экзаменатору

61. Корни

62. Степень с дробным показателем

63. Доказательства числовых неравенств

64. Среднее арифметическое и среднее геометрическое

65. Среднее геометрическое не больше среднего арифметического

66. Задачи на максимум и минимум

67. Геометрические иллюстрации

68. Среднее квадратическое

69. Среднее гармоническое

70. Книги для дальнейшего чтения

---

Загрузить (Mb) djvu (1.35) pdf (-) ps (-) html (-) tex (-)

Постоянный адрес этой страницы: http://math.ru/lib/254

Algebra Formula For Kids: All Algebra Formula & Chart

Автор Dewi Idda Rohmana

Математика — это предмет, который иногда заставляет детей ломать голову. Хотя многие считают его довольно легким предметом, исходя из того, что он требует большого логического мышления, понимания концепций и принципов и практики.

Но поскольку математика включает в себя множество понятий и полей в рамках предмета, понятно, что временами она может быть крепким орешком.

Алгебра, один из основных разделов математики, очень помогает детям усложнить изучение математики.

Хотя алгебра обширна, элементарная алгебра имеет дело с манипулированием переменными, как если бы они были числами, и поэтому требуется во всех математических приложениях.

В этом блоге мы рассмотрим алгебраическую формулу для детей и некоторые алгебраические формулы, которые важны для детей и подростков всех возрастов

Содержание

• Что такое алгебра?
  • Алгебра для представления математических формул
• Таблица формул алгебры
• Формула алгебры для детей

Что такое алгебра?

Алгебра используется в математике, когда мы не знаем точных чисел в расчетах. В алгебре мы используем буквы для обозначения неизвестных значений или значений, которые могут измениться.

Алгебра для представления математической формулы

Например, формула площади прямоугольника представляет собой x b (a представляет собой основание, а b представляет высоту). Если бы высота была 6 см, а основание 4 см, то площадь была бы 24 см ² .

Поскольку значения высоты и основания могут быть изменены, мы можем использовать алгебру для представления формулы.

Таблица формул алгебры

Таблица предоставлена ​​Pinterest

Формула алгебры для детей

Чтобы понять алгебру, мы разделим и организуем основную формулу алгебры на 4 категории.

1. Сложение

При сложении алгебраических выражений необходимо сначала собрать похожие члены, а затем добавить их. Сумма коэффициентов одних и тех же условий будет суммой всех одинаковых условий.

Например, если члены x и x одинаковы, мы можем сложить их вместе, x равно 1x, и результат будет 2x.

Например, если у нас есть 2x + 4x, мы можем добавить 2 и 4 и использовать тот же термин в качестве последнего члена, x. В результате ответ равен 6x.

2. Вычитание

Вычитание — это то же самое, что и сложение, в том смысле, что вы должны найти одинаковые термины, а затем подсчитать их от первого появления термина до последнего.

Например, 4x – x означает 4 – 1 = 3, поэтому мы добавляем термин к конечному числу, чтобы получить 3x.

Другой пример: 7x – 2x, что означает 7x – 2x = 5, а затем добавить x, чтобы получить 5x.

3. Умножение

Умножение отличается от двух предыдущих основных математических формул. Вот некоторые правила формулы алгебры умножения:

• число x термин = число термин
• термин (1) x термин (2) = термин (1) термин (2)

термин x термин = термин ²

4. Деление

Последняя алгебраическая формула — деление; концепция такая же, как умножение, но вы должны добавить / когда между числами есть разные термины.

Например, если a: b содержит два различных термина, мы можем просто вставить/между ними.

Другой пример: если термин включает в себя число, мы должны сначала вычислить число, затем добавить термин, и не забудьте включить/между.

Заключение

Вот и все, что нужно для алгебраических формул для детей и алгебраических формул и таблиц. Поскольку мы будем использовать много динамических данных, вы также можете узнать больше об алгебре в программировании.

Алгебра является одним из основных разделов математики, а также служит основой для различных концепций и тем в других дисциплинах.

Поскольку мир движется с такой головокружительной скоростью, BrightChamps осознала необходимость прививать детям ключевые жизненные/будущие навыки, чтобы держать их впереди игры.

Стремясь заполнить пробел, оставленный традиционным образованием, мы прививаем ключевые будущие навыки с помощью специально разработанных курсов по программированию и финансовой грамотности, которые преподают лучшие умы мира из ведущих институтов, таких как IIT и IIM.

Уравнения алгебры — как их решать

Zave Smith/Stone Collection/Getty Images

Алгебра. Это слово может вселить страх в сердца тех, кто читает это, но мы обещаем, что решение алгебраических математических уравнений не так сложно, как кажется! Этот учебник покажет вам, как решать алгебраические уравнения, с примерами уравнений и их решениями.

Вы можете задаться вопросом: «Когда мне когда-нибудь понадобится решать даже простые алгебраические уравнения в реальной жизни?» Математика в целом и алгебра в частности пригодятся, если вы планируете стать:

• Ученый
• Учитель
• Программист
• Доктор
• Статистик

Решение основных алгебраических уравнений подготавливает ваш мозг к решению других сложных задач, таких как обучение программированию или игра на музыкальном инструменте. Большинство профессий в области технологий требуют понимания математических уравнений алгебры.

Что такое алгебраическое уравнение?

Westend61/Westend61/Getty Images

Прежде чем мы перейдем к некоторым примерам алгебраических уравнений, давайте поговорим об алгебре. Алгебра очень похожа на арифметику с элементом тайны. У вас все те же основные символы:

• Отдел: ÷
• Дополнение: +
• Умножение: ×
• Вычитание: –

Но чтобы найти решение по алгебре, вам нужно найти число, скрытое за буквой, обычно «х».

Давайте рассмотрим некоторые основные термины алгебры:

Переменная

Буква, скрывающая решение, обычно «x».

Константа

Известные числа в уравнении. В уравнении 2+3=x 2 и 3 являются константами.

Уравнение

Часть математики, которую нужно решить. Примеры уравнений: «4x+3=11» и «9÷x=3».

Выражение

Числа и символы на одной стороне уравнения. «4x+3» и «9÷x» являются выражениями.

Термин

Части выражения, разделенные знаком математических символов. В предыдущем примере «4x+3», «4x» и «3» являются терминами.

Коэффициент

Числовая часть члена представляет собой коэффициент, включая знак плюс или минус перед ним. Для «4x+3=11» «4x» будет иметь коэффициент «4». Если бы уравнение было «3-4x=11», коэффициент был бы «-4».

Давайте сравним алгебраические математические уравнения с арифметическими уравнениями. Обычное арифметическое уравнение может выглядеть примерно так:

2+2=

Алгебраическое уравнение будет выглядеть так:

2+2=x

У нас есть буква «x», где будет загадочное число, когда мы найти решение по алгебре. Поскольку мы знаем, что 2 и 2 составляют 4, теперь мы можем найти «x».

Зачем вообще заниматься алгеброй, если простые алгебраические уравнения почти идентичны арифметическим задачам?

Математические уравнения алгебры допускают гораздо большую сложность, чем стандартная арифметика. Такое решение проблем необходимо для детей, изучающих темы STEM. Давайте рассмотрим еще несколько примеров алгебраических уравнений с ответами.

В следующем уравнении мы переместили «x» с другой стороны знака равенства:

x+9=15

Математические уравнения базовой алгебры, подобные этому, легче выполнять без калькулятора или листа бумаги. . Чтобы прийти к решению, мы хотим перевести уравнение в более понятную форму.

Мы знаем, что нужно прибавить число к 9, чтобы получить 15, поэтому мы могли бы переписать уравнение следующим образом:

15-9=x

Изменение порядка выражения делает решение алгебры очевидным. Введите уравнение в калькулятор, и вы получите ответ:

15-9=6

Итак, теперь мы знаем, что:

x=6

Как решать уравнения алгебры

Kryssia Campos/ Moment Open/ Getty Images

До сих пор мы решали довольно простые математические уравнения по алгебре, но давайте придумаем более сложные примеры математических уравнений по алгебре.

Давайте добавим умножение и деление!

(8×2)÷x=4

В скобках указано, что нам нужно умножить 8 и 2, прежде чем делить на «x».

В отличие от предыдущих примеров математических уравнений по алгебре, мы хотим сначала выполнить некоторые математические вычисления в задаче:

16÷x=4

Затем мы можем переписать уравнение, чтобы его было проще читать:

x×4= 16

Поскольку 16, деленное на загадочное число, равно 4, мы знаем, что 4 умножения на загадочное число должны равняться 16. Чтобы найти x, мы можем «сбалансировать уравнение». Другими словами, все, что мы делаем по одну сторону знака равенства, можно делать и по другую:

(x×4)÷4=16÷4

Мы можем разделить обе части на 4, чтобы получить «x»:

x=16÷4

x=4

Теперь вы знаете!

Как найти X в уравнении… и Y тоже?   DNY59 / E+ / Getty Images

Мы можем добавить другие буквы для еще более сложных алгебраических математических уравнений, таких как те, с которыми вы столкнетесь в средней школе и колледже. Важно отметить, что в одном уравнении буква может представлять только одно число. Например: 

 x+x=4 

Несколько разных чисел можно сложить, чтобы получить 4. Но поскольку оба они представлены в уравнении x, они должны быть одним и тем же числом. У вас не может быть x=1 и x=3; они оба должны быть равны 2.  

Теперь, когда мы установили это правило, давайте составим два новых уравнения:

(5×6)-x=10+y

3x=y 

уравнений, когда у нас есть несколько переменных, заключается в том, что нам нужно проверить, правильно ли мы получили «x» и «y», подставив их во второе уравнение.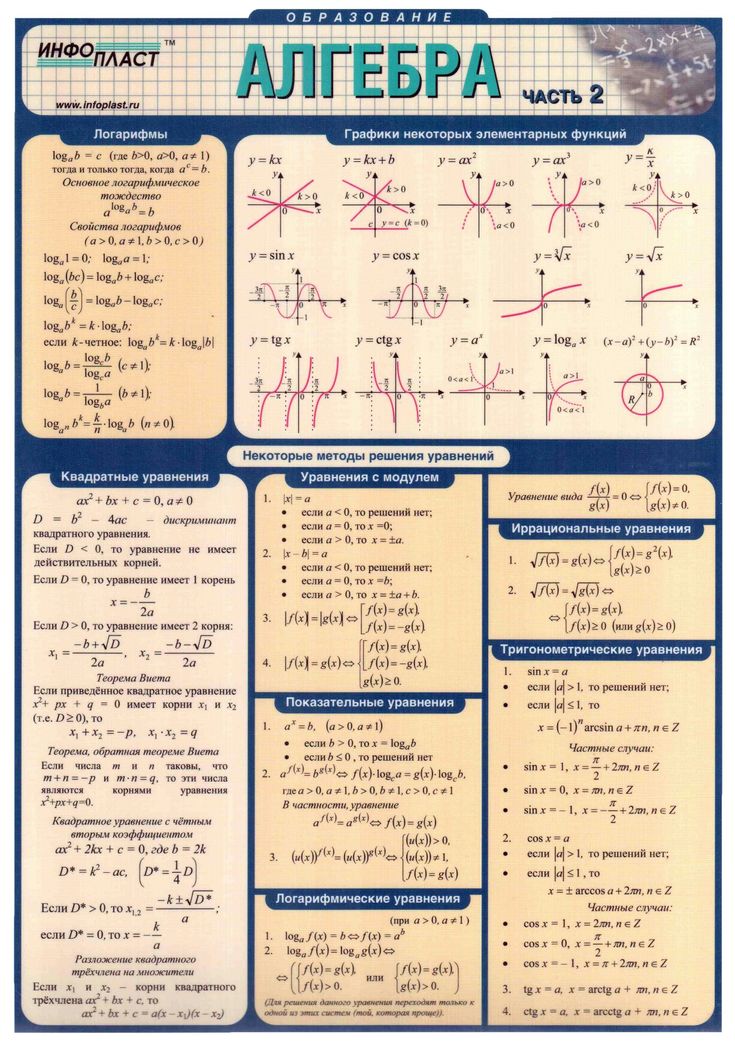

Обратите внимание, что между 3 и x нет символа умножения. Когда у нас есть число рядом с переменной, предполагается, что две цифры будут перемножены. То же самое касается чисел рядом со скобками в математических уравнениях алгебры.

Теперь у нас есть переменные с обеих сторон уравнения, что делает эту задачу более сложной, чем более простые алгебраические уравнения, которые были раньше.

Сначала умножим 5 на 6 в первом уравнении: 

30-x=10+y 

Теперь мы кое-что получили. Давайте изолируем «у». Поскольку мы знаем, что «y» плюс 10 равняется выражению 30 минус «x», мы можем вычесть 10 из обеих частей:  

20-x=y  

Вот сложная часть: многие числа дадут правильные ответы на это уравнение, но есть только два числа, которые будут работать для «x» и «y», если мы также хотим решить второе уравнение.

20-x=y 

3x=y 

Теперь мы можем объединить два уравнения, потому что мы знаем выражения, равные «y».

20-x=3x 

Теперь это выглядит как сложное уравнение само по себе, верно? Вы столкнетесь с математическими уравнениями посложнее! Во-первых, давайте поймем, что 20 минус «x» равно 20 плюс минус «x»:

20+-x=3x

Затем мы изменим порядок, чтобы еще больше изолировать «x»:

-x+20 =3x

Теперь мы можем вычесть 3x с обеих сторон:

-4x+20=0

Теперь добавить 4x к обеим сторонам:

 20=4x

Разделим на 4:

20÷4=4x÷4

И получим:

5=x

Теперь мы можем подставить это обратно в наши исходные уравнения, чтобы найти y:

 (5×6)- 5=10+y

3×5=y

 Мы видим, что второе уравнение даст нам 15=y, но давайте решим первое уравнение, чтобы убедиться:

 30-5=10+y

 Тогда .

Порядок действий   Thomas Winz/The Image Bank/Getty Image

До сих пор вам могло казаться, что алгебра — это совершенно новый язык. Точно так же, как грамматика важна для структуры предложений, порядок операций в алгебраических математических уравнениях действительно важен. Давайте посмотрим на некоторые примеры математических уравнений алгебры.

Распределяющее свойство  

При поиске алгебраического решения есть несколько путей для получения окончательного ответа. Здесь мы рассмотрим свойство распределения. Это свойство называется распределительным, потому что мы распределяем первые 3 как по переменной, так и по 5 в круглых скобках: 

3(x-5)=3

Результат:

3x-15=3

Мы умножили x и 5 на 3, получив 3x и 15. Теперь мы можем добавить 15 к обоим Стороны:

3x = 18

Разделите обе стороны на 3:

3x ÷ 3 = 18 ÷ 3

, чтобы получить наше решение для «x»:

x = 6

Разделение для решения Cristinairanzo / Moment / Getty Images

Division также является отличным способом найти решения математических уравнений алгебры. Вместо того, чтобы распределять 3, мы можем разделить обе части на 3:

3(x-5)÷3=3÷3

Чтобы получить: 

x-5=1 

Затем мы можем добавить 5 к обеим сторонам, чтобы получить: 

x=6 

Возможность решить уравнение несколькими способами также помогает проверить вашу математику. Если вы получаете разные ответы в зависимости от того, как вы решили уравнение, это хороший знак, что вам нужно проверить свой процесс.

Как видите, порядок операций влияет на то, как решать алгебраические уравнения. Но есть еще один сценарий, который мы не рассматривали…

Алгебра: не так уж и страшно   Килито Чан / Moment / Getty Images

Немного терпения и практики, а также знакомство с некоторыми терминами, и вы будете в хорошей форме, чтобы понять, как решать алгебраические уравнения. Конечно, это руководство — лишь верхушка алгебраического айсберга!

Независимо от того, являетесь ли вы школьником или взрослым, оттачивающим свои математические навыки, найти хорошего учителя — лучший способ учиться.