I. Основное тригонометрическое тождество и следствия из него:
II. Формулы (теоремы) сложения аргументов:
III. Формулы приведения:
1) функция меняется на кофункцию при переходе через вертикальную ось и не меняется при переходе через горизонтальную;
2) перед приведенной функцией ставится знак приводимой функции, считая углом первой четверти.
IV. Формулы двойного аргумента:
V. Формулы понижения степени:
Значения тригонометрических функций некоторых углов
таблица 1
0 | | ||||||
sin | 0 | 1 | 0 | –1 | |||
cos | 1 | 0 | –1 | 0 | |||
tg | 0 | 1 | — | 0 | — | ||
ctg | — | 1 | 0 | — | 0 |
Связь между тригонометрическими функциями одного аргумента
таблица 2
Искомая функция | Выражение искомой функции через | |||
sin | cos | tg | сtg | |
sin = | sin | |||
cos | cos | |||
tg = | tg | |||
сtg = | сtg | |||
6.
Графики тригонометрических функцийТригонометрический набор координат:
у = sin x синусоида
у = cos x косинусоида
у = tg x у = ctg x
тангенсоида котангенсоида
7. Свойства синуса и косинуса
Линия синусов | Область значений | Знаки по четвертям | Четность – нечетность |
|sin t| 1 | sin(–t) = –sin t |
Линия косинусов | Область значений | Знаки по четвертям | Четность – нечетность |
|cos t| 1 | cos(–t) = cos t |
Область определения | |
D(sin) = R | D(cos) = R |
| Область значений | |
E(sin) = [–1; 1] | E(cos) = [–1; 1] |
Четность – нечетность | |
нечетная функция | четная функция |
Периодичность | |
sin(x 2) = sin x | cos(x 2) = cos x |
8.
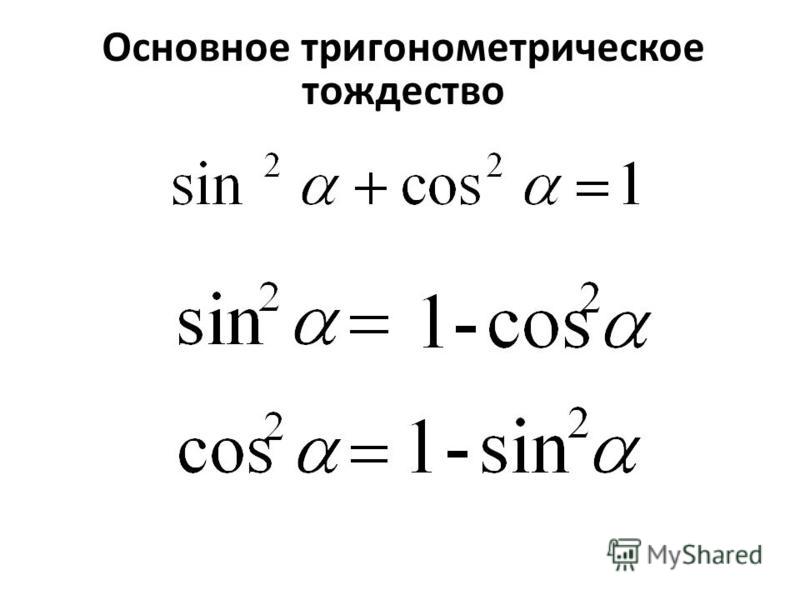Свойства тангенса и котангенсаЛиния тангенсов | Область значений | Знаки по четвертям | |
tg t (–; +) | tg(–t) = –tg t |
Линия котангенсов | Область значений | Знаки по четвертям | Четность – нечетность |
ctg t (–; +) | ctg(–t) = –ctg t |
Область определения | |
Область значений | |
E(tg) = (–; +) | E(ctg) = (–; +) |
Четность – нечетность | |
нечетная функция | нечетная функция |
Периодичность | |
tg(x ) = tg x | ctg(x ) = ctg x |
18 3
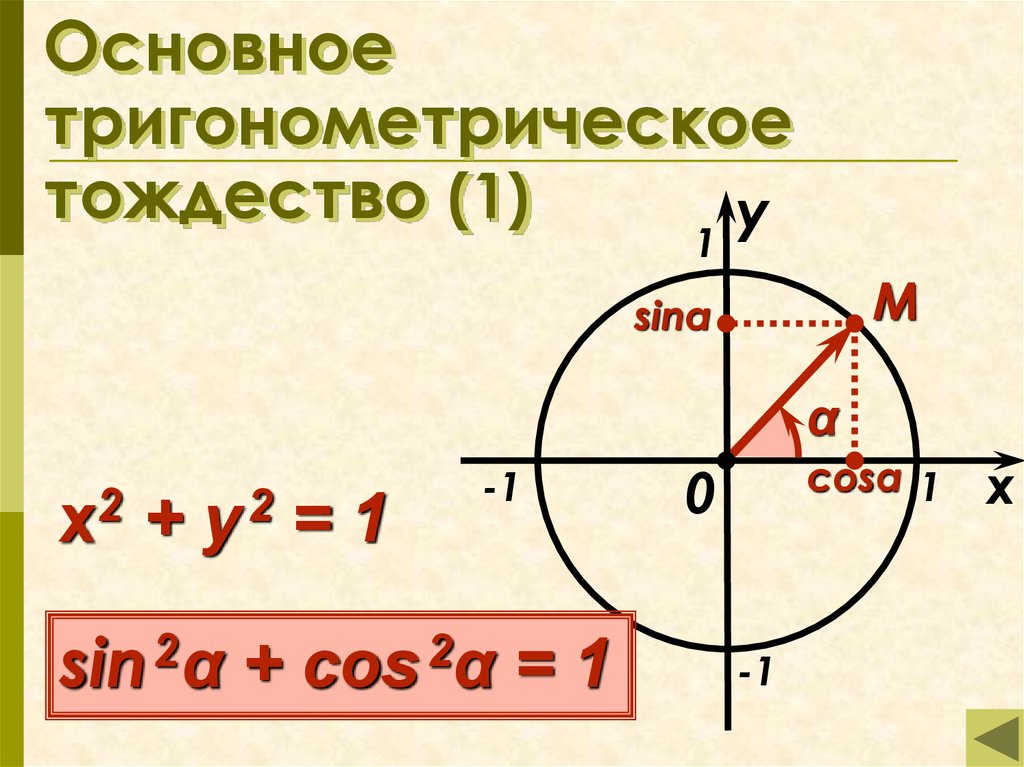
Основное тригонометрическое тождество.
Упрощение выражений. 9-10 класс. Часть 1212+
2 месяца назад
Математика от Баканчиковой161 подписчик
Геометрия 9 класс. Алгебра 10 класс. Что такое основное тригонометрическое тождество? Как доказать основное тригонометрическое тождество? Какие формулы получаются из основного тригонометрического тождества, и как с ними работать? Как применять основное тригонометрическое тождество для упрощения тригонометрических выражений в 9 и 10 классах? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в геометрии», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Вы обратим Ваше внимание на то, что чтобы легко упрощать тригонометрические выражения, Вы должны чётко знать формулы основного тригонометрического тождества и практически все темы алгебры, включая действия с многочленами, дробями, формулы сокращенного умножения многочленов, законы математики, приведение подобных слагаемых и т.
Тригонометрические функции. Часть 7. Геометрия 10-11 класс. https://rutube.ru/video/a246217e2de6f5960fb55a3e77b904d0/
Как найти противо- и прилежащие катеты по углу и другому катету. Как найти площадь треугольника и параллелограмма. Тригонометрические функции. Часть 8. Геометрия 9 класс. https://rutube.ru/video/5b374b4961980532582185a1803b6be0/
Тангенс и котангенс в решении задач по стереометрии. Тригонометрические функции. Часть 9. Геометрия 10-11 класс. https://rutube.ru/video/22ce4c90678e252c22f2084eb1ec14a3/
Как найти гипотенузу по катету и противолежащему или прилежащему углу. Тригонометрические функции. Часть 10. Геометрия 9 класс. https://rutube.ru/video/d4f247808a953357f1ed1c2a66e6fe73/
Как найти значения длин сторон прямоугольного треугольника по значениям тригонометрических функций. Тригонометрические функции. Часть 11. Геометрия 9 класс. https://rutube.ru/video/3f37a5cab19ba4a197de56e09b20237f/
#УпрощениеТригонометрическихВыражений #ОсновноеТригонометрическоеТождество #ДоказатьОсновноеТригонометрическоеТождество #ТождестваТригонометрии #ОсновноеТригонометрическоеТождествоФормулы #ОсновноеТригонометрическоеТождествоСинус #ОсновноеТригонометрическоеТождествоКосинус #ПервоеОсновноеТригонометрическоеТождество #ОсновноеТригонометрическоеТождество9КлассГеометрия #ОсновноеТригонометрическоеТождествоПримеры #МатематикаОтБаканчиковой
Геометрия 9 класс, Алгебра 10 класс, основное тригонометрическое тождество, доказать основное тригонометрическое тождество, упрощение тригонометрических выражений, тождества тригонометрии, основное тригонометрическое тождество формулы, основное тригонометрическое тождество синус, основное тригонометрическое тождество косинустригонометрическое тождество | Platonic Realms
Так называемые тригонометрические тождества представляют собой полезный набор уравнений, которые часто позволяют делать замены в выражении, содержащем тригонометрические функции, чтобы упростить выражение или придать ему более полезную форму.
Большинство тригонометрических тождеств на самом деле довольно легко вывести алгебраически из их определений, и каждый изучающий математику должен вывести их все хотя бы один раз. После этого уже не нужно будет их запоминать; вы сможете получить их всякий раз, когда они понадобятся. 92 \варфи\\
\end{выравнивание*}
\]
Идентичности кофункций
\[ \begin{выравнивание*} \sin\left(\frac{\pi}{2} — \varphi\right) & = & \cos \varphi \\ & & \\ & & \\ \csc\left(\frac{\pi}{2} — \varphi\right) & = & \sec \varphi \\ & & \\ & & \\ \sec\left(\frac{\pi}{2} — \varphi\right) & = & \csc \varphi \\ & & \\ & & \\ \cos\left(\frac{\pi}{2} — \varphi\right) & = & \sin \varphi \\ & & \\ & & \\ \tan\left(\frac{\pi}{2} — \varphi\right) & = & \cot \varphi \\ & & \\ & & \\ \cot\left(\frac{\pi}{2} — \varphi\right) & = & \tan \varphi \\ \end{выравнивание*} \]
Формулы приведения
\[ \begin{выравнивание*} \sin( — \varphi ) & = & -\sin \varphi \\ & & \\ & & \\ \csc( — \varphi ) & = & -\csc \varphi \\ & & \\ & & \\ \sec(-\varphi) & = & \sec\varphi\\ & & \\ & & \\ \cos(-\varphi) & = & \cos\varphi\\ & & \\ & & \\ \tan( — \varphi ) & = & -\tan \varphi \\ & & \\ & & \\ \кот( — \варфи ) & = & -\кот \варфи \\ \end{выравнивание*} \]
Формулы суммы и разности
\[ \begin{выравнивание*} \sin( \varphi \pm \theta ) & = & \sin \varphi \cos \theta \pm \cos \varphi \sin \theta \\ & & \\ & & \\ \cos(\varphi\pm\theta) & = & \cos\varphi\cos\theta\mp\sin\varphi\sin\theta\\ & & \\ & & \\ \ tan ( \ varphi \ pm \ theta ) & = & \ frac {\ tan \ varphi \ pm \ tan \ theta} {1 \ mp \ tan \ varphi \ tan \ theta} \\ \end{выравнивание*} \]
Формулы двойного угла 92 \varphi & = & \frac{1 — \cos 2 \varphi}{1 + \cos 2 \varphi} \\ \end{выравнивание*} \]
Формулы суммы к произведению
\[ \begin{выравнивание*} \sin \varphi + \sin\theta & = & 2 \sin\left(\frac{\varphi +\theta}{2}\right) \cos\left(\frac{\varphi — \theta}{2} \правильно) \\ & & \\ & & \\ \sin \varphi — \sin \theta & = & 2 \cos \left(\frac{\varphi + \theta}{2}\right) \sin \left(\frac{\varphi — \theta}{2} \правильно) \\ & & \\ & & \\ \cos\varphi + \cos\theta & = & 2 \cos\left(\frac{\varphi +\theta}{2}\right) \cos\left(\frac{\varphi — \theta}{2} \правильно) \\ & & \\ & & \\ \cos \varphi — \cos \theta & = & -2 \sin \left(\frac{\varphi + \theta}{2}\right) \sin \left(\frac{\varphi — \theta}{2 }\правильно) \\ \end{выравнивание*} \]
Формулы произведения на сумму
\[ \begin{выравнивание*} \sin \varphi \sin \theta & = & \frac{1}{2}\left( \cos (\varphi — \theta) — \cos (\theta + \varphi) \right) \\ & & \\ & & \\ \cos \varphi \cos \theta & = & \frac{1}{2}\left( \cos (\varphi — \theta) + \cos (\theta + \varphi) \right) \\ & & \\ & & \\ \sin \varphi \cos \theta & = & \frac{1}{2}\left( \sin (\varphi + \theta) + \sin (\theta — \varphi) \right) \\ & & \\ & & \\ \cos \varphi \sin \theta & = & \frac{1}{2}\left( \sin (\varphi + \theta) — \sin (\theta — \varphi) \right) \\ \end{выравнивание*} \]
4.
1: Тригонометрические тождества — Mathematics LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7118
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Что такое личность?
- Как нам подтвердить личность?
Рассмотрим тригонометрическое уравнение \(\sin(2x) = \cos(x)\).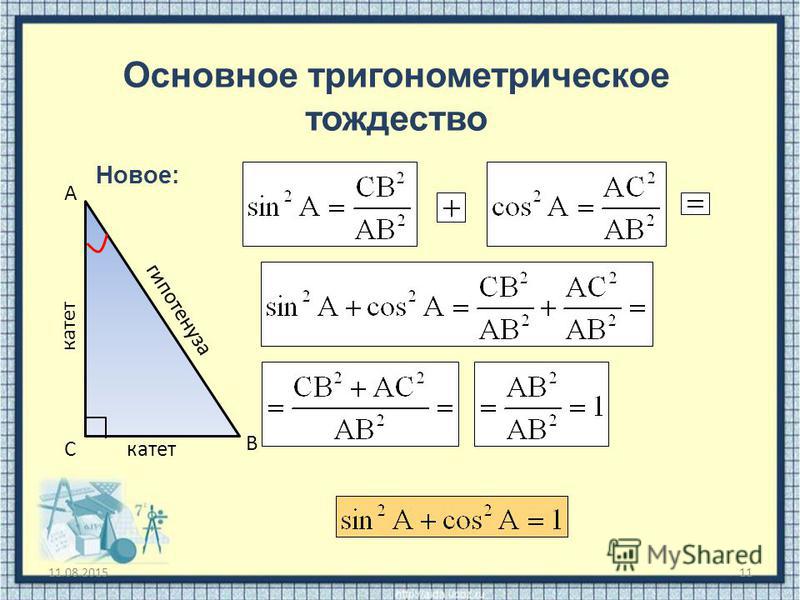
Основываясь на наших текущих знаниях, такое уравнение может быть трудно решить точно, потому что периоды задействованных функций различны. Что позволит нам относительно легко решить это уравнение, так это тригонометрическое тождество, и мы явно решим это уравнение в следующем разделе. Этот раздел представляет собой введение в тригонометрические тождества.
Как мы обсуждали в разделе 2.6, математический 9{2} = 1\), так как это верно для всех вещественных значений \(x\).
Таким образом, пока мы решаем уравнения, чтобы определить, когда справедливо равенство, нет причин решать тождество, поскольку равенство в тождестве всегда действительно. Каждое тождество есть уравнение, но не каждое уравнение есть тождество. Чтобы знать, что уравнение является тождеством, необходимо предоставить убедительный аргумент, что два выражения в уравнении всегда равны друг другу. Такой убедительный аргумент называется доказательство , и мы используем доказательства для проверки тригонометрических тождеств.
Определение: Тождество
Тождество — это уравнение, истинное для всех допустимых значений задействованных переменных.
Начальное задание
- Используйте графическую утилиту, чтобы нарисовать график \(y = \cos(x — \dfrac{\pi}{2})\) и \(y = \sin(x + \dfrac{\ pi}{2})\) на интервале \([-2\pi, 2\pi]\) на том же наборе осей. Являются ли два выражения \(\cos(x — \dfrac{\pi}{2})\) и \(\sin(x + \dfrac{\pi}{2})\) одинаковыми, т.е. они имеют одинаковое значение для каждого входа \(x\)? Если да, объясните, как графики показывают, что выражения одинаковы. Если нет, найдите хотя бы одно значение \(x\), при котором \(\cos(x — \dfrac{\pi}{2})\) и \(y = \sin(x + \dfrac{\pi {2})\) имеют разные значения.
- С помощью графической утилиты нарисуйте график \(y = \cos(x — \dfrac{\pi}{2})\) и \(y = \sin(x)\) на интервале \([- 2\pi , 2\pi]\) на одном и том же наборе осей. Являются ли два выражения \(\cos(x — \dfrac{\pi}{2})\) и \(\sin(x)\) одинаковыми, то есть имеют ли они одинаковое значение для каждого входа \( Икс\)? Если да, объясните, как графики показывают, что выражения одинаковы.
Если нет, найдите хотя бы одно значение \(x\), при котором \(\cos(x — \dfrac{\pi}{2})\) и \(\sin(x)\) имеют разные значения. 9{2} = 1.\]Тождества из определений
Определения функций тангенса, котангенса, секанса и косеканса были введены в разделе 1.6. Следующее справедливо для всех значений \(t\), для которых определена правая часть каждого уравнения.
\[\tan(t) = \dfrac{\sin(t)}{\cos(t)}\]
\[\cot(t) = \dfrac{\cos(t)}{\sin (t)}\]
\[\sec(t) = \dfrac{1}{\cos(t)}\]
\[\csc(t) = \dfrac{1}{\sin(t )}\]
Отрицательные тождества
Отрицательные значения были введены в главе 2, когда обсуждалась симметрия графов. (См. стр. 82 и упражнение (2) на стр. 139.)
\[\cos(-t) = \cos(t)\]
\[\sin(-t) = -\sin(t)\ ]
\[\tan(-t) = -\tan(t)\]
Отрицательные тождества для косинуса и синуса справедливы для всех действительных чисел \(t\), а отрицательное тождество для тангенса справедливо для все действительные числа \(t\), для которых определено \(\tan(t)\).
Проверка личности
9{2}(х)\). Чтобы показать, что уравнение не является тождеством, достаточно продемонстрировать, что две части уравнения имеют разные значения на одном входе.Пример \(\PageIndex{2}\): (Показывая, что уравнение не является тождеством)
Рассмотрим уравнение с уравнением \(\cos(x — \dfrac{\pi}{2}) = \ sin(x + \dfrac{\pi}{2})\), с которым мы столкнулись в нашей начальной деятельности. Хотя вы можете проверить, что \(\cos(x — \dfrac{\pi}{2})\) и \(\sin(x + \dfrac{\pi}{2})\) равны при некоторых значениях, \(\dfrac{\pi}{4}\), например, они не равны при всех значениях –\(\cos(0 — \dfrac{\pi}{2}) = 0\), но \(\sin (0 + \dfrac{\pi}{2}) = 1\). Поскольку тождество должно обеспечивать равенство для все допустимых значения переменной, если два выражения различаются на одном входе, то уравнение не является тождеством. Таким образом, уравнение \(\cos(x — \dfrac{\pi}{2}) = \sin(x + \dfrac{\pi}{2})\) не является тождеством.
Пример 4.2 иллюстрирует важный момент.
чтобы показать, что уравнение не является тождеством, достаточно найти один вход, при котором две части уравнения не равны. Подытожим нашу работу с тождествами следующим образом.- Чтобы доказать, что уравнение является тождеством, нам нужно применить известные тождества, чтобы показать, что одна часть уравнения может быть преобразована в другую.
- Чтобы доказать, что уравнение не является тождеством, нам нужно найти один вход, при котором две части уравнения имеют разные значения.
Важное примечание : При подтверждении личности может возникнуть соблазн начать работать с самим уравнением и манипулировать обеими сторонами, пока вы не придете к чему-то, что, как вы знаете, является правдой. НЕ ДЕЛАЙТЕ ЭТОГО! Работая с обеими частями уравнения, мы делаем предположение, что уравнение является тождеством, но это предполагает именно то, что нам нужно показать. Таким образом, правильный формат доказательства тригонометрического тождества состоит в том, чтобы выбрать одну сторону уравнения и применить существующие тождества, которые мы уже знаем, для преобразования выбранной стороны в оставшуюся часть.
Обычно жизнь проще начинать с более сложной стороны (если она есть). 9{2}(х)\). Любая правильная перестановка тождества также является тождеством, поэтому мы можем манипулировать известными тождествами, чтобы использовать их в наших доказательствах.Повторим еще раз: правильный формат доказательства тригонометрического тождества состоит в том, чтобы выбрать одну сторону уравнения и применить существующие тождества, которые мы уже знаем, чтобы преобразовать выбранную сторону в оставшуюся часть. Жестких и быстрых методов подтверждения личности не существует — это что-то вроде искусства. Вы должны практиковаться, чтобы стать хорошим в этом.
Упражнение \(\PageIndex{1}\) 9{2}(х)\]
- \[\cos(x)\sin(x) = 2\sin(x)\]
Если нет, найдите хотя бы одно значение \(x\), при котором \(\cos(x — \dfrac{\pi}{2})\) и \(\sin(x)\) имеют разные значения. 9{2} = 1.\]
чтобы показать, что уравнение не является тождеством, достаточно найти один вход, при котором две части уравнения не равны. Подытожим нашу работу с тождествами следующим образом.
Обычно жизнь проще начинать с более сложной стороны (если она есть). 9{2}(х)\). Любая правильная перестановка тождества также является тождеством, поэтому мы можем манипулировать известными тождествами, чтобы использовать их в наших доказательствах.- Ответить
1. Графики обеих частей уравнения показывают, что это тождество.
2. Графики обеих частей уравнения показывают, что это не тождество. Например, если мы допустим \(x = \dfrac{\pi}{2}\), то
\[\cos(\dfrac{\pi}{2})\sin(\dfrac{\pi}{2}) = 0\cdot 1 = 0\] и \[2\sin(\dfrac{\pi {2}) = 2\cdot 1 = 2\]
Резюме
В этом разделе мы изучили следующие важные понятия и идеи:
Тождество — это уравнение, верное для всех допустимых значений вовлеченных переменных.