Алгебра логики упрощение выражений: Законы алгебры логики. Упрощение логических выражений.

Законы алгебры логики. Упрощение логических выражений.

Так же как и в привычной нам алгебре есть законы упрощения выражений, в алгебре логики действуют законы алгебры логики. Для удобства обработки информации алгебраические и логические выражения принято упрощать или приводить к нормальному виду. Большинство законов обеих алгебр схожи и уже знакомы вам. И лишь несколько вы узнаете впервые и, возможно, удивитесь. Упрощение сложных высказываний — это замена их на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы.  Нормальная форма выражений — это выражение где нет знаков операций импликации и эквивалентности, а инверсия применена только к отдельным высказываниям. Для обрабатывания выражений вы должны свободно ориентироваться между обозначениями операций. Основные три из них имеют следующие варианты обозначений: Инверсия (отрицание):   Ø ,`A ,  не . Конъюнкция (умножение): & , L ,  × . Дизъюнкция (сложение): V,  +. Для удобства записи и большей наглядности можно записывать знаки операций в логических выражениях в более привычной нам форме: умножение — знаком ×,  а сложение — знаком +.  Иначе говоря, упростить выражение — это найти в нём законы логики и их применить! Первое, что надо знать для упрощения — формулы замены операций (которых не должно быть в нормальной форме записи логических выражений): Итак, а теперь сами законы алгебры логики: Чтобы ими пользоваться их надо знать, т.е. выучить. Но на самом деле эти законы во многом повторяю законы обычной алгебры.  Закон двойного отрицания напоминает нам ситуацию, когда «минус на минус даёт плюс», хотя так говорить и не грамотно, но зато именно так ученики его запоминают быстрее всего! Законы исключения третьего, операции с константами и законы повторения следуют из определения самих логических операций сложения (дизъюнкции) и умножения (конъюнкции).   Переместительный, сочетательный и распределительный законы нам встречались и в обычной алгебре. Они и в алгебре логики работают точно так же! Правда распределительный закон относительно умножения на уроках математики применять никак нельзя, а в алгебре логики пожалуйста: a + b × c = (a + b)× (a + c) И последнее и самое интересное — это законы де Моргана (или двойного отрицания). Никак нельзя допускать при упрощении выражений оставлять знак отрицания более чем над одним высказыванием! С этой проблемой нам помогают бороться именно законы де Моргана.  Запомнить их просто: отрицание раздается каждому высказыванию, находящемуся под общей чертой, а знаки + меняются на × , и наоборот ×  на +. Упрощение нескольких логических выражений представлено в следующем видео. Вы можете его ставить на паузу и сверяться с формулами законов в любом удобном для вас месте:

Упрощение логических выражений | Законы алгебры логики (курс pol 68 ч.) /informatika_10_68_pol/ (68 часов в уч. год)

Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, сокращенный курс, 2 часа в неделю)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, сокращенный курс, 2 часа в неделю) | Упрощение логических выражений

Содержание урока

Законы алгебры логики

Логические уравнения

Задачи

Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — «НЕ», «И» и «ИЛИ».

Закон двойного отрицания означает, что операция «НЕ» обратима: если применить ее два раза, логическое значение не изменится. Закон исключённого третьего основан на том, что в классической (двузначной) логике любое логическое выражение либо истинно, либо ложно («третьего не дано»). Поэтому если А = 1, то А = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.

Операции с константами и закон повторения легко проверяются по таблицам истинности операций «И» и «ИЛИ». Переместительный и сочетательный законы выглядят вполне привычно, так же, как и в арифметике. Почти везде «работает» аналогия с алгеброй чисел, нужно только помнить, что в логике 1 + 1 = 1, а не 2.

Распределительный закон для операции «ИЛИ» — это обычное раскрытие скобок. А вот для операции «И» мы видим незнакомое выражение, в алгебре чисел это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:

(А + В) • (А + С) = А • А + А • С + В • А + В • С.

Дальше используем закон повторения (А • А = А) и заметим, что

А + А • С = А • (1 + С) = А • 1 = А.

Аналогично доказываем, что А + В • А = А • (1 + В) = А, таким образом,

(А + В) • (А + С) = А + В • С.

Равенство доказано. Попутно мы доказали также и закон поглощения для операции «И» (для операции «ИЛИ» вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезное тождество:

А + А • В = (А + А) • (А + В) = А + В.

Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика Огастеса (Августа) де Моргана. Обратите внимание, что при этом не просто «общее» отрицание переходит на отдельные выражения, но и операция «И» заменяется на «ИЛИ» (и наоборот). Доказать законы де Моргана можно с помощью таблиц истинности.

Теперь с помощью приведённых законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме с тремя переменными (§ 20, рис.

3.15):

(А • В • C) + А • В • C = (А + А) • В • C = В • C.

Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключённого третьего.

В общем случае можно рекомендовать такую последовательность действий.

1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции «НЕ», «И» и «ИЛИ».

2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.

3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.

Пример

(А + B) • (А + B) • (А + С)=(А + B) • А • B • (А + C = (А • А + B • А) • B • (А + С) = B • А • B • (А + С) = А • B • B • (А + С) = B • А • (А + С) = B • (А.

Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключённого третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения.

Следующая страница Логические уравнения

Cкачать материалы урока

Калькулятор булевой алгебры — онлайн-упрощение булевых логических выражений

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор логических выражений

Инструмент/калькулятор для упрощения или минимизации логических выражений (булева алгебра), содержащих логические выражения с И, ИЛИ, НЕ, XOR.

Результаты

Калькулятор логических выражений — dCode

Метки: Символьные вычисления, Электроника

Поделиться

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Упрощение логических выражений

Калькулятор логических выражений/упрощение/минификатор
Формат результата
Любой формат
Дизъюнктивная нормальная форма DNF (сумма произведений/SOP/Minterms)
Конъюнктивная нормальная форма CNF (произведение сумм/POS/Maxterms)
Только вентили НЕ-И (НЕ-И ⊼)
Только вентили ИЛИ-НЕ (НЕ-ИЛИ ⊽)

Нотация

Алгебраические (*, +, !) Логические (∧, ∨, ¬) 9000 4 Программирование (&&, ||, ~) Буквенное (И, ИЛИ, НЕ)

См. также: Таблица истинности — Решатель уравнений — Двоичный код

Ответы на вопросы (FAQ)

Что такое логическое выражение? (Определение)

A Логическое выражение (или Логическое выражение) — это математическое выражение, использующее Булева алгебра , которая использует логические значения (0 или 1, истина или ложь) в качестве переменных и имеет логические значения в качестве результата/упрощения. Выражение может содержать такие операторы, как конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).

Как упростить/минимизировать логическое выражение?

Для упрощения булевых уравнений можно использовать различные методы: помимо классического развития через ассоциативность, коммутативность, дистрибутивность и т. д., таблицы истинности или диаграммы Венна обеспечивают хороший обзор выражений.

Пример: Исходное выражение (LaTeX) $$ \overline{a \land b \land (c \lor \bar{d})} \lor \bar{b} $$

dCode допускает несколько синтаксисов:

Алгебраическая запись

Пример: !(ab(c+!d))+!b с неявным умножением ab = a AND b и ! (восклицательный знак) для строки : логический НЕ .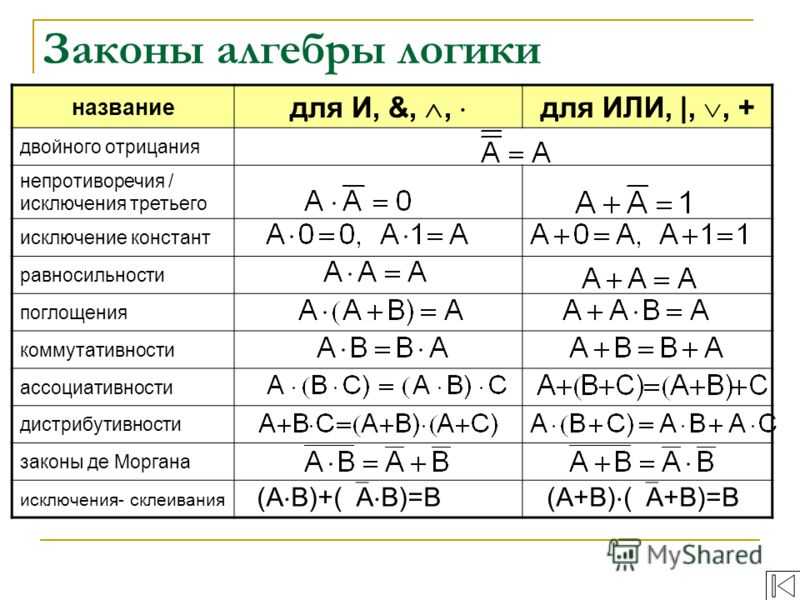

Логические/компьютерные обозначения

Пример: !(a&&b&&(c||!d))||!b с двойным символом и (амперсанд) для И и двойным символом | (прямая, вертикальная черта) для логического ИЛИ .

Буквенное обозначение

Пример: НЕ (a И b И (c ИЛИ НЕ d)) ИЛИ НЕ b

Для одного и того же выражения может быть несколько минимальных представлений, dCode предоставляет решение и выводит алгебраическое обозначение.

Некоторые обозначения неоднозначны, избегайте функционального обозначения ‘XOR(a,b)’ для записи a XOR b , также избегайте суффикса штрих/апостроф перед `a’ и предпочтите !a .

Что такое методы упрощения булевой алгебры?

Булева алгебра обладает многими свойствами (булевыми законами):

1 — Элемент тождества: $0$ нейтрален для логического ИЛИ, тогда как $1$ нейтрален для логического И

$$a + 0 = a \\a .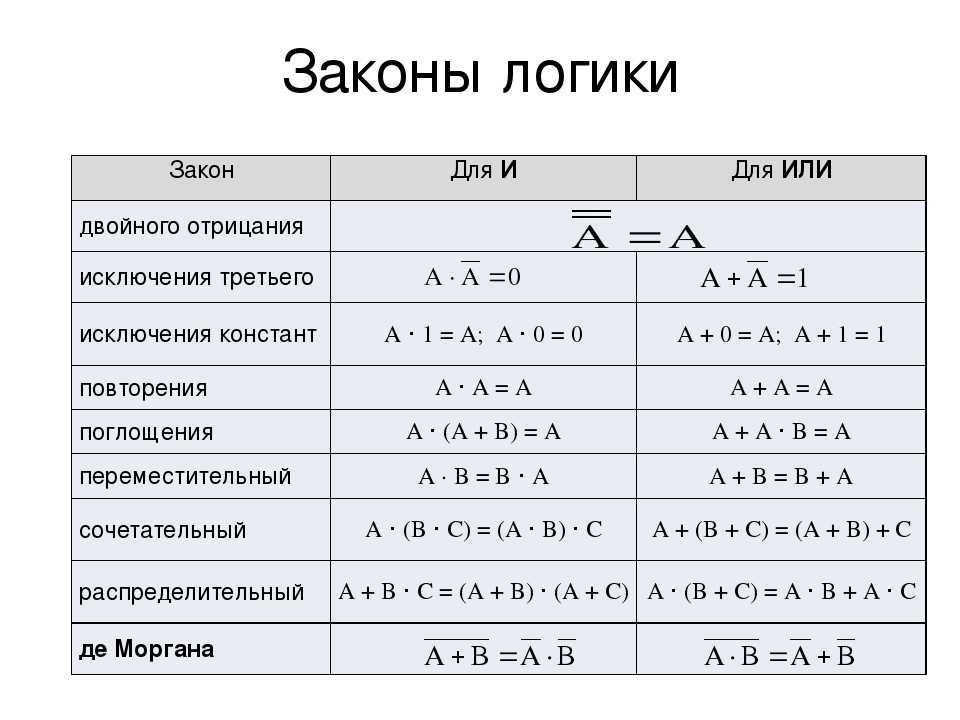 1 = a $$

2 — Поглощение: $1$ поглощает для логического ИЛИ, а $0$ поглощает для логического И

$$ a + 1 = 1 \\ a.0 = 0 $$

3 — Идемпотентность: многократное применение одной и той же операции не меняет значение

$$ a + a = a + a + \cdots + а = а \ а . а = а . а . \cdots . a = a $$

4 — Инволюция или двойное дополнение: противоположность противоположности $ a $ est $ a $

$$ a = \overline{\overline{a}} = !(!a) $$

5 — Дополнительность по противоречию: $ a $ AND $ \text{not}(a) $ невозможно, поэтому ложно и равно $ 0 $

$$ а . \overline{a} = 0 $$

6 — Дополнительность по исключенному третьему: $ a $ OR $ \text{not}(a) $ всегда истинно, поэтому $ 1 $

$$ a + \overline{ a} = 1 $$

7 — Закон ассоциативности: скобки между одинаковыми операторами бесполезны

$$ a.(b.c) = (a.b).c = a.b.c \\ a+(b+c) = (a+b) +c = a+b+c $$

8 — Закон коммуникативности: порядок не имеет значения

$$ a.b = b. a \\ a+b = b+a $$

9 — Закон распределения: И распределено над ИЛИ, но также ИЛИ распределяется по И

$$ a.(b+c) = a.b + a.c \\ a+(b.c) = (a+b).(a+c) $$

10 — Законы Де Моргана (подробнее см. ниже)

$$ \overline{a+b} = \overline{a}.\overline{b} \\ \overline{a.b} = \overline{a}+\overline{b} $$

11 — Другие упрощения комбинации указанных выше

$$ a.(a+b) = a \\ a+(a.b) = a \\ (a.b) + (a.!b) = a \\ (a+b).(a+ !b) = a \\ a + (!a.b) = a + b \\ a.(!a + b) = a.b \\ a.b + \overline{a}.c = a.b + \overline{a}.c + b.c $$

Как показать/продемонстрировать, что 2 логических выражения равны?

Метод 1: упростите их , пока не получите то же самое написание в булевой алгебре .

Метод 2: путем вычисления их таблицы истинности , которая должна быть идентичной.

Что такое закон де Моргана?

Законы де Моргана часто используются для перезаписи логических выражений. Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:

$$ \overline{(a \land b)} \leftrightarrow (\overline{a}) \lor (\overline{b}) \iff \overline{AB} = \overline{a} + \overline{b } $$

$$ \overline{(a \lor b)} ​​\leftrightarrow (\overline{a}) \land (\overline{b}) \iff \overline{a+b} = \overline{a} . \overline{b} $$

Что такое дизъюнктивная или конъюнктивная нормальная форма?

В логике можно использовать разные форматы для обеспечения лучшей читабельности или удобства использования.

Нормальная дизъюнктивная форма (DNF) использует сумму произведений (SOP):

Пример: (a&&c)||b

Нормальная конъюнктивная форма (CNF) или форма предложения использует произведение сумм (POS):

Пример: (a+b).( б +c)

Как показать пошаговые расчеты?

Шаги расчета, какими их может себе представить человек, для решателя не существуют. Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.

Исходный код

dCode сохраняет право собственности на исходный код «Калькулятора логических выражений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор логических выражений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Булевых выражений». Функции калькулятора (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Калькулятора логических выражений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Калькулятор логических выражений» или любых его результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .csv или .txt можно выполнить бесплатно, щелкнув значок export .
Ссылка на источник (библиография):
30, https://www.dcode.fr/boolean-expressions-calculator

Сводка

• Упрощение логических выражений
• Что такое логическое выражение? (Определение)
• Как упростить/минимизировать логическое выражение?
• Что такое методы упрощения булевой алгебры?
• Как показать/продемонстрировать, что 2 логических выражения равны?
• Что такое закон де Моргана?
• Что такое дизъюнктивная или конъюнктивная нормальная форма?
• Как показать пошаговые расчеты?

Похожие страницы

• Таблица истинности
• Решатель уравнений
• Логические двойные
• Логические минитермы и макстермы
• Двоичный код
• Упрощение математических выражений
• Удалить Скобки
• СПИСОК ИНСТРУМЕНТОВ DCODE

Поддержка

• Paypal
• Patreon
• Подробнее

 

Форум/Справка

Ключевые слова

bool,boole,boolean,выражение,алгебра,логика,логический,упрощение,упрощение,и,или,не,xor,амперсанд,труба,восклицательный знак,морган

Ссылки

▲

Упрощение логических выражений

Упрощение логических выражений

Упрощение логических выражений

Примеры булевой алгебры   Двоичный/булев основной индекс

[Примеры таблиц истинности] [Упрощение логических выражений] [Примеры логических вентилей]

Вот несколько примеров упрощений булевой алгебры. Каждая строка дает форму выражения, а правило или правила используется для получения его от предыдущего. Как правило, есть несколько способов достичь результата. Вот список правил упрощения.

• Упрощение: C + BC:

  Выражение	Используемые правила
  C + BC	Исходное выражение
  С+(Б+С)	Закон ДеМоргана.
  (С + С) + В	Коммутативные, ассоциативные законы.
  Т + Б	Закон о дополнении.
  Т	Закон о личности.

• Упрощение: AB(A + B)(B + B):

  Выражение	Используемые правила
  AB(A + B)(B + B)	Исходное выражение
  АВ(А+В)	Закон о дополнении, Закон о личности.
  (А+В)(А+В)	Закон Де Моргана
  А + ВВ	Распределительное право. Этот шаг использует тот факт, что или распределяет по и. Это может выглядеть немного странно так как сложение не распределяется над умножением.
  А	Дополнение, Идентификация.

• Упрощение: (A + C)(AD + AD) + AC + C:

  Выражение	Используемые правила
  (A + C)(AD + AD) + AC + C	Исходное выражение
  (А + С)А(Д + Д) + АС + С	Распределительный.
  (А + С)А + АС + С	Дополнение, Идентификация.
  А((А + С) + С) + С	Коммутативный, Распределительный.
  А(А + С) + С	Ассоциативный, идемпотентный.
  АА + АС + С	Распределительный.
  А + (А + Т )С	Идемпотент, Тождество, Распределение.
  А+С	Личность дважды.

  Вы также можете использовать распределение или более и начиная с A(A+C)+C для достижения того же результата другим путем.

• Упрощение: A(A + B) + (B + AA)(A + B):

  Выражение	Используемые правила
  A(A + B) + (B + AA)(A + B)	Исходное выражение
  АА + АВ + (В + А)А + (В + А)В	Идемпотент (от АА до А), затем Дистрибутив, используется дважды.
  АВ + (В + А)А + (В + А)В	Дополнение, затем Идентификация. (Строго говоря, мы также использовали коммутативный закон для каждого из этих Приложения.)
  АВ + БА + АА + ВВ + АВ	Распределитель, два места.
  АБ + БА + А + АБ	Идемпотент (для А), затем Дополнение и Идентичность для удаления ББ.
  АБ + АБ + А Т + АБ	Коммутативный, Идентичность; подготовка к следующему шагу. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт