Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть exp(x),cos(x),sin(x)
Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции
y» +2y’ = 3ex(cos(x)+sin(x))
Решение уравнения будем искать в виде y = erx с помощью калькулятора. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 +2 r + 0 = 0
D = 22 — 4 • 1 • 0 = 4
Корни характеристического уравнения:
r1 = 0
r2 = -2
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть:
Поиск частного решения.

Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 1, β = 1.
Следовательно, число α + βi = 1 + 1i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y* = ex(Acos(x) + Bsin(x))
Вычисляем производные:
y’ = ex((B-A)•sin(x)+(A+B)•cos(x))
y» = 2•ex(B•cos(x)-A•sin(x))
которые подставляем в исходное дифференциальное уравнение:
y» + 2y’ = (2•ex(B•cos(x)-A•sin(x))) + 2(ex((B-A)•sin(x)+(A+B)•cos(x))) = 3•ex•(cos(x)+sin(x))
или
-4•A•ex•sin(x)+2•A•ex•cos(x)+2•B•ex•sin(x)+4•B•ex•cos(x) = 3•ex•(cos(x)+sin(x))
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-4A + 2B = 3
2A + 4B = 3
Решая ее методом обратной матрицы, находим:
A = -3/10;B = 9/10;
Частное решение имеет вид:
y* = ex(-3/10cos(x) + 9/10sin(x))
Таким образом, общее решение дифференциального уравнения имеет вид:
см.
- Сборник решений линейных дифференциальных уравнений с постоянными коэффициентами
- Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть cos(x),sin(x)
- Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть ex*(Ax + B)
- Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть exp(x),cos(x),sin(x)
- Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть Ax + B
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Вся элементарная математика — Средняя математическая интернет-школа
Тригонометрические уравнения .
Простейшие тригонометрические уравнения .
Методы решения тригонометрических уравнений.
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .
Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения
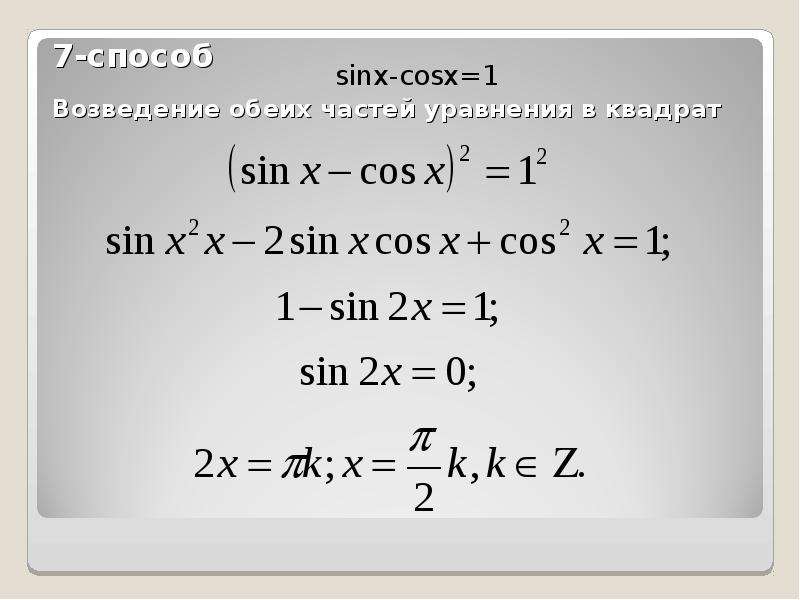 Существует семь
основных методов решения
тригонометрических уравнений.
Существует семь
основных методов решения
тригонометрических уравнений. 1. Алгебраический метод. Этот метод нам хорошо известен из алгебры
( метод замены переменной и подстановки ).
2. Разложение на множители. Этот метод рассмотрим на примерах.
П р и м е р 1. Решить уравнение: sin x + cos x
= 1 .Р е ш е н и е . Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение:
cos 2 x +
sin x ·
cos x = 1.
Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение:
cos
2 x –
cos
8 x +
cos
6 x = 1.
Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4 x cos 2 x = 2 cos ² 4 x ,
cos 4 x · ( cos 2 x – cos 4 x ) = 0 ,
cos 4 x · 2 sin 3 x · sin x = 0 ,
1). cos 4 x = 0 , 2). sin 3 x = 0 , 3). sin x = 0 ,
| 3. | Приведение
к
однородному уравнению.  Чтобы
решить
однородное
уравнение,
надо: Чтобы
решить
однородное
уравнение,
надо:а ) перенести все его члены в левую часть; б ) вынести все общие множители за скобки; в ) приравнять все множители и скобки нулю; г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos ( или sin ) в старшей степени; д ) решить полученное
алгебраическое уравнение относительно tan . П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2. Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x , sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 , tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4 y +3 = 0 , корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда 1) tan x = –1, 2) tan x = –3, |
4. Переход к половинному углу. Рассмотрим этот метод на
примере:
Переход к половинному углу. Рассмотрим этот метод на
примере:
П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
. . . . . . . . . .
. . . . . . . . .
5. Введение вспомогательного угла. Рассмотрим уравнение вида :
a sin x + b cos x = c ,
где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого
из них не больше 1, а сумма их квадратов равна 1 . Тогда можно
обозначить
их соответственно
как
cos
и
sin
( здесь
— так называемый вспомогательный угол ), и
наше уравнение прини
мает
вид:
Тогда можно
обозначить
их соответственно
как
cos
и
sin
( здесь
— так называемый вспомогательный угол ), и
наше уравнение прини
мает
вид:6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
П р и м е р . Решить уравнение: 2 sin 2 x · sin 6 x = cos 4 x .
Р е ш е н и е . Преобразуем левую часть в сумму:
cos 4 x – cos 8 x = cos 4 x ,
cos 8 x = 0 ,
8 x = p / 2 + p k ,
x =
p
/ 16 +
p k / 8 .
7. Универсальная подстановка. Рассмотрим этот метод на примере.
П р и м е р . Решить уравнение: 3 sin
x – 4 cos x = 3 .Таким образом, решение даёт только первый случай.
Назад3
Уравнение cosx+sinx=2 имеет
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10 909 07 Класс 9
- Класс 8
- Класс 7
- Класс 6
- NCERT
- IIT JEE
- Exam
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS 909 07 НЭЭТ
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Neet Все образцы работ
- Образцы работ Биология
- Образцы работ Физика 90 912
- Образцы документов Химия
- Загрузить PDF-файлы
- Класс 6
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Спросите сомнения в том, что app
- Поиск Doubtnut
- Английский словарь
- Toppers Talk
- Блог
- Скачать
- Получить приложение
Вопрос
Обновлено: 26/04/2023C FUNCTIONS — Вопросы WB JEE за предыдущие годы (КАТЕГОРИЯ 2: правильный тип одного варианта ответа (2 балла) ))
4 видеоРЕКЛАМА
Текст Решение
A
Только одно решение
B
Два решения
C
Нет решения
D
Бесконечное число решений
Ответ
Правильный ответ C
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Видео по теме
Решите следующие уравнения: sinx+sqrt(2)=cosx
17336187
02:52
Уравнение sinxcosx=2 имеет:
39181495
01:59
करण sinx−cosx=1 का व्यापक हल है (n∈Z)
104443698
01:18
Докажите, что
1+sinx-cosx1+sinx+cosx+1+sinx+cosx1+sinx-cosx
=2 cosec x
116055283
06:20
Докажите, что
1+sinx−cosx1+sinx+ cosx+1+sinx+cosx1+sinx−cosx
=2 cosec x
116055361
06:20
निम्न अवकल समीकरण को हल कीजिए :
dydx=-cosx-sinxcosx+sinx.
118997962
03:04
Решите уравнение sinx-cosx= sqrt 2 ‘
209196195
02:24
Решить уравнение (cosx−sinx)(2tanx+2)=0
209196222
01:18
Ответьте на уравнение:
∫tan−1(cosx−sinxcosx+ sinx)dx
320218187
03:50
समीकरण sinx−3sin2x=cosx−3cos2x+cos3x का व्याप Номер телефона
358824941
Текст Решение
В интервале [−π4,π4] количество действительных решений уравнений ∣∣ ∣∣sinxcosxcosxcosxsinxcosxcosxcosxsinx∣∣ ∣∣=0
487291809
08:01
निम्न समीकरण को हल कीज िए:
sinx+√2=cosx
642777412
Текстовое решение
Уравнение √3sinx+cosx=4 имеет
642818812
0 2 :48
Уравнение √3sinx+cosx=4 имеет
642850671
02:13
∣∣cosxcosxcosxsinx∣∣∣,x∈(0,π2), то x=… ……. 9(cosx) is
04:25
cos.(2pi)/(7)+cos.(4pi)/(7)+cos.(6pi)/(7)
03:40
- Ask Unlimited Doubts
- Видеорешения на нескольких языках (включая хинди)
- Видеолекции экспертов
- Бесплатные PDF-файлы (документы за предыдущий год, книжные решения и многое другое)
- Посещение специальных семинаров по консультированию для IIT-JEE , НЭИТ и Board Exams
Doubtnut хочет отправлять вам уведомления.


