Произвольный треугольник по заданным параметрам
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1283555449519
418987695398
Настройка.Калькулятор треугольника Флойда онлайн | BBF.
RUТреугольник Флойда — это бесконечный массив натуральных чисел, представленный в виде прямоугольного треугольника. Как и другие числовые построения, таблица Флойда обладает парой интересных свойств, а вывод данной таблицы на экран — стандартная задача для начинающих программистов.
Треугольник Флойда
В математике существует множество бесконечных таблиц и массивов. Среди них особо выделяются треугольник Паскаля и гармонический треугольник Лейбница, построенные по правилам сложения предыдущих или последующих членов строк. Числовые треугольники обладают рядом удивительных свойств и демонстрируют уникальные связи между числами, которые естественным образом возникают в алгебре, комбинаторике, теории чисел или теории вероятностей.
Треугольник Флойда — это элементарная таблица, которая представляет собой массив натуральных чисел. Данная формация была предложена Робертом Флойдом — выдающимся ученым в области теории вычислительных систем. Флойд внес весомый вклад в методологию создания программного обеспечения, поэтому сегодня построение массива натуральных чисел является обязательной задачей для начинающих программистов.
Коэффициенты треугольника Флойда представляют собой простое перечисление целых положительных чисел. Количество членов в каждой строке определяется ее номером. Первые 5 строк таблицы выглядят следующим образом:
- 1
- 2 3
- 4 5 6
- 7 8 9 10
- 11 12 13 14 15
Несмотря на свою простоту, треугольник Флойда также имеет ряд занимательных характеристик. Массив чисел графически выглядит как прямоугольный треугольник, а его стороны обладают удивительными свойствами.
Свойства сторон треугольника
Гипотенуза (ряд 1, 3, 6, 10…) представляет собой последовательность треугольных чисел. Фигурные числа связаны с характеристиками соответствующих геометрических фигур. Последовательность треугольных чисел показывает, сколько элементов требуется помещать в один ряд, чтобы получился треугольник. Если вы захотите построить треугольник из детских кубиков, то вам понадобится выстроить в ряд сначала 10 кубиков, затем 6, потом 3 и 1. Как сделать фигуру еще больше вам подскажет следующее треугольное число в последовательности, то есть 15.
Вертикальный катет (ряд 1, 2, 4, 7…) — это ряд центральных многоугольных чисел. Члены этой последовательности показывают, на сколько «кусков» можно разрезать круг прямыми линиями. В этой последовательности номер коэффициента в ряду отображает количество прямых линий n-1, а его значение — количество кусков. Все это означает следующее:
- при отсутствии линий круг представляет собой один целый кусок, математически это записывается как а(0) = 1;
- одна прямая линия позволяет нам разрезать круг на два кусочка, а(1) = 2;
- две линии режут круг на четыре кусочка, а(2) = 4 и так далее.
Таким образом, если вы хотите узнать, на сколько кусков будет разрезан круг при помощи n линий, вам достаточно узнать значение коэффициента из этого ряда, номер которого определяйся как n-1.
Горизонтальный катет представляет собой часть последовательности натуральных чисел.
Наш онлайн-калькулятор позволяет построить массив натуральных чисел размером от 1 строки до 500.
Вы можете использовать калькулятор как наглядный пример выполнения стандартной задачи программирования, а также воспользоваться свойствами треугольника для решения некоторых практических задач.
Примеры из реальной жизни
Карточный домик
Пусть вы хотите сделать треугольный карточный домик высотой в 12 карт. Для этого вам нужно определить, сколько пар карт будет размещаться в каждом ряду. Вычислить это несложно. Для этого постройте треугольник Флойда для n = 12 и посмотрите на его «гипотенузу». Если читать числа снизу вверх (78, 66, 55, 44…), то вы получите ряды карт, которые при установке друг на друга сформируют правильный треугольник.
Разрезаем блинчик
Классическая задача для центральных многоугольных чисел звучит следующим образом. Возьмем блинчик и попытаемся его разрезать на максимальное количество кусочков при помощи минимального количества разрезов. Кусочки при этом могут быть неодинаковыми. При помощи последовательности чисел мы можем узнать, сколько нам необходимо сделать разрезов, чтобы количество кусков было равно 16.
Для этого построим стандартный треугольник Флойда и посмотрим на его вертикальный катет. Число 16 стоит в нем под шестым номером, следовательно, количество разрезов определится как n-1 = 5.
Заключение
Треугольник Флойда — элегантная таблица натуральных чисел, свойства которой можно использовать в реальных ситуациях. Используйте наш онлайн-калькулятор для построения массива чисел выбранного размера.
Равнобедренные, равнобедренные, тупые, острые и разносторонние
Треугольники можно классифицировать по различным свойствам, относящимся к их углам и сторонам. Наиболее распространенные классификации описаны на этой странице.
Калькулятор треугольника
Классификация треугольников
Прямоугольные треугольники
Прямоугольный треугольник имеет один угол 90° и множество часто изучаемых тем:
- Теорема Пифагора
- Пифагорейские тройки
- Синус, косинус, тангенс
- Изображения прямоугольных треугольников
- 7, 24, 25 Изображения прямоугольного треугольника
- 3, 4, 5 прямоугольных треугольников
- 5, 12, 13 прямоугольных треугольников
- Калькулятор прямоугольного треугольника
Равносторонний треугольник
У равностороннего треугольника, изображенного слева, три равные стороны и три равных угла.
Каждый угол равен 60°.
Равнобедренный треугольник
Равнобедренный треугольник, показанный слева, имеет , две равные стороны и равных углов.
Разносторонний треугольник
У разностороннего треугольника нет конгруэнтных сторон. Другими словами, каждая сторона должна иметь разную длину.
Остроугольный треугольник
Остроугольный треугольник имеет три острых угла (один острый угол меньше 90°).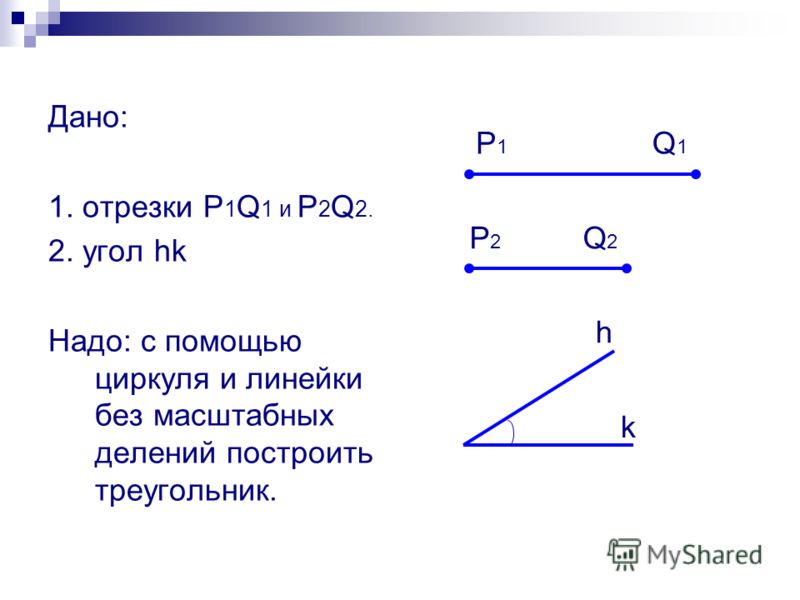
Тупоугольный треугольник
Тупоугольный треугольник имеет тупой угол (тупой угол больше 90°). На картинке слева заштрихованный угол — это тупой угол, отличающий этот треугольник.
Поскольку общее количество градусов в любом треугольнике равно 180°, тупоугольный треугольник может иметь только один угол, размер которого больше 9 градусов.0°.
Практика ПроблемыПрактика 1
Какой треугольник изображен ниже?
Острый треугольник и лестничная клетка.
Практика 2
Какой треугольник изображен ниже?
Тупоугольный треугольник.
Практика 3
Какой тип треугольника изображен ниже?
Так как этот треугольник имеет два равных угла и две равные стороны, то это равнобедренный треугольник.
Практика 4
Классифицируйте треугольник слева.
Предполагая, что изображение выполнено в масштабе, треугольник справа определенно тупой (см. синий угол), а также разносторонний.
Практика 4
Классифицируйте треугольник слева.
Предполагая, что изображение выполнено в масштабе, треугольник справа определенно остроугольный и разносторонний.
Калькулятор треугольника
Здание с треугольниками | Новозеландская математика
Цель
В этом модуле учащиеся будут определять свойства треугольников, строить равносторонние и неправильные треугольники с помощью линейки и транспортира или линейки и циркуля, а также создавать сети для трехмерных фигур (включая платоновые тела и тела, состоящие из треугольников). .
Цели достижения
GM4-1: Используйте соответствующие весы, устройства и метрические единицы измерения длины, площади, объема и емкости, веса (массы), температуры, угла и времени.
Разработка AO и другие учебные ресурсы
GM4-6: Соотнесите трехмерные модели с двумерными представлениями и наоборот.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Построение треугольников заданных размеров с использованием двух разных методов.
- Разработка и создание сетей для трехмерных объектов.
- Назовите основные трехмерные объекты, особенно те, которые состоят из равносторонних треугольников.
Описание математики
В этом разделе рассматриваются некоторые аспекты трехмерной геометрии, а также методы построения треугольников.
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям. Способы дифференциации включают:
- преднамеренное наращивание ступеней в треугольных конструкциях
- позволяет учащимся экспериментировать с конструкциями на цифровой платформе
- непосредственное моделирование и инструктирует учащихся по правильному использованию инструментов, особенно транспортиров и линеек
- сначала строит простые многогранники, прежде чем переходить к более сложным моделям , творческие группы.
Контекст для этого блока математический. Речь идет о треугольниках и их использовании в построении трехмерных тел. Ищите треугольники в окружающей среде, окружающей ваш класс (например, в креплениях каркасов зданий, в купольных конструкциях, используемых для лазанья, в дорожных знаках, еде, мостах, предметах искусства и т. д.). Ты мог бы. Я исследую использование треугольников при строительстве культурно значимых зданий, таких как варенуи, египетские пирамиды, Лувр в Париже и экологический музей биосферы в Монреале. Могут быть другие контексты, включающие треугольники, связанные с интересами и культурным наследием ваших учеников, текущим обучением в других областях учебной программы и текущими событиями, которые можно использовать для вовлечения ваших учеников в эту часть работы.
Te reo Māori kupu, такие как тапатору (треугольник), тапатору хикувару (разносторонний треугольник), тапатору вэрите (равнобедренный треугольник), обряд тапатору (равносторонний треугольник), коки хангай (прямой угол), ине-коки (транспортир), путу ( степень), matawhā (ритуал) (тетраэдр) и koeko (пирамида) могут быть введены в этот раздел и использоваться в других математических исследованиях.
Необходимые материалы
- Карточка или плотная бумага для трехмерных построений
- Линейки/циркули/карандаши/транспортиры/ножницы/изолента
- Модель тетраэдра и других трехмерных форм (цифровых или печатных)
- Примеры сеток (пластиковых, карточных или цифровых) без выступов и с выступами для других трехмерных форм (например, куба, прямоугольного параллелепипеда, цилиндра)
- Зубочистки/палочки для эскимо
- Blu-tack
- Бумага для двухмерных конструкций
- Copymasters One, Two, Three, Four, Five, Six, Seven, Eight and Nine
Упражнение
Начало работы
Начните с повторения знаний о свойствах треугольников, после чего следует обсуждение способов построения треугольников заданных размеров.
- Проведите мозговой штурм с классом «Свойства треугольников».
Возможные ответы могут включать в себя:
Три сторона
Три ракурса/углы
Углы добавляют к 180 O
Различные типы (Скарена/Изоплеры/Равномерные/Право-Англи или все углы одинаковы. Это свойство не треугольников, а правильных многоугольников (включая равносторонние треугольники). Убедитесь, что это подчеркнуто. - Установите связи между знаниями учащихся о треугольниках и контекстами, которые имеют отношение к контексту реальной жизни. Вы можете попросить учащихся найти изображения треугольников в школе, в Интернете или дома.
- Спросите учащихся, как они могли бы построить равносторонний треугольник. Обсудите их идеи – их преимущества и недостатки. Есть три относительно простых метода. Смоделируйте их и дайте учащимся возможность попробовать каждую из них (или продемонстрировать их классу на доске).
- Способ 1: Использование линейки и транспортира
- С помощью линейки начертите одну сторону до необходимой длины.
- Измерьте угол 60 градусов от одного конца первой стороны.
Начертите вторую сторону такой же длины, как и первая, опять же с помощью линейки. - Соедините концы так, чтобы третья сторона была такой же длины, как первые две.
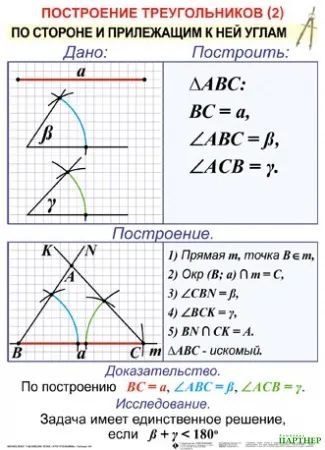
Способ 2. Использование линейки и транспортира
С помощью линейки начертите одну сторону до необходимой длины.
Измерьте угол 60 градусов.
Проведите вторую сторону через отметку под углом 60 градусов.
Измерьте еще один угол в 60 градусов от другого конца первой стороны.
- Нарисуйте третью сторону и сотрите лишние линии.
Способ 3. Использование линейки и циркуля
С помощью линейки начертите одну сторону до необходимой длины.
Установите компас на радиус, равный длине стороны. Поместите острие циркуля на один конец стороны, которую вы нарисовали, и слегка нарисуйте небольшую дугу вокруг того места, где, по вашему мнению, должен быть третий угол.
Переместите точку циркуля на другой конец вашей первой стороны и нарисуйте еще одну дугу, которая должна пересечь первую.
- Точка, в которой пересекаются дуги, является третьим углом. Нарисуйте оставшиеся две стороны, проверяя при этом их правильную длину.
- Способ 1: Использование линейки и транспортира
- Обсудите, можно ли использовать каждый метод для построения треугольников, если стороны не одинаковы. Предложите учащимся перечислить преимущества и недостатки каждого метода и решить, какой из них лучше.
Метод а) можно использовать для построения треугольников, если известны две длины сторон и один угол.
Метод b) можно использовать для построения треугольников, если известны два угла и длина одной стороны.
Метод c) можно использовать для построения треугольников, если известны длины всех сторон.
Метод в) является, вероятно, самым простым и точным, так как измерения транспортиром могут привести к ошибкам. - Дайте учащимся возможность попрактиковаться в построении различных треугольников, используя все три метода. В то время как некоторые учащиеся могут чувствовать себя достаточно уверенно, чтобы делать это самостоятельно, другим может быть полезно работать в парах или в более структурированной группе под руководством учителя. Подумайте, какой подход лучше всего обеспечит доступность учебного контента для всех учащихся. Для расширения учащиеся могут создать бумажную или цифровую презентацию (например, видео, постер, набор слайдов, инфографику), которая демонстрирует и объясняет каждый из этих методов построения.
Это свойство не треугольников, а правильных многоугольников (включая равносторонние треугольники). Убедитесь, что это подчеркнуто.
Подумайте, какой подход лучше всего обеспечит доступность учебного контента для всех учащихся. Для расширения учащиеся могут создать бумажную или цифровую презентацию (например, видео, постер, набор слайдов, инфографику), которая демонстрирует и объясняет каждый из этих методов построения.Помогите учащимся использовать свои знания о построении треугольников для создания трехмерных объектов, состоящих из треугольников.
- Покажите учащимся модель тетраэдра.
- Попросите их определить, какой фигуры и из скольких частей она состоит (4 равносторонних треугольника).
- Попросите учащихся, работающих в группах, использовать зубочистки/палочки для эскимо и Blu-tack для создания 3D-модели тетраэдра. Пока они строят эти фигуры, бродят и поддерживают их, чтобы определить свойства фигуры:
Сколько сторон у фигуры?
Какая двухмерная фигура образует основу фигуры?
Если развернуть эту фигуру, как она будет выглядеть?
Сколько различных вариантов расположения развернутого тетраэдра вы можете составить? - Задайте вышеуказанные вопросы всему классу и дайте учащимся время обсудить свои идеи, прежде чем поделиться ими с остальным классом.
- Раздать бумагу. Предложите учащимся в тех же группах построить сеть без вкладок для тетраэдра. Возможно, вам придется показать учащимся сети для других трехмерных фигур (например, куб, цилиндр, прямоугольный параллелепипед), чтобы убедиться, что они понимают, как будет выглядеть успешная сеть. Напомните учащимся подумать о базовой форме их моделей тетраэдра, о том, сколько сторон было в завершенной форме и как выглядел «развернутый» тетраэдр.
- Проверьте нарисованные сети. Есть два макета из четырех равносторонних треугольников, которые складываются в тетраэдр, и один, который не будет складываться. Попросите учащихся определить, почему (два треугольника складываются, чтобы оказаться друг над другом, поэтому у них есть открытая сторона).
Эти сети образуют тетраэдр:
Эта сеть не образует тетраэдр: - Покажите учащимся примеры сетей с выступами. Позвольте им сделать модель тетраэдра из картона. Учащиеся должны либо соединить края лентой, либо, если они хотят, могут сделать выступы на своей сетке и приклеить края.
Предложите учащимся составить другой трехмерный объект только из равносторонних треугольников. Учащиеся, нуждающиеся в большей поддержке учителя, могут либо спроектировать сеть так, чтобы получился октаэдр (8 равносторонних треугольников — сложить, чтобы получилась форма, подобная двум соединенным вместе пирамидам с квадратным основанием), либо им может быть предоставлена сеть, которую можно вырезать, сложить и склеить. Учащихся, готовых к расширению, можно попросить посмотреть, сколько разных предметов они могут составить и назвать только из равносторонних треугольников. Есть как минимум 9!
4 стороны: тетраэдр
6 сторон: треугольная дипирамида (склейка двух тетраэдров)
8 сторон: октаэдр
10 сторон: пятиугольная дипирамида ( склеить две пятиугольные пирамиды вместе)
12 сторон: курносая дисфеноидная (разбить тетраэдр на два сегмента и соединить их полосой из восьми треугольников)
14 сторон: трехгранная призма (присоединить к треугольной призме три квадратные пирамиды)
16 сторон: гироудлиненная квадратная дипирамида (присоединить две квадратные квадратная антипризма)
20 сторон: икосаэдр
24 стороны: звездчатый октаэдр (прикрепите тетраэдр к каждой грани октаэдра)
Обсудите три платоновых тела, которые можно составить из равносторонних треугольников.
Сколько таких сделал ваш класс?
Некоторые сети, которые вы можете распечатать из прикрепленных файлов и использовать: тетраэдр, октаэдр, икосаэдр.Платоновое тело — это многогранник, все грани которого являются конгруэнтными правильными многоугольниками и в каждой вершине которого встречается одинаковое количество граней.
Другими словами, платоново тело представляет собой трехмерную форму, каждая грань которой представляет собой идентичную плоскую форму со всеми сторонами и углами, одинаковыми, и одинаковое количество этих граней встречается в каждом углу.
Есть 5 платоновых тел, куб (6 квадратов, по 3 сходящихся в каждой вершине), тетраэдр (4 треугольника, по 3 сходящихся в каждой вершине), октаэдр (8 треугольников, по 4 сходящихся в каждой вершине), додекаэдр ( 12 пятиугольников, по 3 сходящихся в каждой вершине) и икосаэдр (20 треугольников, по 5 сходящихся в каждой вершине).
- Посмотрите на другие предметы, сделанные учащимися. Попробуйте назвать их.
Предложите учащимся создать объект, в котором используются равносторонние треугольники в сочетании с другой формой. Обратите внимание, что все длины сторон должны быть одинаковыми, даже если формы разные. По мере необходимости помогайте учащимся создать хотя бы одну из следующих фигур. Учащимся, нуждающимся в дополнительной поддержке учителя, можно либо помочь спроектировать сеть, чтобы сделать треугольную призму (два равносторонних треугольника, соединенных тремя квадратами), либо им можно предоставить сеть, которую нужно вырезать, сложить и склеить. Учащимся, готовым к расширению, может быть предложено увидеть, сколько разных предметов они могут сделать и назвать, и они могут найти примеры этих форм из реального контекста (например, бриллианты, игральные кости, террариумы, футбольные мячи, скульптуры).
Некоторые сети, которые вы можете распечатать из прикрепленных файлов и использовать: треугольная призма, пирамида, пятиугольная пирамида, кубооктаэдр, усеченный тетраэдр, усеченный куб, икосододекаэдр.
9000 2пирамида (4 треугольника и 1 квадрат)
пятиугольная пирамида (5 треугольников и 1 пятиугольник)
треугольная призма (2 треугольника и 3 квадрата (или прямоугольника))
куб. аэдр (8 треугольников и 6 квадратов)
икосододекаэдр (12 пятиугольников и 20 треугольников)
тетраэдр усеченный (4 шестиугольника и 4 треугольника)
куб усеченный (6 восьмиугольников и 8 треугольников)
квадратная антипризма (2 квадрата и 8 треугольников)
- Расскажите о трех типах пирамид ( основания: треугольник, квадрат, пятиугольник). Ваш класс сделал все три? Как называется пирамида с треугольным основанием? (тетраэдр) Могли бы вы построить шестиугольную пирамиду? (Нет) Почему бы и нет? (шесть равносторонних треугольников будут плоско лежать на шестиугольнике, и объект будет плоским. Примечание: вы можете построить шестиугольную пирамиду, но не с равносторонними треугольниками, вам нужно использовать равнобедренные треугольники.
- Посмотрите на другие предметы, сделанные учениками. Попробуйте назвать их. Убедитесь, что у всех учащихся есть время и возможность поделиться своими мыслями и работой.
Сколько таких сделал ваш класс? 
Примечание: вы можете построить шестиугольную пирамиду, но не с равносторонними треугольниками, вам нужно использовать равнобедренные треугольники.Подумайте о предметах, которые сделал класс, и о том, что они о них знают.
- Попросите учащихся назвать как можно больше трехмерных объектов, которые можно составить из равносторонних треугольников.
- Кто-нибудь может придумать, как можно сгруппировать эти объекты? (Количество сторон, другие формы, использованные при построении формы, симметрия)
Самый очевидный способ — сгруппировать объекты на те, которые используют исключительно треугольники, и те, которые включают другие формы в сочетании с равносторонними треугольниками. - Попробуйте сгруппировать модели, созданные классом, по некоторым из этих критериев.
