Модуль в модуле
Среди примеров на модули часто встречаются уравнения где нужно найти корни модуля в модуле, то есть уравнение вида
||a*x-b|-c|=k*x+m.
Если k=0, то есть правая сторона равна постоянной (m) то проще искать решение уравнения с модулями графически. Ниже приведена методика раскрытия двойных модулей на распространенных для практики примерах. Хорошо разберите алгоритм вычисления уравнений с модулями, чтобы не иметь проблем на контрольных, тестах, и просто, чтобы знать.
Пример 1. Решить уравнение модуль в модуле |3|x|-5|=-2x-2.
Решение: Всегда начинают раскрывать уравнения с внутреннего модуля
|x|=0 <-> x=0.
В точке x=0 уравнения с модулем разделяется на 2.
При x < 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
При x>0 или равно, раскрывая модуль получим
|3x-5|=-2x-2.
Решим уравнение для отрицательных переменных (x < 0). Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе — раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная — меняем знак правой или левой части (зависит от методики преподавания).
Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе — раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная — меняем знак правой или левой части (зависит от методики преподавания).
Из первого уравнения получим что решение не должно превышать (-1), т.е.
Это ограничение полностью принадлежит области в которой решаем. Перенесем переменные и постоянные по разные стороны равенства в первой и второй системе
и найдем решение
Оба значения принадлежат промежутку что рассматривается, то есть являются корнями.
Рассмотрим уравнение с модулями при положительных переменных
|3x-5|=-2x-2.
Раскрывая модуль получим две системы уравнений
Из первого уравнения, которое является общим для двух сиcтем, получим знакомое условие
которое в пересечении с множеством, на котором ищем решение дает пустое множество (нет точек пересечения). Итак единственными корнями модуля с модулем являются значения
Итак единственными корнями модуля с модулем являются значения
x=-3; x=-1,4.
Пример 2. Решить уравнение с модулем ||x-1|-2|=3x-4.
Решение: Начнем с раскрытия внутреннего модуля
|x-1|=0 <=> x=1.
Подмодульная функция меняет знак в единице. При меньших значениях она отрицательная, при больших — положительная. В соответствии с этим при раскрытии внутреннего модуля получим два уравнения с модулем
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Обязательно проверяем правую сторону уравнения с модулем, она должна быть больше нуля.
3x-4>=0 -> x>=4/3.
Это означает, что первое из уравнений нет необхидноcти решать, поcкольку оно выпиcано для x< 1,что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 или x-3=4-3x;
4-3=3x-x или x+3x=4+3;
2x=1 или 4x=7;
x=1/2 или x=7/4.
Получили два значения, первое из которых отвергаем, поскольку не принадлежит нужному интервалу. Окончательно уравнение имеет одно решение x=7/4.
Окончательно уравнение имеет одно решение x=7/4.
Пример 3. Решить уравнение с модулем ||2x-5|-1|=x+3.
Решение: Раскроем внутренний модуль
|2x-5|=0 <=> x=5/2=2,5.
Точка x=2,5 разбивает числовую ось на два интервала. Соответственно, подмодульная функция меняет знак при переходе через 2,5. Выпишем условие на решение с правой стороны уравнения с модулем.
x+3>=0 -> x>=-3.
Итак решением могут быть значения, не меньше (-3). Раскроем модуль для отрицательного значения внутреннего модуля
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Этот модуль также при раскрытии даст 2 уравнения
-2x+4=x+3 или 2x-4=x+3;
2x+x=4-3 или 2x-x=3+4;
3x=1; x=1/3 или x=7.
Значение x=7 отвергаем, поскольку мы искали решение на промежутке [-3;2,5]. Теперь раскрываем внутренний модуль для x>2,5. Получим уравнение с одним модулем
|2x-5-1|=x+3;
|2x-6|=x+3.
При раскрытии модуля получим следующие линейные уравнения
-2x+6=x+3 или 2x-6=x+3;
2x+x=6-3 или 2x-x=3+6;
3x=3; x=1 или x=9.
Первое значение x=1 не удовлетворяет условие x>2,5. Так что на этом интервале имеем один корень уравнения с модулем x=9, а всего их два (x=1/3).Подстановкой можно проверять правильность выполненных вычислений
Ответ: x=1/3; x=9.
Пример 4. Найти решения двойного модуля ||3x-1|-5|=2x-3.
Решение: Раскроем внутренний модуль уравнения
|3x-1|=0 <=> x=1/3.
Точка x=2,5 делит числовую ось на два интервала, а заданное уравнение на два случая. Записываем условие на решение, исходя из вида уравнения с правой стороны
2x-3>=0 -> x>=3/2=1,5.
Отсюда следует, что нас интересуют значения >=1,5. Таким образом модульное уравнения рассматриваем на двух интервалах
[1,5; 2,5], [2,5; +бесконечность).
Раскроем модуль при отрицательных значениях внутреннего модуля [1,5; 2,5]
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Полученный модуль при раскрытии делится на 2 уравнения
-3x-4=2x-3 или 3x+4=2x-3;
2x+3x=-4+3 или 3x-2x=-3-4;
5x=-1; x=-1/5 или x=-7.
Оба значения не попадают в промежуток [1,5; 2,5], то есть не являются решениями уравнения с модулями. Далее раскроем модуль для x>2,5. Получим следующее уравнение
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Раскрывая модуль, получим 2 линейные уравнения
3x-6=2x-3 или –(3x-6)=2x-3;
3x-2x=-3+6 или 2x+3x=6+3;
x=3 или 5x=9; x=9/5=1,8.
Второе значение из найденных не соответствует условию x>2,5, его мы отвергаем.
Наконец имеем один корень уравнения с модулями x=3.
Выполняем проверку
||3*3-1|-5|=2*3-3 3=3.
Корень уравнения с модулем вычислено правильно.
Ответ: x=1/3; x=9.
Примеров с модулями где есть один или несколько вложенных модулей в интернете или методичке можно найти немало. Схема их вычислений ничем не отличается от приведенной выше. Для проверки знаний прошу решить следующие задачи.
Равнение на модуль в модуле:
- ||3x-3|-2|=5-2x;
- ||5x-3|-3|=3x-1;
- ||2x-7|-4|=x-2;
- ||5x-4|-8|=x+4;
- ||2x-2|-3|=1;
- ||x-2|-3|=4-x.

Похожие материалы:
- Решение уравнений с модулями
- Модуль в модуле. Графический метод
- Уравнения с модулями. Графический метод
- Решение неравенств с модулями
Время | Деятельность учителя | Деятельность ученика | ||
Слайд-1-2 | 1.Организационный момент 2.Актуализация знаний | 1мин 3мин | «Просто «думать» не умеет никто. Думать можно только над конкретным вопросом. Умение решать задачи в большой мере сводится к обучению тому, над чем надо думать в ходе решения». Доктор педагогических наук, профессор М.Волович Ребята, приглашаю вас к сотрудничеству и предлагаю работать вместе на сегодняшнем уроке. Продолжаем учиться решать. Формируем математическую интуицию, которая поможет ориентироваться в способах решения уравнений. На уроке можно ошибаться, сомневаться, консультироваться. Дать самому себе установку: «Понять и быть тем первым, который увидит ход решения». На слайде записаны уравнения. Что записано? Как называются эти уравнения? | Приветствие учителя. Дежурный докладывает об отсутствующих. Уравнения. Уравнения, содержащие модуль . |
слайд 3-5 мини-проекты Постановка проблемы | 2мин 3мин | Итак тема нашего урока. Чем мы будем заниматься на уроке и какие поставим цели? Сегодня на уроке мы повторим теоретический материал о модуле и его свойствах, геометрический смысл модуля. Научимся решать уравнения, содержащие модуль. Поработаем над основными понятиями, встречающимися в данной теме. — Дайте определение модуля. — Объясните геометрический смысл модуля. — Назовите свойства модуля. — Чему равен ? — Чему равен ? 1) Можно ли свести решение данных уравнений к решению линейных уравнений? 2).Как бы вы сгруппировали данные уравнения по способам решения?( слайд 2-выше записаны уравнения с модулем). Работают в парах, заполняют таблицу. В ходе рассуждений сделали выводы: 1).Если f(x)=g(x) то есть указали способ решения уравнений 3 и 8. 2).Если то должно выполняться условие: , так как модуль величина неотрицательная, тогда по определению модуля То есть указали способ решения уравнений 4 и 9. Как же можно решить уравнение 5,12? Разве уравнение 11 имеет отношение к теме «Модуль»? А как же решить уравнение 6? Каковы ваши предложения по применению метода интервалов? . | Формулируют тему урока. Повторить, отработать, обобщить способы решения уравнений с модулем. Учащиеся показывают и рассказывают информационные мини- проекты | |
Работают в парах .заполняют таблицу № | уравнения | Способ решения | ||
1 | 1,7,10 | На основании определения модуля | ||
2 | 2 | Не имеет решения | ||
3 | 3,8 | │f(x)│=│g(x)│f (x) =g(x) | ||
4 | 4,9 | g(x) ≥0, f(x)│=g(x), f(x)│=—g(x), | ||
5 | 5,12 | Определение модуля(два случая) | ||
6 | 11 | Свойство модуля=│х│ | ||
7 | 6 | Метод интервалов | ||
3.Физкультминутка 4.Актуализация деятельности учащихся | 1 мин | Немного отдохнем Ваша задача: решить предлагаемые уравнения, проанализировать способы их решения, провести классификацию уравнений, содержащих модуль по способам решения, составить таблицу « Решение уравнений, содержащих модуль». Провести защиту вашего проекта. (Вначале более простые примеры выбирают те учащиеся, которым труднее даётся предмет; более сложные примеры выбирают те учащиеся, у которых есть математические способности. После обмена примерами, более сильные учащиеся могут выступать в роли консультантов.) Каждой группе даются карточки с уравнениями (см приложение №1). Каждая группа получает инструкцию. Прежде, чем приступить к работе над проектом, внимательно ознакомьтесь с инструкцией. | Выполняют упражнение(звучит музыка) Работа в группах( 7 групп ) Решают уравнения | |
5.Работа над проектом | 20мин | Инструкция по работе над проектом. 1. Решить уравнения. 2. Проанализировать способы решения. 3. Провести классификацию данных уравнений: а) сгруппировать примеры по способам решения; б) определить, в чём заключается общий вид уравнений в каждой группе; в) дать название каждой группе уравнений. 4. Создать проект таблицы: « Решение уравнений, содержащих модуль». 5. Подготовить защиту проекта. | 1группа-1,2,4 уравнения. 2 группа-3 ,13 ; 3 группа-12 ;9 4группа-10, 7; 5 группа-8 ,11 6 группа-5, 14 7группа- 6 | |
6.Защита проектов | 10мин | Оценочный лист. (5-бальная система) Владеет докладчик терминологией, которую использует своём проекте | ||
Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи | ||||
Выполнила ли группа все поставленные перед ней задачи | ||||
Творческие способности докладчика | ||||
Оформление проекта | В процессе обсуждения участники других групп записывают само уравнение и название метода решения, дома их решают. | |||
7.Домашнее задание | 1мин | Сформировать 2 группы (по3 человека), которые представят результаты исследования в виде презентации к следующему уроку. Задание на карточках. | ||
8 Рефлексия | 1мин | Какая задача стояла перед нами в начале урока? Можно ли считать,что мы ее решили? Сможем ли мы теперь решать уравнения аналогичные данным? Заполните опросный лист(см приложение 2) | Учащиеся отвечают на вопросы, заполняют опорный лист |
|
В математике очень распространены неравенства, содержащие переменную под знаком модуля. На этом уроке мы рассмотрим различные способы решения этих неравенств. |
Тема урока «Неравенства с модулем»
|
|
Для изучения этой темы вспомним определение модуля числа и его геометрический смысл.
|
|
|
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
|
Картинка.
|
|
Геометрически модуль а означает расстояние на координатной прямой от начала отсчета до точки, изображающей число а. Если а не равно нулю, то на координатной прямой существуют две точки а и минус а, равноудаленные от нуля, модули которых равны.
|
Картинка. |
|
Первый способ (геометрический смысл модуля). Рассмотрим на простых примерах. Задание 1 Решить неравенство модуль икс минус трех меньше четырех. Решение Рисуем координатную прямую. Модуль икс минус трех меньше четырех означает, что расстояние от точки икс до точки три меньше четырех единиц. Отмечаем на прямой число три и отсчитываем влево и вправо от него четыре деления. Слева мы придем к точке один, справа – к точке семь. Таким образом, границы точки икс мы просто увидели, не вычисляя их. При этом, согласно условию неравенства, сами минус один и семь не включены во множество решений. Таким образом, ответ: интервал от минус единицы до семи.
|
Текст. Первый способ ( геометрический смысл модуля). Пример1. Решить неравенство |х — 3| Решение. –1 х Ответ:(-1;7)
|
|
Второй способ – графическое решение. Решить неравенство икс минус один меньше модуля квадрата разности икс и двух и минус один. Решение Построим в одной системе координат графики функций: игрек равен икс минус один и игрек равен модуль икс минус два и все в квадрате и минус один. Графиком линейной функции игрек равен икс минус один является прямая, проходящая через точки, например, с координатами один и ноль и четыре и ноль. График функции игрек равен модуль икс минус два и все квадрате и минус один. Находим точки пересечения графиков. В ответе указываем те значения икс, при которых график первой функции расположен ниже графика второй функции. Это объединение открытого числового луча от минус бесконечности до единицы, интервала от одного до двух и открытого числового луча от четырех до плюс бесконечности. Ответ: объединение открытого числового луча от минус бесконечности до единицы, интервала от одного до двух и открытого числового луча от четырех до плюс бесконечности. |
Текст. Второй способ – графическое решение. Пример 2. Решить неравенство x-1 Решение. Построим в одной системе координат графики функций
Картинка.
|
|
Третий способ 
Задание 3 Решить неравенство модуль икс квадрат минус один меньше модуля икс квадрат минус икс плюс один. Решение Возведем обе части неравенства в квадрат. Заметим, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева, и справа стоят модули, поэтому мы можем это сделать. Теперь воспользуемся следующим свойством модуля: квадрат модуля икс равен икс квадрат. Получим икс квадрат минус один и все в квадрате минус икс квадрат минус икс плюс один и все в квадрате меньше нуля. Дальше лучше всего воспользоваться формулой разности квадратов. Можно, конечно, и возводить в квадрат левую и правую скобку, но это займет гораздо больше времени. Имеем произведение трех множителей меньше нуля. Решаем методом интервалов. Из рисунка видно, что решением неравенства является объединение открытого числового луча от минус бесконечности до нуля и интервала от одной второй до двух. Ответ: объединение открытого числового луча от минус бесконечности до нуля и интервала от одной второй до двух. |
Третий способ – возведение в квадрат. Пример3. Решить неравенство |x2 – 1| 2 – x + 1|. Решение. Возведем обе части неравенства в квадрат, получим: (|x2 – 1|)22 – x + 1|)2. По свойству модуля (|x|) (x2 – 1)22 – x + 1)2, (x2 – 1)2 – (x2 – x + 1)2 Дальше лучше всего воспользоваться формулой разности квадратов. (x2 – 1 – x2 + x – 1)( x2 – 1 + x2 – x + 1) (x – 2)(2x2 – x) x(x – 2)(2x – 1) Решаем методом интервалов. |
|
Четвертый способ (определение модуля). Задание 4 Решить неравенство три умноженное на модуль икс минус один меньше либо равно икс плюс три. Решение По определению модуля выражение икс минус один может быть неотрицательным или отрицательным. Если икс минус один больше либо равно нулю, то заданное неравенство примет вид два икс больше либо равно шести. Если икс минус один меньше нуля, то заданное неравенство примет вид минус четыре икс меньше либо равно нулю. Таким образом, данное неравенство равносильно совокупности двух систем. Решаем первую систему совокупности, получим, что решением является числовой отрезок от единицы до трех. Решаем вторую систему совокупности, получим, что решением является числовой отрезок от нуля до единицы. Решением данного неравенства является объединение этих числовых отрезков, то есть числовой отрезок от нуля до трех. Ответ: числовой отрезок от нуля до трех. |
Текст. Четвертый способ (определение модуля). Пример4. Решить неравенство 3|x – 1| ≤ x + 3. Решение. Если х-1≥0, то |x – 1|= х-1 и заданное неравенство примет вид 2х≤6. Если х-1 Имеем, данное неравенство равносильно совокупность двух систем х-1≥0, 2х≤6; х-1 -4х≤0. Решаем первую систему совокупности, получим x ≥ 1 х∈ [1;3] Решаем вторую систему совокупности, получим х-1 -4х≤0 х∈ [0;1] Решением данного неравенства является [0;1] U [1;3]= [0;3]Ответ: [0;3] |
|
Четвертый способ является наиболее универсальным, но в зависимости от ситуации используются и остальные. |
|
|
Задание 5 Решить неравенство модуль икс квадрат минус три минус два икс меньше либо равно нулю. Решение Преобразуем неравенство. Перенесем два икс в правую часть неравенства. Замечаем, что левая часть неравенства неотрицательна, значит, и правая часть должна быть неотрицательной, то есть икс больше либо равно нулю. Так как обе части неравенства неотрицательны, то их можно возвести в квадрат (третий способ) и разложить на множители по формуле разности квадратов. Получаем произведение четырех множителей меньше либо равно нулю. Решим это неравенство методом интервалов. Из рисунка видно, что решение этого неравенства — объединение числовых отрезков от минус трех до минус единицы и от единицы до трех. Учитывая условие икс больше либо равно нулю, получим решение исходного неравенства — отрезок от одного до трех. Ответ: отрезок от одного до трех. |
Текст. Пример5. Решить неравенство │х2-3│-2х≤0. Решение. Преобразуем неравенство в виде │х2-3│≤2х. Замечаем, что 2х≥0,х≥0. Поэтому, обе части неравенства можно возвести в квадрат: ( х2-3)2-(2х)2≤0, (х2-3-2х)( х2-3+2х) ≤0, (х+1)(х-1)(х-3)(х+3) ≤0. Решим это неравенство методом интервалов и получим х[-3;-1]U[1;3].Учитывая условие х≥0, получим х[1;3]. Ответ: [1;3]. |
|
Задание 6 Решить неравенство модуль икс минус четыре больше модуля икс плюс шесть. Решение Обе части данного неравенства неотрицательны для любых значений икс, поэтому их можно возвести в квадрат, затем разложить на множители по формуле разности квадратов, привести подобные члены, разделить на минус десять. Получим неравенство икс меньше минус одного. Решением этого неравенства, а значит, и равносильного ему данного неравенства является открытый числовой луч от минус бесконечности до минус единицы. Ответ: открытый числовой луч от минус бесконечности до минус единицы.
|
Текст. Пример 6. Решить неравенство │х-4│>│х+6│. Решение. Так как обе части данного неравенства неотрицательны для любых значений х, то каждую возведем в квадрат, получим (х-4)2>(х+6)2, (х-4)2-(х+6)2>0, (х-4-х-6)(х-4+х+6) >0, -10(2х+2) >0, 2х+2 х Решение этого неравенства- (-∞;-1)а, значит, решение равносильного ему данного неравенства тоже есть (-∞;-1). Ответ: (-∞;-1). |
|
Задание 7 Решить неравенство икс минус один больше кубического корня из икс в кубе минус два икс в квадрате плюс четыре икс минус семь. Решение Возведя обе части этого неравенства в третью степень, получим неравенство, равносильное данному. Применив формулу куба разности, перенеся все члены неравенства в правую часть и приведя подобные члены многочлена, получим квадратное неравенство икс в квадрате плюс икс минус шесть меньше нуля, равносильное данному неравенству. Решением этого неравенства, а значит, и равносильного ему исходного неравенства является интервал от минус трех до двух. Ответ: интервал от минус трех до двух. |
Текст. Пример7. Решить неравенство Решение. Возведя обе части этого неравенства в третью степень, получим неравенство (х-1)3 >х3-2х2+4х-7 равносильное данному. Или х2+х -6 х(-3;2) Так как неравенство х2+х -6 Ответ: (-3;2) |
|
Задание 8 Решить неравенство два икс плюс три и все в квадрате минус модуль двух икс плюс три меньше либо равно тридцати. Решение Заметим, что два икс плюс три и все в квадрате равно квадрату модуля два икс плюс три. Тогда получим квадратное неравенство, в котором сделаем замену: игрек равен модулю два икс плюс три. Перепишем наше неравенство с учетом замены, разложим на множители и получим неравенство игрек минус шесть умноженное на игрек плюс пять меньше либо равно нулю. Решим методом интервалов и получим: игрек меньше либо равен минус пять и меньше либо равен шести. Вернемся к замене, и данное двойное неравенство равносильно системе неравенств. Решим первое неравенство из этой системы. Оно равносильно системе неравенств. Два икс плюс три меньше либо равно шести и два икс плюс три больше либо равно минус шести. Ее решением является отрезок от минус четырех целых пяти десятых до одной целой пяти десятых. Второе неравенство системы — модуль двух икс плюс три больше либо равно минус пяти — очевидно выполняется для всех икс, так как модуль по определению число положительное. Так как решение системы неравенств – это все икс, которые удовлетворяют одновременно и первому и второму неравенству системы, то ее решением, а значит, и исходного неравенства, будет решение ее первого неравенства (ведь решением системы будет решение ее первого неравенства, то есть числовой отрезок от минус четырех целых пяти десятых до одной целой пяти десятых. Ответ: числовой отрезок от минус четырех целых пяти десятых до одной целой пяти десятых. |
Текст. Пример8. Решить неравенство (2x + 3)2 – |2x + 3| ≤ 30. Решение. Заметим, что (2x + 3)2 = (|2x + 3|)2. Тогда получим неравенство (|2x + 3|)2 – |2x + 3| ≤ 30. Сделаем замену y = |2x + 3|. Перепишем наше неравенство с учетом замены. y2 – y ≤ 30, y2 – y – 30 ≤ 0. Разложим квадратный трехчлен, стоящий слева, на множители. D = 121, y1 = (1 + 11) / 2, y2 = (1 – 11) / 2, y1 = 6, y2 = -5. (y – 6)(y + 5) ≤ 0. Решим методом интервалов и получим: -5 ≤ y ≤ 6. Вернемся к замене: -5 ≤ |2x + 3| ≤ 6. Данное двойное неравенство равносильно системе неравенств: |2x + 3| ≤ 6 Решим каждое из неравенств в отдельности. Первое равносильно системе 2x + 3 ≤ 6
Решим ее. x ≤ 1.5 х∈[-4,5; 1,5]. Второе неравенство очевидно выполняется для всех x. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то ее решением, а, значит, и исходного неравенства будет решение ее первого неравенства (ведь второе верно для всех x),то есть х∈[-4,5; 1,5].
Ответ: [-4,5; 1,5].
|
|
|
|
Элективный курс «Уравнения, содержащие знак модуль»
Количество часов — 34.
АнатацияЭлективный курс по предпрофильной подготовке учащихся 9 классов посвящен систематическому изложению учебного материала, связанного с понятием абсолютной величины (модуля числа) и аспектами его применения. В нем рассматриваются различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации. Это все необходимо любому ученику, желающему не только успешно выступить на математических конкурсах и олимпиадах, но и хорошо подготовиться к поступлению в высшие учебные заведения.
Присутствует идея психического здоровья. Ученики, кроме усвоения фактического материала, смогли обрести уверенность в своей компетентности по предмету алгебра, повысить культуру общения в дискуссии, развить способность отстаивать собственную точку зрения, распределять обязанности при выполнении совместной работы с другими учениками.
Ученики, кроме усвоения фактического материала, смогли обрести уверенность в своей компетентности по предмету алгебра, повысить культуру общения в дискуссии, развить способность отстаивать собственную точку зрения, распределять обязанности при выполнении совместной работы с другими учениками.
Исторические аспекты. Термин «модуль» (от латинского modulus — мера) ввел английский математик Р.Котек (1682-1716). Знак «| |» ввел немецкий математик К.Вейерштрасс (1815-1897) в 1841 году.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку, достаточных для изучения смежных дисциплин и продолжения образования. Кроме того, задания единого экзамена по математике предполагают умение оперировать с модулем. Материал данного курса содержит «нестандартные» методы, которые позволяют более эффективно решать широкий класс заданий, содержащий модуль.
Элективный курс «Уравнения и неравенства, содержащие знак модуля» предусматривает углубленное изучение математики, формирование учащихся 9 классов устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессию, связанную с математикой, подготовку к обучению в вуз.
Пояснительная запискаКурс написан на 34часа и составлен из 3-х частей т.е. главы: I — 14 часов, II — 15 часов, III — 5 часов. Применяю дифференцированное обучение, для этого учеников разбиваю на три группы по уровню усвоения сложного материала. Первая группа ребят изучает главу I, вторая группа изучает главы I и II, третья группа изучает главы I, II, III.
Глава I. Линейные уравнения и неравенства, содержащие знак модуля, и их методы решения.
Глава II. Уравнения и неравенства, содержащие знак модуля, сводящиеся к квадратным уравнениям и их методы решения.
Глава III. Решение уравнений и неравенств с параметром и модулем.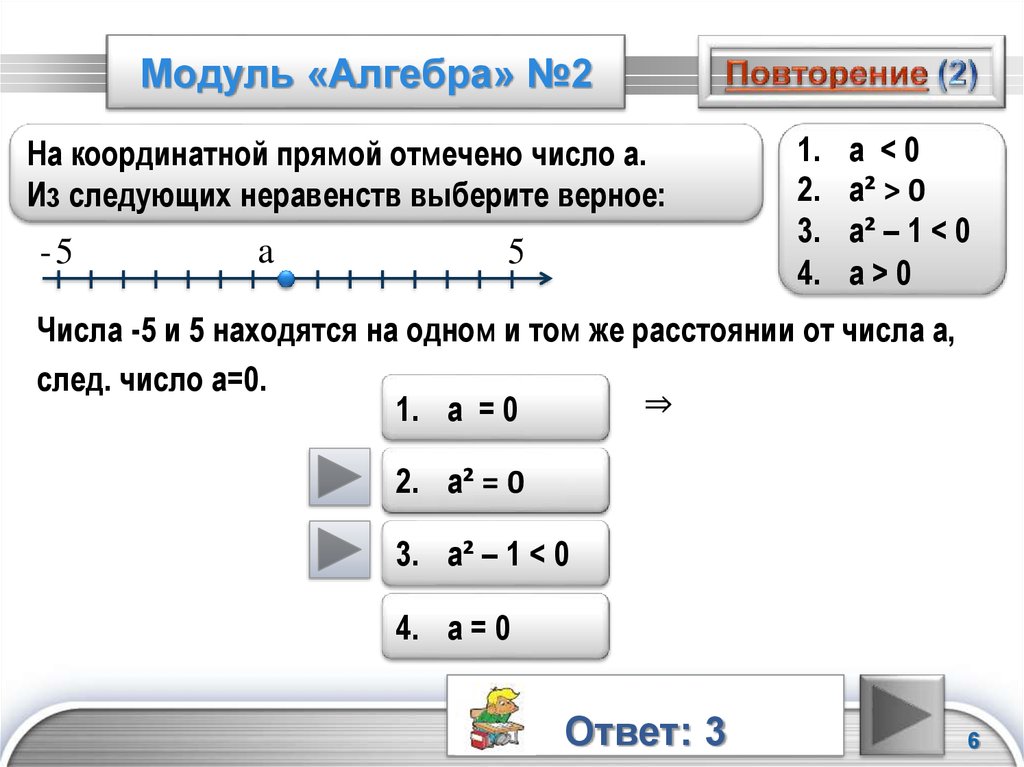
Главы разделены на отдельные темы. Каждая глава заканчивается контрольной работой из 3-х-5-ти заданий. Третью главу завершает тема «Защита творческих работ учащихся»
Глава I состоит из 10-ти тем:
Тема 1.1.Водная беседа. Определение модуля и его применение при решении уравнений и неравенств(1ч).
Тема 1.2.Множества и элементы комбинаторики.
Решение уравнений и неравенств с модулями на координатной прямой.(1ч)
Тема 1.3.Решение неравенств вида |x| < 0, |x| > 0 посредством равносторонних переходов.
Тема 1.4. Решение уравнений и неравенств по формуле.
Тема 1.5.Метод интервалов решения уравнений и неравенств, содержащих модуль.
Тема 1.6.Свойство модуля. Применение свойств модуля при решении уравнений и неравенств.
Тема 1.7.Решение уравнений и неравенств, содержащих знак модуля под знаком модуля.
Тема 1.8.Построение графиков линейных функций, содержащих знак модуля.
Тема 1.9. Графическое решение уравнений и неравенств с модулем.
Тема 1.10. Контрольная работа №1
В этой главе учащиеся учатся применять определение модуля числа, выражения при решении линейных уравнений и неравенств, решают уравнения и неравенства, содержащих знак модуля под знаком модуля, рассматривают легкие задания с параметром. Осваивают структуру работы с модулем, знакомятся с множествами и элементами комбинаторики, терминологией и символикой системы и совокупности, со свойствами модуля. Учащиеся знакомятся с дробно-линейной функцией и ее графиком. Рассматривают различные методы решения уравнений и неравенств: а) по определению модуля; б) методом интервалов в) графический метод; г) по формуле.
Каждая тема содержит изложение теории с поясняющими примерами содержит систему уравнений и неравенств с модулем ( многие из которых с решениями или указаниями).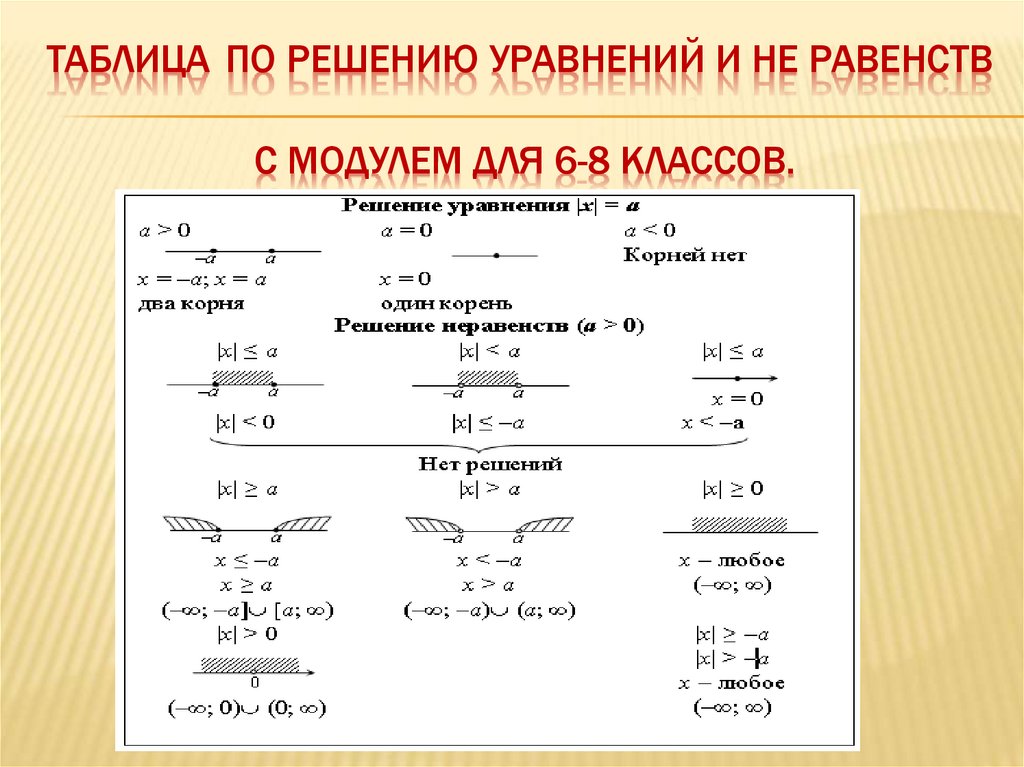 В конце каждой темы предлагается ряд заданий для самостоятельной работы с указанием ответов, помогающих закрепить теоретический материал. В конце каждой темы предлагается домашнее задание.
В конце каждой темы предлагается ряд заданий для самостоятельной работы с указанием ответов, помогающих закрепить теоретический материал. В конце каждой темы предлагается домашнее задание.
Выступления учащихся с лекцией, рефератом, докладом, с творческим сообщением, с проектными заданиями, проведение семинаров, диспутов занимают первое место при проведении занятий по данному курсу.
Глава II состоит из 9-ти тем:
Тема 2.1.Квадратный трехчлен в уравнениях и неравенствах, содержащих модули.
Тема 2.2.Уравнения и неравенства с модулем, сводящиеся к квадратным уравнениям, решаемые методом интервалов.
Тема 2.3. Решение квадратных уравнений и неравенств с модулем по формулам.
Тема 2. 4.Модуль и преобразование корней.
Тема 2.5. Модуль и иррациональные уравнения.
Тема 2.6. Решение квадратных уравнений с модулем с помощью построения графиков.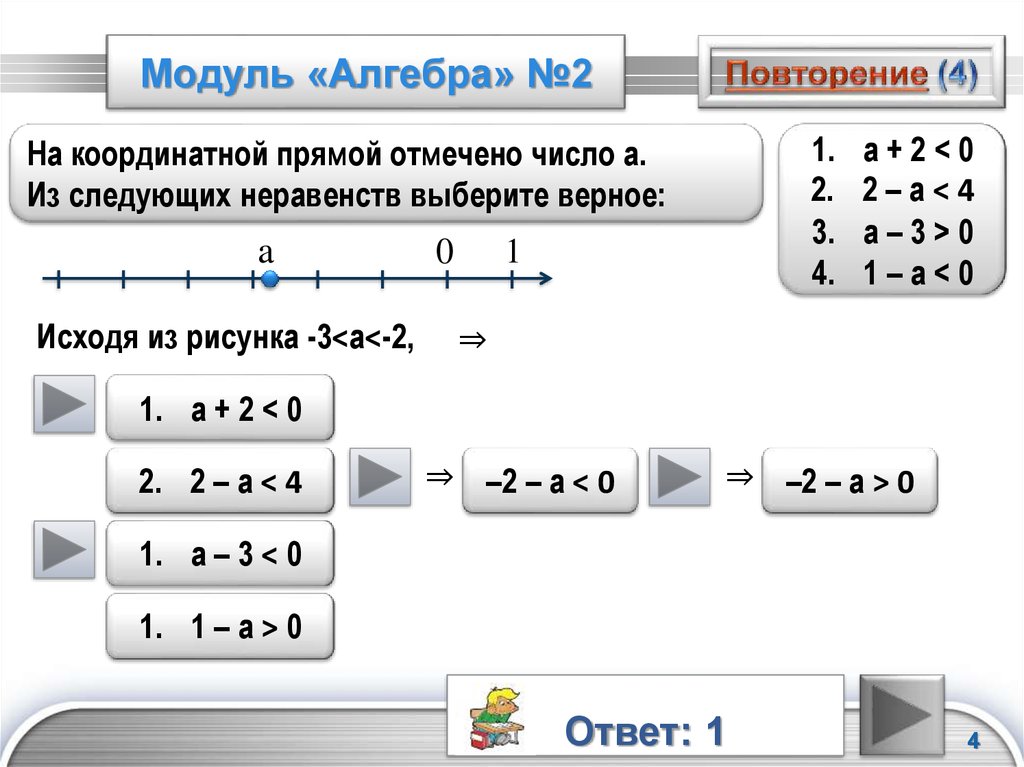
Тема 2.7. Тестовые задачи с модулем в КИМах ЕГЭ и на вступительных экзаменах.
Тема 2.8. Тестовые задачи с модулем, содержащие тригонометрические выражения, из КИМов ЕГЭ.
Тема 2.9. Контрольная работа №2.
В этой главе учащиеся изучают квадратный трехчлен в уравнениях и неравенствах с модулем, учатся оперировать арифметическими корнями и учатся преобразовывать иррациональные выражения.
Представлена работа на перспективу (рассматриваются задания с тригонометрией), так же в этой главе учащиеся решают олимпиадные задачи с применением уравнений и неравенств с модулем, устанавливаются межпредметные связи. Рассматриваем тестовые задачи с модулем из КИМов ЕГЭ.
В этой главе осуществляется подготовка к экзамену по алгебре в 9-ом классе, идет повторение всего курса алгебры.
В главе III три темы:
Тема 3.1. Уравнения с параметром и модулем.
Тема 3.2 .Неравенства с параметром и модулем.
Тема 3.3. Защита творческих работ и рефератов.
Эту главу изучают одаренные и способные учащиеся. Предлагается лекционное изложение теоретического материала.
Рассматриваются разнообразные и нестандартные уравнения и неравенства с параметрами, так как на олимпиадах всех уровней и вступительных экзаменах в престижные вузы без них, как правило, не обходятся. Учащимся предлагают решать неравенства с двумя параметрами.
Задачи курса
- научить учащихся преобразовывать выражения, содержащие модуль;
- научить учащихся решать уравнения и неравенства, содержащие модуль;
- научить строить графики, содержащие модуль;
- работать на перспективу по тригонометрии;
- научить работать с литературой;
- научить составлять проектные задания, составлять математическую модель.
Цели курса: помочь повысить уровень понимания и практической подготовки в таких вопросах, как:
а) освоить рациональные способы организации своей деятельности для эффективного решения заданий повышенного уровня;
б) способствовать приобщению к творческой и исследовательской деятельности по алгебре;
в) создать в совокупности с основными разделами курса базу для развития способностей учащихся;
г) помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы.
Требования к математической подготовке учащихся.
В результате изучения курса «Уравнения и неравенства, содержащие знак модуля», учащиеся должны:
— усвоить алгебраическое определение модуля и геометрическое определение модуля;
— усвоить основные приемы решения уравнений и неравенств, содержащих знак модуля:
а) по определению модуля;
б) методом интервалов;
в) графический метод;
г) по формуле.
Содержание данного элективного курса включает ряд более сложных уравнений, содержащих знак модуля, которые не включены в программу по математике для классов общеобразовательных школ. Однако этот курс является важным содержательным компонентом системы непрерывного математического образования.
Содержание программы включает три части — теоретическую, практическую и проектную. В теоретическом разделе рассматриваются уравнения и неравенства с модулем и способы их решения. Практическая часть включает задания различного уровня сложности для закрепления и контроля усвоенного материала. Эти задачи предназначены для индивидуальной, парной, групповой и коллективной форм работы. Большое внимание в курсе уделяется формированию у учащихся умения конструировать задания. В проектной части учащиеся должны показать свои умения в составлении и представлении сообщений, рефератов, самостоятельно составленных заданий.
Эти задачи предназначены для индивидуальной, парной, групповой и коллективной форм работы. Большое внимание в курсе уделяется формированию у учащихся умения конструировать задания. В проектной части учащиеся должны показать свои умения в составлении и представлении сообщений, рефератов, самостоятельно составленных заданий.
Этот курс создает базу для удовлетворения интересов и развития способностей учащихся, а также восполнение пробелов основного курса решения уравнений и неравенств, содержащих знак модуля.
Этот курс поможет при подготовке к ЕГЭ (единому государственному экзамену) по математике в 11классе.
Конечным продуктом должна быть творческая работа каждого ученика.
В результате изучения курса учащиеся должны уметь:
- точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
- применять изученные алгоритмы для решения заданий и отстаивать свою точку зрения;
- преобразовывать выражения, содержащие модуль;
- решать уравнения и неравенства, содержащие модуль;
- строить графики функций, содержащих модуль;
- решать самостоятельно задания из единого государственного экзамена;
- решать типовые задачи с модулем, содержащие тригонометрию.

Возможные критерии оценок.
- Оценка «отлично» — учащийся освоил теоретический курс и демонстрирует ответственное отношение, сопровождающееся ярко выраженным интересом к учению; получил навыки при решении конкретных заданий; продемонстрировал умение работать самостоятельно, показал знания и умения применять стандартные методы решения при выполнении творческой работы.
- Оценка «хорошо» — учащийся освоил идеи и методы курса и может справиться со стандартными заданиями; прилежно выполняет домашние задания; наблюдаются результаты возрастания общих умений учащихся. Успешно выполнил творческую работу.
- Оценка «удовлетворительно» — учащийся освоил наиболее простые идеи и методы курса, что позволило ему достаточно успешно выполнять простые задания.
См. продолжение элективного курса
Решение уравнений и неравенств c модулем
Версия для печати
1.
 4`;
4`;
1.3 Модуль неизвестного числа
`abs(x)=[({(x >= 0),(abs(x) = x):}), ({(x < 0),(abs(x)=-x):}) :}`
1.4 Упражнения к определению модуля
1.4.1 Решить уравнение `abs(2x-1)=2x-1`
`2x-1>=0`;
`x >= 1/2`
Ответ: `[1/2; +infty)`
1.4.2 Решить уравнение `abs(7x-14)=14-7x`
`7x-14 <= 0`; `x <= 2`Ответ: `(-infty; 2]`
1.4.3 Решить уравнение `abs(3x-19)=1`
`[(3x-19=1), (3x-19=-1) :}`; `[(x=20/3), (x=6) :}`Ответ: `{6; 20/3}`
1.4.4 Решить уравнение `abs(5x-11)=3x+4`
`{( 3x+4 >= 0 ), ( [(5x-11=3x+4), (5x-11=-3x-4):}) :}`; `{(x >= -4/3), ( [(x=15/2), (x=7/8):} ) :}`;Ответ: `{7/8; 15/2}`
1.
 4.5 Решить неравенство `abs(x+4) <=1`
4.5 Решить неравенство `abs(x+4) <=1`
`-1 <= x+4 <= 1`;
`-5 <= x <= -3`
Ответ: `[-5; -3]`
1.4.6 Решить неравенство `1/5 abs(1-7x) > 3`
`abs(1-7x) > 15`;
`[(1-7x > 15), (1 — 7x < -15) :}`; `[(7x < -14), ( 7x > 16) :}`;
`[(x < -2), (x > 16/7) :}`
Ответ: `(-infty; -2) uu (16/7; +infty)`
2. Решение уравнений, содержащих неизвестную функцию под знаком модуля
`abs(f(x))=varphi(x)`
— Если `varphi(x) < 0`, уравнение не имеет решения (по определению модуля).
— Если `varphi(x) >= 0`, то решаем систему:
`{( varphi(x) >= 0 ), ( [(f(x)=varphi(x)), (f(x)=-varphi(x)) :}) :}`
Примеры уравнений, содержащих неизвестную функцию под знаком модуля
Решить уравнение `abs(x^2-x)=3x-4`
`{( 3x-4 >= 0 ), ( [ (x^2-x=3x-4), (x^2-x=4-3x) :}) :}`; `{ (x >= 4/3 ), ( [ (x^2-4x+4 = 0), (x^2+2x-4=0) :}) :}`;
`[( { (x >= 4/3), ((x-2)^2=0) :} ), ( { (x >= 4/3), (x^2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;
Сравним `4/3 vv sqrt5-1`
`4 vv 3sqrt5-3`; `7 vv 3sqrt5`; `49 vv 45 (>)`
`4/4 > sqrt5-1`
Ответ: 2
3.
 10`
10`
Итоговое объединение двух систем: `x < -5/3 uu [-3/2; 2] uu x>=2`
Ответ: `(-infty; -5/3) uu (-3/2; +infty)`
3.1.3 Найти область определения функции `f(x)=sqrt(1/2-abs(3/(5-x))`
`D_f(x)`:
`1/2-abs(3/(5-x)) >= 0`;
`abs(3/(5-x)) <= 1/2`;
` -1/2 <= 3/(5-x) <= 1/2`;
`{( 3/(5-x) <= 1/2), ( 3/(5-x) >= -1/2) :}`; `{( 3/(5-x) — 1/2 <= 0), ( 3/(5-x) + 1/2 >= 0):}`;
`{( (6-5+x)/(2(5-x)) <= 0 ), ( (6+5-x)/(2(5-x)) >= 0 ):}`; `2 > 0`; `{( (x +1)/(5-x) <= 0 ), ( (11-x)/(5-x) >= 0 ):}`;
Ответ: `(-infty; -1] uu [11; +infty)`
3.
 2 <= 0) :}
)
:}`
2 <= 0) :}
)
:}`
Ответ: `[-5; -2] uu [2; 3) uu (3; 5]`
3.2 Смысл неравенства больше либо равно
`abs(f(x)) >= varphi(x)`
Если `varphi(x) <= 0` — то неравенство справедливо для всех `x`, удовлетворяющих области допустимых значений (ОДЗ).
Если `varphi(x) > 0` — то необходимо решить совокупность двух неравенств:
`[(f(x) >= varphi(x)), (f(x) <= -varphi(x)) :}`
Примеры с модулем на неравенства со смыслом больше либо равно
3.2.1 Решить неравенство `abs((x+1)/(x-1)) >= 1-2x`
а) `{(ОДЗ: x != 1), (1-2x < 0) :}`
В ответ: `(1/2; 1) uu (1; +infty)` (a)
б) `{(ОДЗ: x != 1), (1-2x >= 0), ([((x+1)/(x-1) >= 1-2x), ((x+1)/(x-1) <= 2x — 1) :} ) :}`; `{(x <= 1/2), ([((x+1)/(x-1) + (2x -1)/1 >= 0), ((x+1)/(x-1)+ (1-2x)/1 <= 0) :} ) :}`;
`{(x <= 1/2), ( [ ((x^2-x+1)/(x-1) >= 0), ((1-x)^2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
В ответ: `[-1; 1/2]` (б)
В ответ `[ ( a: (1/2; 1) uu (1; +infty)), ( б: [-1; 1/2]) :}`
Ответ: `[-1; 1) uu (1; +infty)`
4.
 Уравнения и неравенства, содержащие неизвестные под несколькими модулями
Уравнения и неравенства, содержащие неизвестные под несколькими модулями4.1 Решить неравенство `abs(x-4)-2abs(1-x) >= 1`
На числовом луче отметим значения x, при которых подмодульные значения обращаются в «0»: `x=1; x=4`. Луч разбился на три интервала.
Необходимо на каждом интервале найти решение данного неравенства, то есть решить совокупность трёх систем неравенств:
`[
(
{
(x <= 1), (4-x-2(1-x) >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2(1-x) >= 1) :}
),
(
{(x > 4), (x-4+2(1-x) >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (4-x-2+2x >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2-2x >= 1) :}
),
(
{(x > 4), (x-4+2-2x >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (x+1 >= 0)
:}
),
(
{(1 < x <= 4), (5-3x >= 0) :}
),
(
{(x > 4), (-x-3 >= 0) :}
)
:}` ;
`[
(
{
(x <= 1), (x >= -1)
:}
),
(
{(1 < x <= 4), (x <= 5/3) :}
),
(
{(x > 4), (x <= -3) :}
)
:}` ;
Ответ: `[-1; 5/3]`
4.
 2-9 >= 0), (x+3 >= 0) :}`
2-9 >= 0), (x+3 >= 0) :}`
Ответ: `{-3} uu [3; +infty)`
4.5 Решить неравенство `3x-abs(x+10) — abs (2-x) <= 6`
`[ ( { (x <= -10), (3x+x+10-2+x <= -6) :} ), ( {(-10 < x <= 2), (3x-x-10-2+x <= -6) :} ), ( {(x > 2), (3x-x-10+2-x <= -6) :} ) :}` ; `[ ( { (x <= -10), (5x <= -14) :} ), ( {(-10 < x <= 2), (3x <= 6) :} ), ( {(x > 2), (x <= 2) :} emptyset ) :}` ;
`[(x <= -10), (-10 < x <= 2):}`
Ответ: `(-infty; 2]`
5. Неравенства, содержащие модуль, повышенной сложности
5.
 2 -3abs(x)+1)`
2 -3abs(x)+1)`Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`
6.9 Решить неравенство `3x — abs(x+8) — abs(1-x) <= -6`
Ответ: `(-infty; 1]`
Много задач с решениями на неравенства с модулем можно посмотреть здесь:
Решения неравенств с модулем
Уравнения с параметром, содержащие модуль — Мегаобучалка
Решить в зависимости от значений параметра а.
| x – 3 | = a
По свойству модуля при всех левая часть уравнения неотрицательна, следовательно, при a < 0 уравнение не имеет решений.
При a = 0 x = 3.
При a > 0 x – 3 = ± a, откуда x = 3 ± a.
Ответ: при a = 0 x = 3.
при a > 0 x = 3 + a. x = 3 – a.
при a < 0 уравнение не имеет решений.
При каких значениях параметра a уравнение x = a · | x – 5 | имеет единственное решение, два решения, не имеет решения. Найдите их.
Для решения уравнения найдём нули модули x – 5 = 0 x = 5.
Раскроем модуль на двух промежутках: x ≥ 5 и x < 5.
1) x ≥ 5, 2) x < 5,
x = a ( x – 5 ) x = a ( – x + 5 )
x ≥ 5, x < 5,
x – ax = – 5a;x + ax = 5a;
x ≥ 5, x < 5,
x ( 1– a )= – 5a;x ( 1+ a )= 5a ;
Исследуем линейное уравнение Исследуем линейное уравнение
в зависимости от параметра a. в зависимости от параметра a.
в зависимости от параметра a.
x ( 1– a )= – 5a ; x ( 1+ a )= 5a;
Если 1– a = 0, т.е. a = 1, то Если 1+ a = 0, т.е. a = – 1, то
x · 0 = – 5 Уравнение не имеет x · 0 = – 5 Уравнение не имеет
решения. решений.
Если 1– a ≠ 0, т.е. a ≠ 1, то Если 1+ a ≠ 0, т.е. a ≠ – 1, то
— уравнение имеет — уравнение имеет
единственное решение. единственное решение.
x ≥ 5, x < 5,
, a ≠ 1; , a ≠ –1;
Учтем, что x ≥ 5, т.е. Учтем, что x < 5, т.е.
решим методом интервалов решим методом интервалов
неравенство. неравенство.
Получим a > 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1
Т.е. при a > –1
уравнение будет иметь уравнение будет иметь
единственное решение единственное решение
на промежутке x ≥ 5. на промежутке x < 5.
Ответим на поставленные вопросы. Наши решения покажем на координатных прямых.
одно решение
нет одно два
решения решение решения
При a > 1 уравнение имеет два корня ; ;
При a < – 1 уравнение не имеет решения.
При – 1< a ≤ 1 уравнение имеет одно решение, т.е. .
Ответ: a > 1, ; .
a < – 1, решений нет.
– 1< a ≤ 1, .
Решить самостоятельно:
При каком a уравнение имеет решения. Найдите их.
При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения?
Найдем нули модуля: x + 3 =0; x = – 3.
Раскроем модуль на двух промежутках:
x ≥ – 3 x < – 3
x ≥ – 3, x < – 3
( x + 3) ( x – 3 ) + a = 0; (– x – 3) ( x – 3 ) + a = 0;
Исследуем уравнение Исследуем уравнение
( x + 3) ( x – 3 ) + a = 0; (– x – 3) ( x – 3 ) + a = 0;
x2 – 9 + a = 0; – ( x2 – 9 ) = – a ;
x2 = 9 – a ; x2 – 9 = a ;
при 9 – a ≥ 0, т.е. a ≤ 9 x2 = a + 9;
уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9
. уравнение имеет два корня
x ≥ – 3; a ≥ – 9
; a ≤ 9 x < – 3;
Учтем, что x ≥ – 3 Учтем, что x < – 3
при 9 – a ≥ 0
неравенство имеет решение, решения нет.
т.е. a ≤ 9.
a + 9 ≥ 0,
a + 9 > 9,
неравенство имеет решение Т.е. при a > 0
a ≤ 9; уравнение имеет один корень
a ≥ 0; т.е. 0 ≤ a ≤ 9;
Т.е. при 0 ≤ a ≤ 9 уравнение
имеет два различных корня.
, при a = 3
уравнение имеет два равных
корня .
Ответим на поставленный вопрос.
При 0 ≤ a < 9 уравнение имеет 3 корня.
нет три одно
решения решения решение
два два
решения решения
Ответ: при 0 ≤ a < 9 три корня.
При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения? (Графический способ).
| x + 3| · ( x – 3 ) = – a
Построим графики, заданные в левой и правой частях:
1) y = | x + 3| · ( x – 3 )
Найдем нули модуля: x + 3 =0; x = – 3.
Раскроем модуль на двух промежутках: x < – 3; x ≥ – 3.
x ≥ – 3; x < – 3;
y = ( x + 3) ( x – 3 ) = x2 – 9; y = – ( x + 3) ( x – 3 ) = 9 – x2;
2) y = – a – линейная функция, график прямая, параллельная оси OY.
Эскиз графиков. y
y = – a
Ответ: 0 < a < 9.
При каких значениях a уравнение имеет единственное решение?
ОДЗ: x2+ 8x + 12 ≠ 0; x ≠ – 6; x ≠ –2;
Найдем нули модуля: 2x + 6 = 0; x = –3;
Раскроем модуль на двух промежутках: x ≥ –3 и x < –3.
1) x ≥ –3; и 2) x < –3.
x ≥ –3; x < –3.
x ≥ –3; x < –3.
Исследуем уравнение: Исследуем уравнение
x ≠ – 6; x ≠ –2;
Если a = 0; 0 ∙ x = 3 Если a = 0; 0 ∙ x = – 1
решения нет. решения нет.
a ≠ 0; a ≠ 0;
единственное решение. единственное решение.
x ≥ –3; x < –3;
a ≠ 0; a ≠ 0;
Учтем, что x ≥ –3; т.е. Учтем, что x < –3; т.е.
Решим методом интервалов Решим методом интервалов
неравенство. неравенство
Получим 0 < a ≤ 1. Получим 0 < a < 1.
Т.е. при 0 < a ≤ 1 уравнение Т.е. при 0 < a < 1 уравнение
будет иметь единственное будет иметь единственное
решение решение
Ответим на поставленный вопрос. Наши решения покажем на координатных прямых.
Наши решения покажем на координатных прямых.
нет два нет
решения решения решений
нет одно
решения решение
При a = 1 уравнение имеет одно решение.
Учтем ОДЗ x ≠ – 2; x ≠ –6;
x ≥ –3; x < –3;
x ≠ –6; x ≠ – 2; x ≠ –6; x ≠ – 2;
a ≠ 0;
С учетом ОДЗ
При и уравнение имеет одно решение.
Ответ: — единственное решение.
Решить самостоятельно:
При каких значениях a уравнение имеет единственное решение? Ответ:
При каких значениях параметра a уравнение имеет два различных корня?
Так как то сделав замену где получим новое квадратное уравнение
Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:
Это будет в двух следующих случаях:
а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;
б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.
Таким образом, получим совокупность двух систем.
1) Д > 0, 2) Д = 0,
y1 ∙ y2 < 0; y1 + y2 > 0;
Так как
то системы будут иметь вид:
Откуда или
Ответ: ;
При каких значениях с уравнение x2 – ( 3c – 2 ) ∙ | x | + 2c2 – c = 0 имеет 4 различных корня?
Так как | x |2 = x2, то сделав замену | x | = y, где y ≥ 0, получим новое квадратное уравнение y 2 – ( 3c – 2 ) ∙ y + 2c2 – c = 0.
Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.
Таким образом, получим систему неравенств:
Д > 0;
Так как Д = ( 3c – 2 )2 – 4∙ ( 2c2 – c ) = 9c2 – 12c + 4– 8c2 +4c= c2 – 8c +4
то система будет иметь вид:
c2 – 8c +4 > 0;
3c – 2 > 0; Откуда имеем
2c2 – c > 0;
Ответ:
СПИСОК ЛИТЕРАТУРЫ
1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000
2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986
3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994
5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999
6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003
Теория модулей | Задачи по математике
Теория модулей
Задача 449
Пусть $R$ — коммутативное кольцо с $1$ и $M$ — $R$-модуль.
Докажите, что $R$-модуль $M$ неприводим тогда и только тогда, когда $M$ изоморфен $R/I$, где $I$ — максимальный идеал $R$, как $R$-модуль .
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 434
Пусть $R$ — кольцо с $1$.
Ненулевой $R$-модуль $M$ называется неприводимым , если $0$ и $M$ являются единственными подмодулями в $M$.
(Его также называют простым -модулем.)
(a) Докажите, что ненулевой $R$-модуль $M$ неприводим тогда и только тогда, когда $M$ — циклический модуль с любым ненулевым элементом в качестве его генератор.
(б) Определить все неприводимые $\Z$-модули.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 432
(a) Пусть $R$ — область целостности, $M$ — конечно порожденный $R$-модуль кручения.
Докажите, что модуль $M$ имеет ненулевой аннулятор.
Другими словами, покажите, что существует ненулевой элемент $r\in R$ такой, что $rm=0$ для всех $m\in M$.
Здесь $r$ не зависит от $m$.
(b) Приведите пример области целостности $R$ и $R$-модуля кручения $M$, аннулятором которого является нулевой идеал.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 431
Пусть $R$ — коммутативное кольцо и $I$ — нильпотентный идеал кольца $R$.
Пусть $M$ и $N$ — $R$-модули, а $\phi:M\to N$ — гомоморфизм $R$-модулей.
Докажите, что если индуцированный гомоморфизм $\bar{\phi}: M/IM \to N/IN$ сюръективен, то $\phi$ сюръективен.
Чтение решения
Добавить для решения позже
Теория модулей
Задача 422
Пусть $R$ — кольцо с $1$, и рассмотрим $R$ как модуль над собой.
(a) Определите, является ли гомоморфизм модулей $\phi:R\to R$ гомоморфизмом колец.
(b) Определите, является ли гомоморфизм колец $\phi: R\to R$ модульным гомоморфизмом.
(c) Если $\phi:R\to R$ является одновременно гомоморфизмом модулей и гомоморфизмом колец, что мы можем сказать о $\phi$?
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 418
Если $M$ — конечная абелева группа, то $M$, естественно, является $\Z$-модулем.
Можно ли расширить это действие, чтобы превратить $M$ в $\Q$-модуль?
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 417
Пусть $R$ — кольцо с $1$, а $M$ — $R$-модуль. Пусть $I$ — идеал в $R$. 9{\infty} N_i\] является подмодулем в $M$.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 415
(a) Пусть $R$ — коммутативное кольцо. Если рассматривать $R$ как левый $R$-модуль, то докажите, что любые два различных элемента модуля $R$ линейно зависимы.
(b) Пусть $f: M\to M’$ — гомоморфизм левых $R$-модулей. Пусть $\{x_1, \dots, x_n\}$ — подмножество в $M$. Докажите, что если множество $\{f(x_1), \dots, f(x_n)\}$ линейно независимо, то множество $\{x_1, \dots, x_n\}$ также линейно независимо. 9{\prime\prime}$ конечно порождены, то $M’$ также конечно порождены.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 410
Пусть $R$ — кольцо с $1$ и $M$ — левый $R$-модуль.
Пусть $S$ — подмножество $M$. Аннулятор кольца $S$ в $R$ — это подмножество кольца $R$, определяемое как
\[\Ann_R(S)=\{ r\in R\mid rx=0 \text{ для всех } х\в S\}. \]
(Если $rx=0, r\in R, x\in S$, то говорят $r$ аннулирует $x$.)
\]
(Если $rx=0, r\in R, x\in S$, то говорят $r$ аннулирует $x$.)
Предположим, что $N$ — подмодуль в $M$. Затем докажите, что аннулятор
\[\Ann_R(N)=\{ r\in R\mid rn=0 \text{ для всех } n\in N\}\]
$M$ в $R$ является двусторонним идеалом в $R$.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 409
Пусть $R$ — кольцо с $1$. Элемент $R$-модуля $M$ называется элементом кручения если $rm=0$ для некоторого ненулевого элемента $r\in R$.
Множество элементов кручения обозначается
\[\Tor(M)=\{m \in M \mid rm=0 \text{ для некоторого ненулевого} r\in R\}.\]
(a) Докажите, что если $R$ — область целостности, то $\Tor(M)$ — подмодуль в $M$.
(Замечание: область целостности является коммутативным кольцом по определению.) В этом случае подмодуль $\Tor(M)$ называется подмодулем кручения в $M$.
(b) Найдите пример кольца $R$ и $R$-модуля $M$ таких, что $\Tor(M)$ не является подмодулем.
(c) Если $R$ имеет ненулевые делители нуля, то показать, что каждый ненулевой $R$-модуль имеет ненулевой элемент кручения.
Прочитать решение
Добавить для решения позже
Теория модулей
Задача 408
Пусть $R$ — кольцо с $1$ и $M$ — левый $R$-модуль.
(a) Докажите, что $0_Rm=0_M$ для всех $m \in M$.
Здесь $0_R$ — нулевой элемент в кольце $R$, а $0_M$ — нулевой элемент в модуле $M$, т. е. единичный элемент аддитивной группы $M$.
Для упрощения обозначений мы игнорируем индексы и пишем просто
\[0m=0.\]
Вы должны уметь и должны судить, какие нулевые элементы используются из контекста.
(b) Докажите, что $r0=0$ для всех $s\in R$. Здесь оба нуля равны $0_M$.
Здесь оба нуля равны $0_M$.
(c) Докажите, что $(-1)m=-m$ для всех $m \in M$.
(d) Предположим, что $rm=0$ для некоторого $r\in R$ и некоторого ненулевого элемента $m\in M$. Докажите, что $r$ не имеет левого обратного.
Прочитать решение
Добавить для решения позже
Python Math Module — GeeksforGeeks
Иногда при работе с какими-то финансовыми или научными проектами возникает необходимость реализовать в проекте математические расчеты. Python предоставляет математический модуль для выполнения таких вычислений. Модуль Math предоставляет функции для работы как с основными операциями, такими как сложение (+), вычитание (-), умножение (*), деление (/), так и с дополнительными операциями, такими как тригонометрические, логарифмические, экспоненциальные функции.
В этой статье мы узнаем о математическом модуле от основ до продвижения с помощью огромного набора данных, содержащего функции, объясненные с помощью хороших примеров.
Константы, предоставляемые математическим модулем
Математический модуль предоставляет различные значения различных констант, таких как пи, тау. Наличие таких констант экономит время записи значения каждой константы каждый раз, когда мы хотим ее использовать, и это также с большой точностью. Константы, предоставляемые математическим модулем: –
- Число Эйлера
- Пи
- Тау
- Бесконечность
- Не число (NaN)
Рассмотрим каждую константу подробно.
Число ЭйлераКонстанта math.e возвращает число Эйлера: 2,71828182846.
Синтаксис:
MATH.E
Пример:
Python3
|
Выход:
2,71828182845
2,71828182845. Пи изображается как 22/7 или 3,14. math.pi обеспечивает более точное значение числа пи.
Синтаксис:
math.pi
Пример 1:
Python3
00016 import math
|
Output:
3.1415589793
Example 2: Let's find the area of the circle
Python3
|
Output:
50.26548245743669
Tau
Тау определяется как отношение длины окружности к радиусу окружности. Константа math.tau возвращает значение тау: 6,283185307179586.
Синтаксис:
math.tau
Example:
Python3
|
Output:
6.283185307179586
Бесконечность
Бесконечность в основном означает нечто бесконечное или безграничное в обоих направлениях, т.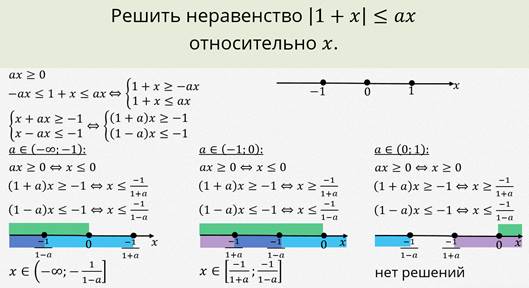 е. отрицательное и положительное. Его нельзя изобразить числом. math.inf постоянный возврат положительной бесконечности. Для отрицательной бесконечности используйте -math.inf .
е. отрицательное и положительное. Его нельзя изобразить числом. math.inf постоянный возврат положительной бесконечности. Для отрицательной бесконечности используйте -math.inf .
Syntax:
math.inf
Example 1:
Python3
|
Вывод:
инф -inf
Example 2: Comparing the values of infinity with the maximum floating point value
Python3
|
Вывод:
Правда True
NaN
Константа math.nan возвращает значение nan (не число) с плавающей запятой. Это значение не является допустимым числом. Константа nan эквивалентна float("nan").
Пример:
Python3
935 печать 0352 (math.nan) |
Вывод:
nan
Числовые функции
факториал числа.
Определение максимального и минимального значения
Потолочное значение означает наименьшее целое значение, большее числа, а нижнее значение означает наибольшее целое значение, меньшее числа. Это можно легко рассчитать с помощью ceil() и floor() соответственно.
Это можно легко рассчитать с помощью ceil() и floor() соответственно.
Example:
Python3
|
Вывод:
Максимальное значение 2.3: 3 Этаж 2.3: 2
Нахождение факториала числа
С помощью функции factorial() мы можем найти факториал числа в одной строке кода. Сообщение об ошибке отображается, если число не является целым.
Example:
Python3
|
Факториал 5: 120
Нахождение НОД
gcd() Функция используется для нахождения наибольшего общего делителя двух чисел, переданных в качестве аргументов.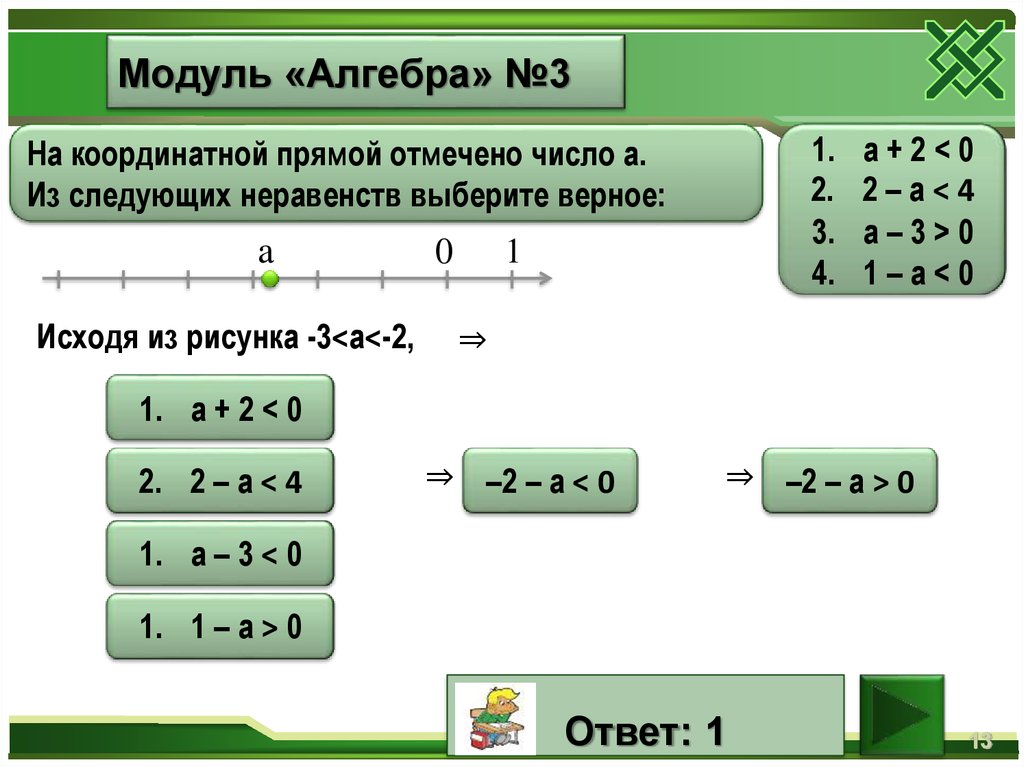
Example:
Python3
|
Вывод:
НОД 5 и 15: 5
Нахождение абсолютного значения
Функция 2bs9 возвращает 900.
Пример:
Python3
Нахождение степени expМетод exp() используется для вычисления мощности e, т. е. или, можно сказать, экспоненциальной величины y. Example: Python3
Вывод: 54.34 0,049787068367863944 1.0 Нахождение степени числафункция pow() вычисляет x**y. Эта функция сначала преобразует свои аргументы в число с плавающей запятой, а затем вычисляет мощность. Пример: Python3
Выход: Значение 3 ** 4 IS: 81,0 Обнаружение логарита
. база б. Если база не указана, вычисленное значение соответствует натуральному логарифму. база б. Если база не указана, вычисленное значение соответствует натуральному логарифму.Python3
Выход: . Значение log2 из 16: 4,0 Значение log10 из 10000: 4.0 Нахождение квадратного корняФункция sqrt() возвращает квадратный корень из числа. Пример: Python3
Выход: 77777777.0367 |
.
2.0
1.8708286 Обратитесь к статье ниже, чтобы получить подробную информацию о логарифмических и степенных функциях Вы все должны знать о тригонометрии и о том, как трудно найти значения синуса и косинуса любого угла. Модуль Math предоставляет встроенные функции для поиска таких значений и даже для изменения значений между градусами и радианами. sin(), cos() и tan() 9Функции 0029 возвращают синус, косинус и тангенс значения, переданного в качестве аргумента. Example: Вывод: Example: Output: Обратитесь к статьям ниже, чтобы получить подробную информацию о тригонометрических и угловых функциях. Помимо всех числовых и логарифмических функций, которые мы уже обсудили, математический модуль предоставляет еще несколько полезных функций, которые не подпадают ни под одну из описанных выше категорий, но могут пригодиться в некоторых случаях. точка во время кодирования. Функция gamma() используется для возврата значения гаммы аргумента. Example: Выход: Функция isinf() используется для проверки того, является ли значение бесконечностью или нет. Пример: Вывод: Функция isnan() возвращает true, если число равно «NaN», иначе возвращает false. Example: Подробнее о специальных функциях см. в статье ниже. Список математической функции в Python К концу этого модуля вы: Классное упражнение 1: Мы рассмотрим 10 различных приложений линейного
алгебра. Начните с выполнения этих инструкций . Рассмотрим эти одновременных линейных уравнения :
$$
\eqb{
х + 3у & = 7,5\
4х+2у&=10\
}
$$
который мы также можем записать как
$$
\eqb{
х_1+3х_2&=7,5\
4x_1+2x_2&=10\
}
$$ Классное упражнение 2: Решите эти уравнения вручную, используя систематический подход. Классное упражнение 3: Покажите, как ваш алгоритм применим к приведенным выше уравнениям.
Проверьте, используя данные в файле Problem2.txt.
(Для использования демо на
проблема2.txt
копировать
проблема2.txt
к
уравнения.txt,
который является входным файлом для программы.) Классное упражнение 4: Каковы два параметра методаsolveEquations()?
Что возвращается из метода? Классное упражнение 5: Покажи, что происходит
когда ваш алгоритм применяется к этим уравнениям. Классное упражнение 6: Изучите данные в Problem4.txt
и запишите соответствующие уравнения. Почему проблема
есть несколько решений? Классное упражнение 7: Изучите данные в Problem5.txt, запишите
соответствующие уравнения и применить ваш алгоритм.
Имеют ли эти уравнения решение? Что ты видишь
когда вы запускаете демо?
Сравните уравнения с первым набором данных (в
проблема1.txt). Классное упражнение 8: Запустите демонстрацию данных в файле problem6.txt.
Запишите, затем сравните эти уравнения с уравнениями в Problem5.txt.
Что вас не устраивает в выводе демо? Классное упражнение 9: Какие желательные функции в решателе общего назначения для
одновременные линейные уравнения? Карл Фридрих Гаусс, считающийся одним из величайших математиков
все время разрабатывал метод предсказания орбит на основе наблюдений: Классное упражнение 10: В файле curveFittingDemo скомпилируйте и
выполнить CurveFittingDemo.java. Затем попробуйте каждый из
четыре примера по очереди, как указано в main().
Прочитайте код в методе ellipse(). Любой инструмент графического дизайна должен позволять дизайнерам рисовать кривые.
а затем хранить их. Три варианта: Классное упражнение 11: Каковы сравнительные преимущества и недостатки A и B выше? Классное упражнение 12: Запустите BezierDemo. Наши устройства просмотра все 2D. Классное упражнение 13: Рассмотрим кубоид с углами в этих координатах:
(5,1,8), (5,3,8), (9,3,8), (9,1,8)
(5,1,11), (5,3,11), (9,3,11), (9,1,11).
На листе бумаги нарисуйте оси x, y, z осью z вверх, ось x
идет примерно на юго-запад, а ось Y на юго-восток. Затем нарисуйте куб.
Теперь рассмотрим левый край бумаги как ось Y двумерной плоскости;
нижний край бумаги является осью Z. Какие координаты
углов прямоугольного параллелепипеда в этом двухмерном мире? Классное упражнение 14: Запустите демо-версию координат в координатахDemo
каталог. Затем изучите код. Зачем нужно положение глаз? Целью почти каждого медиаформата является сжатие необработанного
данные во что-то меньшее. Существует два основных типа сжатия: Давайте посмотрим на сжатие изображений. Классное упражнение 15: Изучите простое изображение testimage.png в CompressDemo.
каталог. Теперь изучите код в ImageExample.java, затем
скомпилировать и выполнить. Линейная алгебра играет ключевую роль в сжатии с потерями. Давайте рассмотрим пример. Классное упражнение 16: Попробуйте одну за другой три демонстрации в CompressionDemo.java.
(Первый — одномерное изображение: одномерный массив).
В каждом случае сравните несжатое изображение с исходным.
чтобы понять, насколько «с потерями» было сжатие. В задаче распознавания лиц : Это всего лишь частный случай более общего изображения .
поиск проблема: найти ближайшее изображение к заданному изображению запроса
в базе изображений. Классное упражнение 17: Войдите в каталог eigenImageSearchDemo и
изучите примеры изображений в trainingImages, а затем
изображения запроса в queryImages. Какие образы наиболее близки
к изображениям запроса? Классное упражнение 18: Запустите ImageSearchDemo. Рассмотрим граф гиперссылок: Классное упражнение 19: Предположим, что важность веб-страницы определяется как количество
входящие ребра в графе гиперссылок. Классное упражнение 20: В директорию pageRankDemo скопируйте
файл network1.txt в network.txt. Классное упражнение 21: Скопируйте файл network2.txt в network.txt. Классное упражнение 22: Изучите код. Где в коде появляется
линейная алгебра в действии? Следующим шагом в поиске, помимо простого сопоставления ключевых слов, является
чтобы найти релевантный текст, который соответствует интересующей теме Классное упражнение 23: Приведите пример двух фрагментов текста с одинаковыми
тему, но где простое соответствие ключевому слову может не сработать
идентифицировать их как похожие. Классное упражнение 24: Изучите файлы
в wikinews/trainingТекст в
в
скрытый каталог SADemo
и группа
их в темы. Создайте вручную таблицу 7 x 7 и в
ячейка таблицы (i,j), запишите то, что, по вашему мнению, является корреляцией
(число от -1 до 1) в теме между текстом i и текстом j. Классное упражнение 25: Запустите демонстрацию LSA и сравните свои корреляции с
корреляции «до» и «после», обнаруженные демонстрацией.
Что такое «стоп-слова» и почему мы их удаляем?
Прочтите код, чтобы увидеть, где используется линейная алгебра. Цель механизма рекомендаций фильмов – изучить
пользовательские рейтинги фильмов и давать рекомендации, которые
вместить индивидуальных предпочтения согласно рейтингам. Например: Здесь: Обработка сигналов — инженерная дисциплина, посвященная
для обнаружения и обработки электрических сигналов всех видов,
особенно аудио. Тип обработки звука, с которым мы все знакомы: настройка
бас или высокие частоты. Дискретное преобразование Фурье (ДПФ) является ключевым методом, используемым
во многих приложениях обработки сигналов. И линейная алгебра обеспечивает теоретическую основу для ДПФ. Посмотрим, как уменьшается содержание «высоких частот» (высокая нота)
изменяет звук. Вот почему: На практике многие из вышеперечисленных приложений имеют
большие объемы данных. Рассмотрим этот простой и распространенный пример: Большие примеры: В целом по линейной алгебре есть три направления работы: В двух словах: В линейной алгебре будут представлены две повторяющиеся темы. К концу этого курса вы должны: КМ = квантовая механика КК = квантовые вычисления Изображение: http://science.iit.edu/sites/science/files/elements/am/images/as2014-Header-800w.jpg Нажмите на ссылку ниже, чтобы пройти предварительный тест для модуля 56. Если вы набрали 80% или более баллов по предварительному тесту, вы хорошо знаете основы алгебры и можете перейти к следующему модулю или просмотреть материалы модуля 5. Если вы набрали менее 80 %, проработайте модуль и в конце пройдите тест, чтобы проверить свои знания. Манипуляции с уравнениями основаны на том факте, что если две величины равны, то «выполнение одних и тех же действий с каждой из них» сохранит равенство. Другими словами, если уравнение визуализируется в виде шкалы, всегда должен соблюдаться баланс, чтобы то, что вы делаете с одной стороной знака "=", вы также должны делать с другой стороной! Изображение: http://mathbitsnotebook. Пример Следующая ссылка на страницу Maths is fun Введение в алгебру страница посвящена идее «сохранения баланса» по обе стороны от знака равенства. Неуместное использование знака равенства 1. Это заблуждение часто возникает, когда знак равенства рассматривается только как инструкция «что-то вычислить». Например, рассмотрим пример 8 + 4 = + 5 . Некоторые люди неправильно помещают 12 в ячейку, потому что считают, что им нужно поставить «ответ» на то, что находится слева. Пример. Рассмотрим следующую текстовую задачу «У мальчика пять шариков, а потом друг дал ему еще десять, а потом он потерял два. Сколько сейчас шариков у мальчика?» Некоторые неправильно пишут 5 + 10 = 15 - 2 = 13 Несмотря на то, что окончательный «ответ» правильный, математические рассуждения написаны неверно. Это потому, что равенство не поддерживается. Правильным ответом на задачу может быть: 5 + 10 = 15 Следовательно, у мальчика есть 13 мраморных Заполните следующие уравнения: 8 = 3 + 3 + 5 = 2 + 17 = + 17 + 4 = 5 + 7 9 + 7 = + 9 Нажмите здесь , чтобы проверить свои ответы Прочислительные — это буквы, используемые в алгебре, и они обозначают значение (или неизвестную сумму). Повторяющиеся вхождения одного и того же местоимения в выражении представляют одно и то же значение. Например, в уравнении x + x + x = 12 мы знаем, что x равно 4. Алгебру можно рассматривать как обобщенную арифметику. То есть алгебра позволяет нам делать утверждения об отношениях между числами, которые справедливы для всех чисел, а не только для конкретных чисел, с которыми мы имеем дело в арифметических вычислениях. В алгебре выполняются законы арифметики (коммутативной, ассоциативной и дистрибутивной). Обратите внимание, что символ ≠ означает «не равно» или «не равно». Commutative Property Arithmetic Generalised Meaning 3 + 4 = 4 + 3 a + b = b + a Любые 2 числа можно складывать в любом порядке, это не повлияет на результат. 3 x 4 = 4 x 3 a x b=b x a (т. 3 - 4 ≠ 4 - 3 A - B ≠ B - A 12 12. 12. 12. Ассоциативное свойство Арифметика Обобщение (5 + 6) + 5 + + (6 + 8) (5 + 6) + 8 + (6 + 8). (7 – 3) – 2 ≠ 7 – (3 – 2) a x b=b x a (т. ) x 4 = 5 x (2 x 4) (a x b) x c = a x (b x c) (20 ÷ 5) ÷ 2 ≠ 20 ÷ (5 ÷ 2) (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) Смотрите следующее видео, оно обсуждает коммутативные, ассоциативные и дистрибутивные свойства. Distributive Property Arithmetic Generalised 35 x 6 = (30 x 6) + (5 x 6) Еще один способ сокращения в алгебре — опустить знак «x», чтобы получилось 6 (30 + 5) и так: 6(30 + 5)= (6 х 30) + (6 х 5) а х (б + в) Возможно, вы помните, что это называлось «раскрывающиеся скобки» 48 ÷ 4 = (40 ÷ 4) + (8 ÷ 4) Что эквивалентно: = = Посмотрите следующее видео, в нем объясняется, как объединять одинаковые термины в алгебраических выражениях, работая с некоторыми примерами Пример 1 Рассмотрим уравнение: x + y + z = x + p + z Верно ли это уравнение? Это всегда/никогда/иногда верно? Объясните Решение: Повторяющиеся вхождения одного и того же местоимения представляют одно и то же значение. В случае этого уравнения x в левой части равен x в правой части, а z в левой части уравнения равен z в правой части уравнения. Следовательно, мы можем сделать вывод, что это уравнение может быть верным только тогда, когда y = p. Пример 2 Напишите уравнение для следующей ситуации: На каждого преподавателя приходится 6 студентов. Решение: Пусть количество студентов равно S, а количество профессоров равно P. S = 6 x P Которое мы можем переписать как S = 6 P Пример 3 Используйте свойство распределения, чтобы расширить следующее выражение: (x+y) 2 Мы можем увидеть это визуально, используя модель области ниже ysquared.GIF Как видно из прямоугольника слева, площадь маленького белого квадрата внутри прямоугольника равна x 2 , а площадь каждого из желтых прямоугольников внутри основного прямоугольника равна xy, поэтому они вместе сделать 2xy и тогда площадь большего квадрата внутри основного прямоугольника y 2 . Итак, вместе мы имеем x 2 + 2xy + y 2 Использование сопоставления в качестве сокращения для умножения распространено в алгебре. Например, 6y используется для обозначения 6, умноженного на y. Примеры Упростите следующие выражения без использования символа умножения. Винкулум (горизонтальная дробная черта) действует как набор скобок для выражений, в числителе и знаменателе он равен (6x+4)÷2 В приведенном выше выражении сначала x было умножается на 6, затем к результату добавляется 4, а затем новый результат делится на 2. Эквивалентный способ представления выражения (пожалуйста, обратитесь к Большой Идее для более подробной информации о том, что мы подразумеваем под алгебраическим выражением) : Мы можем объяснить алгебраическое выражение в терминах последовательности действий над неизвестным числом. Например, 3 (x + 4) + 2 можно объяснить как серию действий над x на блок-схеме. Следующее интерактивное задание от Академии Хана может оказаться полезным, редакция 9.0003 1. Напишите эквивалентный способ выражения следующего алгебраического выражения без использования дробной черты (vinculum) 2. Объясните, чем выражение 3x + 2 отличается от выражение 3(х + 2). 3. Упростите выражение2753 При написании алгебраических выражений из слов полезно знать такие термины, как: 3x + 8 х (х - 3) (x не должен быть равен 5. Сопоставьте каждое алгебраическое выражение с соответствующим объяснением. Изображение: http://www.educationaldesigner.org/ed/volume1/issue1/article3/images/figure_3a_large.png Изображение: http://www.educationaldesigner.org/ed/volume1/issue1 /article3/images/figure_3b_large.png Нажмите здесь , чтобы проверить свои ответы Упростите выражение Нажмите здесь , чтобы проверить свой ответ может подумать, что после того, как 2 было сокращено в 6, а 2 (знаменатель) больше не может быть сокращено как множитель 4). www.washoe.k12.nv.us/ecollab/washoemath/dictionary/vmd/images/i/erationsoppositeoperations.gif 4.bp.blogspot.com/-VjfFvPQpAKA/UepNgexVv7I/AAAAAAAAAcY/8KYNSsJJYfY/s1600/Square-Root.jpg Подумайте, как вы используете обратные операции для решения уравнений. Одношаговые уравнения Двухэтапные уравнения Все материалы Академии Хана доступны бесплатно по адресу www.khanacademy.org/ Решите следующие уравнения и запишите все обратные операции, которые вы использовали на каждом шаге для каждого уравнения. . 1. 14x = 98 2. 5y + 10 = 3y 3. 4. При каком значении x следующие выражения не определены: а) б) в) Нажмите здесь , чтобы проверить свои ответы www.ndt-ed.org/EducationResources/Math/mathimages/algeq.jpg x 2 – 81 = 0 x 2 = 81 x= +9 или x = -9 В некоторых ситуациях требуется «найти x» (т. Пример 1 Найдите длину гипотенузы (h) прямоугольного треугольника ниже. Решить Изображение : http://www.cimt.plymouth.ac.uk/projects/mepres/book8/bk8i3/bk8_3i2.htm длина гипотенузы (h). Вы можете вспомнить теорему Пифагора, которая говорит нам: квадрат гипотенузы равен сумме квадратов двух меньших сторон. В данном случае это означает, что h² равно 5² + 12². h²=5² + 12² (вычислите квадраты двух более коротких сторон) Примечание: для нашего ответа нас интересуют только положительные 13 метров. Напомним, что квадратный корень из 169 может быть либо положительным 13, либо отрицательным 13. Мы можем опустить отрицательный ответ, потому что -13 метров не имеет практического смысла. Пример 2 Решите следующее уравнение относительно x. 9x + 3 = 21 9x + 3 – 3 = 21 – 3 ( Примечание: 3 было вычтено из обеих частей уравнения, чтобы сохранить равенство, как обсуждалось в Большой идее 1). 9х = 18 (обе части уравнения были поделены на 9) х = 2 Пример 3 Решите следующее уравнение относительно x. Изображение : http://tkendall.edublogs.org/files/2010/03/Notation2_350.jpg Следующая ссылка на Академию Хана представляет собой интерактивное задание, которое предоставит вам с возможностью построения и решения уравнений. Весь контент Академии Хана доступен бесплатно в www. Существуют и другие ситуации, когда прочислительные используются для описания взаимосвязи между изменяющимися величинами (например, v = s/t, что представляет взаимосвязь между скоростью (v), перемещением (s) и время (t), или y = 3x+2, что описывает линейную функцию, связывающую y и x; каждая из переменных может изменяться, но только способами, ограниченными отношением). В подобных ситуациях мы называем неизвестные переменными, потому что они могут изменяться и действительно изменяются по отношению к другим переменным в отношениях. Эти идеи лежат в основе многих расчетов, которые выполняются в научных областях, включая науки о здоровье. Формула, используемая для расчета индекса массы тела (ИМТ), показанная ниже, иллюстрирует взаимосвязь между несколькими переменными, индексом массы тела, ростом и весом. То есть по мере увеличения веса ИМТ увеличивается, поэтому ИМТ пропорционален весу. Индекс массы тела = вес/(рост) 2 Существует линейная зависимость между ИМТ и весом (например, половина веса -> половина ИМТ). Существует нелинейная зависимость между ИМТ и ростом (например, рост в два раза -> 4 x ИМТ). ш=ИМТ×ч 2 Пример 1 Давайте еще раз рассмотрим пример 1 из «Большой идеи 4». Был задан вопрос: верно ли следующее соотношение? Это всегда/никогда/иногда верно? Объясните x + y + z = x + p + z Это соотношение верно, когда y = p Теперь мы называем y и p переменными, поскольку они могут изменяться при условии, что значение y равно значению п. В этом случае y и p могут принимать любые значения при условии, что y = p. Таким образом, мы можем сказать, что соотношение истинно тогда и только тогда, когда y = p Пример 2 Рассмотрим соотношение y = 2x + 3 Прочислительные в этом соотношении являются переменными , поскольку значение y зависит от значения x определенным образом. Пример 3 Археологи могут оценить рост человека по длине бедренной кости (бедренной кости). Формула для этого: H = 2,3 L + 61,4 Где все измерения даны в сантиметрах, где H представляет рост (человека), а L представляет длину (бедренной кости). Эта формула предполагает, что рост человека равен 2,3 длины его бедренной кости плюс 61,4. Допустим, археолог нашел бедренную кость человека, длина кости 45см. Как мы думаем, какого роста должен был быть этот человек? Решение: Отношение между ростом и длиной бедренной кости равно H = 2,3 L + 61,4 мы знаем, что длина бедренной кости 45см Таким образом, археолог предсказывает, что рост человека был около 165 см. Обратите внимание, что H и L являются переменными, поскольку значение H зависит от значения L. Пример 4 Предположим, что археолог нашел другое бедро человека длиной 52 см. Как мы думаем, какого роста должен был быть этот человек? Н = 2,3 л + 61,4 Таким образом, археолог предсказывает, что рост человека должен был быть 181 см. Нажмите здесь , чтобы проверить свои ответы Не помогает и то, что многие ресурсы, учебники и пояснения склонны использовать термин «переменная» для описания местоимений даже в ситуациях, когда местоимение представляет конкретное неизвестное число. Нажмите на ссылку ниже, чтобы пройти онлайн-тест для самооценки. В викторине 10 вопросов по математике, и они касаются информации в этом модуле. Чтобы пройти этот тест, вам нужно получить оценку 80%. В конце викторины будет предоставлена обратная связь как для правильных, так и для неправильных ответов. Если вы отвечаете на вопросы неправильно, настоятельно рекомендуется просмотреть разделы модулей, чтобы просмотреть эти темы. При необходимости вы сможете пройти тест повторно. Обязательно введите свое имя и адрес электронной почты в тесте, чтобы ваши результаты могли быть отправлены вам по почте для ваших записей. Возможно, вам придется показать свои результаты в вашем университете. Какой у вас угол?, Целые числа и порядок операций, Введение в алгебру и Word Комбинированные модули: 8/1/–8/4 98 уроков 131,00 $ Финальный тест «Какой у тебя угол» Ответы на финальный тест What’s Your An Angle Этот модуль посвящен геометрии. Есть 27 уроков на DVD и 2 дополнительных Начнем с меры углов и видов углов. Мы также рассмотрим уникальные символы, используемые в геометрии. Охватываются альтернативные внутренние, альтернативные внешние, соответствующие, вертикальные, дополнительные и дополнительные углы. Используя их, мы научимся вычислять углы, образованные параллельными прямыми, пересекаемыми секущей. Мы также научимся вычислять сумму углов различных многоугольников. Преподается косвенное измерение с использованием соответствующих углов и сторон. Мы изучаем теорему Пифагора и то, как с ее помощью решать задачи, в том числе о том, как раскладывать лестницы и стропила для строительства домов. Мы также рассматриваем распределение сил в сегменте по механическому преимуществу с использованием подъемников, лебедок, наклонных плоскостей, цепных талей и резьбовых стержней. Этот модуль включает: Целые числа и порядок операций Окончательный тест Целые числа и порядок операций Ответы на финальный тест Это второй модуль из серии «Введение в алгебру». Это наш первый модуль по алгебре. В этом модуле из 15 DVD-уроков мы расскажем о значении положительных и отрицательных чисел и их Мы покрываем противоположности и инверсии. Мы выполняем все четыре операции с положительными и отрицательными числами, а также правила и их обоснование. Обрабатываются как положительные, так и отрицательные показатели. Абсолютное значение, скобки, скобки и фигурные скобки покрыты. Мы также рассмотрим сложение, вычитание, умножение и деление экспоненциальных чисел. Этот модуль включает: 22,00 $ Введение в итоговый тест по алгебре Введение в итоговый тест по алгебре Ответы Это третий модуль из серии «Введение в алгебру». Мы рассмотрим свойства и обоснование линейных уравнений в 23 уроках на DVD. 34,00 $ Словесные задачи. Финальный тест Задания на слова. Этот модуль является последним в серии «Введение в алгебру» и содержит 27 уроков на DVD и 4 дополнительных урока (без видео). Он следует за «Целыми числами и порядком операций» и «Введением в алгебру» и стоит перед «Алгеброй А». В этом модуле мы уделяем много времени разработке обоснования для работы с текстовыми задачами. Прежде чем учащиеся смогут успешно решать текстовые задачи, необходимо разработать логику и процедуру. Как только стратегия Этот модуль включает: Функции линейной алгебры NumPy полагаются на BLAS и LAPACK для обеспечения эффективного
низкоуровневые реализации стандартных алгоритмов линейной алгебры. Те
библиотеки могут быть предоставлены самим NumPy с использованием C-версий подмножества их
эталонные реализации, но, по возможности, высокооптимизированные библиотеки,
использовать специализированные функциональные возможности процессора. Примеры
таких библиотек являются OpenBLAS, MKL (TM) и ATLAS. Потому что эти библиотеки
являются многопоточными и зависят от процессора, переменных среды и внешних
пакеты, такие как threadpoolctl, могут быть необходимы для управления количеством потоков
или указать архитектуру процессора. Библиотека SciPy также содержит подмодуль Примечание Термин матрица , используемый на этой странице, указывает на 2d Представленный в NumPy 1.10.0 оператор Скалярное произведение двух массивов. Вычисление скалярного произведения двух или более массивов в одном вызове функции с автоматическим выбором самого быстрого порядка вычисления. Возвращает скалярное произведение двух векторов. Внутреннее произведение двух массивов. Вычисление внешнего произведения двух векторов. Матричное произведение двух массивов. Вычисление тензорного скалярного произведения вдоль заданных осей. Оценивает соглашение Эйнштейна о суммировании операндов. Оценивает порядок сокращения с наименьшей стоимостью для выражения einsum с учетом создания промежуточных массивов. Возведение квадратной матрицы в (целую) степень n . Произведение Кронекера двух массивов. Распад Холецкого. Вычисление qr-факторизации матрицы. Разложение по сингулярным значениям. Вычислить собственные значения и правые собственные векторы квадратного массива. Возвращает собственные значения и собственные векторы комплексной эрмитовой (сопряженной симметричной) или вещественной симметричной матрицы. Вычисление собственных значений общей матрицы. Вычисление собственных значений комплексной эрмитовой или вещественной симметричной матрицы. Матричная или векторная норма. Вычислить число обусловленности матрицы. Вычислить определитель массива. Вернуть ранг матрицы массива с помощью метода SVD Вычислить знак и (натуральный) логарифм определителя массива. Возвращает сумму по диагоналям массива. Решите линейное матричное уравнение или систему линейных скалярных уравнений. Решите тензорное уравнение Возвращает решение линейного матричного уравнения методом наименьших квадратов. Вычисление (мультипликативной) обратной матрицы. Вычисление псевдообратной матрицы Мура-Пенроуза. Вычисление «обратного» N-мерного массива. Общий объект, производный от исключения Python, вызванный функциями linalg. Новое в версии 1.8.0. Некоторые из перечисленных выше подпрограмм линейной алгебры могут
вычислять результаты сразу для нескольких матриц, если они сложены в
тот же массив. Это указывается в документации через входной параметр
такие спецификации, как
9707 Тригонометрические и угловые функции
Нахождение синуса, косинуса и тангенса
 Значение, переданное в эту функцию, должно быть в радианах .
Значение, переданное в эту функцию, должно быть в радианах . Python3
import math a = math.pi / 6 print ( "Значение синуса пи/6 равно:" , конец = "") Печать (математика. " , конец = " ") Печать (Math.cos (a)) . : " , конец = "") print (math. tan(a))
tan(a)) Значение синуса пи/6: 9999999
Значение косинуса пи/6: 0,8660254037844387
Значение тангенса пи/6 равно: 0,57735026
257 Преобразование значений из градусов в радианы и наоборот
Python3
import math a = math.pi / 6 b = 30 print ( "Преобразованное значение из радианов в градусы:" , конец = ") Печать (Math. Degrees (A))
Degrees (A)) . , end = "") print (math.radians(b)) The converted value from radians to degrees is : 29.999999999999996
Преобразованное значение из градусов в радианы: 0,5235987755982988
Специальные функции
Поиск значения гаммы

Python3
import math gamma_var = 6 print ( "The gamma value of данный аргумент: " + Str (Math.gamma (Gamma_VAR))
Python3
импорт математика print (math.  isinf(math.pi))
isinf(math.pi)) print (math.isinf(math.e)) print (math.isinf( float ( 'inf' ))) Ложь
ЛОЖЬ
True
Python3
import math print (math.isnan(math.pi)) print (math.isnan(math .E) Печать (Math.  isnan (
isnan ( Float ( 'NAN' )) 'NAN' )) 9 'NAN' ))) 'NAN' ))))0373 Ложь
ЛОЖЬ
True Наименование функции Описание SIGLEST SIGLAST SIGLAST SIGHLEST. копизнак(х, у) Возвращает число со значением 'x', но со знаком 'y' fabs(x) Возвращает абсолютное значение числа числа floor(x) Возвращает наибольшее целое значение, меньшее числа gcd(x, y) Вычислить наибольший общий делитель двух чисел у) Возвращает остаток от деления x на y frexp(x) Возвращает мантиссу и показатель степени x в виде пары (m, e) -point значение суммы элементов в итерируемом isfinite(x) Проверить, является ли значение ни бесконечным, ни Nan isinf(x) Проверить, является ли значение бесконечным или нет isnan(x) Возвращает true, если число равно «nan», иначе возвращает false ldexp(x, i) Возвращает x * (2**i) modf(x) Возвращает дробную и целую части x trunc(x) Возвращает усеченное целое значение x exp(x) Возвращает значение e в степени x(e** x) expm1(x) Возвращает значение e, возведенное в степень a (x-1) log(x[ b]) Возвращает логарифмическое значение a по основанию b log1p(x) Возвращает натуральное логарифмическое значение 1+x log 93(x3) Вычисляет значение log a по основанию 2 log10(x) Вычисляет значение log a по основанию 10 pow(x, y) Вычисляет значение x х**у) sqrt(x) Возвращает квадратный корень числа acos(x) Возвращает арккосинус значения, переданного в качестве аргумента asin(x) Возвращает арксинус значения, переданного в качестве аргумента atan(x) Возвращает арктангенс значения, переданного в качестве аргумента.  как аргумент
как аргумент hypot(x, y) Returns the hypotenuse of the values passed in arguments sin(x) Returns the sine of value passed as argument tan(x) Returns тангенс значения, переданного в качестве аргумента градусов(х) Преобразование значения аргумента из радиан в градусы радиан(х) Преобразование значения аргумента из градусов в радианы ACOSH (x) Возвращает обратный гиперболический косинус значения, переданный как аргумент ASINH (x) Возвращает обратную гиперболическую синус. cosh(x) Возвращает гиперболический косинус значения, переданного в качестве аргумента0365 TANH (x) Возвращает гиперболическую тангенс значения, передаваемая как аргумент ERF (x) Возвращает функцию ошибки по адресу x Function Function x . 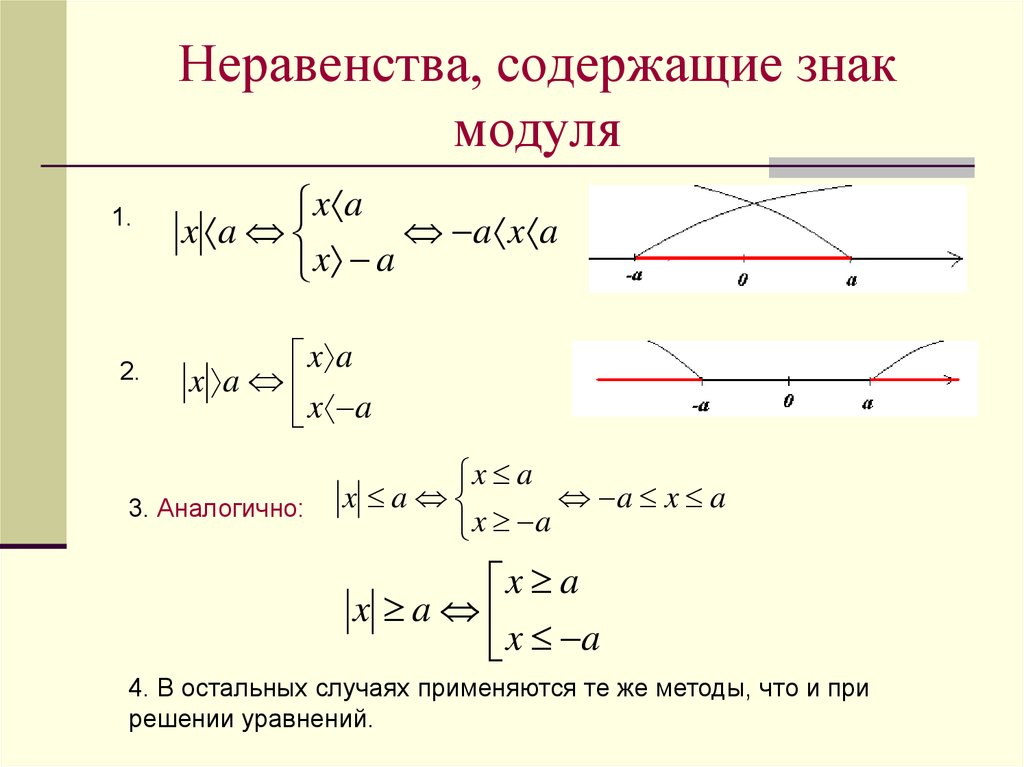 at x
at x gamma(x) Возвращает гамма-функцию аргумента lgamma(x) Возвращает натуральный логарифм абсолютного значения гамма-функции Линейная алгебра
Цели модуля
1,0
Демонстрации приложений
1.1
Приложение №1: самое старое приложение
 Описывать
ваш "алгоритм" на простом английском языке. Затем проверьте свое решение:
Описывать
ваш "алгоритм" на простом английском языке. Затем проверьте свое решение:
Изучите файл Problem1.txt и объясните, как данные
соответствует вышеуказанной проблеме. Что Вы
сделать вывод? Проверьте с помощью Problem3.txt.
Что Вы
сделать вывод? Проверьте с помощью Problem3.txt.
Любые другие? 1,2
Приложение №2: открытие Гаусса

Примечание: исходная (истинная) кривая выделена красным цветом, тогда как
подогнанная кривая - синяя. В этот момент возникает несколько вопросов:
В этот момент возникает несколько вопросов: 1,3
Приложение № 3: дилемма автомобильного дизайнера
 Нарисуйте интересную кривую с четырьмя
или несколько контрольных точек. Какие требования к хранению
такая кривая с использованием традиционного (типа А) подхода? Какие
требования к хранилищу с использованием подхода Безье?
Прочтите код. Каковы входные данные для линейной алгебры?
Нарисуйте интересную кривую с четырьмя
или несколько контрольных точек. Какие требования к хранению
такая кривая с использованием традиционного (типа А) подхода? Какие
требования к хранилищу с использованием подхода Безье?
Прочтите код. Каковы входные данные для линейной алгебры?
Вопросы на данный момент: 1,4
Приложение № 4: 3D в 2D
 Что делает это проблемой
для представления трехмерного объекта.
Что делает это проблемой
для представления трехмерного объекта.
1,5
Приложение № 5: меньше значит больше

1,6
Приложение №6: кто этот человек?
 Сравните изображения, найденные собственным алгоритмом, с изображениями
вы нашли ранее. Теперь изучите изображения в eigenImages.
каталог. Что ты заметил?
Изучите код. Как преобразуется изображение запроса перед предоставлением
это как ввод в линейную алгебру?
Сравните изображения, найденные собственным алгоритмом, с изображениями
вы нашли ранее. Теперь изучите изображения в eigenImages.
каталог. Что ты заметил?
Изучите код. Как преобразуется изображение запроса перед предоставлением
это как ввод в линейную алгебру? 1,7
Приложение №7: генезис поисковой системы
Теперь рассмотрим проблему важности страниц :
Общий принцип: веб-страница, на которую ссылаются другие веб-страницы
должно быть важно . Опишите некоторые
преимущества и недостатки этого подхода.
Опишите некоторые
преимущества и недостатки этого подхода.
⇒ вероятность того, что серфер посетит узел Какой узел имеет наибольшую вероятность посещения?
Какой узел имеет наибольшую вероятность посещения? 1,8
Приложение №8: актуален ли этот текст?
⇒ веб-страницы, текст которых соответствует теме текста поиска.
1,9
Приложение №9: если вам понравился этот фильм, попробуйте этот

Классное упражнение 26: В CollabFilteringDemo просмотрите файл ratings.txt.
с 9пользователей и 6 фильмов.
Классное упражнение 27: Запустите CollabFilteringDemo и проверьте предсказанные рейтинги. Прочтите код. Что такое вход и выход, когда линейная алгебра используется для
прогнозировать рейтинги?
Прочтите код. Что такое вход и выход, когда линейная алгебра используется для
прогнозировать рейтинги? 1.10
Приложение № 10: больше басов, меньше высоких частот
1.11
Зачем изучать линейную алгебру?
Классное упражнение 29: Воспользуйтесь поиском, чтобы узнать, сколько PDF-документов содержат слово «матрица».
⇒
просто предполагается, что вы знаете обозначения и значения.
⇒
Большинство (но не все) результатов приводят к полезному алгоритму
⇒
Математика средней школы
⇒
написание кода, который «делает линейную алгебру», — это интересный способ научиться Сколько из них научных публикаций?
Сколько из них научных публикаций? 1.11
Размеры проблем
\(\rhd\)
Вот данные
1.12
Ландшафт линейной алгебры
⇒
Этот курс.
⇒
Даже кто-то вроде фон Неймана признал, что ему бросили вызов. 1.
 13
Архитектура линейной алгебры
13
Архитектура линейной алгебры
Удивительно, что такая простая операция имеет так много
приложения и богатая теория.
Второй: линейных преобразования :
⇒ Это линейная комбинация .
Идея линейного преобразования окажется важной
абстракция для теории линейной алгебры.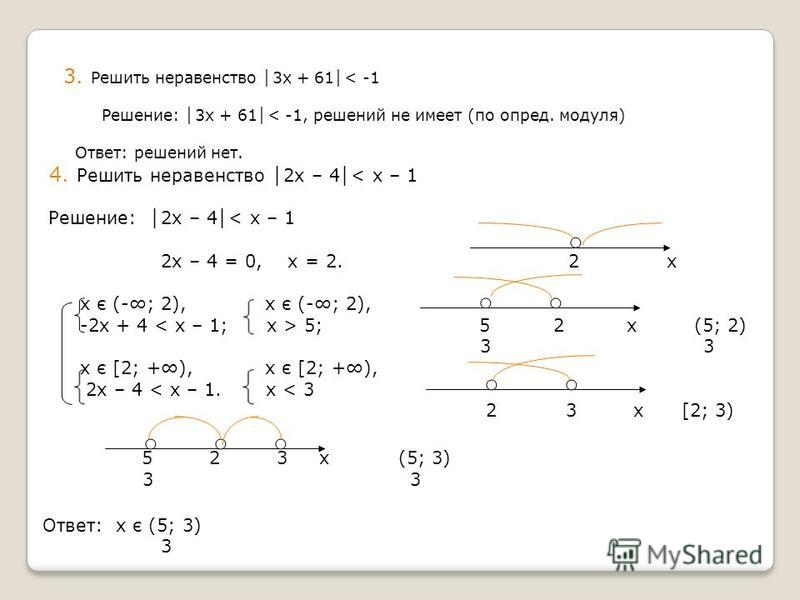 (Хотя для практических приложений нам не понадобится использовать эту идею.)
(Хотя для практических приложений нам не понадобится использовать эту идею.) 1.14
Цели этого курса
⇒ основные понятия, стандартные обозначения
⇒ оставшись один на необитаемом острове, вы сможете восстановить
теория
⇒ С красотой линейной алгебры, то есть. 1,15
Конечная отдача: QM и QC,
два убийственных приложения линейной алгебры


Модуль 5: Алгебра — математические пути
Модуль 5: Алгебра Алгебра используется во многих расчетах и математическом моделировании, связанных с науками о здоровье. От простых расчетов, включающих нахождение неизвестной величины с помощью пропорциональных рассуждений, до более сложной системы уравнений для моделирования контекста реального мира, лежащие в основе алгебраические концепции проистекают всего из нескольких больших идей.
Предварительный тест по алгебре
Предварительный тест для модуля 5: Алгебра
 Предварительный тест необязателен, но мы рекомендуем пройти его, чтобы проверить свои знания по алгебре. Всего 5 вопросов, и на их выполнение уйдет около 10 минут.
Предварительный тест необязателен, но мы рекомендуем пройти его, чтобы проверить свои знания по алгебре. Всего 5 вопросов, и на их выполнение уйдет около 10 минут. Модуль 5: Алгебра
Знак равенства указывает, что количества или выражения по обе стороны от знака равенства эквивалентны.
Манипуляции с уравнениями
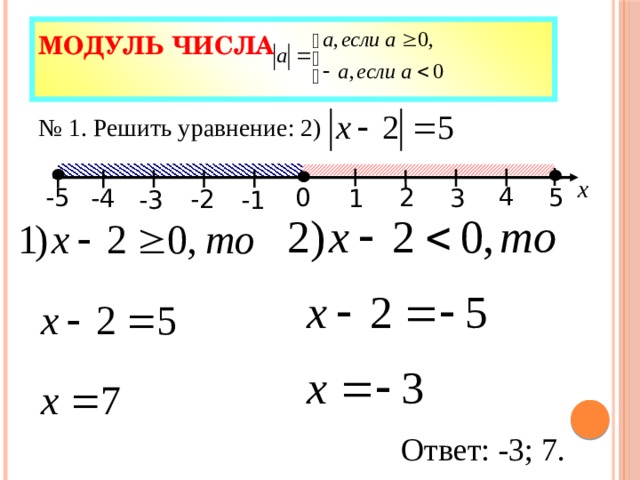 com/Algebra1/LinearEquations/scales.jpg
com/Algebra1/LinearEquations/scales.jpg
8 + 4 = 7 + 5
8 + 4 – 4 = 7 + 5 – 4 (здесь мы вычитаем 4 из обеих частей уравнения)
8 = 7 + 1
( Примечание: в первой строке сумма левой и правой частей уравнения равна 12, а в третьей строке сумма двух сторон равна 8. Важно то, что равенство сохраняется всегда). Распространенные заблуждения
 В то время как правильным ответом было бы поместить 7 в квадрат так, чтобы сохранялось равенство между левой и правой частями уравнения.
В то время как правильным ответом было бы поместить 7 в квадрат так, чтобы сохранялось равенство между левой и правой частями уравнения.
2. Аналогичное неуместное использование знака равенства происходит, когда вычисления завершаются как вычисления, выполняемые на ходу.
15 - 2 = 13 Вопросы практических практических средств
Пронумералы обозначают значение (неизвестное количество), и к ним применяются числовые свойства.

Прочислительные
Commutative, Associative and Distributive Properties

9296 12 9296 12 9296 12 .  (b + c)
(b + c)
Let us look как это работает:
6 x (30 + 5) вы видите, что мы разделили 35 на 30 + 5.
= а (б + в)
= (а х б) + (а х с)
= ab + ac
Давайте посмотрим, как это работает:
Мы перепишем 48 как (40 + 8), так что теперь мы можем записать:
(40 + 8) ÷ 4
Мы можем переписать это как:
=( 40 ÷ 4) + (8 ÷ 4)
= 10 + 2
= 12
Нет необходимости включать все эти шаги, они приведены здесь, чтобы показать вам, как это работает.
(а + б) ÷ в (5 x 2) x 4 = 5 x (2 x 4) (a x b) x c = a x (b x c) (20 ÷ 2 ÷ 5) (20 ÷ 2 ÷ 5) (5 ÷ 2) (a ÷ b) ÷ c ≠ a ÷ (b ÷ c) Примеры
= (х + у) (х + у)
= х 2 + ху + ху + у 2
= x 2 + 2xy + y 2
Мы можем видеть это визуально, используя модель области ниже.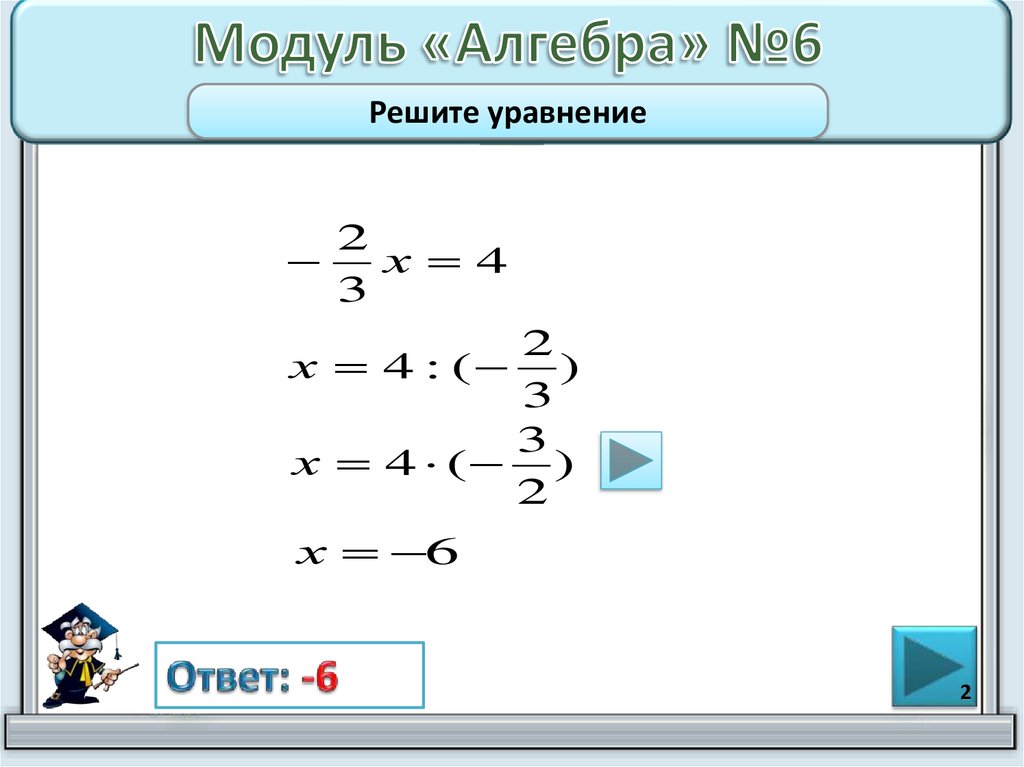 Общее количество студентов равно шестикратному количеству профессоров. Итак, у нас есть уравнение:
Общее количество студентов равно шестикратному количеству профессоров. Итак, у нас есть уравнение: Распространенные заблуждения
 Это приводит к классической неправильной интерпретации, когда отношение «на каждого профессора приходится 6 студентов» представляется как 6S = P, что на самом деле является неправильной формулировкой, если S представляет количество студентов, а P количество профессоров.
Это приводит к классической неправильной интерпретации, когда отношение «на каждого профессора приходится 6 студентов» представляется как 6S = P, что на самом деле является неправильной формулировкой, если S представляет количество студентов, а P количество профессоров. Существуют соглашения, связанные с порядком записи и вычисления числовых операций.

Сопоставление
Винкулум
 Это выражение можно еще упростить. Один из подходов состоит в том, чтобы признать, что выражение также может быть записано как:
Это выражение можно еще упростить. Один из подходов состоит в том, чтобы признать, что выражение также может быть записано как: Эквивалентные формы выражения
Практическое задание 1
 Почему?)
Почему?) Практическое задание 2
Практическое задание 3
Причина, по которой это неверно, заключается в том, что учащийся разделил только 6x на 2, а не 4 на 2. Помните, что винкулум действует как набор скобок вокруг 6x + 4, и, поскольку деление является распределительным, мы должны разделить как 6x, так и 4 на 2.

Многие операции над действительными числами имеют обратные операции. Операции — это сложение, вычитание, умножение, деление и многие другие.
Обратные операции
 Вы не можете делить на 0 никогда. Деление на 0 не определено (узнайте больше о том, что означает деление на ноль не определено, на сайте Maths is Fun Dividing by Zero)
Вы не можете делить на 0 никогда. Деление на 0 не определено (узнайте больше о том, что означает деление на ноль не определено, на сайте Maths is Fun Dividing by Zero) Одно- и двухшаговые уравнения
9000 . Первая ссылка посвящена уравнениям одного шага, а вторая ссылка касается уравнений двух шагов.
Практическое задание 1
Распространенные заблуждения
 Подумайте об обратных операциях, которые выполняются, чтобы в конечном итоге получить решение, что x = 4,
Подумайте об обратных операциях, которые выполняются, чтобы в конечном итоге получить решение, что x = 4, Часто только одно решение является физически разумным.
Часто только одно решение является физически разумным. Как объяснялось в «Большой идее 2», местоимения обозначают числа. Есть два основных способа, которыми местоимения используются для обозначения чисел в алгебре:
1. Прочислительное может представлять неизвестное число, которое необходимо определить или «решить».
2. В других случаях местоимение может использоваться для представления переменной, то есть числа, которое может принимать ряд значений.
Прочислительное, представляющее неизвестное число
 е. найти конкретное значение x) или какое-либо другое прочислительное, как в следующих примерах:
е. найти конкретное значение x) или какое-либо другое прочислительное, как в следующих примерах:
h²=25 + 144 (сложите квадраты двух более коротких сторон вместе)
h²=169 (квадратный корень с обеих сторон, чтобы найти значение h)
ч=13
Построить и решить уравнения
Построение и решение уравнений
 khanacademy.org/
khanacademy.org/ Прочислительные для представления переменной
 С другой стороны, по мере увеличения роста ИМТ уменьшается, поэтому существует обратно пропорциональная зависимость между ростом и ИМТ.
С другой стороны, по мере увеличения роста ИМТ уменьшается, поэтому существует обратно пропорциональная зависимость между ростом и ИМТ. Например, когда х = 1, у = 5, когда х = 2, у = 7 и так далее. Другими словами, значение y равно удвоенному значению x плюс 3.
Например, когда х = 1, у = 5, когда х = 2, у = 7 и так далее. Другими словами, значение y равно удвоенному значению x плюс 3.
Н = 2,3 х 45 + 61,4
Н = 164,9
Н = 2,3 х 52 + 61,4
Н = 181 Практическое задание 1

Модуль 5: Викторина по алгебре
Модуль 5: Викторина по алгебре
Алгебра 1. Систематическая математика
АЛГЕБРА I - Уровень 8 (больше не доступен)
Представляем комбинированный набор алгебры - (Алгебра I)
Задачи составляют наш объединенный набор 8-го уровня. Хотя это начало нашего материала по алгебре, первый модуль в наборе – отличный практический модуль по геометрии. Остальная часть набора начинается с материала студента по алгебре I. Модули алгебры следует заполнять в том порядке, в котором они перечислены.
Хотя это начало нашего материала по алгебре, первый модуль в наборе – отличный практический модуль по геометрии. Остальная часть набора начинается с материала студента по алгебре I. Модули алгебры следует заполнять в том порядке, в котором они перечислены. Модуль 8/1 — модуль геометрии. 8/2, 8/3 и 8/4 соответствуют алгебре I
Скачать файл 2whatsouranglefinal.pdf
Скачать файл 2answers_whatsouranglefinal.pdf Какой у вас угол 8/1
уроков (без видео). Он охватывает измерение и производство углов.
Он охватывает измерение и производство углов.
1 компакт-диск с данными (печатные материалы)
3 DVD-диска с уроками (27 уроков)
2 дополнительных урока (без видео)
Скачать файл 2integersorderopfinal.  pdf
pdf
Скачать файл 2answers_integersandorderopfinal.pdf Целые числа и порядок операций 8/2
отношениях друг с другом.
1 CD с данными (печатные материалы)
2 DVD с уроками (15 уроков)
Скачать файл 2introалгебраfinal.  pdf
pdf
Скачать файл 2answers_introалгебраfinal.pdf Введение в алгебру 8/3
Учащийся сможет решать все уравнения с одной переменной и применять их для решения формул. Мы учим студента не только тому, как найти числовой ответ, но и метку.
Этот модуль включает:
1 CD с данными (печатные материалы)
3 DVD с уроками (23 урока)
Скачать файл 2wordproblemsfinal.pdf  Ответы на итоговый тест
Ответы на итоговый тест
Скачать файл 2answers_wordproblemsfinal.pdf Проблемы со словами 8/4
выучен, мы решаем ряд сюжетных задач, связанных с различными числами и их отношениями друг к другу, используя возраст, монеты и т. д. простота.
1 компакт-диск с данными (печатные материалы)
3 DVD с уроками (27 уроков)
4 дополнительных урока (без видео)
31 уроков всего Линейная алгебра (numpy.
 linalg) — Руководство NumPy v1.23
linalg) — Руководство NumPy v1.23 linalg , и есть
перекрываются функциональные возможности, предоставляемые подмодулями SciPy и NumPy. SciPy
содержит функции, не найденные в numpy.linalg , такие как функции, связанные с
Разложение LU и разложение Шура, несколько способов вычисления
псевдообратные и трансцендентные матрицы, такие как матричный логарифм. Немного
функции, существующие в обоих, имеют расширенную функциональность в
Немного
функции, существующие в обоих, имеют расширенную функциональность в scipy.linalg .
Например, scipy.linalg.eig может принимать второй аргумент матрицы для решения
обобщенные задачи на собственные значения. Однако некоторые функции в NumPy имеют более
гибкие настройки вещания. Например, numpy.linalg.solve может обрабатывать
«сложенные» массивы, в то время как scipy.linalg.solve принимает только один квадрат
массив в качестве первого аргумента. numpy.array объект и не объект numpy.matrix . Последний уже не
рекомендуется даже для линейной алгебры. Видеть
документация матричного объекта для
Дополнительная информация. Оператор
@ @ предпочтительнее, чем
другие методы при вычислении произведения матриц между двумерными массивами. Функция
Функция numpy.matmul реализует оператор @ . Матричные и векторные произведения
точка (a, b[ out]) linalg.multi_dot (массивы, *[ out]) вдот (а, б, /) внутренний (a, b, /) внешний (a, b[ out]) матмул (x1, x2, /[ out, casting, order, . ..])
..]) тенсордот (а, б[ оси]) einsum (индексы, *operands[ out, dtype, ...]) einsum_path (индексы, *операнды[ оптимизировать]) linalg.matrix_power (a, n) крона (а, б) Разложения
линалг. (а) холецкий
холецкий linalg.qr (a[ режим]) linalg.svd (a[full_matrices,compute_uv, ...]) Собственные значения матрицы
linalg.eig (a) linalg.eigh (a[ UPLO]) linalg.eigvals (a) линалг. (а[ УПЛО]) эйгвальш
эйгвальш Нормы и другие номера
linalg.norm (x[ ord, ось, keepdims]) linalg.cond (x[ p]) linalg.det (a) linalg.matrix_rank (A[ tol, ermitian]) linalg.slogdet (a) трасса (a[ смещение, ось 1, ось 2, dtype, выход])
Решение уравнений и обращение матриц
linalg.solve (a, b) linalg.tensorsolve (a, b[ оси]) a x = b относительно x. linalg.lstsq (а, б[ гконд]) линалг.инв (а) linalg.pinv (a[ rcond, эрмитов]) linalg.tensorinv (а[ инд])
Исключения
linalg.LinAlgError Линейная алгебра сразу на нескольких матрицах
a : (..., M, M) array_like . Это означает, что
если, например, задан входной массив a.shape == (N, M, M) , это
интерпретируется как «стек» из N матриц, каждая из которых имеет размер M на M. Похожий
спецификация применяется к возвращаемым значениям, например определитель
имеет det : (...) и в этом случае вернет массив формы det(a).




 Сформулируйте.
Сформулируйте.







 Используя алгоритм, делаем построения графика функции игрек равен модуль эф от икс.
Используя алгоритм, делаем построения графика функции игрек равен модуль эф от икс.


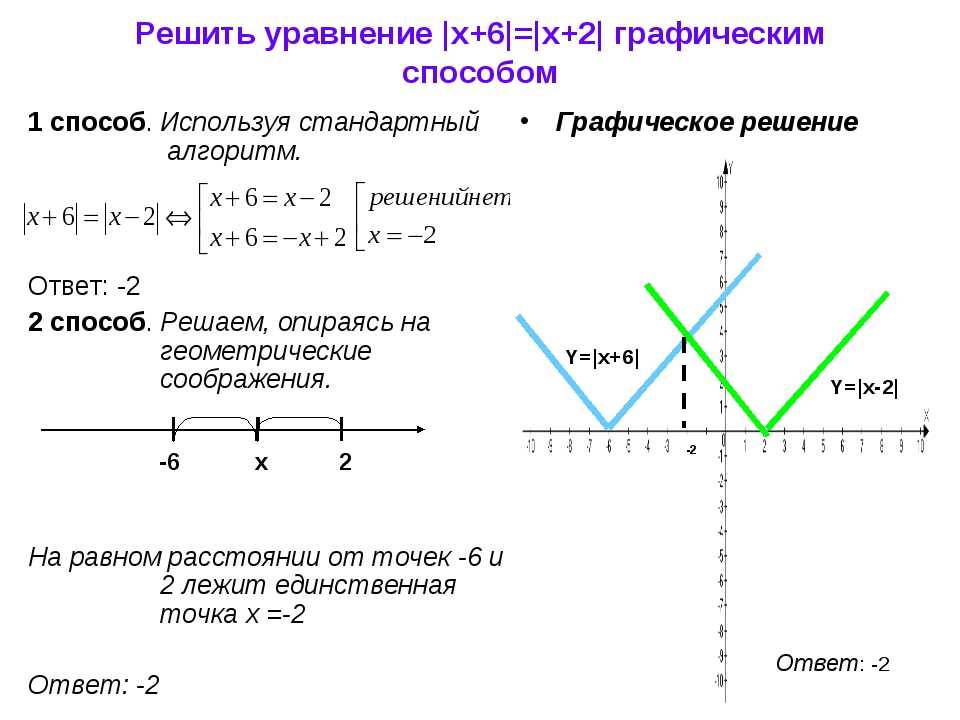



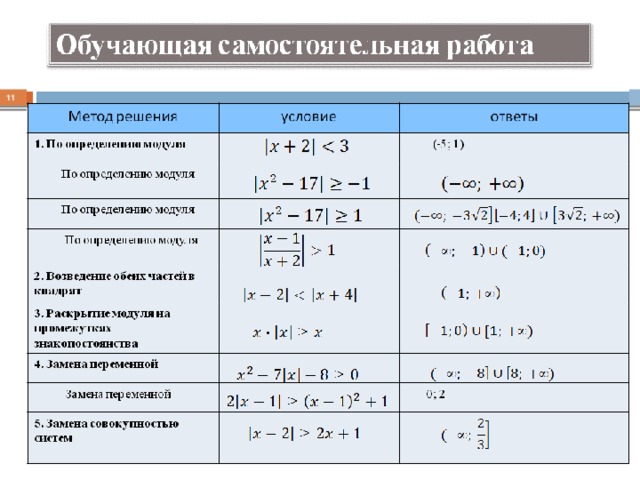


 E)
E)  pi
pi  inf >
inf > 
 9n, где n - степень x, тогда как логарифмические функции считаются обратными экспоненциальным функциям.
9n, где n - степень x, тогда как логарифмические функции считаются обратными экспоненциальным функциям. exp(test_neg_int ))
exp(test_neg_int )) 
 sqrt(
sqrt(