Формулы площади выпуклого четырехугольника — Студопедия.Нет
Стр 1 из 2Следующая ⇒
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
S = | 1 | a · h |
2 |
- Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = | 1 | a · b · sin γ |
2 |
- Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = | a · b · с |
4R |
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
| S = p · r |
- где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,
p = | a + b + c | — полупериметр треугольника. |
2 |
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
S = a2
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
S = | 1 | d2 |
2 |
где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.
Формула площади прямоугольника
Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
- Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sin α
- Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = | 1 | d1d2 sin γ |
2 |
- где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h
- Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S = a2 · sin α
- Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
S = | 1 | d1 · d2 |
2 |
- где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d1, d2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
S = | a + b | √(p-a)(p-b)(p-a-c)(p-a-d) |
|a — b| |
- Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту
S = | 1 | (a + b) · h |
2 |
где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = | a + b + c + d | — полупериметр трапеции. |
2 |
Формулы площади выпуклого четырехугольника
- Формула площади четырехугольника по длине диагоналей и углу между ними Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
S = | 1 | d1 d2 sin α |
2 |
где S — площадь четырехугольника,
d1, d2 — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.
- Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
3.
Дата добавления: 2018-05-12; просмотров: 538;
12Следующая ⇒
Мы поможем в написании ваших работ!
Формулы площади выпуклого четырёхугольника и задачи, связанные с ней
Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»
Индивидуальный проект по теме:
«Формулы площади выпуклого четырёхугольника и задачи, связанные с ней»
Автор работы:
ученица 11 класса А
Казакова Ольга
Научный руководитель:
Козадаев В.С., учитель математики
ТАМБОВ 2017
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 1
ЧТО ТАКОЕ ЧЕТЫРЁХУГОЛЬНИК? 2
ЗАДАЧА №1 3
ЗАДАЧА №2 4
ЗАДАЧА №3 5
ЗАДАЧА №4 6
ЗАДАЧА №5 9
ЗАДАЧА №6 11
ЗАКЛЮЧЕНИЕ 12
СПИСОК ЛИТЕРАТУРЫ 13
ВВЕДЕНИЕ
Геометрия — раздел математики, изучающий формы и размеры предметов, а также взаимное размещение фигур. Можно ли представить себе мир без четырехугольников? В современном мире огромное количество предметов имеют именно эту форму. В архитектуре используются разные геометрические фигуры, но чаще всего используются именно четырёхугольники. В данном проекте я знакомлюсь с формулой площади выпуклого четырёхугольника и с её дальнейшим применением.
Можно ли представить себе мир без четырехугольников? В современном мире огромное количество предметов имеют именно эту форму. В архитектуре используются разные геометрические фигуры, но чаще всего используются именно четырёхугольники. В данном проекте я знакомлюсь с формулой площади выпуклого четырёхугольника и с её дальнейшим применением.
Актуальность проекта заключается в том, что знание данной формулы помогает облегчить процесс решения задач с четырёхугольниками и расширить диапазон способов решения геометрических задач.
Цель: знакомство с формулой для площади выпуклого четырёхугольника по его сторонам и сумме противоположных углов и её применение к решению некоторых задач.
Задачи:
• изучить литературу по данному вопросу;
• вывести формулу площади для выпуклого четырёхугольника;
• рассмотреть дальнейшее применение этой формулы;
• доказать некоторые свойства выпуклого четырёхугольника.
Практическая значимость проекта состоит в возможности использования данных формул и свойств для решения геометрических задач в школьном курсе геометрии и на ЕГЭ.
ЧТО ТАКОЕ ЧЕТЫРЁХУГОЛЬНИК?
Четырёхугольник — это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений.
Основные сведения
1.Многоугольник называют выпуклым, если он лежит по одну сторону от любой прямой, соединяющей его соседние вершины.
2.Выпуклый многоугольник называют вписанным, если все его вершины лежат на одной окружности. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда .
ЗАДАЧА №1
Вывести формулу для площади выпуклого четырёхугольника, если даны его стороны , , , и известна сумма его противоположных углов .
Решение:
Пусть , , и , ,
1)
По теореме косинусов в : .
2)Возведём в квадрат и получим:
Но
Следовательно, (1)
3)
Возведём обе части в квадрат:
(2)
4) Подставим (2) неравенство в (1) и получим:
, через формулу понижения степени, равную получаем, что
Из всего вышесказанного следует, что – полупериметр четырёхугольника, ч.т.д.
ЗАДАЧА №2
Доказать, что их всех четырёхугольников с данными сторонами , , , наибольшую площадь имеет тот, около которого можно описать окружность. Как в этом случае будет выглядеть формула для площади этого четырёхугольника?
Решение:
Если около четырёхугольника можно описать окружность, то
Тогда =
, а это и будет наибольшая площадь.
ЗАДАЧА №3
Из формулы предыдущей задачи получите формулу Герона для треугольника.
Решение:
Так как в треугольнике всего 3 стороны =
Тогда формула площади для треугольника будет равна .
ЗАДАЧА №4
Постройте по четырём сторонам четырёхугольник, около которого можно описать окружность.
Решение:
Пусть имеется 4 стороны четырёхугольника:, , ,
1) Если около четырёхугольника описана окружность, то сумма противоположных углов четырёхугольника равна 180.
2) Введём декартову систему координат:
3) Возьмём две стороныи и проведём их из начала координат, построив произвольный угол :
4) Найдём координаты точек , , :
(0;0;), (, (
5) Найдём угол через скалярное произведение векторов и :
=
Координаты вектора :
Координаты вектора:
Тогда
Найдём длины этих векторов:
,
Тогда
6) Так как сумма противоположных углов в четырёхугольнике, около которого описана окружность, равна 180, тогда найдём угла , противоположному : cos(180 (по формуле приведения).
7) Пусть координаты точки, которые нужно найти, равны .
Найдём также по скалярному произведению, но уже через векторы и :
=
Координаты вектора {;
Координаты вектора {;
Скалярное произведение
Длина вектора
Длина вектора
Тогда ==
Чтобы найти координаты точки , составим систему уравнений:
Решим отдельно 1 и 2 уравнение:
Раскроем скобки, вычтем одно уравнение из другого и получим:
Выразим отсюда и подставим его в 3 уравнение в 1 системе.
Оттуда найдём , а затем , подставив в это предыдущее равенство.
Таким образом, найдя координаты точки , строим эту точку, согласно координатам и достраиваем до полного четырёхугольника.
Получим искомый четырёхугольник. Задача выполнена.
Задача выполнена.
ЗАДАЧА №5
Доказать, что для всякого выпуклого четырёхугольника со сторонами , , , и диагоналями m и n имеет место равенство , где – угол между диагоналями, а , .
Решение:
Пусть – точка пересечения диагоналей четырёхугольника , где , , ,, а .
Найдём и по теореме косинусов.
Вычтем одно равенство из другого:
(1)
Аналогично найдём и и вычтем одно равенство из другого:
(2)
Сложим обе части (1) и (2) равенства:
Возведём обе части в квадрат и получим:
ч.т.д.
ЗАДАЧА №6
Доказать, что для всякого выпуклого четырёхугольника со сторонами ,, , , площадью и диагоналями и имеет место равенство .
Решение:
Площадь выпуклого четырёхугольника равна , где — длины диагоналей четырёхугольника, а – угол между диагоналями.
1) Возведём в квадрат:
Отсюда
2) Возьмём выведенную формулу из предыдущей задачи:
Подставим из 1 пункта :
= , ч.т.д.
ЗАКЛЮЧЕНИЕ
Работая над проектом, я выполнила поставленную перед собой цель, т.е. ознакомилась с формулой для площади выпуклого четырёхугольника по его сторонам и её применением к решению некоторых задач. Я рассмотрела задачи, где нужно было вывести формулы, которые могут помочь при решении олимпиадных задач.
Для достижения этой цели я изучила литературу по данному вопросу и множество задач.
Знания, полученные в ходе выполнения проекта, позволяют разнообразить методы решения геометрических задач. Эти знания могут пригодиться также и в дальнейшем, например, для подготовки к ЕГЭ.
СПИСОК ЛИТЕРАТУРЫ
1. В.В. Прасолов. Задачи по планиметрии.
В.В. Прасолов. Задачи по планиметрии.
2. https://egemaximum.ru/formula-braxmagupty/
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оснащения врачебно-сестринской бригады. Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы. Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 Теорема. Площадь выпуклого четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения его диагоналей. Дано: ABCD – выпуклый четырехугольник. Доказать: Доказательство: I) По 4-му свойству площади: II) III) Что и требовалось доказать. Теорема об отношении площадей треугольников. Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Дано: Доказать: Доказательство:
I) Д.П.: Наложим так, чтобы совпали вершины А и А1, лучи АС и А1С1, лучи АВ и А1В1 ( ). II) Рассмотрим У них общая высота ВН. Тогда по лемме III) Рассмотрим У них общая высота С1Н1. Тогда по лемме IV) Перемножим равенство из пункта II на равенство из пункта III: Сократим, и получим. Что и требовалось доказать. Теорема Пифагора. Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Дано: – прямоугольный треугольник. АС и ВС – катеты. АВ – гипотенуза. АС = b , ВС = а, АВ = с. Доказать: Доказательство: I) Д.П.: Достроим треугольник до квадрата со стороной (а + b). II) По 4-му свойству площади: III) Что и требовалось доказать. Примеры. 1) Дано: а = 3см, b = 4см. Найти: с. Решение:
с = 5см Ответ: с = 5см. 2) Дано: а = 5см, b = 6см. Найти: с. Решение:
Ответ: . 3) Дано: с = 50см, а = 14см. Найти: b . Решение:
b = 48см Ответ: b = 48см. Пифагоровы тройки чисел. 3, 4, 5 – Египетский треугольник.
Теорема, обратная теореме Пифагора. Теорема. Если в треугольнике квадрат большей стороны равен сумме квадратов 2-х других сторон, то этот треугольник прямоугольный. Дано: Доказать: Доказательство: I) Д.П.: Построим прямоугольный в котором В1С1= ВС, А1С1=АС. II) (По построению). По теореме Пифагора А1В12 = В1С12 + А1С12 = ВС2 +АС2 = АВ2(по условию). Тогда А1В12 = АВ2. Отсюда А1В1 = АВ. III) Рассмотрим и . 1) АВ = А1В1(по доказанному во II-м). 2) АС = А1С1(по построению). 3) ВС = В1С1 (по построению). Из условий 1), 2), 3) получаем, что = по 3-м сторонам. В равных треугольниках напротив равных сторон лежат равные углы. Значит, Что и требовалось доказать. Следствие. В : АВ = с, ВС = а, АС = b . АВ = с – большая сторона. 1) Если с2 = а2 + b 2 , то — прямоугольный. 2) Если с2 < а2 + b 2 , то — остроугольный. 3) Если с2 > а2 + b 2 , то — прямоугольный. Площадь равностороннего треугольника. Теорема. Площадь равностороннего треугольника вычисляется по формуле , где а сторона треугольника. Дано: — равносторонний. АВ = а. Доказать: . Доказательство: I) Д.П.: высота ВН. II) III) Рассмотрим — прямоугольный (по построению). АВ = а, ВН = h , АН = (по свойству равнобедренного треугольника). ВН2 = АВ2 – АН2(по теореме Пифагора).
IV) То есть Что и требовалось доказать. Пример. Дано: — равносторонний. АВ = дм. Найти: Решение: Ответ: ⇐ Предыдущая12 Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. |
Формула площади четырехугольника по четырем сторонам — dj-sensor.ru
Содержание
- Через диагонали и угол между ними
- Через стороны и противолежащие углы
- Площадь вписанного четырехугольника в окружность
- Площадь описанного четырехугольника около окружности через радиус
- Площадь четырехугольника по диагоналям и углу между ними
- Площадь четырехугольника через стороны и углы между этими сторонами
- Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
- Площадь четырехугольника в который можно вписать окружность
- Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
- Определения
- Площадь выпуклого четырехугольника
- Площадь четырехугольника по четырем сторонам и двум противолежащим углам
- Площадь четырехугольника по четырем сторонам и двум диагоналям
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Через диагонали и угол между нимиЧетырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углыФормула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружностьФормула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиусФормула для нахождения площади описанного четырехугольника около окружности через радиус:
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
Читайте также: Уравнение движения точки в полярных координатах
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Площадь четырехугольника по диагоналям и углу между ними
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться нашим «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
В статье собраны несколько калькуляторов, вычисляющих площади неправильных четырехугольников.
Читайте также: Что такое диптих в живописи
Есть несколько способов найти площадь неправильного четырехугольника.
- Вы знаете длины диагоналей и размер угла между ними. Тогда площадь четырехугольника можно найти по формуле
Площадь выпуклого четырехугольника
- Вы знаете длины четырех сторон и размеры двух противолежащих углов.
 Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.
Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.
,
где s — полупериметр.
Площадь четырехугольника по четырем сторонам и двум противолежащим углам
- Вы знаете длины четырех сторон и длины диагоналей. Тогда площадь четырехугольника тоже можно найти по формуле Бретшнайдера.
,
где s — полупериметр
Площадь четырехугольника по четырем сторонам и двум диагоналям
- Вы знаете длины четырех сторон и то, что четырехугольник является вписанным в окружность. Тогда вы имеете дело с частным случаем формулы Бретшнайдера (сумма двух противолежащих углов известна и равна 180), известным как формула Брахмагупты.
,
где s — полупериметр
Для вычисления можно использовать калькулятор выше, введя произвольно два угла так, чтобы их сумма составляла 180.
Вывод самих формул Бретшнайдера можно посмотреть здесь.
Ну и напоследок еще раз упомяну, что зная только длины четырех сторон вычислить площадь четырехугольника нельзя, так как нельзя однозначно определить его вид — нужно еще какое-нибудь ограничивающее условие. Так как у нас на сайте довольно часто просили посчитать площадь четырехугольника только по четырем сторонам, то еще есть вот такой вот шуточный калькулятор: Площадь неправильного четырехугольника с заданными сторонами, который бесконечно рассчитывает такие площади.
Так как у нас на сайте довольно часто просили посчитать площадь четырехугольника только по четырем сторонам, то еще есть вот такой вот шуточный калькулятор: Площадь неправильного четырехугольника с заданными сторонами, который бесконечно рассчитывает такие площади.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
решение четырехугольников. Площадь параллелограмма Задачи для самостоятельного решения
Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:
Теорема 3. Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними:
Теорема 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема 6. Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности:
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника:
Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2 .
Статья опубликована при поддержке компании «ДКРОСТ». Горки детские , домики, песочницы и многое
другое — изготовление и продажа детских площадок оптом и в розницу.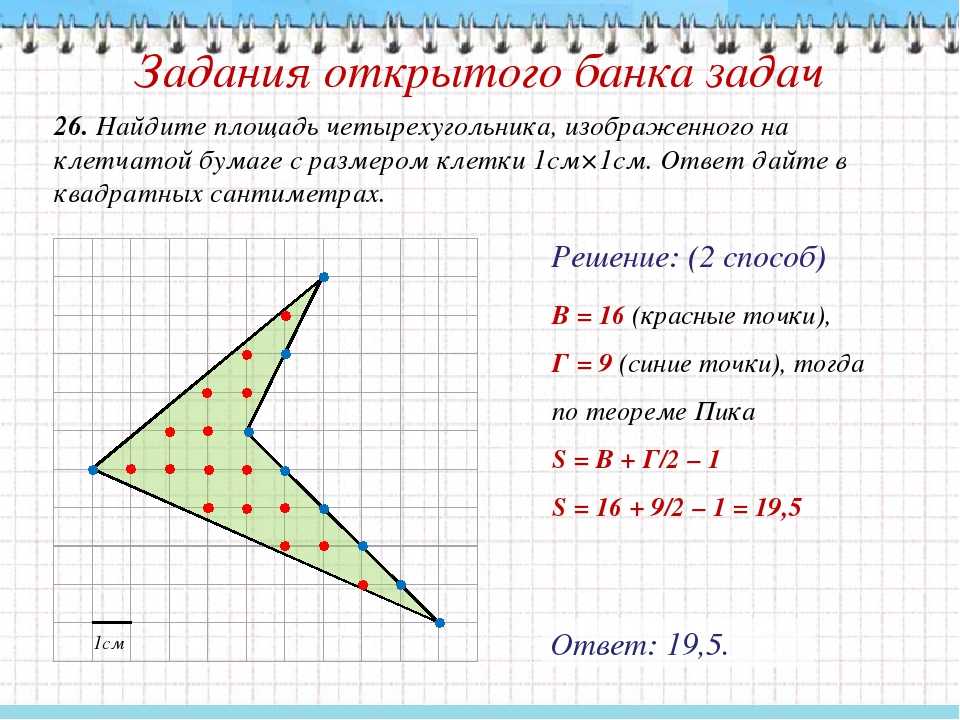 Самые низкие
цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия
качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты
Вы сможете на сайте, который располагается по адресу: http://dkrost.ru/.
Самые низкие
цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия
качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты
Вы сможете на сайте, который располагается по адресу: http://dkrost.ru/.
Доказательства некоторых теорем
Доказательство теоремы 2 . Пусть ABCD — данная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна
А площадь треугольника ACD равна
Так как BP = CQ, то и S∆ABD = S∆ACD . Но площадь треугольника AOB есть разность площадей треугольников ABD и AOD, а площадь треугольника COD — разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.
Доказательство теоремы 4 . Пусть ABCD — параллелограмм, AB = CD = a , AD = BC = b,
AC = d1
, BD = d2
, ∠BAD = α, ∠ADC = 180° – α. Применим к треугольнику ABD теорему косинусов:
Применим к треугольнику ABD теорему косинусов:
Применив теперь теорему косинусов к треугольнику ACD, получим:
Складывая почленно полученные равенства, получаем, что что и требовалось доказать.
Доказательство теоремы 5. Пусть ABCD — произвольный выпуклый четырехугольник, E — точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180° – ϕ. Имеем:
что и требовалось доказать.
Доказательство теоремы 6 . Пусть ABCD — произвольный четырехугольник, описанный около окружности, O — центр этой окружности, OK, OL, OM и ON — перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. Имеем:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7 . Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Так как KL — средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN — параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Аналогично,
Это значит, что
откуда вытекает, что
Доказательство теоремы 8 . Пусть ABCD — произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a , BE = b, CE = c, DE = d. Применим к треугольникам ABE и CDE теорему Пифагора:
AB2
= AE2
+ BE2
= a 2
+ b2
,
CD2
= CE2
+ DE2
= c2
+ d2
,
следовательно,
AB2
+ CD2
= a 2
+ b2
+ c2
+ d2
.
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2
= AE2
+ DE2
= a 2
+ d2
,
BC2
= BE2
+ CE2
= b2
+ c2
,
откуда вытекает, что
AD2
+ BC2
= a 2
+ b2
+ c2
+ d2
.
Значит, AB2
+ CD2
= AD2
+ BC2
, что и требовалось доказать.
Решения задач
Задача 1 . Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.
Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.
Решение . Пусть ABCD — данная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то
Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:
AB + CD = AD + BC,
откуда находим
Значит, площадь трапеции есть
и искомое отношение равно
Ответ :
Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.
Доказательство .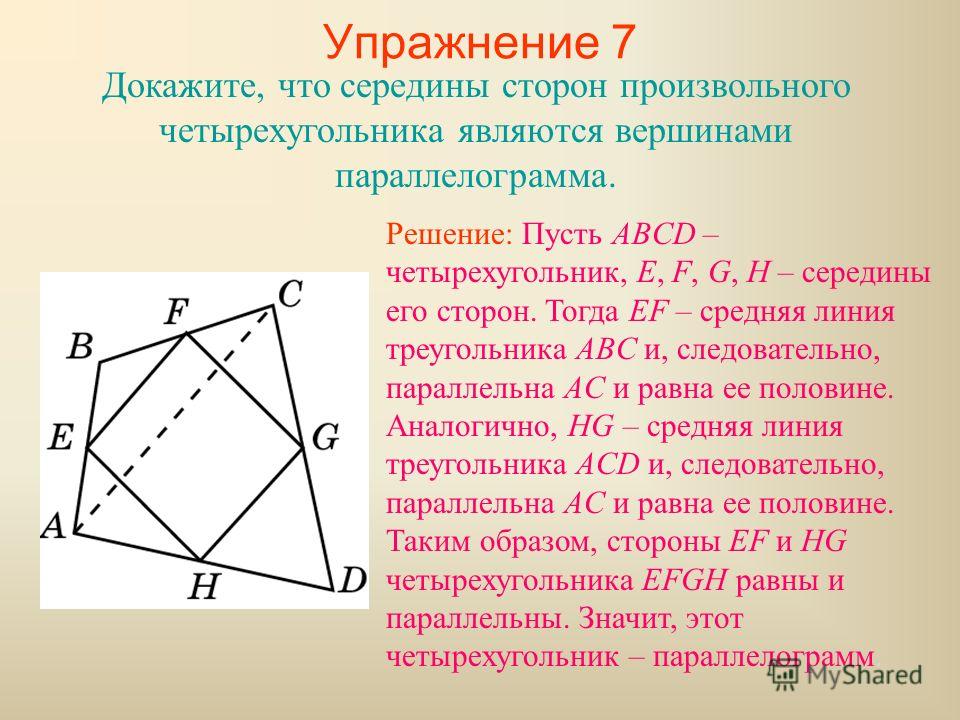 Так как угол A равен 90°,
Так как угол A равен 90°,
а угол C не превосходит 90°, то точки E и F лежат на диагонали AC. Без ограничения общности мы можем считать, что AE
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как
откуда получаем, что что и требовалось доказать.
Задача 3 . Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен α.
Решение . Пусть ABCD — данная равнобочная трапеция с основаниями AD и BC, пусть BH — высота этой трапеции, опущенная из вершины B.
Так как в данную трапецию можно вписать окружность, то
Следовательно,
Из прямоугольного треугольника ABH находим,
Ответ :
Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD — в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
Решение . Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD — равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔
Нам требуется вычислить отношение:
Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O — точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.
Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.
Решение . Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм. В нашем случае EFHG — параллелограмм и O — точка пересечения его диагоналей. Тогда
Применим к треугольнику FOH теорему косинусов:
Так как FH — средняя линия треугольника BCD, то
Аналогично, применив теорему косинусов к треугольнику EFO, получим, что
Ответ :
Задача 6. Боковые стороны трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно Найти основания трапеции.
Решение . Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM.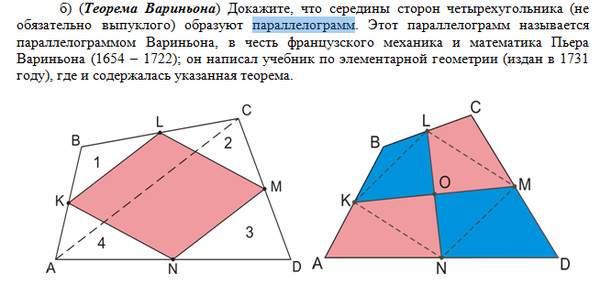 Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем:
Значит, BC = 1 и AD = 7.
Ответ: 1 и 7.
Задача 7 . Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина боковой стороны BC равна b. Найти площадь трапеции.
Решение . Пусть E — точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда
AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана.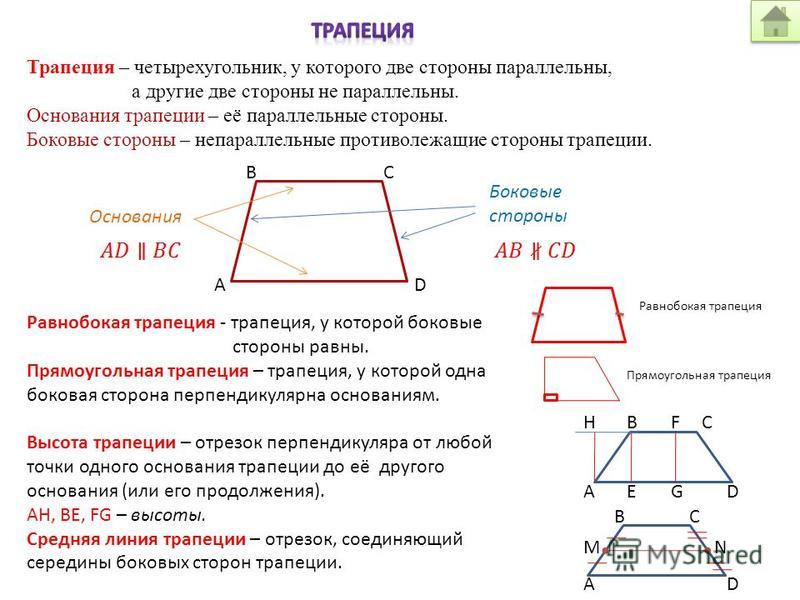 Поэтому AC является и высотой этого треугольника, и значит,
Поэтому AC является и высотой этого треугольника, и значит,
Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то
Ответ :
Задача 8 . Диагонали трапеции ABCD пересекаются в точке E. Найти площадь треугольника BCE, если длины оснований трапеции AB = 30, DC = 24, боковой стороны AD = 3 и угол DAB равен 60°.
Решение . Пусть DH — высота трапеции. Из треугольника ADH находим, что
Так как высота треугольника ABC, опущенная из вершины C, равна высоте DH трапеции, имеем:
Ответ :
Задача 9 . В трапеции средняя линия равна 4, а углы при одном из оснований равны 40° и 50°. Найти основания трапеции, если отрезок, соединяющий середины оснований, равен 1.
Решение . Пусть ABCD — данная трапеция, AB и CD — ее основания (AB
AB + CD = 8. Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°,
следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
EN = x + 1. Из подобия треугольников AEM и DEN имеем:
Это означает, что AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 . Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2. Найти периметр четырехугольника ABCD.
Решение . Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO — прямоугольные. Применив к этим треугольникам теорему Пифагора, получим, что
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности.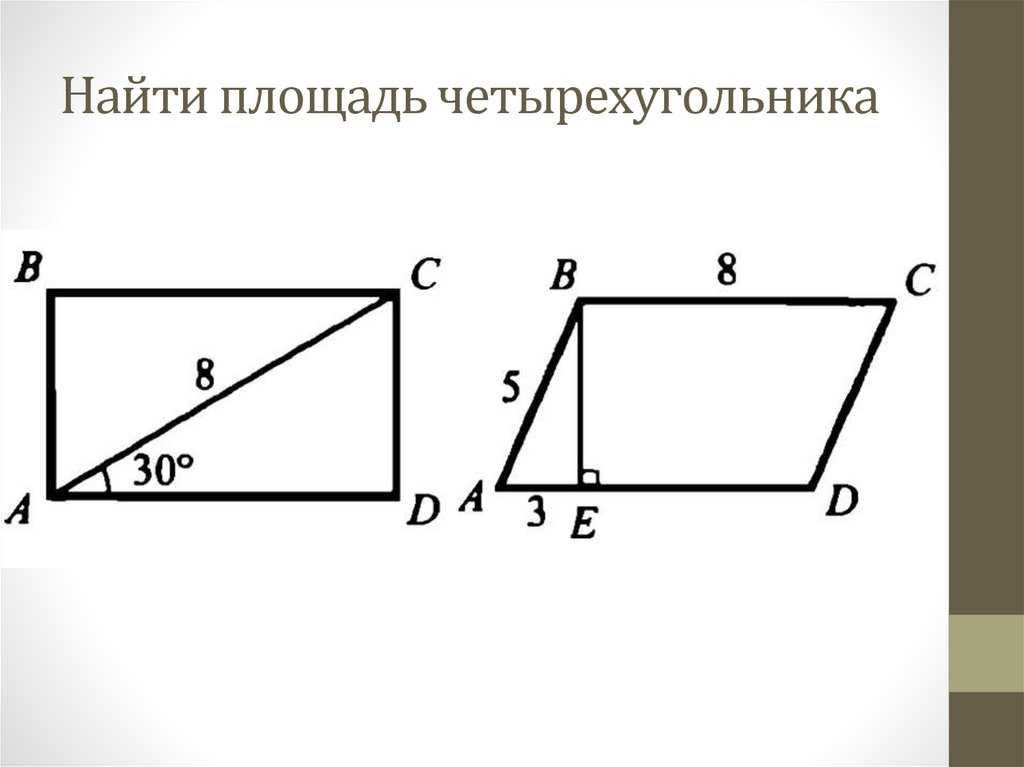 Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1. Около окружности радиуса r описана равнобочная трапеция ABCD. Пусть E и K — точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции равен 60°. Докажите, что EK параллелен AB, и найдите площадь трапеции ABEK.
С-2. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2.
Найдите площадь трапеции.
С-3 . Можно ли вокруг четырехугольника ABCD описать окружность, если ∠ADC = 30°, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB — основание) величины углов DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O так, что OB = OD = 13. Найдите расстояние от точки O до наиболее удаленной от нее вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Величина угла ABC равна 120°. Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
С-8. Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на прямую AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD. Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен угол BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна
С-10. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90°, и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Найдите длину стороны BC.
С-11. Пусть M — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны между собой. Найдите угол CMD, если известно, что DM = MC,
а ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74°, ∠D = 120°. Найдите угол между биссектрисами углов B и C.
С-13. В четырехугольник ABCD можно вписать окружность. Пусть K — точка пересечения его диагоналей. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.
С-14. В трапеции, описанной около окружности, известно, что BC AD, AB = CD, ∠BAD =
= 45°. Найдите AB, если площадь трапеции ABCD равна 10.
С-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60°. Найдите площадь параллелограмма.
С-17 . В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность. Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
С-18. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. При этом ∠BAC =
= ∠BDC, а площадь круга, описанного около треугольника BDC, равна
а) Найдите радиус окружности, описанной около треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90°, найдите площадь четырехугольника ABCD.
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.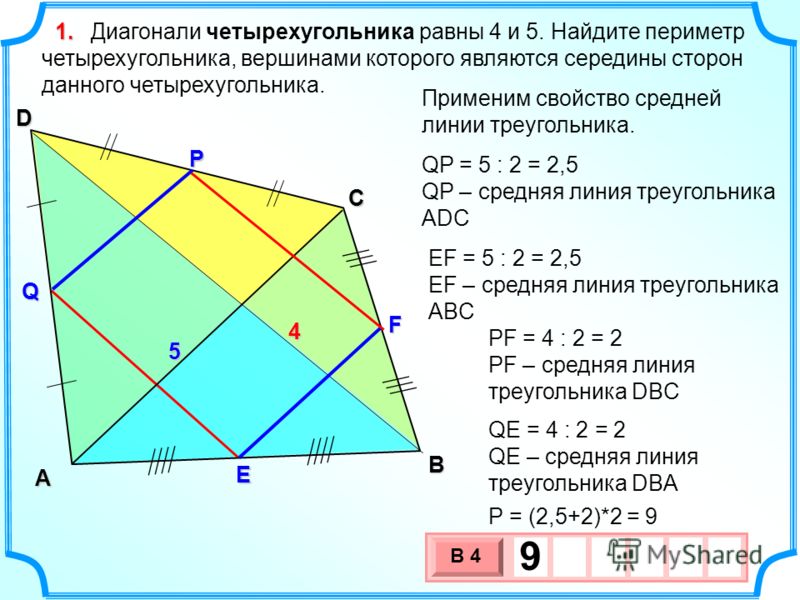
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.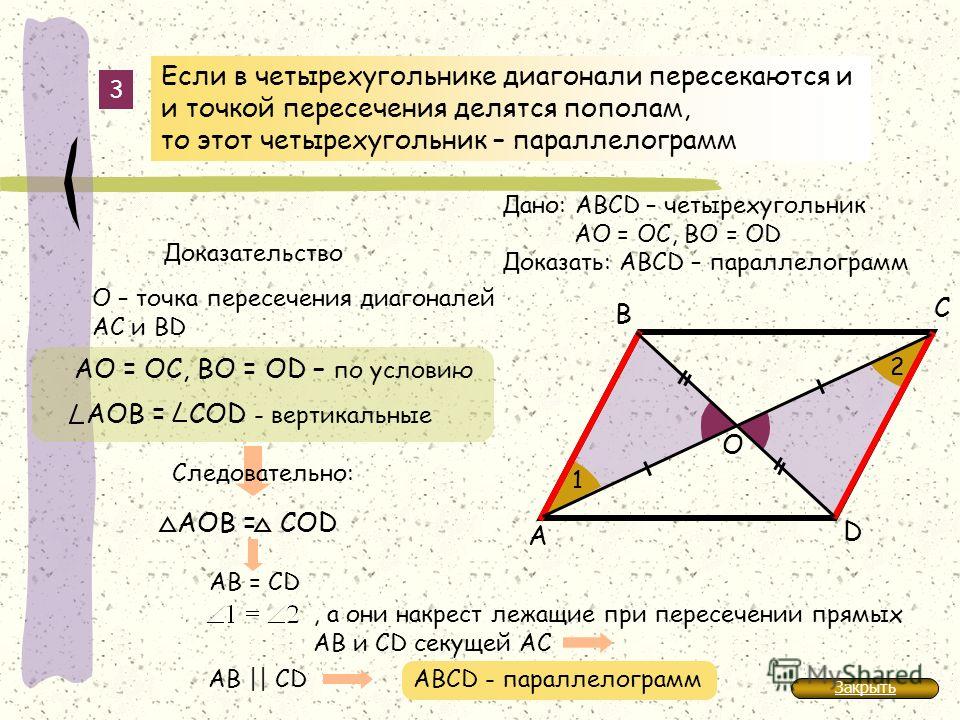
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD.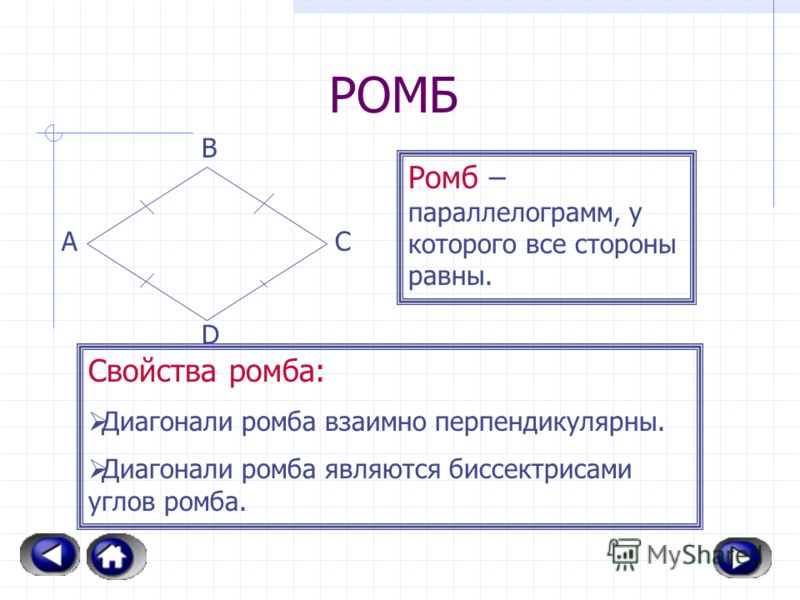 ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.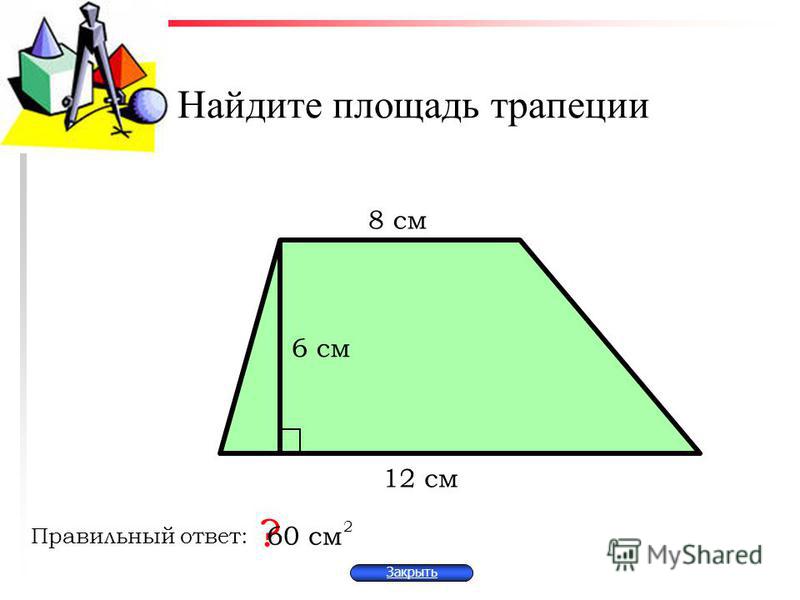
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.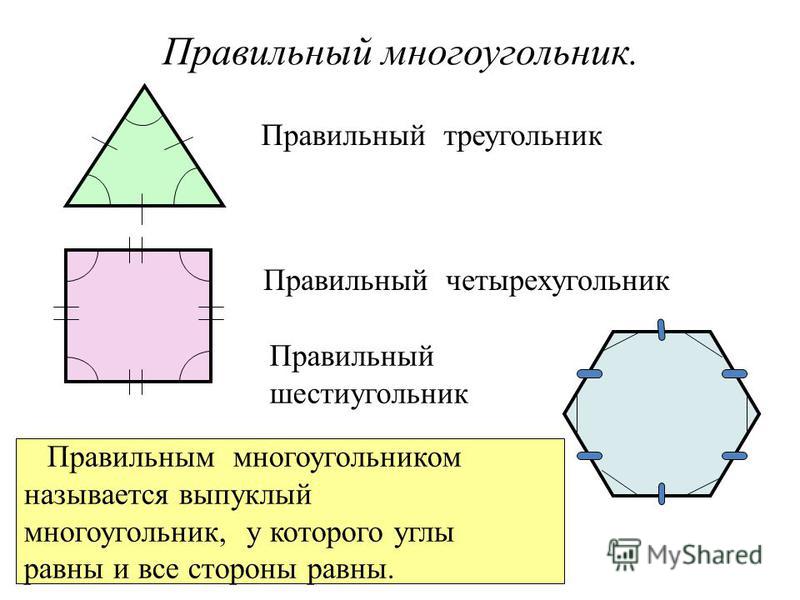
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .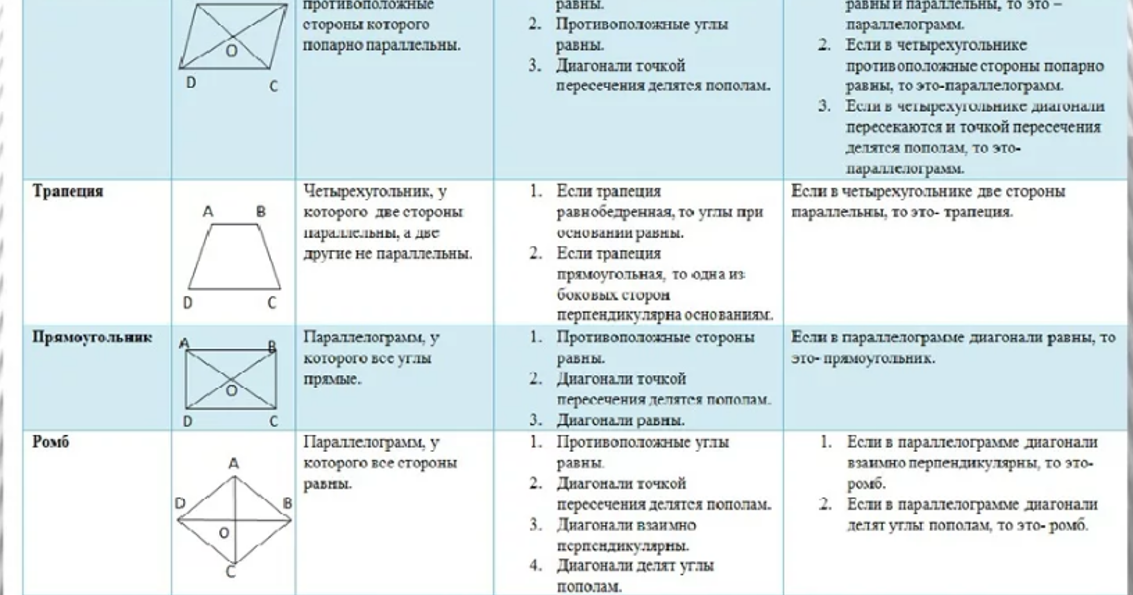
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Формула для площади параллелограмма
Площадь параллелограмма равна произведению его стороны на высоту, опущенную на эту сторону.
Доказательство
Если параллелограмм — прямоугольник, то равенство выполнено по теореме о площади прямоугольника. Далее считаем, что углы параллелограмма не прямые.
Далее считаем, что углы параллелограмма не прямые.
Пусть в параллелограмме $ABCD$ угол $\angle BAD$ острый и $AD > AB$. Иначе переименуем вершины. Тогда высота $BH$ из вершины $B$ на прямую $AD$ падает на сторону $AD$, так как катет $AH$ короче гипотенузы $AB$, а $AB
Сравним площадь параллелограмма $ABCD$ и площадь прямоугольника $HBCK$. Площадь параллелограмма больше на площадь $\triangle ABH$, но меньше на на площадь $\triangle DCK$. Так как эти треугольники равны, то и их площади равны. Значит, площадь параллелограмма равна площади прямоугольника со сторонами длиной в сторону и высоту параллелограмма.
Формула для площади параллелограмма через стороны и синус
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
Доказательство
Высота параллелограмма $ABCD$, опущенная на сторону $AB$ равна произведению отрезка $BC$ на синус угла $\angle ABC$. Осталось применить предыдущее утверждение.
Формула для площади параллелограмма через диагонали
Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними. \circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
\circ — \angle AOD$. Значит, синусы углов при пересечении диагоналей равны $\sin \alpha$.
$S_{ABCD}=S_{\triangle AOB} + S_{\triangle BOC} + S_{\triangle COD} + S_{\triangle AOD}$
по аксиоме измерения площади. Применяем формулу площади треугольника $S_{ABC} = \dfrac{1}{2} \cdot AB \cdot BC \sin \angle ABC$ для этих треугольников и углов при пересечении диагоналей. Стороны каждого равны половинам диагоналей, синусы также равны. Следовательно, площади всех четырёх треугольников равны $S = \dfrac{1}{2} \cdot \dfrac{AC}{2} \cdot \dfrac{BD}{2} \cdot \sin \alpha = \dfrac{AC \cdot BD}{8} \sin \alpha$. Суммируя всё вышесказанное, получаем
$S_{ABCD} = 4S = 4 \cdot \dfrac{AC \cdot BD}{8} \sin \alpha = \dfrac{AC \cdot BD \cdot \sin \alpha}{2}$
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как найти площадь четырехугольника? Площадь четырехугольника
Если на плоскости последовательно начертить несколько отрезков так, чтобы каждый следующий начинался в том месте, где закончился предыдущий, то получится ломаная линия. Эти отрезки называют звеньями, а места их пересечения — вершинами. Когда конец последнего отрезка пересечется с начальной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из них является конечной, а вторая бесконечной.
Когда конец последнего отрезка пересечется с начальной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из них является конечной, а вторая бесконечной.
Простая замкнутая линия вместе с заключенной в ней частью плоскости (той, которая конечна) называют многоугольником. Отрезки являются сторонами, а образованные ими углы — вершинами. Количество сторон любого многоугольника равно числу его вершин. Фигура, которая имеет три стороны, называется треугольником, а четыре — четырехугольником. Многоугольник численно характеризуется такой величиной, как площадь, которая показывает размер фигуры. Как найти площадь четырехугольника? Этому учит раздел математики — геометрия.
Чтобы найти площадь четырехугольника, нужно знать к какому типу он относится — выпуклому или невыпуклому? весь лежит относительно прямой (а она обязательно содержит какую-либо из его сторон) по одну сторону. Кроме того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными противоположными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и четырьмя равными сторонами), трапеция с двумя параллельными противоположными сторонами и дельтоид с двумя парами смежных сторон, которые равны.
Площади любого многоугольника находят, применяя общий метод, который заключается в том, чтобы разбить его на треугольники, для каждого вычислить площадь произвольного треугольника и сложить полученные результаты. Любой выпуклый четырехугольник делится на два треугольника, невыпуклый — на два или три его в этом случае может складываться из суммы и разности результатов. Площадь любого треугольника вычисляют как половину произведения основания (a) на высоту (ħ), проведенную к основанию. Формула, которая применяется в этом случае для вычисления, записывается как: S = ½ . a . ħ.
Как найти площадь четырехугольника, например, параллелограмма? Нужно знать длину основания (a), длину боковой стороны (ƀ) и найти синус угла α, образованного основанием и боковой стороной (sinα), формула для расчета будет выглядеть: S = a . ƀ . sinα. Так как синус угла α есть произведение основания параллелограмма на его высоту (ħ = ƀ) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a .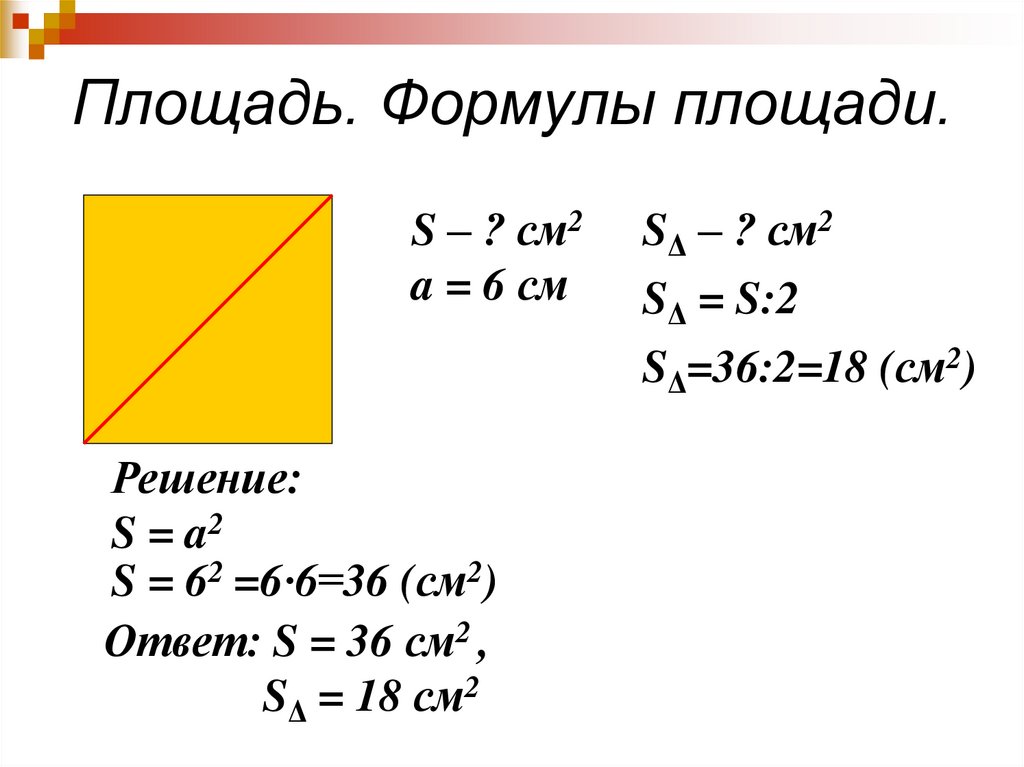 ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a . ƀ. потому что a = ƀ, будет равняться квадрату его стороны: S = a . a = a². вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ . (a + ƀ) . ħ.
ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a . ƀ. потому что a = ƀ, будет равняться квадрату его стороны: S = a . a = a². вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ . (a + ƀ) . ħ.
Как найти площадь четырехугольника, если неизвестны длины его сторон, но известны его диагонали (e) и (f), а также синус угла α? В этом случай площадь вычисляют, как половину произведения его диагоналей (линии, которые соединяют вершины многоугольника), умноженное на синус угла α. Формула может быть записана в таком виде: S = ½ . (e . f) . sinα. В частности в этом случае будет равняться половине произведения диагоналей (линии, соединяющие противоположные углы ромба): S = ½ . (e . f).
Как найти площадь четырехугольника, который не является параллелограммом или трапецией, его обычно принято называть произвольный четырехугольник. Площадь такой фигуры выражают через его полупериметр (Ρ — сумма двух сторон с общей вершиной), стороны a, ƀ, c, d и сумму двух противоположных углов (α + β): S = √[(Ρ — a) . (Ρ — ƀ) . (Ρ — c) . (Ρ — d) — a . ƀ . c . d . cos² ½ (α + β)].
Площадь такой фигуры выражают через его полупериметр (Ρ — сумма двух сторон с общей вершиной), стороны a, ƀ, c, d и сумму двух противоположных углов (α + β): S = √[(Ρ — a) . (Ρ — ƀ) . (Ρ — c) . (Ρ — d) — a . ƀ . c . d . cos² ½ (α + β)].
Если четырехугольник вписан в окружность, а φ = 180о, то для расчета его площади используют формулу Брахмагупты (индийский астроном и математик, живший в 6—7 веках нашей эры): S = √[(Ρ — a) . (Ρ — ƀ) . (Ρ — c) . (Ρ — d)]. Если четырехугольник описан окружностью, то (a + c = ƀ + d), а его площадь вычисляют: S = √[ a . ƀ . c . d] . sin ½ (α + β). Если четырехугольник одновременно является описанным одной окружностью и вписанным в другую окружность, то для вычисления площади используют следующую формулу: S = √.
При решении планиметрических заданий курса геометрии нередко встречается фигура с 4-мя сторонами. Да, речь идет о четырехугольнике. Произвольный многоугольник с четырьмя углами встречается реже, чем его частные случаи, – трапеции, дельтоиды, параллелограммы. В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
В последнюю «группу» входят также ромбы, прямоугольники, квадраты.
Рассмотрим, какие данные фигуры необходимо знать, чтобы рассчитать ее площадь.
Как найти площадь четырехугольника
Многоугольник произвольный
Для нахождения его площади вам потребуются диагонали фигуры, а также угол, полученный как результат их пересечения.
- S = (d1*d2*sinα)/2,
- d1, d2 – диагонали,
- α – угол, полученный путем их пересечения.
Многоугольник в окружности
Если заданный четырехугольник помещен в окружность, известна длина сторон фигуры, то в определении площади многоугольника поможет соотношение:
S = √(p – m)(p – k)(p – l)(p – e), p = (m + k + l + e)/2.
m, k, l, e – его стороны.
Как найти площадь четырехугольника — трапеции
Данную фигуру отличает наличие параллельных 2-ух сторон. Чтобы определить площадь такого многоугольника воспользуйтесь такими параметрами:
- Если известны величины параллельных сторон и перпендикуляра-высоты, проведенной к ним, площадь вычисляется с помощью выражения S = ((a + b)*h)/2,
a и b – основания,
h – перпендикуляр-высота.
- Исходя из определения линии средины (k = (a + b)/2)), предыдущая формула приобретет следующий вид: S = k*h,
k – линия средины.
Известные диагонали трапеции и градусная мера угла, образованная в результате их пересечения, также помогут определить площадь фигуры: S = (d1*d2*sinβ)/2,
d1, d2 – диагонали,
β – угол, полученный путем их пересечения. - Заданы 4 стороны: S = ((m + l)√k 2 – ((m – l) 2 + k 2 – d 2) 2 /(4(m – l) 2))/2,
m, l — стороны параллельные,
k, d — стороны боковые.
Как найти площадь четырехугольника — дельтоида
Многоугольник-дельтоид характеризуется наличием 2-ух пар равных сторон. Вычислить площадь такого четырехугольника рассчитывается следующим образом:
- Известны стороны фигуры и угол, образованный сторонами разной длины:
S = m*l*sinϕ,
m, l – стороны дельтоида,
ϕ – угол между ними. - Известны стороны фигуры и углы, образованные сторонами равной длины:
S = m 2 *sinα/2 + l 2 *sinβ/2,
m, l – стороны дельтоида,
α, β — углы между равными сторонами.
- Наличие известных диагоналей также позволяет определить площадь фигуры:
S = d1*d2/2,
d1, d2 – диагонали дельтоида. - Если в фигуру вписана окружность, то знание ее радиуса позволяет вычислить площадь дельтоида: S = (m + l)*r,
m, l – стороны дельтоида,
r – радиус в случае вписанной окружности.
Как найти площадь четырехугольника — параллелограмма
Если выпуклый многоугольник имеет 2 пары непересекающихся сторон, то перед вами – параллелограмм.
Общее выражение
Для определения площади данного вида фигуры потребуются:
- Сторона четырехугольника и высота, на нее опущенная: S = k*h(k),
k – сторона фигуры,
h(k) – высота к ней. - Длина двух сторон, имеющих одну вершину, и градусная мера угла при данной вершине:
S = l*k*sinϕ,
k, l – стороны многоугольника,
ϕ – угол между ними. - Диагонали фигуры и угол, полученный как результат их пересечения: S = d1*d2*sinβ/2,
d1, d2 – диагонали,
β – угол — результат их пересечения.
Ромб
Данный четырехугольник – частный случай параллелограмма, имеющий 4 равные стороны. Поэтому выражения, справедливые для параллелограмма, верны и для него. Тогда
- S = k*h(k),
k – сторона фигуры, h(k) – высота к ней. - S = k 2 *sinϕ,
k – сторона четырехугольника, ϕ – угол между сторонами. - S = d1*d2/2 (т.к. диагонали фигуры при пересечении образую прямой угол, а sin90° = 1),
d1, d2 – диагонали многоугольника.
Прямоугольник
Такой многоугольник имеет 2 пары равных сторон, а градусная мера его углов – 90°. Для нахождения его площади справедливы следующие выражения:
- S = k*l,
k, l – стороны фигуры. - S = d 2 *sinβ/2,
d – диагонали четырехугольника, β – угол – результат их пересечения. - S = 2R 2 *sinβ,
R – радиус в случае описанной окружности.
Квадрат
В данном случае у соотношения, полученные на предыдущем этапе, приобретут следующий вид (т. к. стороны такого вида прямоугольника равны):
к. стороны такого вида прямоугольника равны):
- S = k 2 , k – сторона фигуры.
- S = d 2 /2, d – диагональ квадрата.
- S = 2R 2 , R – радиус в случае описанной окружности.
- S = 4r 4 , r – радиус в случае вписанной окружности.
Теорема 1. Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Теорема 2. Диагонали трапеции делят ее на четыре треугольника, два из которых подобны, а два другие имеют одинаковую площадь:
Теорема 3. Площадь параллелограмма равна произведению основания на высоту, опущенную на данное основание, или произведению двух сторон на синус угла между ними:
Теорема 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон:
Теорема 5. Площадь произвольного выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
Теорема 6.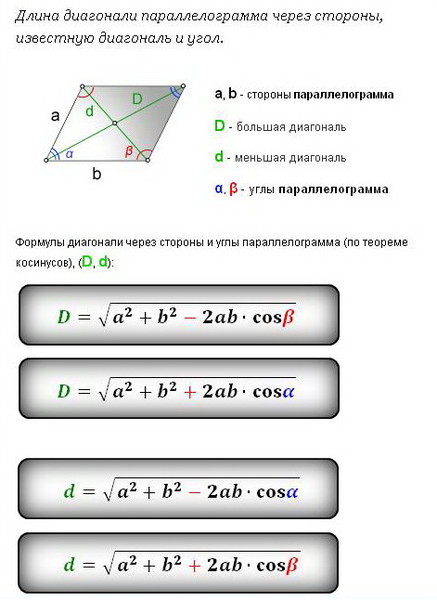 Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности:
Площадь четырехугольника, описанного около окружности, равна произведению полупериметра этого четырехугольника на радиус данной окружности:
Теорема 7. Четырехугольник, вершинами которого являются середины сторон произвольного выпуклого четырехугольника, есть параллелограмм, площадь которого равна половине площади исходного четырехугольника:
Теорема 8. Если у выпуклого четырехугольника диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон этого четырехугольника равны:
AB2 + CD2 = BC2 + AD2 .
Статья опубликована при поддержке компании «ДКРОСТ». Горки детские , домики, песочницы и многое
другое — изготовление и продажа детских площадок оптом и в розницу. Самые низкие
цены, скидки, сжатые сроки изготовления, выезд и консультация специалиста, гарантия
качества. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты
Вы сможете на сайте, который располагается по адресу: http://dkrost.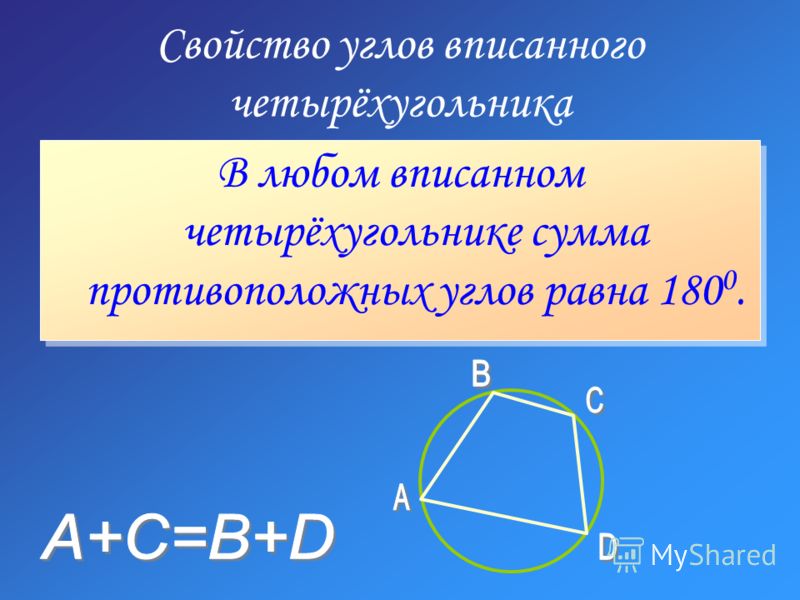 ru/.
ru/.
Доказательства некоторых теорем
Доказательство теоремы 2 . Пусть ABCD — данная трапеция, AD и BC — ее основания, O — точка пересечения диагоналей AC и BD этой трапеции. Докажем, что треугольники AOB и COD имеют одинаковую площадь. Для этого опустим из точек B и C на прямую AD перпендикуляры BP и CQ. Тогда площадь треугольника ABD равна
А площадь треугольника ACD равна
Так как BP = CQ, то и S∆ABD = S∆ACD . Но площадь треугольника AOB есть разность площадей треугольников ABD и AOD, а площадь треугольника COD — разность площадей треугольников ACD и AOD. Следовательно, площади треугольников AOB и COD равны, что и требовалось доказать.
Доказательство теоремы 4 . Пусть ABCD — параллелограмм, AB = CD = a , AD = BC = b,
AC = d1
, BD = d2
, ∠BAD = α, ∠ADC = 180° – α. Применим к треугольнику ABD теорему косинусов:
Применив теперь теорему косинусов к треугольнику ACD, получим:
Складывая почленно полученные равенства, получаем, что что и требовалось доказать.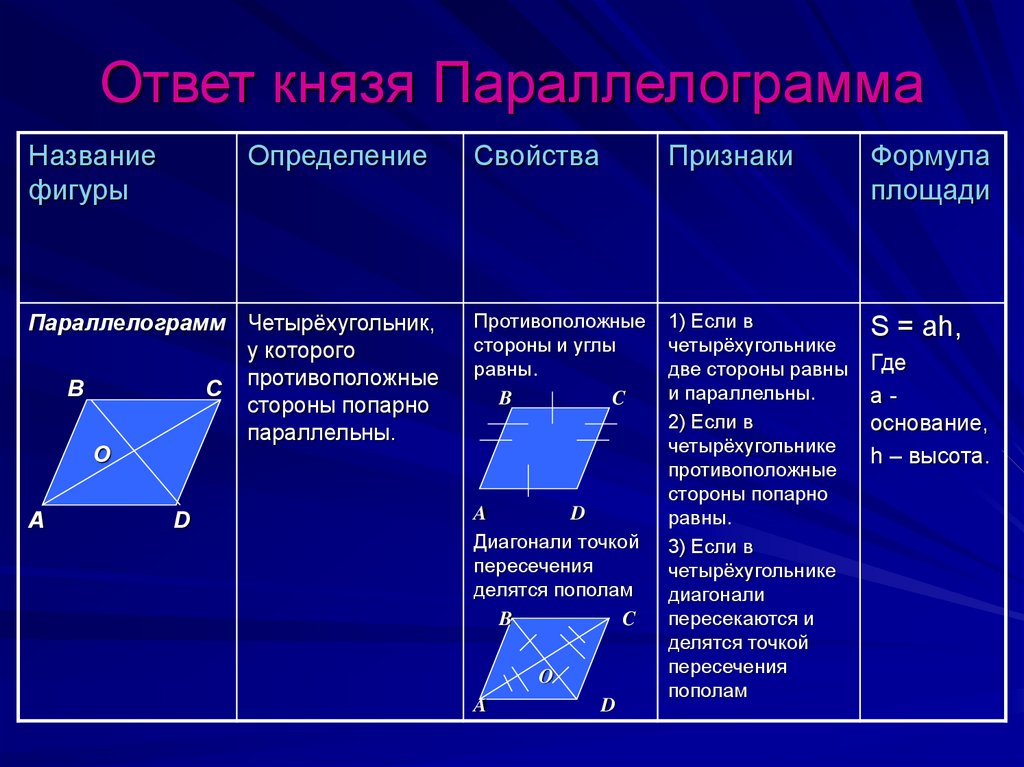
Доказательство теоремы 5. Пусть ABCD — произвольный выпуклый четырехугольник, E — точка пересечения его диагоналей, AE = a , BE = b,
CE = c, DE = d, ∠AEB = ∠CED = ϕ, ∠BEC =
= ∠AED = 180° – ϕ. Имеем:
что и требовалось доказать.
Доказательство теоремы 6 . Пусть ABCD — произвольный четырехугольник, описанный около окружности, O — центр этой окружности, OK, OL, OM и ON — перпендикуляры, опущенные из точки O на прямые AB, BC, CD и AD соответственно. Имеем:
где r — радиус окружности, а p — полупериметр четырехугольника ABCD.
Доказательство теоремы 7 . Пусть ABCD — произвольный выпуклый четырехугольник, K, L, M и N — середины сторон AB, BC, CD и AD соответственно. Так как KL — средняя линия треугольника ABC, то прямая KL параллельна прямой AC и Аналогично, прямая MN параллельна прямой AC и Следовательно, KLMN — параллелограмм. Рассмотрим треугольник KBL. Его площадь равна четверти площади треугольника ABC. Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Площадь треугольника MDN также равна четверти площади треугольника ACD. Следовательно,
Аналогично,
Это значит, что
откуда вытекает, что
Доказательство теоремы 8 . Пусть ABCD — произвольный выпуклый четырехугольник, у которого диагонали взаимно перпендикулярны, пусть E — точка пересечения его диагоналей,
AE = a , BE = b, CE = c, DE = d. Применим к треугольникам ABE и CDE теорему Пифагора:
AB2
= AE2
+ BE2
= a 2
+ b2
,
CD2
= CE2
+ DE2
= c2
+ d2
,
следовательно,
AB2
+ CD2
= a 2
+ b2
+ c2
+ d2
.
Применив теперь теорему Пифагора к треугольникам ADE и BCE, получим:
AD2
= AE2
+ DE2
= a 2
+ d2
,
BC2
= BE2
+ CE2
= b2
+ c2
,
откуда вытекает, что
AD2
+ BC2
= a 2
+ b2
+ c2
+ d2
.
Значит, AB2
+ CD2
= AD2
+ BC2
, что и требовалось доказать.
Решения задач
Задача 1 . Около круга описана трапеция с углами при основании α и β. Найти отношение площади трапеции к площади круга.
Найти отношение площади трапеции к площади круга.
Решение . Пусть ABCD — данная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна π, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то
Аналогично, из прямоугольного треугольника BCM находим, что Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:
AB + CD = AD + BC,
откуда находим
Значит, площадь трапеции есть
и искомое отношение равно
Ответ :
Задача 2 . В выпуклом четырехугольнике ABCD угол A равен 90°, а угол C не превосходит 90°. Из вершин B и D на диагональ AC опущены перпендикуляры BE и DF. Известно, что AE = CF. Доказать, что угол C прямой.
Доказательство . Так как угол A равен 90°,
а угол C не превосходит 90°, то точки E и F лежат на диагонали AC. Без ограничения общности мы можем считать, что AE
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как
Без ограничения общности мы можем считать, что AE
∠EBC = β, ∠FDA = γ, ∠FDC = δ. Нам достаточно доказать, что α + β + γ + δ = π. Так как
откуда получаем, что что и требовалось доказать.
Задача 3 . Периметр равнобочной трапеции, описанной около круга, равен p. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен α.
Решение . Пусть ABCD — данная равнобочная трапеция с основаниями AD и BC, пусть BH — высота этой трапеции, опущенная из вершины B.
Так как в данную трапецию можно вписать окружность, то
Следовательно,
Из прямоугольного треугольника ABH находим,
Ответ :
Задача 4 . Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке O, а прямые AB и CD — в точке K. Прямая KO пересекает стороны BC и AD в точках M и N соответственно, а угол BAD равен 30°. Известно, что в трапеции ABMN и NMCD можно вписать окружность. Найти отношение площадей треугольника BKC и трапеции ABCD.
Решение . Как известно, для произвольной трапеции прямая, соединяющая точку пересечения диагоналей и точку пересечения продолжений боковых сторон, делит каждое из оснований пополам. Итак, BM = MC и AN = ND. Далее, так как в трапеции ABMN и NMCD можно вписать окружность, то
BM + AN = AB + MN,
MC + ND = CD + MN.
Отсюда следует, что AB = CD, то есть трапеция ABCD — равнобокая. Искомое отношение площадей не зависит от масштаба, поэтому мы можем принять, что KN = x, KM = 1. Из прямоугольных треугольников AKN и BKM получаем, что Записывая вновь уже использованное выше соотношение
BM + AN = AB + MN ⇔
Нам требуется вычислить отношение:
Здесь мы использовали тот факт, что площади треугольников AKD и BKC относятся как квадраты сторон KN и KM, то есть как x2.
Ответ:
Задача 5. В выпуклом четырехугольнике ABCD точки E, F, H, G являются серединами сторон AB, BC, CD, DA соответственно и O — точка пересечения отрезков EH и FG. Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.. Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Известно, что EH = a , FG = b, Найти длины диагоналей четырехугольника.. Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:
Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем:
Значит, BC = 1 и AD = 7.
Ответ: 1 и 7.
Задача 7 . Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна a , а длина боковой стороны BC равна b. Найти площадь трапеции.
Решение . Пусть E — точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда
AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Поэтому AC является и высотой этого треугольника, и значит,
Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда
AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Поэтому AC является и высотой этого треугольника, и значит,
Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия то
AB + CD = 8. Продлим боковые стороны DA и CB до пересечения в точке E. Рассмотрим треугольник ABE, в котором ∠EAB = 50°. ∠EBA = 40°,
следовательно, ∠AEB = 90°. Медиана EM этого треугольника, проведенная из вершины прямого угла, равна половине гипотенузы: EM = AM. Пусть EM = x, тогда AM = x, DN = 4 – x. Согласно условию задачи MN = 1, следовательно,
EN = x + 1. Из подобия треугольников AEM и DEN имеем:
Это означает, что AB = 3 и CD = 5.
Ответ : 3 и 5.
Задача 10 . Выпуклый четырехугольник ABCD описан около окружности с центром в точке O, при этом AO = OC = 1, BO = OD = 2.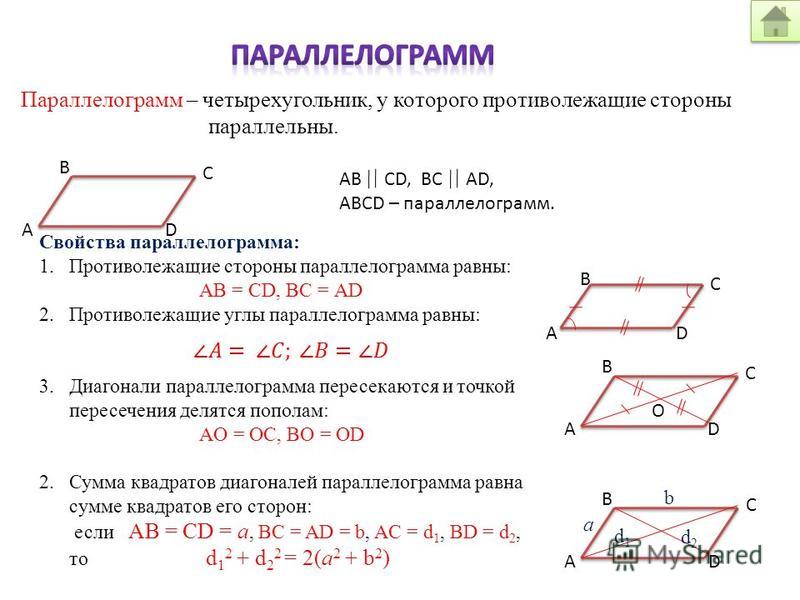 Найти периметр четырехугольника ABCD.
Найти периметр четырехугольника ABCD.
Решение . Пусть K, L, M, N — точки касания окружности со сторонами AB, BC, CD, DA соответственно, r — радиус окружности. Так как касательная к окружности перпендикулярна радиусу, проведенному в точку касания, то треугольники AKO, BKO, BLO, CLO, CMO, DMO, DNO, ANO — прямоугольные. Применив к этим треугольникам теорему Пифагора, получим, что
Следовательно, AB = BC = CD = DA, то есть ABCD — ромб. Диагонали ромба перпендикулярны друг другу, и точка их пересечения является центром вписанной окружности. Отсюда легко находим, что сторона ромба равна и значит, периметр ромба равен
Ответ :
Задачи для самостоятельного решения
С-1. Около окружности радиуса r описана равнобочная трапеция ABCD. Пусть E и K — точки касания этой окружности с боковыми сторонами трапеции. Угол между основанием AB и боковой стороной AD трапеции равен 60°. Докажите, что EK параллелен AB, и найдите площадь трапеции ABEK.
С-2. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2.
Найдите площадь трапеции.
С-3 . Можно ли вокруг четырехугольника ABCD описать окружность, если ∠ADC = 30°, AB = 3, BC = 4, AC = 6?
С-4. В трапеции ABCD (AB — основание) величины углов DAB, BCD, ADC, ABD и ADB образуют арифметическую прогрессию (в том порядке, в котором они написаны). Найдите расстояние от вершины C до диагонали BD, если высота трапеции равна h.
С-5. Дана равнобедренная трапеция, в которую вписана окружность и около которой описана окружность. Отношение высоты трапеции к радиусу описанной окружности равно Найдите углы трапеции.
С-6. Площадь прямоугольника ABCD равна 48, а длина диагонали равна 10. На плоскости, в которой расположен прямоугольник, выбрана точка O так, что OB = OD = 13. Найдите расстояние от точки O до наиболее удаленной от нее вершины прямоугольника.
С-7. Периметр параллелограмма ABCD равен 26. Величина угла ABC равна 120°. Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
Радиус окружности, вписанной в треугольник BCD, равен Найдите длины сторон параллелограмма, если известно, что AD > AB.
С-8. Четырехугольник ABCD вписан в окружность с центром в точке O. Радиус OA перпендикулярен радиусу OB, а радиус OC перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки C на прямую AD, равна 9. Длина отрезка BC в два раза меньше длины отрезка AD. Найдите площадь треугольника AOB.
С-9. В выпуклом четырехугольнике ABCD вершины A и C противоположны, а длина стороны AB равна 3. Угол ABC равен угол BCD равен Найдите длину стороны AD, если известно, что площадь четырехугольника равна
С-10. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. Известно, что
AD = 2, ∠ABD = ∠ACD = 90°, и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно Найдите длину стороны BC.
С-11. Пусть M — точка пересечения диагоналей выпуклого четырехугольника ABCD, в котором стороны AB, AD и BC равны между собой. Найдите угол CMD, если известно, что DM = MC,
Найдите угол CMD, если известно, что DM = MC,
а ∠CAB ≠ ∠DBA.
С-12. В четырехугольнике ABCD известно, что ∠A = 74°, ∠D = 120°. Найдите угол между биссектрисами углов B и C.
С-13. В четырехугольник ABCD можно вписать окружность. Пусть K — точка пересечения его диагоналей. Известно, что AB > BC > KC, а периметр и площадь треугольника BKC равны соответственно 14 и 7. Найдите DC.
С-14. В трапеции, описанной около окружности, известно, что BC AD, AB = CD, ∠BAD =
= 45°. Найдите AB, если площадь трапеции ABCD равна 10.
С-15. В трапеции ABCD с основаниями AB и CD известно, что ∠CAB = 2∠DBA. Найдите площадь трапеции.
С-16. В параллелограмме ABCD известно, что AC = a , ∠CAB = 60°. Найдите площадь параллелограмма.
С-17 . В четырехугольнике ABCD диагонали AC и BD пересекаются в точке K. Точки L и M являются соответственно серединами сторон BC и AD. Отрезок LM содержит точку K. Четырехугольник ABCD таков, что в него можно вписать окружность.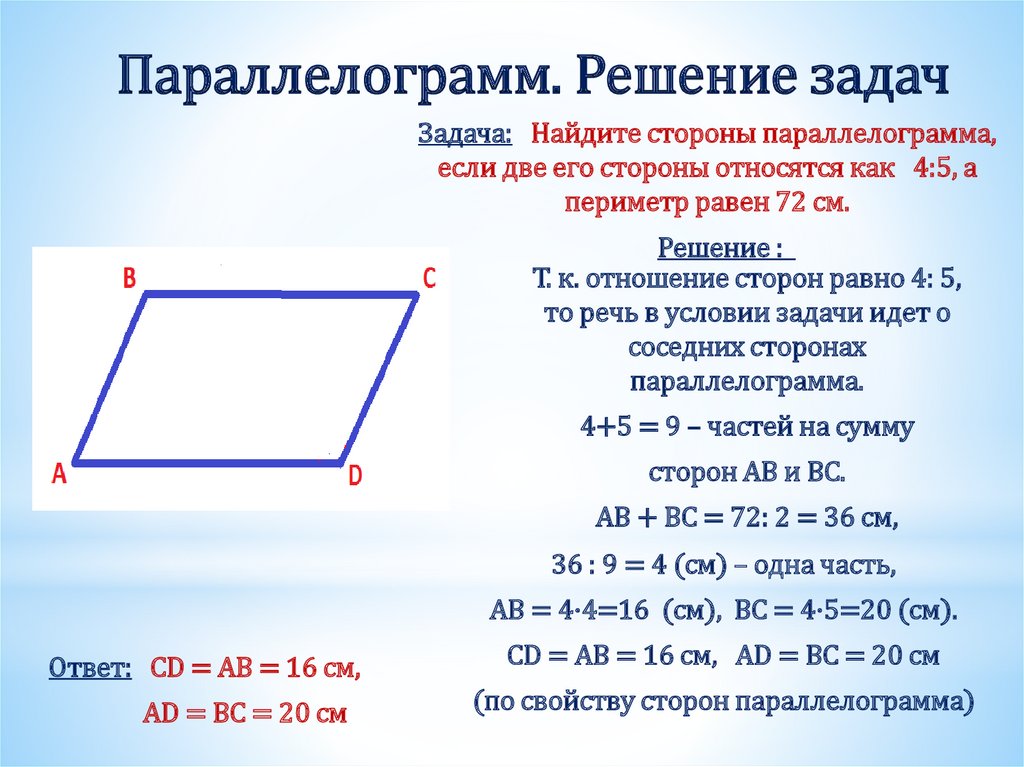 Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
Найдите радиус этой окружности, если AB = 3, и LK: KM = 1: 3.
С-18. В выпуклом четырехугольнике ABCD проведены диагонали AC и BD. При этом ∠BAC =
= ∠BDC, а площадь круга, описанного около треугольника BDC, равна
а) Найдите радиус окружности, описанной около треугольника ABC.
б) Зная, что BC = 3, AC = 4, ∠BAD = 90°, найдите площадь четырехугольника ABCD.
Определение .
Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.
Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?
Теорема 1 .
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны .
В четырехугольник ABCD можно вписать окружность, если
И обратно, если суммы противоположных сторон четырехугольника равны:
то в четырехугольник ABCD можно вписать окружность.
Теорема 2 .
Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис .
O — точка пересечения биссектрис четырехугольника ABCD.
AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,
то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.
3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.
AM=AN,
5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
Четырехугольником называется фигура, состоящая из четырех вершин, три из которых не лежат на одной прямой, и отрезков, соединяющих их.
Существует множество четырехугольников. К ним относятся параллелограммы, квадраты, ромбы, трапеции. Найти можно найти по сторонам, легко вычисляется по диагоналям. В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ. Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними. Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле:
Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Пусть дан четырехугольник с двумя диагоналями d1
=5 см;d2
=4см. Острый угол между ними равен α
= 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий. Подставим данные:
На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет .
Площадь четырехугольника по сторонам
Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры. Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d
формула полупериметра будет выглядеть так:
В нашем прямоугольнике со сторонами a, b, c, d
формула полупериметра будет выглядеть так:
Зная стороны, выводим формулу. Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны:
Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a
= 5 см, b
= 4 см, с
= 3 см, d
= 6 см. Для начала найдем полупериметр:
используем найденное значение для расчета площади:
Площадь четырехугольника, заданного координатами
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY .
Выпуклый четырехугольник — определение, формы, свойства, использование
Выпуклый четырехугольник — одна из наиболее часто используемых фигур во многих отраслях и областях. Они даже используются в астрономии . Выпуклые четырехугольники являются не только одной из наиболее часто используемых форм, но и одной из самых основных форм с четырьмя сторонами, которые заключают в себе пространство.
Они даже используются в астрономии . Выпуклые четырехугольники являются не только одной из наиболее часто используемых форм, но и одной из самых основных форм с четырьмя сторонами, которые заключают в себе пространство.
Выпуклый четырехугольник можно найти где угодно, если внимательно присмотреться. Например, стены зданий представляют собой выпуклые четырехугольники, прямоугольники и даже книги имеют одинаковую форму.
ИсторияИстория четырехугольников очень давняя. В эпоху sulbasutra представление о четырехугольнике ограничивалось некоторыми правильными и циклическими четырехугольниками, такими как квадрат, прямоугольник и равнобедренная трапеция.
Бхаскара-I был первым, кто упомянул четырехугольник с неравными сторонами, который позже был идентифицирован как четырехугольник, вершины которого лежат на окружности, которые теперь известны как вписанных четырехугольников . Все древнеиндийские ученые, кроме Арьябхаты-II , изучали только выпуклые четырехугольники.
Но есть также отчеты, которые предполагают, что четырехугольники были впервые обнаружены древними греками и впервые нарисованы Пифагором .
Форма Выпуклый четырехугольникВыпуклый четырехугольник представляет собой многоугольник с четырьмя сторонами и углами. Все углы при вершинах меньше 180°, а их сумма 360°.
Четырехугольник также называют четырехугольником , четырехугольником и 4-угольником . Четырехугольники с вершинами A, B, C и D часто представляются как □ABCD .
Диагонали выпуклого четырехугольника лежат и пересекаются внутри фигуры.
В четырехугольниках тоже есть некоторые условия эквивалентности, подобные условиям эквивалентности треугольников. Условия эквивалентности четырехугольников:
- Противоположные стороны должны быть параллельны.
- Диагонали равны по длине и перпендикулярно делят друг друга пополам.

Вот некоторые распространенные выпуклые четырехугольники, с которыми мы чаще всего сталкиваемся в повседневной жизни.
1. Квадрат: Квадрат обычно также называют правильным четырехугольником. Это потому, что все стороны квадрата равны, и все углы также равны, каждый из которых равен 90 O . Квадрат также является равносторонним четырехугольником.
Квадрат2. Прямоугольник: Прямоугольник – это выпуклый четырехугольник, все углы которого прямые, а противоположные стороны равны и параллельны. Диагонали прямоугольника делят друг друга пополам и имеют одинаковую длину. Квадраты и прямоугольники также являются прямоугольниками.
A Прямоугольник 3. Ромб: У ромба все четыре стороны одинаковой длины, противоположные стороны параллельны, его противоположные углы также равны. Его диагонали перпендикулярно делят друг друга пополам, но не равны. Сумма смежных с ним углов равна 180°. Квадраты тоже ромбы, но с вершинами углов 90°.
Сумма смежных с ним углов равна 180°. Квадраты тоже ромбы, но с вершинами углов 90°.
4. Параллелограмм: Параллелограмм является одним из важнейших выпуклых четырехугольников, его противоположные стороны параллельны и равны. Его противоположные углы равны, а сумма смежных углов равна 180°. Его диагонали не равны, но делят друг друга пополам. Прямоугольники также являются параллелограммами с углами при вершинах 90°.
A Параллелограмм5. Трапеция: Трапеция представляет собой выпуклый четырехугольник с одной парой параллельных сторон. У трапеции все стороны и углы различны.
A Трапеция 6. Равнобедренная трапеция: Равнобедренная трапеция, как следует из названия, представляет собой трапецию, две непараллельные стороны которой равны. При этом углы при основании или углы, находящиеся по обе стороны от одной из параллельных сторон, равны. Сумма углов, существующих между параллельными прямыми. составляет 180°.
7. Неправильный четырехугольник: Неправильный выпуклый четырехугольник, как следует из названия, не имеет двух сторон и углов. Его диагонали лежат внутри области, образованной его сторонами, а все углы острые, что делает его выпуклым четырехугольником.
Неправильный четырехугольник8. Воздушный змей: Воздушный змей — это выпуклый четырехугольник, имеющий две пары равных смежных сторон, и каждая пара имеет разную длину. Его диагонали не равны, но пересекают друг друга перпендикулярно, и диагональ, на каждой стороне которой лежит пара равных сторон, делится пополам другой диагональю.
Воздушный змей 9. Вписанный четырехугольник: Вписанный четырехугольник — один из наиболее важных типов выпуклых четырехугольников. Четырехугольник, вершины которого лежат на окружности, называется вписанным четырехугольником.
Одним из основных и важных свойств вписанного четырехугольника является то, что сумма его противоположных углов равна 180°.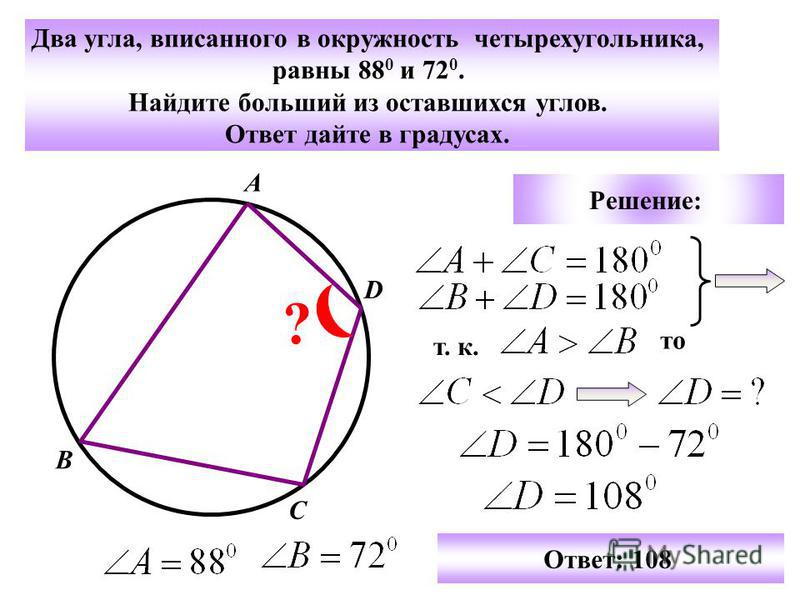
ПРИМЕЧАНИЕ: Узнайте больше о вписанных четырехугольниках
Свойства выпуклого четырехугольникаТеперь давайте перейдем к обсуждению свойств этих четырехугольников.
Площадь выпуклого четырехугольникаМы рассмотрим различные способы нахождения площади выпуклого четырехугольника. 92(\frac{A + C}{2})]}\)
Здесь \(a\), \(b\), \(c\) и \(d\) — стороны четырехугольника, \(s\) — его полупериметр, а \(A\) и \(C\) — любые два противоположных угла.
Использование сторон и углов\(\mbox{Площадь } = \frac{ad}{2} \sin A + \frac{bc}{2} \sin C\)
Здесь \(a \), \(b\), \(c\) и \(d\) — стороны четырехугольника, а \(A\) — угол между \(a\) и \(d\) и \(C\) — это угол между \(b\) и \(c\).
92 + 2ab \cos \alpha)}}{4}\)
Здесь \(a\), \(b\), \(c\) и \(d\) — стороны четырехугольника, а \ (\alpha\) — это угол между \(a\) и \(b\).
\(\mbox{Площадь } = \sqrt{(s – a)(s – b)(s – c)(s – d) – \frac{ac + bd + pq}{4}(ac + bd – pq)}\)
Здесь \(a\), \(b\), \(c\) и \(d\) — стороны четырехугольника, а \ )p\) и \(q\) — его диагонали.
Использование диагоналей в качестве векторов\(\mbox{Площадь } = \frac{|AC \times BD|}{2}\)
Здесь \(AC\) и \(BD\) — векторы диагоналей четырехугольника ABCD.
ПРИМЕЧАНИЕ: Узнайте больше о площади четырехугольника
Длины диагоналейДлины диагоналей выпуклого четырехугольника можно найти с помощью правила косинусов в треугольниках, которые образуются при проведении диагонали.
Пусть диагонали четырехугольника равны \(p\) и \(q\). Затем 92 – 2bc \cos C}\)
Биссектрисы Внутренние биссектрисы четырехугольника либо совпадают, либо точки их пересечения совпадают и, следовательно, образуют вписанный четырехугольник.
Бимедианы четырехугольника — это отрезки, соединяющие середины его противоположных сторон. Точка пересечения бимедиан является центром тяжести четырехугольника.
Если середины смежных сторон четырехугольника соединены, то получившийся четырехугольник всегда является параллелограммом. Этот параллелограмм называется параллелограммом Вариньона .
Параллелограмм Вариньона обладает некоторыми уникальными свойствами, связанными с исходным четырехугольником.
- Каждая пара параллельных сторон вариньонного параллелограмма также параллельна одной из диагоналей четырехугольника.
- Длина сторон параллелограмма вариньона равна половине длины соответствующей им диагонали.
- Площадь вариньонного параллелограмма равна половине площади исходного четырехугольника. Это справедливо как для выпуклых, так и для вогнутых четырехугольников.
- Периметр вариньонного параллелограмма равен сумме диагоналей исходного четырехугольника.

Рассмотрим четырехугольник со сторонами \(a\), \(b\), \(c\) и \(d\) и диагоналями \(p\) и \ (к\).
- Стороны:
- 92)}\)
- \(A \le \sqrt{(s – a)(s – b)(s – c)(s – d)}\) ; здесь \(s\) — полупериметр
- \(A \le \frac{1}{2} \sqrt[3]{(ab + cd)(ac + bd)(ad + bc)}\)
- \(A \le \frac{1}{2} pq\)
- Центроид: В четырехугольнике есть 3 типа центроидов на основе ссылки, с помощью которой они формируются.
- Центроид вершины: Это точка пересечения медиан четырехугольника.
- Центроид области: Это точка пересечения отрезков, соединяющих центроиды треугольников, образованных диагональю.
- Центроид стороны: Образуется путем рассмотрения стороны четырехугольника с постоянной массой на единицу длины.

- Центр описанной окружности: Центр описанной окружности четырехугольника называется центром описанной окружности, поскольку нет естественных аналогий центру описанной окружности четырехугольника. Это точка пересечения отрезков, соединяющих центры описанных окружностей треугольников, образованных диагональю.
- Квазиортоцентр: ортоцентр четырехугольника называется квазиортоцентром, так как нет естественных аналогий ортоцентру четырехугольника. Это точка пересечения отрезков, соединяющих ортоцентры треугольников, образованных диагональю.
- Квази-ортоцентр(H), центроид площади(G) и квази-центр окружности(O) коллинеарны и имеют отношение
\(HG = 2GO\) - Точка Микеля: четырехугольника ABCD, а P и Q — точки пересечения прямых AD и BC и AB и CD соответственно. Тогда точка, через которую проходят окружности (PAB), (PCD), (QAD) и (QBC), является точкой Микеля.
- Линия Ньютона: Это отрезок, соединяющий середины диагоналей.
 Эта линия делится пополам центром тяжести вершины.
Эта линия делится пополам центром тяжести вершины. - Линия, соединяющая точку пересечения диагоналей и центр тяжести вершины, она также содержит центр тяжести площади. Эта линия делится центроидом вершины в отношении 3:1.
Четырехугольники используются в самых разных областях, от искусства и дизайна до космоса и астрономии. Вот некоторые из их применений:
- Свойства четырехугольников используются в чертежах планов этажей зданий.
- Даже Леонардо да Винчи использовал четырехугольники в своих рисунках, он использовал свойства четырехугольников в знаменитой картине Monalisa .
- Они используются в украшениях , чтобы сделать их более блестящими.
- Птолемей использовал свою теорему, связывающую стороны и диагонали вписанного четырехугольника, для создания тригонометрической таблицы, которую он применил к астрономии .

Вопрос 1. Найдите площадь четырехугольника, длины сторон которого равны 2 см, 4 см, 5 см и 9 см для сторон a, b, c и d соответственно, и угол между a и d равен 60°, а между b и c равен 30°. Найдите площадь четырехугольника.
Решение. Данные длины и углы четырехугольника:
\(a\) = 2см
\(b\) = 4см
\(c\) = 5см
\(d\) = 9см
\(A\) = 60 °
\(C\) = 30°
Площадь данного четырехугольника можно найти по следующей формуле:
\(\mbox{Площадь } = \frac{ad}{2} \sin A + \frac {bc}{2} \sin C\)
\(\mbox{Площадь } = \frac{2*9}{2} \sin 60° + \frac{4*5}{2} \sin 30° \)
\(\mbox{Площадь} = 9 * \frac{\sqrt{3}}{2} + 10 * \frac{1}{2} = 7,79 + 5\) 92\).
Вопрос 2. Какова максимальная площадь четырехугольника, длины сторон которого равны 2 см, 5 см, 7 см и 3 см для сторон a, b, c и d четырехугольника соответственно?
Раствор. Данные длины сторон четырехугольника равны:
Данные длины сторон четырехугольника равны:
\(a\) = 2см
\(b\) = 5см
\(c\) = 7см
\(d\) = 3см
Мы можем найти максимальную площадь этого четырехугольника по следующей формуле:
\(\mbox{Площадь} \le frac{1}{4} (a + c)(b + d)\) 92\)
Максимальная площадь четырехугольника с такими длинами сторон равна 18 см 2 .
Часто задаваемые вопросыЧто такое выпуклый четырехугольник?
Многоугольник с четырьмя сторонами и всеми внутренними углами меньше 180° называется выпуклым четырехугольником.
Задайте выпуклый четырехугольник.
Выпуклый четырехугольник – это четырехугольник, все диагонали которого лежат внутри площади, ограниченной его четырьмя сторонами.
Что такое невыпуклый четырехугольник?
Как следует из названия, это четырехугольник, в котором один угол больше 180°.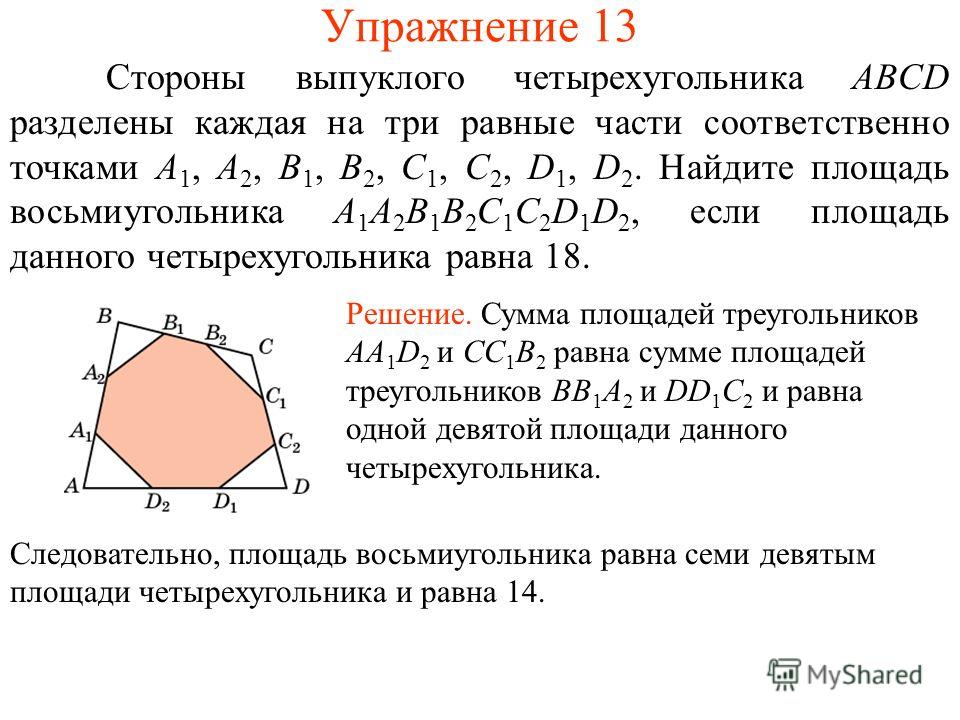 Итак, невыпуклый четырехугольник по существу является вогнутым четырехугольником.
Итак, невыпуклый четырехугольник по существу является вогнутым четырехугольником.
Каковы свойства параллелограмма вариньона?
Вариньонный параллелограмм образован соединением середины сторон параллелограмма:
1 . Его пара параллельных сторон равна половине длины диагонали, которой они параллельны.
2 . Площадь параллелограмма вариньона равна половине площади его четырехугольника.
3 . Периметр вариньонного параллелограмма равен сумме диагоналей четырехугольника.
4 . Диагонали вариньонного параллелограмма являются бимедианами четырехугольника.
Площадь четырехугольника – формула, определение и примеры
Площадь четырехугольника – это количество области, которая находится внутри него. Вспомним, что такое четырехугольник. Четырехугольник — это замкнутая фигура, ограниченная четырьмя отрезками. Четырехугольник может быть правильным и неправильным. Правильный четырехугольник – это четырехугольник, у которого все стороны имеют одинаковую длину. Четырехугольник, который не является правильным, называется неправильным четырехугольником. Существует 6 видов четырехугольников.
Четырехугольник может быть правильным и неправильным. Правильный четырехугольник – это четырехугольник, у которого все стороны имеют одинаковую длину. Четырехугольник, который не является правильным, называется неправильным четырехугольником. Существует 6 видов четырехугольников.
- квадратный
- прямоугольник
- параллелограмм
- трапеция
- ромб
- воздушный змей
На этой странице мы увидим, как найти площадь четырехугольника, разделив его на два треугольника, и как найти площадь четырехугольника, используя его 4 стороны. Кроме того, мы изучим формулы для нахождения площади каждого из этих различных типов четырехугольников.
| 1. | Что такое площадь четырехугольника? |
| 2. | Формула площади четырехугольника путем деления на два треугольника |
| 3. | Формула площади четырехугольника с использованием сторон |
4. | Формулы площади различных типов четырехугольников |
| 5. | Площадь четырехугольника по формуле Герона |
| 6. | Площадь четырехугольника с использованием координат |
| 7. | Часто задаваемые вопросы о площади четырехугольника |
Что такое площадь четырехугольника?
Площадь четырехугольника есть не что иное, как область, ограниченная сторонами четырехугольника. Она измеряется в квадратных единицах, таких как м 2 , 2 см , 2 см и т. Д. Процесс нахождения площади четырехугольника зависит от его типа и информации, доступной о четырехугольнике. Если четырехугольник не принадлежит ни к одному из упомянутых выше типов, то его площадь можно найти либо разбив его на два треугольника, либо воспользовавшись формулой (которая называется формулой Бретшнейдера) нахождения площади четырехугольника используя четыре стороны. Здесь вы можете увидеть формулы для нахождения площади четырехугольника, который не принадлежит ни к одному из стандартных типов.
Здесь вы можете увидеть формулы для нахождения площади четырехугольника, который не принадлежит ни к одному из стандартных типов.
Давайте узнаем больше об этих формулах в следующих разделах.
Формула площади четырехугольника путем деления на два треугольника
Рассмотрим четырехугольник ABCD, длина диагонали BD которого известна как d. ABCD можно разделить на два треугольника диагональю BD. Чтобы найти его площадь, нужно знать высоты треугольников ABD и BCD. Предположим, что высоты треугольников BCD и ABD равны \(h_1\) и \(h_2\) соответственно. Найдем площадь четырехугольника ABCD, сложив площади треугольников BCD и ABD.
Здесь площадь треугольника BCD = (1/2) × d × \(h_1\).
Площадь треугольника ABD = (1/2) × d × \(h_2\).
На приведенном выше рисунке площадь четырехугольника ABCD = площадь ΔBCD + площадь ΔABD.
Таким образом, площадь четырехугольника ABCD = (1/2) × d × \(h_1\) + (1/2) × d × \(h_2\) = (1/2) × d × (\( h_1+h_2\)). {2} \frac{\theta}{2}}\), где
{2} \frac{\theta}{2}}\), где
- s = полупериметр четырехугольника = (a + b + c + d)/2
- θ = θ\(_1\) + θ\(_2\)
Площадь четырехугольника по формуле Герона
По формуле Герона площадь треугольника с тремя сторонами a, b и c равна \(\sqrt{s(s-a)(s-b)(s-c)}\), где s – полупериметр треугольника. треугольник, т. е. s = (a + b + c)/2. Чтобы найти площадь четырехугольника по формуле Герона,
- Разделите его на два треугольника с помощью диагонали (используйте диагональ, длина которой известна).
- Примените формулу Герона к каждому треугольнику, чтобы найти его площадь.
- Сложите площади двух треугольников, чтобы получить площадь четырехугольника.
Формулы площади четырехугольников различных типов
Мы уже узнали, что существует 6 типов четырехугольников: квадрат, прямоугольник, параллелограмм, трапеция, ромб и воздушный змей. У нас есть специальная формула для нахождения площади каждого из этих четырехугольников.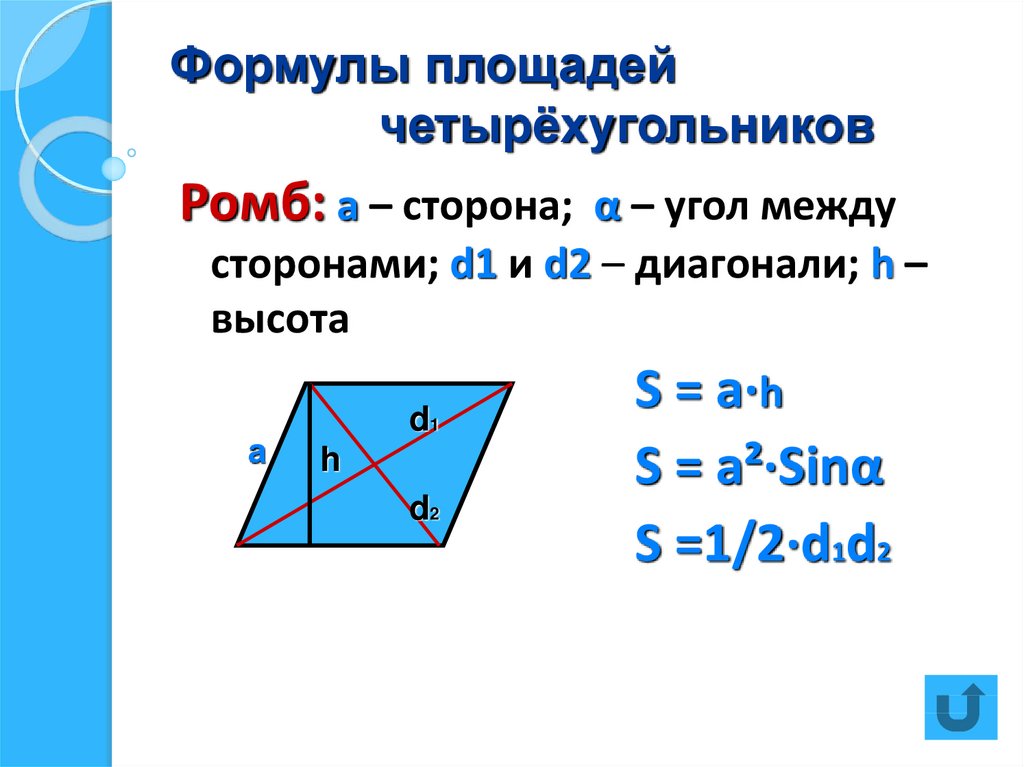 Давайте посмотрим на них.
Давайте посмотрим на них.
Площадь четырехугольника с использованием координат
Площадь четырехугольника можно вычислить, если известны координаты его вершин. Рассмотрим четырехугольник в координатной плоскости, как показано ниже:
. (_2\)), C(x\(_3\), y\(_3\)) и D(x\(_4\), y\(_4\)) — вершины.
Чтобы найти площадь четырехугольника ABCD, возьмем вершины A(x\(_1\), y\(_1\)), B(x\(_2\), y\(_2\)), C( x\(_3\), y\(_3\)) и D(x\(_4\), y\(_4\)) четырехугольника ABCD и запишите их, как показано ниже,
Сложите диагональные произведения x\(_1\)y\(_2\), x\(_2\)y\(_3\), x\(_3\)y\(_4\) и x\( _4\)y\(_1\) , которые показаны синими стрелками на изображении выше.
(х\(_1\)у\(_2\) + х\(_2\)у\(_3\) + х\(_3\)у\(_4\) + х\(_4\)у \(_1\)) → (1)
Складываем диагональные произведения x\(_2\)y\(_1\), x\(_3\)y\(_2\), x\(_4\)y\ (_3\) и x\(_1\)y\(_4\), которые показаны оранжевыми стрелками.
(х\(_2\)у\(_1\) + х\(_3\)у\(_2\) + х\(_4\)у\(_3\) + х\(_1\) у\(_4\)) → (2)
Вычтите (2) из (1) и умножьте разницу на 1/2, чтобы получить площадь четырехугольника ABCD.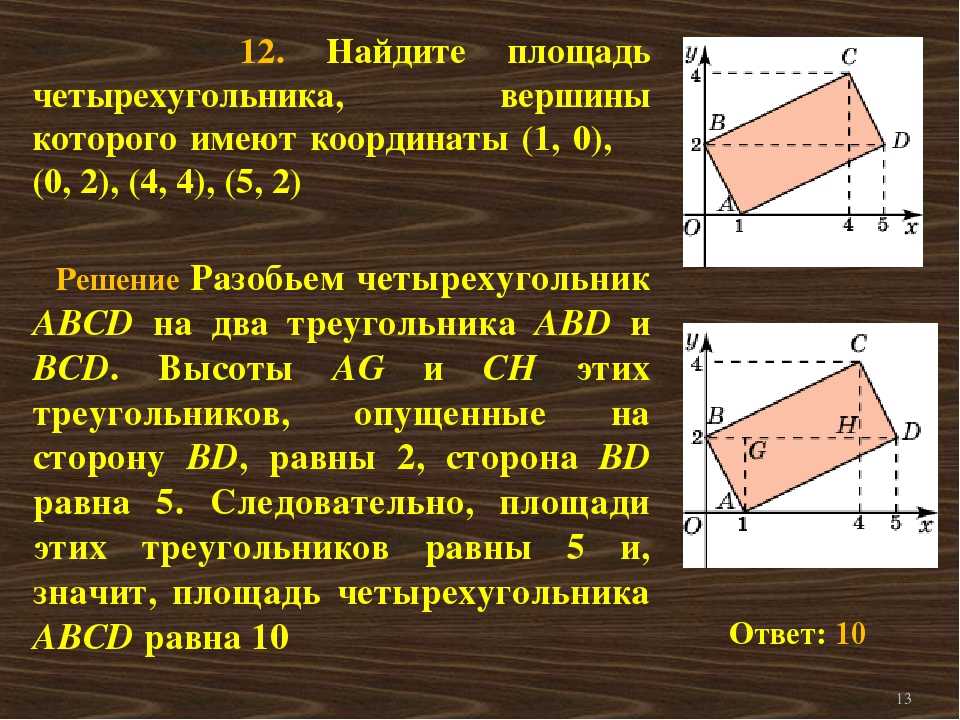
Итак, площадь четырехугольника ABCD определяется как
A = (1/2) ⋅ {(x\(_1\)y\(_2\) + x\(_2\)y\(_3\) + х\(_3\)у\(_4\) + х\(_4\)у\(_1\)) — (х\(_2\)у\(_1\) + х\(_3\) y\(_2\) + x\(_4\)y\(_3\) + x\(_1\)y\(_4\))}
Примечание: Мы также можем вычислить площадь четырехугольника используя координаты вершин, разделив его на два треугольника и добавив их соответствующие площади. Давайте разберемся с этой техникой на примере, приведенном ниже,
Пример: Рассмотрим следующие четыре точки: A(−3, 1), B(−1, 4), C(3, 2), D(1, −2). Эти четыре точки являются вершинами четырехугольника:
Здесь мы разделим четырехугольник на два треугольника (используя любую из диагоналей), вычислим (положительное значение) площади каждого треугольника и добавим эти значения к получить общую площадь. На следующем рисунке четырехугольник ABCD разделен на ΔABD и ΔADC.
Теперь вычислим площади двух треугольников по отдельности.
Площадь треугольника ABC:
= (1/2) |−3 × (4 − 2) + (−1) × (2 − 1) + 3 × (1 − 4)| = (1/2) |−6−1−9| = (1/2) × 16 = 8 квадратных единиц
Площадь треугольника ACD:
= (1/2) |−3 × (−2 − 2) + 1 × (2 − 1) + 3 × (1 −(−2))|
= (1/2)|12 + 1 + 9| = (1/2) × 22 = 11 квадратных единиц
Площадь четырехугольника ABCD:
Площадь (ABCD) = площадь (ΔABC) + площадь (ΔADC) = 8 + 11 = 19 квадратных единиц
Ниже перечислены некоторые темы, связанные с площадью четырехугольников.
- Типы четырехугольников
- Периметр четырехугольника
- 2D-фигуры
- 3D-фигуры
Площадь четырехугольника Примеры
Пример 1: Найдите площадь прямоугольника, длина которого 10 дюймов, а ширина 15 дюймов.
Решение:
Длина прямоугольника l = 10 дюймов. = 15 дюймов.
Используя формулы площади четырехугольника, площадь (A) данного прямоугольника равна,
А = l × b = 10 × 15 = 150 в 2 .

Ответ: Площадь данного прямоугольника = 150 в 2 .
Пример 2: Найдите площадь воздушного змея, диагонали которого составляют 18 единиц и 15 единиц.
Решение:
Диагонали данного воздушного змея равны, d\(_1\) = 18 единиц и d\(_2\) = 15 единиц.
Используя формулы площади четырехугольника, площадь (A) данного воздушного змея составляет,
A = (1/2) × d\(_1\) × d\(_2\) = (1/2) × 18 × 15 = 135 квадратных единиц.
Ответ: Площадь данного воздушного змея = 135 квадратных единиц.
Пример 3: Найдите площадь следующего четырехугольника. Округлите ответ до двух знаков после запятой.
Решение:
Стороны данного четырехугольника равны,
а = 15; б = 12; с = 8; и d = 10,
Его полупериметр равен s = (a + b + c + d)/2 = (15 + 12 + 8 + 10)/2 = 22,5. 9{2} \frac{180}{2}}\) ≈ 119,47
Ответ: Площадь данного четырехугольника = 119,47 квадратных единиц.

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по площади четырехугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади четырехугольника
Какова площадь четырехугольника в математике?
Площадь четырехугольника – это площадь, заключенная в нем. Он измеряется в квадратных единицах, таких как 2 , см 2 , м 2 и т. д.
Что такое формула площади четырехугольника?
Площадь четырехугольника можно найти, разделив его на два треугольника диагональю. Когда длина диагонали и высоты двух треугольников известны, площадь (A) четырехугольника равна A = (1/2) × Диагональ × (Сумма высот). 9{2} \frac{\theta}{2}}\), где s – полупериметр четырехугольника. т. е. s = (a + b + c + d)/2.
9{2} \frac{\theta}{2}}\), где s – полупериметр четырехугольника. т. е. s = (a + b + c + d)/2.
Как найти площадь четырехугольника по формуле Герона?
Мы знаем, что площадь четырехугольника можно найти, разделив его диагональю на два треугольника. Кроме того, мы знаем, что площадь треугольника с тремя сторонами можно найти по формуле Герона. По формуле Герона площадь треугольника со сторонами a, b и c определяется выражением \(\sqrt{s(s-a)(s-b)(s-c)}\), где s – полупериметр треугольника. треугольник. т. е. s = (a + b + c)/2. Используя эту формулу, мы можем найти площади двух треугольников (которые образованы четырехугольником) и сложить их, чтобы получить площадь четырехугольника.
Какие существуют формулы для нахождения площадей четырехугольников различных типов?
Для нахождения площадей различных типов четырехугольников используются разные формулы. Вот они:
- Площадь квадрата со стороной x равна x 2 .
- Площадь прямоугольника с размерами l и b равна l × b.

- Площадь параллелограмма с основанием b и высотой h равна b × h.
- Площадь трапеции, параллельные стороны которой равны «a» и «b», а высота (перпендикулярное расстояние между «a» и «b») «h» равна (1/2) (a + b) h.
- Площадь ромба с диагоналями d\(_1\) и d\(_2\) равна (1/2) × d\(_1\) × d\(_2\).
- Площадь воздушного змея с диагоналями d\(_1\) и d\(_2\) равна (1/2) × d\(_1\) × d\(_2\).
Как найти площадь четырехугольника с координатами?
Когда вершины четырехугольника заданы координатами, сначала найдите длины 4 сторон и длину диагонали, используя формулу расстояния. Затем разделите четырехугольник на две части с помощью найденной диагонали, найдите площадь каждого треугольника по формуле Герона, а затем сложите площади двух треугольников, чтобы получить площадь четырехугольника.
Четырехугольники
Обзор
[Вернитесь к началу страницы]
Четырехугольник (от латинского «quadri», что означает «квадрат» и «latus», что означает «сторона») — это четырехсторонний многоугольник (многоугольник — это плоская замкнутая форма с несколькими прямыми ребрами).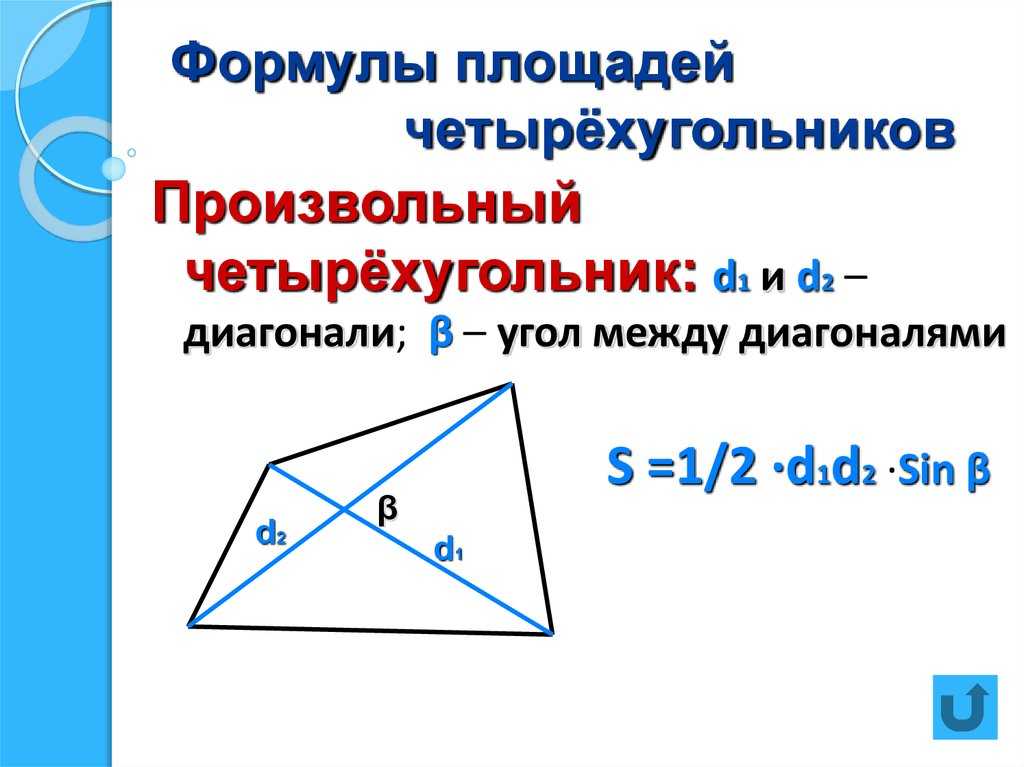 Существует несколько типов четырехугольников, каждый со своими отличительными характеристиками. Однако есть некоторые характеристики, общие для всех простых четырехугольников. Существует также тип четырехугольника, называемый сложным или пересеченным четырехугольником , о котором мы поговорим позже. Если не указано иное, термин четырехугольник используется здесь для обозначения простых четырехугольников. Четырехугольники не только имеют четыре стороны, но и имеют четыре вершины, четыре внутренних угла и две диагонали ( диагональ — это воображаемая линия, соединяющая противоположные вершины). Сумма внутренних углов всегда равна триста шестьдесят градусов (360°). Кстати, стоит отметить, что сумма внутренних углов S для любого многоугольника связана с количеством сторон n , которые имеет многоугольник, следующей формулой:
Существует несколько типов четырехугольников, каждый со своими отличительными характеристиками. Однако есть некоторые характеристики, общие для всех простых четырехугольников. Существует также тип четырехугольника, называемый сложным или пересеченным четырехугольником , о котором мы поговорим позже. Если не указано иное, термин четырехугольник используется здесь для обозначения простых четырехугольников. Четырехугольники не только имеют четыре стороны, но и имеют четыре вершины, четыре внутренних угла и две диагонали ( диагональ — это воображаемая линия, соединяющая противоположные вершины). Сумма внутренних углов всегда равна триста шестьдесят градусов (360°). Кстати, стоит отметить, что сумма внутренних углов S для любого многоугольника связана с количеством сторон n , которые имеет многоугольник, следующей формулой:
S = ( n — 2) 180°
Простой четырехугольник имеет четыре стороны и четыре внутренних угла
Говоря о четырехугольниках, мы часто имеем в виду отношения между различными сторонами и углами. Возможно, наиболее важно то, что мы различаем стороны или углы, равные 9.0005 подряд и те, что напротив друг друга. Чтобы избежать возможной путаницы в дальнейшем, вот несколько кратких определений со ссылкой на простой четырехугольник, показанный выше, того, что на самом деле означают эти термины:
Возможно, наиболее важно то, что мы различаем стороны или углы, равные 9.0005 подряд и те, что напротив друг друга. Чтобы избежать возможной путаницы в дальнейшем, вот несколько кратких определений со ссылкой на простой четырехугольник, показанный выше, того, что на самом деле означают эти термины:
- Смежные углы — два угла являются последовательными, если их вершины соединены общей стороной. Углы ABC и BCD являются последовательными.
- Противоположные углы — два угла противоположны, если они , а не последовательных. Углы ABC и CDA противоположны.
- Последовательные стороны — две стороны являются последовательными, если они пересекаются в одной вершине. Стороны CD и DA идут последовательно.
- Противоположные стороны — две стороны противоположны, если они не последовательных.
 Стороны BC и DA противоположны.
Стороны BC и DA противоположны.
Виды четырехугольника
[Вернитесь к началу страницы]
Различные типы четырехугольников имеют разные свойства, которые определяются конкретным соотношением между сторонами и углами четырехугольника. Вполне возможно иметь четырехугольник, у которого нет двух одинаковых сторон и двух одинаковых углов. С другой стороны, любые две или более сторон могут быть равны по длине, и любые два или более углов могут иметь одинаковую величину. Кроме того, одна или обе пары противоположных сторон могут быть параллельными. Результатом многих конфигураций являются формы с определенными именами, и по крайней мере некоторые из этих имен, вероятно, вам знакомы. Примеры различных конфигураций показаны ниже вместе с названием каждой формы и кратким описанием ее характеристик.
- Квадрат — вероятно, самый простой тип четырехугольника для работы из-за его простоты, и, безусловно, один из самых узнаваемых.
 Квадрат называется равносторонним , потому что все четыре стороны имеют одинаковую длину (это делает квадрат как правильным многоугольником , так и правильным четырехугольником ), и все четыре внутренних угла прямые (т.е. девяносто градусов). . Диагонали квадрата имеют одинаковую длину, делят друг друга пополам и равны ортогональны (т.е. они пересекаются под прямым углом). По определению, квадрат также является прямоугольником , параллелограммом и ромбом (см. ниже).
Квадрат называется равносторонним , потому что все четыре стороны имеют одинаковую длину (это делает квадрат как правильным многоугольником , так и правильным четырехугольником ), и все четыре внутренних угла прямые (т.е. девяносто градусов). . Диагонали квадрата имеют одинаковую длину, делят друг друга пополам и равны ортогональны (т.е. они пересекаются под прямым углом). По определению, квадрат также является прямоугольником , параллелограммом и ромбом (см. ниже).
У квадрата четыре равные стороны и четыре прямых угла
- Прямоугольник — как и у квадрата, все четыре внутренних угла прямые (т.е. девяносто градусов), противоположные стороны имеют одинаковую длину, диагонали также имеют одинаковую длину и делят друг друга пополам. При этом соседние стороны могут иметь разную длину. По определению прямоугольник также является параллелограммом.

Только противоположные стороны прямоугольника должны быть равны
- Параллелограмм — обе пары противоположных сторон параллельны (отсюда и название), противоположные стороны имеют одинаковую длину, а противоположные углы равны по величине. Диагонали, хотя и имеют одинаковую длину только тогда, когда параллелограмм представляет собой квадрат или прямоугольник , всегда делят друг друга пополам. Каждая из диагоналей делит параллелограмм на два равных треугольника. Смежные углы равны дополнительный (т.е. они всегда в сумме составляют сто восемьдесят градусов). Обратите внимание, что параллелограмм, в котором смежные стороны имеют разную длину, а все внутренние углы косые, иногда называют ромбом (в отличие от ромба , который является параллелограммом, в котором все четыре стороны равны ). одинаковая длина — см. ниже).
Показанный здесь параллелограмм является ромбовидным
- Ромб — ромб является равносторонним параллелограммом, т.
 е. имеет четыре стороны одинаковой длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют одинаковую величину, последовательные углы являются дополнительными (т. Е. В сумме они составляют сто восемьдесят градусов), а диагонали делят друг друга пополам. Диагонали ромба также делят внутренние углы пополам и составляют ортогональных (т.е. они пересекаются под прямым углом).
е. имеет четыре стороны одинаковой длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют одинаковую величину, последовательные углы являются дополнительными (т. Е. В сумме они составляют сто восемьдесят градусов), а диагонали делят друг друга пополам. Диагонали ромба также делят внутренние углы пополам и составляют ортогональных (т.е. они пересекаются под прямым углом).
Ромб – это равносторонний параллелограмм
- Трапеция — это название используется за пределами Северной Америки, где его называют трапецией . Хотя мнения относительно строгого определения трапеции различаются, здесь мы будем использовать то, что трапеция — это четырехугольник, у которого есть одна пара, а только одна пара , противоположных сторон, которые параллельны. На иллюстрации ниже показаны три возможных варианта трапеции. цифра слева равнобедренная трапеция , у которой углы, прилежащие к каждой из параллельных сторон, равны, а непараллельные стороны и диагонали равны по длине.
 У центральной фигуры одна сторона перпендикулярна обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. У последней (самой правой) фигуры непараллельные стороны разной длины, и все внутренние углы разные.
У центральной фигуры одна сторона перпендикулярна обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. У последней (самой правой) фигуры непараллельные стороны разной длины, и все внутренние углы разные.
Возможны различные конфигурации трапеции
- Воздушный змей — воздушный змей отличается тем, что имеет две пары конгруэнтных (т.е. одинаковой длины) смежных сторон. Ни одна пара противоположных сторон не параллельна (если бы они были параллельны, учитывая, что соседние стороны равны, то полученный четырехугольник был бы либо ромбом, либо квадратом). Диагонали воздушного змея ортогональны (т.е. они пересекаются под прямым углом), а самая длинная диагональ делит воздушного змея на два конгруэнтных треугольника. Противоположные углы по обе стороны от большей диагонали равны по величине.
Воздушный змей имеет две пары конгруэнтных сторон
- Дротик — как и воздушный змей, дротик — иногда называемый наконечником стрелы или шевроном — имеет две пары конгруэнтных (т.
 е. одинаковой длины) смежных сторон. Ни одна из сторон не параллельна, а диагонали воздушного змея ортогональны (т.е. они пересекаются под прямым углом). В отличие от воздушного змея, диагонали пересекают вне форму, а один из углов (угол, примыкающий к обеим более коротким сторонам) представляет собой рефлекторный угол (т.е. больше 180°). Противоположные углы по обе стороны от диагонали, делящей этот рефлекторный угол пополам, равны по величине. Все четырехугольники до этого момента были выпуклыми (т. е. ни один из внутренних углов не превышал ста восьмидесяти градусов). Наличие внутреннего угла свыше ста восьмидесяти градусов означает, что дротик вогнутая четырехугольная. Также возможен подобный (вогнутый) четырехугольник, у которого нет двух сторон одинаковой длины.
е. одинаковой длины) смежных сторон. Ни одна из сторон не параллельна, а диагонали воздушного змея ортогональны (т.е. они пересекаются под прямым углом). В отличие от воздушного змея, диагонали пересекают вне форму, а один из углов (угол, примыкающий к обеим более коротким сторонам) представляет собой рефлекторный угол (т.е. больше 180°). Противоположные углы по обе стороны от диагонали, делящей этот рефлекторный угол пополам, равны по величине. Все четырехугольники до этого момента были выпуклыми (т. е. ни один из внутренних углов не превышал ста восьмидесяти градусов). Наличие внутреннего угла свыше ста восьмидесяти градусов означает, что дротик вогнутая четырехугольная. Также возможен подобный (вогнутый) четырехугольник, у которого нет двух сторон одинаковой длины.
Дротик представляет собой вогнутый четырехугольник
Надписываемые четырехугольники
[Вернитесь к началу страницы]
Любой четырехугольник, все четыре стороны которого касаются вписанной окружности (т. е. круг, нарисованный полностью внутри четырехугольника, который касается всех четырех сторон) называется записываемым (или касательным ). Из четырехугольников, которые мы рассмотрели выше, надписываемыми являются только квадрат, ромб и воздушный змей (см. иллюстрацию ниже). Чтобы четырехугольник был надписываемым, он должен быть выпуклым четырехугольником, а длины любой пары противоположных сторон должны в сумме давать одинаковую общую длину.
е. круг, нарисованный полностью внутри четырехугольника, который касается всех четырех сторон) называется записываемым (или касательным ). Из четырехугольников, которые мы рассмотрели выше, надписываемыми являются только квадрат, ромб и воздушный змей (см. иллюстрацию ниже). Чтобы четырехугольник был надписываемым, он должен быть выпуклым четырехугольником, а длины любой пары противоположных сторон должны в сумме давать одинаковую общую длину.
Квадрат, ромб и воздушный змей — все это примеры четырехугольников, которые можно написать.
Описываемые четырехугольники
[Вернитесь к началу страницы]
Любой четырехугольник, все четыре вершины которого лежат на одной окружности, называется описанным (или циклическим ). Из четырехугольников, которые мы рассмотрели выше, квадрат, прямоугольник, воздушный змей и равнобедренная трапеция являются описанными (см. иллюстрацию ниже). Четырехугольник, который является описанным и inscriptable считаются бицентрическими . Квадрат является примером двухцентрового четырехугольника. Воздушный змей также может быть бицентрическим, если у него есть два противоположных угла, которые являются прямыми углами (такие воздушные змеи называются прямыми воздушными змеями ).
иллюстрацию ниже). Четырехугольник, который является описанным и inscriptable считаются бицентрическими . Квадрат является примером двухцентрового четырехугольника. Воздушный змей также может быть бицентрическим, если у него есть два противоположных угла, которые являются прямыми углами (такие воздушные змеи называются прямыми воздушными змеями ).
Квадрат, прямоугольник, прямой воздушный змей и равнобедренная трапеция являются описанными четырехугольниками.
Квадрат и правый воздушный змей являются примерами двухцентровых четырехугольников.
Бимедианы и центроид
[Вернитесь к началу страницы]
Бимедиана — это отрезок, соединяющий середины противоположных сторон четырехугольника. Бимедианы четырехугольника делят друг друга пополам, и в случае параллелограмма точка, в которой они пересекаются, известна как центр тяжести .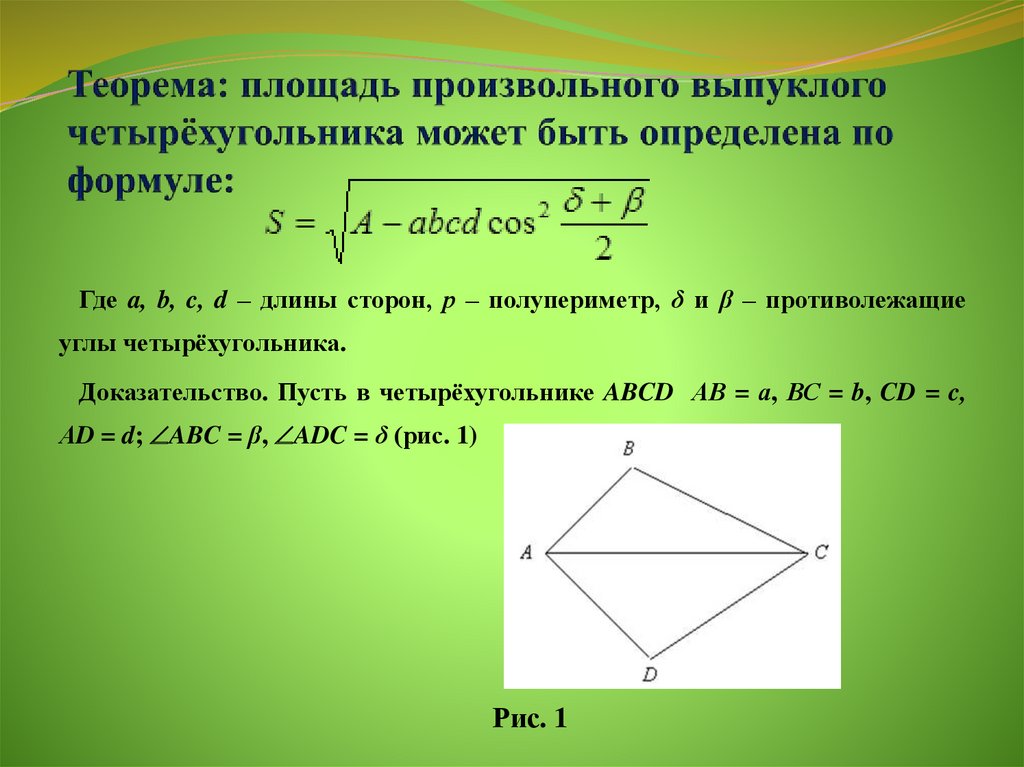 Любая прямая, проходящая через центр тяжести параллелограмма, разделит параллелограмм на две равные части. Если бы параллелограмм был изготовлен из плоского листа какого-либо подходящего материала одинаковой толщины и плотности, центр тяжести был бы центром масс этого четырехугольного объекта. На приведенной ниже диаграмме бимедианы помечены, а точка, в которой они пересекаются, является центроидом. Показана третья линия, проходящая через центр тяжести и делящая параллелограмм на две равные части.
Любая прямая, проходящая через центр тяжести параллелограмма, разделит параллелограмм на две равные части. Если бы параллелограмм был изготовлен из плоского листа какого-либо подходящего материала одинаковой толщины и плотности, центр тяжести был бы центром масс этого четырехугольного объекта. На приведенной ниже диаграмме бимедианы помечены, а точка, в которой они пересекаются, является центроидом. Показана третья линия, проходящая через центр тяжести и делящая параллелограмм на две равные части.
Любая линия, проходящая через центр тяжести, делит параллелограмм на две равные части.
Нахождение площади четырехугольника
[Вернитесь к началу страницы]
Найти площадь квадрата или прямоугольника несложно, если вы знаете длину основания b и высоту h четырехугольника, и в этом случае площадь A определяется по формуле:
А = б × ч
Площадь квадрата или прямоугольника равна произведению длины основания на высоту
Найти площадь параллелограмма или ромба (который является просто равносторонним параллелограммом) также относительно просто. Мы можем думать о параллелограмме как о прямоугольнике, у которого прямоугольный треугольник удален с одного конца и приклеен к другому концу. Принцип проиллюстрирован ниже. На диаграмме видно, что если обратить этот процесс вспять, получится прямоугольник с той же площадью, что и у параллелограмма, поскольку на самом деле мы ничего не удаляли. Размер основания также останется для прямоугольника таким же, как и для параллелограмма, так как мы просто взяли часть основания с одного конца параллелограмма и прилепили его к другому концу. Зная длину основания (b) и высоту (h) четырехугольника, вы можете использовать ту же формулу для нахождения площади параллелограмма или ромба, что и для квадрата или прямоугольника ( площадь = б × ч ).
Мы можем думать о параллелограмме как о прямоугольнике, у которого прямоугольный треугольник удален с одного конца и приклеен к другому концу. Принцип проиллюстрирован ниже. На диаграмме видно, что если обратить этот процесс вспять, получится прямоугольник с той же площадью, что и у параллелограмма, поскольку на самом деле мы ничего не удаляли. Размер основания также останется для прямоугольника таким же, как и для параллелограмма, так как мы просто взяли часть основания с одного конца параллелограмма и прилепили его к другому концу. Зная длину основания (b) и высоту (h) четырехугольника, вы можете использовать ту же формулу для нахождения площади параллелограмма или ромба, что и для квадрата или прямоугольника ( площадь = б × ч ).
Площадь параллелограмма или ромба также равна произведению длины основания на высоту.
Найти площадь трапеции не так просто. Однако, как и в случае с параллелограммом, мы можем разбить трапецию на простые формы, чтобы посмотреть, как можно вычислить площадь:
Трапецию можно разбить на простые фигуры
Из диаграммы видно, что общая площадь трапеции ABCD будет равна сумме площадей прямоугольника FBCE и прямоугольных треугольников ABF и ECD.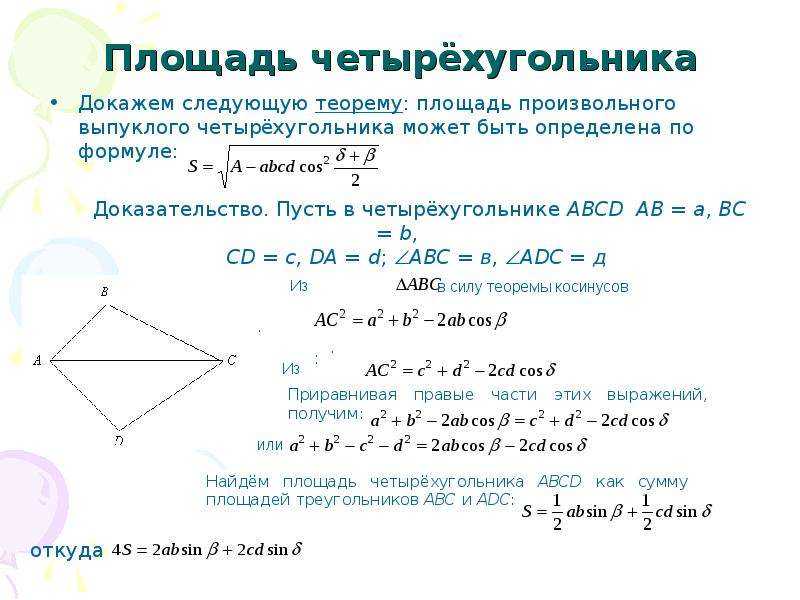 Теперь добавим длину более короткой параллельной стороны трапеции (вершина трапеции) к более длинной параллельной стороне (основание трапеции) и создадим прямоугольник, как показано ниже. В дополнение к прямоугольнику FBCE и треугольникам ABF и ECD наш новый прямоугольник содержит точные копии этих фигур и, таким образом, имеет площадь, вдвое превышающую площадь исходной трапеции. Таким образом, чтобы получить площадь трапеции, просто сложите длины двух параллельных сторон, умножьте результат на высоту трапеции (это будет перпендикулярное расстояние между двумя параллельными сторонами), а затем разделите результат на два.
Теперь добавим длину более короткой параллельной стороны трапеции (вершина трапеции) к более длинной параллельной стороне (основание трапеции) и создадим прямоугольник, как показано ниже. В дополнение к прямоугольнику FBCE и треугольникам ABF и ECD наш новый прямоугольник содержит точные копии этих фигур и, таким образом, имеет площадь, вдвое превышающую площадь исходной трапеции. Таким образом, чтобы получить площадь трапеции, просто сложите длины двух параллельных сторон, умножьте результат на высоту трапеции (это будет перпендикулярное расстояние между двумя параллельными сторонами), а затем разделите результат на два.
Площадь прямоугольника вдвое больше площади исходной трапеции.
Мы можем выполнить аналогичное упражнение с воздушным змеем. Поскольку диагонали воздушного змея перпендикулярны (под прямым углом) друг к другу, воздушный змей можно разбить на две пары конгруэнтных прямоугольных треугольников. Мы можем нарисовать прямоугольник EFGH вокруг воздушного змея ABCD, как показано ниже. Из диаграммы вы должны увидеть, что треугольники ABO, AEB, AOD и ADH равны. Точно так же равны треугольники BCO, BFC, DOC и DCG. Сумма площадей треугольников внутри форма воздушного змея и сумма площадей треугольников вне форма воздушного змея должны быть равны. Отсюда следует, что площадь прямоугольника EFGH должна быть ровно в раз больше площади змея ABCD. Мы видим, что длина основания GH прямоугольника равна длине диагонали AC , а высота EH прямоугольника равна длине диагонали BD . Таким образом, площадь прямоугольника можно рассчитать как произведение диагоналей воздушного змея, а площадь самого воздушного змея будет равна половина прямоугольника.
Из диаграммы вы должны увидеть, что треугольники ABO, AEB, AOD и ADH равны. Точно так же равны треугольники BCO, BFC, DOC и DCG. Сумма площадей треугольников внутри форма воздушного змея и сумма площадей треугольников вне форма воздушного змея должны быть равны. Отсюда следует, что площадь прямоугольника EFGH должна быть ровно в раз больше площади змея ABCD. Мы видим, что длина основания GH прямоугольника равна длине диагонали AC , а высота EH прямоугольника равна длине диагонали BD . Таким образом, площадь прямоугольника можно рассчитать как произведение диагоналей воздушного змея, а площадь самого воздушного змея будет равна половина прямоугольника.
Прямоугольник имеет двойную площадь воздушного змея, который он содержит.
Нахождение площади дротика представляет собой другую задачу, потому что форма вогнутая (в отличие от выпуклых форм, которые мы рассмотрели выше).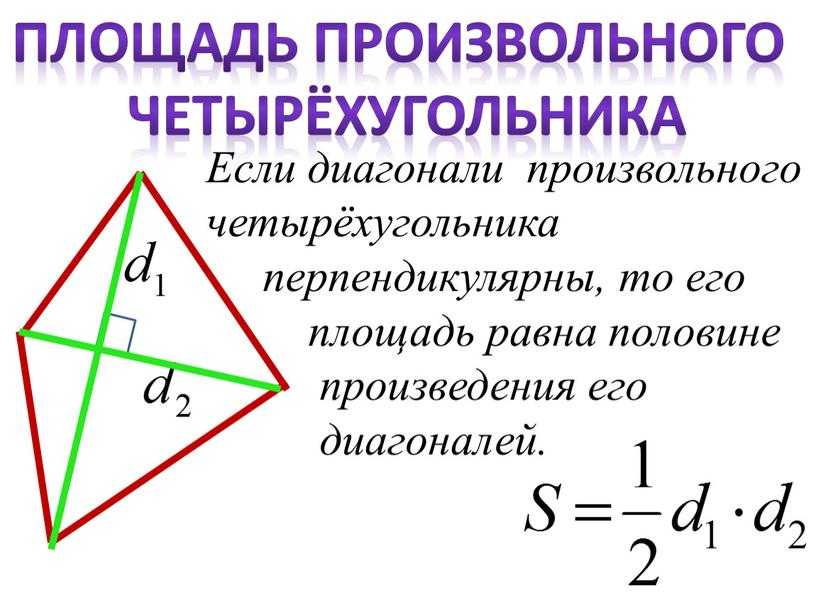 Однако мы можем применить тот же принцип, что и раньше, и разбить дротик на два конгруэнтных треугольника. Площадь треугольника можно легко вычислить, умножив длину основания треугольника на его высоту, а затем разделив результат на два. Поскольку треугольники ABC и ACD (см. иллюстрацию ниже) равны, все, что нам нужно сделать, чтобы найти площадь дротика ABCD, — это найти длину основания и высоту треугольника ACD и вычислить их произведение.
Однако мы можем применить тот же принцип, что и раньше, и разбить дротик на два конгруэнтных треугольника. Площадь треугольника можно легко вычислить, умножив длину основания треугольника на его высоту, а затем разделив результат на два. Поскольку треугольники ABC и ACD (см. иллюстрацию ниже) равны, все, что нам нужно сделать, чтобы найти площадь дротика ABCD, — это найти длину основания и высоту треугольника ACD и вычислить их произведение.
Дротик можно рассматривать как два конгруэнтных треугольника.
До сих пор мы имели дело с нахождением площадей различных видов четырехугольников в каждом конкретном случае. Однако не все четырехугольники вписываются в одну из категорий, которые мы рассматривали до сих пор, и было бы полезно иметь общую формулу для нахождения площади любого выпуклого четырехугольника. Как и следовало ожидать, формула, которая работает для всех случаев, несколько сложнее, чем формула, применимая только к одному конкретному типу четырехугольника. Однако существует несколько таких формул. Один из самых известных из них дается как:
Однако существует несколько таких формул. Один из самых известных из них дается как:
| Площадь = √ | ( | ( S — A ) ( S — B ) ( S — C ) ( S —5555555 годы — C ) ( — 55555 гг. — | ( ac + bd + pq )( ac + bd — pq ) | ) |
| 4 |
куда:
- а , б , c и d представляют собой длины сторон четырехугольника ( a и c составляют одну пару противоположных сторон, b и d составляют другую)
- p и q — диагонали четырехугольника
- s — это сумма длин четырех сторон, деленная на два (т.
 е. половина периметра четырехугольника, иначе известного как полупериметр ):
е. половина периметра четырехугольника, иначе известного как полупериметр ):
| S = | A + B + C + D |
| 2 |
Чтобы проверить формулу, мы будем использовать неправильный выпуклый четырехугольник ABCD (показан ниже). Четырехугольник не имеет двух одинаковых сторон или углов, но, как и все выпуклые четырехугольники, его можно разбить на два треугольника с помощью одной из диагоналей. Мы воспользуемся этим фактом, чтобы перепроверить ответ, который мы получим, используя общую формулу площади четырехугольника.
У этого четырехугольника нет двух одинаковых сторон или углов
Длины сторон a , b , c и d , а также длины диагоналей p и q найдены путем измерения упражнения) и с точностью до двух знаков после запятой выглядят следующим образом:
а = 5,10
B = 4,12
C = 3,61
D = 3,16
P = 4,47
Q = 6,40
Значение s определяется следующим образом:
| s = | (5.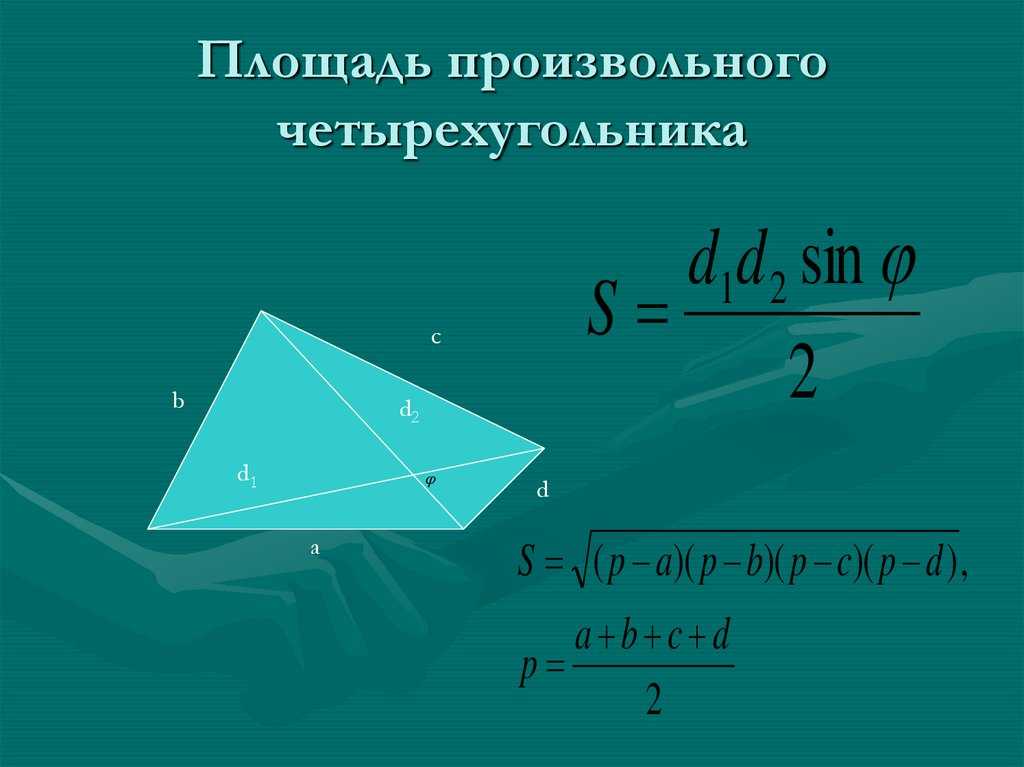 10 + 4.12 + 3.61 + 3.16) 10 + 4.12 + 3.61 + 3.16) | = | 15.99 | = 8.0 |
| 2 | 2 |
Значение ( s — a )( s — b )( s — c )( s — d ) определяется как:
(2,9)(3,88)(4,39)(4,84) = 239,08
Значение ( ac + bd + pq )( ac + bd — pq ) определяется по формуле:
(18,41 + 13,02 + 28,61) × (18,41 + 13,02 – 28,61) = 60,04 × 2,82 = 169.31
Таким образом, площадь четырехугольника равна:
| Area = √ | ( | 239.08 — | 169.31 | ) |
| 4 |
Район = √(239,08 — 42,33)
Район = √196,75 = 14,03
Мы можем перепроверить ответ, используя треугольники ABD и BCD. Сначала возьмем треугольник ABD, пусть основание треугольника будет стороной 9.0005 AD , а высота треугольника равна отрезку BF (перпендикулярному отрезку от стороны AD до вершины B). Мы уже знаем, что сторона AD имеет длину 3,16 единицы, а отрезок BF измеряется как 4,43 единицы (с точностью до двух знаков после запятой), поэтому мы получаем:
Сначала возьмем треугольник ABD, пусть основание треугольника будет стороной 9.0005 AD , а высота треугольника равна отрезку BF (перпендикулярному отрезку от стороны AD до вершины B). Мы уже знаем, что сторона AD имеет длину 3,16 единицы, а отрезок BF измеряется как 4,43 единицы (с точностью до двух знаков после запятой), поэтому мы получаем:
| Площадь треугольника ABD = | AD · BF | = | 3,16 × 4,43 | = 7,0 |
| 2 | 2 |
Теперь возьмем треугольник BCD, пусть основание треугольника будет стороной CD , а высота треугольника будет отрезком BE (это отрезок перпендикулярной линии от стороны CD к вершине B). Мы знаем, что сторона CD имеет длину 3,61 единицы, а отрезок BE измеряется как 3,88 единицы (с точностью до двух знаков после запятой), поэтому мы получаем:
| Area of triangle ABD = | CD · BE | = | 3. 61 × 3.88 61 × 3.88 | = 7.0 |
| 2 | 2 |
Площадь четырехугольника ABCD равна площади треугольника ABD плюс площадь треугольника BCD, поэтому получаем:
Площадь четырехугольника ABCD = 7,0 + 7,0 = 14,0
В двух полученных нами результатах есть очень незначительное различие, которое можно объяснить ошибками округления. В расчеты (при использовании любого метода) также может вкрадываться некоторая неточность в зависимости от точности, с которой проводятся измерения. Глядя на вышеизложенное, вы можете подумать, что разбить неправильный выпуклый четырехугольник на два треугольника для получения площади — это более простой вариант, и с точки зрения сложности вычислений вы были бы правы. С другой стороны, в то время как мы можем легко измерить стороны и диагонали четырехугольника, нахождение высоты треугольника может быть немного сложнее, потому что это обычно включает в себя нахождение перпендикуляра от любой стороны, которую вы выбрали в качестве основания, к противоположной вершине.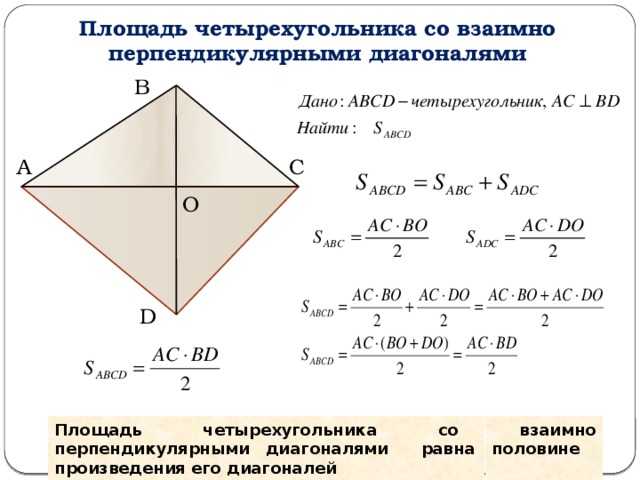 Это может потребовать от вас выполнения какой-либо конструкции (например, с помощью транспортира или циркуля), чтобы найти указанный перпендикуляр, прежде чем вы сможете его измерить.
Это может потребовать от вас выполнения какой-либо конструкции (например, с помощью транспортира или циркуля), чтобы найти указанный перпендикуляр, прежде чем вы сможете его измерить.
Сложные четырехугольники
[Вернитесь к началу страницы]
Сложный четырехугольник (часто называемый скрещенным четырехугольником или четырехугольником-бабочкой , среди прочего) — это тот, в котором две несмежные стороны пересекают друг друга, как показано ниже. Вопреки тому, что вы можете интуитивно предположить, существует только четыре вершин и четыре 9 вершины.0006 внутренних углов (хотя два из них эффектно вывернуты наизнанку). Точка пересечения противоположных сторон не образует дополнительной пары вершин. Один из способов визуализировать образование сложного четырехугольника — представить себе простой выпуклый четырехугольник (скажем, квадрат или прямоугольник). Представьте, что произойдет, если вы возьмете одну из сторон четырехугольника и повернете ее вокруг середины на сто восемьдесят градусов. Представьте на мгновение, что соседние стороны сделаны из резины, чтобы они могли приспособиться к этому вращению, не отрываясь. В результате получится сложный четырехугольник, как показано ниже.
Представьте на мгновение, что соседние стороны сделаны из резины, чтобы они могли приспособиться к этому вращению, не отрываясь. В результате получится сложный четырехугольник, как показано ниже.
Сумма внутренних углов сложного четырехугольника равна 720°.
Обратите внимание на диаграмму, что сложный четырехугольник может иметь две параллельные стороны, и в этом случае диагонально противоположные внутренние углы будут дополнительными или сопряженными (т. Е. В сумме они составляют триста шестьдесят градусов). Самая левая фигура выше имеет две пары равносторонних сторон, одна из которых параллельна. Такую форму иногда называют антипараллелограмм . Общим для всех сложных четырехугольников является то, что их можно рассматривать как пару треугольников, имеющих по крайней мере один общий внутренний угол. Хотя мы не предлагаем здесь общей формулы для нахождения площади сложного четырехугольника, площадь можно вычислить как сумму площадей составляющих его треугольников. Эти площади рассчитываются как произведение длины основания и высоты каждого треугольника. Вам нужно будет сделать произвольный выбор того, какую сторону использовать в качестве базы в каждом конкретном случае. Тогда высота — это длина перпендикулярного отрезка, соединяющего основание с противоположной вершиной.
Эти площади рассчитываются как произведение длины основания и высоты каждого треугольника. Вам нужно будет сделать произвольный выбор того, какую сторону использовать в качестве базы в каждом конкретном случае. Тогда высота — это длина перпендикулярного отрезка, соединяющего основание с противоположной вершиной.
Площадь сложного четырехугольника можно найти с помощью треугольников
В сложном четырехугольнике ABCD (см. выше) площадь четырехугольника можно вычислить, найдя сумму площадей треугольников ADE и BCE. Мы взяли основание треугольника AED за сторону AD , а основание треугольника BCE за сторону BC . Высота треугольников будет равна длине перпендикуляра EG (для треугольника ADE) и длине перпендикуляра EF (для треугольника BCE). Таким образом, формулу площади четырехугольника можно записать так:
| Площадь четырехсторонней ABCD = | г. н.э.
[Вернитесь к началу страницы] н.э.
[Вернитесь к началу страницы] Формула площади четырехугольника — объяснение, типы и часто задаваемые вопросыбазовая линия; пробел: предварительно; четыре внутренних угла 360 или . Кроме того, он имеет 4 ребра (стороны) и четыре вершины (углы). Есть два разных типа четырехугольников, а именно правильные четырехугольники и неправильные четырехугольники. Несколько известных примеров четырехугольников — это квадрат, прямоугольник, трапеция, ромб, воздушный змей и параллелограмм. Площадь четырехугольника — это количество квадратных единиц, которые можно составить из него. Здесь мы рассмотрим важные формулы площади для четырехугольников и то, как найти площадь четырехугольника. Общая формула площади четырехугольникаДавайте научимся выводить общую формулу площади четырехугольника. Рассмотрим четырехугольник PQRS, приведенный ниже:
Площадь четырехугольника PQRS можно рассчитать, сложив площади двух треугольников, то есть PQR и PSR. Вычислим площадь треугольника PQR и площадь треугольника PSR. Площадь ΔPSR = 1/2 x основание x высота = 1/2 x PR x h 1 Площадь ΔPQR = 1/2 x основание x высота = 1/2 x PR x h площадь четырехугольника PQRS равна Площадь ΔPSR + площадь ΔPQR = 1/2 x PR x h 1 + 1/2 x PR x h 2 = PR(h 1 + h 2 /2) = 1/2 PR (ч 1 + ч 2 ) Следовательно, формула для нахождения площади четырехугольника получается следующим образом: Общая формула площади четырехугольника = 1/2 x длина диагоналей x (сумма высот двух треугольников). Формулы площади четырехугольника в тригонометрических терминахФормула для нахождения площади четырехугольника в тригонометрических терминах дается следующим образом: Площадь = ½ x ab x Sin θ четырехугольник и угол между ними. В случае ортогональных четырехугольников (таких как квадрат, воздушный змей и ромб) формулы минимизируются до Площадь = ½ x ab (поскольку θ равно 90 o ). Площадь четырехугольника Формула Координаты ГеометрияЕсли ABCD — четырехугольник с диагональю AC, то мы можем разделить четырехугольник на два треугольника ABC и ACD. Теперь, используя формулу площади треугольника, зная его вершины, мы можем определить площади треугольников ABC и ACD Следовательно, площадь четырехугольника по формуле координатной геометрии задается как: Площадь четырехугольника ABCD = площадь треугольника ABC + площадь треугольника ACD Используя эту информацию, мы можем найти площадь четырехугольника, если его вершины даны: Пусть вершины четырехугольника ABCD равны A ( x₁,y₁), B(x₂,y₂), C(x₃,y₃), D(x₄,y₄) Площадь четырехугольника ABCD = площадь треугольника ABD + площадь Треугольник BCD +1/2{(x₁y₂ + x₂y₄ + x₄y₁) — (x₂y₁ + x₄y₂ + x₁y₄)} = 1/2 {(x₂y₃ + x₃y₄ + x₄y₂) — (x₃y₂ + x₄y₃ + x₂y₄)} = 1/2 {(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) — (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)) — (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄) =1/2(x₁ — x₃) (y₂ — y₄) -(x₂ -x₄) (y₁ — y₃) квадратных единиц Формулы для нахождения площади четырехугольника Вот список формул для нахождения площади четырехугольников, таких как квадрат, воздушный змей, параллелограмм, трапеция, прямоугольник и ромб.
Заключение Здесь мы рассмотрели формулу площади для различных типов четырехугольников. Как правильно выбрать калькулятор четырехугольника для вашего бизнесаЕсли вам нужно рассчитать площадь или периметр четырехугольника, вам может быть интересно, подойдет ли конкретный калькулятор четырехугольника для нужд вашего бизнеса. Если да, то полезно знать, как выбрать правильный. Четырехугольник можно определить двумя способамиЧетырехугольник можно определить как замкнутую фигуру с четырьмя отрезками (сторонами) и четырьмя углами (углами). Или его можно определить более формально как многоугольник с четырьмя сторонами и четырьмя вершинами. В любом случае четырехугольник — это двумерная фигура с четырьмя сторонами. Существует множество различных типов четырехугольников, каждый из которых обладает своими уникальными свойствами. Выбирая калькулятор четырехугольника для своего бизнеса, важно учитывать, с каким типом четырехугольника вы будете работать чаще всего. Существует множество доступных онлайн-калькуляторов, которые помогут вам определить свойства различных типов четырехугольников. Если вы не уверены, с каким типом четырехугольника вам нужно работать, то, возможно, лучше выбрать обычный калькулятор четырехугольника, который имеет дополнительные функции, такие как построение графика координат или тригонометрические функции. Эти функции позволят вам производить необходимые расчеты, не переключаясь между несколькими калькуляторами. Читайте также: Как использовать калькулятор параметрических уравнений 3D Четырехугольник в математике (от латинского quadri + latus, что означает «четырехсторонний») — это плоская фигура с четырьмя сторонами. Четырехугольник имеет четыре вершины (углы) и четыре ребра (стороны). Сумма углов четырехугольника равна 360°. Если две стороны четырехугольника параллельны, то он называется параллелограммом. Если четырехугольник имеет четыре равные стороны, то он называется квадратом. Если четырехугольник имеет четыре прямых угла, то он называется прямоугольником. Если все четыре угла четырехугольника острые (меньше 90°), то он называется тупоугольным четырехугольником. Если все четыре угла четырехугольника прямые, то такой четырехугольник называется остроугольным. Теорема Пифагора связывает одну сторону прямоугольного треугольника с другой. Он гласит, что в любом прямоугольном треугольнике квадрат гипотенузы (сторона, противоположная прямому углу) в два раза больше любой из сторон, примыкающих по обе стороны. Слово «тупой» означает угол больше 90° и меньше 180°. Слово «острый» означает угол меньше 90°, но больше 0°. Остроугольный четырехугольник также называют прямоугольным четырехугольником. Если вы занимаетесь бизнесом, вполне возможно, что в какой-то момент вам понадобится вычислить площадь четырехугольника. Но с таким количеством различных четырехугольных калькуляторов на рынке, как вы узнаете, какой из них подходит для вашего бизнеса? Вот несколько советов, которые помогут вам найти идеальный калькулятор для ваших нужд: *Подумайте, какую работу вы выполняете – используйте калькулятор, который будет наиболее полезен в этом контексте. Например, если вы работаете с дизайном интерьера и вам нужно измерить и оценить вещи, рассмотрите возможность использования четырехугольника метрического калькулятора . * Спросите себя, является ли точность проблемой. Если да, то выберите расчет, который может выполнять измерения с точностью до миллиметров или даже микрометров; в противном случае выберите недорогой вариант, который даст вам приблизительное измерение и сэкономит деньги. Существуют разные способы вычисления площади четырехугольника, и каждый из них имеет свои преимущества и недостатки. Самый распространенный метод — использовать формулу A = 1/2bh, где b — основание, а h — высота. Однако это работает только в том случае, если вы знаете размеры основания и высоты. Другой метод — использовать формулу Герона, которая немного сложнее, но не требует знания размеров обеих сторон. Наконец, вы также можете использовать метод биссектрисы угла, который прост, но может быть неточным, если ваши углы не точно измерены. Чтобы выбрать правильный четырехугольник калькулятор для вашего бизнеса, важно учитывать, как вы хотите его использовать. Вам нужно долгосрочное решение или что-то быстрое? Вы бы предпочли тот, который дает точный ответ, или что-то, что допускает некоторую степень ошибки? Как часто вам нужно будет вычислять площади? С какими типами фигур вам нужно работать? Над этим проектом одновременно будут работать несколько человек? Если да, то будут ли все они иметь доступ к одному и тому же устройству? Эти вопросы должны помочь вам определить, какой тип четырехугольного калькулятора лучше всего соответствует вашим потребностям. Существует несколько различных способов вычисления площади четырехугольника, каждый из которых имеет свои преимущества и недостатки. Наиболее распространенными методами являются метод трапеций и формула Герона. Метод трапеций быстрый и простой, но он может быть неточным, если стороны четырехугольника не параллельны. Формула цапли точнее, но сложнее и требует больше информации о сторонах четырехугольника. Если вы не уверены, какой метод использовать, спросите у математика или обратитесь к калькулятору четырехугольника. Хорошим выбором может быть онлайн-калькулятор четырехугольника, который предоставляет пошаговые инструкции о том, как выполнять расчеты с использованием различных методов. Вы также должны принять во внимание свой уровень опыта, прежде чем решить, какой тип калькулятора лучше всего соответствует вашим потребностям. Если вы никогда раньше не занимались расчетами, вам может понадобиться простой четырехугольный калькулятор, который поможет вам в этом процессе. Центр масс выпуклого четырехугольника С помощью Geometer’s Sketch Pad (GSP) можно построить центр тяжести
треугольник с легкостью. Мы продемонстрируем это в свое время.
Что может быть не сразу очевидно, так это то, что мы можем расширить
это построение для определения центра масс выпуклой
четырехугольник. Нужно только отметить, что использование любой диагонали
выпуклого четырехугольника можно разделить четырехугольник на два
различные треугольники, которые в общем случае не будут иметь одинаковую площадь или массу
как бы для этого задания. В общем треугольнике выше мы уже построили середины каждой стороны треугольника, используя инструмент выбора на каждый сегмент, затем с помощью команды построения для определения середина. Далее мы хотим построить медианы, соединяющие каждый средней точки к вершине, противоположной стороне, на которой он находится. Наконец,
в качестве последнего шага мы помечаем общие пересечения медиан как
центроид, который мы ищем (хотя на самом деле необходимы только две медианы). Один
может спросить, почему это производит центр масс данного треугольника.
Сначала мы должны обратиться к важному техническому допущению, которое
необходимо для того, чтобы наше утверждение было верным. Будем считать, что все полигоны
имеют одинаковую толщину и плотность, иначе наше утверждение вполне могло бы быть
ЛОЖЬ. Теперь, согласно первому предположению, каждая медиана делит
треугольник на две части, и это главное, одинакового размера.
Это можно увидеть, рассматривая любую из трех сторон как основу
треугольник. Когда мы делим отрезок пополам и строим медиану
мы эффективно создаем два треугольника одинаковой длины основания и
одинаковая высота; чистый результат состоит в том, что каждый треугольник имеет то же самое
область. Теперь рассмотрим один из двух оставшихся сегментов и
треугольник из только что построенных с ним в качестве стороны. Когда мы
разделите эту сторону пополам и постройте медиану мы, затем повторите то же самое
процесс для последнего сегмента мы создаем два треугольника с равным основанием
длина на сегменте, с медианой, прикрепленной к сегменту как
общая высота и исключенные медианы, действующие как соответствующие стороны,
так что эти два треугольника равны. Ниже приведен общий выпуклый четырехугольник. Если для данного четырехугольника провести поочередно одну из двух диагоналей, то образуются два треугольника: Теперь мы хотим построить центры масс для каждого из четырех треугольников и указать их в нашем исходном четырехугольнике. Работая сначала с ранее указанной диагональю, мы повторяем построение центроида для нашего исходного треугольника. Аналогичным образом мы строим центроиды треугольников на последнем изображении. Давайте посмотрим на наш четырехугольник с нашими четырьмя центроидами, указанными вместе, после построения отрезка, соединяющего те, которые связаны с каждой из указанных диагоналей. Теперь, если построить середину отрезка между центроидом A и центроидом B, то середина будет центром масс четырехугольника в направлении отрезка через середину. Точно так же середина отрезка между центроидом C и центроидом D будет центром масс четырехугольника в направлении отрезка через середину. Это показано на следующем изображении. То, что я сказал вам, что это два центра масс для данного четырехугольника, это прекрасно, но почему вы должны мне доверять? Любой центр масс четырехугольника должен отражать, что поперек линии в направлении баланса четырехугольник должен иметь одинаковую массу с обеих сторон. |



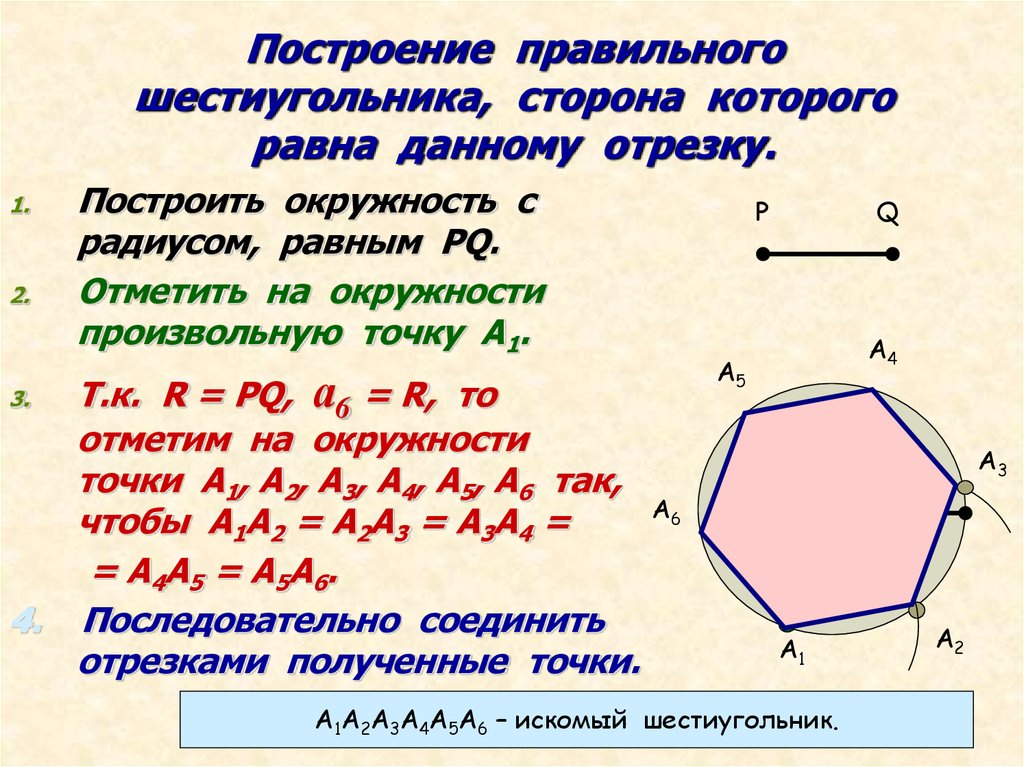
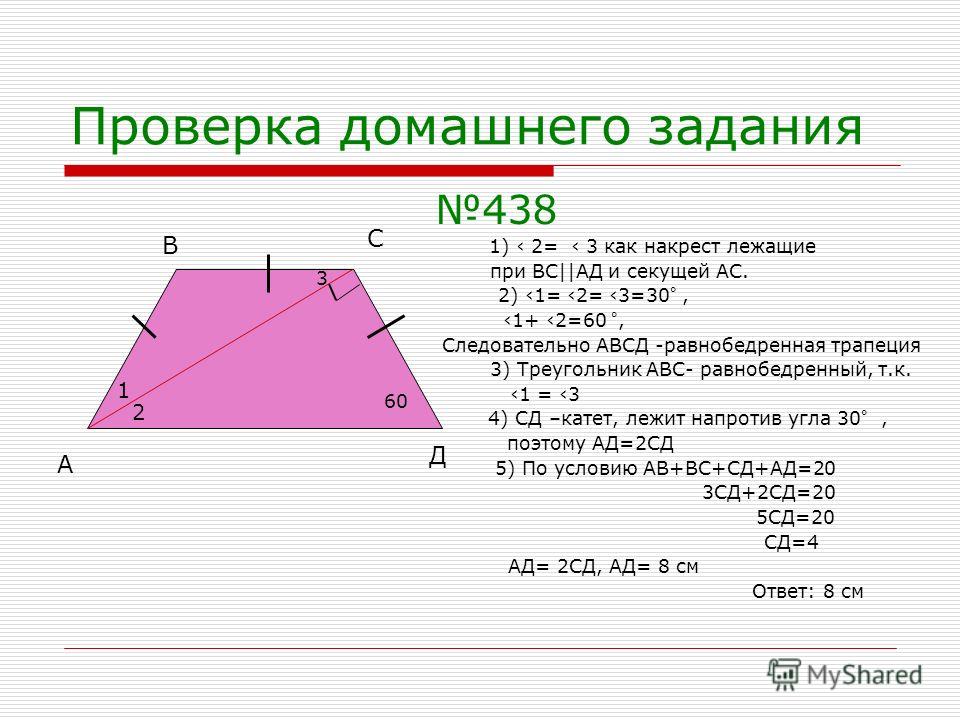
 ..
..
 Проведем В1С1. ВН и С1Н1 .
Проведем В1С1. ВН и С1Н1 .


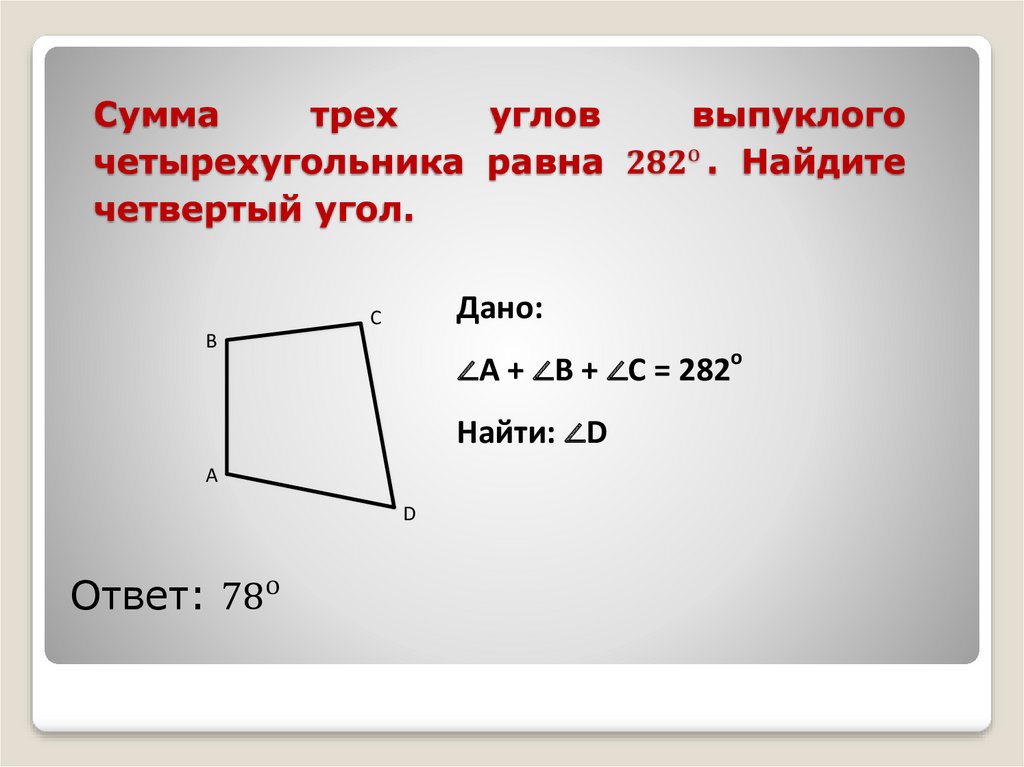
 ..
.. Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.
Тогда площадь четырехугольника можно найти по формуле Бретшнайдера.

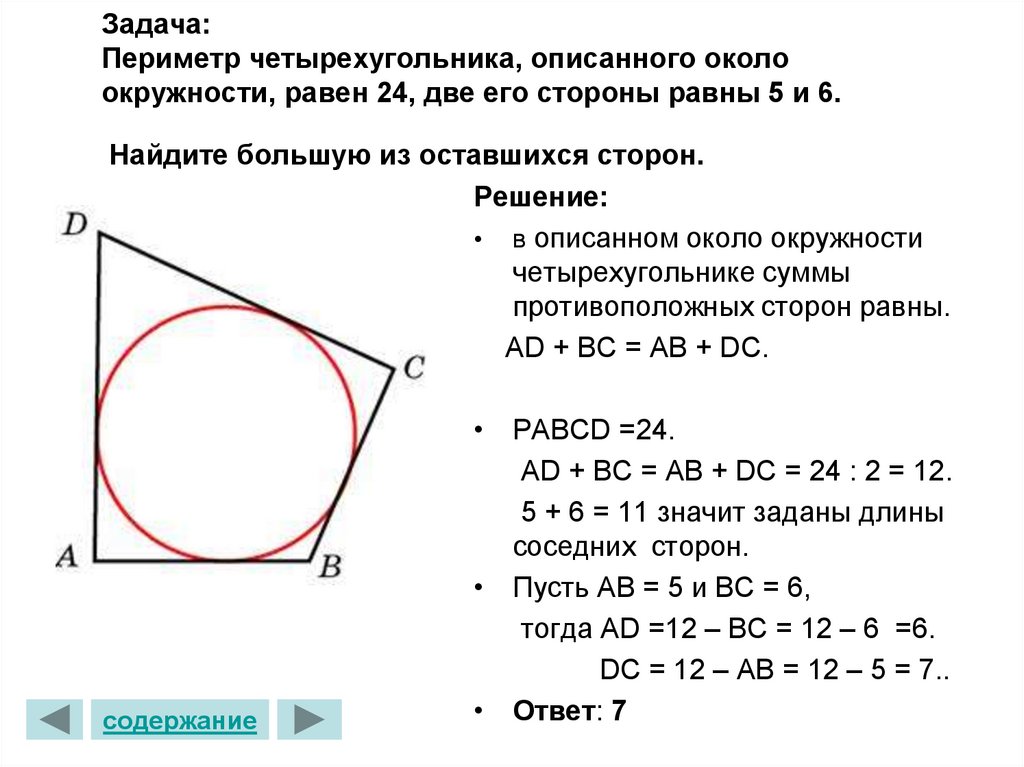
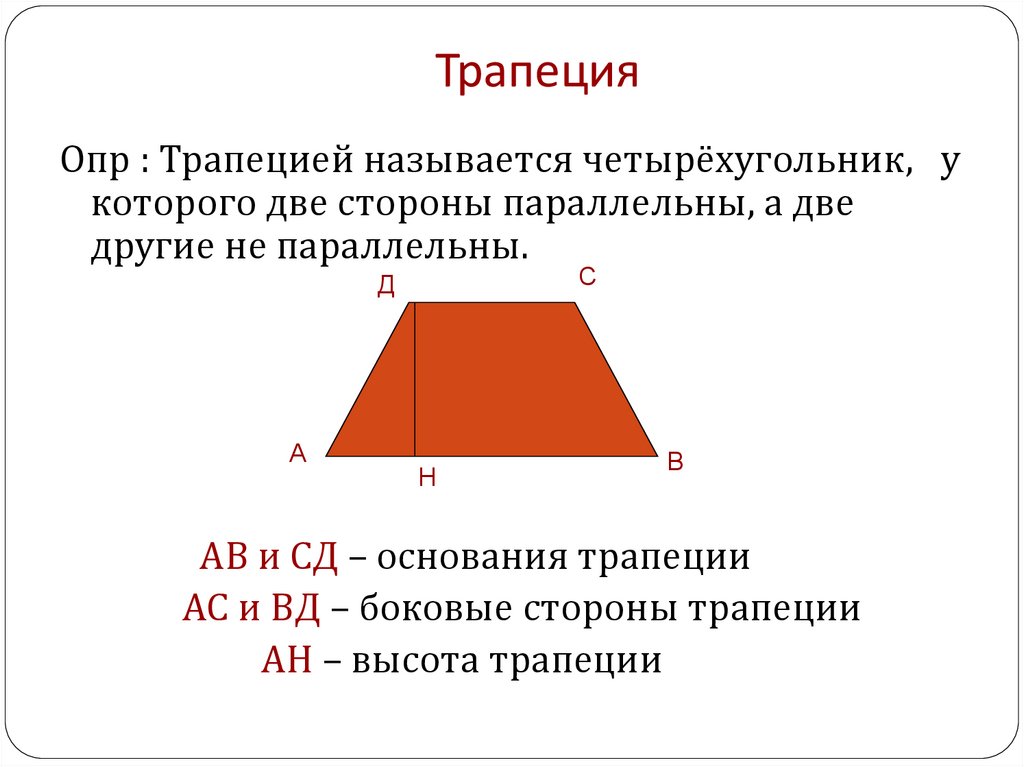

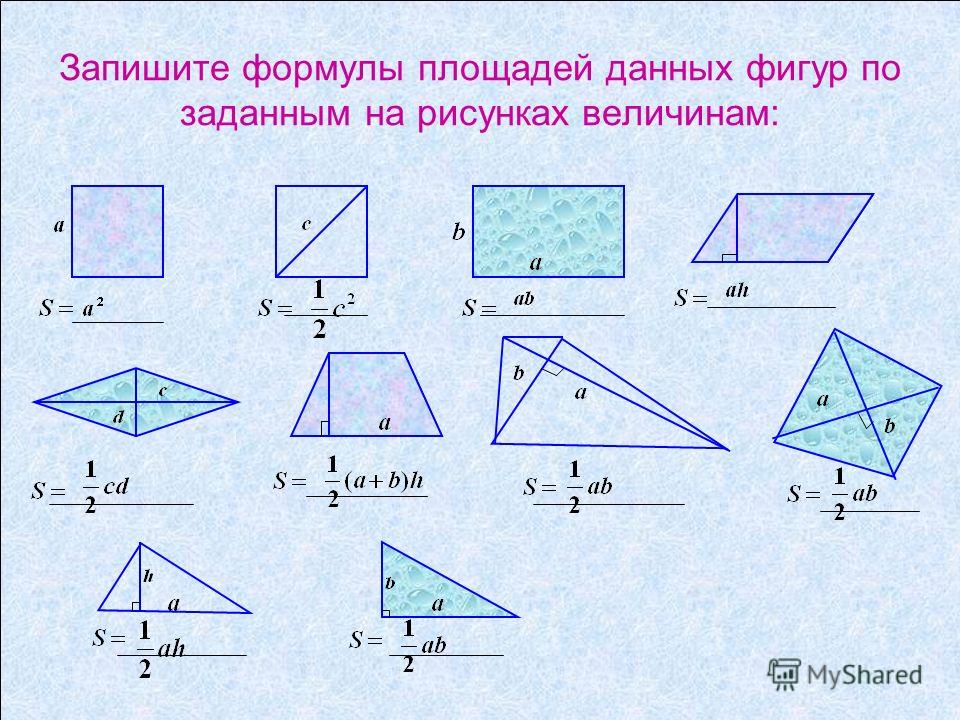
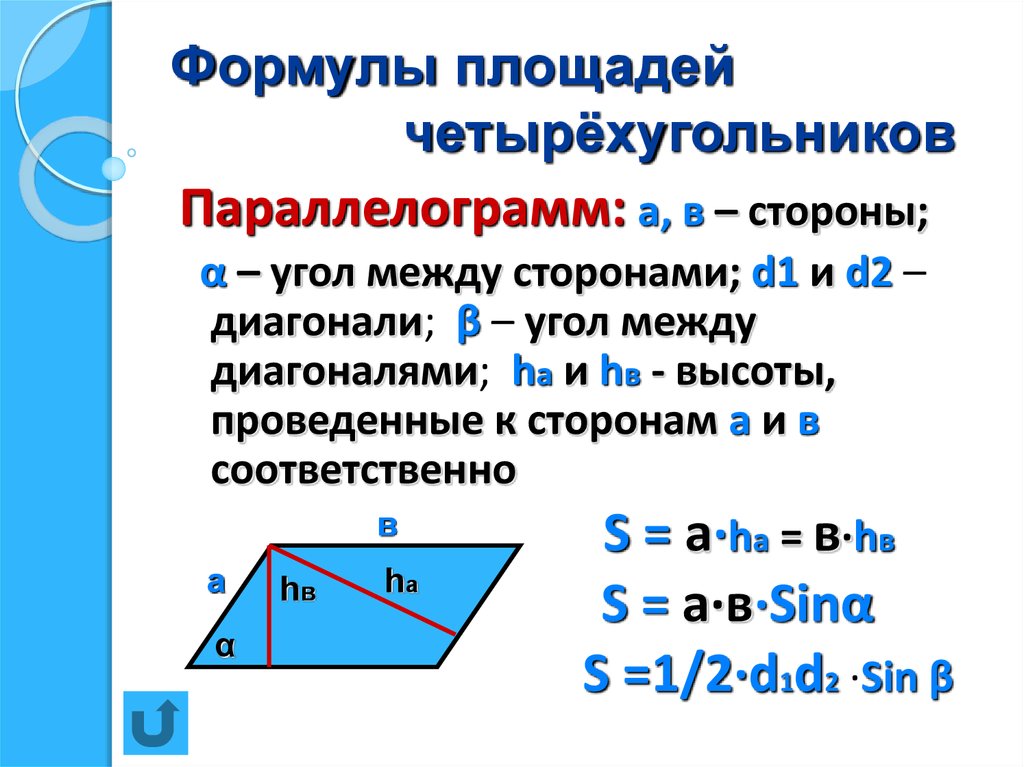 Эта линия делится пополам центром тяжести вершины.
Эта линия делится пополам центром тяжести вершины.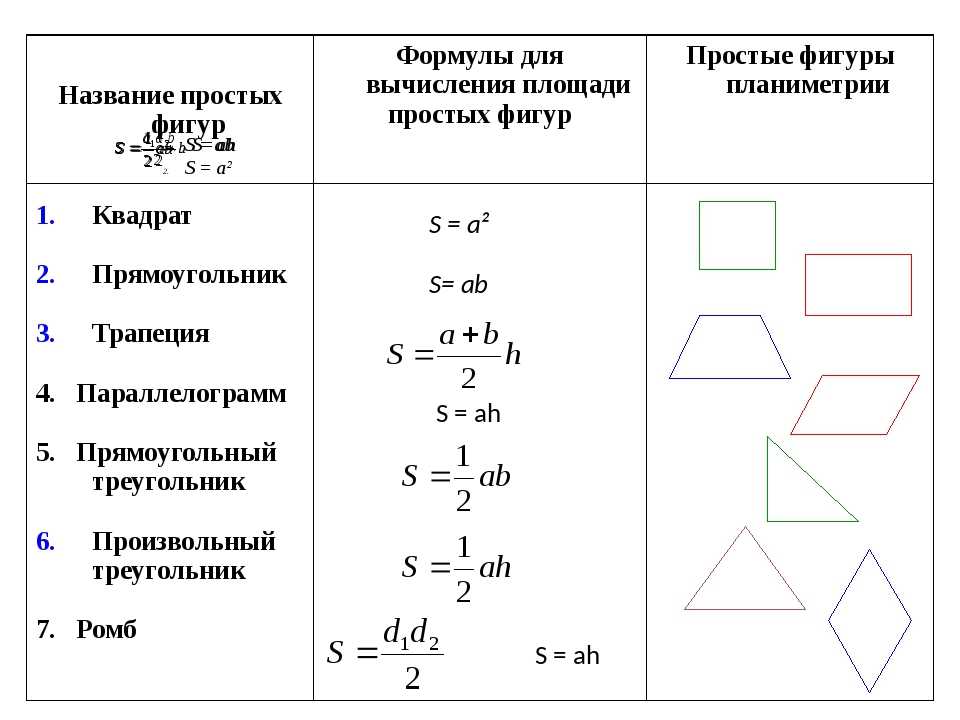
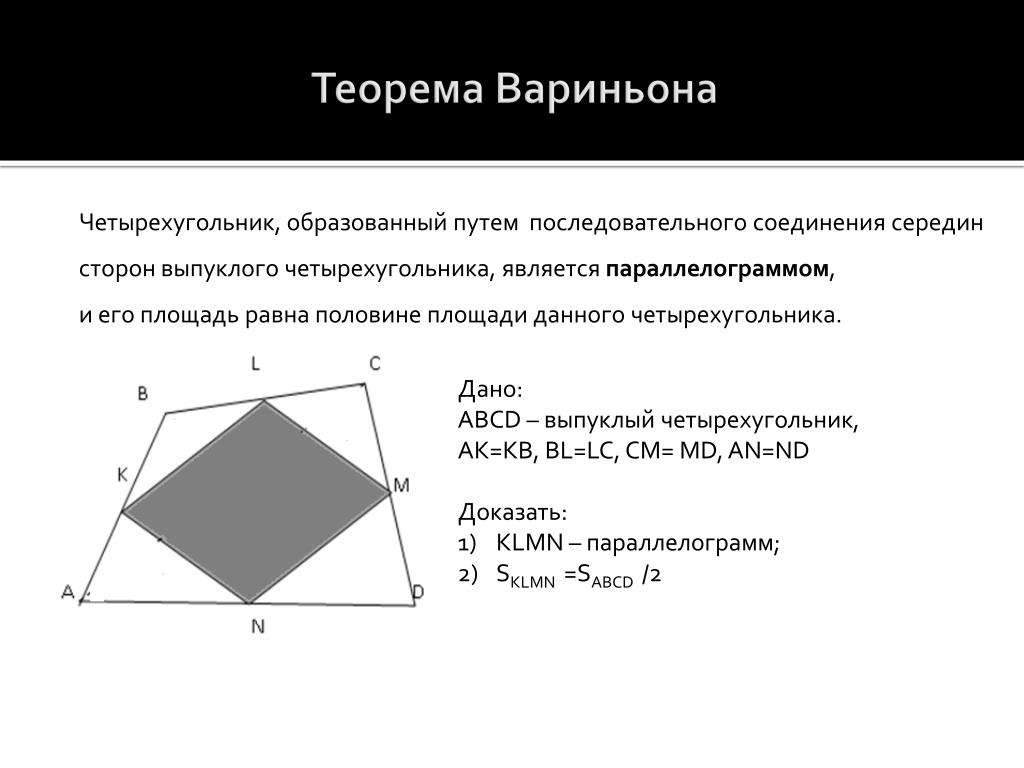


 Стороны BC и DA противоположны.
Стороны BC и DA противоположны. Квадрат называется равносторонним , потому что все четыре стороны имеют одинаковую длину (это делает квадрат как правильным многоугольником , так и правильным четырехугольником ), и все четыре внутренних угла прямые (т.е. девяносто градусов). . Диагонали квадрата имеют одинаковую длину, делят друг друга пополам и равны ортогональны (т.е. они пересекаются под прямым углом). По определению, квадрат также является прямоугольником , параллелограммом и ромбом (см. ниже).
Квадрат называется равносторонним , потому что все четыре стороны имеют одинаковую длину (это делает квадрат как правильным многоугольником , так и правильным четырехугольником ), и все четыре внутренних угла прямые (т.е. девяносто градусов). . Диагонали квадрата имеют одинаковую длину, делят друг друга пополам и равны ортогональны (т.е. они пересекаются под прямым углом). По определению, квадрат также является прямоугольником , параллелограммом и ромбом (см. ниже).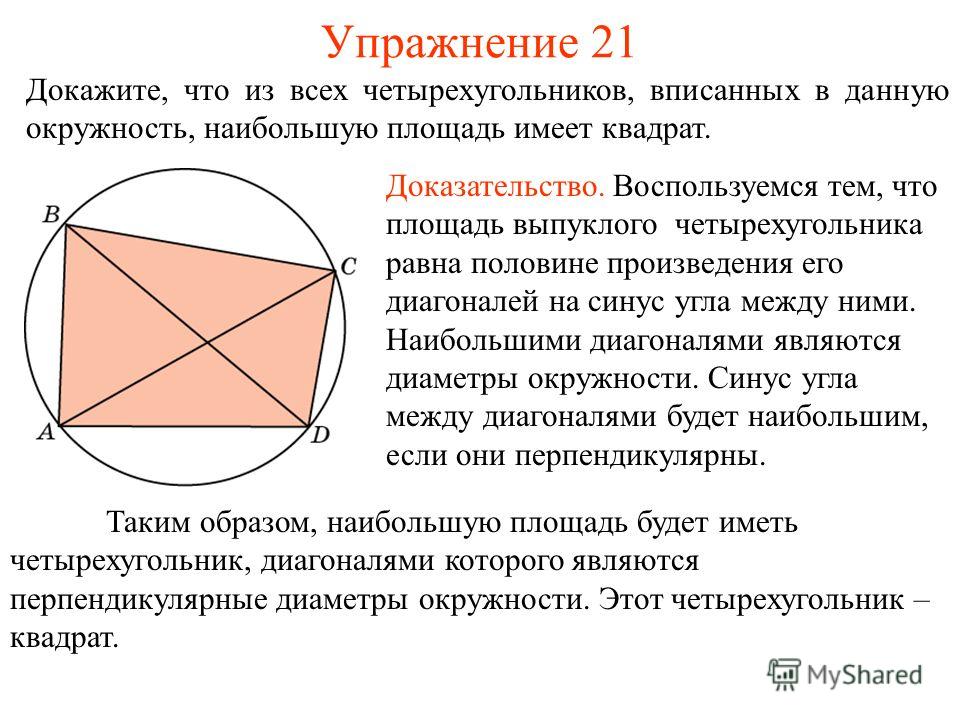
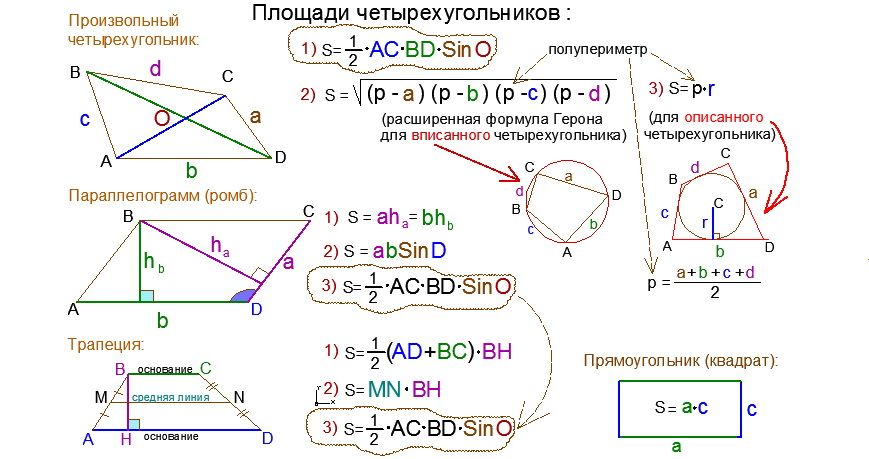 е. имеет четыре стороны одинаковой длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют одинаковую величину, последовательные углы являются дополнительными (т. Е. В сумме они составляют сто восемьдесят градусов), а диагонали делят друг друга пополам. Диагонали ромба также делят внутренние углы пополам и составляют ортогональных (т.е. они пересекаются под прямым углом).
е. имеет четыре стороны одинаковой длины. Поскольку это параллелограмм, противоположные стороны параллельны, противоположные углы имеют одинаковую величину, последовательные углы являются дополнительными (т. Е. В сумме они составляют сто восемьдесят градусов), а диагонали делят друг друга пополам. Диагонали ромба также делят внутренние углы пополам и составляют ортогональных (т.е. они пересекаются под прямым углом). У центральной фигуры одна сторона перпендикулярна обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. У последней (самой правой) фигуры непараллельные стороны разной длины, и все внутренние углы разные.
У центральной фигуры одна сторона перпендикулярна обеим параллельным сторонам, поэтому трапеция содержит два прямых угла. У последней (самой правой) фигуры непараллельные стороны разной длины, и все внутренние углы разные. е. одинаковой длины) смежных сторон. Ни одна из сторон не параллельна, а диагонали воздушного змея ортогональны (т.е. они пересекаются под прямым углом). В отличие от воздушного змея, диагонали пересекают вне форму, а один из углов (угол, примыкающий к обеим более коротким сторонам) представляет собой рефлекторный угол (т.е. больше 180°). Противоположные углы по обе стороны от диагонали, делящей этот рефлекторный угол пополам, равны по величине. Все четырехугольники до этого момента были выпуклыми (т. е. ни один из внутренних углов не превышал ста восьмидесяти градусов). Наличие внутреннего угла свыше ста восьмидесяти градусов означает, что дротик вогнутая четырехугольная. Также возможен подобный (вогнутый) четырехугольник, у которого нет двух сторон одинаковой длины.
е. одинаковой длины) смежных сторон. Ни одна из сторон не параллельна, а диагонали воздушного змея ортогональны (т.е. они пересекаются под прямым углом). В отличие от воздушного змея, диагонали пересекают вне форму, а один из углов (угол, примыкающий к обеим более коротким сторонам) представляет собой рефлекторный угол (т.е. больше 180°). Противоположные углы по обе стороны от диагонали, делящей этот рефлекторный угол пополам, равны по величине. Все четырехугольники до этого момента были выпуклыми (т. е. ни один из внутренних углов не превышал ста восьмидесяти градусов). Наличие внутреннего угла свыше ста восьмидесяти градусов означает, что дротик вогнутая четырехугольная. Также возможен подобный (вогнутый) четырехугольник, у которого нет двух сторон одинаковой длины. е. половина периметра четырехугольника, иначе известного как полупериметр ):
е. половина периметра четырехугольника, иначе известного как полупериметр ):


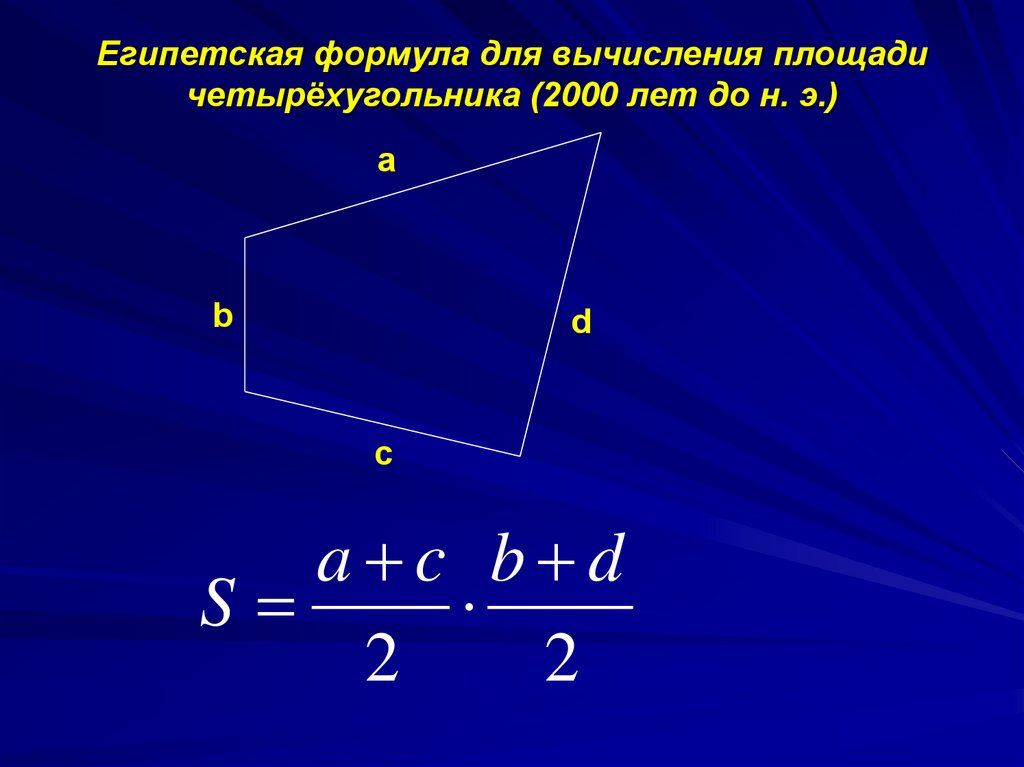 Эти формулы четырехугольника помогут вам вычислить площадь квадрата, прямоугольника, параллелограмма, воздушного змея, ромба и трапеции. Мы также обсудили площадь четырехугольника с формулой координатной геометрии, которая получается путем деления четырехугольника на два треугольника, вычисления площади каждого треугольника с учетом его вершин и сложения этих значений для получения общей площади четырехугольника.
Эти формулы четырехугольника помогут вам вычислить площадь квадрата, прямоугольника, параллелограмма, воздушного змея, ромба и трапеции. Мы также обсудили площадь четырехугольника с формулой координатной геометрии, которая получается путем деления четырехугольника на два треугольника, вычисления площади каждого треугольника с учетом его вершин и сложения этих значений для получения общей площади четырехугольника.