Натуральные целые: Числа: натуральные, целые, рациональные, иррациональные, действительные

Содержание

1.1. Натуральные и целые числа

Понятия «число» и «операция» не так просты, как это может показаться с первого взгляда. Почему, пользуясь одними и теми же числами, мы можем считать камушки и звезды? Это позволяет нам думать, что, сколько бы ни было объектов, мы всегда сможем их пересчитать, и операции сложения, умножения будут также применимы к ним. Подобные вопросы ставились и древними греками, и в наше время.

В этом курсе мы будем исходить из того, что умение считать и различать разные количества предметов – врожденные способности человека. Возьмем в руки камушки, как это делали пифагорейцы, будем прибавлять их по одному, называть последовательно каждое количество своим именем и таким «наглядным» способом определим сразу два основных для алгебры понятия – число и операцию увеличения на единицу. Повторяя эту процедуру и предполагая, что ничто не мешает нам делать это бесконечно, мы сможем определить сложение и умножение на бесконечном множестве натуральных чисел.

Натуральными называются числа, которые используются для счёта предметов или обозначения номера предмета в ряду однородных предметов: 1, 2, 3, 4, 5, …

При сложении и умножении натуральных чисел снова получается натуральное число.

Пусть p и q – натуральные числа. Тогда:

s = p + q – натуральное число, s – сумма, p и q – слагаемые;
t = pq – натуральное число, t – произведение, p и q – сомножители.

Приведем без доказательства законы, которые впоследствии позволят определить операции сложения и умножения не только для чисел, но и для гораздо более сложных объектов, таких, как множества, функции, группы и так далее.

Сложение и умножение натуральных чисел обладают следующими свойствами:

a + b = b + a (переместительный закон сложения).
(a + b) + c = a + (b + c) (сочетательный закон сложения).
ab = ba (переместительный закон умножения).
(ab)c = a(bc) (сочетательный закон умножения).
a(b + c) = ab + ac (распределительный закон умножения относительно сложения).

К сложению и умножению можно добавить обратные операции – вычитание и деление.

Если p, q и k – натуральные числа, то при натуральном k = p – q говорят, что

Если же натуральное k = p : q, то говорят, что

При этом число p называется кратным числа q, а число q – делителем числа p. Другими словами, если число p кратно числу q, то существует такое число k, что k = p : q.

Вычитание и деление натуральных чисел, вообще говоря, не всегда приводит опять к натуральному числу: 15 – 3 = 12 – натуральное число, но 4 – 9 = –5 – не натуральное число. 25 : 5 = 5 – натуральное число, 22 : 7 – не натуральное число.

Увы, нам придется вводить ограничения на применимость новых операций, так как в некоторых случаях они выводят нас за рамки натуральных чисел, а другие числа мы еще не определили. Так что будем пока считать, что нельзя вычитать большее из меньшего, и делить на число, которое не укладывается нацело в делимом. Но с этими ограничениями мы можем уже записывать числовые выражения.

Числовым называется выражение, составленное из чисел с помощью знаков арифметических действий. Если в числовом выражении выполнить все указанные действия, то получится число, которое называется значением данного выражения.

Для того, чтобы определить порядок действий в выражении, введем еще один, парный, знак – скобки.

Приоритет арифметических операций в числовом выражении следующий: вначале выполняются действия в скобках; внутри скобок вначале выполняют умножение и деление, после чего сложение и вычитание.

Пример 1

В каком порядке нужно выполнять действия в выражении

Решение

Порядок действий указан цифрами над знаками арифметических действий:

Пример 2

В каком порядке нужно выполнять действия в выражении

Решение

Порядок действий указан цифрами над знаками арифметических действий:

Еще один простой вопрос – можем ли мы наше множество упорядочить? Существует ли последовательность действий, выполнив которую, мы можем перечислить все элементы множества? Это было бы равнозначно введению какого-то однозначного отношения между элементами. Самым простым упорядочивающим отношением служит понятие «больше», и, чтобы ввести его, расположим натуральные числа на числовой прямой.

Рисунок 1.1.1.1.

Координатная прямая

Нарисуем горизонтальную прямую x, выберем на ней точку O и назовём её началом отсчёта, выберем на этой прямой направление (обычно слева направо) и единичный отрезок (то есть отрезок, длина которого по определению равна 1) (см. рисунок). Говорят, что задана координатная прямая. Каждому натуральному числу можно поставить в соответствие одну и только одну точку. Именно, если, например, задано число 5, отложим от точки O вправо выбранный единичный отрезок 5 раз. Точно так же можно поступить с любым натуральным числом. Если некоторая точка A соответствует некоторому числу a, то говорят, что число a является координатой точки A.

В этом случае пишут A (a).

Говорят, что натуральное число a меньше другого натурального числа b, и записывают этот факт так: a < b, если точка на числовой оси, отвечающая числу a, лежит левее точки, отвечающей числу b.
Говорят, что натуральное число a больше другого натурального числа b, и записывают этот факт так: a > b, если точка на числовой оси, отвечающая числу a, лежит правее точки, отвечающей числу b.

Ясно, что число 0 (нуль) – координата точки O – меньше любого натурального числа.

Для любых двух натуральных различных чисел a и b справедливо одно и только одно утверждение: a < b, a > b или a = b. Знаки < и > называются знаками строгих неравенств, знаки ≤ и ≥ – знаками нестрогих неравенств. Запись a ≤ b означает, что верно одно из двух утверждений: либо a < b, либо a = b. Неравенства a < b и c < d называют неравенствами одного знака; неравенства a < b и c > d называют неравенствами разных знаков.

Арабские цифры. Натуральные и целые числа. История натуральных чисел.

Альфашкола
Статьи
Натуральные и целые числа

Натуральные числа — это положительные числа, которые используются при счете предметов. Натуральные числа существуют не одно тысячелетие, как сказал однажды знаменитый математик Кронекер: «Бог создал натуральные числа, все остальное — работа человека.»

Основные потребности повседневной жизни людей привели к введению дробных чисел, как \(\frac{1}{2};\frac{2}{3};\frac{5}{4}.\)

Позже, индусы изобрели число \(0\), он показывает, что какого-то объекта нет или он не существует. В начале нового времени итальянские алгебраисты ввели отрицательные числа.

Так образовались целые числа – это натуральные, отрицательные числа и 0.

Когда математики говорят о рациональных числах — это значит целые и дробные числа.

Арабские цифры

Арабские цифры возникли в Индии не позднее V века. Мы используем арабскую десятичную систему счисления цифр:

Цифры – система знаков для записи конкретного значения чисел, причем такие, что каждый знак в отдельности описывает определенное число. Это одно из величайших человеческих изобретений в математики. Числа формируются путем объединения цифр системы счисления по определенному механизму, то есть при помощи цифр можно записать любое число, например, число \(6 324 354\). Самая правая цифра в числе определяется как наименее значащая цифра, а самая левая как наиболее значимая цифра. Это связано с тем, что значение места самой правой цифры является наименьшим, а левая цифра — наибольшая.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Елена Германовна Пухова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 5-9 классов и информатике 9 класса. Имею опыт работы подготовки к ОГЭ по математике и информатике. Важным в своей работе считаю изучение и учет личностных особенностей ребенка, независимо от его успеваемости. Люблю математику за то, что она придает мыслям логичность, ясность и точность, развивает критичность мышления, интуицию, тренирует силу воли и учит преодолевать трудности.

Амаяк Варданович Варданян

Репетитор по математике

Стаж (лет)

Образование:

Российский университет дружбы народов

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-9 классов. Подбираю метод работы, отталкиваясь от уровня ученика, говорю с ним на «одном» языке, объясняю сложные вещи на простых примерах. Имею опыт работы по учебникам Школа России, Школа 21 век. Готовлю учеников по программе Петерсона, готовлю к олимпиадам. Самый главный принцип, которого я придерживаюсь — это индивидуальный подход к ребенку. Занятия провожу в легкой и непринужденной обстановке.

Юлия Геннадьевна Ючко

Репетитор по математике

Стаж (лет)

Образование:

Минский государственный лингвистический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-9 классов. Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.

Полностью натуральный — frwiki.

wiki

Для одноименных статей см. Integer .

В математике , натуральное число является положительным число , которое в основном позволяет рассчитывать объектов каждый подсчет , как один , и поэтому рассчитывать объекты считаются эквивалентными: токен, две фишки … карты, две карты, три карты … Такое целое число можно записать конечной последовательностью цифр в десятичной позиционной системе счисления (без знака и без запятой).

У каждого целого числа есть уникальный преемник , то есть целое число непосредственно над ним, а список натуральных целых чисел бесконечен .

Первоначальное определение множества натуральных чисел, данное Ричардом Дедекиндом , не включает число ноль; совсем недавно было предложено другое определение, включающее ноль. Эти два определения сосуществуют и сегодня. Таким образом, по значениям список натуральных чисел выглядит следующим образом:

1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; …

или же

0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; . ..

Изучение натуральных чисел и их отношений, в частности, операций сложения и умножения , было разделом математики, называемым « арифметикой », начиная с греческой античности .

Структура натуральных чисел была аксиоматизирована впервые по Пеано и Дедекиндом в конце XIX — ^го века. В то время ноль не считался натуральным числом (и некоторые авторы до сих пор делают этот выбор), что принципиально не меняет аксиоматизацию. Эрнст Цермело , когда он аксиоматизировал теорию множеств, показал, что натуральные целые числа могут быть определены в терминах множеств (сегодня чаще всего используется метод фон Неймана ).

Набор натуральных чисел, независимо от того, содержит он число ноль или нет, обозначается » » или » «. Обозначение принадлежит Дедекинду в 1888 году, который использует его для набора ненулевых натуральных чисел. Сегодня этот последний набор также часто называют « » (или « »). НЕТ{\ displaystyle \ mathbf {N}}НЕТ{\ Displaystyle \ mathbb {N}}НЕТ⋆{\ displaystyle \ mathbf {N} ^ {\ star}}НЕТ⋆{\ displaystyle \ mathbb {N} ^ {\ star}}

Натуральные числа идентифицируются с положительными или нулевыми относительными целыми числами , а также с положительными или нулевыми рациональными числами, которые могут быть записаны в форме дроби знаменателя 1, и, в более общем смысле, с положительными или нулевыми действительными числами дробной части нуля.

Натуральные числа позволяют считать (яблоко, два яблока, три яблока и т. Д.).

Резюме

1 Дизайн
- 1.1 От перечисления к абстракции
- 1.2 Прерванное определение целых чисел в терминах класса биективности
- 1.3 Построение по ординалам
2 Обозначение
- 2.1 Заявление
- 2.2 Зашифрованная запись
- 2.3 Кодирование
3 Арифметика
- 3.1 Представление операций
- 3.2 Кратное и делитель
- 3.3 простое число
4 Набор натуральных чисел
- 4.1 Рейтинги
- 4.2 Теория множеств
- 4.3 Свойства
- 4.4 Аксиоматика Пеано
5 Примечания
6 Библиография
7 См. Также
- 7.1 Статьи по теме
- 7.2 Внешняя ссылка

Дизайн

От перечисления к абстракции

Понятие натурального числа, занимая первое (и до XVII — ^го века), вся идея числа , вероятно , после того, как понятие коллекции: целое число в первую очередь предназначен как кардинал. Некоторые предметы или животные, хотя и отличаются друг от друга, могут допускать общее обозначение из-за их сходства или другой общей характеристики. Их собрание представляет собой собрание, как стадо коров, жемчужное ожерелье, груду камней.

Число прорастает в перечислении коллекции, то есть в факте прокрутки всех ее элементов один за другим и без повторения. Требуется последовательность в наблюдении, что два одновременных подсчета (например, от стада до загона и камней в мешке) заканчиваются либо всегда в одно и то же время, либо всегда не в одном шаге. Число, наконец, отображается, когда мешок с камешками или зубчатая палка используется для обозначения количества.

Однако понятие целого по-настоящему рождается только тогда, когда оно оставило своего представителя, то есть когда оно больше не представляет никаких камешков, выемок или коровы: существует первая абстракция, в которой каждый объект рассматривается как чистая единица и без качество. Этот умственный процесс известен как абстракция : он абстрагируется от качества объекта и касается только количества. Вторая абстракция затем приводит к рассмотрению этих единиц как совокупности единиц.

Евклид дает в Книге VII Элементов следующее определение: «Единство — это то, относительно которого каждый объект называется Единицей». Эта абстракция позволяет ему затем определить число (натуральное целое) как «совокупность единиц».

*Представление первых ненулевых натуральных чисел наборами точек.*
0	1	2	3	4	5	6	7	8	9	10

Прерванное определение целых чисел в терминах класса биэквивалентности

Фреге думал (в «Основах арифметики» , 1884 г.) определять целые числа в терминах класса биективности .

Эта идея заключается в определении каждого целого числа п как сбор всех множеств , имеющих п элементы.

Это очень привлекательное определение вступает в противоречие с парадоксом Рассела, если с точки зрения онтологического монизма кто-то желает, чтобы такое собрание также было единым целым.

Это потому, что, за исключением целого числа 0, идентифицированного с набором, содержащим только пустой набор, для любого другого целого числа n набор наборов, имеющих n элементов, является надлежащим классом и, следовательно, не является набором.

Построение по ординалам

Натуральные целые числа можно определить как порядковые , то есть с помощью метода фон Неймана , как хорошо упорядоченные множества, все сравнимые по включению . Натуральные числа являются конечными порядковыми числами, те, чей обратный порядок также является хорошим порядком, или последующие порядковые числа, у которых все нижние границы также являются последующими порядковыми числами.

Обозначение

Произнесение

Обозначение целых чисел в языке отличается от одного языка к другому, хотя обычно оно основано на нескольких простых методах.

Первые целые числа имеют определенное имя, не связанное друг с другом. Во французском языке это целые числа от одного до десяти (названия целых чисел от одиннадцати до шестнадцати на самом деле являются деформациями составных имен). В некоторых языках нет определенного слова, кроме двух .

Соединение двух существительных может обозначать результат сложения (как в семнадцати ) или умножения (как в восьмидесяти ) соответствующих целых чисел. Существуют и другие методы с использованием вычитания, деления или удлинения .

Некоторое «большое» число также дано имя конкретного, как правило , определенные полномочия по более конкретной базе . База десять наиболее распространенными сегодня, но обозначение чисел на французском языке, например , сохраняет следы частичного использования базы двадцать . Противоречивые международные конвенции предлагают стандартизированные обозначения для первой сотни степеней от тысячи до миллиона.

За пределами, налагаемыми словарным запасом, язык может предлагать обозначения только по придаткам: «тысяча миллиардов миллиардов …»

Зашифрованная запись

Если написание целых чисел сильно менялось в истории цивилизаций, то сегодня оно почти везде основано на одной и той же системе позиционного десятичного счисления , даже если написание чисел может претерпевать более или менее значительные вариации от страны к стране. .

Каждое натуральное число уникальным образом разлагается на сумму кратных степеней десяти, так что каждый коэффициент умножения строго меньше десяти, поэтому он представлен одной из десяти арабских цифр от 0 до 9. Это число записывается так. затем получается путем соединения этих фигур, расположенных в порядке убывания соответствующих степеней десяти.

Основным интересом этой статьи является общая простота вычислительных алгоритмов для четырех элементарных арифметических операций.

Кодирование

Практика вычислений может основываться на манипуляциях с галькой или другими конкретными символами, сначала для обозначения одной единицы на гальку, а затем путем дифференцирования значений символов (например, раковина, обозначающая десять камешков).

Позиционное обозначение позволило дифференцировать значения символов в соответствии с их положением и более не их характер, что привело к развитию Абак и счеты . Этот принцип до сих пор действует в калькуляторах и компьютерах .

Арифметика

Представление операций

Представляя каждое целое число набором объектов (например, камешков или жетонов), операция сложения представляется объединением двух коллекций, в то время как вычитание сводится к удалению одной коллекции из другой. Это представление ясно показывает невозможность вычитания (в натуральных числах) одного числа из другого строго меньшего.

Умножение два натуральных числа соответствуют заполнению прямоугольника из которых две смежных сторон каждый представляют собой один из факторов.

Евклидово деление целого числа (называется дивидендов ) другим ( так называемый делитель и обязательно ненулевых) иллюстрируется расположением коллекции , представляющей дивиденды в виде прямоугольника, одна сторона которого представляет собой делитель. Тогда количество полных строк представляет собой частное, в то время как возможная неполная строка представляет собой остаток , обязательно строго меньший, чем делитель.

Множественный и делитель

Учитывая ненулевое натуральное число, множество его кратным является бесконечным , но равномерно распределен и легко описать с помощью арифметической последовательности . Например, числа, кратные 2, являются четными числами , которые чередуются с нечетными числами среди всех целых чисел.

Напротив, множество делителей ненулевого целого числа всегда конечно, и его распределение вообще не имеет такой же регулярности. Он, безусловно, всегда содержит число, которое нужно разделить, и число 1, любые другие делители, лежащие между этими двумя крайностями. Но, как правило, трудно перечислить эти другие делители, записав число в данной системе счисления .

Эта проблема частично связана с нехваткой простых критериев для определения без расчета, делится ли одно число на другое. В десятичной позиционной системе счисления для малых делителей известны несколько критериев делимости (особенно для 2, 3, 5, 9 и 10), но помимо этих нескольких случаев, по существу, именно евклидово деление позволяет нам ответить на этот вопрос.

простое число

Следовательно, кроме числа 1, которое является его единственным делителем, любое число допускает по крайней мере два различных делителя. Те, кто допускают ровно два, называются простыми числами . Только они могут уменьшать другие числа путем деления, не будучи разложенными на произведения строго меньших чисел. Их бесконечное количество, и каждое число уникальным образом разлагается на произведение простых чисел. Это разложение позволяет, среди прочего, понять структуру набора разделителей.

Набор натуральных чисел

Обозначения

НЕТзнак равнояНЕТзнак равноНЕТзнак равноНЕТ*знак равноНЕТ1знак равно{1,2,. {*} = \ mathbb {N} _ {1} = \ {1, 2, \ ldots \}}

яНЕТзнак равноНЕТзнак равноНЕТ0знак равно{0,1,2,…}{\ Displaystyle \ mathrm {I _ {\,} \! \! N} = \ mathbb {N} = \ mathbb {N} _ {0} = \ {0,1,2, \ ldots \}}

НЕТ≠0знак равноНЕТ>0знак равно{1,2,…}{\ Displaystyle \ mathbb {N} _ {\ neq 0} = \ mathbb {N} _ {> 0} = \ {1,2, \ ldots \}}

НЕТ≥0знак равно{0,1,2,…}{\ Displaystyle \ mathbb {N} _ {\ geq 0} = \ {0,1,2, \ ldots \}}

Различные обозначения для набора целых чисел, включая или ненулевые.

В 1894 году Джузеппе Пеано использовал обозначения «N» для «положительного целого числа» и «N ₀ » для «положительного или нулевого целого числа» в своих « Обозначениях математической логики», которые послужили введением в его великий проект формализации математики, « Математическая форма». . Он использует его как предикат, понятие, очень близкое к понятию целого. Таким образом, Пеано пишет « x ε N» (которое мы теперь пишем « »), что для него читается как « x — натуральное число». Икс∈НЕТ{\ Displaystyle х \ в \ mathbb {N}}

Историческое обозначение всех натуральных чисел в печати становится « N », жирной заглавной буквой. В почерке (и особенно на доске ) этот символ отличается от буквы «N», используемой для других целей, путем удвоения первой вертикальной черты или косой черты « ». Последний вариант был выбран для полужирного шрифта на классной доске . В современном математическом редактировании теперь используются «удвоенные» символы, но также продолжается использование жирного шрифта. НЕТ{\ Displaystyle \ mathbb {N}}

Теория множеств

Наименьший бесконечный ординал — это верхняя граница всех конечных ординалов, которые являются натуральными целыми числами. Он был введен Георгом Кантором, который отметил его ω (греческая строчная буква омега ) или ω ₀ . Джон фон Нейман показал, что ординалы могут быть определены таким образом, чтобы отождествлять ординал с множеством его строгой нижней границы, а ординал ω затем отождествляется с множеством натуральных чисел (натуральное число само отождествляется с множеством натуральных чисел, которые ему строго подчиняются). Поэтому в теории множеств буква ω также используется для обозначения множества натуральных чисел. Аксиома бесконечности позволяет показать существование этого множества.

Счетное множество представляет собой набор , который имеет то же самое, что и кардинальное множество натуральных чисел (иногда указать «счетную бесконечность», который также может означать «конечный или одного и тот же кардинальный как N »). Кардинал из счетных , что из N , является наименьшим бесконечный кардинал, следует отметить , ℵ ₀ , алеф-ноль .

В теории множеств формально ₀ определяется как наименьший счетный бесконечный ординал, а именно, и, следовательно, снова как набор натуральных целых чисел.

Характеристики

Поскольку операции сложения и умножения ассоциативны , коммутативны , снабжены нейтралами и удовлетворяют свойству дистрибутивности , множество натуральных чисел представляет собой полукольцо .

Он упорядочен для обычного отношения порядка, индуцированного сложением, что дает ему структуру хорошего порядка , т. е. любая непустая часть допускает меньший элемент. Это свойство лежит в основе рассуждений по индукции .

Множество также имеет отношение делимости, которое является частичным порядком .

Его кардинал — это наименьшее бесконечное кардинальное число , обозначаемое ℵ ₀ ( алеф ноль ), что определяет понятие счетности . В самом деле, мы говорим о любом множестве, что оно счетно, если существует биекция этого множества в множество натуральных чисел. Иногда довольствуется инъекцией, чтобы включить в нее и готовые наборы.

Пеано Аксиоматик

Независимо от того, как вы вводите натуральные целые числа, они обладают теми же фундаментальными свойствами, на основе которых развивается арифметика. Ричард Дедекинд и Джузеппе Пеано независимо друг от друга предложили аксиоматизацию, которая была по существу эквивалентной. Речь шла об аксиоматизации, о которой сегодня иногда говорят о втором порядке: понятие множества (или предиката ) предполагается известным и не принимается во внимание аксиоматизацией. Вот современное представление этих аксиом (известных как аксиомы Пеано):

Элемент, называемый нулем и отмеченный 0, является натуральным числом.
Каждое натуральное число n имеет уникального преемника, часто обозначаемого s ( n ) или S n (или другие варианты).
Никакое натуральное число не имеет преемника 0.
Два натуральных числа с одним и тем же преемником равны.
Если множество натуральных чисел содержит 0 и содержит преемника каждого из ее элементов, то это множество равно N .

Первая аксиома позволяет утверждать, что множество натуральных чисел не пусто , вторая — что преемник является функцией , четвертая — что эта функция является инъективной , третья — что у нее есть первый элемент (эти две аксиомы гарантируют, что множество натуральных чисел бесконечно). Пятый — это формулировка принципа повторяемости .

Важное свойство, продемонстрированное Ричардом Дедекиндом из этих аксиом, — это принцип определения по индукции . Это позволяет, например, определять обычные операции.

Заметки

↑ Георг Кантор — первый математик, изучавший различные бесконечности, он полагался на упорядоченный набор натуральных чисел, чтобы определить первый базис бесконечности, а затем лучше открыть другие бесконечные множества.
↑ Ричард Дедекинд. Был ли sind und sollen die Zahlen? (1888) 2 ^е изд. Friedrich Vieweg et fils 1893. Читать онлайн.
↑ Под записью «число» Лексис (1975) определяет «натуральное число» как «каждое из целых чисел последовательности 1,2,3 и т. Д. » , А Ле Пети Робер (1977) дает « В начале и в простейшем случае натуральных чисел (1,2,3,4…) […] » ; Французская академия , в девятом издании своего словаря, по въездному «целому числу» определяет «натуральное число» , как «положительное целое», и при входе «положительный» указует , что «положительное число„Is“больше нуля «.
↑ (in) Эрик В. Вайстейн , « Натуральное число » на MathWorld .
↑ Кристиан Хаузель , «Что такое число? », История чисел , Tallandier 2007.
↑ Номер числа обрабатываются в III — ^е тысячелетия до н.э. в месопотамской цивилизации, но они не имеют теоретический статус номера.
↑ Философское построение понятия числа подробно раскрывается в книге Луи Кутюра « Из математической бесконечности» .
↑ Это определение может быть ретроспективно применено к нулю , совокупности, не содержащей единиц.
↑ Жорж Ифра , Введение во Всеобщую историю фигур , том 1, издание Роберта Лаффона (1994), стр. 9 , § Первые попытки и ошибки.
↑ Слово «расчет» связано со словом «caillou».
↑ В относительных целых числах всегда возможно вычитание .
↑ Джузеппе Пеано (1894 г. ), Обозначения математической логики , Гуаданьини, Турин (1894 г.), стр. 4 читать онлайн
↑ (in) Флориан Каджори , История математических обозначений [ розничные издания ]полет. 2 шт. 299 .
↑ Пеано на самом деле использует 1 (один), что соответствует обычаям того времени, но принципиально ничего не меняет

Библиография

Питер Дж. Бентли, Книга чисел, их история и их секреты, от истоков до наших дней , Eyrolles, Париж, 2009 г., 272 страницы ( ISBN 978-2-212-54226-4 ) . Перевод Анн-Мари Терель и Лоуренса Николаева из Книги Чисел , Cassel Illustrated, Лондон, 2008.
Пьер Дамфусс, Арифметика или искусство счета , издания Le Pommier, 2002.
Жорж Ифра, Всеобщая история фигур , издания Seghers, Париж, Лозанна, 1981, 567 страниц ( ISBN 2-221-50205-1 ) .
Бенуа Ритто, что такое число? , Les Petites Pommes du savoir, Le Pommier editions, Париж, 2011 г., 64 страницы ( ISBN 978-2-7465-0565-0 ) .

Смотрите также

Статьи по Теме

Список номеров
простое число
Счастливое число
Номер гармоники
Хроматическое число

Внешняя ссылка

Числа: курьезы, теория и использование , сайт Г. Виллемена

Числовое понятие
Обычные наборы	Целое число ( ) НЕТ{\ Displaystyle \ scriptstyle \ mathbb {N}} · относительно Целого числа ( ) Z{\ Displaystyle \ scriptstyle \ mathbb {Z}} · Десятичного числа ( ) D{\ Displaystyle \ scriptstyle \ mathbb {D}} · рационального числа ( ) Q{\ Displaystyle \ scriptstyle \ mathbb {Q}} · Фактического ( ) р{\ Displaystyle \ scriptstyle \ mathbb {R}} · Комплексного числа ( )ПРОТИВ{\ Displaystyle \ scriptstyle \ mathbb {C}}
Расширения	Кватерниона ( ) ЧАС{\ Displaystyle \ scriptstyle \ mathbb {H}} · октонионы ( ) О{\ Displaystyle \ scriptstyle \ mathbb {O}} · седенионы ( ) S{\ Displaystyle \ scriptstyle \ mathbb {S}} · Комплексного число развернет · Tessarine · Количество бикомплекс ( ) ПРОТИВ2{\ Displaystyle \ scriptstyle \ mathbb {C} _ {2}} · Числа мультикомплекс ( ПРОТИВнет{\ displaystyle \ scriptstyle \ mathbb {C} _ {n}} · ) · бикватернионных · расщепленные кватернионы · гиперболических кватернионы · октонионы развернуты · Число hypercomplexe · Число р-адический ( ) · Число гиперреальное · Число superréel · Число двойственное · законченное действительное Справа · Число Кардинал · Порядковое число · Число сюрреалистическое · Число псевдореальноеMПРОТИВнет{\ Displaystyle \ scriptstyle {\ mathcal {M}} \ mathbb {C} _ {n}} Qп{\ Displaystyle \ scriptstyle \ mathbb {Q} _ {p}}
Особые свойства	Четность · Номер первое · Номер состоит · Количества фигурного · Номер идеально · Количество положительного · Количество отрицательна · доли диадического · Число иррациональное · Алгебраического Количество · Количество трансцендентный · Количество чисто мнимое · Количество Лиувилля · Период · Количество Нормального · Номер вселенная · Номер здание · Актуально вычислимое · число трансфини · бесконечно малое
Примеры	Пи ( π ) · квадратный корень из двух ( ) · Число золота (φ) · Ноль (0) · Мнимая единица ( i ) · Константа Непер ( e ) · Алеф-ноль (ℵ ₀ ) · Табличные математические константы2{\ displaystyle \ scriptstyle {\ sqrt {2}}}
Статьи по Теме	Продажи · Количество · Дробь · Операция · Вычисление · Алгебра · Арифметика · Следующее целое число · бесконечность ( ∞ ) · Значащая цифра

Наборы из целых чисел , основанные на их делимость
Формы факторизации	Премьер · Номер состоит · Количество мощный · Integer бесквадратным
Суммы делителей	Номер идеально · Номер почти идеальный · Номер около совершена · совершенного Multiple Количества · Количества hyperparfait · Номер унитарные совершенный · Номер полусовершено · Количества совершенного пол-примитивный · Номера практики
Множество разделителей	Численность многочисленна · Численность очень многочисленна · Число суперабондант · Число колоссально обильно · Численность очень сложная · Число высокоразвитых соединений
Другой	Количество дефицитного · Количество странно · дружелюбные номера · Количество дружеский · Количество одинока · Количества возвышенный · Количество полный гармонический среднее · Количество скудный · Номер équidigital · Номер экстравагантным

Полномочия по целым числам
Степень 2	2 ¹ · 2 ² · 2 ³ · 2 ⁴ · 2 ⁵ · 2 ⁶ · 2 ⁷ · 2 ⁸ · 2 ⁹ · 2 ¹⁰ · 2 ¹¹ · 2 ¹² · 2 ¹³ · 2 ¹⁴ · 2 ¹⁵ · 2 ¹⁶ · 2 ¹⁷ · 2 ¹⁸ · 2 ¹⁹ · 2 ²⁰ · 2 ²¹ · 2 ²² · 2 ²³ · 2 ²⁴ · 2 ²⁵ · 2 ²⁶ · 2 ²⁷ · 2 ²⁸ · 2 ²⁹ · 2 ³⁰ · 2 ³¹ · 2 ³² · 2 ³³
Степени 3	3 ¹ · 3 ² · 3 ³ · 3 ⁴ · 3 ⁵ · 3 ⁶ · 3 ⁷ · 3 ⁸ · 3 ⁹ · 3 ¹⁰ · 3 ¹¹ · 3 ¹² · 3 ¹³ · 3 ¹⁴ · 3 ¹⁵ · 3 ¹⁶ · 3 ¹⁷ · 3 ¹⁸ · 3 ¹⁹ · 3 ²⁰
Степени 5	5 ¹ · 5 ² · 5 ³ · 5 ⁴ · 5 ⁵ · 5 ⁶ · 5 ⁷ · 5 ⁸ · 5 ⁹ · 5 ¹⁰ · 5 ¹¹ · 5 ¹² · 5 ¹³ · 5 ¹⁴
Степени 6	6 ¹ · 6 ² · 6 ³ · 6 ⁴ · 6 ⁵ · 6 ⁶ · 6 ⁷ · 6 ⁸ · 6 ⁹ · 6 ¹⁰ · 6 ¹¹ · 6 ¹²
Степени 7	7 ¹ · 7 ² · 7 ³ · 7 ⁴ · 7 ⁵ · 7 ⁶ · 7 ⁷ · 7 ⁸ · 7 ⁹ · 7 ¹⁰ · 7 ¹¹
Степени 10	10 ¹ · 10 ² · 10 ³ · 10 ⁴ · 10 ⁵ · 10 ⁶ · 10 ⁷ · 10 ⁸ · 10 ⁹
Степени 11	11 ¹ · 11 ² · 11 ³ · 11 ⁴ · 11 ⁵ · 11 ⁶ · 11 ⁷ · 11 ⁸ · 11 ⁹
Степени 12	12 ¹ · 12 ² · 12 ³ · 12 ⁴ · 12 ⁵ · 12 ⁶ · 12 ⁷ · 12 ⁸ · 12 ⁹
Степени 13	13 ¹ · 13 ² · 13 ³ · 13 ⁴ · 13 ⁵ · 13 ⁶ · 13 ⁷ · 13 ⁸
Степени 14	14 ¹ · 14 ² · 14 ³ · 14 ⁴ · 14 ⁵ · 14 ⁶ · 14 ⁷ · 14 ⁸
Степени 15	15 ¹ · 15 ² · 15 ³ · 15 ⁴ · 15 ⁵ · 15 ⁶ · 15 ⁷ · 15 ⁸
Степени 17	17 ¹ · 17 ² · 17 ³ · 17 ⁴ · 17 ⁵ · 17 ⁶ · 17 ⁷ · 17 ⁸
Полномочия 18	18 ¹ · 18 ² · 18 ³ · 18 ⁴ · 18 ⁵ · 18 ⁶ · 18 ⁷
Полномочия 19	19 ¹ · 19 ² · 19 ³ · 19 ⁴ · 19 ⁵ · 19 ⁶ · 19 ⁷
Степени 20	20 ¹ · 20 ² · 20 ³ · 20 ⁴ · 20 ⁵ · 20 ⁶ · 20 ⁷

В чем разница между натуральными и целыми числами?

Определяющее понятие математики – число, которое используется для количественной характеристики объектов. Наука оперирует их несколькими видами. Осознание особенностей этого понятия поможет избежать ошибок, приблизит открытие новых горизонтов познания точной науки.

Считать человек научился тогда, когда научился говорить. Первоначально это было определение количества предметов, товара. При появлении письменности придумали специальные значки – цифры. В этой стать речь пойдёт о натуральных и целых числах, как самых простых.

Натуральные числа

На заре цивилизации первобытные люди обходились понятиями «один» и «много». Древние охотники не утруждали себя подсчётами. При возникновении товарообменных отношений назрела потребность усложнить счёт.

Во время торговли приходилось считать количество товара. Тогда появились самые простые числа. Их называют натуральными, так как возникли естественным образом при счёте. Ими описывают количество предметов или порядковый номер ряда подобных объектов. Для письменного отображения этих величин используют специальные знаки, которые называют цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Пример записи: двести тридцать один – 231.

Самая маленькая величина – единица (1), самой большой нет. Если возьмём самое большое, на наш взгляд, значение, к нему всегда можно добавить ещё 1, получить большее, и так до бесконечности.

При их расположении последовательно в порядке возрастания получаем числовой ряд. Каждый следующий элемент ряда увеличивается на 1 по отношению к предыдущему. Этот массив элементов обозначают N={1, 2, 3, …n, …}. Сюда не входит ноль, он применяется только для описания многозначных величин.

Если выражение содержит только один значок, то оно называется однозначным. Например: 1, 3, 7. Если запись имеет больше одной цифры, то она многозначная. К примеру, числа: 15, 23, 78 – двузначные, 125, 561, 938 – трёхзначные, 2589, 1596, 3564 – четырёхзначные. Математика использует десятичную систему исчисления. При записи каждому значку соответствует своё определённое значение в зависимости от расположения. Например, 286:

Последняя шесть означает 6 единиц.
Предпоследняя восемь – 8десятков.
Первая двойка – 2 сотни.

В этой записи две сотни, восемь десятков и шесть единиц.

С ними производят математические действия: сложение, вычитание, умножение, деление, а также возведение в степень и извлечение корня. Но только при умножении и сложении получают натуральные числа. Если выполнять другие действия, то получим целую или дробную величину.

Целые числа

У этого понятия определение шире. Сюда входят элементы, описанные выше, а также противоположные по значению и 0. В итоге, имеем бесконечное количество натуральных (1, 2, 3, 4, …) и столько же противоположных значений.

Совокупность их с нолём называется целыми.Они бывают положительными и отрицательными. Первые подразумевают знак плюс (обычно не пишется). Примеры таких записей: 8, 15, 127, 3259.

Отрицательные целые имеют знак минус (всегда пишется): −9, −21, −832, −4785. Они появились при развитии товарообменных отношений. Так было удобно считать долги. Например, торговцу заплатили за мешок вяленой рыбы одну шкурку лисы, а надо было три, то долг составит ещё две шкурки: 1− 3 = −2.

Ноль стоит обособленно. Он не принадлежит ни к тем, ни к другим. Все что больше него – положительные, меньше – отрицательные. Множество этих элементов обозначают Z={… −3, −2, −1, 0, 1, 2, 3, …}. С ними выполняют основные математические действия, нельзя только делить на ноль. Этими значениями принято описывать количественное изменение предметов или физических явлений во времени.

Общие черты понятий

Оба выполняют количественную характеристику предметов или каких-то параметров.
Натуральные значения входят во множество целых, то есть любое из них будет целым.
Математические действия кроме деления и извлечения корня с обоими видами даёт целое.
Самого большого числа для них нет – исчезает в бесконечности.

Отличия чисел

Наряду с общими признаками у этих понятий есть различия в написании, значениях и функциях.

Натуральные всегда больше ноля, целые – положительные, отрицательные и 0, поэтому не каждое целое будет натуральным.

У первых самое маленькое значение единица, у вторых его нет, оно бесконечно малое. Какую бы маленькую величину мы не придумали, от неё всегда можно отнять единицу и получить ещё меньшую и так бесконечно много раз.

Целыми легче описывать изменение количества, чем натуральными. При этом нет необходимости конкретно указывать увеличение или уменьшение численности. Само число характеризует эту перемену, а знак перед ним указывает направление. Вот примеры такого описания. Пусть в библиотеке есть некоторое количество книг. Если туда привезут еще восемьдесят, то их станет больше, а 80 выражает это изменение перечня в сторону повышения. Если же из библиотеки заберут тридцать книг, то их станет меньше, а 30 будет выражать перемену в сторону снижения. В библиотеку не будут привозить и увозить издания, то говорят о неизменности наличия литературы, то есть произошла нулевая перемена.

Этот пример показывает преобразование объёма книг с помощью целых чисел 80, −30 и 0 соответственно. Положительное 80 передаёт рост численности, отрицательное −30 выражает её понижение (отрицательная величина). Ноль показывает, что сумма предметов осталось без изменения.

Целыми хорошо описывается варьирование физических величин. При увеличении температуры на 3 градуса, это указывается значением 3. Уменьшение температуры на 10 градусов записывается как число с минусом: −10. А постоянство температуры определяется нолём.

Не каждый из нас математик, но понимание основ этой науки сыграет позитивную роль для каждого. Элементарные математические знания не раз выручат в трудной ситуации.

НаукаКомментировать

Натуральное число: определение и примеры

Определения статистики > Натуральные числа и целые числа

Содержание (Нажмите, чтобы перейти к этому разделу)

Натуральное число
Целые числа
Почему натуральное число является целым числом?
Целые числа Пример
Закрытые комплекты и целые изделия
Свойства целых чисел

Натуральные числа — это числа, которые мы используем для счета. Они целые, неотрицательных чисел. Мы часто видим их представленными в числовой строке .

Строка на изображении выше начинается с 1 и увеличивается в значении до 5. Однако значения чисел могут увеличиваться навсегда (обозначено пунктирной линией на изображении). Следовательно, натуральные числа могут продолжаться до бесконечности.

Набор натуральных чисел обычно обозначается символом ℕ . Например:

ℕ = {1, 2, 3, 4, 5, 6, 7…}

Набор натуральных чисел, включающий ноль, известен как целых чисел . Набор целых чисел обычно обозначается как W . Например, ниже представлен набор целых чисел:

W = {0, 1, 2, 3, 4, 5, 6, 7…}

Возможно, это сбивает с толку, некоторые авторы не включают ноль в числовое значение. набор целых чисел. В этом случае это то же самое, что и множество натуральных чисел.

Как упоминалось выше, натуральные числа должны быть целыми и положительными. Это имеет смысл по ряду причин, включая тот факт, что они считают числа. Допустим, учитель хочет посчитать количество учеников в своем классе: она может сосчитать только всех детей целиком.

Мы часто видим в статистике, опубликованной в Интернете, цифры, которые, кажется, противоречат «целостности» людей. Например, «средний размер семьи составляет 3,1 человека». Должно быть совершенно ясно, что невозможно иметь 0,1 человека, но это число является лишь средним. Среднее количество автомобилей на домохозяйство рассчитывается путем сложения общего количества автомобилей и деления на количество домохозяйств. Как только мы разделим, мы больше не будем работать с натуральными числами. Скорее, у нас остается действительное число, в данном случае дробь.

Сумма или произведение натуральных чисел также являются натуральными числами. Например, 5 + 5 = 10 (все три числа натуральные), или 10 · 15 = 150.

Точно так же в физическом мире «натуральных» чисел нет смысла говорить, что у нас есть «что-то отрицательное». . Скорее мы говорим, что у нас есть ноль чего-то там, где их нет. Используя приведенный выше пример с учителем, если у учителя в настоящее время нет учеников в классе, у него нет учеников; В реальном мире нет никакого смысла иметь отрицательных учеников.

Полный набор целых чисел равен набору из неотрицательных целых чисел. Целые числа похожи на целые числа, за исключением того, что они также могут быть отрицательными или нулевыми. Например: -10, -3, 0, 1 5.
Статья по теме: Целочисленные последовательности (CalculusHowTo.com).

Несколько примеров целых чисел: 3, 15, 998, 2, 232, 589.

Все следующие , а не целые числа:

.
Дроби : ½, 1/27, 2 ½, 99/100.
Отрицательные числа: -10, -99, -521.

В теории множеств целые числа подчиняются нескольким правилам. Множество целых чисел:
Замкнуто при сложении и умножении. Возьмите два целых числа a и b. Если добавить потом (a + b = c), то «c» тоже будет целым числом. То же верно и для умножения: a · b = d.

Давайте рассмотрим пару конкретных примеров с числами вместо переменных:

6 + 7 = 13
6 · 7 = 42

Множество целых чисел не замкнуто для деления и вычитания. Если a — целое число, то существует другое целое число b, которое дает нецелочисленное решение. В обозначениях это:

a – b = c
а/б = д

Где «b», «c» и «d» не являются целыми числами.

Примеры :

Вычитание:
6 и 10 — целые числа,
, но 7–9 = -2, что не является целым числом.
Деление :
4 и 5 — целые числа, но 4/5 — не целое число.

Целые числа являются коммутативными для сложения и умножения. Вы не можете вычесть два целых числа в любом порядке и получить тот же результат.
В обозначениях: Для любых a, b в наборе целых чисел a + b = b + a и a · b = b a.
Пример : 10 – 1 не то же самое, что 1 – 10.
Целые числа ассоциативны для сложения и умножения. Порядок добавления не важен (они могут быть сгруппированы в разном порядке).
Для любых a, b и c в множестве целых чисел a(b·c) = (a·b) · c и (a + b) + c = a + (b + c).
Набор целых чисел включает аддитивную единицу (0). Ноль — это аддитивная идентичность целых чисел. В обозначениях а + 0 = а для каждого целого числа а.
Мультипликативная идентичность равно 1. Умножьте любое целое число на 1, и вы получите тот же результат. В обозначениях 1 · а = а.

Натуральные числа: ссылки

Распространение натуральных чисел на целые

ПРИЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Натуральное число: определение и примеры» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/natural-number/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Полностью натуральная цельная утка | Maple Leaf Farms

Описание

Наша полностью натуральная цельная утка — идеальный вариант для воплощения вашего кулинарного творчества. Готовьте целиком, разделывайте на грудку и ноги или даже запекайте тушку для утиного бульона. Это один из наших самых простых продуктов, с которым можно проявить творческий подход на кухне или приготовить звездный праздничный ужин.

Вес: 3–7 фунтов
Доступен: свежий или замороженный
Срок годности: 14 дней в холодильнике / 2 года в замороженном виде с минимальной обработкой (без маринования)
Без глютена
Без добавления гормонов
Без антибиотиков для стимуляции роста

Наша цельная утка полностью натуральная, выращенная и выращенная в свободном выгуле на небольшой семейной утке фермы по всей Северной Индиане. Maple Leaf Farms уделяет первостепенное внимание благополучию наших уток в рамках нашей программы Trident Stewardship.

Ингредиенты:
Duck -Маринация Добавлена 

Купить сейчас

Время подготовки: 10 минут

Время приготовления: 2-3 часа

Время готовой: 2-3 часы

Инструкции по приготовлению

1
Если заморожено, разморозить в холодильнике.
2
Разогрейте духовку до 350 градусов по Фаренгейту.
3
Вынуть из сумки. Удалить шею и потроха из полости тела.
4
Промокните утку бумажными полотенцами.
5
Приправить по вкусу.
6
Жарить без крышки, грудкой вверх, на решетке в жаровне в течение 30 минут на фунт или до тех пор, пока внутренняя температура не достигнет 180 градусов F (82 градуса C) при измерении в бедренном суставе.
7
Ножки свободно двигаются, а сок становится прозрачным, когда утка готова.
8
Перед нарезкой дайте постоять 10 минут.

Как разделать целую утку

Другие продукты, которые могут вам понравиться…

Разница между натуральными и целыми числами [Обновлено в 2022 г.]

Последнее обновление: 3 сентября 2022 г. / Автор Сандип Бхандари / Факт проверен / 5 минут

Сегодня существует несколько математических концепций и источников, которые помогают нам, людям, гладко выполнять различные задачи. Эти термины и концепции были придуманы различными интеллектами и математиками.

Эти математики и интеллектуалы позаботились о том, чтобы их знания по предмету дошли до самых разных людей.

Некоторые люди находят математику и статистику сложными и непреодолимыми, но они не знают, что как только человек поймет определенную концепцию, математика может быть очень интересной и увлекательной для изучения.

Основные понятия математики и статистики требуют глубокого понимания различных типов чисел. В математике есть несколько типов чисел. Два из которых 1. Натуральные числа и 2. Целые числа.

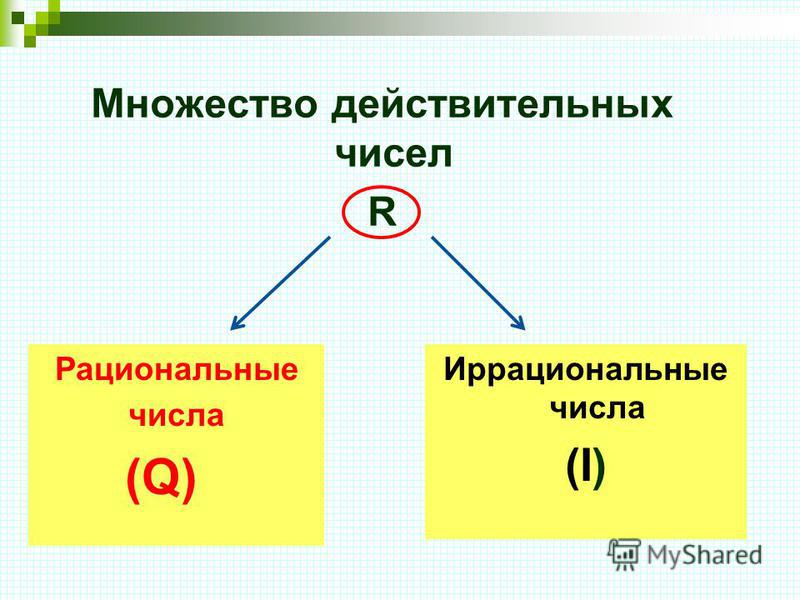
Натуральные и целые числа

Основное различие между натуральными числами и целыми числами заключается в наличии числа «ноль». Множество натуральных чисел не состоит из числа «ноль». С другой стороны, набор целых чисел состоит из числа «ноль».

Числа, которые используются для счета, а также числа, которые являются неотрицательными или положительными, называются натуральными числами. Для счета используются натуральные числа.

Набор натуральных чисел представлен как «N». Это бесконечный набор чисел, начинающихся с единицы.

Есть несколько свойств и функций натуральных чисел. За каждым натуральным числом следует другое натуральное число — это одно из наиболее широко известных свойств.

Набор чисел, состоящий из числа «ноль», известен как целые числа. Все целые числа считаются действительными числами, но, с другой стороны, не все действительные числа считаются целыми числами.

Они состоят из положительных чисел и целых чисел, но не из дробей. Набор целых чисел обозначается буквой «W».

Таблица сравнения между натуральными и целыми числами

Параметры сравнения	Натуральные номера	. которые неотрицательны или положительны, известны как натуральные числа.	Набор чисел, состоящий из числа «ноль», известен как целые числа.
Число «Ноль»	Отсутствует	Присутствует
Множество	Бесконечное множество представлено «N».	Бесконечное множество обозначается буквой «W».
Счетный номер	Счетный номер начинается с цифры «один».	Счетный номер начинается с цифры «ноль».
Установить обозначение	{1,2,3,4,5,6,7,……. }	{0,1,2,3,4,5,6,7,8,…… }

Что такое натуральные числа?

Числа, которые используются для счета, а также числа, которые являются неотрицательными или положительными, называются натуральными числами. Теоретизировано несколько свойств натуральных чисел.

История натуральных чисел насчитывает несколько лет и является довольно древней. Различные интеллекты постулировали несколько теорий и свойств натуральных чисел.

Для счета используются натуральные числа. Набор натуральных чисел представлен как «N». Это бесконечный набор чисел, начинающихся с единицы.

В 19 веке в Европе велось несколько дискуссий о системе счисления. Велись как математические, так и философские дискуссии.

Некоторые умы даже постулировали, что натуральные числа были результатом человеческого интеллекта. Самотеоретические значения и определения были инициированы Фреге.

Существует несколько свойств и функций натуральных чисел. Множество натуральных чисел бесконечно, но оно известно как счетная бесконечность.

Подсчет и упорядочивание — два наиболее значительных обобщения натуральных чисел. Эти числа помогают многим людям в различных задачах.

Что такое целые числа?

Набор чисел, состоящий из числа «ноль», известен как целые числа. Все целые числа существуют на числовой прямой, и все они действительные числа.

Примеры целых чисел: 0, 44, 19, 13, 45, 67, 24, 5 и т. д. Целые числа не содержат дробей и включают число «ноль».

Все целые числа считаются действительными числами, но, с другой стороны, не все действительные числа считаются целыми числами. Они состоят из положительных чисел и целых чисел, но не состоят из дробей.

Набор целых чисел обозначается буквой «W». Есть несколько фактов и свойств, касающихся целых чисел.

Все натуральные числа, счетные числа, положительные целые числа являются целыми числами, включая число «ноль». Также говорят, что все целые числа являются действительными числами, но не все действительные числа являются целыми числами.

Эти факты и свойства были постулированы несколькими учеными и математиками с течением времени.

В основе свойств целых чисел лежат различные арифметические операции. К таким операциям относятся сложение, вычитание, умножение и деление.

Умножение или сложение двух целых чисел дает целое число, в отличие от вычитания двух целых чисел, которое может дать или не дать целое число, поскольку иногда результаты также являются целыми числами.

Если разделить два целых числа, получится дробь.

Основные различия между натуральными и целыми числами

Числа, используемые для счета, а также неотрицательные или положительные числа называются натуральными числами. С другой стороны, набор чисел, состоящий из числа «ноль», известен как целые числа.
Множество натуральных чисел не состоит из числа «ноль». С другой стороны, множество целых чисел состоит из числа «ноль».
Набор натуральных чисел представлен буквой «N». С другой стороны, набор целых чисел представлен буквой «W».
Счетное число в натуральных числах начинается с цифры «один». С другой стороны, счетным числом в целых числах является число «ноль».
Установленная запись натуральных чисел {1,2,3,4,5,6,7,8,9…….}, с другой стороны, установленная запись целых чисел {0,1,2,3,4,5,6,7,8,9….}.
Все натуральные числа считаются целыми числами, но не все целые числа считаются натуральными числами.

Заключение

Как натуральные, так и целые числа облегчили людям выполнение различных математических задач. Многие умы и ученые выдвинули несколько теорий относительно этих чисел и их нескольких типов.

Многие люди следуют и используют эти теории.

Однако всегда нужно знать различные математические и статистические термины и понятия.

Изучение этих предметов играет важную роль в жизни человека, поскольку они применимы в различных повседневных жизненных событиях и происшествиях. Нужно, по крайней мере, знать основы предмета, чтобы выполнять несколько задач.

Ссылки

https://www.researchgate.net/profile/Grzegorz-Bancerek/publication/243767436_Segments_of_Natural_Numbers_and_Finite_Sequences/links/5470776e0cf216f8cfa9f888/Segments-of-Natural-Numbers-and-Finite-Sequences.pdf
https://library.oapen.org/bitstream/handle/20.500.12657/27709/1002297.pdf?sequence=1

Поиск для «Спроси любую разницу» в Google. Оцените этот пост!

[Всего: 0]

Один запрос?

Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы он был вам полезен. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. ДЕЛИТЬСЯ ♥️

Содержание

сообщите об этом объявлении

Whole Natural | Classic Almonds

Show more flavors

Whole Natural Almonds

Lightly Salted Low Sodium Almonds

Roasted Salted Almonds

Smokehouse® Almonds

Honey Roasted Almonds

Toasted Coconut Almonds

Blueberry Almonds

Dark Chocolate Flavored Almonds

Миндаль с морской солью

Миндаль со вкусом корицы и клена

Миндаль со вкусом темного шоколада и перца чили

Вкусный, полезный для сердца* суперпродукт**, цельный натуральный миндаль от Blue Diamond — идеальное дополнение к вашей повседневной жизни. Наш превосходный натуральный миндаль Nonpareil является хорошим источником витамина Е, биотина и магния, которые являются важными питательными веществами для поддержания красоты изнутри.

Съедайте 28 миндальных орехов Blue Diamond в день. Feel Beauty Full.™

* Научные данные предполагают, но не доказывают, что употребление 1,5 унции. в день большинство орехов, таких как миндаль, как часть диеты с низким содержанием насыщенных жиров и холестерина может снизить риск сердечных заболеваний. Содержание жира см. в информации о пищевой ценности

** 28 Миндаль содержит 5 г растительного белка на порцию и является отличным источником антиоксиданта витамина Е и хорошим источником магния.

СМОТРЕТЬ

Богатый биотин

0:16

Посмотреть

Хороший источник магния

0:15

Найдите Alck Almonds

FULTION FAUL 160

% Daily Value
Total Fat 14g 18% Saturated Fat 1g 5% Trans Fat 0g Polyunsaturated Fat 3. 5g Monounsaturated Fat 9g Cholesterol 0mg Sodium 0mg Total Carbohydrate 6g 2% Dietary Fiber 3g 11% Total Sugars 1g Added Sugars 0g Protein 6g Vitamin D  0mcg Calcium 70mg 6% Iron 1. 1mg 6% Potassium 200mg 4% Vitamin E 7.4mg 50% Magnesium 75mg 20%
Ингредиенты
МИНДАЛЬ.
Обзоры продуктов
Другие продукты с миндалем
Будьте смелее. Закуска жирный.
Посмотреть больше продуктов
XTREMES
Посмотреть больше продуктов
More Blue Diamond Products
Almond BreezeShelf Stable Coconut Unsweetened Original Almondmilk
Snack AlmondsCayenne Pepper Not for the Faint of Tongue
ProteinUnsweetened Almond Protein Powder Drink Mix
Nut-Thins® Мед Корица Nut-Thins®
Nut-Thins®Pepper Jack Nut-Thins®
Snack AlmondsSmokehouse® Almonds
Свежая полностью натуральная молодая индейка
Информация о HPAI стрелка вправо
Ссылка скопирована!
Вам больше не нужно искать, где купить свежую индейку! Забудьте о размораживании: полностью натуральная* цельная индейка готова к отправке в духовку, и ее приготовление не займет целый день! Удобный всплывающий таймер сообщит вам, когда это будет сделано. Выберите из разных размеров подходящее блюдо для случая, будь то будний день или праздник. Чтобы узнать больше о приготовлении свежей полностью натуральной* молодой индейки, посмотрите наше простое видео с практическими рекомендациями и найдите свежую индейку в холодильном отделе своего продуктового магазина.
* Минимальная обработка. Никаких искусственных ингредиентов.

Калории 140
Всего жиров 6г
Насыщенный жир 2г
Трансжиры 0г
Холестерин 70 мг
натрий 80 мг
Всего углеводов 0 г
Пищевые волокна 0 г
Всего сахаров 0г
Включает 0 добавленных сахаров 0
белок 24г 48%
Кальций 0 0%
Утюг 2%
Витамин А 0%
Витамин C 0%
* % дневной нормы (DV) показывает, сколько питательных веществ содержится в порция еды способствует ежедневному рациону. 2000 калорий день используется для общих рекомендаций по питанию.
Young Turkey содержит до 6% остаточной воды.
Бытовая печь:
Охладить при температуре 28-36°F или заморозить до 0°F или ниже.
Разморозьте в холодильнике 3-4 дня или поместите упакованную индейку в раковину с холодной водой.
Часто меняйте воду и дайте оттаять 1/2 часа на фунт.
Охладить после оттаивания.
Готовьте целую индейку при температуре 325°F, пока термометр для мяса, вставленный в самую толстую часть бедра, не зарегистрирует 180°F.
Соки должны быть прозрачными.
ДЛЯ ЖАРКИ:
Нагрейте духовку до 325°F.
Удалить шею и потроха.
Их можно использовать для приготовления соуса или начинки.
Во время приготовления можно оставить пластиковый зажим для ног.
Положите индейку на решетку в неглубокую сковороду грудкой вверх и неплотно накройте фольгой.
Обжарка при 325°F.
Снимите фольгу через 1 час приготовления.
Продолжайте жарить при температуре 325°F до тех пор, пока термометр для мяса, вставленный в самую толстую часть бедра, не зарегистрирует 180°F.
Соки должны быть прозрачными.
Перед нарезкой дайте индейке постоять 20 минут.
Для оптимальной безопасности готовьте фарш и индейку отдельно.
При желании добавьте полностью приготовленную начинку в готовую индейку непосредственно перед подачей на стол.
Приблизительное время запекания в духовке при 325°F:
ВЕС ВРЕМЯ ПРИГОТОВЛЕНИЯ 8-12 фунтов от 3-1/2 до 4 часов 12-18 фунтов от 4-1/4 до 4-3/4 часов 18-22 фунтов 4-1/ от 2 до 5 часов 22-24 фунта от 4-3/4 до 5-1/4 часов
ТЕГИ Не содержит глютен Натрий Смарт Свежий Вся Турция Специальные диеты
Рекомендуемые продукты
Посмотреть больше
Популярные рецепты
Посмотреть больше
Узнайте больше о нас
Посмотреть больше
Синтетические и натуральные питательные вещества: имеет ли это значение?
Мэри Джейн Браун, доктор философии, доктор медицинских наук (Великобритания), 17 августа 2016 г.
Многие люди не получают достаточного количества питательных веществ только из пищи (1).
В настоящее время более половины населения США принимает синтетические питательные вещества, такие как поливитамины (2).
Тем не менее, было много споров о том, обеспечивают ли синтетические питательные вещества те же преимущества, что и натуральные питательные вещества.
Некоторые источники даже предполагают, что синтетические питательные вещества могут быть опасны.
В этой статье объективно рассматривается наука о синтетических и натуральных питательных веществах.
Что такое синтетические и натуральные питательные вещества?
Вот разница между натуральными и синтетическими питательными веществами:
Натуральные питательные вещества: Получаются из цельных пищевых источников в рационе.
Синтетические питательные вещества: Также называемые изолированными питательными веществами, они обычно производятся искусственно в промышленном процессе.
Синтетические питательные вещества не включают «цельные пищевые добавки», которые изготавливаются из концентрированных обезвоженных цельных продуктов.
Большинство пищевых добавок, доступных сегодня на рынке, производятся искусственно. К ним относятся, среди прочего, витамины, антиоксиданты, минералы и аминокислоты.
Их можно принимать в виде пилюль, капсул, таблеток, порошка или жидкости, и они созданы для имитации того, как естественные питательные вещества действуют в нашем организме.
Чтобы выяснить, является ли ваша добавка синтетической или натуральной, проверьте этикетку. Натуральные добавки обычно содержат список источников пищи или помечены как 100% растительные или животные продукты.
Добавки, в которых питательные вещества перечислены отдельно, например, витамин С, или используются химические названия, такие как аскорбиновая кислота, почти наверняка являются синтетическими.
Итог:
Синтетические питательные вещества — это пищевые добавки, искусственно изготовленные в лабораторных условиях или в промышленных условиях. Натуральные питательные вещества содержатся в цельных продуктах.
Отличаются ли натуральные и синтетические питательные вещества?
Принято считать, что синтетические питательные вещества химически почти идентичны тем, которые содержатся в пищевых продуктах.
Однако процесс производства синтетических питательных веществ сильно отличается от того, как их создают растения и животные. Таким образом, несмотря на схожую структуру, ваше тело может по-разному реагировать на синтетические питательные вещества.
Кроме того, неясно, насколько хорошо синтетические питательные вещества усваиваются и используются организмом. Одни могут усваиваться легче, другие нет (3).
Это потому, что когда вы едите настоящую пищу, вы потребляете не отдельные питательные вещества, а целый ряд витаминов, минералов, кофакторов и ферментов, которые обеспечивают оптимальное использование организмом.
Без этих дополнительных соединений синтетические питательные вещества вряд ли будут использоваться организмом так же, как их натуральные аналоги (4).
Например, исследования показывают, что натуральный витамин Е усваивается в два раза эффективнее, чем синтетический витамин Е (5).
Итог:
Неясно, насколько хорошо синтетические питательные вещества усваиваются и используются организмом. Ваше тело будет лучше использовать питательные вещества, если принимать их в виде цельных продуктов с широким спектром пищевых соединений.
Питательные вещества в цельных продуктах полезны для здоровья
Натуральные цельные продукты могут помочь в лечении и профилактике сердечных заболеваний, диабета, рака и ранней смерти.
Эти преимущества были связаны с широким спектром витаминов, минералов, антиоксидантов, клетчатки и жирных кислот, содержащихся в цельных продуктах.
Фрукты и овощи
Фрукты и овощи снабжают нас клетчаткой, витаминами, минералами и растительными соединениями, которые, как считается, полезны для здоровья.
Наблюдательные исследования показывают, что более высокое потребление фруктов и овощей связано с более низким риском сердечных заболеваний, рака, диабета, артрита и некоторых заболеваний головного мозга (6, 7, 8).
Увеличение потребления фруктов также связано со снижением артериального давления, уменьшением окислительного стресса и улучшением контроля уровня сахара в крови (9, 10).
Один обзор показал, что с каждой ежедневной порцией съеденных фруктов или овощей риск сердечных заболеваний снижается на 4–7% (11).
Жирная рыба
Ученые считают, что высокий уровень омега-3 жирных кислот в жирной рыбе способствует улучшению здоровья сердца.
Многие крупные обсервационные исследования показали, что люди, которые регулярно едят рыбу, имеют более низкий риск сердечных приступов, инсультов и смерти от сердечных заболеваний (12, 13, 14, 15).
Одно исследование, в котором приняли участие более 40 000 мужчин в возрасте 40–75 лет, показало, что у тех, кто регулярно ел одну или несколько порций рыбы в неделю, риск сердечных заболеваний был на 15 % ниже (16).
Фасоль и бобовые
Эксперты считают, что высокое содержание растворимой клетчатки и широкий спектр витаминов, минералов и антиоксидантов в фасоли и бобовых могут помочь снизить риск сердечных заболеваний, диабета и некоторых видов рака (
17
,
18
,
19
) .
Ежедневное употребление одной порции бобовых, таких как фасоль, горох и нут, снижает уровень холестерина ЛПНП на 5% и снижает риск сердечно-сосудистых заболеваний на 5-6% (20).
Орехи и семена
Орехи и семена богаты антиоксидантами, минералами и полезными жирами. Они были связаны со сниженным риском ранней смерти, сердечных заболеваний и диабета (9).0004 21
,
22
).
Один обзор показал, что 4 порции орехов в неделю снижают риск сердечно-сосудистых заболеваний на 28% и диабета на 22% (22).
Цельнозерновые продукты
Цельнозерновые продукты содержат много ценных питательных веществ, в том числе клетчатку, витамины группы В и минералы, такие как железо, магний и селен.
Потребление цельного зерна также связано с защитой от рака, сердечных заболеваний, диабета и ожирения (23).
Итог:
Данные подтверждают идею о том, что натуральные питательные вещества, содержащиеся в цельных продуктах, могут предотвратить широкий спектр хронических заболеваний, таких как болезни сердца, диабет, рак и преждевременная смерть.
Исследования пищевых добавок дали неоднозначные результаты
Хотя очевидно, что натуральные питательные вещества связаны со многими преимуществами для здоровья, данные о синтетических добавках неоднозначны.
Поливитамины
Некоторые обсервационные исследования показали, что прием поливитаминов связан с более низким риском сердечных заболеваний и рака (
24
,
25
,
26
,
27
,
28
).
Однако другие исследования не выявили эффекта (29, 30, 31, 32, 33, 34).
Некоторые даже связывают использование поливитаминов с повышенным риском развития рака (35, 36, 37, 38).
Одно большое исследование изучало влияние поливитаминов в высоких дозах на здоровье сердца. Спустя почти 5 лет исследование показало, что поливитамины не оказывают положительного эффекта (39).
Однако несколько других исследований связывают поливитаминные добавки с улучшением памяти у пожилых людей (40, 41, 42, 43).
Тем не менее, Исследование здоровья врачей II показало, что 12 лет ежедневного приема поливитаминов не повлияли на функцию мозга или память у мужчин старше 65 лет (44).
Отдельные и парные витамины
В одном обзоре не было обнаружено явных доказательств того, что отдельные или парные добавки полезны при сердечных заболеваниях (
45
).
Однако некоторые предыдущие исследования показывают, что витамины группы В, такие как фолиевая кислота, могут улучшать работу мозга (46).
Другие убедительные исследования показывают, что пищевые добавки, включая витамины группы В, не улучшают работу мозга (47, 48).
Несмотря на то, что известно, что достаточный уровень витамина D имеет решающее значение для хорошего здоровья и профилактики заболеваний, добавки витамина D также находятся под пристальным вниманием (49, 50).
Добавки витамина D были связаны с многочисленными преимуществами, связанными с раком, здоровьем костей и функцией мозга, и это лишь некоторые из них. Тем не менее, эксперты согласны с тем, что необходимы дополнительные доказательства (50, 51).
Эксперты в целом согласны с тем, что добавки витамина D в сочетании с кальцием могут улучшить здоровье костей у пожилых людей (50).
Антиоксиданты
В нескольких обзорах не было найдено доказательств в поддержку антиоксидантных добавок, включая бета-каротин, витамины A, C, E и селен (по отдельности или в комбинации), для снижения риска смерти и рака (
52
,
53
).
На самом деле было показано, что добавки с бета-каротином повышают риск развития рака у курильщиков (54).
Тем не менее витамины-антиоксиданты и минералы могут помочь замедлить прогрессирование заболеваний, вызывающих слепоту. Однако необходимы дополнительные исследования (55, 56).
Итог:
Исследования благотворного воздействия на здоровье многих синтетических питательных веществ были непоследовательными, слабыми или не показали никакого эффекта.
Стоит ли принимать синтетические питательные вещества?
Нет четких доказательств того, что большинство синтетических питательных веществ полезны для здоровых, хорошо питающихся людей.
Тем не менее, есть определенные группы, которым могут быть полезны добавки с синтетическими питательными веществами. К ним относятся:
Пожилые люди: Эта группа, как правило, подвержена более высокому риску дефицита витамина D и может также нуждаться в большем количестве витамина B12 и кальция для здоровья костей (57, 58).
Веганы и вегетарианцы: Поскольку некоторые витамины и минералы содержатся в основном в продуктах животного происхождения, эта группа часто подвергается высокому риску дефицита витамина B12, кальция, цинка, железа и витамина D (59, 60).
Беременные и кормящие женщины: Этим женщинам, возможно, придется дополнять свой рацион дополнительными витаминами и/или минералами (такими как витамин D) и избегать других (таких как витамин A) (61).
Женщинам детородного возраста: Этой группе часто рекомендуется принимать добавки фолиевой кислоты, чтобы снизить риск дефектов нервной трубки в случае беременности. Однако прием большего количества, чем вам нужно, может иметь некоторые риски.
Люди с дефицитом питательных веществ: Некоторые пищевые добавки могут лечить дефицит питательных веществ, например, добавки железа для лечения железодефицитной анемии (62).
Итог:
Определенным группам людей, подверженным риску дефицита питательных веществ, могут быть полезны определенные синтетические добавки.
Синтетические питательные вещества могут быть откровенно вредными
В общем, прием добавок в соответствии с количеством, указанным на упаковке, безопасен для большинства людей.
Однако FDA не проверяет пищевые добавки на безопасность и эффективность до того, как они поступят в продажу. Следовательно, может произойти мошенничество с добавками.
Это означает, что добавки могут содержать больше или меньше питательных веществ, чем указано на этикетке. Другие могут содержать вещества, не указанные на этикетке.
Если вы уже потребляете широкий спектр питательных веществ с пищей, прием дополнительных добавок может превысить рекомендуемую суточную норму многих питательных веществ.
При избыточном приеме водорастворимые витамины, такие как витамин С и витамины группы В, вымываются из организма с мочой. Однако жирорастворимые витамины — витамины А, D, Е и К — могут накапливаться в организме. Это означает, что существует риск их накопления до высоких уровней, что приводит к гипервитаминозу.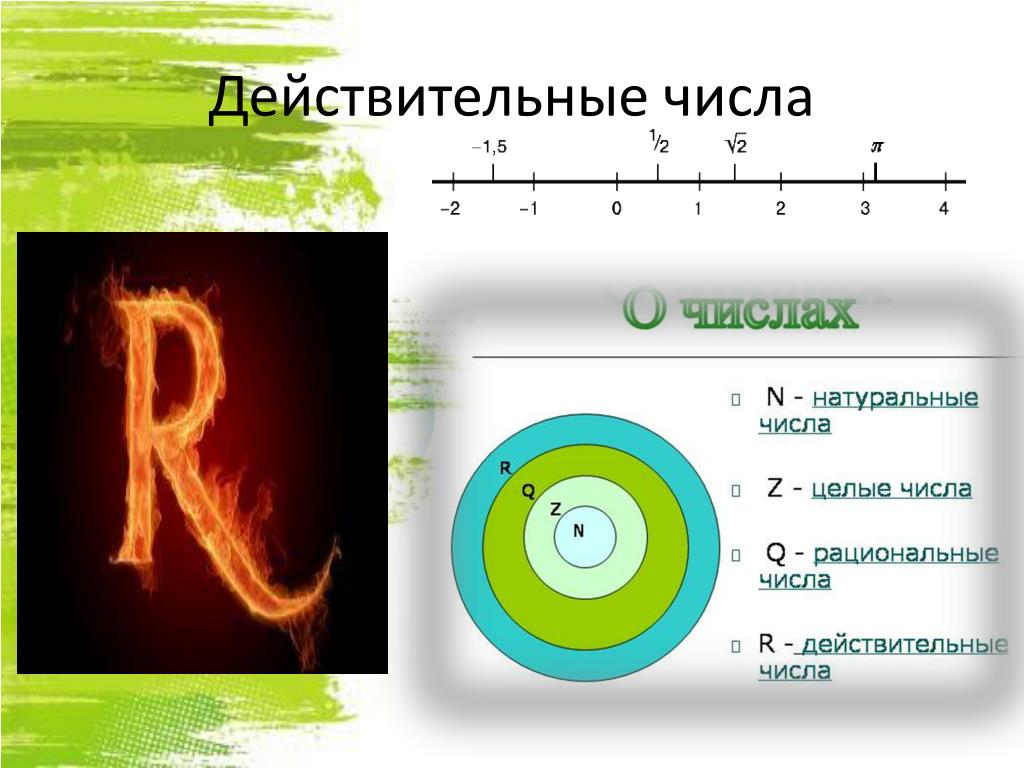
Беременные женщины должны быть особенно осторожны с потреблением витамина А, поскольку избыточное его количество связано с врожденными дефектами (63).
Результаты многих клинических испытаний показывают, что бета-каротин, витамин Е и, возможно, высокие дозы витамина А могут повышать риск преждевременной смерти (64, 65).
Другие исследования связывают использование поливитаминов с повышенным риском рака, а добавки железа могут быть вредными для людей, которые в них не нуждаются (66, 67, 68, 69).
Есть также некоторые свидетельства того, что синтетическая фолиевая кислота более вредна, чем натуральная фолиевая кислота в пищевых продуктах. Он может накапливаться в организме и повышать риск развития рака (70, 71, 72).
Итог:
Прием большого количества синтетических питательных веществ может иметь вредные последствия для здоровья. Рекомендуемые суточные дозы безопасны для большинства людей, но рекомендуется соблюдать осторожность.
No related posts.