log online
Вы искали log online? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и online log, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «log online».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как log online,online log,антилогарифм калькулятор онлайн,антилогарифм онлайн,антилогарифм онлайн калькулятор,вычислить логарифм онлайн с подробным решением,двоичный логарифм,калькулятор логарифмические уравнения,калькулятор логарифмических выражений,калькулятор логарифмических уравнений,калькулятор логарифмов с дробями,калькулятор логарифмов с решением онлайн,калькулятор решение логарифмов,калькулятор решения логарифмов,калькулятор уравнений логарифмов,калькулятор уравнений с логарифмами,логарифмирование онлайн,логарифмические уравнения калькулятор,логарифмические уравнения калькулятор онлайн,логарифмические уравнения калькулятор онлайн с подробным решением,логарифмический калькулятор онлайн с решением,логарифмы онлайн калькулятор с подробным решением,логарифмы онлайн примеры,онлайн калькулятор логарифмических уравнений,онлайн калькулятор логарифмов уравнений,онлайн калькулятор решение логарифмов,онлайн калькулятор с подробным решением логарифмы,онлайн решение логарифмических выражений,онлайн решение натуральных логарифмов,онлайн считать логарифмы,решение логарифмических выражений онлайн,решение логарифмов калькулятор,решение логарифмов калькулятор онлайн,решение логарифмов онлайн калькулятор,решение логарифмов онлайн калькулятор с подробным решением,решение логарифмов онлайн калькулятор с решением,решение логарифмов онлайн с решением калькулятор,решение примеров с логарифмами онлайн,решения логарифмов калькулятор,решить логарифм,решить логарифм онлайн,решить логарифмическое уравнение онлайн с подробным решением,решить логарифмы онлайн,решить онлайн логарифмы,считать логарифмы онлайн.
Решить задачу log online вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор инженерный BRAUBERG SC-880-N
Непрограммируемый инженерный калькулятор BRAUBERG SC-880-N выполняет все основные вычисления, которые понадобятся школьникам на экзаменах и контрольных работах по физике, химии, биологии и географии. Сертифицирован для использования на ЕГЭ и ОГЭ.
Сертифицирован для использования на ЕГЭ и ОГЭ.417 встроенных научных и статистических функций позволяют вычислять степени и корни, факториалы, логарифмы и антилогарифмы, интегралы и дифференциалы, а также производить статистические расчеты и вычисления с прямыми и обратными гиперболическими и тригонометрическими функциями (в том числе в градусах, радианах и градах).
Калькулятор поддерживает систему естественного ввода/вывода математических выражений и позволяет выводить на дисплей обыкновенные дроби, степени, корни, логарифмы и экспоненты в привычном всем еще со школы виде. Это делает интерфейс более «дружелюбным» для пользователя и позволяет снизить количество вычислительных ошибок.
Калькулятор может переключаться между двоичной, восьмеричной и шестнадцатеричной системами исчисления. Имеет 40 встроенных команд для перевода значений из одной единицы измерения в другую, а также 40 научных констант, которые отображаются уникальными символами и могут быть использованы внутри вычисления. Наряду с кнопкой выключения OFF в калькулятор встроена функция автоматического отключения (через 8-10 минут бездействия), которая позволяет максимально продлить срок его службы без замены батареи.
Наряду с кнопкой выключения OFF в калькулятор встроена функция автоматического отключения (через 8-10 минут бездействия), которая позволяет максимально продлить срок его службы без замены батареи.
Позаботьтесь об успехе на экзаменах заранее. Закажите калькулятор BRAUBERG SC-880-N в интернет-магазине Calculators-Online.ru
Больше информации в руководстве пользователя
Инструкция к инженерному калькулятору BRAUBERG SC-880-N
Технические характеристики
Разрядность дисплея: 12
Тип дисплея: жидкокристаллический
Количество функций: 417
Тип калькулятора: инженерный
Серия: SC-880
Функционал: алгебраический ввод/вывод данных (S.V.P.A.M.), вычисление абсолютного значения, вычисления с комплексными числами, матрицами и векторами, генерирование случайных чисел, естественный ввод/вывод данных (N.V.P.A.M.), логические операции, построение таблиц значений функций, расчеты в нескольких системах исчисления, регрессионный анализ, редактор данных с последовательным просмотром, решение систем линейных уравнений, статистические расчеты одной переменной, суммирование, численное интегрирование и дифференцирование
Число строк дисплея: 2
Регулировка контрастности дисплея: да
Конструктивные особенности: сдвижной пластиковый футляр
Тип питания: 1 батарейка CR2032
Цвет панели: белый
Материал кнопок — пластик
Производитель: Китай
Длина корпуса: 165 мм
Ширина корпуса: 84 мм
Вес: 130 г
Добавить комментарий
Уведомлять меня о новых комментариях по E-mail
Наши покупатели уже неоднократно заказывали этот калькулятор и делились с нами информацией, зачем он им необходим, планируют ли они использовать его для учебы или работы.

Прочитайте комментарии — и, возможно, вы откроете для себя новые варианты использования калькулятора:
- Школа 2048
- школа
- Школа/институт
Записей не найдено.
Вычисление логарифма и обратного логарифма
Логарифм против логарифма
Калькулятор логарифма
Калькулятор антилогарифма
Математические формулы
Вычисление логарифма (log): 0016
log b x = y подразумевает b у = х.
Где,
- b = основание,
- г = число,
- x = значение журнала.
Вычисление Antilog:
y = 10 x
Где,
- x = число,
- y = антилогарифмическое значение.
Логарифмы и антилогарифмы: как это работает и их значение
— Руководство Автор: Корин Б. Аренас и глобальные темпы экономического роста, то вы попали в нужное место.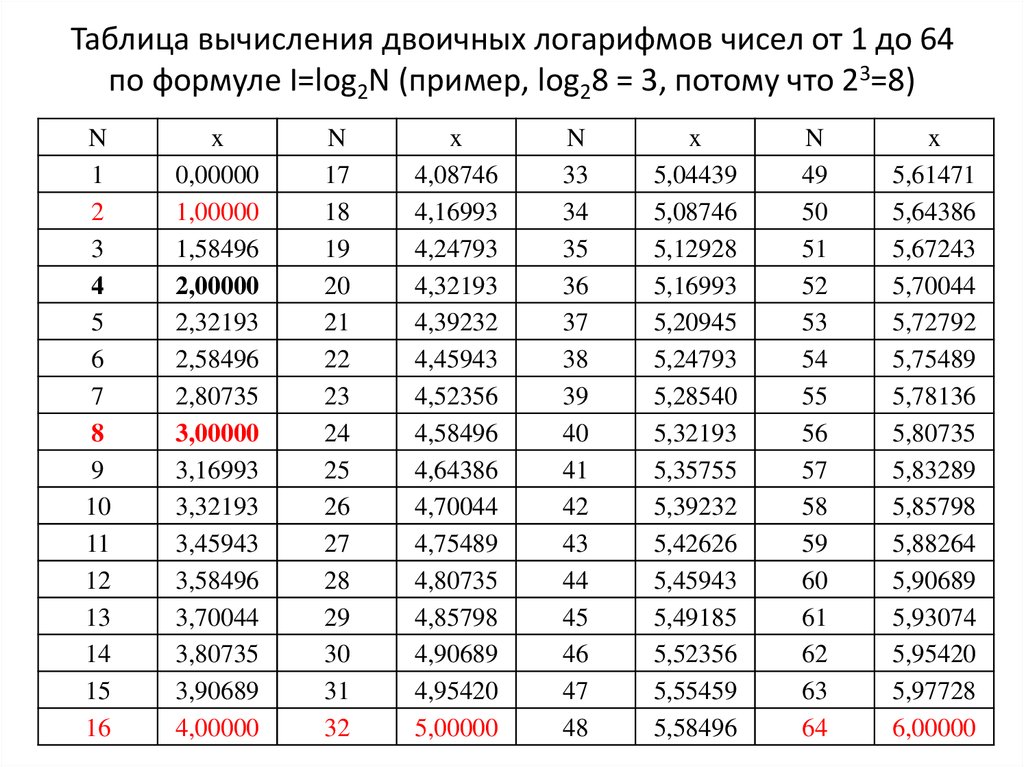
Расчет очень больших сумм может быть медленным и запутанным. Но с помощью логарифмов (log) и антилогарифмов (antilog) вычисления можно упростить.
Читайте дальше, чтобы узнать больше о log и antilog, о том, как они работают, и почему это важные математические концепции.
Что такое логарифм?
Логарифм — это степень, в которую число (называемое основанием ) должно быть умножено само на себя, чтобы получить данное число. Проще говоря, логарифм решает задачу:
Сколько раз нужно умножить на , чтобы получить еще одно число y ?
Логарифм подсчитывает, сколько раз нужно умножить один и тот же множитель, чтобы получить заданное число.
Кто это придумал?
Бревно было изобретено в 16 -м -м веке шотландским математиком, физиком и астрономом Джоном Нейпиром в качестве инструмента для расчетов. Он написал книгу Mirifici Logarithmorum Canonis Descriptio с таблицами и числами, в которых обсуждаются натуральные логарифмы, заложив основу для его основной концепции.
Нейпир ввел термин логарифм от греческого слова logos , что означает «отношение или пропорция», и arithmos , что означает «число». В сочетании это буквально означает «число отношения».
2 Типы логарифмов
Натуральный логарифм числа — это его логарифм по основанию константы e , где e приблизительно равно 2,718281828459. Уравнение записывается как log e (x) .
Если логарифм не указывает основание , как в этом примере: log(1000) , он известен как десятичный логарифм , который использует по основанию 10 .
log(1000) , он известен как десятичный логарифм , который использует по основанию 10 .
Как используется журнал?
Как только вы начнете считать цифры миллионами, миллиардами и триллионами, это может стать довольно утомительным. Касается ли это подсчета больших денег, роста населения или преодоления больших расстояний, журнал может работать на вас. Он может упростить больших сумм, содержащих длинные и запутанные уравнения, облегчая их понимание.
Касается ли это подсчета больших денег, роста населения или преодоления больших расстояний, журнал может работать на вас. Он может упростить больших сумм, содержащих длинные и запутанные уравнения, облегчая их понимание.
Вот стандартное уравнение для log:
log b (x) = y
Где,
- Число, умноженное само на себя (b), является основанием .
- Количество умножений (y) равно логарифму .
- В скобках записывается число , полученное (x).
Чтобы понять, как работает эта концепция, вот пример с меньшим числом:
b = 2, x = 32
log 2 (32) = y
Ответ: 2 x 2 x 2 x 2 x 2 = 32
32.
Ответ: log 2 (32) = 5
Следовательно, в этом примере: Логарифм числа 32 по основанию 2 равен 5, или логарифм 2 по основанию 32 равен 5.
Кроме того, log — это обратная функция возведения в степень, где математическая операция записывается как млрд . b — это основание, которое умножается в соответствии со степенью n, то есть количеством раз, когда оно умножается на себя.
Что это значит? Лог числа равен степени , на которую умножается основание b для получения данного числа. Чтобы дать вам лучшее представление, обратитесь к приведенному ниже примеру уравнения журнала вместе с его экспоненциальным уравнением.
Теперь попробуем с большим числом.
Вопрос: Сколько десятков нужно умножить, чтобы получить 150 000 000 000?
b = 10, x = 150 000 000 000
log b (x) = y
log(150 000 000 000) = y
log(150 000 000 000) = 11,17609125
Это решается с помощью логарифмическая функция в научном калькуляторе. Или воспользуйтесь калькулятором на этой странице, чтобы получить ответ.
Или воспользуйтесь калькулятором на этой странице, чтобы получить ответ.
Как антилогарифм связан с логарифмом?
Затем номер журнала может быть возвращен к исходному номеру. Это можно сделать с помощью антилогарифм (антилогарифм). Таким образом, антилогарифм — это обратная функция логарифма. Аналогично, антилогарифмические функции для
Чтобы вычислить антилогарифм числа y, вы должны возвести основание логарифма b (обычно 10, иногда константу e) в степень, которая даст число y.
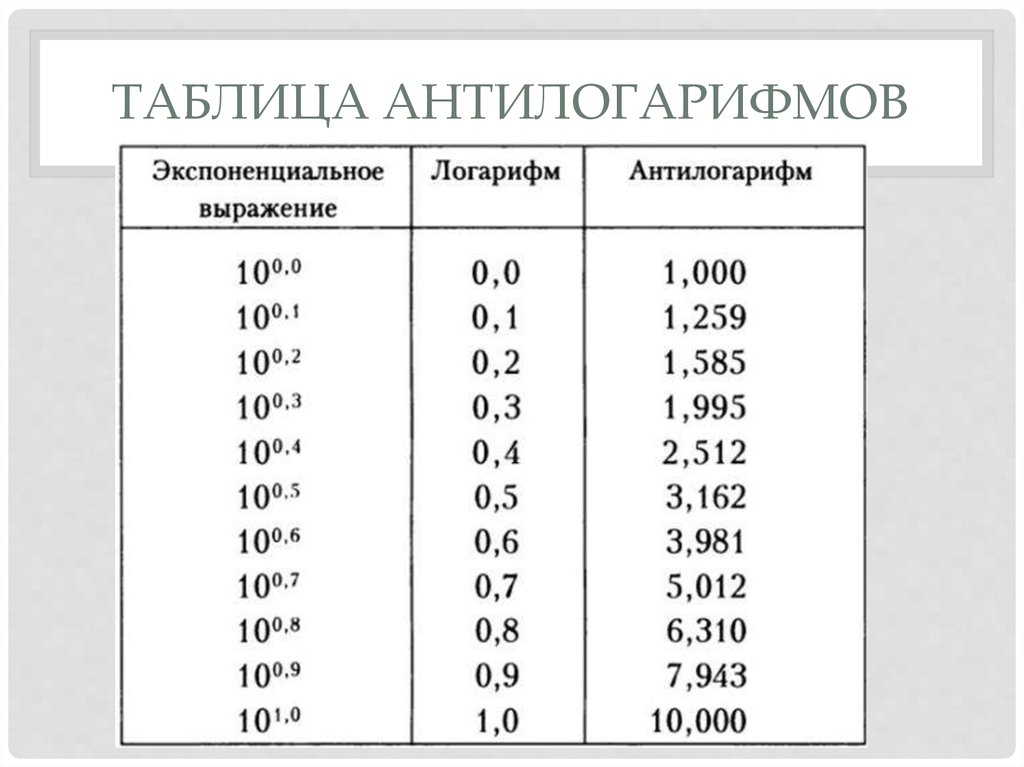
Вот уравнение для антилогарифма с основанием 10:
10 x = y
Где x — показатель степени, а y — антилогарифмическое значение.
Например, если мы возьмем это уравнение, log(5) = x, его антилогарифм будет 10x = 5.
- Log: log(5) = 0,698970004336019
- Антилог: 10 0,698970004336019 = 5
Теперь попробуем с большим числом.
Если мы возьмем log(150 000 000 000) = x, его антилогарифм будет 10x = 150 000 000 000.
- Лог: лог 10 (150 000 000 000) = 11,17609125
- Антилог: 10 11.17609125
= 150 000 000 000 Важность и практическое применение
До изобретения калькуляторов логарифмы использовались для упрощения вычислений в различных областях знаний, таких как навигация, геодезия, астрономия, а позже и инженерия.
Представьте, что вы плывете в глуши 16 века. В то время навигаторы полагались на положение звезд и механизм секстанта, чтобы определить их точное местоположение. Без современных технологий, помогающих вычислять большие расстояния, вы можете использовать логарифм для упрощения вычислений. Точность важна, иначе вы рискуете провести больше дней в море со скудными припасами. Чем меньше уравнений, тем меньше места для ошибки.
А как насчет других практических применений? Живая наука утверждает, что логарифмы связывают геометрические прогрессии с арифметическими.
 Если вы когда-нибудь замечали повторяющиеся формы и узоры в природе, архитектуре и искусстве, эти образования обладают собственными логарифмическими значениями.
Если вы когда-нибудь замечали повторяющиеся формы и узоры в природе, архитектуре и искусстве, эти образования обладают собственными логарифмическими значениями.Сегодня знания о том, как работают эти шаблоны, влияют на то, как человечество строит и проектирует дома, здания и городские ландшафты.
Логарифмы также используются для выражения степени и интенсивности определенных шкал. Помимо больших расстояний и высоких скоростей, он измеряет и другие параметры, такие как:
- Сила звука
- Звуковая частота
- Сила урагана
- Сила землетрясений
- Коррозионный уровень кислот
- Твердость минералов
- Яркость звезд
Возьмем для примера децибелы. Чтобы громкоговорители стали громче на 10 децибел, необходимо подать в 10 раз больше мощности. При увеличении его до +20 дБ потребуется в 100 раз больше мощности, а при +30 дБ потребуется мощность в 1000 раз.
Более того, интенсивность звука увеличивается арифметически.
Он также изменяется пропорционально логарифму звуковой волны, которая развивается геометрически.
Ниже приведена таблица из Live Science, в которой перечислены различные логарифмические шкалы с соответствующими им линейными шкалами.
In Measuring Rates and Ranks
По словам Калида Азада, преподавателя математики из BetterExplained.com, логарифмы — это то, как мы определяем, насколько быстро что-то растет.
Простые логарифмы в основном описывают числа с точки зрения их степеней 10. Когда дело доходит до процентной ставки, логарифмом является рост инвестиций .
При определении темпов роста ВВП страны аналитики рассматривают ВВП в последующие годы. Они берут ВВП предыдущего года и ВВП следующего года, а затем вычисляют логарифм, чтобы найти расчетный темп роста.
Поисковые системы используют график ссылок для оценки важности, надежности и авторитетности документов в Интернете. Google PageRank стал важным этапом эволюции в поиске, который повысил релевантность поиска и помог Google увеличить долю рынка поиска.

Согласно Азаду, по шкале от 1 до 10 целевая страница с PageRank 2 в 10 раз популярнее, чем страница с PageRank 1. Если сайт имеет PageRank 5, а сайт конкурента PageRank равен 9, тогда разница составляет на 4 порядка .
порядок величины означает примерно 10-кратную разницу, или ранжирование на 1 цифру больше по сравнению с другим. В этом случае сайт с PageRank 9 на 100 000 000 популярнее, чем сайт с PageRank 1.
Практический результат
Лог и антилогарифм — важные вычислительные методы, позволяющие упростить большие суммы. Упрощение сокращает процесс вычислений и упрощает их понимание. Это помогает уменьшить место для ошибки.
Кроме того, использование логарифма обеспечивает измеримые масштабы для оценки природных явлений, таких как интенсивность землетрясений, сила ураганов и яркость звезд. С точки зрения финансов логарифмы позволяют точно определить процентные ставки и темпы экономического роста.

Практически используется во многих областях. Большие значения, которые зависят от точности измерения, выигрывают от использования логарифмических вычислений.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также способы помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.
Калькулятор антилогарифма с шагами
Формула антилогарифмаАнтилогарифм a (log a (x)) = x
Для расчета антилогарифмического калькулятора используется произвольное число. Он может вычислить значение антилогарифма с любой заданной базой. Калькулятор обратного логарифма находит обратную функцию логарифма с указанным базовым числом.
 В этом содержании мы расскажем об антилогарифме, как рассчитать антилогарифм на калькуляторе, что такое обратный логарифм 10 и многое другое.
В этом содержании мы расскажем об антилогарифме, как рассчитать антилогарифм на калькуляторе, что такое обратный логарифм 10 и многое другое.Как пользоваться нашим антилогарифмическим калькулятором?
Чтобы вычислить антилогарифмическое значение с помощью калькулятора, обратного логарифмическому основанию 10, выполните следующие действия:
- Введите антилогарифмическое значение в заданное поле ввода.
- Введите базу антилогарифма в следующем поле ввода.
- Нажмите кнопку Вычислить , чтобы увидеть антилог.
- Нажмите кнопку Сброс , чтобы сбросить все значения для нового расчета.
Калькулятор антилогарифма мгновенно вычисляет значение антилогарифма для заданного числа и основания. Чтобы рассчитать логарифм любого числа, вы можете в любое время воспользоваться нашим калькулятором логарифмов.
Что такое антилог?
В некоторых задачах известен логарифм x и основание, но неизвестно x .
 Противоположная или обратная функция логарифма является антилогарифмом. Антилогарифмическое основание всегда является положительным числом, потому что корень экспоненциальной функции не является отрицательным. Поскольку обратная функция является экспоненциальной функцией логарифма,
Противоположная или обратная функция логарифма является антилогарифмом. Антилогарифмическое основание всегда является положительным числом, потому что корень экспоненциальной функции не является отрицательным. Поскольку обратная функция является экспоненциальной функцией логарифма,Antilog a (log a (x)) = x
If log a x=b, , тогда x называется антилогарифмом b и записывается как: 68 с основание a соответственно a b . Если основа антилога не записана, то по умолчанию основанием антилога будет 10 b , так как log x означает логарифм по основанию 10.
Как найти антилог?
Когда числа записываются миллиардами и триллионами, работать с этими числами относительно сложно. Журнал будет работать на вас, независимо от того, касается ли это доходов, прироста населения или больших расстояний.
 Это может облегчить понимание большого количества длинных и сложных уравнений.
Это может облегчить понимание большого количества длинных и сложных уравнений.Antilog используется для реверсирования функции журнала в любом числе. Мы используем антилогарифм, чтобы вернуть исходное число, которое мы получили после использования логарифма.
Чтобы найти антилогарифм числа по основанию, выполните следующие действия:
- Запишите число для вычисления антилогарифма.
- Укажите основание числа для расчета антилог.
- Возведение антилогарифмического числа в степень основания b .
- Полученное число будет антилогарифмическим числом с указанным основанием.
Пример:
Давайте разберемся с вычислением антилогарифма на примере.
Вычислить антилогарифм 2 по основанию 10.
Решение:
Шаг 1 9013 6 Запишите число как 900 67 a для расчета антилог.

a = 2
Шаг 2 : Укажите основание числа для вычисления антилог.
b = 10
Шаг 3 : Возведение антилогарифмического числа в степень основания б .
x = антилогарифмический 2 10 = 2 10
x = 2 10 = 100
9004 Шаг : Результирующее число будет номером антилога с указанной базой.
Таким образом, антилогарифм 2 с основанием 10 равен 100. Точно так же вы можете найти антилогарифм любого числа, используя описанный выше метод.
Некоторые важные антилогарифмические значения
антилог(2) 10 2 100 3 антилогарифмический(1) 10 1 10 антилогарифмический (10) 10 10 10000000000 антилог 2 5 5 2 9 02232 антилогарифмический 2 2 2 2 4 1000 антилог 3 5,5 3 5.  5
5 420.8883 антилог. антилогарифмический (15,6) 10 15,6 3.981071705535E+15 антилог. 0000 антилог(0) 10 0 1 антилогарифмический(4) 10 4 10000 антилогарифмический(5) 2 09 1 905 5 100000 антилогарифмический(9) 10 9 1000000000 антилогарифмический(12) 2 1905 221000000000000 антилог(20) 10 20 1.0E+20 антилог(22) 10 22 1.0E+22 65 0013 антилог(13) 10 13 10000000000000 антилог(18) 10 18 7 5 1. 
- Антилог: 10 11.17609125

 Если вы когда-нибудь замечали повторяющиеся формы и узоры в природе, архитектуре и искусстве, эти образования обладают собственными логарифмическими значениями.
Если вы когда-нибудь замечали повторяющиеся формы и узоры в природе, архитектуре и искусстве, эти образования обладают собственными логарифмическими значениями.
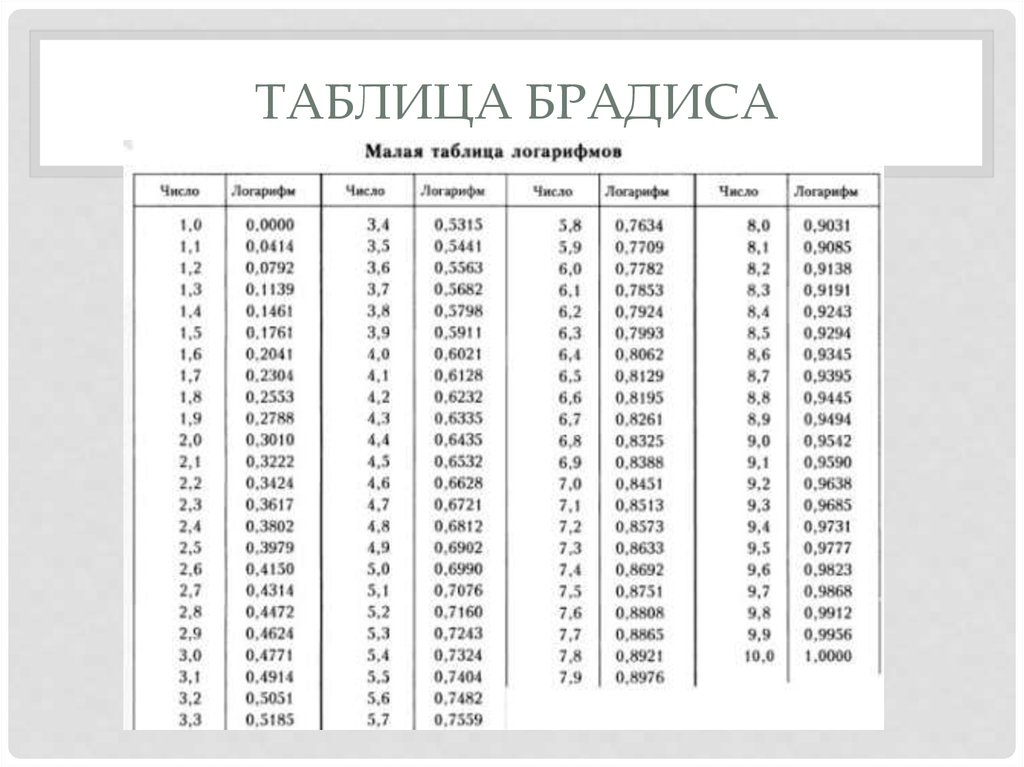
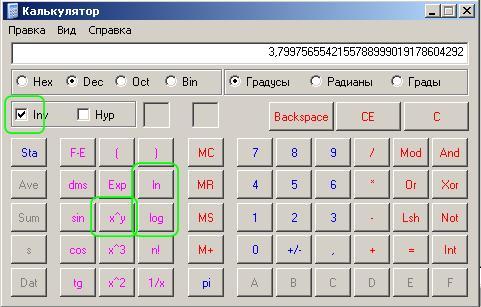 В этом содержании мы расскажем об антилогарифме, как рассчитать антилогарифм на калькуляторе, что такое обратный логарифм 10 и многое другое.
В этом содержании мы расскажем об антилогарифме, как рассчитать антилогарифм на калькуляторе, что такое обратный логарифм 10 и многое другое. Противоположная или обратная функция логарифма является антилогарифмом. Антилогарифмическое основание всегда является положительным числом, потому что корень экспоненциальной функции не является отрицательным. Поскольку обратная функция является экспоненциальной функцией логарифма,
Противоположная или обратная функция логарифма является антилогарифмом. Антилогарифмическое основание всегда является положительным числом, потому что корень экспоненциальной функции не является отрицательным. Поскольку обратная функция является экспоненциальной функцией логарифма, Это может облегчить понимание большого количества длинных и сложных уравнений.
Это может облегчить понимание большого количества длинных и сложных уравнений.
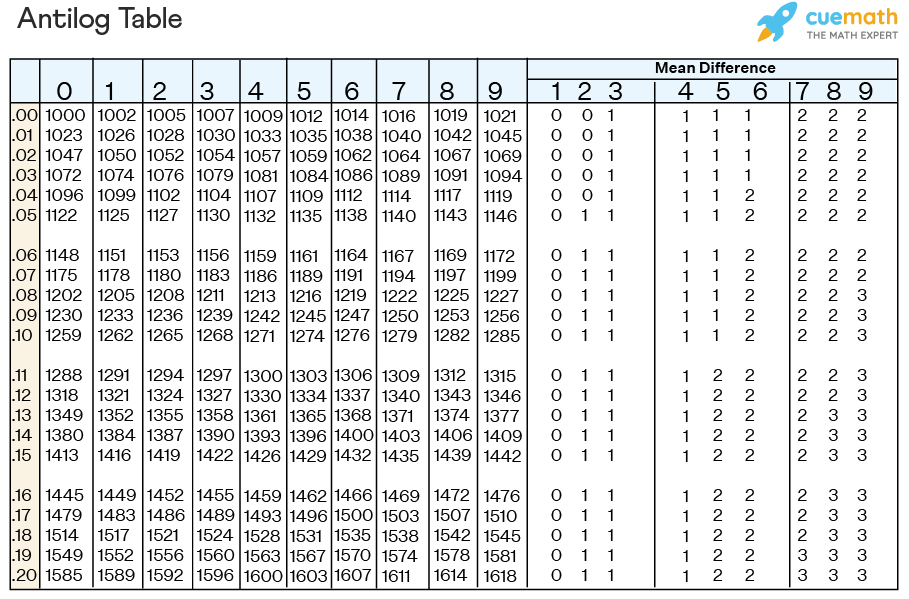 5
5 