Методы статистики
Фрэнк Уилкоксон
Критерий Уилкоксона для связанных выборок (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) – непараметрический статистический критерий, используемый для сравнения двух связанных (парных) выборок по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.
Суть метода состоит в том, что сопоставляются абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
1. История разработки критерия Уилкоксона для связанных выборок
Тест был впервые предложен в 1945 году американским статистиком и химиком Фрэнком Уилкоксоном (1892-1965). В той же научной работе автором был описан еще один критерий, применяемый в случае сравнения независимых выборок.
В той же научной работе автором был описан еще один критерий, применяемый в случае сравнения независимых выборок.
2. Для чего используется критерий Уилкоксона?
Т-критерий Уилкоксона используется для оценки различий между двумя рядами измерений, выполненных для одной и той же совокупности исследуемых, но в разных условиях или в разное время. Данный тест способен выявить направленность и выраженность изменений — то есть, являются ли показатели больше сдвинутыми в одном направлении, чем в другом.
Классическим примером ситуации, в которой может применяться Т-критерий Уилкоксона для связанных совокупностей, является исследование «до-после», когда сравниваются показатели до и после лечения. Например, при изучении эффективности антигипертензивного средства сравнивается артериальное давление до приема препарата и после приема.
3. Условия и ограничения применения Т-критерия Уилкоксона
- Критерий Уилкоксона является непараметрическим критерием, поэтому, в отличие от парного t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.

- Число исследуемых при использовании T-критерия Уилкоксона должно быть не менее 5.
- Изучаемый признак может быть измерен как в количественной непрерывной (артериальное давление, ЧСС, содержание лейкоцитов в 1 мл крови), так и в порядковой шкале (число баллов, степень тяжести заболевания, степень обсемененности микроорганизмами).
- Данный критерий используется только в случае сравнения двух рядов измерений. Аналогом Т-критерия Уилкоксона для сравнения трех и более связанных совокупностей является Критерий Фридмана.
4. Как рассчитать Т-критерий Уилкоксона для связанных выборок?
- Вычислить разность между значениями парных измерений для каждого исследуемого. Нулевые сдвиги далее не учитываются.
- Определить, какие из разностей являются типичными, то есть соответствуют преобладающему по частоте направлению изменения показателя.
- Проранжировать разности пар по их абсолютным значениям (то есть, без учета знака), в порядке возрастания.
 Меньшему абсолютному значению разности приписывается меньший ранг.
Меньшему абсолютному значению разности приписывается меньший ранг. - Рассчитать сумму рангов, соответствующих нетипичным сдвигам.
Таким образом, Т-критерий Уилкоксона для связанных выборок рассчитывается по следующей формуле:
T = ΣRr
где ΣRr — сумма рангов, соответствующих нетипичным изменениям показателя.
5. Как интерпретировать значение критерия Уилкоксона?
Полученное значение T-критерия Уилкоксона сравниваем с критическим по таблице для избранного уровня статистической значимости (p=0.05
или p=0.01) при заданной численности сопоставляемых выборок n:- Если расчетное (эмпирическое) значение Тэмп. меньше табличного Ткр. или равно ему, то признается статистическая значимость изменений показателя в типичную сторону (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение Т.
- Если Тэмп. больше Ткр.
 , принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя.
, принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя.
Пример расчета критерия Уилкоксона для связанных выборок
Фармацевтической компанией проводится исследование нового препарата из группы нестероидных противовоспалительных средств. Для этого отобрана группа из 10 добровольцев, страдающих ОРВИ с гипертермией. У них была измерена температура тела до и через 30 минут после приема нового препарата. Требуется сделать вывод о значимости снижения температуры тела в результате приема препарата.
- Исходные данные оформлены в виде следующей таблицы:
N Фамилия t тела до приема препарата t тела после приема препарата 1. Иванов 39.0 37.6 2. 
Петров 39.5 38.7 3. Сидоров 38.6 38.7 4. Попов 39.1 38.5 5. Николаев 40.1 38.6 6. Козлов 39.3 37.5 7. Игнатьев 38.9 38.8 8. Семенов 39.2 38.  0
09. Егоров 39.8 39.7 10. Алексеев 39.3 - Для расчета Т-критерия Уилкоксона рассчитаем разности парных показателей и проранжируем их абсолютные значения. При этом нетипичные ранги выделим красным шрифтом:
Как мы видим, типичным сдвигом показателя является его снижение, отмеченное в 7 случаях из 10. В одном случае (у пациента Егорова) — температура после приема препарата не изменилась, в связи с чем данный случай не использовался в дальнейшем анализе. В двух случаях (у пациентов Сидорова и Алексеева) отмечался нетипичный сдвиг температуры в сторону повышения. Ранги, соответствующие нетипичному сдвигу, равны 1.5 и 3.N Фамилия t тела до приема препарата t тела после приема препарата Разность показателей, d |d| Ранг 1. Иванов 39.0 37.  6
6-1.4 1.4 7 2. Петров 39.5 38.7 -0.8 0.8 5 3. Сидоров 38.6 38.7 0.1 0.1 1.5 4. Попов 39.1 38.5 -0.6 0.6 4 5. Николаев 40.1 38.  6
6-1.5 1.5 8 6. Козлов 39.3 37.5 -1.8 1.8 9 7. Игнатьев 38.9 38.8 -0.1 0.1 1.5 8. Семенов 39.2 38.0 -1.2 1.2 6 9. Егоров 39.8 39.  8
80 — — 10. Алексеев 38.8 39.3 0.5 0.5 3 - Рассчитаем Т-критерий Уилкоксона, который равен сумме рангов, соответствующих нетипичному сдвигу показателя:
T = ΣRr = 3 + 1.
 5 = 4.5
5 = 4.5 - Сравниваем Тэмп. с Ткр., который при уровне значимости p=0.05 и n=9 равен 8. Следовательно, Тэмп.<Tкр., изменения показателя статистически значимы при p<0.05.
- Делаем вывод: снижение температуры тела у пациентов с ОРВИ в результате приема нового препарата является статистически значимым (р<0.05).
Показать таблицу критических значений Т-критерия Уилкоксона
Критерий Вилкоксона (Уилкоксона): две зависимые выборки
Краткое описание:
Сазонов В.Ф. Критерий Вилкоксона (Уилкоксона): две зависимые выборки [Электронный ресурс] // Кинезиолог, 2009-2016: [сайт]. Дата обновления: 22.02.2016. URL: http://kineziolog.su/content/content/kriterii-vilkoksona-uilkoksona-dve-zavisimye-vyborki (дата обращения: __.__.201_).
_Сравнение двух зависимых выборок (n от 12 до 40) по непараметрическому критерию Вилкоксона, определение достоверности различий.
Итак, у вас есть данные обследования, полученные в двух опытах (или в двух замерах), но на одной и той же группе испытуемых (подопытных, объектов и т.д.).
Понятие «зависимые выборки»
Зависимые выборки — это два замера одного и того же параметра, сделанные на одной и той же совокупности объектов либо в разное время, либо при разных условиях. В итоге получаются две группы данных, попарно связанные между собой через одни и те же объекты. © Сазонов В.Ф., 2016. © kineziolog.su, 2016.
Две выборки считаются зависимыми друг от друга, если каждому значению одной выборки можно однозначно поставить в соответствие ровно одно значение другой выборки. Аналогично определяется зависимость друг от друга нескольких выборок.
Или такое определение:
Зависимые (связанные, попарно сопряженные) выборки — это выборки, представляющие собой параметры одной и той же совокупности до и после воздействия некоторого фактора.
Чаще всего зависимые выборки – это измерения одной и той же группы объектов в разные моменты времени (например, до и после воздействия какого-либо фактора). Таким образом, зависимые выборки всегда должны содержать одинаковое количество наблюдений. В электронной таблице зависимые переменные располагаются в разных столбцах одной таблицы под разными названиями (например, показатели чего-то до воздействия и показатели чего-то после воздействия).
И вам надо из этих двух столбиков данных получить какие-то обобщённые результаты, сделать выводы. И самое главное — вам надо сравнить между собой две эти выборки.
Например:
| ФИО | Замер 1 | Замер 2 |
Ив. | 5,05 | 7,20 |
| Петр. | 6,48 | 7,43 |
Сид. | 5,16 | 5,58 |
| Ник. | 7,30 | 7,46 |
| Серг. | 4,70 | 7,05 |
| Павл. | 7,25 | 12,95 |
| Сем. | 5,85 | 5,55 |
| Фр. | 6,62 | 9,85 |
| Григ. | 5,15 | 7,50 |
| Пуш. | 4,83 | 6,38 |
Саз. | 6,20 | 14,35 |
Как видим, люди-то одни и те же, но с каждого из них снимали показатели дважды. И нам не важно, какие именно это показатели: секунды, килограммы или сантиметры…
Наводящие вопросы:
1. Вы собираетесь проверять, что в этих выборках соблюдается закон нормального распределения?
— Да. Мне не лень возиться с этим, и я обязательно проверю, соблюдается ли в этих выборках закон нормального распределения.
ОК, тогда после проверки вы сможете сделать обоснованный вывод о том, можно ли применять для сравнения ваших выборок параметрическием методы статистической обработки. Или же вам всё равно придётся вернуться сюда, на эту же страничку, к методу Вилкоксона…
— Нет, мне лень возиться с проверками на нормальность распределения, и я хочу сравнить свои две зависимые выборки прямо сейчас.
Тогда за дело! Нам нужен Т—критерий Вилкоксона
Т—критерий Вилкоксона
Тест Уилкоксона (Вилкоксона), он же: знаковый ранговый критерий Уилкоксона, критерий знаковых рангов Уилкоксона, одновыборочный критерий Вилкоксона, Wilcoxon signed-ranks test for matched pairs.
Т-критерий Вилкоксона применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке (группе) испытуемых. Рекомендуется для выборок умеренной численности (численность каждой выборки от 12 до 40).
Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.
АЛГОРИТМ 9 (Сидоренко Е.В., 2001)
Подсчет критерия Т Вилкоксона
1. Составить список испытуемых в любом порядке, например, алфавитном.
2. Вычислить разность между индивидуальными значениями во втором и первом замерах (в каждой паре чисел от значения «после» отнять значение «до»). Определить, что будет считаться «типичным» сдвигом (т.е. наиболее частым) и сформулировать соответствующие гипотезы.
Получится такая табличка:
№ п\п | ФИО | Замер №1 | Замер №2 | №2 — №1 |
1 | Ив. | 5,05 | 7,2 | 2,15 |
2 | Петр. | 6,48 | 7,43 | 0,95 |
3 | Сид. | 5,16 | 5,58 | 0,42 |
4 | Ник. | 7,3 | 7,46 | 0,16 |
5 | Серг. | 4,7 | 7,05 | 2,35 |
6 | Павл. | 7,25 | 12,95 | 5,7 |
7 | Сем. | 5,85 | 5,55 | -0,3 |
8 | Фр. | 6,62 | 9,85 | 3,23 |
9 | Григ. | 5,15 | 7,5 | 2,35 |
10 | Пуш. | 4,83 | 6,38 | 1,55 |
11 | Саз. | 6,2 | 14,35 | 8,15 |
Как видим, большинство сдвигов — выше нуля, т.е. имеют положительные знаки. Их и будем считать типичными, потому что их больше. Итак, типичные сдвиги — положительные.
3. Перевести разности в абсолютные величины и записать их отдельным столбцом (иначе трудно отвлечься от знака разности).
4. Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.
5. Отметить кружками, звёздочками или другими знаками ранги, соответствующие сдвигам в «нетипичном» направлении. В нашем примере это ранги для отрицательных сдвигов.
6. Подсчитать сумму этих рангов по формуле:
T=∑Rr
где Rr — ранговые значения сдвигов с более редким знаком.
7. Определить критические значения Т для данного n по Табл. VI Приложения 1. Если Тэмп (т.е. полученный в нашем опыте) меньше или равен Ткр, (т.е. табличному) то это означает, что сдвиг в «типичную» сторону по интенсивности достоверно преобладает. Кроме того в нашем примере видно, что положительные «типичные» сдвиги говорят о том, что показатели в замере №2 выше, чем в замере №1.
Если Тэмп (т.е. полученный в нашем опыте) меньше или равен Ткр, (т.е. табличному) то это означает, что сдвиг в «типичную» сторону по интенсивности достоверно преобладает. Кроме того в нашем примере видно, что положительные «типичные» сдвиги говорят о том, что показатели в замере №2 выше, чем в замере №1.
Выводы:
- Между замером №1 и замером №2 обнаружены достоверные различия по критерию Вилкоксона.
- По критерию Вилкоксона показатели в замере №2 достоверно выше, чем в замере №1.
Определение в статистике, типах и расчетах
К
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 01 декабря 2021 г.
Рассмотрено
Гордон Скотт
Рассмотрено Гордон Скотт
Полная биография
Гордон Скотт был активным инвестором и техническим аналитиком более 20 лет. Он дипломированный специалист по рынку (CMT).
Узнайте о нашем Совет финансового контроля
Факт проверен
Скайлар Кларин
Факт проверен Скайлар Кларин
Полная биография
Скайлар Кларин занимается проверкой фактов и экспертом по личным финансам с большим опытом, включая ветеринарные технологии и исследования фильмов.
Узнайте о нашем редакционная политика
Что такое тест Уилкоксона?
Критерий Уилкоксона, который может относиться либо к критерию суммы рангов, либо к варианту критерия знаковых рангов, представляет собой непараметрический статистический критерий, который сравнивает две парные группы. Тесты, по сути, вычисляют разницу между наборами пар и анализируют эти различия, чтобы установить, отличаются ли они друг от друга статистически значимо.
Ключевые выводы
- Тест Уилкоксона сравнивает две парные группы и существует в двух версиях: тест суммы рангов и критерий знакового ранга.
- Цель теста — определить, отличаются ли два или более набора пар друг от друга статистически значимым образом.
- Обе версии модели предполагают, что пары в данных происходят из зависимых популяций, т. е. следят за одним и тем же человеком или ценой акции во времени или месте.
Понимание теста Уилкоксона
Критерии суммы рангов и знаковых рангов были предложены американским статистиком Фрэнком Уилкоксоном в новаторской исследовательской работе, опубликованной в 1945 году. числовые значения, такие как удовлетворенность клиентов или музыкальные обзоры. Непараметрические распределения не имеют параметров и не могут быть определены уравнением, в отличие от параметрических распределений.
числовые значения, такие как удовлетворенность клиентов или музыкальные обзоры. Непараметрические распределения не имеют параметров и не могут быть определены уравнением, в отличие от параметрических распределений.
Типы вопросов, на которые может помочь ответить тест Уилкоксона, включают такие вещи, как:
- Различаются ли результаты тестов в 5-м и 6-м классах для одних и тех же учащихся?
- Влияет ли конкретное лекарство на здоровье при испытаниях на одних и тех же людях?
Эти модели предполагают, что данные поступают от двух совпадающих или зависимых популяций, следящих за одним и тем же человеком или группой во времени или месте. Данные также предполагаются непрерывными, а не дискретными. Поскольку это непараметрический тест, он не требует определенного распределения вероятностей зависимой переменной в анализе.
Типы критерия Уилкоксона
- Критерий суммы рангов Уилкоксона можно использовать для проверки нулевой гипотезы о том, что две совокупности имеют одинаковое непрерывное распределение.
 Нулевая гипотеза — это статистический тест, который говорит об отсутствии существенной разницы между двумя популяциями или переменными. Базовые предположения, необходимые для использования теста суммы рангов, заключаются в том, что данные взяты из одной и той же совокупности и являются парными, данные могут быть измерены, по крайней мере, по интервальной шкале, и данные были выбраны случайным и независимым образом.
Нулевая гипотеза — это статистический тест, который говорит об отсутствии существенной разницы между двумя популяциями или переменными. Базовые предположения, необходимые для использования теста суммы рангов, заключаются в том, что данные взяты из одной и той же совокупности и являются парными, данные могут быть измерены, по крайней мере, по интервальной шкале, и данные были выбраны случайным и независимым образом. - Критерий знакового ранга Уилкоксона предполагает наличие информации о величинах и знаках различий между парными наблюдениями. В качестве непараметрического эквивалента парного t-критерия Стьюдента ранг со знаком может использоваться в качестве альтернативы t-критерию, когда данные населения не подчиняются нормальному распределению.
Расчет статистики критерия Вилкоксона
Шаги для получения статистики знакового рангового теста Уилкоксона, W, , следующие:
- Для каждого элемента в выборке из n элементов получить оценку разницы D i между двумя измерениями (т.
 е. вычесть одно из другого).
е. вычесть одно из другого). - Пренебречь положительными или отрицательными знаками и получить набор из n абсолютных разностей |D i |.
- Опустить нулевые баллы разности, получив набор из n ненулевых абсолютных баллов разности, где n’ ≤ n . Таким образом, n’ становится фактическим размером выборки.
- Затем присвойте ранги R i от 1 до n каждому из |D i | таким образом, наименьшая абсолютная разность получает ранг 1, а наибольшая — ранг n . Если два или более |D i | равны, каждому из них присваивается средний ранг рангов, которые им были бы присвоены по отдельности, если бы не было совпадений в данных.
- Теперь переназначить символ «+» или «–» каждому из n рангов R i , в зависимости от того, D i изначально был положительным или отрицательным.
- Статистика критерия Уилкоксона W впоследствии получается как сумма положительных рангов.

На практике этот тест выполняется с использованием программного обеспечения для статистического анализа или электронной таблицы.
Источники статей
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.
Международное биометрическое общество. «Индивидуальные сравнения методами ранжирования». По состоянию на 5 октября 2021 г.
Критерий суммы рангов Уилкоксона
Критерий суммы рангов Уилкоксона часто называют непараметрической версией двухвыборочного t-критерия. Иногда вы видите его в блок-схемах анализа после вопроса, например, «нормальны ли ваши данные?» Ответ «нет» на этот вопрос будет рекомендовать тест Уилкоксона, если вы сравниваете две группы непрерывных измерений.
Так что же это за тест Уилкоксона? Что делает его непараметрическим? Что это вообще значит? И как мы это реализуем и интерпретируем? Вот некоторые из вопросов, на которые мы стремимся ответить в этом посте.
Во-первых, давайте вспомним предположения двухвыборочного t-критерия для сравнения двух средних совокупностей:
1. Две выборки независимы друг от друга
2. Две совокупности имеют одинаковую дисперсию или разброс
3. Две совокупности нормально распределены
#1 никуда не деться. Это предположение должно выполняться для двухвыборочного t-критерия. Когда предположения № 2 и № 3 (равная дисперсия и нормальность) не выполняются, но выборки большие (скажем, более 30), результаты приблизительно правильные. Но когда наши выборки малы, а наши данные искажены или ненормальны, мы, вероятно, не должны слишком доверять двухвыборочному t-критерию Стьюдента.
Здесь на помощь приходит критерий суммы рангов Уилкоксона. Он делает только первые два предположения о независимости и равной дисперсии. Это не предполагает, что наши данные имеют известное распределение. Известные распределения описываются математическими формулами. Эти формулы имеют параметры, определяющие форму и/или положение распределения. Например, дисперсия и среднее — это два параметра нормального распределения, которые определяют его форму и расположение соответственно. Поскольку критерий суммы рангов Уилкоксона не предполагает известных распределений, он не имеет дело с параметрами, и поэтому мы называем его непараметрическим критерием.
Это не предполагает, что наши данные имеют известное распределение. Известные распределения описываются математическими формулами. Эти формулы имеют параметры, определяющие форму и/или положение распределения. Например, дисперсия и среднее — это два параметра нормального распределения, которые определяют его форму и расположение соответственно. Поскольку критерий суммы рангов Уилкоксона не предполагает известных распределений, он не имеет дело с параметрами, и поэтому мы называем его непараметрическим критерием.
В то время как нулевая гипотеза двухвыборочного t-критерия равна среднему значению, нулевая гипотеза теста Уилкоксона обычно принимается за равные медианы. Другой способ думать о нуле состоит в том, что две совокупности имеют одинаковое распределение с одной и той же медианой. Если мы отклоняем нулевое значение, это означает, что у нас есть свидетельство того, что одно распределение сдвинуто влево или вправо по отношению к другому. Поскольку мы предполагаем, что наши распределения равны, отклонение нуля означает, что у нас есть доказательства того, что медианы двух популяций различаются. Среда статистического программирования R, которую мы используем для реализации теста суммы рангов Уилкоксона ниже, называет это «сдвигом местоположения».
Среда статистического программирования R, которую мы используем для реализации теста суммы рангов Уилкоксона ниже, называет это «сдвигом местоположения».
Давайте рассмотрим быстрый пример на R. Приведенные ниже данные взяты из Hogg & Tanis, пример 8.4-6. Он включает в себя вес упаковки от двух компаний, продающих один и тот же продукт. У нас есть 8 наблюдений от каждой компании, A и B. Мы хотели бы знать, является ли распределение весов одинаковым в каждой компании. Быстрая диаграмма показывает, что данные имеют схожий разброс, но могут быть искаженными и ненормальными. С такой маленькой выборкой может быть опасно предполагать нормальность.
А <- с(117,1, 121,3, 127,8, 121,9, 117,4, 124,5, 119,5, 115,1)
В <- с(123,5, 125,3, 126,5, 127,9, 122,1, 125,6, 129,8, 117,2)
dat <- data.frame(вес = c(A,B),
компания = rep(c("A","B"), каждый=8))
boxplot(вес ~ компания, данные = dat)
Теперь мы запускаем тест суммы рангов Уилкоксона, используя функцию wilkox.. Опять же, ноль в том, что распределения одинаковы и, следовательно, имеют одинаковую медиану. Альтернатива двусторонняя. Мы понятия не имеем, смещено ли одно распределение влево или вправо по отношению к другому. test
test
wilkox.test(вес ~ компания, данные = дата) Критерий суммы рангов Уилкоксона данные: вес по компаниям W = 13, p-значение = 0,04988. альтернативная гипотеза: истинное смещение местоположения не равно 0
Сначала мы замечаем, что значение p чуть меньше 0,05. На основании этого результата мы можем заключить, что медианы этих двух распределений различаются. Альтернативная гипотеза формулируется как «истинный сдвиг местоположения не равен 0». Это еще один способ сказать, что «распределение одной популяции смещено влево или вправо относительно другой», что подразумевает разные медианы.
Статистика Уилкоксона возвращается как W = 13. Это НЕ оценка разницы в медианах. На самом деле это количество раз, в которое вес посылки от компании B меньше веса посылки от компании A. Мы можем рассчитать это вручную, используя вложенные циклы for следующим образом (хотя мы должны отметить, что это не так, как
Мы можем рассчитать это вручную, используя вложенные циклы for следующим образом (хотя мы должны отметить, что это не так, как wilcox. функция test вычисляет W):
Вт <- 0
для (я в 1: длина (B)) {
для (j в 1: длина (A)) {
если (B[j] < A[i]) W <- W + 1
}
}
Вт
[1] 13
Другой способ сделать это — использовать внешнюю функцию , которая может принимать два вектора и выполнять операцию над всеми парами. Результатом является матрица 8 x 8, состоящая из значений TRUE/FALSE. Использование суммы в матрице подсчитывает все экземпляры TRUE.
сумма (внешняя (B, A, "<")) [1] 13
Конечно, мы могли бы пойти другим путем и подсчитать, сколько раз вес посылки от компании А меньше, чем вес посылки от компании Б. Это дает нам 51.
сумма (внешняя (A, B, "<")) [1] 51
Если мы изменим уровень переменной нашей компании в data.frame dat, чтобы иметь «B» в качестве опорного уровня, мы получим тот же результат в выводе wilcox.. test
test
dat$company <- relevel(dat$company, ref = "B") wilkox.test(вес ~ компания, данные = дата) Критерий суммы рангов Уилкоксона данные: вес по компаниям W = 51, p-значение = 0,04988 альтернативная гипотеза: истинное смещение местоположения не равно 0
Так почему же мы считаем пары? Напомним, что это непараметрический тест. Мы не оцениваем такие параметры, как среднее значение. Мы просто пытаемся найти доказательства того, что одно распределение смещено влево или вправо по отношению к другому. На нашей блочной диаграмме выше видно, что распределения от обеих компаний достаточно похожи, но B смещено вправо или выше, чем A. Один из способов подумать о проверке, являются ли распределения одинаковыми, — это рассмотреть вероятность случайного выбранное наблюдение от компании A меньше, чем случайно выбранное наблюдение от компании B: P (A < B). Мы могли бы оценить эту вероятность как количество пар, у которых А меньше В, деленное на общее количество пар. В нашем случае получается \(51/(8\times8)\) или \(51/64\). Точно так же мы могли бы оценить вероятность того, что B меньше, чем A. В нашем случае это \(13/64\). Итак, мы видим, что статистика W является числителем в этой оценочной вероятности.
В нашем случае получается \(51/(8\times8)\) или \(51/64\). Точно так же мы могли бы оценить вероятность того, что B меньше, чем A. В нашем случае это \(13/64\). Итак, мы видим, что статистика W является числителем в этой оценочной вероятности.
Точное значение p определяется из распределения статистики суммы рангов Уилкоксона. Мы говорим «точно», потому что распределение статистики суммы рангов Уилкоксона является дискретным. Он параметризован двумя размерами выборки, которые мы сравниваем. «Но подождите, я думал, что критерий Уилкоксона непараметрический?» Это! Но тестовая статистика W имеет распределение, не зависящее от распределения данных.
Мы можем рассчитать точные двусторонние p-значения явно, используя pwilkox (они двусторонние, поэтому умножаем на 2):
Для W = 13, \(P(W \leq 13)\):
pwilcox(q = 13, m = 8, n = 8) * 2 [1] 0,04988345
Для W = 51, \(P(W \geq 51)\), мы должны получить \(P(W \leq 50)\), а затем вычесть из 1, чтобы получить \(P(W \geq 51) \):
(1 - pwilkox(q = 51 - 1, m = 8, n = 8)) * 2 [1] 0,04988345
По умолчанию функция wilcox. вычисляет точные p-значения, если выборки содержат менее 50 конечных значений и в значениях нет совпадений. (Подробнее о «связях» чуть позже.) В противном случае используется нормальное приближение. Для принудительного нормального приближения установите  test
test точно = ЛОЖЬ .
dat$company <- relevel(dat$company, ref = "A") wilkox.test(вес ~ компания, данные = dat, точно = ЛОЖЬ) Критерий суммы рангов Вилкоксона с коррекцией непрерывности данные: вес по компаниям W = 13, p-значение = 0,05203 альтернативная гипотеза: истинное смещение местоположения не равно 0
При использовании нормального приближения к названию теста добавляется фраза «с коррекцией непрерывности». Поправка на непрерывность — это корректировка, которая выполняется, когда дискретное распределение аппроксимируется непрерывным распределением. Нормальная аппроксимация очень хороша и в вычислительном отношении быстрее для выборок больше 50.
Вернемся к "галстукам". Что это значит и почему это важно? Чтобы ответить на эти вопросы, сначала рассмотрим название «тест суммы рангов Уилкоксона». Название связано с тем, что статистику теста можно рассчитать как сумму рангов значений. Другими словами, возьмите все значения из обеих групп, ранжируйте их от самого низкого до самого высокого в соответствии с их значением, а затем просуммируйте ранги из одной из групп. Вот как мы можем сделать это в R с нашими данными:
Название связано с тем, что статистику теста можно рассчитать как сумму рангов значений. Другими словами, возьмите все значения из обеих групп, ранжируйте их от самого низкого до самого высокого в соответствии с их значением, а затем просуммируйте ранги из одной из групп. Вот как мы можем сделать это в R с нашими данными:
сумма(ранг(dat$вес)[dat$company=="A"]) [1] 49
Выше мы ранжируем все веса, используя функцию rank , выбираем только те ранги для компании A, а затем суммируем их. Это классический способ расчета статистики теста суммы рангов Уилкоксона. Обратите внимание, что это не соответствует тестовой статистике, предоставленной wilcox.test , которая была 13. Это потому, что R использует другой расчет из-за Манна и Уитни. Их тестовая статистика, иногда называемая U, является линейной функцией исходной статистики суммы рангов, обычно называемой W:
\[U = W – \frac{n_2(n_2 + 1)}{2}\]
где \(n_2\) — количество наблюдений в другой группе, ранги которых не суммировались. Мы можем проверить эту связь для наших данных
Мы можем проверить эту связь для наших данных
сумма (ранг (вес $ данных) [компания $ данных = = "A"]) - (8 * 9/2) [1] 13
Именно так функция wilcox.test вычисляет тестовую статистику, хотя она помечает ее W вместо U.
Ранжирование значений должно быть изменено в случае равенства. Например, в приведенных ниже данных 7 встречается дважды. Одному из 7 может быть присвоено 3-е место, а другому 4-е. Но тогда одно из них будет иметь более высокий ранг, чем другое, а это неправильно. Мы могли бы поставить их обеим на 3 или обе на 4, но это тоже было бы неправильно. Что мы делаем, так это берем среднее значение их рангов. Ниже это \((3 + 4)/2 = 3,5\). R делает это по умолчанию при ранжировании значений.
vals <- c(2, 4, 7, 7, 12) ранг (валы) [1] 1,0 2,0 3,5 3,5 5,0
Влияние связей означает, что распределение ранговой суммы Уилкоксона нельзя использовать для расчета точных p-значений. Если в наших данных встречаются связи и у нас менее 50 наблюдений, функция wilkox. возвращает нормальное аппроксимированное значение p вместе с предупреждающим сообщением о том, что «невозможно вычислить точное значение p при наличии связей». test
test
Точные или приблизительные p-значения ничего не говорят нам о том, насколько различны эти распределения. Для теста Уилкоксона p-значение — это вероятность получить статистику теста как большую или большую при условии, что оба распределения одинаковы. В дополнение к p-значению нам нужна некоторая оценочная мера того, как эти распределения различаются. 9Функция 0165 wilkox.test предоставляет эту информацию, когда мы устанавливаем conf.int = TRUE .
wilcox.test(вес ~ компания, данные = dat, conf.int = TRUE)
Критерий суммы рангов Уилкоксона
данные: вес по компаниям
W = 13, p-значение = 0,04988.
альтернативная гипотеза: истинное смещение местоположения не равно 0
95-процентный доверительный интервал:
-8,5 -0,1
примерные оценки:
разница в местоположении
-4,65
Возвращает меру «разницы в местоположении» -4,65. В документации к функции
В документации к функции wilcox.test говорится, что она «оценивает не разницу в медианах (распространенное заблуждение), а скорее медиану разницы между выборкой из x и выборкой из y».
Опять же, мы можем использовать внешнюю функцию , чтобы проверить это вычисление. Сначала мы вычисляем разницу между всеми парами, а затем находим медиану этих разностей.
медиана (внешняя (A, B, "-")) [1] -4,65
Доверительный интервал довольно широк из-за небольшого размера выборки, но, похоже, мы можем с уверенностью сказать, что средний вес упаковки компании А как минимум на -0,1 меньше, чем средний вес упаковки компании Б.
Если нас явно интересует разница в медианах между двумя популяциями, мы можем попробовать загрузочный подход с использованием загрузочного пакета. Идея состоит в том, чтобы передискретизировать данные (с заменой) много раз, скажем, 1000 раз, каждый раз принимая во внимание разницу в медианах. Затем мы берем медиану этих 1000 различий, чтобы оценить разницу в медианах. Затем мы можем найти доверительный интервал на основе наших 1000 различий. Простой способ - использовать 2,5-й и 9-й7,5-й процентиль как верхняя и нижняя границы 95% доверительного интервала.
Затем мы можем найти доверительный интервал на основе наших 1000 различий. Простой способ - использовать 2,5-й и 9-й7,5-й процентиль как верхняя и нижняя границы 95% доверительного интервала.
Вот один из способов выполнить это в R.
Сначала мы загружаем загрузочный пакет, поставляемый с R, и создаем функцию с именем med.diff для вычисления разницы в медианах. Чтобы работать с функцией boot пакета загрузки, нашей функции нужны два аргумента: один для данных и один для индексации данных. Мы условно назвали эти аргументы d и и . Функция загрузки возьмет наши данные, d , и передискретизирует их в соответствии со случайно выбранными номерами строк, i . Затем он вернет разницу в медианах для данных с повторной выборкой.
библиотека (загрузочная)
med.diff <- function(d, i) {
tmp <- d[i,]
медиана (tmp$вес[tmp$company=="A"]) -
медиана (tmp$вес[tmp$company=="B"])
}
Теперь мы используем функцию boot для повторной выборки наших данных 1000 раз, каждый раз беря разницу в медианах и сохраняя результаты в объект с именем boot. out.
out.
boot.out <- boot(data = dat, statistic = med.diff, R = 1000)
Объект boot.out является объектом списка. Элемент с именем «t» содержит 1000 различий в медианах. Взятие медианы этих значений дает нам точечную оценку оценочной разницы в медианах. Ниже мы получаем -5,05, но вы, скорее всего, получите что-то другое.
медиана (boot.out $ t) [1] -5,05
Далее мы используем функцию boot.ci для расчета доверительных интервалов. Указываем type = "perc" , чтобы получить процентильный интервал начальной загрузки.
boot.ci(boot.out, тип = "perc") ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА BOOTSTRAP Основано на 1000 репликах начальной загрузки ВЫЗОВ : boot.ci(boot.out = boot.out, type = "perc") Интервалы: Процентиль уровня 95% (-9,399, -0,100) Расчеты и интервалы в исходном масштабе
Мы заметили, что интервал не слишком отличается от того, что wilcox.test 9Возврат функции 0166, но, безусловно, больше на нижней границе.


 Меньшему абсолютному значению разности приписывается меньший ранг.
Меньшему абсолютному значению разности приписывается меньший ранг. , принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя.
, принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя.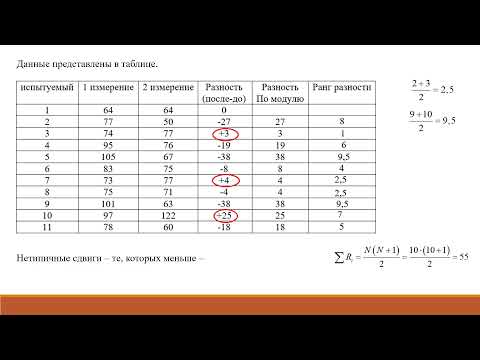
 0
0 6
6
 8
8 5 = 4.5
5 = 4.5


 Нулевая гипотеза — это статистический тест, который говорит об отсутствии существенной разницы между двумя популяциями или переменными. Базовые предположения, необходимые для использования теста суммы рангов, заключаются в том, что данные взяты из одной и той же совокупности и являются парными, данные могут быть измерены, по крайней мере, по интервальной шкале, и данные были выбраны случайным и независимым образом.
Нулевая гипотеза — это статистический тест, который говорит об отсутствии существенной разницы между двумя популяциями или переменными. Базовые предположения, необходимые для использования теста суммы рангов, заключаются в том, что данные взяты из одной и той же совокупности и являются парными, данные могут быть измерены, по крайней мере, по интервальной шкале, и данные были выбраны случайным и независимым образом. е. вычесть одно из другого).
е. вычесть одно из другого).