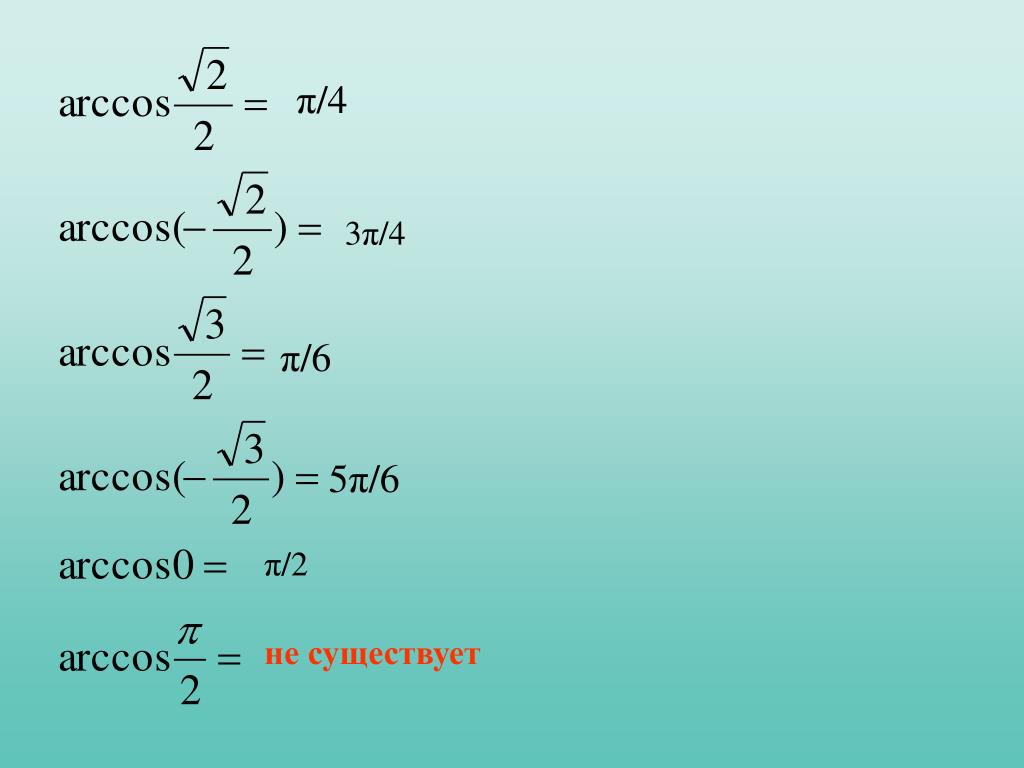Как решать С1. Урок 4 (часть 1). ЕГЭ по математике 2014 — решения.егэцентр.рф
Здравствуйте!
Как решать уравнение `\sin x = \frac{\sqrt{3}}{2}` мы уже знаем. Но что если в правой части уравнения окажется другое число, до сих пор не встречавшееся нам, например, безобидное `0{,}8`?
В этом уроке мы научимся решать уравнения вида `\sin x = a` и `\cos x = a` для любых значений `a`.
Так же по многочисленным просьбам учеников во второй части урока, я расскажу, что такое тангенс и как решать уравнения для него.
Итак, приступим.
Определение арксинуса
Для того, чтобы лучше понять вопрос, давайте схематически нарисуем, как работает синус:
Он берет известную нам точку на окружности и как бы переносит ее на ось `y`.
А что если нам известно значение синуса на оси `y`? Было бы неплохо научиться «переносить» его на круг.
Для этого существует специально обученная для этого функция — арксинус.
Поскольку функция обязана быть однозначной — одному значению переменной должно соответствовать только одно значение функции, то договоримся, что арксинус будет «переносить» точки с оси `y` только на правую половину окружности, причем без всяких `\pi k` (чтобы добиться однозначности).
Тогда, для `x\in \left[ -\frac{\pi}{2},\frac{\pi}{2}\right]` будет работать такая схема (это определение арксинуса):
$$\sin x = a \Leftrightarrow x = \arcsin a, \quad a\in [-1,1], x\in \left[ -\frac{\pi}{2},\frac{\pi}{2}\right].$$
Что такое арксинус, разобрались. Осталось два вопроса: как быть с левой половиной, и что делать, если мы хотим получить все точки на окружности, а не только на одном обороте вокруг нее.
С оборотами поступим просто: добавим `\pi k`: `x =\arcsin a + 2\pi k`.
А как быть с левой половиной? Мы ведь знаем, что точки, симметричные относительно `Oy` дадут нам один и тот же синус.
Давайте внимательнее изучим точки, синусы которых равны.
Сделаем такой рисунок:
Длины дуг, отмеченных красным, равны. Получается, что для того, чтобы получить точку на левой половине круга, нам нужно из `\pi` вычесть дугу длиной `\arcsin a`.
Таким образом, общее решение простого тригонометрического уравнения с синусом будет записано так:
$$\left[ \begin{array}{l}x=\arcsin a +2\pi k, \\ x = 2 — \arcsin a +2\pi k, \end{array}\right. \quad k\in \mathbb{Z}.$$
Можно переходить к арккосинусу.
Определение арккосинуса
Вновь сперва рассмотрим, как работает косинус.
Как видно, косинус «переносит» точки с круга на ось `x`. Арккосинус будет «переносить» точки с оси `x` на круг. Опять же, чтобы функция была однозначной, договоримся, что арккосинус переносит точки с оси `x` только на верхнюю половину круга.
Определение арккосинуса можно записать так:
$$\cos x =a \Leftrightarrow x = \arccos a,\quad a \in [-1,1], x\in [0, \pi ].$$
Что делать если нам нужно обобщить это на любое количество оборотов по окружности, я думаю, вы догадываетесь: прибавить `2\pi k`.
2 x = 0`.
На этом урок закончим. Ваши лайки поднимают боевой дух и помогают писать новые статьи, так что ставим,не стесняемся 🙂 Есть вопросы? Оставляйте их в комментариях.
| 1 | грех(30) | ||
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | желтовато-коричневый(60) | ||
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | ||
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — arccos(5) — Solumaths
Arccos, расчет онлайн
Резюме:
Функция arccos позволяет вычислить арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
arccos online
Описание:
Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .
Число, к которому вы хотите применить функцию функции арккосинуса, должно принадлежать диапазону [-1,1].
- Расчет арккосинуса
- Таблица замечательных значений
Чтобы вычислить арккосинус числа , просто введите число и примените функция arccos . Таким образом, для , вычисляющего , арккосинус числа, следующего за 0,4, вы должны ввести arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть, результат 1.1592)`.
| arccos(`-1`) | `pi` | |
| arccos(`-sqrt(3)/2`) | `5*pi/6` | |
| `3*pi/4` | ||
| arccos(`-1/2`) | `2*pi/3` | |
| arccos(`0`) | ``2*pi/3` pi/2` | |
| arccos(`1/2`) | `pi/3` | |
| arccos(`sqrt(2)/2`) | `pi/4` | |
| Arccos (` sqrt (3)/2`) | `pi/6` | |
| Arccos (` 1`) | `0` |
arccos(x), где x — число.
Иногда используются другие обозначения: acos
Примеры:
arccos(`1`) возвращает 0
Производная арккосинуса :
Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)`
Предел арккосинуса :
Калькулятор предела позволяет вычислить пределы функции арккосинуса.
предел arccos(x) is limit(`»arccos»(x)`)
Обратная функция арккосинуса :
обратная функция арккосинуса — это функция косинуса, отмеченная как cos.
Графический арккосинус :
Графический калькулятор может отображать функцию арккосинуса в заданном интервале.
Расчет онлайн с арккосинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.