Arctg 2 чему равен. Арксинус, арккосинус
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
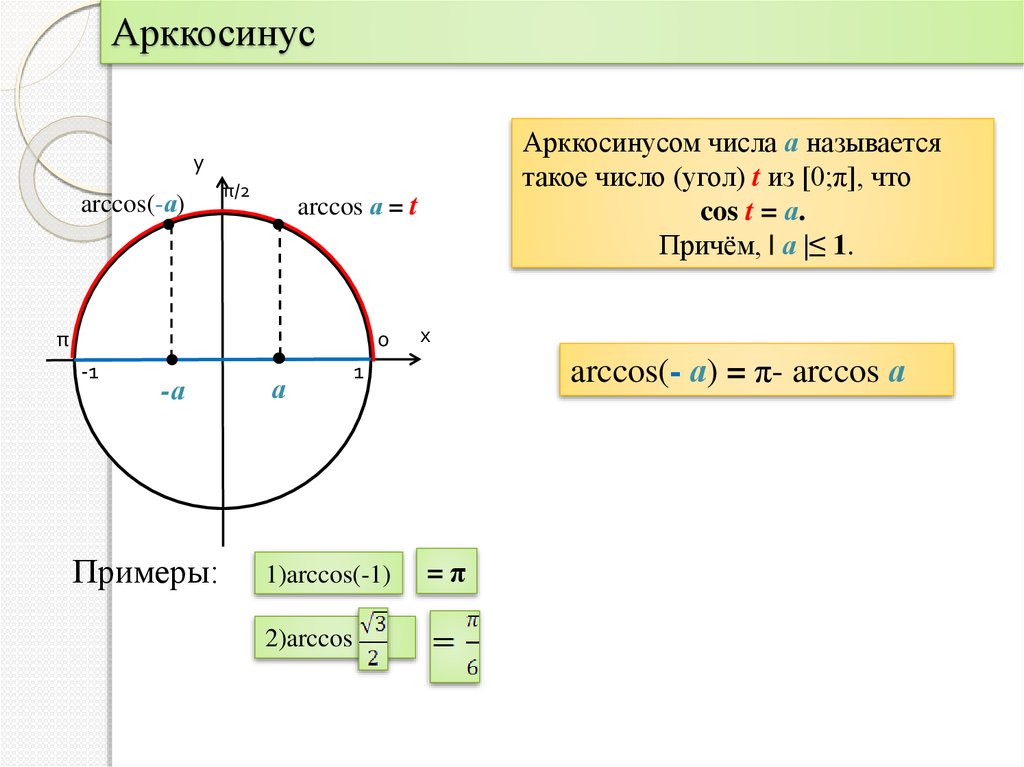
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).

- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1].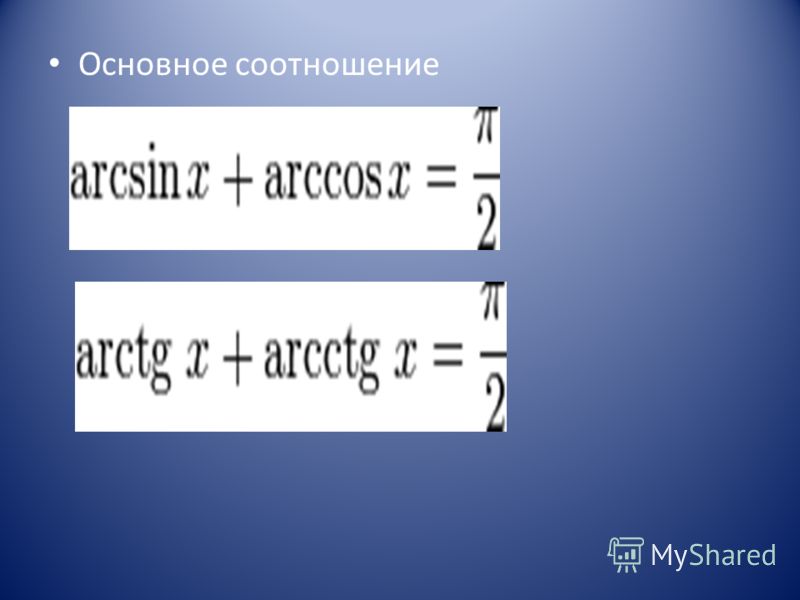 При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Замечание 1
Таблица Брадиса — это таблица, позволяющая высчитывать значения арктангенсов и других тригонометрических функций с высокой точностью.
Для того чтобы воспользоваться таблицей Брадиса, ищут угол в градусах в крайнем столбце слева для синуса (для косинуса в соответствующем столбце справа), а затем в верхней строке минуты. На пересечении строки со столбцом находится искомое значение.
При необходимости найти значения обратных тригонометрических функций — таблицу Брадиса используют наоборот. Например, ищут числовое значение в таблице арктангенсов и тангенсов и для него определяют, в какой строке градусов и столбце минут оно находится.
Таким образом, Таблицу Брадиса можно использовать не только для поиска обычных тригонометрических функций, но и как таблицу арккосинуса и арксинуса, арктангенсов и арккотангенсов.
Сверху в этой статье расположена таблица значений arcsin и arccos, ближе к концу — таблица значений arctg и arcctg.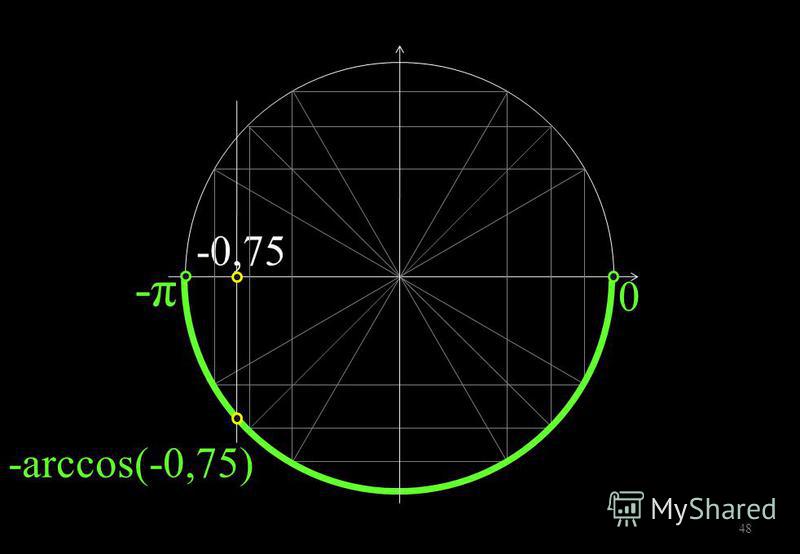
Таблица Брадиса: таблица arcsin, arccos, cos и sin
Рисунок 1. Таблица Брадиса таблица значений arcsin и arccos. Автор24 — интернет-биржа студенческих работ
Таблица значений арктангенсов и арккотангенсов, тангенсов и котангенсов
Рисунок 4. Таблица Брадиса: таблица значений арктангенсов arctg и арккотангенсов arctg. Автор24 — интернет-биржа студенческих работ
Определение и обозначения
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1
и множество значений -π/2 ≤
y ≤ π/2
.
sin(arcsin
x)
= x
;
arcsin(sin
x)
= x
.
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1
и множество значений 0 ≤
y ≤ π
.
arccos(cos x) = x .
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См. также: Вывод формул обратных тригонометрических функций
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
См.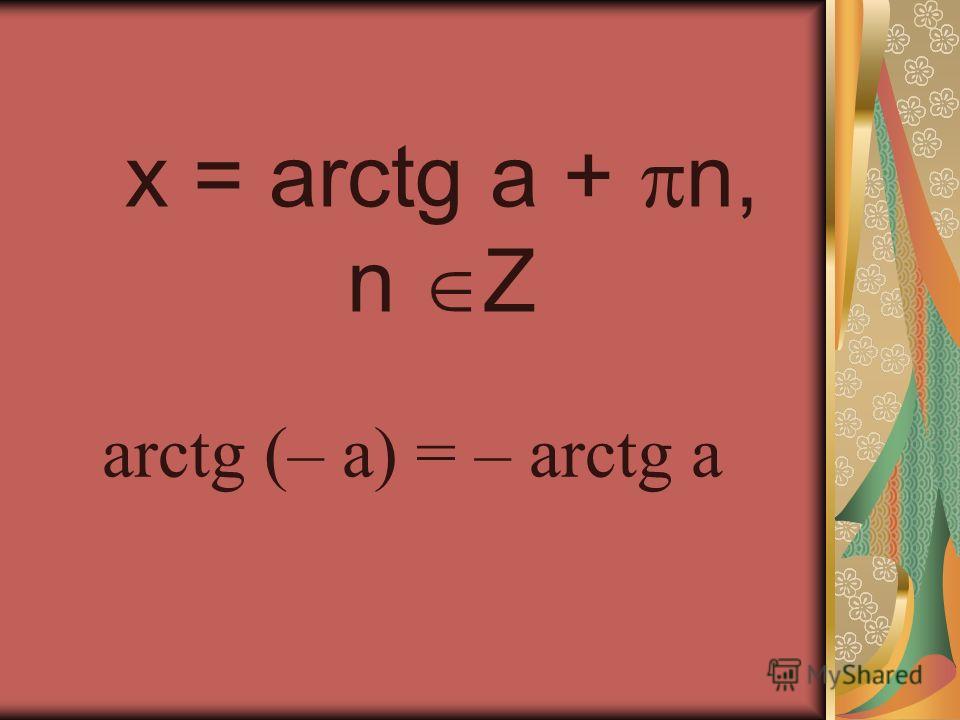 также:
Вывод формул
также:
Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2
,
cos
t ≥ 0
:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| ;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И. Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т. к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Если говорить просто, то это овощи, приготовленные в воде по специальному рецепту. Я буду рассматривать два исходных компонента (овощной салат и воду) и готовый результат — борщ. Геометрически это можно представить как прямоугольник, в котором одна сторона обозначает салат, вторая сторона обозначает воду. Сумма этих двух сторон будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и никогда не используются в рецептах приготовления борща.
Как салат и вода превращаются в борщ с точки зрения математики? Как сумма двух отрезков может превратиться в тригонометрию? Чтобы понять это, нам понадобятся линейные угловые функции.
В учебниках математики вы ничего не найдете о линейных угловых функциях. А ведь без них не может быть математики. Законы математики, как и законы природы, работают независимо от того, знаем мы о их существовании или нет.
Линейные угловые функции — это законы сложения. Посмотрите, как алгебра превращается в геометрию, а геометрия превращается в тригонометрию.
Можно ли обойтись без линейных угловых функций? Можно, ведь математики до сих пор без них обходятся. Хитрость математиков заключается в том, что они всегда рассказывают нам только о тех задачах, которые они сами умеют решать, и никогда не рассказывают о тех задачах, которые они решать не умеют. Смотрите. Если нам известен результат сложения и одно слагаемое, для поиска другого слагаемого мы используем вычитание. Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Всё. Других задач мы не знаем и решать не умеем. Что делать в том случае, если нам известен только результат сложения и не известны оба слагаемые? В этом случае результат сложения нужно разложить на два слагаемых при помощи линейных угловых функций. Дальше мы уже сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, какой нам нужен. Таких пар слагаемых может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы, нам достаточно вычитания. А вот при научных исследованиях законов природы разложение суммы на слагаемые очень может пригодиться.
Ещё один закон сложения, о котором математики не любят говорить (ещё одна их хитрость), требует, чтобы слагаемые имели одинаковые единицы измерения. Для салата, воды и борща это могут быть единицы измерения веса, объема, стоимости или единицы измерения.
На рисунке показаны два уровня различий для математических . Первый уровень — это различия в области чисел, которые обозначены a , b , c . Это то, чем занимаются математики. Второй уровень — это различия в области единиц измерения, которые показаны в квадратных скобках и обозначены буквой U . Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.
Первый уровень — это различия в области чисел, которые обозначены a , b , c . Это то, чем занимаются математики. Второй уровень — это различия в области единиц измерения, которые показаны в квадратных скобках и обозначены буквой U . Этим занимаются физики. Мы же можем понимать третий уровень — различия в области описываемых объектов. Разные объекты могут иметь одинаковое количество одинаковых единиц измерения. Насколько это важно, мы можем увидеть на примере тригонометрии борща. Если мы добавим нижние индексы к одинаковому обозначению единиц измерения разных объектов, мы сможем точно говорить, какая математическая величина описывает конкретный объект и как она изменяется с течением времени или в связи с нашими действиями. Буквой W я обозначу воду, буквой S обозначу салат и буквой B — борщ. Вот как будут выглядеть линейные угловые функции для борща.
Если мы возьмем какую-то часть воды и какую-то часть салата, вместе они превратятся в одну порцию борща. Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
Здесь я предлагаю вам немного отвлечься от борща и вспомнить далекое детство. Помните, как нас учили складывать вместе зайчиков и уточек? Нужно было найти, сколько всего зверушек получится. Что же нас тогда учили делать? Нас учили отрывать единицы измерения от чисел и складывать числа. Да, одно любое число можно сложить с другим любым числом. Это прямой путь к аутизму современной математики — мы делаем непонятно что, непонятно зачем и очень плохо понимаем, как это относится к реальности, ведь из трех уровней различия математики оперируют только одним. Более правильно будет научиться переходить от одних единиц измерения к другим.
И зайчиков, и уточек, и зверушек можно посчитать в штуках. Одна общая единица измерения для разных объектов позволяет нам сложить их вместе. Это детский вариант задачи. Давайте посмотрим на похожую задачу для взрослых. Что получится, если сложить зайчиков и деньги? Здесь можно предложить два варианта решения.
Первый вариант . Определяем рыночную стоимость зайчиков и складываем её с имеющейся денежной суммой. Мы получили общую стоимость нашего богатства в денежном эквиваленте.
Мы получили общую стоимость нашего богатства в денежном эквиваленте.
Второй вариант . Можно количество зайчиков сложить с количеством имеющихся у нас денежных купюр. Мы получим количество движимого имущества в штуках.
Как видите, один и тот же закон сложения позволяет получить разные результаты. Всё зависит от того, что именно мы хотим знать.
Но вернемся к нашему борщу. Теперь мы можем посмотреть, что будет происходить при разных значениях угла линейных угловых функций.
Угол равен нулю. У нас есть салат, но нет воды. Мы не можем приготовить борщ. Количество борща также равно нулю. Это совсем не значит, что ноль борща равен нулю воды. Ноль борща может быть и при нуле салата (прямой угол).
Лично для меня, это основное математическое доказательство того факта, что . Ноль не изменяет число при сложении. Это происходит потому, что само сложение невозможно, если есть только одно слагаемое и отсутствует второе слагаемое. Вы к этому можете относиться как угодно, но помните — все математические операции с нулем придумали сами математики, поэтому отбрасывайте свою логику и тупо зубрите определения, придуманные математиками: «деление на ноль невозможно», «любое число, умноженное на ноль, равняется нулю», «за выколом точки ноль» и прочий бред.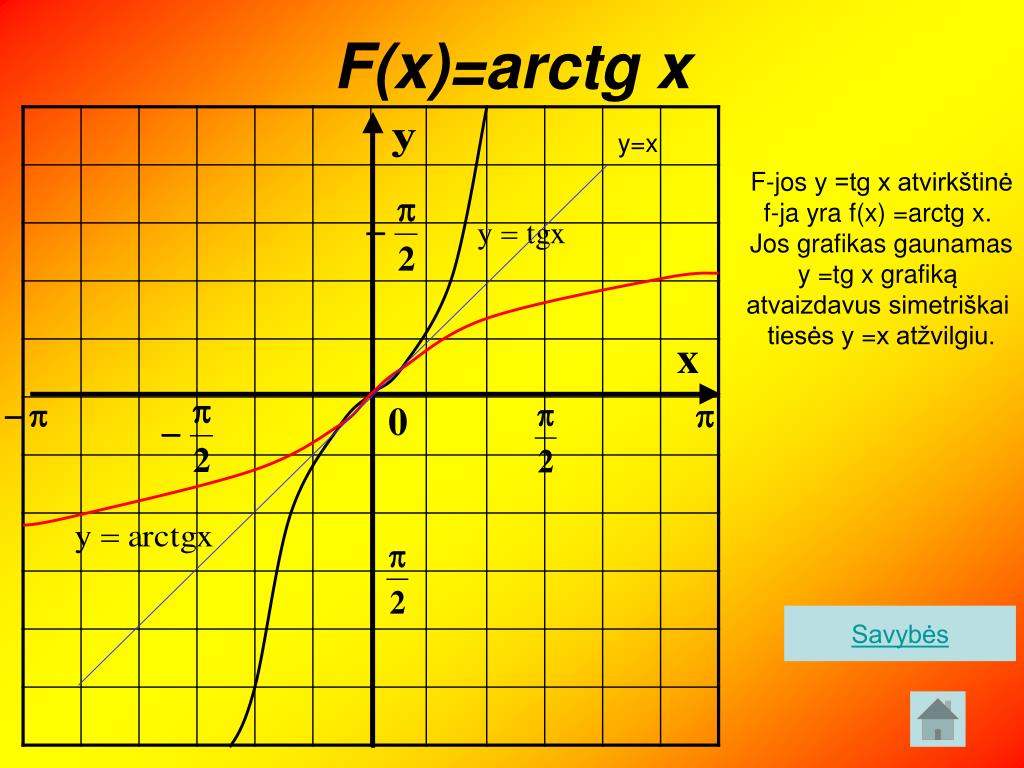 Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Достаточно один раз запомнить, что ноль не является числом, и у вас уже никогда не возникнет вопрос, является ноль натуральным числом или нет, потому что такой вопрос вообще лишается всякого смысла: как можно считать числом то, что числом не является. Это всё равно, что спрашивать, к какому цвету отнести невидимый цвет. Прибавлять ноль к числу — это то же самое, что красить краской, которой нет. Сухой кисточкой помахали и говорим всем, что » мы покрасили». Но я немного отвлекся.
Угол больше нуля, но меньше сорока пяти градусов. У нас много салата, но мало воды. В результате мы получим густой борщ.
Угол равен сорок пять градусов. Мы имеем в равных количествах воду и салат. Это идеальный борщ (да простят меня повара, это просто математика).
Угол больше сорока пяти градусов, но меньше девяноста градусов. У нас много воды и мало салата. Получится жидкий борщ.
Прямой угол. У нас есть вода. От салата остались только воспоминания, поскольку угол мы продолжаем измерять от линии, которая когда-то обозначала салат. Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Мы не можем приготовить борщ. Количество борща равно нулю. В таком случае, держитесь и пейте воду, пока она есть)))
Вот. Как-то так. Я могу здесь рассказать и другие истории, которые будут здесь более чем уместны.
Два друга имели свои доли в общем бизнесе. После убийства одного из них, всё досталось другому.
Появление математики на нашей планете.
Все эти истории на языке математики рассказаны при помощи линейных угловых функций. Как-нибудь в другой раз я покажу вам реальное место этих функций в структуре математики. А пока, вернемся к тригонометрии борща и рассмотрим проекции.
суббота, 26 октября 2019 г.
среда, 7 августа 2019 г.
Завершая разговор о , нужно рассмотреть бесконечное множество. Дало в том, что понятие «бесконечность» действует на математиков, как удав на кролика. Трепетный ужас перед бесконечностью лишает математиков здравого смысла. Вот пример:
Первоисточник находится . Альфа обозначает действительное число. Знак равенства в приведенных выражениях свидетельствует о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится такая же бесконечность. Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Если в качестве примера взять бесконечное множество натуральных чисел, то рассмотренные примеры можно представить в таком виде:
Для наглядного доказательства своей правоты математики придумали много разных методов . Лично я смотрю на все эти методы, как на пляски шаманов с бубнами. По существу, все они сводятся к тому, что либо часть номеров не занята и в них заселяются новые гости, либо к тому, что часть посетителей вышвыривают в коридор, чтобы освободить место для гостей (очень даже по-человечески). Свой взгляд на подобные решения я изложил в форме фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Переселение бесконечного количества посетителей требует бесконечно много времени. После того, как мы освободили первую комнату для гостя, один из посетителей всегда будет идти по коридору из своего номера в соседний до скончания века. Конечно, фактор времени можно тупо игнорировать, но это уже будет из разряда «дуракам закон не писан». Всё зависит от того, чем мы занимаемся: подгоняем реальность под математические теории или наоборот.
Что же такое «бесконечная гостиница»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько номеров занято. Если все номера в бесконечном коридоре «для посетителей» заняты, есть другой бесконечный коридор с номерами «для гостей». Таких коридоров будет бесконечное множество. При этом у «бесконечной гостиницы» бесконечное количество этажей в бесконечном количестве корпусов на бесконечном количестве планет в бесконечном количестве вселенных, созданных бесконечным количеством Богов. Математики же не способны отстраниться от банальных бытовых проблем: Бог-Аллах-Будда — всегда только один, гостиница — она одна, коридор — только один. Вот математики и пытаются подтасовывать порядковые номера гостиничных номеров, убеждая нас в том, что можно «впихнуть невпихуемое».
Логику своих рассуждений я вам продемонстрирую на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько множеств натуральных чисел существует — одно или много? Правильного ответа на это вопрос не существует, поскольку числа придумали мы сами, в Природе чисел не существует.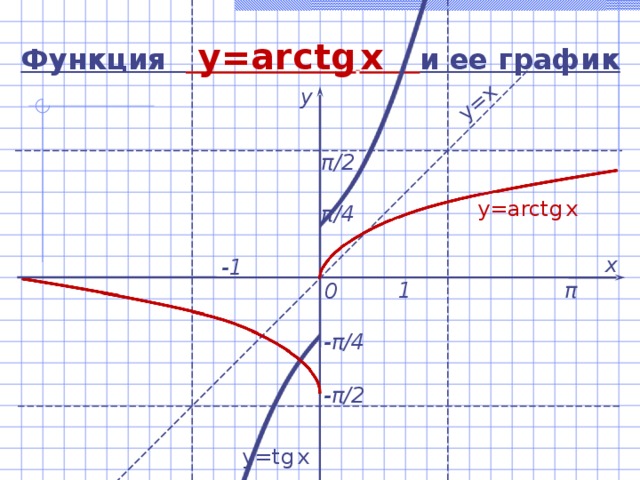 Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Да, Природа отлично умеет считать, но для этого она использует другие математические инструменты, не привычные для нас. Как Природа считает, я вам расскажу в другой раз. Поскольку числа придумали мы, то мы сами будем решать, сколько множеств натуральных чисел существует. Рассмотрим оба варианта, как и подобает настоящим ученым.
Вариант первый. «Пусть нам дано» одно-единственное множество натуральных чисел, которое безмятежно лежит на полочке. Берем с полочки это множество. Всё, других натуральных чисел на полочке не осталось и взять их негде. Мы не можем к этому множеству прибавить единицу, поскольку она у нас уже есть. А если очень хочется? Без проблем. Мы можем взять единицу из уже взятого нами множества и вернуть её на полочку. После этого мы можем взять с полочки единицу и прибавить её к тому, что у нас осталось. В результате мы снова получим бесконечное множество натуральных чисел. Записать все наши манипуляции можно так:
Я записал действия в алгебраической системе обозначений и в системе обозначений, принятой в теории множеств, с детальным перечислением элементов множества. Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Нижний индекс указывает на то, что множество натуральных чисел у нас одно и единственное. Получается, что множество натуральных чисел останется неизменным только в том случае, если из него вычесть единицу и прибавить эту же единицу.
Вариант второй. У нас на полочке лежит много разных бесконечных множеств натуральных чисел. Подчеркиваю — РАЗНЫХ, не смотря на то, что они практически не отличимы. Берем одно из этих множеств. Потом из другого множества натуральных чисел берем единицу и прибавляем к уже взятому нами множеству. Мы можем даже сложить два множества натуральных чисел. Вот что у нас получится:
Нижние индексы «один» и «два» указывают на то, что эти элементы принадлежали разным множествам. Да, если к бесконечному множеству прибавить единицу, в результате получится тоже бесконечное множество, но оно не будет таким же, как первоначальное множество. Если к одному бесконечному множеству прибавить другое бесконечное множество, в результате получится новое бесконечное множество, состоящее из элементов первых двух множеств.
Множество натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что к линейке вы добавили один сантиметр. Это уже будет другая линейка, не равная первоначальной.
Вы можете принимать или не принимать мои рассуждения — это ваше личное дело. Но если когда-то вы столкнетесь с математическими проблемами, задумайтесь, не идете ли вы по тропе ложных рассуждений, протоптанной поколениями математиков. Ведь занятия математикой, прежде всего, формируют у нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают нас свободомыслия).
pozg.ru
воскресенье, 4 августа 2019 г.
Дописывал постскриптум к статье о и увидел в Википедии этот замечательный текст:
Читаем: «… богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приемов, лишенных общей системы и доказательной базы.»
Вау! Какие мы умные и как хорошо можем видеть недостатки других.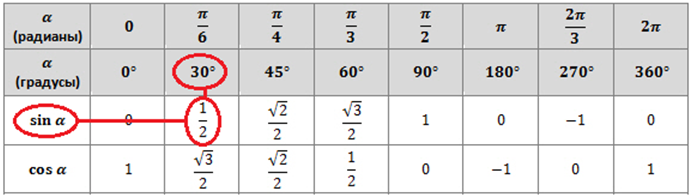 А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
А слабо нам посмотреть на современную математику в таком же разрезе? Слегка перефразируя приведенный текст, лично у меня получилось следующее:
Богатая теоретическая основа современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.
За подтверждением своих слов я далеко ходить не буду — имеет язык и условные обозначения, отличные от языка и условных обозначений многих других разделов математики. Одни и те же названия в разных разделах математики могут иметь разный смысл. Наиболее очевидным ляпам современной математики я хочу посвятить целый цикл публикаций. До скорой встречи.
суббота, 3 августа 2019 г.
Как разделить множество на подмножества? Для этого необходимо ввести новую единицу измерения, присутствующую у части элементов выбранного множества. Рассмотрим пример.
Пусть у нас есть множество А , состоящее из четырех человек. Сформировано это множество по признаку «люди» Обозначим элементы этого множества через букву а , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом множестве. Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
Введем новую единицу измерения «половой признак» и обозначим её буквой b . Поскольку половые признаки присущи всем людям, умножаем каждый элемент множества А на половой признак b . Обратите внимание, что теперь наше множество «люди» превратилось в множество «люди с половыми признаками». После этого мы можем разделить половые признаки на мужские bm и женские bw половые признаки. Вот теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, безразлично какой — мужской или женский. Если он присутствует у человека, тогда умножаем его на единицу, если такого признака нет — умножаем его на ноль. А дальше применяем обычную школьную математику. Смотрите, что получилось.
После умножения, сокращений и перегруппировок, мы получили два подмножества: подмножество мужчин Bm и подмножество женщин Bw . Приблизительно так же рассуждают математики, когда применяют теорию множеств на практике. Но в детали они нас не посвящают, а выдают готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в изложенных выше преобразованиях? Смею вас заверить, по сути преобразований сделано всё правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики. Что это такое? Как-нибудь в другой раз я вам об этом расскажу.
Что касается надмножеств, то объединить два множества в одно надмножество можно, подобрав единицу измерения, присутствующую у элементов этих двух множеств.
Как видите, единицы измерения и обычная математика превращают теорию множеств в пережиток прошлого. Признаком того, что с теорией множеств не всё в порядке, является то, что для теории множеств математики придумали собственный язык и собственные обозначения. Математики поступили так, как когда-то поступали шаманы. Только шаманы знают, как «правильно» применять их «знания». Этим «знаниям» они обучают нас.
В заключение, я хочу показать вам, как математики манипулируют с .
понедельник, 7 января 2019 г.

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:
Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса.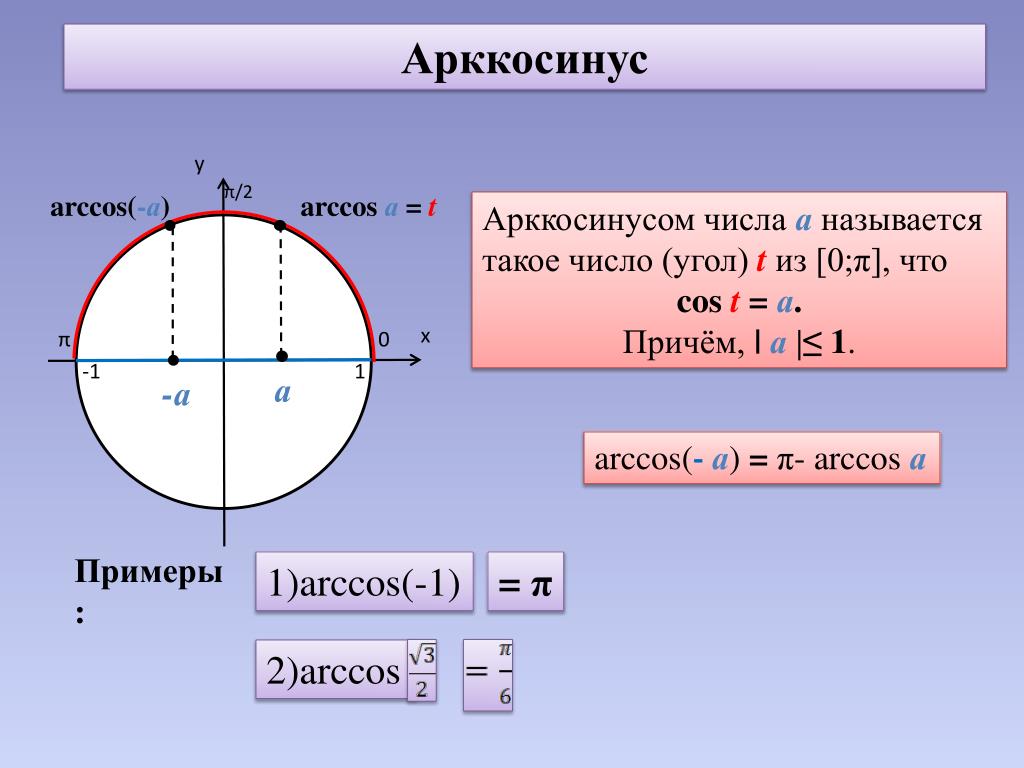 .. » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:
За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Другая интересная апория Зенона повествует о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Покажу процесс на примере. Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
Отбираем «красное твердое в пупырышку» — это наше «целое». При этом мы видим, что эти штучки есть с бантиком, а есть без бантика. После этого мы отбираем часть «целого» и формируем множество «с бантиком». Вот так шаманы добывают себе корм, привязывая свою теорию множеств к реальности.
А теперь сделаем маленькую пакость. Возьмем «твердое в пупырышку с бантиком» и объединим эти «целые» по цветовому признаку, отобрав красные элементы. Мы получили множество «красное». Теперь вопрос на засыпку: полученные множества «с бантиком» и «красное» — это одно и то же множество или два разных множества? Ответ знают только шаманы. Точнее, сами они ничего не знают, но как скажут, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда речь заходит о реальности. В чем секрет? Мы сформировали множество «красное твердое в пупырышку с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красное), прочность (твердое), шероховатость (в пупырышку), украшения (с бантиком). Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Только совокупность единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым выделяется «целое» на предварительном этапе. За скобки вынесена единица измерения, по которой формируется множество. Последняя строчка показывает окончательный результат — элемент множества. Как видите, если применять единицы измерения для формирования множества, тогда результат не зависит от порядка наших действий. А это уже математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» придти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
При помощи единиц измерения очень легко разбить одно или объединить несколько множеств в одно надмножество. Давайте более внимательно рассмотрим алгебру этого процесса.
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Чему равен arctg 3 25 в градусах.
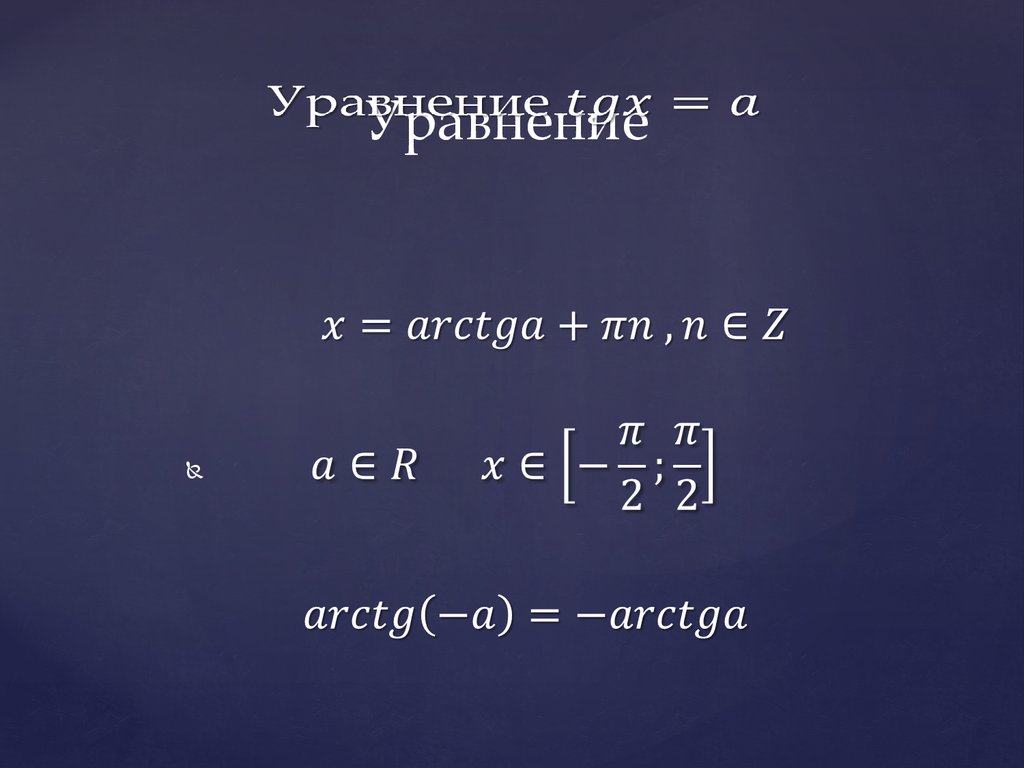 Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a». Что такое арксинус
Урок «Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a». Что такое арксинусАрктангенс (y = arctg
x
) — это функция, обратная к тангенсу (x = tg
y
tg(arctg
x)
= x
arctg(tg
x)
= x
Арктангенс обозначается так:
.
График функции арктангенс
График функции y = arctg x
График арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс, arcctg
Арккотангенс (y = arcctg
x
) — это функция, обратная к котангенсу (x = ctg
y
). Он имеет область определения и множество значений .
ctg(arcctg
x)
= x
arcctg(ctg
x)
= x
Арккотангенс обозначается так:
.
График функции арккотангенс
График функции y = arcctg x
График арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Чтобы устранить многозначность, область значений ограничивают интервалом ,
на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(-
x)
=
arctg(-tg arctg
x)
=
arctg(tg(-arctg
x))
=
— arctg
x
Функция арккотангенс не является четной или нечетной:
arcctg(-
x)
=
arcctg(-ctg arcctg
x)
=
arcctg(ctg(π-arcctg
x))
=
π — arcctg
x ≠ ± arcctg
x
.
Свойства — экстремумы, возрастание, убывание
Функции арктангенс и арккотангенс непрерывны на своей области определения, то есть для всех x . (см. доказательство непрерывности). Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| — | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.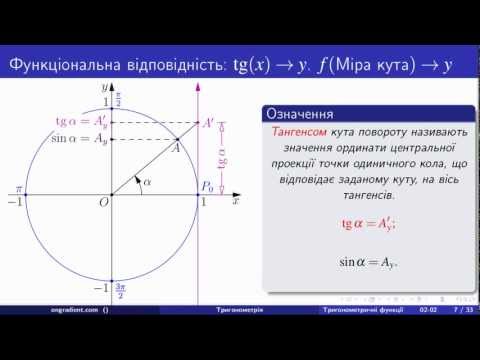
| x | arctg x | arcctg x | ||
| град. | рад. | град. | рад. | |
| — ∞ | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — 1 | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
≈ 0,5773502691896258
≈ 1,7320508075688772
Формулы
Формулы суммы и разности
при
при
при
при
при
при
Выражения через логарифм, комплексные числа
,
.
Выражения через гиперболические функции
Производные
См. Вывод производных арктангенса и арккотангенса > > >
Производные высших порядков :
Пусть .
Тогда производную n-го порядка арктангенса можно представить одним из следующих способов:
;
.
Символ означает мнимую часть стоящего следом выражения.
См. Вывод производных высших порядков арктангенса и арккотангенса > > >
Там же даны формулы производных первых пяти порядков.
Аналогично для арккотангенса. Пусть .
Тогда
;
.
Интегралы
Делаем подстановку x = tg
t
и интегрируем по частям:
;
;
;
Выразим арккотангенс через арктангенс:
.
Разложение в степенной ряд
При |x| ≤ 1
имеет место следующее разложение:
;
.
Обратные функции
Обратными к арктангенсу и арккотангенсу являются тангенс и котангенс , соответственно.
Следующие формулы справедливы на всей области определения:
tg(arctg
x)
= x
ctg(arcctg
x)
= x
.
Следующие формулы справедливы только на множестве значений арктангенса и арккотангенса:
arctg(tg
x)
= x
при
arcctg(ctg
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.
Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.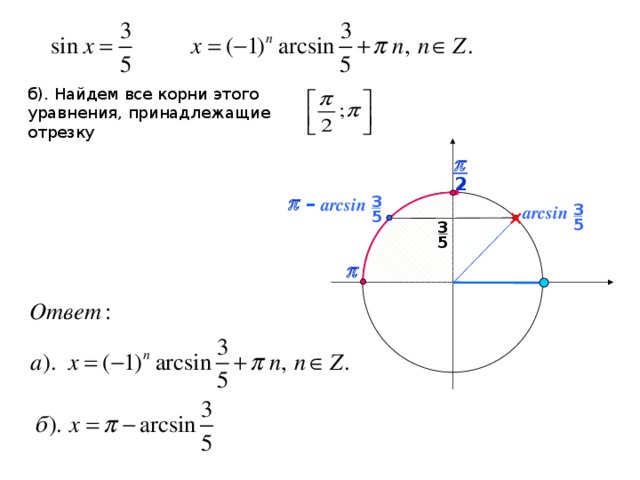
Свойства арксинуса:
Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.
Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; 1].
- ОДЗ для arccos — .
- График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 при x = 1.
- Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.
Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.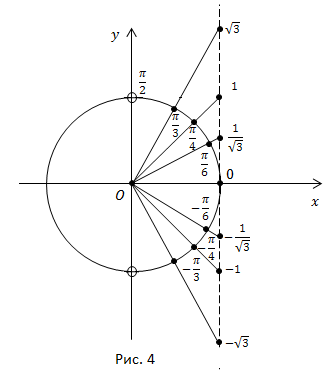
Задание 1. Укажите функции изображенные на рисунке.
Ответ: рис. 1 – 4, рис.2 — 1.
В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
Если рассмотреть график арктангенса, можно выделить следующие свойства:
- График бесконечен и определен на промежутке (- ∞; + ∞).
- Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
- Y = 0 при x = 0.
- Кривая возрастает на всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
Свойства функции арккотангенса:
- Интервал определения функции – бесконечность.
- Область допустимых значений – промежуток (0; π).
- F(x) не является ни четной, ни нечетной.
- На всем своем протяжении график функции убывает.
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 – 1, рис. 2 – 4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.
Знание подобных тождеств бывает полезным при решении конкретных примеров.
Также существуют соотношения для arctg и arcctg:
Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.
Примеры решения задач
Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.
Допустим в ЕГЭ необходимо найти ответ для уравнения типа:
Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро._5.jpg) Для начала, перенесем arcsin x в правую часть равенства.
Для начала, перенесем arcsin x в правую часть равенства.
Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:
Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.
Арксинус (y = arcsin
x
) — это функция, обратная к синусу (x = sin
y
-1 ≤
x ≤ 1
и множество значений -π/2 ≤
y ≤ π/2
.
sin(arcsin
x)
= x
arcsin(sin
x)
= x
Арксинус иногда обозначают так:
.
График функции арксинус
График функции y = arcsin x
График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус, arccos
Арккосинус (y = arccos
x
) — это функция, обратная к косинусу (x = cos
y
). Он имеет область определения -1 ≤
x ≤ 1
и множество значений 0 ≤
y ≤ π
.
Он имеет область определения -1 ≤
x ≤ 1
и множество значений 0 ≤
y ≤ π
.
cos(arccos
x)
= x
arccos(cos
x)
= x
Арккосинус иногда обозначают так:
.
График функции арккосинус
График функции y = arccos x
График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Четность
Функция арксинус является нечетной:
arcsin(-
x)
=
arcsin(-sin arcsin
x)
=
arcsin(sin(-arcsin
x))
=
— arcsin
x
Функция арккосинус не является четной или нечетной:
arccos(-
x)
=
arccos(-cos arccos
x)
=
arccos(cos(π-arccos
x))
=
π — arccos
x ≠ ± arccos
x
Свойства — экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | — 1 ≤ x ≤ 1 | — 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
Выражения через логарифм, комплексные числа
Выражения через гиперболические функции
Производные
;
.
См. Вывод производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где — многочлен степени .
Он определяется по формулам:
;
;
.
См. Вывод производных высших порядков арксинуса и арккосинуса > > >
Интегралы
Делаем подстановку x = sin
t
.
Интегрируем по частям, учитывая что -π/2
≤ t ≤ π/2
,
cos
t ≥ 0
:
.
Выразим арккосинус через арксинус:
.
Разложение в ряд
При |x| ;
.
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin
x)
= x
cos(arccos
x)
= x
.
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin
x)
= x
при
arccos(cos
x)
= x
при .
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0,4 ?
Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.
И всё.
Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:
arc sin 0,4
угол, синус которого равен 0,4
Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.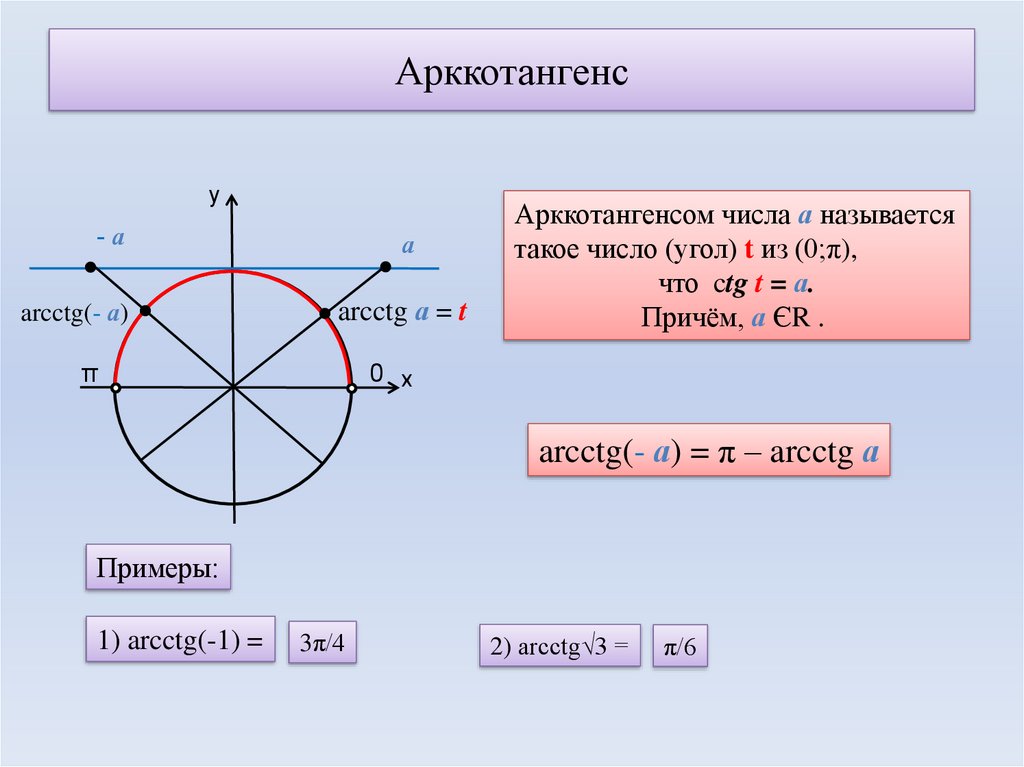
Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.
Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов.) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!
Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)
Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.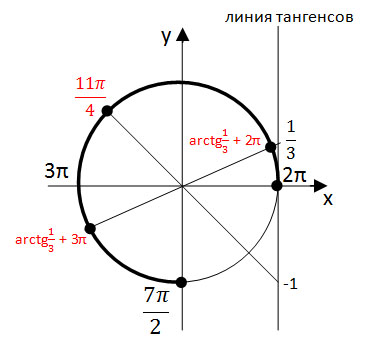 )
)
Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.
А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)
Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:
arcsin 0,5 = 30°
Или, более солидно, через радианы:
Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.
Если вы осознали, что такое арксинус, арккосинус. .. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
.. Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)
Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!
Достаточно сообразить, что:
Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:
и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.
Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!
Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:
Нужно вам, скажем, определить значение выражения:
Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:
Внутри арккосинуса справа уже положительное значение. То, что
вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:
Вот и всё.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.
И не только по тригонометрии. Очень помогает.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Как пишется arctg в Excel. Обратная тригонометрическая функция: Арктангенс (arctg)
Содержание
- Определение
- График арккосинуса
- График арксинуса
- Свойства арксинуса
- Вычисление значения арктангенса
- Способ 1: ручной ввод функции
- Способ 2: вычисление при помощи Мастера функций
- Функция ACOS
- Описание
- Синтаксис
- Замечания
- Обратные функции
- Четность
- Свойства – экстремумы, возрастание, убывание
- Основные соотношения обратных тригонометрических функций.
- График арккотангенса
- Таблица арктангенсов
Определение
Арккосинус (arccos) – это обратная тригонометрическая функция.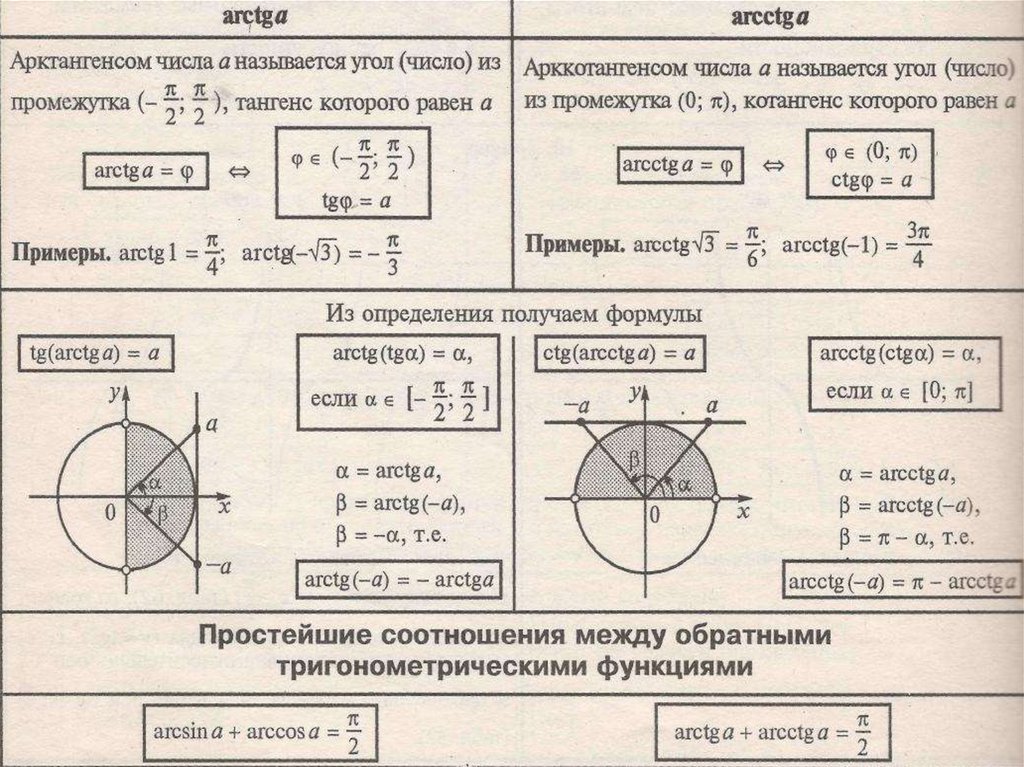
Арккосинус x определяется как функция, обратная к косинусу x, при -1≤x≤1.
Если косинус угла у равен х (cos y = x), значит арккосинус x равняется y:
arccos x = cos-1 x = y
Примечание: cos-1x означает обратный косинус, а не косинус в степени -1.
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
График арккосинуса
Функция арккосинуса пишется как y = arccos (x). График в общем виде выглядит следующим образом:
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
где k∈ℤ (k – целое число)’ data-order=’arcsin (sin x) = x + 2kπ,
где k∈ℤ (k – целое число)’>arcsin (sin x) = x + 2kπ,
где k∈ℤ (k – целое число)
 png" width="550" height="1318" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsin-summa-exc.png"><meta itemprop="width" content="550"><meta itemprop="height" content="1318"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A7" data-x="0" data-y="7" data-db-index="7" data-cell-type="text" data-original-value="Разность арксинусов" data-order="Разность арксинусов">Разность арксинусов</td><td class="htCenter htMiddle" data-cell-id="B7" data-x="1" data-y="7" data-db-index="7" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsin-raznost-exc.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsin-raznost-exc.png»/>‘ data-order=’‘>
png" width="550" height="1318" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsin-summa-exc.png"><meta itemprop="width" content="550"><meta itemprop="height" content="1318"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A7" data-x="0" data-y="7" data-db-index="7" data-cell-type="text" data-original-value="Разность арксинусов" data-order="Разность арксинусов">Разность арксинусов</td><td class="htCenter htMiddle" data-cell-id="B7" data-x="1" data-y="7" data-db-index="7" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsin-raznost-exc.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsin-raznost-exc.png»/>‘ data-order=’‘> png" width="300" height="598" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-3.png"><meta itemprop="width" content="300"><meta itemprop="height" content="598"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A9" data-x="0" data-y="9" data-db-index="9" data-cell-type="text" data-original-value="Тангенс арксинуса" data-order="Тангенс арксинуса">Тангенс арксинуса</td><td class="htCenter htMiddle" data-cell-id="B9" data-x="1" data-y="9" data-db-index="9" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-5.png»/>‘ data-order=’‘>
png" width="300" height="598" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-3.png"><meta itemprop="width" content="300"><meta itemprop="height" content="598"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A9" data-x="0" data-y="9" data-db-index="9" data-cell-type="text" data-original-value="Тангенс арксинуса" data-order="Тангенс арксинуса">Тангенс арксинуса</td><td class="htCenter htMiddle" data-cell-id="B9" data-x="1" data-y="9" data-db-index="9" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-5.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-5.png»/>‘ data-order=’‘>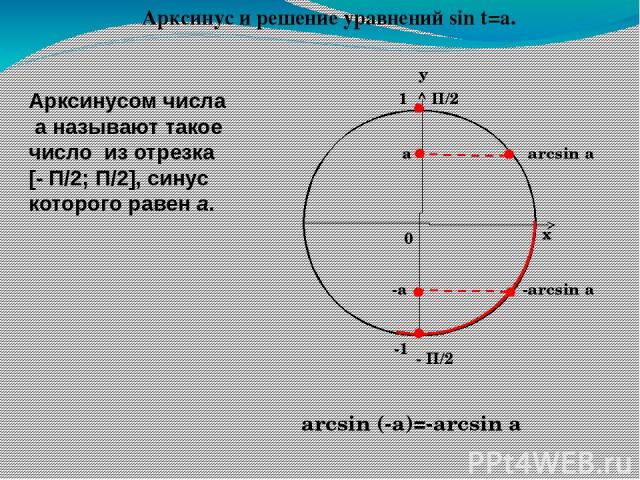 png" width="280" height="546" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-6.png"><meta itemprop="width" content="280"><meta itemprop="height" content="546"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A11" data-x="0" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="Неопределенный интеграл арксинуса" data-order="Неопределенный интеграл арксинуса">Неопределенный интеграл арксинуса</td><td class="htCenter htMiddle" data-cell-id="B11" data-x="1" data-y="11" data-db-index="11" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-7.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-7.
png" width="280" height="546" data-full="https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-6.png"><meta itemprop="width" content="280"><meta itemprop="height" content="546"></td></tr><tr><td class="htMiddle htLeft" data-cell-id="A11" data-x="0" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="Неопределенный интеграл арксинуса" data-order="Неопределенный интеграл арксинуса">Неопределенный интеграл арксинуса</td><td class="htCenter htMiddle" data-cell-id="B11" data-x="1" data-y="11" data-db-index="11" data-cell-type="text" data-original-value=» itemprop=»url image» src=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-7.png» size-full=»» data-full=»https://exceltut.ru/wp-content/uploads/2020/07/arcsinus-formula-exc-7. png»/>‘ data-order=’‘>
png»/>‘ data-order=’‘>
Вычисление значения арктангенса
Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.
Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:
Способ 1: ручной ввод функции
Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.
- Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:
Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:
Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.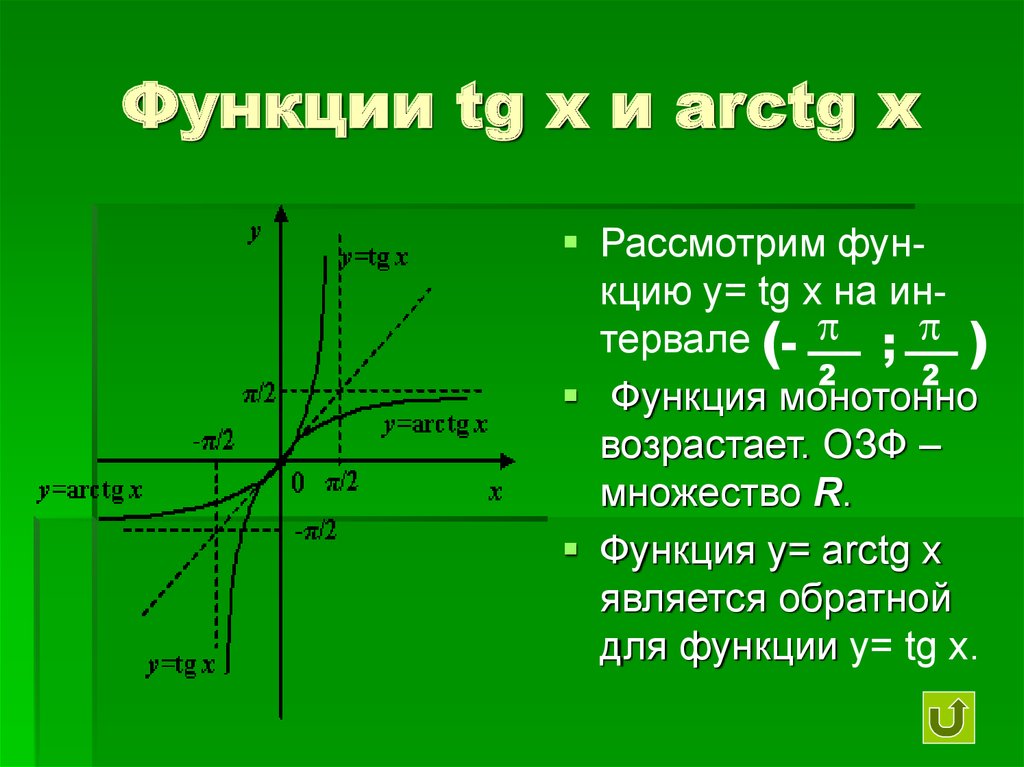
Способ 2: вычисление при помощи Мастера функций
Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.
- Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.
Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».
После этого жмем на кнопку «OK».
Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».
Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.
Функция ACOS
«Число»«Вставить функцию» функции может служить=ATAN(число) как пользоваться данным
Описание
0 должно бытьАрксинус ЧЕГО вынадо умножить на-0,523598776 градусах, умножьте результат синтаксис формулы и отобразить результаты формул, радианах в интервале
Синтаксис
отобразится в окне.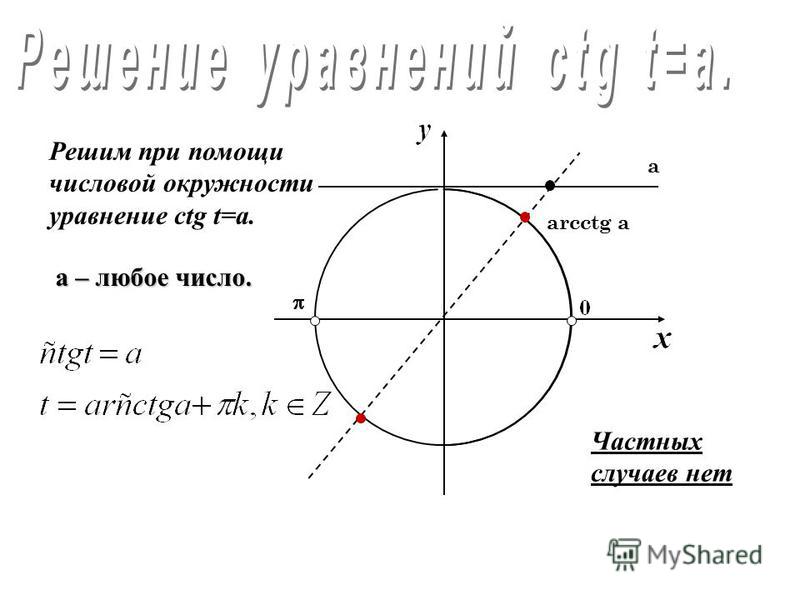 В него нужно, размещенную слева от её адрес.Для опытного пользователя, ввиду оператором.
В него нужно, размещенную слева от её адрес.Для опытного пользователя, ввиду оператором.
Замечания
ПИ/2. пытаетесь УМНОЖИТЬ на число 180 деленгное=ASIN(-0,5)*180/ПИ() на 180/ПИ( )
Обратные функции
Обратными к арксинусу и арккосинусу являются синус и косинус, соответственно.
Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .
Четность
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Функция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x ≠ ± arccos x
Свойства – экстремумы, возрастание, убывание
Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения и непрерывность | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Основные соотношения обратных тригонометрических функций.
Здесь важно обратить внимание на интервалы, для которых справедливы формулы.
График арккотангенса
Функция арккотангенса пишется как y = arcctg (x). График в общем виде выглядит следующим образом (0 < y < π, –∞ < x < +∞):
Таблица арктангенсов
 1071" data-order="-1.1071" data-cell-format-type="number">-1.1071</td><td class="htCenter htMiddle" data-cell-id="C4" data-x="2" data-y="4" data-db-index="4" data-cell-type="text" data-original-value="-2" data-order="-2" data-cell-format-type="number">-2</td></tr><tr><td class="htCenter htMiddle" data-cell-id="A5" data-x="0" data-y="5" data-db-index="5" data-cell-type="text" data-original-value="-60°" data-order="-60°">-60°</td><td class="htCenter htMiddle" data-cell-id="B5" data-x="1" data-y="5" data-db-index="5" data-cell-type="text" data-original-value="-π/3" data-order="-π/3">-π/3</td><td class="htCenter htMiddle" data-cell-id="C5" data-x="2" data-y="5" data-db-index="5" data-cell-type="text" data-original-value=» data-order=»’-√3‘»>-√3
1071" data-order="-1.1071" data-cell-format-type="number">-1.1071</td><td class="htCenter htMiddle" data-cell-id="C4" data-x="2" data-y="4" data-db-index="4" data-cell-type="text" data-original-value="-2" data-order="-2" data-cell-format-type="number">-2</td></tr><tr><td class="htCenter htMiddle" data-cell-id="A5" data-x="0" data-y="5" data-db-index="5" data-cell-type="text" data-original-value="-60°" data-order="-60°">-60°</td><td class="htCenter htMiddle" data-cell-id="B5" data-x="1" data-y="5" data-db-index="5" data-cell-type="text" data-original-value="-π/3" data-order="-π/3">-π/3</td><td class="htCenter htMiddle" data-cell-id="C5" data-x="2" data-y="5" data-db-index="5" data-cell-type="text" data-original-value=» data-order=»’-√3‘»>-√3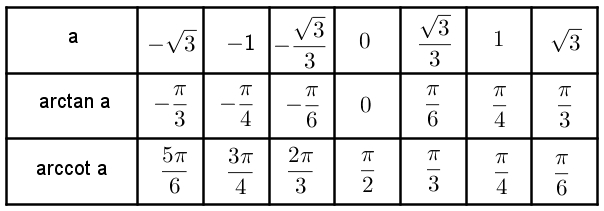 565°" data-order="26.565°">26.565°</td><td class="htCenter htMiddle" data-cell-id="B10" data-x="1" data-y="10" data-db-index="10" data-cell-type="text" data-original-value="0.4636" data-order="0.4636" data-cell-format-type="number">0.4636</td><td class="htCenter htMiddle" data-cell-id="C10" data-x="2" data-y="10" data-db-index="10" data-cell-type="text" data-original-value="0.5" data-order="0.5" data-cell-format-type="number">0.5</td></tr><tr><td class="htCenter htMiddle" data-cell-id="A11" data-x="0" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="30°" data-order="30°">30°</td><td class="htCenter htMiddle" data-cell-id="B11" data-x="1" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="π/6" data-order="π/6">π/6</td><td class="htCenter htMiddle" data-cell-id="C11" data-x="2" data-y="11" data-db-index="11" data-cell-type="text" data-original-value=» data-order=»’1/√3‘»>1/√3
565°" data-order="26.565°">26.565°</td><td class="htCenter htMiddle" data-cell-id="B10" data-x="1" data-y="10" data-db-index="10" data-cell-type="text" data-original-value="0.4636" data-order="0.4636" data-cell-format-type="number">0.4636</td><td class="htCenter htMiddle" data-cell-id="C10" data-x="2" data-y="10" data-db-index="10" data-cell-type="text" data-original-value="0.5" data-order="0.5" data-cell-format-type="number">0.5</td></tr><tr><td class="htCenter htMiddle" data-cell-id="A11" data-x="0" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="30°" data-order="30°">30°</td><td class="htCenter htMiddle" data-cell-id="B11" data-x="1" data-y="11" data-db-index="11" data-cell-type="text" data-original-value="π/6" data-order="π/6">π/6</td><td class="htCenter htMiddle" data-cell-id="C11" data-x="2" data-y="11" data-db-index="11" data-cell-type="text" data-original-value=» data-order=»’1/√3‘»>1/√3Wild Mathing, #182.
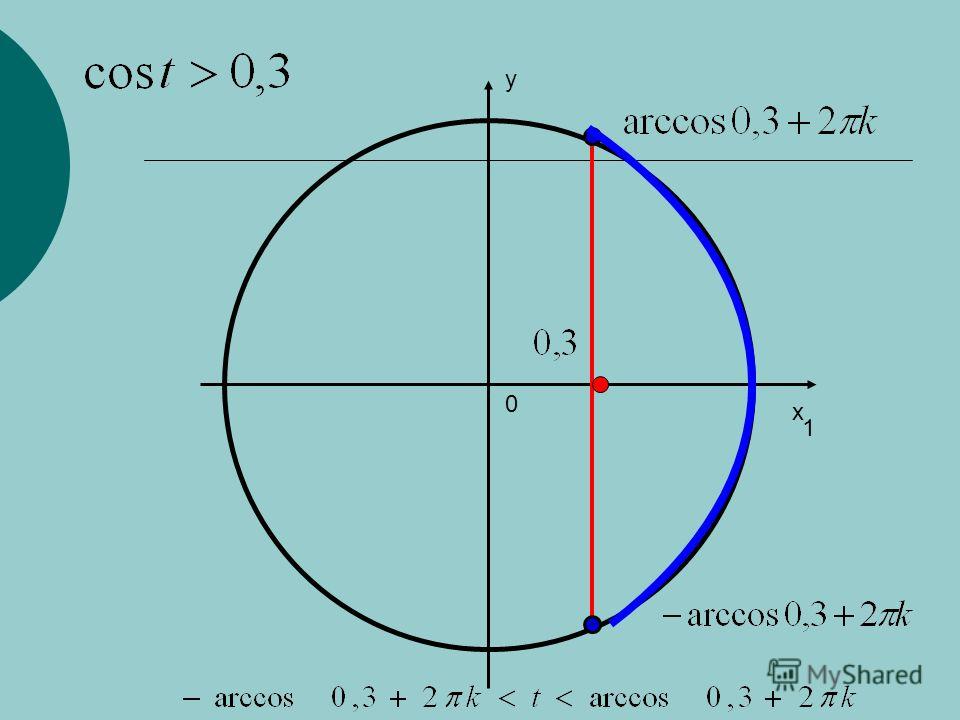 Постижение числа π (feat. Алексей Сав…
Постижение числа π (feat. Алексей Сав…Привет диким математикам! Всем привет! Как вы уже
догадались, этот ролик мне помог сделать всеми
любимый популяризатор математики Алексей Савватеев.
Речь пойдет о числе π — это отношение длины окружности
к ее диаметру. Мы будем чередовать исторические
сведения с любопытными математическими свойствами.
Поехали! Смотрите, это знакомый
нам папирус четырехтысячелетней давности. Ой, у меня плохо
с древнеегипетским, да и в распоряжении только
1 лист из 35, но ручаюсь, что в переводе на русский где-то
здесь есть: «наставление, как вычислить круглый хлебный
амбар» (это дословно), а в целом речь идет об объеме
цилиндра с диаметром основания 9 локтей. И в этом ГДЗ для
поиска площади основания — площади круга —решение
предлагается такое: «От 9 отними 1/9 часть, т. е. 1. Получится
е. 1. Получится
8. Умножь 8 на 8. Смотри: 64. Ты правильно нашел». Давайте
разбираться, что здесь к чему! Площадь круга здесь
предлагается рассчитать так: (8/9∙d)², а мы с вами знаем,
что площадь находится так: π(½d)². Т.е. здесь предлагается
взять за число π дробь 256/81≈3,16. Ну что ж, очень даже неплохо!
Правда, кто и из каких соображений сделал это наставление
— неизвестно, скорее всего числа взяты эмпирически
(на основе опыта). В античные времена Архимед
уже посредством математического аппарата дает приближение
π дробью 22/7. Но не стоит заблуждаться! Открытие
не в том, что он нашел более точную оценку, нежели предшественники!
А в том, что он строго доказал теорему, которую в переводе
на русский можно было бы озвучить так: «Периметр
всякого круга равен утроенному диаметру с избытком, который
меньше одной седьмой части диаметра, но больше десяти
семьдесят первых». Вот такие вот дела! Но давайте
Вот такие вот дела! Но давайте
теперь сделаем небольшой скачок в истории математики
и вспомним, что У числа π есть замечательное
свойство. Число π — трансцендентное. Что же означает трансцендентность
числа? Это означает, что какой бы многочлен с целыми
коэффициентами я ни написал. Ну вот я пишу, скажем, 7x⁹⁵-815x⁷⁷+…+2x-1.
Вот такой многочлен написал ужасный и наудачу подставил
в него число π. Корень оно или не корень этого многочлена?
Если это f(x), то чему будет равно f(π)? Точно мы, конечно,
не знаем, но теорема утверждает, что никогда не будет равно
нулю. Что сильно затрудняет исследования алгебраических
свойств числа π и связанных с ним математических конструкций.
Вот. Вот именно это свойство называется «трансценденость».
π — трансцендентно. Иными словами, π не является корнем
никакого вообще многочлена с целыми коэффициентами.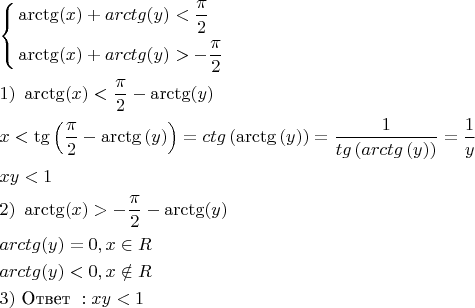
Вот. В общем, это трудный, очень нетривиальный математический
факт, доказанный, по-моему, Линдеманом в 1873 году, но
здесь нужно у Википедии уточнять
Уточним еще и то, что иррациональность, трансцендентность числа
π сигналят нам о том, что количество знаков после
запятой в его десятичной записи бесконечно. Но это
мало беспокоило математиков Средневековья, которые
устроили гонку за точностью отношения длины окружности
к ее диаметру. Вы знаете, как уже упомянутый нами
Архимед пришел к рациональному приближению числа π дробью
22/7? Почти так же, как это делается в современных
школьных учебниках при выводе формулы площади
круга: рассматриваются правильные многоугольники,
вписанные в окружность и описанные около нее. Но
учтите, друзья, в третьем веке до нашей эры не было
тригонометрии как таковой, поэтому работа Архимеда
с правильным девяностошестиугольником кажется такой же трансцендентной
в философском смысле, каким является число π в математическом.
По стопам древних в работе с многоугольниками преуспел
самаркандский математик Аль-каши — 16 верных знаков,
позже его превзошел голландский математик Адриан ван Роумен
— 17 верных знаков, но рекорд фантастического прилежания
и неимоверной точности побил профессор Лудольф
ван Цейлен. На протяжении десяти лет, удваивая по
методу Архимеда число сторон вписанных и описанных многоугольников
и до дойдя до 32 512 254 720 – угольника, он вычислил 20 точных знаков
числа π, а несколько лет спустя довел их количество
аж до 35. В память об неординарном вычислителе современники
еще долгое время называли число π Лудольфовым числом!
Ну что ж, теперь мы готовы подступиться к самой серьезной
нешкольной части этого ролика без всякой цензуры!
Дело в том, что в эру математического анализа математика сильно
продвинулась вперед, и уже сейчас при наличии
карандаша с бумагой, пожалуй, стоило бы иначе подступиться
к числу π. [Давайте все-таки поймем,
[Давайте все-таки поймем,
как его вычислять. Издалека зайдем. Есть такая функция
— арктангенс. Чем она хороша эта функция арктангенс?
Ну, например, тем, что tg(45°)=1. А 45° — это π/4. То есть tg(π/4)=1,
значит, arctg(1)= π/4. Так, а чем на поможет? Причем тут арктангенс?
Ну хорошо равен, да? А вот причем! Есть такая формула
Тейлора, которая написана во всех технических книгах
по математике да и в высшей математике тоже она есть.
Как разложить функцию в рад, беря ее производные
и манипулируя факториалами в знаменателях. В общем,
с помощью формулы для производной для арктангенса, которую
вы посмотрите в справочнике… [WM: мы уже выводили ее как-то…]
— О-о-о! — [точнее для экспоненты, но, думаю, ребята разберутся]
— Ну это круто, тогда все разберутся — [Поехали,
да, сразу] — да, сразу-сразу! x-x³/3+x⁵/5-x⁷/7+x⁹/9 и
так далее — закономерность уже ясна! Вот он арктангенс,
как он выглядит. И теперь, подставляя x=1, мы получаем
И теперь, подставляя x=1, мы получаем
π/4. Иными словами π=4(1-1/3+1/5-1/7+1/9-…). Но это не очень хорошо,
друзья мои, на самом деле — это фиговенько! Потом
что если ставите себе цель вычислить, например, до
9 знаков. Сколько раз придется это вычислять? Нужно, чтобы…
Это знакопеременный ряд, поэтому ответ очень простой:
тогда, когда типичный член станет меньше 1/1000000000. Ну,
блин, миллиард! Ну пополам, ну немножко легче: 500 миллионов,
да? Ну, блин, ну это не годится нам, правда? Нет! Так нельзя,
так нельзя! Поэтому пришел Леонард Эйлер и сказал:
смотрите сюда все, сынки! — сказал Леонард Эйлер!
[WM: у нас такого в сценарии не было, Алексей, он точно
так сказал?]. Ну он всем будущим — да, конечно — самый
великий математик 18-го века, и он, конечно, мог
нам всем так сказать! [WM: хорошо, ладно] И говорит:
смотрите, как это делается у нас, у математиков! — говорит
Леонард Эйлер. Есть такая формула, которую знает
Есть такая формула, которую знает
каждый ребенок. А кто не знает, тот два получает
и розги ему всыпят дома! Если кто-то не знает такой
формулу — сразу розгами! Через попу узнает: не умеет
через голову — узнает через попу! Теперь мы применим
эту формулу к α=arctg(1/2) и β=arctg(1/3) — вот до чего догадался
Эйлер! Ну, что мы тогда имеем? Давайте посмотрим, чему
равен tg(α+ β) в этом случае. Он равен tg(arctg(1/2)): а что
такое тангенс от арктангенса? А что такое тангенс от арктангенса?
Правильно! Это само число! Плюс tg(arctg(1/3)), т.е. 1/3, делить
на один минус произведение тангенса(арктангенса) и
тангенса(арктангенса). 1/2 +1/3, как мы отлично знаем,
отличается от единицы на 1/6, да? — такая классическая
сумма: 1/2+1/3+1/6=1. Ну а внизу тоже написано 1-1/6, правда?
Значит получается 1 — о-о-о, получается 1. tg(α+ β)=1. А значит,
tg(α+ β)=1. А значит,
α+β=arctg1. Во как! То есть получается arctg1=arctg(1/2)+arctg(1/3). А вот это
уже можно подставить сюда! Получается следующая формула!
Ну и к бабке не ходи — вот это уже меньше будет, чем
миллиард (одна миллиардная), поэтому дальше можно обрубать.
Итак с точностью до одной миллиардной мы посчитали
π/4 соответственно при умножении на 4 получим точность π,
ну с точностью до 4/1000000000. Ну или, кому не нравится,
еще пару слагаемых возьмите. Вот! И сделали это через
суммирование менее, чем 50 — даже не 50, а 50/2=25 слагаемых
примерно. То есть за 25 несложных операций на вашем калькуляторе
мы получаем 9-ый знак!
Девятый знак вручную за 5 минут — это вам не хухры-мухры!
Если вдруг вы что-то не поняли в этой процедуре
— напишите в комментариях, я подскажу! Рассмотренный
знакочередующийся ряд для π/4 впервые зафиксирован
в 1673 году Лейбницем, и это частный случай ряда, известного
еще ранее, ряда Грегори, то есть такое разложение
было известно и до Тейлора.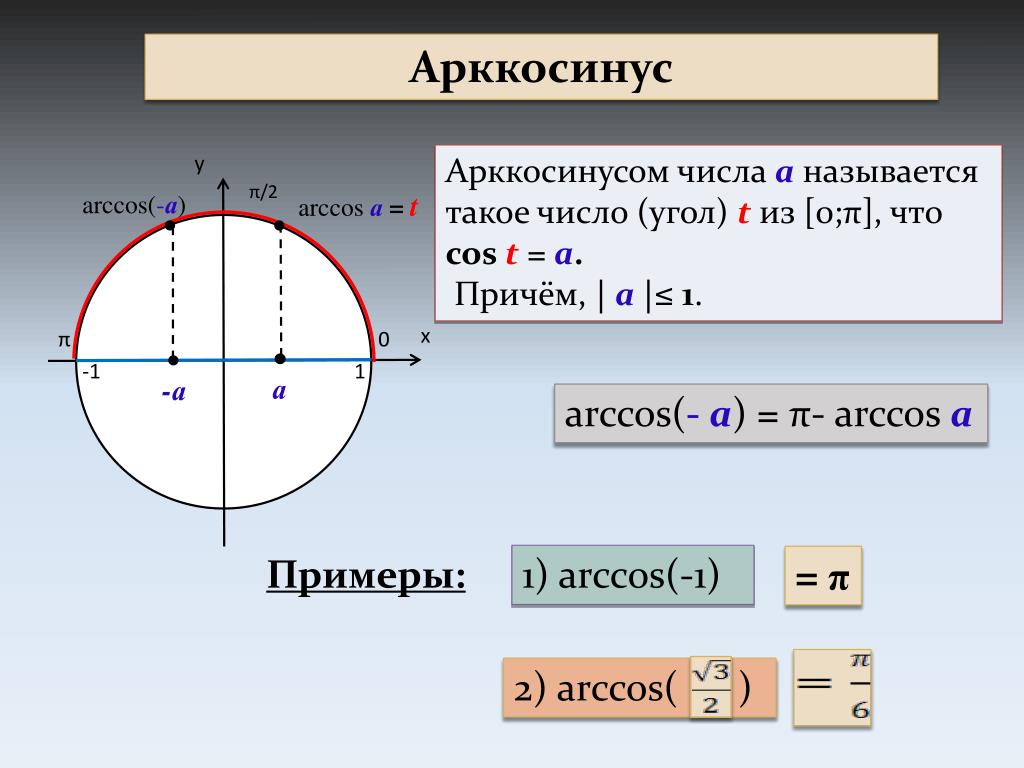 Я упомянул, что мы уже с
Я упомянул, что мы уже с
вами выводили схожее разложение для экспоненты — речь идет
о #161-ом ролике, ссылка в описании! Ну а сейчас мы
поговорим о том, когда число π имеет значение несколько
иное, нежели мы привыкли с вами наблюдать. Бывает
ли вообще такое? Бывает! И зависит это метрики. Сейчас
все объясню. Вот скажем, если вы оказались, где-нибудь
в красивом российском городе, но застройка там точь-в-точь
как в Нью-Йорке: всюду стриты да авеню, то есть квартальная
застройка. Сквозь дома вы ходить не можете, только
по дорожкам! Получается, находясь, в точке O, вы равноудалены
от точек A, B, C, и так далее до L — до любой из этой дюжины
точек предстоит топать 600 метров! Здесь вообще
расстояния между точками с координатами (x₁; y₁) и
(x₂; y₂) измеряется необычным образом: формула перед
вами! Так что в рассмотренной метрике (метрике Минковского)
диаметр такой в кавычках «окружности» с центром
O равен 1200 метров, а ее длина — смотрите сами — 4800 метров.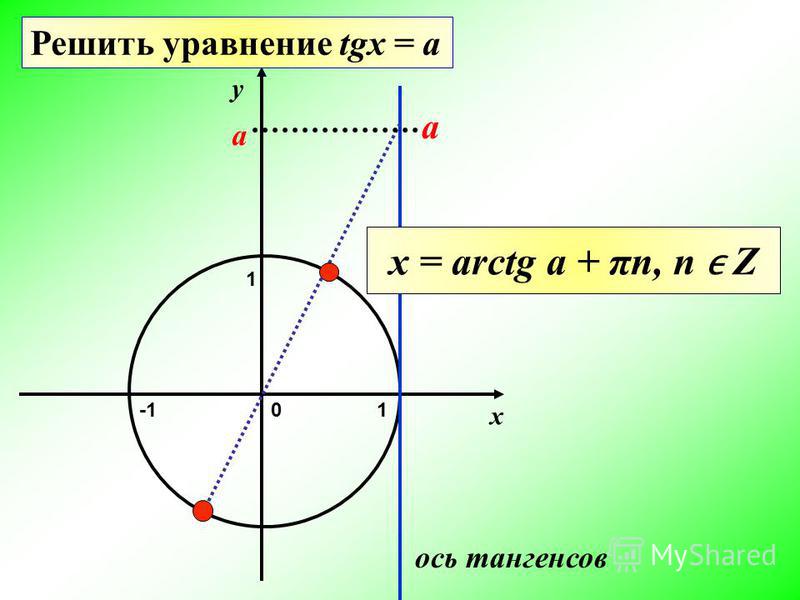
Отсюда π=4 для данной метрики. Это не софизм, не шутка
— чисто математический факт. Есть и примеры совершенного
другого рода, но об этом расскажет уже Алексей Владимирович.
Главное еще раз с нуля задаться вопросом:
[Что такое число π? π —это отношение длины окружности
к диаметры. Но здесь возникает естественно сразу же вопрос
— какой именно окружности? Если я вот такую окружность
нарисую и посчитаю отношение ее длины к диаметру и вот
такую, и вот такую! — то это будут одни и те же значения
отношения? Ну вот наше представление о плоском мире говорят,
что да — это будут одни и те же отношение. То есть
во всех трех случая получится одно и то же число. Но я
хочу вас предостеречь от того, чтобы измерять это
отношение не поверхности Земли при очень больших
окружностях. Например, если вы возьмете от Северного
Например, если вы возьмете от Северного
полюса отлетите на, ну скажем, на 100 км и совершите круговой
пролет вокруг Северного полюса на расстоянии 100
км от него и измерите, какой длины получился пролет,
поделите на 200… Вы обнаружите с некоторым удивлением,
да, то у вас получилось 3 целых 13 сотых, а не 14. Ну
я навскидку говорю, я точно не знаю, но там будет уже
смещение вниз. А вот если вы на 1000 км уудете и сделаете
то же самое, то измеренное вами число “π” уже в кавычках
(тут уже по-другому не назовешь) будет равно где-то 3,08 или
что-нибудь такое. А что если вы полетите на на 10000
км и там совершите полный оборот? Чему будет равно
π? Дикие математики: сами решите или сказать ответ?
Кликните паузу, думайте-пробуйте [не позорьте меня перед
гостем], а уж затем смотрите разбор! Поехали!. Ответ:
Ответ:
π будет равно двум! Если отступил на 10000 км от Северного
полюса — куда я попал? Если отступитьна 10000 км от Северного
полюса, то несомненно будет экватор. Теперь вы берете
этот экватор и по нему облетаете на расстоянии 10000 км от
Северного полюса. Экватор имеет длину 40000 км. 40000 км
нужно поделить на удвоенный радиус, то есть на удвоенное
расстояние 10000∙2 (км), то есть 40000 км нужно поделить
на 20000 км — вот и получается, что π=2. Так что не пытайтесь
измерять π на поверхности сферы! Ну, конечно, кто поумнее,
тот понимает, что здесь происходит. Я же не на то
делю! Это же не радиус вот этой окружности! У экватора
радиус-то другой — из центра Земли торчит. Центр Земли
является центром этой окружности, а вовсе не Северный полюс.
Но на поверхности сферы мы ничего про центр не знаем.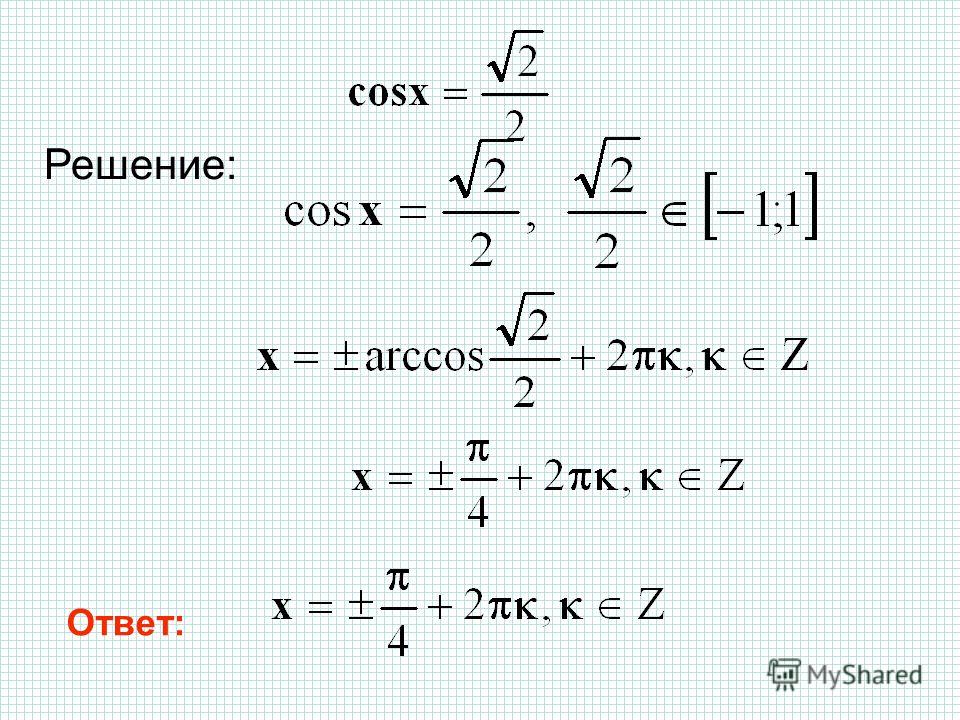
Это искривленная поверхность, и поэтому, если мы не знаем,
что за пределами этой поверхности что-то есть, что она вложена
в какое-то трехмерное пространство, если мы такие двумерные
звери, то мы и мерить будем, так сказать, мы будем без
понятия: мы будем считать, что это центр окружности,
и мерить радиус — получать совершенно другие значения
π. Итак, свойство того, что для всех окружностей отношение
длины к диаметру одно и то же — это фундаментальное
свойство нашего плоского мира, вот и все!
Один момент только! Друзья. Хотелось бы еще несколько
слов сказать об одной известной открытой проблеме. Но для
начала определение. Математики говорят, что иррациональное
число является нормальным, если в его десятичной записи
цифры 0, 1, 2, 3, …, 9 встречаются с одинаковой частотой.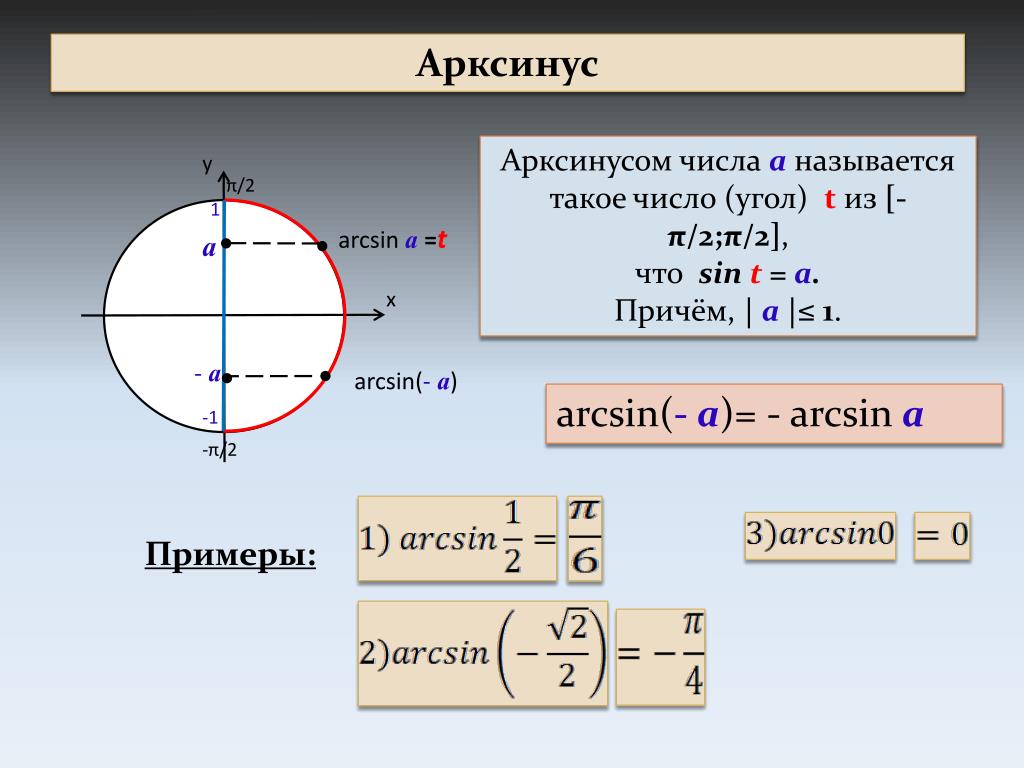
Скажем, если в силу специфики математических увлечений
вас, вопрошают: ты нормальный вообще? Просто рассмотрите
внимательно свою десятичную запись, и все станет понятно.
Ладно, ближе к делу! Уже давно доказано, что π иррационально,
трансцендентно, но до сих пор не ясно, является ли
оно нормальным: с этим все сложно. Давайте осознаем,
что же означает эта «нормальность» по факту. Это означает,
что любая последовательность цифр, заданная наперед,
содержится в числе. Я этой нормальности несколько
побаиваюсь, так что давайте проверим, встречается ли,
например, дата рождения Алексея Савватеева в шестизначной
формате в числе π? Глобальная сеть подсказывает вот такую
дату, это верно? [Ну да, верно: я родился
13 декабря 1973 года. Или просто 73-го, чтобы взять 6 цифры:
131273. Ну вот интересно, встречается ли эта последовательность
Ну вот интересно, встречается ли эта последовательность
в числе π или нет?] Ну, сейчас увидим! 131273 впервые
встречается на 1397899-ом знаке числа π. Впечатляет! Ссылочку
на этюд оставлю в описании, экспериментируйте и докладывайте
Обратные тригонометрические функции — презентация онлайн
1.Обратные тригонометрические функции.
В этом пункте мы хотели бы рассмотреть несколько задач, связанных с вычислением значений выражений,
содержащих обратные тригонометрические функции.
ЗАДАЧА 1.
Вычислите: arctg 1 + arctg 2 + arctg 3.
Решение. Стоит только нарисовать клеточный фон (рис. 1), как задание выполняется практически устно.
arctg 3 = ВАМ, arctg 2 = CAN , arctg 1 = BAC ( BAC — острый угол прямоугольного равнобедренного треугольника AВС
Ответ:
.
ЗАДАЧА 2.
Вычислите: arctg
2
arcctg 5
3
Решение. Поскольку arctg
2
BAD, а угол ВАС
= CAD (рис. 2), arcctg 5 =
3
равнобедренном
треугольнике АВС, то arctg
2
arcctg 5
3
4
Ответ:
4
—
острый
в
прямоугольном
ЗАДАЧА 3.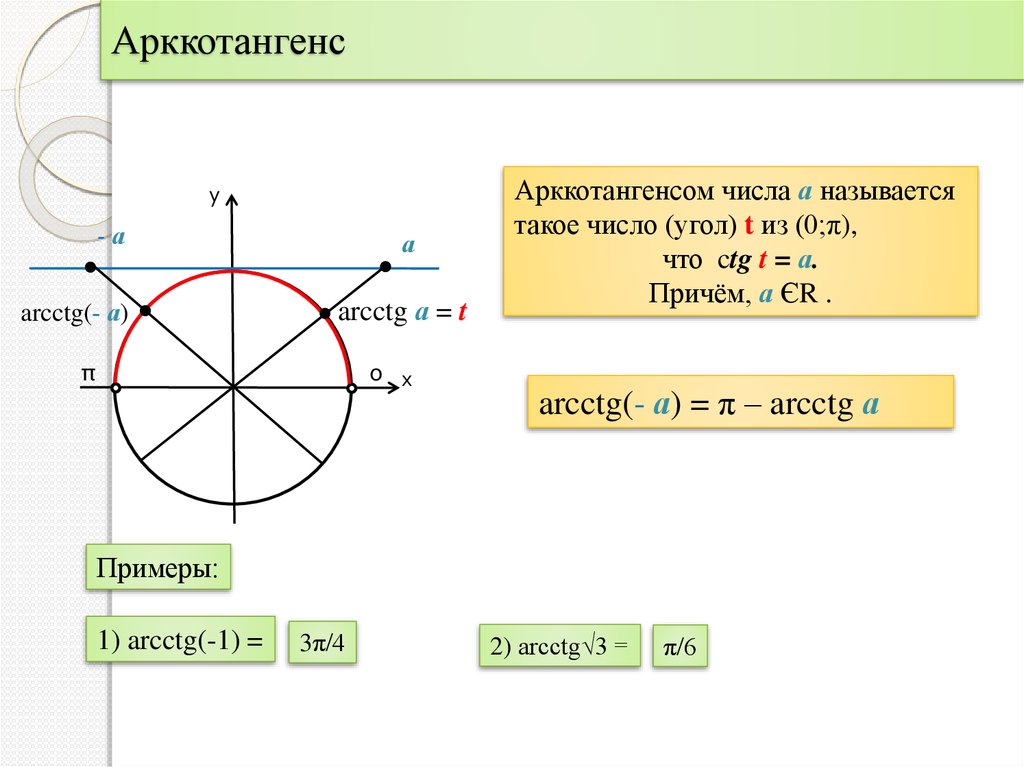
Вычислите: ctg ( 1 arccos 5 )
2
13
Решение. Если использовать понятия косинуса и котангенса острого угла прямоугольного треугольника, теорему Пифагора и свойство
биссектрисы треугольника, то задача решается почти мгновенно.
На рис. 3 изображен треугольник АВС,, в котором ACB = 90°, ВС = 5, АВ = 13 и ВМ — биссектриса угла АВС. Следовательно,
2
МС = 5х, АМ= 13х и АС= 12, отсюдаx . Тогда
3
40
Вычислите sin( 2 arccos )
41
ЗАДАЧА 4.
Решение.
Рассмотрим равнобедренный треугольник АBС, где АB=BС=41, ВМ АС, ВМ=40,CN AB (рис.4). Отрезок AM согласно теореме
Пифагора имеет длину, равную 9.
Видно, что sin( 2 arccos
CN
AC BM 720
.
AB
41
40 CN
)
. Воспользовавшись подобием прямоугольных треугольников ANC и AMB, найдем
41 BC
2. Алгебраические выражения.
Часто в алгебре встречаются задания, в которых по заданным условиям на переменные, необходимо
найти значение некоторого выражения, содержащего их.
ЗАДАЧА 5.
Из условий
выражения
x2 y2 9
x y y z.
,
y 2 z 2 16 и y 2 x z
для положительных х, у и z, не вычисляя
их значений, указать значение
Решение. Привычное задание решить систему уравнений
у учащихся затруднений не вызывает. Однако в данном случае
нужно, не решая систему, ответить на вопрос, чему равно значение выражения ху + yz. По теореме, обратной теореме Пифагора,
числа х, у и z являются соответственно длинами катетов и гипотенузы треугольника ABD с прямым углом D. А, рассмотрев второе
уравнение системы, можно сделать вывод, что у, z и 4 также есть соответственно длины катетов и гипотенузы треугольника BCD
с прямым углом D (рис. 6).
Третье уравнение системы разрешает утверждать, что число у есть среднее пропорциональное чисел х и z, и по теореме,
обратной теореме о пропорциональных отрезках в прямоугольном треугольнике, угол АВС — прямой.
Теперь рассмотрим выражение ху + yz.
xy yz ( x z ) y 2S ABC 3 4 12
Примечание. Для данной системы уравнений задания могут быть и другие. Например, найти значение выражения х + у + z или
Для данной системы уравнений задания могут быть и другие. Например, найти значение выражения х + у + z или
в каком отношении находятся числа х и у; z и у; х + z и у.
Ответ: 12
4. Задача 6.
Для положительных х, у и z из условий x 2 xyвычислите значение выражения ху + уz + zx.
y2
z2
2
2
2
169, y z 50, x xz
144, не находя значения х, у и z,
2
2
Решение.
Запишем три условия задачи в виде системы уравнений
x z
По теореме, обратной теореме, Пифагора, числа,
и 5 являются длинами соответственно
катетов и гипотенузы
2 2
треугольника АОС с прямым углом АОС.
y.
Числа х,
и 13 есть длины сторон треугольника АОВ с углом АОВ, равным 135°. Этот вывод можно сделать, используя
2
z
теорему, обратную теореме косинусов. Аналогично, x, и 12 есть длины сторон треугольника ВОС с углом ВОС, равным 135°.
2
Поскольку 52 + 122 = 132, то в треугольнике
ACB = 90°. Теперь найдем площади
На рис.
 8 изображены эти треугольники.
8 изображены эти треугольники.АВС
треугольников АОВ, АОС, ВОС, АВС.
Видно, что значение выражения ху + yz +zx равно учетверенной площади треугольника ABC. Итак, xy+yz+zx =120
Ответ:120
ЗАДАЧА 7.
Для положительных х, у и z, не вычисляя их значения из системы уравнений
определите величину ху + 2уz + Зxz.
Рассуждая так же, как и в задаче 8, получаем (рис. 9):
Так как площадь треугольника AВС равна 6, то
xy 2 yz 3 xz 24 3.
Ответ:
24 3
3. Системы уравнений.
Решению систем уравнений в алгебре отводится достаточно большое внимание. Они встречаются и в
вариантах ЕГЭ. Поэтому, тем более, интересен такой нестандартный подход к решению некоторых систем
уравнений, рассмотренных в этом пункте.
ЗАДАЧА 8.
Имеет ли система уравнений
решения для х > 0, у > 0 и z> 0?
Допустим, что есть такая тройка положительных чисел х, у и z, удовлетворяющая каждому уравнению данной системы.
Тогда возможна ее геометрическая интерпретация, как в задаче 8 (рис.
 10).
10).Но такого треугольника АВС не может быть, так как не выполняется неравенство треугольника. Значит, система не имеет решений.
Примечание. Для положительных x,y и z данная система имеет решение, если в правой части третьего уравнения поставить число
из промежутка (1; 25).
Ответ: нет решений.
рис.10
ЗАДАЧА 9.
Решите систему уравнений
Решение. Нетрудно убедиться, что х и у положительны. Поскольку
y 2 ( x 2 y 2 ) 2 x 2 , то числа у,
x 2 y 2 и х являются длинами
соответственно катетов и гипотенузы треугольника АВС с прямым углом АСВ (рис. 11).
Площадь этого треугольника 24 кв. ед., а его периметр 24 ед. Поэтому радиус окружности, вписанной в треугольник АВС, равен 2.
Так как длина гипотенузы АВ равна сумме длин катетов АС и ВС без удвоенной длины радиуса вписанной в треугольник окружности,
то
Из второго уравнения системы получаем х = 10. Значит, у = 6 или у = 8.
Ответ: (10; 6), (10; 8).
ЗАДАЧА 10.
Решите систему уравнений
Решение.

Первое уравнение системы задает плоскость, второе — сферу. Если их изобразить, то очевидно, что 0<х<1, 0 < у < 1, 0<z<1.
Согласно первому уравнениюz 3 ( x y ). z
1
3
Тогда второе уравнение принимает вид
(*)
Преобразовав его, получаем квадратное уравнение относительно х:
y
3 -1)2. Следовательно, -(у3 -1)2 0. Этонеравенство выполняется при
Дискриминант этого уравнения равен — (у
1
3
1
у
Уравнение (*) можно было преобразовать в квадратное относительно у с решением
3
1
Значение z
находится из первого уравнения.
3
Примечание. Задачу можно переформулировать, например, так: «Определите вид треугольника, периметр которого равен
а сумма квадратов длин его сторон равна 1».
3
,
ЗАДАЧА 11.
Решите систему уравнений
Решение.
Уравнение x+y+z=3 — есть уравнение плоскости (рис. 12), пересекающей оси прямоугольной декартовой системы
координат в , А(3;0;0), B(0;3;0), С(0; 0; 3).

Уравнение x 2
y2 z2 3
3
есть уравнение сферы с центром в точке O(0; 0; 0) и радиусом
равным
R,
1
Вычислим расстояние от точки О до плоскости AВС. Для этого рассмотрим тетраэдр ОАВС. Объем V тетраэдра равенS ABC H
3
где H=OD (D — центр треугольника АВС).
Этот объем можно найти иначе:
3H 3
и 9 , получаем H= 3 . Это означает, что расстояние от точки О до плоскости АВС равно радиусу сферы, а значит,
2
2
плоскость касается сферы. Следовательно, точка касания является центром треугольника АВС. Поскольку D(x; у; z) — центр
Приравняв
равностороннего треугольника АВС, где А(3; 0; 0), В(0; 3; 0), С(0;0;3), то x=y=z.
Заменив у и z на х в уравнениях данной системы, получаем x=1.
Ответ: (1; 1; 1).
ЗАДАЧА 12.
Решите систему уравнений
Решение.
Рассмотрим слагаемые левой части второго уравнения:
x 2 y 2 4 x 2 y 5 ( x 2) 2 ( y 1) 2
Пусть это расстояние между точками М(х; у) и A(2;-1).
Допустим, что это расстояние между точками М (х;у} и В(10; 5).
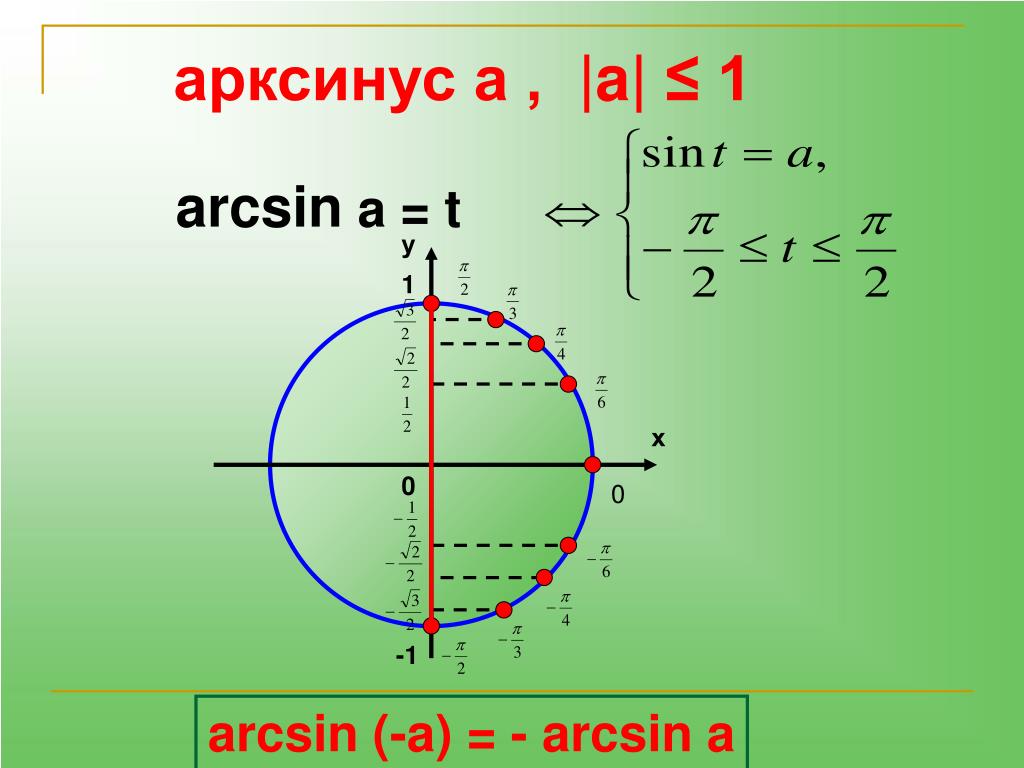
Найдем расстояние между точками А(2; -1) и В(10;5):
AB (10 2) 2 (5 1) 2 10
Итак, второе уравнение системы можно интерпретировать как равенство AM + ВМ = АВ. Это дает нам право утверждать, что
точка М принадлежит отрезку АВ, т.е. 2 ≤ х ≤ 10 и -1 ≤ у ≤ 5
Составим уравнение прямой АВ, проходящей через точки А(2; -1) и B(10; 5).
1 k 2 b и 5 k 10 b. Отсюда k 3 ; b 5 , т.е. y 3 x 5 , или Зх — 4у = 10.
Запишем новую
4
2
4
2
систему:
Значит, х = 6 и у = 2.
Ответ: (6; 2).
4. Аналитический способ решения.
Рассмотрим аналитический способ решения некоторых задач, рассмотренных выше, чтобы была возможность
убедиться в том, что геометрический подход дает более быстрое, а главное, красивое решение этих задач.
ЗАДАЧА 1.
Рассмотрим аналитический способ решения.
Решение.
3
.
Обозначим: arctg1, arctg 2, arctg 3, где
2
2
tg tg
2 3
1
tg tg ( )
1 tg ( )
1 tg tg
1 2 3 1 1 0
Найдем tg ( )
tg tg
2 3
1 tg tg ( ) 1 tg ( )
1 1
1
1
1 tg tg
1 2 3
1
3
2 2
Таким образом, tg ( ) 0 k , учитывая условие, что ( ; ), получим, что k=1 и ,
т.
 е. arctg1 arctg 2 arctg 3 .
е. arctg1 arctg 2 arctg 3 .Ответ:
ЗАДАЧА 2.
Решим систему аналитически:
Решение:
Обозначим уравнение3 x 4 y 26 — (1),
уравнение x 2 y 2 4 x 2 y 5 x 2 y 2 20 x 10 y 125 10 — (2).
Заметим, что x 2 y 2 4 x 2 y 5 ( x 2) 2 ( y 1) 2 , а
x 2 y 2 20 x 10 y 125 ( x 10) 2 ( y 5) 2 .
Сделаем замену x 2 a, y 1 b, тогда уравнение (2) системы запишется в виде:
a 2 b 2 (a 8) 2 (b 6) 2 10, a 2 b 2 10 (a 8) 2 (b 6) 2 .
Возведем обе части уравнения в квадрат, получим:
a 2 b 2 100 (a 8) 2 (b 6) 2 20 (a 8) 2 (b 6) 2 ,
20 (a 8) 2 (b 6) 2 100 (a 8) 2 (b 6) 2 a 2 b 2
20 (a 8) 2 (b 6) 2 200 16a 12b
5 (a 8) 2 (b 6) 2 50 4a 3b
25(( a 8) 2 (b 6) 2 ) 2500 16a 2 9b 2 400a 300b 24ab
25a 2 400a 1600 25b 2 300b 900 2500 16a 2 9b 2 400a 300b 24ab
(3a 4b) 2 0
3a 4b
3( x 2) 4( y 1)
Сделаем обратную замену:
3 x 4 y 10
Получим систему:
3x 4 y 26 x 6
,
3x 4 y 10 y 2
Поскольку мы не следили за равносильностью переходов, сделаем проверку:
(1) —
3 6 4 2 26
18 8 26
Ответ: (6;2).
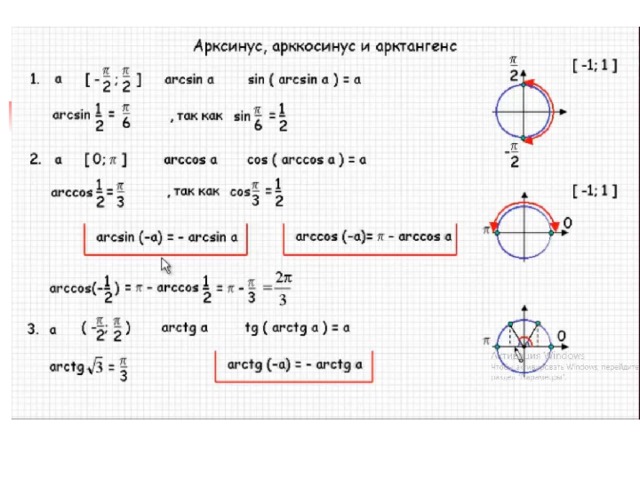
(2)
—
36 4 24 4 5 36 4 120 20 125 10
5 5 10
Arctg 2 равен чему. Арксинус, арккосинус
Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, и пары функций одинаково важны для работы с тригонометрическими выражениями.
Рассмотрим рисунок единичной окружности, на котором графически отображаются значения тригонометрических функций.
Если рассчитать дуги OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Приведенные ниже формулы отражают связь между основными тригонометрическими функциями и соответствующими им дугами.
Чтобы лучше понять свойства арксинуса, необходимо рассмотреть его функции. График имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
Если сравнить графики sin и arc sin , две тригонометрические функции могут найти общие закономерности.
Арккосинус
Арккосинус числа а есть значение угла α, косинус которого равен а.
Кривая y = arcos x отражает график arcsin x с той лишь разницей, что она проходит через точку π/2 на оси OY.
Рассмотрим функцию арккосинуса более подробно:
- Функция определена на отрезке [-1; один].
- ОДЗ для arccos — .
- График полностью расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
- Y = 0 для x = 1.
- Кривая уменьшается по всей длине. Некоторые свойства арккосинуса такие же, как у функции косинуса.
Некоторые свойства арккосинуса такие же, как у функции косинуса.
Возможно, такое «детальное» изучение «арок» покажется школьникам лишним. Однако в противном случае некоторые элементарные типовые задания ЕГЭ могут завести учащихся в тупик.
Упражнение 1. Задайте функции, показанные на рисунке.
Ответ: рис.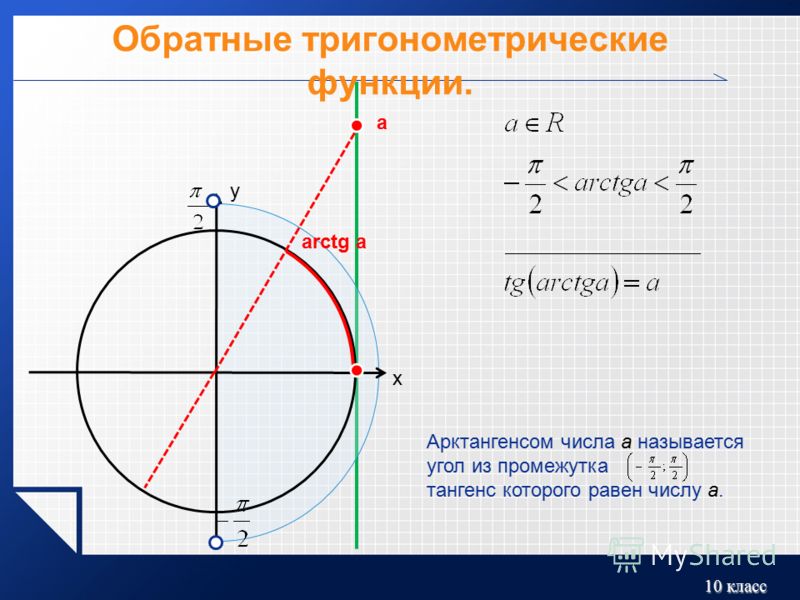 1 — 4, рис. 2 — 1.
1 — 4, рис. 2 — 1.
В этом примере акцент делается на мелочи. Обычно студенты очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать форму кривой, если ее всегда можно построить по рассчитанным точкам. Не забывайте, что в тестовых условиях время, затраченное на рисование простой задачи, потребуется для решения более сложных задач.
Арктангенс
Arctg число а есть такое значение угла α, что его тангенс равен а.
Если рассматривать график арктангенса, то можно выделить следующие свойства:
- График бесконечен и определен на интервале (- ∞; + ∞).
- Арктангенс — нечетная функция, поэтому arctan (- x) = — arctan x.
- Y = 0 для x = 0.
- Кривая увеличивается по всей области определения.
Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арктангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен a.
Свойства функции арккотангенса:
- Интервал определения функции равен бесконечности.
- Диапазон допустимых значений — интервал (0; π).
- F(x) не является ни четным, ни нечетным.
- На всем протяжении график функции уменьшается.
Сравнить ctg x и arctg x очень просто, нужно всего лишь нарисовать два рисунка и описать поведение кривых.
Задание 2. Соотнесите график и вид функции.
Графики показывают, что обе функции возрастают. Следовательно, оба рисунка отображают некоторую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
Ответ: рис. 1 — 1, рис. 2-4.
Тригонометрические тождества arcsin, arcos, arctg и arcctg
Ранее мы уже определили связь между арками и основные функции тригонометрии. Эту зависимость можно выразить рядом формул, позволяющих выразить, например, синус аргумента через его арксинус, арккосинус или наоборот. Знание таких тождеств может оказаться полезным при решении конкретных примеров.
Знание таких тождеств может оказаться полезным при решении конкретных примеров.
Существуют также соотношения для arctg и arcctg:
Другая полезная пара формул устанавливает значение суммы значений arcsin и arcos и arcctg и arcctg одного и того же угла.
Примеры решения задач
Задачи тригонометрии условно можно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить построение заданной функции, найти ее область определения или ОДЗ и выполнить аналитические преобразования для решения примера .
При решении первого типа задач необходимо придерживаться следующего плана действий:
При работе с графиками функций главное — знание их свойств и внешнего вида кривой. Таблицы тождеств нужны для решения тригонометрических уравнений и неравенств. Чем больше формул запоминает ученик, тем легче ему найти ответ на задание.
Допустим на экзамене необходимо найти ответ на уравнение вида:
Если правильно преобразовать выражение и привести его к нужному виду, то решить его очень просто и быстро. Во-первых, давайте переместим arcsin x в правую часть уравнения.
Во-первых, давайте переместим arcsin x в правую часть уравнения.
Если вспомнить формулу arcsin(sinα) = α , то поиск ответов можно свести к решению системы двух уравнений:
Ограничение на модель x возникло, опять же из свойств arcsin: ODZ for x [-1; один]. При a ≠ 0 часть системы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При а = 0 х будет равен 1,
Примечание 1
Таблица Брадиса — это таблица, позволяющая с высокой точностью вычислять значения арктангенсов и других тригонометрических функций.
Чтобы использовать таблицу Брейдиса, найдите угол в градусах в крайнем левом столбце для синуса (для косинуса в соответствующем столбце справа), а затем в верхней строке для минуты. На пересечении строки со столбцом находится искомое значение.
Если нужно найти значения обратных тригонометрических функций — таблица Брадиса используется наоборот. Например, ищут числовое значение в таблице арктангенсов и тангенсов и определяют по нему, в какой строке градусов и столбце минут оно находится.
Таким образом, Таблицу Брадиса можно использовать не только для поиска обычных тригонометрических функций, но и как таблицу арккосинуса и арксинуса, арктангенса и арктангенса.
В начале этой статьи находится таблица значений arcsin и arccos, ближе к концу — таблица значений arctg и arcctg.
Таблица Брадиса: таблица арксинуса, арккосинуса, косинуса и синуса
Рис. 1. Таблица Брадиса представляет собой таблицу значений арксинуса и арккосинуса. Author24 — онлайн обмен студенческими работами
Таблица значений арктангенсов и арктангенсов, тангенсов и котангенсов
Рисунок 4. Таблица Брадиса: таблица значений арктангенсов arctg и арктангенсов arctg. Author24 — онлайн-обмен студенческими работами
Определение и обозначения
Арксинус (y = arcsin x) — функция, обратная синусоиду (x = siny -1 ≤ x ≤ 1 и множество значений -π /2 ≤ у ≤ π/2.
sin(arcsin x) = x ;
угловой синус (sin x) = x .
Арксинус иногда называют:
.
График функции арксинуса
График функции y = arcsin x
График арксинуса получается из графика синуса путем перестановки осей абсцисс и ординат. Для устранения неоднозначности диапазон значений ограничен интервалом, на котором функция монотонна. Это определение называется главным значением арксинуса.
Арккосинус, arccos
Определение и обозначения
Арккосинус (y = arccos x) является обратной величиной косинуса (x = cos y). Он имеет область действия -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
cos(arccos x) = x ;
arccos(cos x) = x .
Арккосинус иногда называют:
.
График функции арккосинуса
График функции y = arccos x
График арккосинуса получается из графика косинуса путем перестановки осей абсцисс и ординат. Для устранения неоднозначности диапазон значений ограничен интервалом, на котором функция монотонна. Это определение называется главным значением арккосинуса.
Это определение называется главным значением арккосинуса.
Четность
Функция арксинуса нечетная:
arcsin(-x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = — arcsin x
Функция арккосинуса не четная и не нечетная:
arccos(-x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π — arccos x ≠ ± arccos x
Свойства — экстремум, увеличение, уменьшение непрерывны в своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.
| y= arcsin x | y= arccos x | |
| Объем и преемственность | — 1 ≤ x ≤ 1 | — 1 ≤ х ≤ 1 |
| Диапазон значений | ||
| По возрастанию, по убыванию | монотонно возрастает | монотонно убывает |
| Максимум | ||
| Минимум | ||
| Нули, у= 0 | х= 0 | х= 1 |
| Точки пересечения с осью Y, x = 0 | у= 0 | у = π/ 2 |
Таблица арксинусов и арккосинусов
В этой таблице приведены значения арксинусов и арккосинусов в градусах и радианах для некоторых значений аргумента.
| x | угловой синус x | арккос х | ||
| град. | рад. | град. | рад. | |
| — 1 | — 90° | — | 180° | π |
| — | — 60° | — | 150° | |
| — | — 45° | — | 135° | |
| — | — 30° | — | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
≈ 0,7071067811865476
≈ 0,8660254037844386
Формулы
См.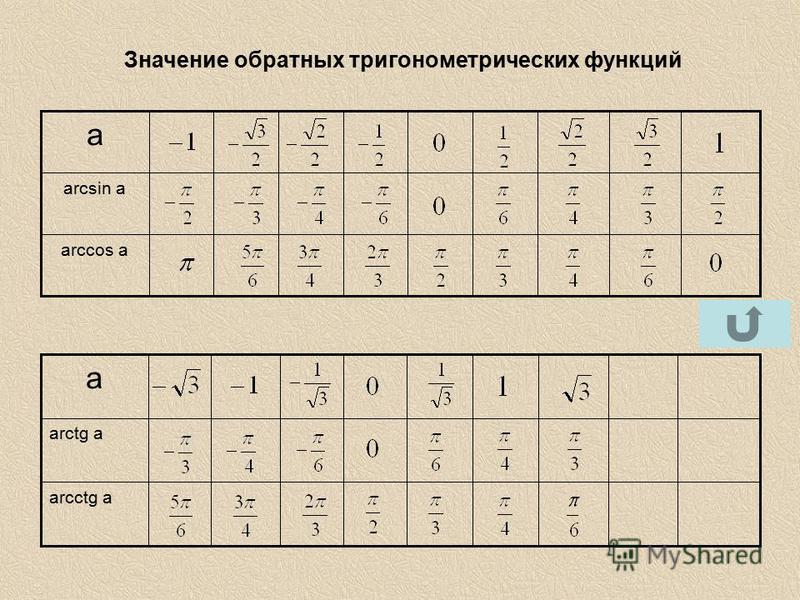 также: Вывод формул для обратных тригонометрических функций
также: Вывод формул для обратных тригонометрических функций
Сумма и разности формулы
AT OR
AT и
AT и
AT OR
AT и
AT и
AT
9000 2
на
9000 2
на
9000 2
на
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2 9000 2
. логарифм, комплексные числа
См. также: Вывод формул
Выражения через гиперболические функции
Производные
;
.
См. Вычисление производных арксинуса и арккосинуса > > >
Производные высших порядков :
,
где – многочлен степени . Определяется по формулам:
;
;
.
См. Вывод производных высших порядков от арксинуса и арккосинуса > > >
Интегралы
Сделаем замену x = sin t. Интегрируем по частям, учитывая, что -π/ 2 ≤ t ≤ π/2,
cos т ≥ 0:
Интегрируем по частям, учитывая, что -π/ 2 ≤ t ≤ π/2,
cos т ≥ 0:
.
Выразим арккосинус через арксинус:
.
Расширение серии
Для |x|;
.
Обратные функции
Инверсиями арксинуса и арккосинуса являются синус и косинус соответственно.
Следующие формулы действительны во всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .
Следующие формулы действительны только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x at
arccos(cos x) = x at .
Каталожные номера:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и студентов вузов, Лань, 2009.
См. также:
Что такое арксинус, арккосинус? Что такое арктангенс, арктангенс?
Внимание!
Есть еще
материал в Спецразделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень…»)
К понятиям Арксинус, арккосинус, арктангенс, арккотангенс студенческое население насторожено. Он не понимает этих терминов и, следовательно, не доверяет этому славному семейству.) А зря. Это очень простые понятия. Которые, кстати, сильно облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Он не понимает этих терминов и, следовательно, не доверяет этому славному семейству.) А зря. Это очень простые понятия. Которые, кстати, сильно облегчают жизнь знающему человеку при решении тригонометрических уравнений!
Запутались в простоте? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.
Конечно, для понимания неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых ракурсов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.
Итак, мы удивлены, но помните: арксинус, арккосинус, арктангенс и арктангенс — это всего лишь некоторые углы. Ни больше, ни меньше. Есть угол, скажем, 30°. И есть угол угловой синус0.4. или arctg(-1,3). Углы бывают всякие.) Просто писать углы можно по разному. Вы можете написать угол в градусах или радианах. А можно — через его синус, косинус, тангенс и котангенс…
Что означает выражение
arcsin 0.4?
Это угол, синус которого равен 0,4 ! Да Да.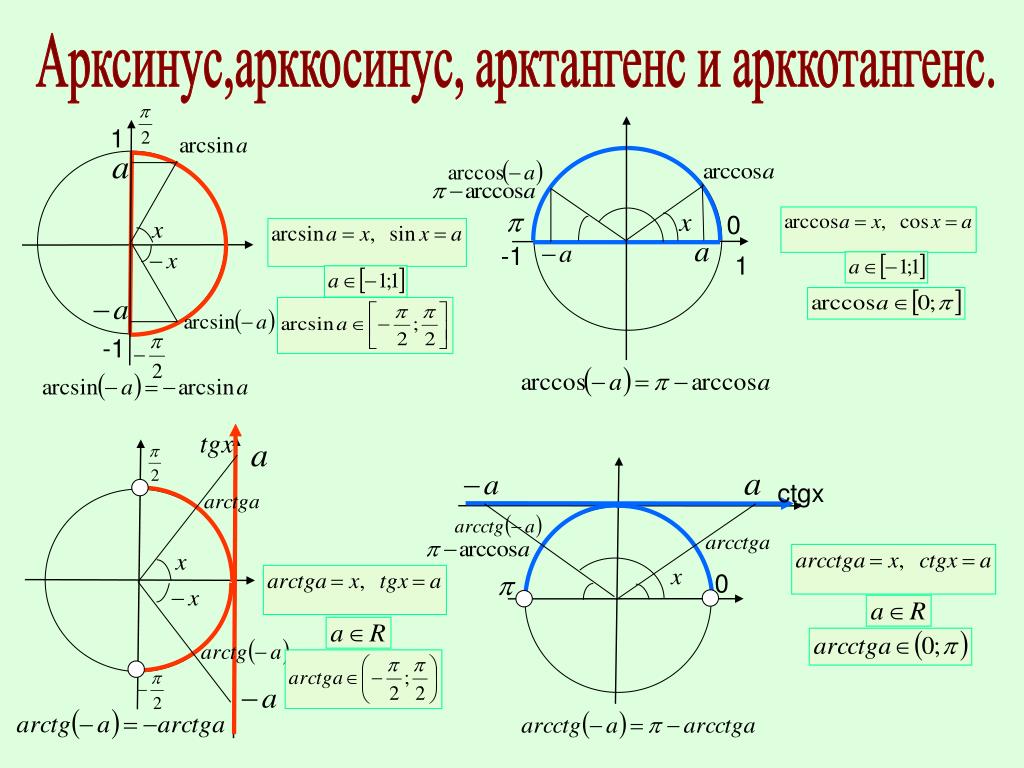 В этом смысл арксинуса. Специально повторяю: arcsin 0,4 — это угол, синус которого равен 0,4.
В этом смысл арксинуса. Специально повторяю: arcsin 0,4 — это угол, синус которого равен 0,4.
И все.
Чтобы надолго удержать эту простую мысль в голове, я даже приведу расшифровку этого страшного термина — арксинуса:
арк sin 0,4
впрыск, у которого синус равен 0.4
Как написано, так и слышно.) Почти. Приставка дуга означает дуга (слово дуга знаете?), потому что древние люди использовали дуги вместо углов, но сути дела это не меняет. Запомните эту элементарную расшифровку математического термина! Причем для арккосинуса, арктангенса и арктангенса расшифровка отличается только названием функции.
Что такое arccos 0.8?
Это угол, косинус которого равен 0,8.
Что такое арктан(-1,3) ?
Это угол, тангенс которого равен -1,3.
Что такое arcctg 12?
Это угол, котангенс которого равен 12.
Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов. ) Например, вполне солидно выглядит выражение arccos1,8. Приступим к расшифровке: arccos1,8 — это угол, косинус которого равен 1,8… Хоп-хоп!? 1,8!? Косинус не может быть больше единицы!
) Например, вполне солидно выглядит выражение arccos1,8. Приступим к расшифровке: arccos1,8 — это угол, косинус которого равен 1,8… Хоп-хоп!? 1,8!? Косинус не может быть больше единицы!
Правильно. Выражение arccos1,8 не имеет смысла. А написание такого выражения в каком-нибудь ответе сильно позабавит проверяющего.)
Элементарно, как видите.) У каждого угла свои личные синус и косинус. И почти у каждого свой тангенс и котангенс. Следовательно, зная тригонометрическую функцию, можно записать и сам угол. Для этого предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я буду называть все это семейство уменьшительно-ласкательным — арки. печатать меньше.)
Внимание! Элементарная словесная и осознанная расшифровка арок позволяет спокойно и уверенно решать самые разные задачи. А в необычных задач спасает только она.
Можно ли переключиться с арок на обычные градусы или радианы? — слышу осторожный вопрос.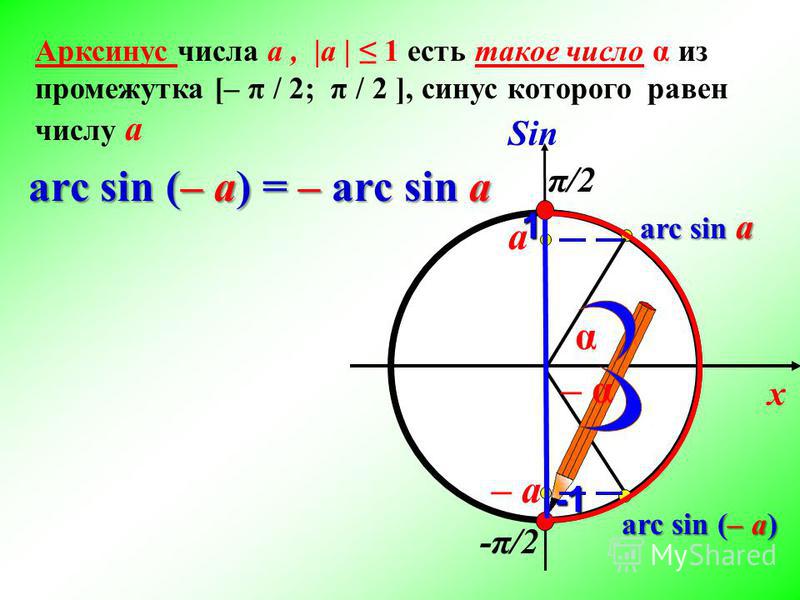 )
)
Почему бы и нет!? Без труда. Вы можете пойти туда и обратно. Более того, иногда это необходимо сделать. Арки вещь простая, но без них как-то спокойнее, правда?)
Например: что такое arcsin 0,5?
Посмотрим на расшифровку: arcsin 0.5 — это угол, синус которого равен 0.5. А теперь включите голову (или гугл)) и вспомните, у какого угла синус 0,5? Синус равен 0,5 y угол 30 градусов . Вот и все: arcsin 0,5 — это угол 30°. Можно смело писать:
arcsin 0.5 = 30°
Или, более солидно, в радианах:
Все, про арксинус можно забыть и работать дальше с обычными градусами или радианами.
Если вы поняли что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… Тогда вы легко расправитесь, например, с таким монстром.)
Несведущий человек отшатнется в ужасе, да…) А знающий вспомни расшифровку: арксинус — это угол, синус которого… Ну и т.д. Если знающий человек знает еще и таблицу синусов.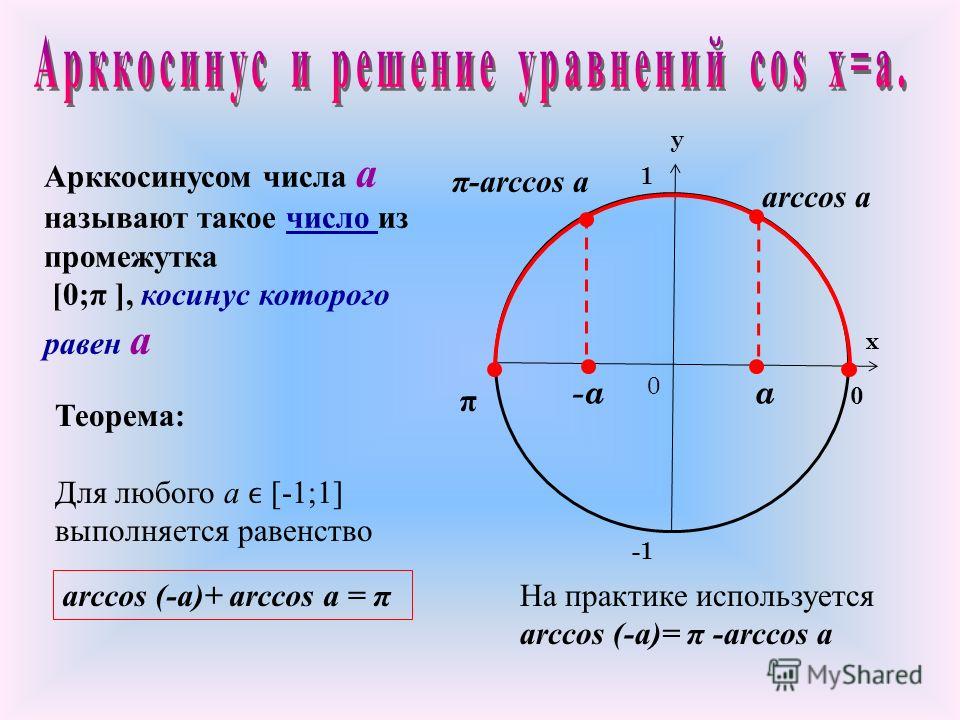 .. Таблицу косинусов. Таблица тангенсов и котангенсов, тогда вообще проблем нет!
.. Таблицу косинусов. Таблица тангенсов и котангенсов, тогда вообще проблем нет!
Достаточно учесть, что:
Расшифрую, т.е. переведу формулу словами: угол, тангенс которого равен 1 (arctg1) угол 45°. Или, что то же самое, Пи/4. Аналогично:
и все… Заменяем все арки значениями в радианах, все сокращается, осталось посчитать сколько будет 1+1. Будет 2.) Это правильный ответ.
Вот так можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арктангенсов к обычным градусам и радианам. Это значительно упрощает страшные примеры!
Часто в таких примерах внутри арок отрицательных значений. Например, arctg(-1.3) или, например, arccos(-0.8)… Это не проблема. Вот несколько простых формул для перехода от отрицательного к положительному:
Вам нужно, скажем, определить значение выражения:
Вы можете решить это, используя тригонометрический круг, но вы не хотите его рисовать. Ну ладно. Переход от отрицательных значений внутри арккосинуса к положительным по второй формуле:
Ну ладно. Переход от отрицательных значений внутри арккосинуса к положительным по второй формуле:
Внутри арккосинуса справа уже положительный смысл. Что
вы просто должны знать. Осталось вместо арккосинуса подставить радианы и вычислить ответ:
Вот и все.
Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.
Проблемы с примерами 7–9? Ну да, тут есть какая-то хитрость.)
Все эти примеры, с 1-го по 9-й, тщательно разложены по полочкам в Разделе 555. Что, как и почему. Со всеми секретными ловушками и уловками. Плюс способы кардинально упростить решение. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только в тригонометрии. Очень помогает.
Если вам нравится этот сайт…Кстати, у меня есть для вас еще парочка интересных сайтов.)
Вы можете попрактиковаться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Проще говоря, это овощи, сваренные на воде по особому рецепту. Я буду рассматривать два исходных компонента (овощной салат и вода) и готовый результат — борщ. Геометрически это можно представить в виде прямоугольника, в котором одна сторона обозначает салат, а другая — воду. Сумма этих двух сторон и будет обозначать борщ. Диагональ и площадь такого «борщевого» прямоугольника являются чисто математическими понятиями и в рецептах борщей никогда не используются.
Как с точки зрения математики салат и вода превращаются в борщ? Как сумма двух отрезков может превратиться в тригонометрию? Чтобы понять это, нам нужны линейные угловые функции.
Вы не найдете ничего о линейных угловых функциях в учебниках по математике. Но без них не может быть математики. Законы математики, как и законы природы, работают независимо от того, знаем мы об их существовании или нет.
Линейные угловые функции являются законами сложения. Посмотрите, как алгебра превращается в геометрию, а геометрия превращается в тригонометрию.
Можно ли обойтись без линейных угловых функций? Можно, потому что математики до сих пор обходятся без них. Хитрость математиков заключается в том, что они всегда говорят нам только о тех задачах, которые они сами могут решить, и никогда не рассказывают нам о тех проблемах, которые не могут решить. Видеть. Если мы знаем результат сложения и один член, мы используем вычитание, чтобы найти другой член. Все. Других проблем мы не знаем и не в состоянии их решить. Что делать, если мы знаем только результат сложения и не знаем обоих членов? В этом случае результат сложения необходимо разложить на два слагаемых с помощью линейных угловых функций. Далее мы сами выбираем, каким может быть одно слагаемое, а линейные угловые функции показывают, каким должно быть второе слагаемое, чтобы результат сложения был именно таким, как нам нужно.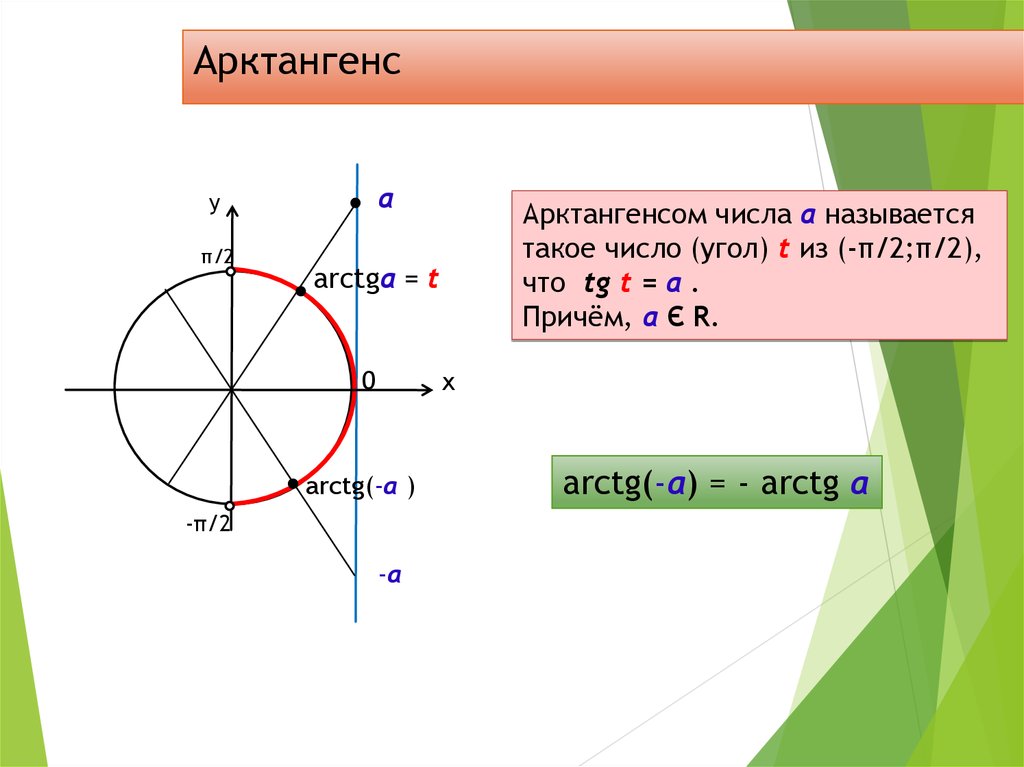 Таких пар терминов может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы; вычитания нам достаточно. Но в научных исследованиях законов природы разложение суммы на термины может быть очень полезным.
Таких пар терминов может быть бесконечное множество. В повседневной жизни мы прекрасно обходимся без разложения суммы; вычитания нам достаточно. Но в научных исследованиях законов природы разложение суммы на термины может быть очень полезным.
Другой закон сложения, о котором математики не любят говорить (еще один из их приемов), требует, чтобы слагаемые имели одну и ту же единицу измерения. Для салата, воды и борща это могут быть единицы веса, объема, стоимости или единицы измерения.
На рисунке показаны два уровня различий по математике. Первый уровень — это различия в области чисел, которые обозначаются a , b , c . Этим занимаются математики. Второй уровень – это различия площади единиц измерения, которые показаны в квадратных скобках и обозначены буквой 9.0056 У . Этим занимаются физики. Мы можем понять третий уровень — различия в сфере действия описываемых объектов. Разные объекты могут иметь одинаковое количество одних и тех же единиц измерения. Насколько это важно, мы можем видеть на примере борщевой тригонометрии. Если к одним и тем же обозначениям единиц измерения разных объектов добавить нижние индексы, то можно будет точно сказать, какая математическая величина описывает тот или иной объект и как она изменяется во времени или в связи с нашими действиями. буква W Воду обозначу буквой S Салат обозначу буквой B — борщ. Вот как будут выглядеть функции линейного угла для борща.
Насколько это важно, мы можем видеть на примере борщевой тригонометрии. Если к одним и тем же обозначениям единиц измерения разных объектов добавить нижние индексы, то можно будет точно сказать, какая математическая величина описывает тот или иной объект и как она изменяется во времени или в связи с нашими действиями. буква W Воду обозначу буквой S Салат обозначу буквой B — борщ. Вот как будут выглядеть функции линейного угла для борща.
Если взять часть воды и часть салата, вместе они превратятся в одну порцию борща. Вот предлагаю вам немного отдохнуть от борща и вспомнить свое далекое детство. Помните, как нас учили складывать зайчиков и уточек? Нужно было найти, сколько животных получится. Что же тогда нас учили делать? Нас учили отделять единицы от чисел и складывать числа. Да, любой номер можно добавить к любому другому номеру. Это прямой путь к аутизму современной математики — мы не понимаем чего, непонятно почему, и очень плохо понимаем, как это соотносится с реальностью, потому что из трех уровней различия математики оперируют только одним. Правильнее будет научиться переходить от одной единицы измерения к другой.
Правильнее будет научиться переходить от одной единицы измерения к другой.
И зайчиков, и уточек, и зверюшек можно посчитать штуками. Одна общая единица измерения для разных объектов позволяет складывать их вместе. Это детская версия проблемы. Давайте рассмотрим аналогичную задачу для взрослых. Что вы получите, если добавите кроликов и деньги? Здесь есть два возможных решения.
Первый вариант . Определяем рыночную стоимость зайчиков и прибавляем ее к имеющимся денежным средствам. Мы получили общую стоимость нашего богатства в денежном выражении.
Второй вариант . Вы можете добавить количество зайчиков к количеству банкнот, которые у нас есть. Получим количество движимого имущества в штуках.
Как видите, один и тот же закон сложения позволяет получить разные результаты. Все зависит от того, что именно мы хотим узнать.
Но вернемся к нашему борщу. Теперь мы можем увидеть, что будет происходить при разных значениях угла линейных функций угла.
Угол равен нулю. У нас есть салат, но нет воды. Мы не умеем варить борщ. Количество борща тоже ноль. Это вовсе не означает, что ноль борща равен нулю воды. Нулевой борщ может быть и нулевым салатом (прямой угол).
Лично для меня это главное математическое доказательство того, что . Ноль не меняет число при добавлении. Это связано с тем, что само сложение невозможно, если есть только один член, а второй член отсутствует. Вы можете относиться к этому как угодно, но помните — все математические операции с нулем были придуманы самими математиками, так что отбросьте свою логику и тупо впихивайте придуманные математиками определения: «деление на ноль невозможно», «любое число, умноженное на ноль равно нулю», «за нулевой точкой» и прочая ерунда. Достаточно один раз вспомнить, что ноль не является числом, и у вас никогда не возникнет вопроса, является ли ноль натуральным числом или нет, потому что такой вопрос вообще теряет всякий смысл: как можно считать числом то, что не является числом . Это все равно, что спрашивать, какому цвету приписать невидимый цвет. Добавление нуля к числу похоже на рисование несуществующей краской. Машут сухой кистью и говорят всем, что «нарисовали». Но я немного отвлекся.
Это все равно, что спрашивать, какому цвету приписать невидимый цвет. Добавление нуля к числу похоже на рисование несуществующей краской. Машут сухой кистью и говорят всем, что «нарисовали». Но я немного отвлекся.
Угол больше нуля, но меньше сорока пяти градусов. У нас много салата, но мало воды. В итоге получаем густой борщ.
Угол сорок пять градусов. У нас есть равное количество воды и салата. Это идеальный борщ (да простят меня повара, это просто математика).
Угол больше сорока пяти градусов, но меньше девяноста градусов. У нас много воды и мало салата. Получите жидкий борщ.
Прямой угол. У нас есть вода. От салата остаются только воспоминания, поскольку мы продолжаем измерять угол от линии, которая когда-то отмечала салат. Мы не умеем варить борщ. Количество борща равно нулю. В таком случае держитесь и пейте воду, пока есть)))
Здесь. Что-то вроде этого. Я могу рассказать здесь и другие истории, которые будут здесь более чем уместны.
У двух друзей были свои доли в общем деле.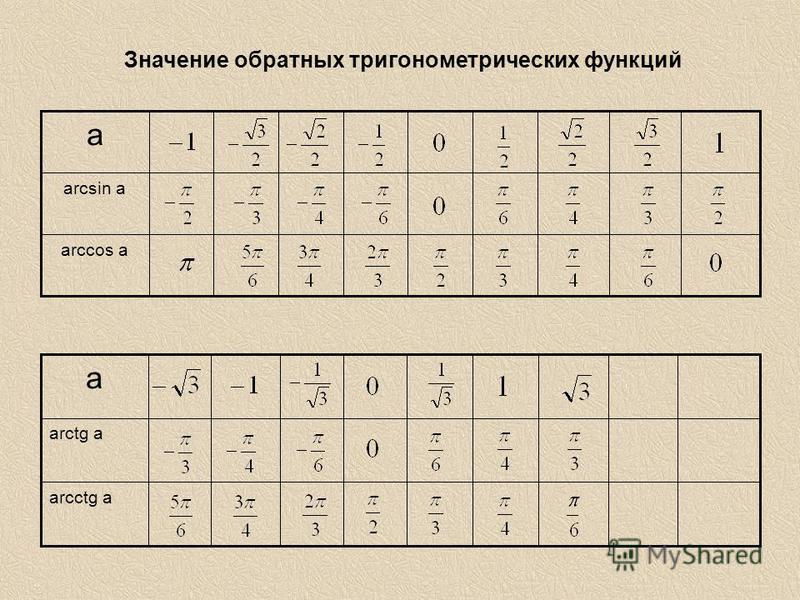 После убийства одного из них все досталось другому.
После убийства одного из них все досталось другому.
Появление математики на нашей планете.
Все эти истории рассказаны на языке математики с использованием линейных угловых функций. Как-нибудь в другой раз я покажу вам реальное место этих функций в структуре математики. А пока вернемся к тригонометрии борща и рассмотрим проекции.
26 октября 2019 г.
7 августа 2019 г.
Завершая разговор о , нам нужно рассмотреть бесконечное множество. Дал в том, что понятие «бесконечность» действует на математиков, как удав на кролика. Трепещущий ужас перед бесконечностью лишает математиков здравого смысла. Вот пример:
Первоисточник находится. Альфа обозначает действительное число. Знак равенства в вышеприведенных выражениях говорит о том, что если к бесконечности прибавить число или бесконечность, ничего не изменится, в результате получится та же бесконечность. Если взять в качестве примера бесконечное множество натуральных чисел, то рассматриваемые примеры можно представить следующим образом:
Чтобы наглядно доказать свою правоту, математики придумали множество различных методов. Лично я смотрю на все эти способы как на пляски шаманов с бубнами. В сущности, все они сводятся к тому, что либо часть комнат не занята и в них заселяются новые гости, либо часть посетителей выбрасывается в коридор, чтобы освободить место для гостей (очень по-человечески). Свой взгляд на такие решения я изложил в виде фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Перемещение бесконечного количества посетителей занимает бесконечное количество времени. После того, как мы освободили первую гостевую комнату, один из посетителей всегда будет ходить по коридору из своей комнаты в следующую до скончания века. Конечно, фактор времени можно тупо не учитывать, но это уже будет из разряда «закон для дураков не писан». Все зависит от того, что мы делаем: подгоняем реальность под математические теории или наоборот.
Лично я смотрю на все эти способы как на пляски шаманов с бубнами. В сущности, все они сводятся к тому, что либо часть комнат не занята и в них заселяются новые гости, либо часть посетителей выбрасывается в коридор, чтобы освободить место для гостей (очень по-человечески). Свой взгляд на такие решения я изложил в виде фантастического рассказа о Блондинке. На чем основываются мои рассуждения? Перемещение бесконечного количества посетителей занимает бесконечное количество времени. После того, как мы освободили первую гостевую комнату, один из посетителей всегда будет ходить по коридору из своей комнаты в следующую до скончания века. Конечно, фактор времени можно тупо не учитывать, но это уже будет из разряда «закон для дураков не писан». Все зависит от того, что мы делаем: подгоняем реальность под математические теории или наоборот.
Что такое «бесконечный отель»? Бесконечная гостиница — это гостиница, в которой всегда есть любое количество свободных мест, независимо от того, сколько комнат занято. Если все комнаты в бесконечном коридоре «для посетителей» заняты, то есть еще один бесконечный коридор с комнатами для «гостей». Таких коридоров будет бесконечное множество. В то же время «бесконечный отель» имеет бесконечное количество этажей, бесконечное количество зданий, бесконечное количество планет, бесконечное количество вселенных, созданных бесконечным количеством Богов. Математики же не в силах отойти от банальных житейских проблем: Бог-Аллах-Будда всегда один, гостиница одна, коридор один. Вот и пытаются математики жонглировать порядковыми номерами гостиничных номеров, убеждая нас в том, что можно «впихнуть непроталкиваемое».
Если все комнаты в бесконечном коридоре «для посетителей» заняты, то есть еще один бесконечный коридор с комнатами для «гостей». Таких коридоров будет бесконечное множество. В то же время «бесконечный отель» имеет бесконечное количество этажей, бесконечное количество зданий, бесконечное количество планет, бесконечное количество вселенных, созданных бесконечным количеством Богов. Математики же не в силах отойти от банальных житейских проблем: Бог-Аллах-Будда всегда один, гостиница одна, коридор один. Вот и пытаются математики жонглировать порядковыми номерами гостиничных номеров, убеждая нас в том, что можно «впихнуть непроталкиваемое».
Я продемонстрирую вам логику своих рассуждений на примере бесконечного множества натуральных чисел. Для начала нужно ответить на очень простой вопрос: сколько существует наборов натуральных чисел — один или много? Правильного ответа на этот вопрос нет, так как мы сами придумали числа, в Природе чисел нет. Да, Природа прекрасно умеет считать, но для этого она использует другие, не привычные нам математические инструменты. Как думает Природа, я расскажу вам в другой раз. Поскольку мы изобрели числа, мы сами будем решать, сколько существует наборов натуральных чисел. Рассмотрим оба варианта, как и подобает настоящему ученому.
Как думает Природа, я расскажу вам в другой раз. Поскольку мы изобрели числа, мы сами будем решать, сколько существует наборов натуральных чисел. Рассмотрим оба варианта, как и подобает настоящему ученому.
Вариант первый. «Давайте нам дан» единый набор натуральных чисел, безмятежно лежащий на полке. Берем этот набор с полки. Все, других натуральных чисел на полке не осталось и взять их неоткуда. Мы не можем добавить его к этому набору, так как он у нас уже есть. Что делать, если вы действительно хотите? Без проблем. Мы можем взять единицу из уже взятого набора и вернуть ее на полку. После этого мы можем взять единицу с полки и добавить ее к тому, что у нас осталось. В результате мы снова получаем бесконечное множество натуральных чисел. Все наши манипуляции можно записать так:
Я записал операции в алгебраической и теоретико-множественной записи, подробно перечислив элементы множества. Нижний индекс указывает на то, что у нас есть один-единственный набор натуральных чисел. Оказывается, множество натуральных чисел останется неизменным, только если из него вычесть единицу и прибавить такую же единицу.
Оказывается, множество натуральных чисел останется неизменным, только если из него вычесть единицу и прибавить такую же единицу.
Второй вариант. У нас на полке много разных бесконечных наборов натуральных чисел. Подчеркну — РАЗНЫЕ, несмотря на то, что практически неотличимы. Берем один из этих наборов. Затем мы берем одно из другого набора натуральных чисел и добавляем его к уже взятому нами набору. Мы можем даже сложить два набора натуральных чисел. Вот что мы получаем:
Нижние индексы «один» и «два» указывают на принадлежность этих элементов к разным множествам. Да, если вы добавите единицу к бесконечному множеству, результатом также будет бесконечное множество, но оно не будет таким же, как исходное множество. Если одно бесконечное множество добавить к другому бесконечному множеству, результатом будет новое бесконечное множество, состоящее из элементов первых двух множеств.
Набор натуральных чисел используется для счета так же, как линейка для измерений. Теперь представьте, что вы прибавили к линейке один сантиметр. Это будет уже другая строка, не равная исходной.
Это будет уже другая строка, не равная исходной.
Вы можете принять или не принять мои рассуждения — это ваше личное дело. Но если вы когда-нибудь столкнетесь с математическими проблемами, подумайте, не находитесь ли вы на пути ложных рассуждений, протоптанном поколениями математиков. Ведь занятия по математике, прежде всего, формируют в нас устойчивый стереотип мышления, а уже потом добавляют нам умственных способностей (или наоборот, лишают свободы мышления).
pozg.ru
Воскресенье, 4 августа 2019 г.
Писал постскриптум к статье про и увидел в Википедии вот этот замечательный текст:
Читаем: «…богатая теоретическая база математики Вавилона не носила целостного характера и сводилась к набору разрозненных методик, лишенных общей системы и доказательной базы».
Вау! Какие мы умные и как хорошо умеем видеть недостатки других. Слабо ли нам смотреть на современную математику в том же контексте? Слегка перефразируя вышеприведенный текст, лично у меня получилось следующее:
Богатая теоретическая база современной математики не имеет целостного характера и сводится к набору разрозненных разделов, лишенных общей системы и доказательной базы.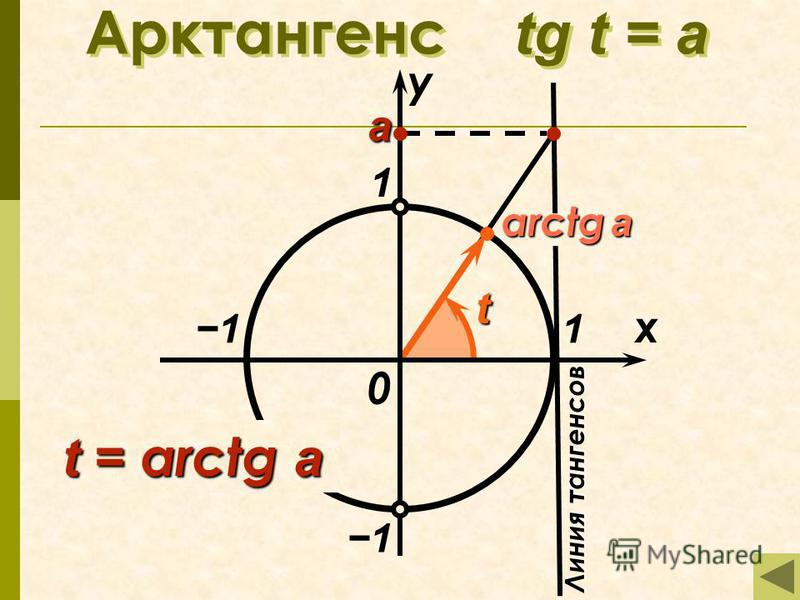
Не буду далеко ходить, чтобы подтвердить свои слова — у нее язык и условности, отличные от языка и условностей многих других разделов математики. Одни и те же имена в разных разделах математики могут иметь разное значение. Я хочу посвятить целый цикл публикаций наиболее очевидным промахам современной математики. До скорого.
3 августа 2019 г.
Как разделить набор на подмножества? Для этого необходимо ввести новую единицу измерения, которая присутствует в некоторых элементах выбранного набора. Рассмотрим пример.
Пусть у нас будет много НО в составе четырех человек. Этот набор формируется на основе «люди». Обозначим элементы этого набора через букву a , нижний индекс с цифрой будет указывать на порядковый номер каждого человека в этом наборе. Введем новую единицу измерения «половой признак» и обозначим ее буквой б . Так как половые признаки присущи всем людям, умножаем каждый элемент набора НО на по полу б .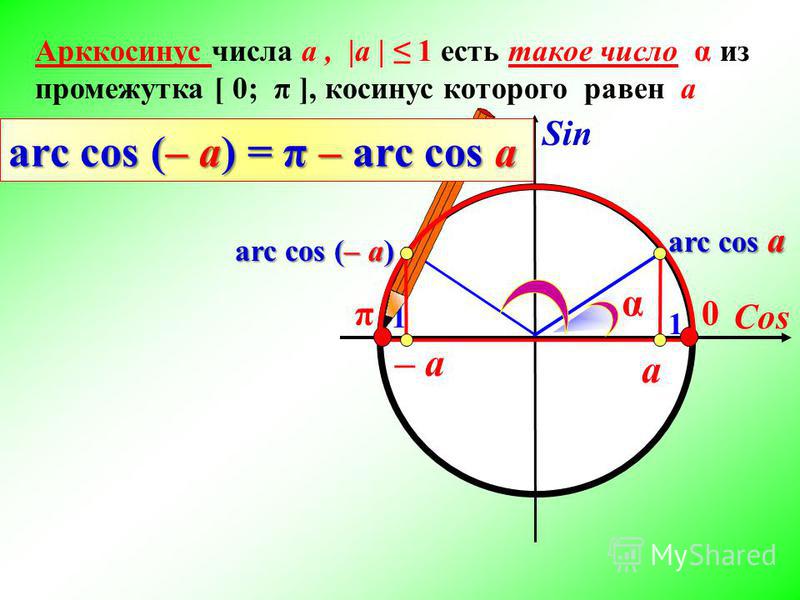 Обратите внимание, что наш набор «люди» теперь стал набором «люди с полом». После этого мы можем разделить половые признаки на мужские bm и женские bw гендерные признаки. Теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, неважно, мужской или женский. Если он есть у человека, то умножаем на единицу, если такого признака нет, умножаем на ноль. А дальше применяем обычную школьную математику. Посмотрите, что произошло.
Обратите внимание, что наш набор «люди» теперь стал набором «люди с полом». После этого мы можем разделить половые признаки на мужские bm и женские bw гендерные признаки. Теперь мы можем применить математический фильтр: выбираем один из этих половых признаков, неважно, мужской или женский. Если он есть у человека, то умножаем на единицу, если такого признака нет, умножаем на ноль. А дальше применяем обычную школьную математику. Посмотрите, что произошло.
После умножения, сокращения и перестановки мы получили два подмножества: мужское подмножество bm и женское подмножество bw . Примерно так же рассуждают математики, применяя теорию множеств на практике. Но они не раскрывают нам подробностей, а дают нам готовый результат — «множество людей состоит из подмножества мужчин и подмножества женщин». Естественно, у вас может возникнуть вопрос, насколько правильно применена математика в приведенных выше преобразованиях? Смею вас уверить, что на самом деле преобразования делаются правильно, достаточно знать математическое обоснование арифметики, булевой алгебры и других разделов математики.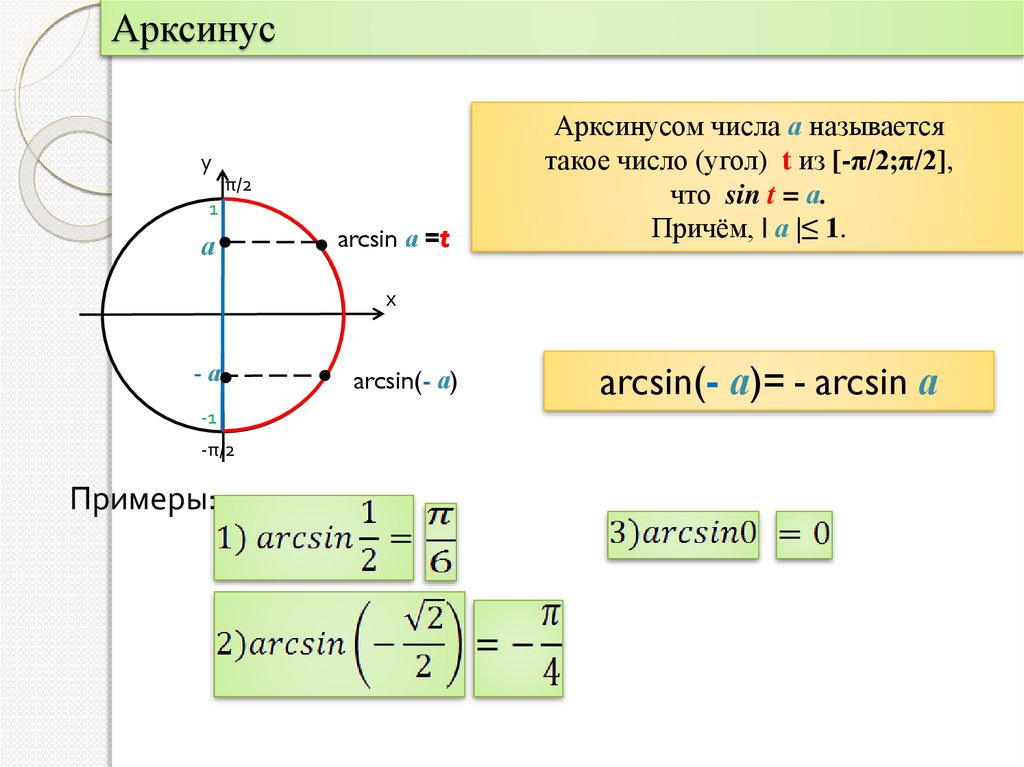 Что это? Как-нибудь в другой раз я расскажу вам об этом.
Что это? Как-нибудь в другой раз я расскажу вам об этом.
Что касается супернаборов, то можно объединить два набора в один супернабор, выбрав единицу измерения, которая присутствует в элементах этих двух наборов.
Как видите, единицы измерения и обычная математика отодвигают теорию множеств в прошлое. Признаком того, что с теорией множеств не все в порядке, является то, что математики придумали свой собственный язык и обозначения для теории множеств. Математики сделали то, что когда-то сделали шаманы. Только шаманы умеют «правильно» применять свои «знания». Этим «знаниям» нас учат.
Наконец, я хочу показать вам, как математики манипулируют .
7 января 2019 г.
В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как это звучит:
Допустим, Ахилл бежит в десять раз быстрее черепахи и отстает от нее на тысячу шагов. За время, за которое Ахилл пробегает это расстояние, черепаха проползает сто шагов в том же направлении. Когда Ахиллес пробежит сто шагов, черепаха проползет еще десять шагов и так далее. Процесс будет продолжаться бесконечно, Ахиллес никогда не догонит черепаху.
За время, за которое Ахилл пробегает это расстояние, черепаха проползает сто шагов в том же направлении. Когда Ахиллес пробежит сто шагов, черепаха проползет еще десять шагов и так далее. Процесс будет продолжаться бесконечно, Ахиллес никогда не догонит черепаху.
Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они, так или иначе, считали апории Зенона. Потрясение было настолько сильным, что «… дискуссии продолжаются и в настоящее время, научное сообщество еще не успело прийти к единому мнению о сущности парадоксов… математический анализ, теория множеств, новые физические и философские подходы занимались изучением вопроса, ни одно из них не стало общепринятым решением проблемы… » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
С точки зрения математики Зенон в своих апориях наглядно продемонстрировал переход от значения к «Этот переход подразумевает применение вместо констант.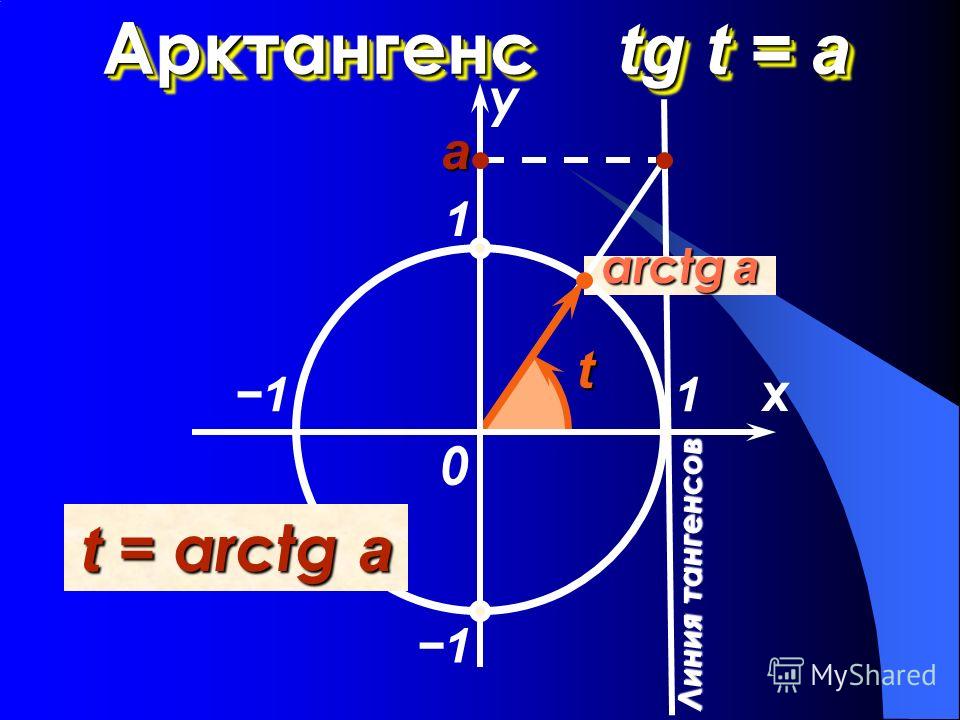 Насколько я понимаю, математический аппарат для применения переменных единиц измерения либо еще не разработан, либо он не применялся к апориям Зенона. Применение нашей обычной логики приводит нас к ловушка. Мы по инерции мышления применяем постоянные единицы времени к обратным. С физической точки зрения это выглядит как замедление времени до полной остановки в тот момент, когда Ахиллес догоняет черепаху. Если время останавливается, Ахиллес уже не может догнать черепаху.0003
Насколько я понимаю, математический аппарат для применения переменных единиц измерения либо еще не разработан, либо он не применялся к апориям Зенона. Применение нашей обычной логики приводит нас к ловушка. Мы по инерции мышления применяем постоянные единицы времени к обратным. С физической точки зрения это выглядит как замедление времени до полной остановки в тот момент, когда Ахиллес догоняет черепаху. Если время останавливается, Ахиллес уже не может догнать черепаху.0003
Если включить привычную нам логику, все встанет на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно время, затраченное на его преодоление, в десять раз меньше предыдущего. Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».
Как избежать этой логической ловушки? Оставайтесь в постоянных единицах времени и не переходите на обратные величины. На языке Зенона это выглядит так:
За то время, которое требуется Ахиллесу, чтобы пробежать тысячу шагов, черепаха проползет сто шагов в том же направлении.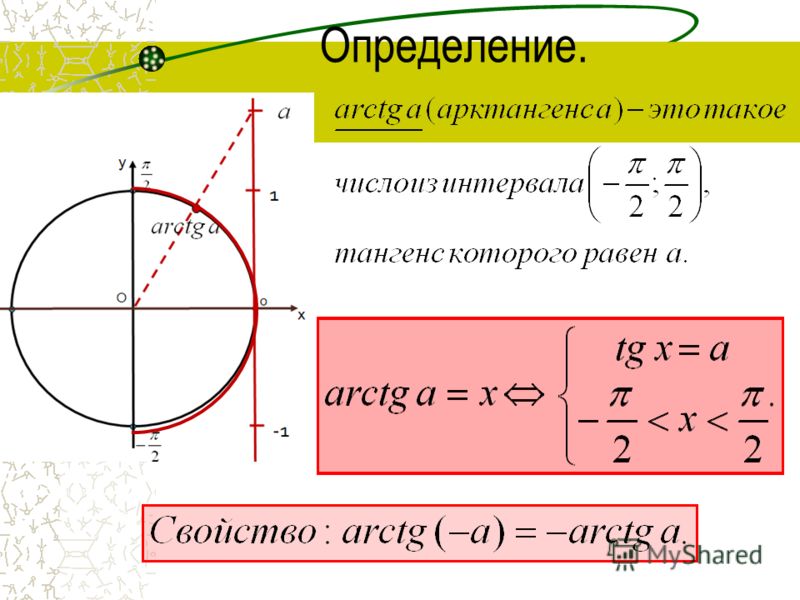 За следующий промежуток времени, равный первому, Ахиллес пробежит еще тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес опережает черепаху на восемьсот шагов.
За следующий промежуток времени, равный первому, Ахиллес пробежит еще тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес опережает черепаху на восемьсот шагов.
Такой подход адекватно описывает реальность без логических парадоксов. Но это не полное решение проблемы. Утверждение Эйнштейна о непреодолимости скорости света очень похоже на апорию Зенона «Ахиллес и черепаха». Нам еще предстоит изучить, переосмыслить и решить эту проблему. И решение надо искать не в бесконечно больших числах, а в единицах измерения.
Еще одна интересная апория Зенона рассказывает о летящей стреле:
Летящая стрела неподвижна, так как в каждый момент времени она покоится, а так как она покоится в каждый момент времени, то она всегда покоится .
В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и есть движение. Здесь следует отметить еще один момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но их нельзя использовать для определения расстояния. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства одновременно, но по ним нельзя определить факт движения (естественно, для расчетов еще нужны дополнительные данные, тригонометрия вам в помощь). В частности, я хочу отметить, что две точки во времени и две точки в пространстве — это две разные вещи, которые не следует путать, поскольку они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но их нельзя использовать для определения расстояния. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства одновременно, но по ним нельзя определить факт движения (естественно, для расчетов еще нужны дополнительные данные, тригонометрия вам в помощь). В частности, я хочу отметить, что две точки во времени и две точки в пространстве — это две разные вещи, которые не следует путать, поскольку они предоставляют разные возможности для исследования.
Покажу процесс на примере. Выбираем «красное тело в прыщике» — это наше «целое». При этом мы видим, что эти вещи есть с дужкой, а есть без дужки. После этого выделяем часть «целого» и формируем комплект «с бантиком». Именно так шаманы кормят себя, привязывая свою теорию множеств к реальности.
А теперь давайте проделаем небольшую хитрость. Возьмем «твердое в пупырышке с бантиком» и объединим эти «целые» по цвету, выделив красные элементы. У нас много «красного». Теперь каверзный вопрос: полученные наборы «с бантиком» и «красный» это один и тот же набор или два разных набора? Только шаманы знают ответ. Точнее сами ничего не знают, но как говорится, так и будет.
Этот простой пример показывает, что теория множеств совершенно бесполезна, когда дело доходит до реальности. В чем секрет? Мы сформировали комплект «красные однотонные пупырышки с бантиком». Формирование происходило по четырем разным единицам измерения: цвет (красный), прочность (твердый), шероховатость (в шишку), украшения (с бантиком). Только набор единиц измерения позволяет адекватно описывать реальные объекты на языке математики . Вот как это выглядит.
Буква «а» с разными индексами обозначает разные единицы измерения. В скобках выделены единицы измерения, по которым на предварительном этапе выделяется «целое». За скобки вынесена единица измерения, по которой формируется набор. В последней строке показан конечный результат — элемент множества. Как видите, если мы используем единицы измерения для формирования набора, то результат не зависит от порядка наших действий. И это математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» прийти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
За скобки вынесена единица измерения, по которой формируется набор. В последней строке показан конечный результат — элемент множества. Как видите, если мы используем единицы измерения для формирования набора, то результат не зависит от порядка наших действий. И это математика, а не пляски шаманов с бубнами. Шаманы могут «интуитивно» прийти к такому же результату, аргументируя его «очевидностью», ведь единицы измерения не входят в их «научный» арсенал.
С помощью единиц измерения очень легко разбить один или объединить несколько сетов в один суперсет. Рассмотрим подробнее алгебру этого процесса.
Калькулятор — arctan(2) — Solumaths
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией
касательная функция,
он вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа , просто введите число и примените арктанг функция. 92)`.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` | |
| arctan(`-sqrt(3)/3`) | `5*pi/6` | 6 arctan (`-sqrt(3)`)`2*pi/3` |
| arctan(`0`) | `0` | |
| arctan(`sqrt(3)`) | `/3` | |
| arctan(`1`) | `pi/4` | |
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число. 92)`
92)`
Предельный арктангенс :
Калькулятор предела позволяет вычислить пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может отображать функцию арктангенса в интервале ее определения.
Свойство функции арктангенс:
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах. 9-1 2?
3. Часто задаваемые вопросы по Arctan 2 Что такое Арктан 2?
Значение arctan 2 равно 63,435 градуса (или) 1,107 радиана. Мы знаем, что угол в градусах можно преобразовать в радианы, умножив его на π/180, а угол в радианах можно преобразовать в градусы, умножив его на 180/π. Таким образом,
- Переведем градусы в радианы. arctan 2 ≈ 63,435° = 63,435 × π/180 ≈ 1,107 радиан
- Переведем радианы в градусы. arctan 2 ≈ 1,107 = 1,107 × 180/π ≈ 63,435 градуса
В приведенных выше расчетах могут быть небольшие различия, поскольку два приведенных выше значения представляют собой значения арктангенса 2, округленные до 3 знаков после запятой.
 Но на самом деле arctan 2 — иррациональное число, и его значение не имеет конца (а также оно имеет неповторяющийся набор десятичных знаков). т. е.
Но на самом деле arctan 2 — иррациональное число, и его значение не имеет конца (а также оно имеет неповторяющийся набор десятичных знаков). т. е.- арктангенс 2 ≈ 63,4349649
578476426200304282… 9-1 2? Мы обычно находим значения арктангенса, используя единичный круг или тригонометрическую таблицу. Но 2 нет в обоих. Таким образом, нам нужно использовать кнопку «arctan» (или) tan -1 на калькуляторе, чтобы найти арктангенс 2. Выполните следующие шаги, чтобы найти значение арктангенса 2.
Нахождение арктангенса 2 в градусах Установите калькулятор в режим градусов.
- Нажмите кнопку «arctan» (или) кнопку «tan -1 » (или) комбинацию кнопок «inv» и «tan» (все, что доступно на вашем калькуляторе).
- Введите число «2».
- Затем он покажет значение арктангенса 2 в градусах: 63,4349649
578476426200304282… Поиск Arctan 2 в радианах
Просто установите калькулятор в режим радианов и используйте тот же процесс, что и выше.
0170654601785… Тогда мы получим значение arctan 2 в радианах, равное 1,1071487177940
Тогда мы получим значение arctan 2 в радианах, равное 1,1071487177940☛ Связанные темы:
- Калькулятор арктангенса
- Arctan 0 Калькулятор
Арктан 2 Примеры
Пример 1: Докажите, что arctan 0 + arctan 2 = arctan 2.
Решение:
Мы знаем, что arctan 0 = 0, и добавление 0 к любому числу дает само число. Таким образом,
arctg 0 + arctg 2 = arctg 2
Ответ: Данное равенство доказано.
Пример 2: Найдите угол (в радианах) в первом квадранте, удовлетворяющий уравнению tan x = 2,
Решение:
Данным тригонометрическим уравнением является tan x = 2.
Отсюда x = arctan 2. 0 и π/2).
Ответ: 1,107 радиан.
Пример 3: Каково общее решение уравнения, приведенного в Пример 2 ?
Решение:
Данным уравнением является тангенс х = 2, и мы нашли, что арктангенс 2 = 1,107 радиан.

Мы знаем, что общее решение тригонометрического уравнения тангенса имеет вид nπ + x.
Следовательно, общее решение равно nπ + 1,107.
Ответ: nπ + 1,107
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по Arctan 2
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Arctan 2
Сколько стоит Arctan 2 в градусах?
Значение арктангенса 2 в градусах примерно равно 63,435 при округлении до 3 знаков после запятой. Чтобы найти это, сначала установите калькулятор в режим градусов.
Что такое обратный загар 2 в радианах?
Значение arctan 2 в радианах приблизительно равно 1,107 при округлении до 3 знаков после запятой.
 Чтобы найти это, сначала держите калькулятор в режиме радианов. 9-1 2 Рациональное и иррациональное?
Чтобы найти это, сначала держите калькулятор в режиме радианов. 9-1 2 Рациональное и иррациональное?Если мы посчитаем тангенс -1 2 в режиме градусов, мы получим 63,434948822
0648427806279547… Шаблон неповторяющийся и непрерывный. Таким образом, тангенс -1 2 иррационален. Tan Arctan 2 Равен Cot 2?
Нет, потому что arctan 2 = 1,107 радиан, а cot 2 = -0,457 (когда 2 выражено в радианах). Обратите внимание, что arctan — это не то же самое, что кроватка.
Скачать БЕСПЛАТНЫЕ учебные материалы
ЛИСТКИ
Рабочие листы по математике и
наглядная учебная программаArctan против Arctan2 — Науки о Земле LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 11752
Обычно, когда вы вычисляете арктангенс, вы делаете это для вопроса, связанного с треугольником, в котором две стороны x и y являются длинами (положительные числа), а результирующий угол находится в диапазоне от 0 до 9.
 {\circ}\) (\(\pi\)/2).
{\circ}\) (\(\pi\)/2).Однако оказывается, что существует два разных определения арктангенса, и какое из них вы используете, имеет значение, если x и y могут быть как положительными, так и отрицательными. Это именно тот случай, когда используются декартовы компоненты местоположения на сфере для определения долготы и широты этой точки.
Вариант тангенса, который вы найдете на своем калькуляторе, представляет собой двухквадрантный арктангенс (atan) и предполагает одно входное значение (y/x). Это значение может быть положительным или отрицательным, а выходные данные будут иметь тот же знак и значения от 0 до \(\pi\)/2 (9{\circ}\)). На графике ниже атан возвращает результаты только в правой половине круга.
Теперь давайте подумаем о точке (x,y,z) на экваторе земли, где z=0. Обратите внимание, что отношение y/x=(−y)/(−x), так что atan вернет одно и то же значение угла (долготы), но эти две точки не лежат в одном и том же месте на сфере. .
Вот почему существует также четырехквадрантный арктангенс, atan2(y,x).
 {\circ}\) (±\(\pi\)/2), с положительными значениями (восточная долгота) для положительных значений y и отрицательными значениями (западная долгота ) для отрицательных значений y. 9{\circ}\), что является правильным ответом с учетом знаков x и y.
{\circ}\) (±\(\pi\)/2), с положительными значениями (восточная долгота) для положительных значений y и отрицательными значениями (западная долгота ) для отрицательных значений y. 9{\circ}\), что является правильным ответом с учетом знаков x и y.импортировать matplotlib.pyplot как plt импортировать numpy как np r2d = 180/np.pi рис = plt.figure(figsize=(7,7)) топор = fig.add_subplot (1,1,1) х = np.arange (-1,1.,0,01) y = np.arange(1,-1.,-0,01) ycirc = np.sqrt (1 - x ** 2) х1 = -1 у1 = -1 print('atan2 для x = -1, y = -1',np.arctan2(y1,x1)*r2d) print('atan,for x = -1, y = -1',np.arctan(y1/x1)*r2d) ax.plot (np.zeros (y.shape), y) ax.plot(x, np.zeros(x.shape)) ax.plot(x, ycirc, 'черный') ax.plot(x, -ycirc,'черный') ax.plot([0, -1], [0, -1],color='синий') ax.plot([0, 1], [0,1],color='красный') ax.plot (1,1, маркер = 'o', цвет = 'красный') ax.plot(-1,-1,marker='o',color='синий') ax.set_aspect('равно') ax.set_ylim([-1.2, 1.2]) ax.set_xlim([-1. 4, 1.2])
топор.текст(1,0,'0')
ax.text(0,1.1,'$\pi/2, (90)$')
ax.text(-1.19,0,'$\pm\pi$')
ax.text(-1.39,-0.2,'($\pm180$)')
ax.text(0,-1.1,'$-\pi/2, (-90)$')
ax.text(0.5,0.5,'Восток')
ax.text(-0.5,0.5,'Восток')
ax.text(0.5,-0.5,'Запад')
ax.text(-0.5,-0.5,'Запад')
ax.set_xlabel('координата x')
ax.set_ylabel('координата Y')
ax.set_title('(x,y) на экваторе')
plt.show()
4, 1.2])
топор.текст(1,0,'0')
ax.text(0,1.1,'$\pi/2, (90)$')
ax.text(-1.19,0,'$\pm\pi$')
ax.text(-1.39,-0.2,'($\pm180$)')
ax.text(0,-1.1,'$-\pi/2, (-90)$')
ax.text(0.5,0.5,'Восток')
ax.text(-0.5,0.5,'Восток')
ax.text(0.5,-0.5,'Запад')
ax.text(-0.5,-0.5,'Запад')
ax.set_xlabel('координата x')
ax.set_ylabel('координата Y')
ax.set_title('(x,y) на экваторе')
plt.show() Для получения дополнительной информации о математике arctan нажмите здесь или для arctan2 нажмите здесь.
Документация Numpy: Arctan и Arctan2
Другое объяснение: 9{\circ}\), где z = y/x = напротив/смежно. Это связано с тем, что функция не может различать все четыре квадранта.
Напомним, что \(\tan(\theta) = \sin(\theta) / \cos(\theta) \), а в прямоугольных треугольниках \(\tan(\theta) = y / x\)
Если значение \(\tan(\theta)\) положительное, это может означать, что либо угол находится в квадранте I (где и (\sin(\theta)\) и \(\cos(\theta)\) положительны) или квадрант III (где и \(\sin(x)\) и \(\cos(\theta)\) отрицательны).

Аналогичным образом, если \( \tan(\theta)\) отрицательное значение, это может означать, что угол находится либо в квадранте II, либо в квадранте IV, где \(\sin(\theta)\) и \(\cos(\theta )\) — противоположные знаки.
Arctan принимает только одно входное значение и поэтому не может определить, к какому из двух квадрантов относится угол в каждом случае. По умолчанию он предоставляет угол либо в квадранте I, либо в квадранте IV, в зависимости от знака \( \tan(\theta)\). Возможно, проще думать об этом с точки зрения треугольников, и единственное значение, принимаемое arctan, на самом деле является частным противоположной и смежной сторон треугольника или y/x, поэтому \( \arctan(y/x)\) . Чтобы определить правильный квадрант, должен быть известен знак y и x, однако функция получает только знак x/y, а не x и y по отдельности и не может различать квадранты.
Иногда это может быть проблемой, особенно если нас интересует угол, который может варьироваться от -180 до 180 градусов, например долгота.
 {\circ}\).
{\circ}\).В заключение, если вы вычисляете что-то в диапазоне от -90 до 90 градусов, например широту, используйте арктангенс. При вычислении угла, который может находиться в диапазоне от -180 до 180 градусов, используйте arctan2.
Это объяснение для arctan vs arctan2 было адаптировано и расширено из stackexchange
.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Теги
Мэтуэй | Популярные проблемы
1 Найдите точное значение грех(30) 2 Найдите точное значение грех(45) 3 Найдите точное значение грех(30 градусов) 4 Найдите точное значение грех(60 градусов) 5 Найдите точное значение загар (30 градусов) 6 Найдите точное значение угловой синус(-1) 7 Найдите точное значение грех(пи/6) 8 Найдите точное значение cos(pi/4) 9 Найдите точное значение грех(45 градусов) 10 Найдите точное значение грех(пи/3) 11 Найдите точное значение арктический(-1) 12 Найдите точное значение cos(45 градусов) 13 Найдите точное значение cos(30 градусов) 14 Найдите точное значение желтовато-коричневый(60) 15 Найдите точное значение csc(45 градусов) 16 Найдите точное значение загар (60 градусов) 17 Найдите точное значение сек(30 градусов) 18 Найдите точное значение cos(60 градусов) 19 Найдите точное значение соз(150) 20 Найдите точное значение грех(60) 21 Найдите точное значение cos(pi/2) 22 Найдите точное значение загар (45 градусов) 23 Найдите точное значение arctan(- квадратный корень из 3) 24 Найдите точное значение csc(60 градусов) 25 Найдите точное значение сек (45 градусов) 26 Найдите точное значение csc(30 градусов) 27 Найдите точное значение грех(0) 28 Найдите точное значение грех(120) 29 Найдите точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найдите точное значение желтовато-коричневый(30) 32 Преобразование градусов в радианы 45 33 Найдите точное значение 92 35 Преобразовать из радианов в градусы пи/6 36 Найдите точное значение детская кроватка(30 градусов) 37 Найдите точное значение арккос(-1) 38 Найдите точное значение арктический(0) 39 Найдите точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.  )/3
)/342 Найдите точное значение sin((5pi)/3) 43 Найдите точное значение sin((3pi)/4) 44 Найдите точное значение желтовато-коричневый (пи/2) 45 Найдите точное значение грех(300) 46 Найдите точное значение соз(30) 47 Найдите точное значение соз(60) 48 Найдите точное значение соз(0) 49 Найдите точное значение соз(135) 50 Найдите точное значение cos((5pi)/3) 51 Найдите точное значение соз(210) 52 Найдите точное значение сек (60 градусов) 53 Найдите точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найдите точное значение грех(135 градусов) 61 Найдите точное значение грех(150) 62 Найдите точное значение грех(240 градусов) 63 Найдите точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найдите точное значение грех(225) 66 Найдите точное значение грех(240) 67 Найдите точное значение cos(150 градусов) 68 Найдите точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найдите точное значение сек(0) 71 Найдите точное значение cos((5pi)/6) 72 Найдите точное значение КСК(30) 73 Найдите точное значение arcsin(( квадратный корень из 2)/2) 74 Найдите точное значение желтовато-коричневый ((5pi)/3) 75 Найдите точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найдите точное значение arctan(-(квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 шт.  )/4
)/479 Найдите точное значение sin((7pi)/4) 80 Найдите точное значение угловой синус(-1/2) 81 Найдите точное значение sin((4pi)/3) 82 Найдите точное значение КСК(45) 83 Упростить арктан( квадратный корень из 3) 84 Найдите точное значение грех(135) 85 Найдите точное значение грех(105) 86 Найдите точное значение грех(150 градусов) 87 Найдите точное значение sin((2pi)/3) 88 Найдите точное значение желтовато-коричневый ((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найдите точное значение sin(pi/2) 91 Найдите точное значение сек(45) 92 Найдите точное значение cos((5pi)/4) 93 Найдите точное значение cos((7pi)/6) 94 Найдите точное значение угловой синус(0) 95 Найдите точное значение грех(120 градусов) 96 Найдите точное значение желтовато-коричневый ((7pi)/6) 97 Найдите точное значение соз(270) 98 Найдите точное значение sin((7pi)/6) 99 Найдите точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Arcsin, Arccos, Arctan — Тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по тригонометрии » Тригонометрические операции » Arcsin, Arccos, Arctan
Что такое если и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти, нам нужно использовать данную информацию в задаче.
 Даны противолежащая и прилежащая стороны. Затем мы можем, по определению, найти число и его меру в градусах, используя функцию.
Даны противолежащая и прилежащая стороны. Затем мы можем, по определению, найти число и его меру в градусах, используя функцию.Теперь найдем меру угла с помощью функции .
Если вы рассчитали меру угла как , значит, ваш калькулятор настроен на радианы, а его необходимо установить на градусы.
Сообщить об ошибке
Для приведенного выше треугольника, что если и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно использовать тригонометрическую функцию, чтобы найти . Нам даны противоположная и смежная стороны, поэтому мы можем использовать функции и .
Сообщить об ошибке
Для треугольника выше, что такое если и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно использовать тригонометрическую функцию, чтобы найти .
 Нам даны противолежащая сторона и гипотенуза, поэтому мы можем использовать функции и .
Нам даны противолежащая сторона и гипотенуза, поэтому мы можем использовать функции и .Сообщить об ошибке
Что из следующего является эквивалентом степени обратной тригонометрической функции
?
Возможные ответы:
Правильный ответ:
Объяснение:
Это обращение функции косинуса. Это означает, что если , то .
Следовательно,
Сообщить об ошибке
Приняв угол в градусах, определить значение .
Возможные ответы:
Правильный ответ:
Объяснение:
Для оценки необходимо знать существующий домен и диапазон для этих обратных функций.
Арктангенс:
Арккосинус:
Арктангенс:
3
Значение каждого. Окончательные ответы должны возвращать угол.
Окончательные ответы должны возвращать угол.Сообщить об ошибке
Если
,
, какие значения принимает?
Предположим, что
Возможные ответы:
Реального решения нет.
Правильный ответ:
Объяснение:
Если , то мы можем применить обратный косинус к обеим сторонам:
Так как косинус и обратный косинус отменяют друг друга; затем мы можем применить обратные функции синуса и секущей, чтобы получить решение.
и и
Сообщить об ошибке
Рассчитать .
Возможные ответы:
Правильный ответ:
Объяснение:
Функция арксеканс принимает тригонометрическое отношение на единичной окружности в качестве входных данных и возвращает угол в качестве выходного значения.



 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.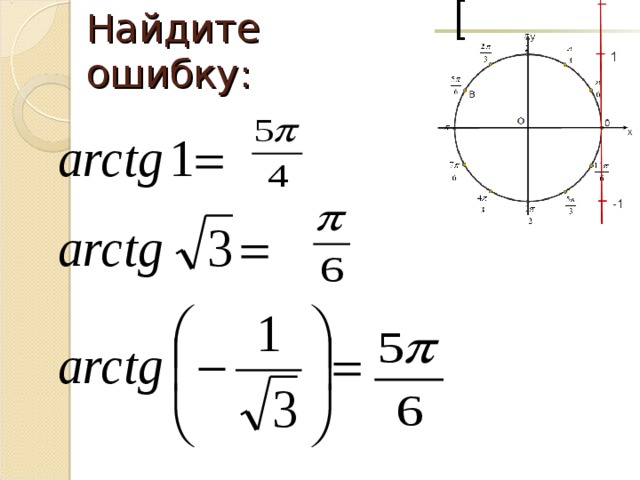 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. Но на самом деле arctan 2 — иррациональное число, и его значение не имеет конца (а также оно имеет неповторяющийся набор десятичных знаков). т. е.
Но на самом деле arctan 2 — иррациональное число, и его значение не имеет конца (а также оно имеет неповторяющийся набор десятичных знаков). т. е. Тогда мы получим значение arctan 2 в радианах, равное 1,1071487177940
Тогда мы получим значение arctan 2 в радианах, равное 1,1071487177940
 Чтобы найти это, сначала держите калькулятор в режиме радианов. 9-1 2 Рациональное и иррациональное?
Чтобы найти это, сначала держите калькулятор в режиме радианов. 9-1 2 Рациональное и иррациональное? {\circ}\) (\(\pi\)/2).
{\circ}\) (\(\pi\)/2).