§ Квадратичная функция. Как построить параболу
Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Запомните!
Квадратичная функция — это функция вида
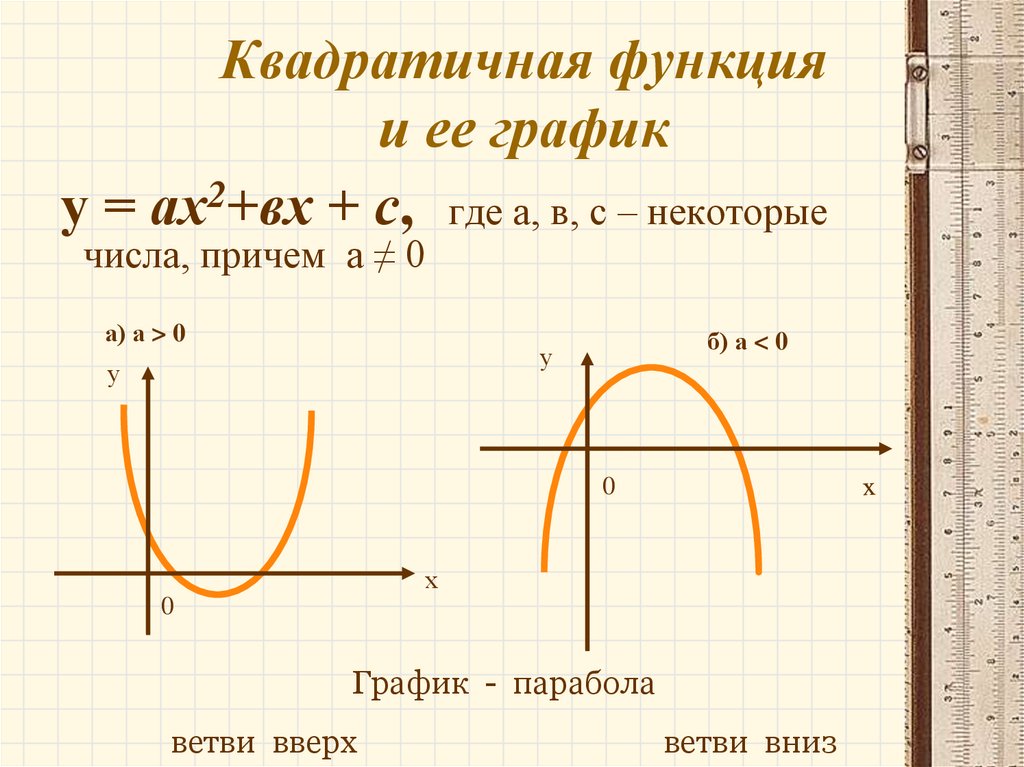
y = ax2 + bx + c,
где a, b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит «x» — это «2», то перед нами квадратичная функция.
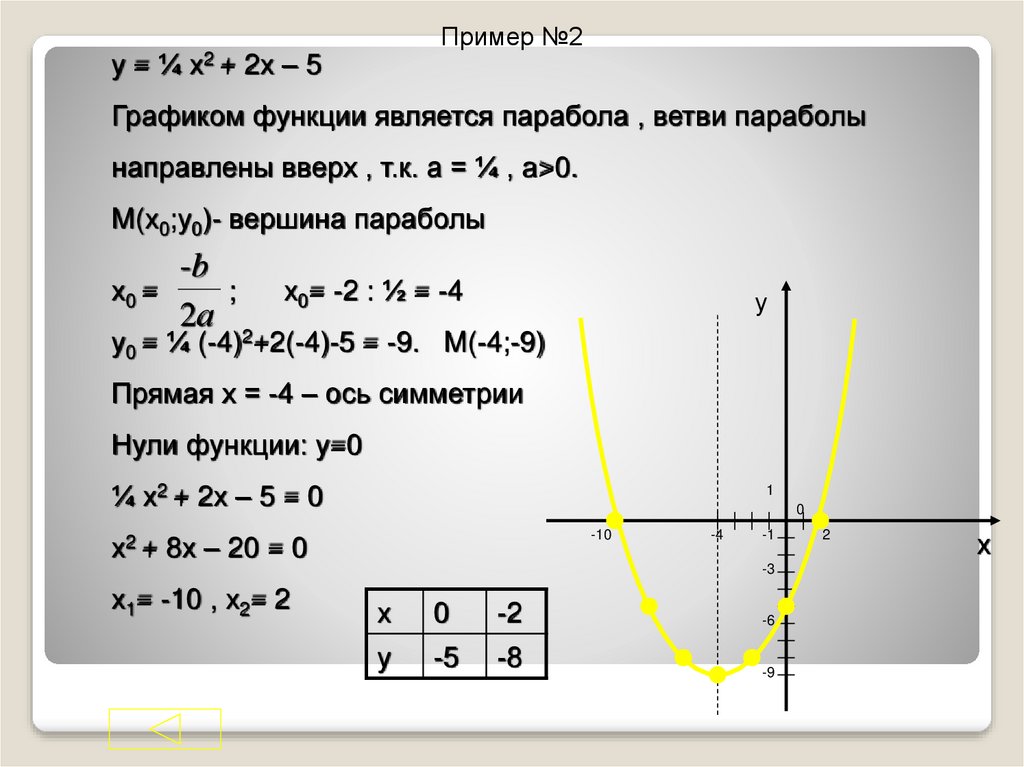
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».
| Квадратичная функция | |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
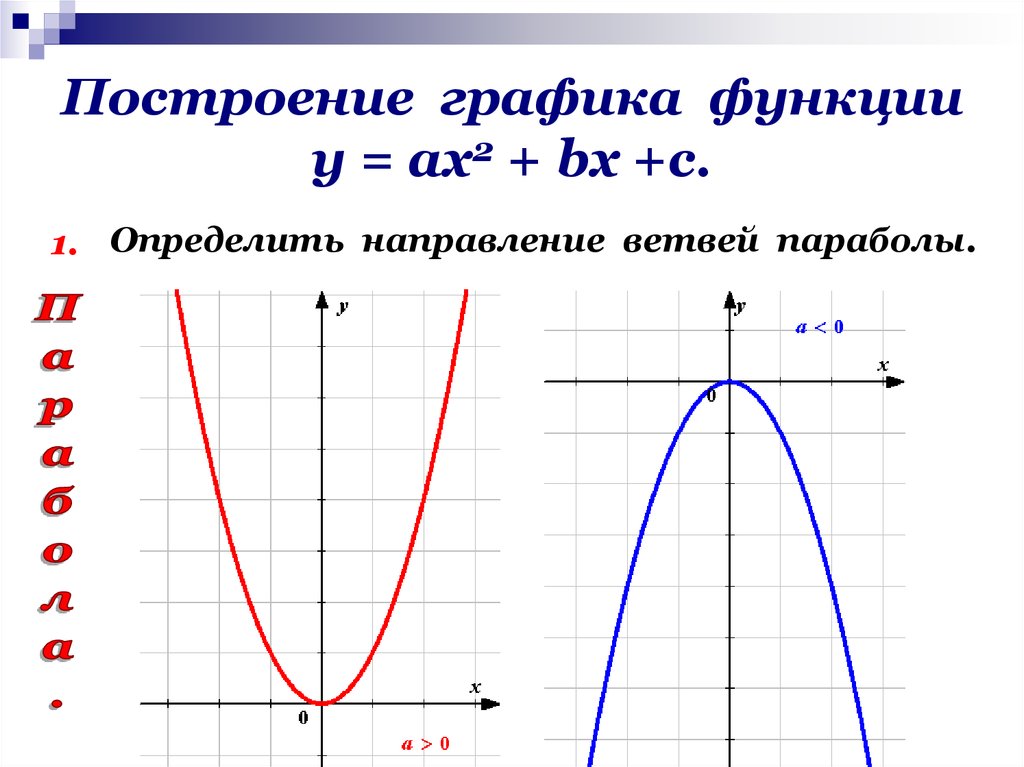
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
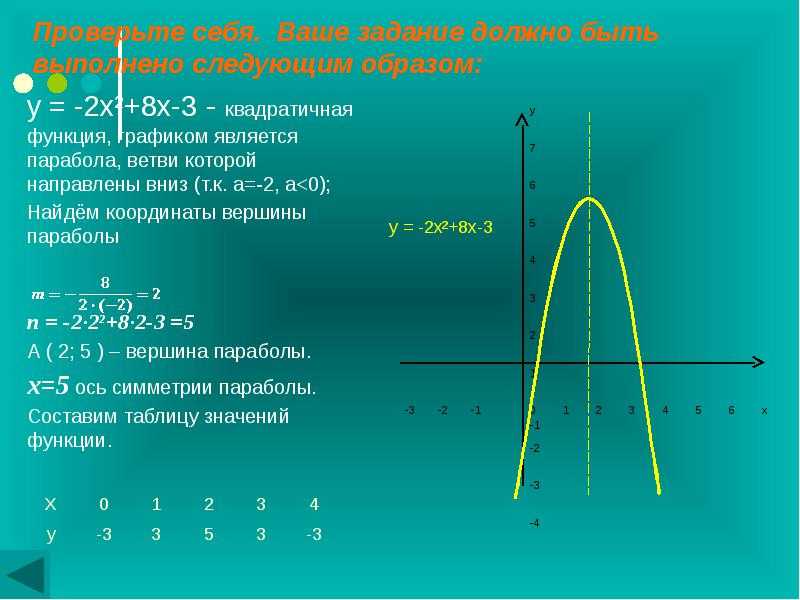
Построим график квадратичной функции «y = x2 −7x + 10».
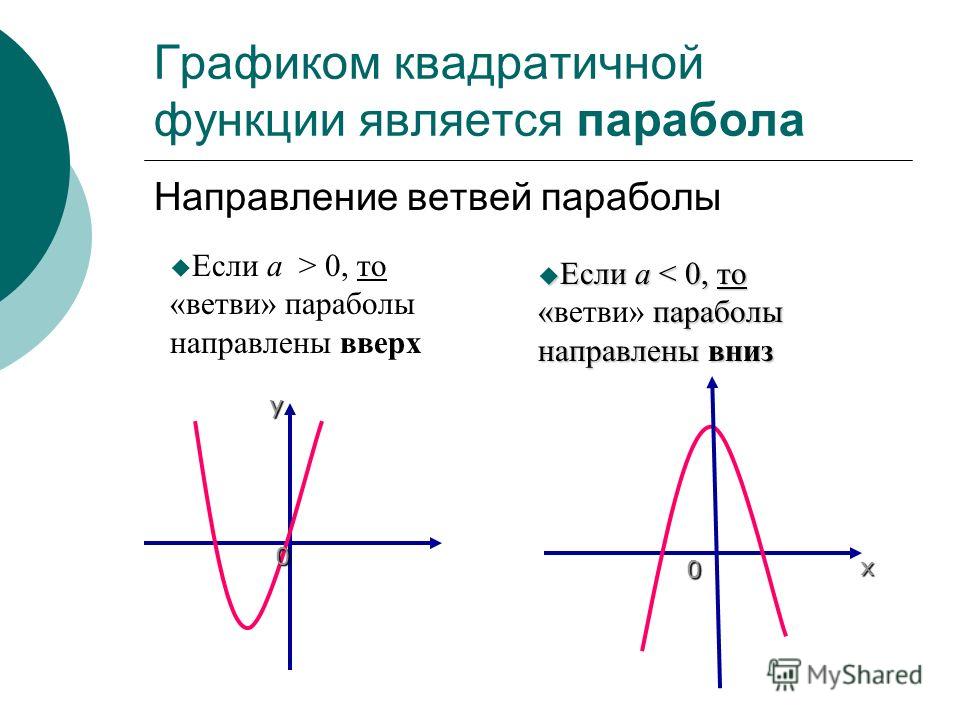
- Направление ветвей параболы
Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
- Координаты вершины параболы
Запомните!
Чтобы найти «x0» (координата вершины по оси «Ox») нужно использовать формулу:
x0 =
Найдем «x0» для нашей функции «y = x2 −7x + 10».

x0 =
= = 3,5− (−7) 2 · 1 Теперь нам нужно найти «y0» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x0» в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
y0(3,5) = (3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 = −12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.

Запомните!
Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».
Подставим в заданную функцию «y = x2 −7x + 10» вместо «y = 0» и решим полученное квадратное уравнение относительно «x» .
0 = x2 −7x + 10
x2 −7x + 10 = 0
x1;2 =7 ± √49 − 4 · 1 · 10 2 · 1
x1;2 =7 ± √9 2
x1;2 =7 ± 3 2 x1 = x2 = 7 − 3 2 x1 = x2 = x1 = 5 x 2 = 2 Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox».
 Назовем эти точки и выпишем их координаты.
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.
- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
x 1 3 4 6 y Для каждого выбранного значения «x» рассчитаем «y».

- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 = 4
- y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 = −2
- y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 = −2
- y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 = 4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции «y = −3x2 − 6x − 4».
- Направление ветвей параболы «a = −3» — ветви параболы направлены вниз.
- Координаты вершины параболы
x0 =
x0 =
−(−6) 2 · (−3) =
= −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
- Нули функции Точки пересечения с осью «Ox» (y = 0).

0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ± √62 − 4 · 3 · 4 2 · 1 x1;2 =
−6 ± √36 − 48 2 x1;2 =
−6 ± √−12 2 Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось «Ox».
- Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x
- y(−3) = −3 · (−3)2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
- y(−2) = −3 · (−2)2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
- y(0) = −3 · 02 − 6 · 0 − 4 = −4
- y(1) = −3 · 12 − 6 · 1 − 4 = −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13
Отметим вспомогательные точки.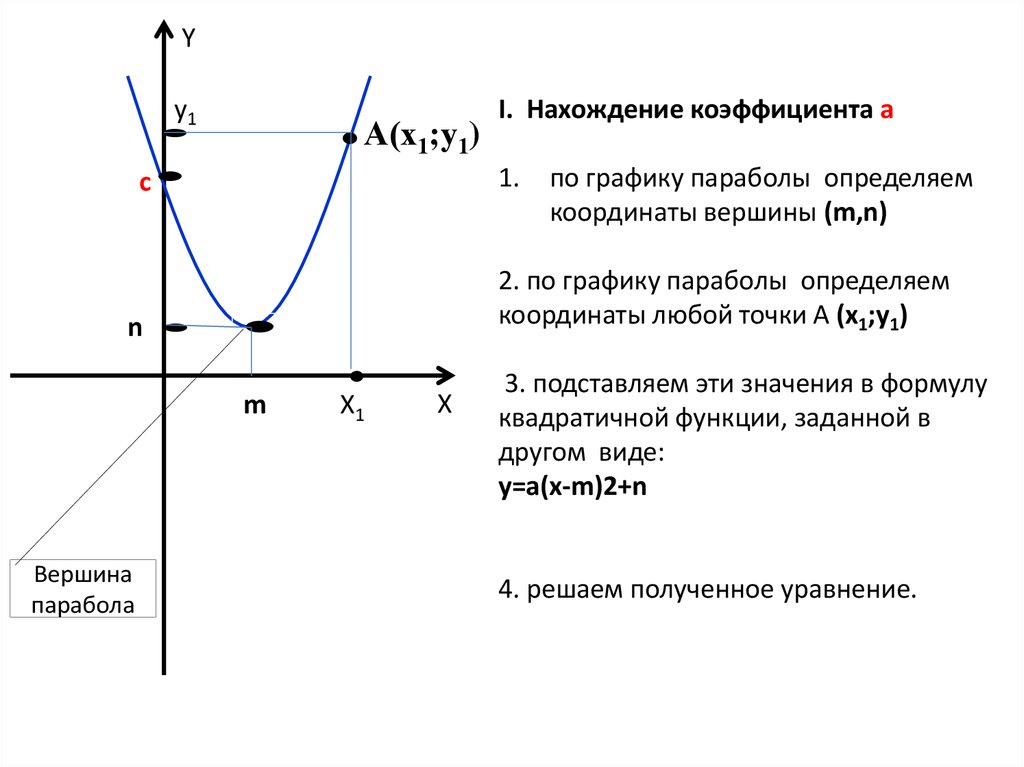 2+bx_в+с\)
2+bx_в+с\)
Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.
3 параметра позволяющих сопоставить формулу квадратичной функции и график:
|
1. |
\(a>0\) — ветви параболы направлены вверх |
|
||||
|
\(a<0\) — ветви параболы направлены вниз |
|
|||||
|
2. |
\(c\) равна ординате точки пересечения |
|
||||
|
3. Ответ:
Как построить график квадратичной функции (параболу)?Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.
|
Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства
Пошаговое руководство построение графика квадратичной функции
Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения.
У точки в этой системе есть две координаты.
M(x, y): M это название точки, x это абсцисса и она измеряется по Ox, а y это ордината и мерится по Oy.
Две координаты отображают расстояние от точки до двух осей.
Если мы рассмотрим функцию f: A -> B (где A — область определения, B — область значений функции), тогда точку на графике данной функции можно представить в форме P(x, f(x)).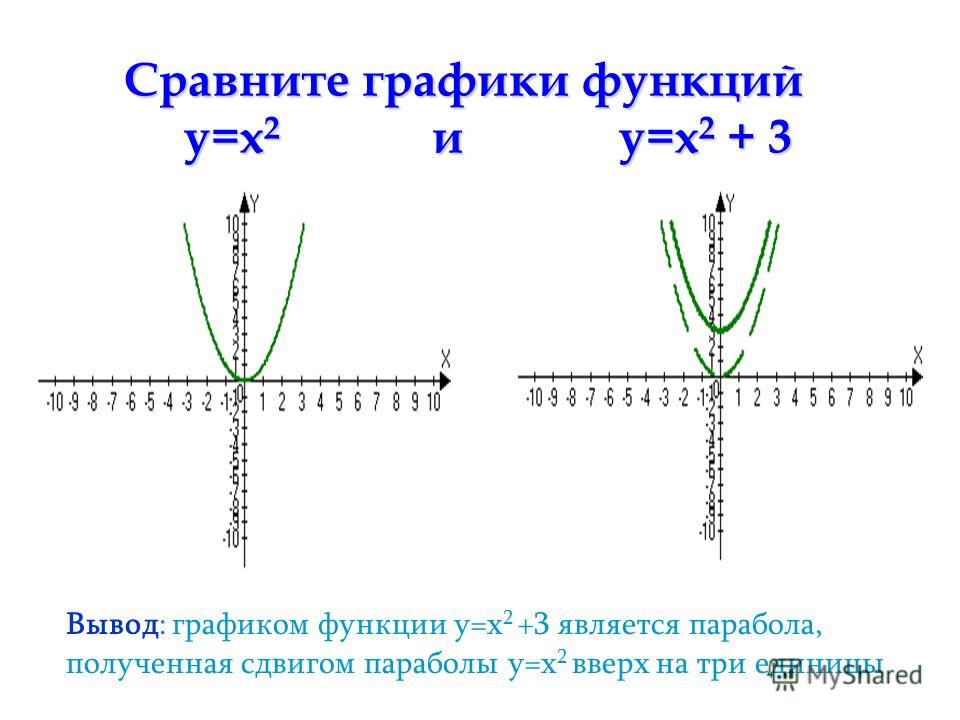 2-\frac{\Delta}{4a}$
2-\frac{\Delta}{4a}$
где Δ = b2 — 4ac
Если a > 0, то минимальным значением f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, то минимальное значение f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, которую она пересекает $x=-\frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, когда мы присваиваем знаячения x, то вибираем их симметричными относительно $-\frac{b}{2a}$.
При построении графика, точки пересечения с осями координат очень важны.
|. Точка, расположенная на оси Ox имеет форму P(x, 0), потому что расстояние от неё до Ox равно 0. Если точка находиться и на Ox и на графике функции,то она также имеет вид P(x, f(x)) ⇒ f(x) = 0.
Если точка находиться и на Ox и на графике функции,то она также имеет вид P(x, f(x)) ⇒ f(x) = 0.
Таким образом, для того чтобы найти координаты точки пересечения с осью Ox, мы должны решить уравнение f(x)=0. Мы получаем уравнение a2 + bx + c = 0.
Решение уравнения зависит от знака Δ = b2 — 4ac.
Иммем следующие варианты:
1) Δ < 0,
тогда у уравнения нет решений в R (множестве действительных чисел) и график не пересекает Ox. Форма графика будет:
или
2) Δ = 0,
тогда у уравнения два решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы. Форма графика будет:
или
3) Δ > 0,
тогда у уравнения два разных решения.
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ox в точках M(x1 и Ox. Форма графика будет:
Форма графика будет:
или
||. Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).
В случае квадратичной функции,
f(0) = a×02 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax2 + bx + c
1. Составляем таблицу переменных, куда заносим некоторые важные значения x.
2. Вычисляем координаты вершины$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также записываем 0 в таблицу и нулевые значения симметричные $-\frac{b}{2a}$.
или
4. Мы определяем точку пересечения с осью Ox,решая уравнение f(x)=0 и записываем корни x1 и x2 в таблице.
Δ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-\frac{b}{2a}$
Δ = 0 ⇒ график касается Ox прямо в вершине параболы. Мы снова выберем два удобных значения, симметричных $-\frac{b}{2a}$. Для лучшего определения формы графика мы может выбрать другие пары значений для x, но они должны быть симметричны $-\frac{b}{2a}$.
5. Мы наносим эти значения на систему координат и строим график, соединяя эти точки.
Пример 1
f: R → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметричное 0 значение относительно 1 равно 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет иметь вид:
Пример 2
f: R → R
f(x) = -x2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b2 — 4×a×c = (-2)2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}=-1$
⇒ V(-1; 9)
1. $-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
$-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
f(-2) = 8 (симметричное 0 значение относительно -1 равно -2)
3. f(x) = 0 ⇒ -x2 — 2x + 8 = 0
Δ = 36
x1 = 2 и x2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b2 — 4×a×c = (-4)2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1. $-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ x2 — 4x + 4 = 0
Δ = 0
x1 = x2 = $-\frac{b}{2a}$ = 2
A(-2; 9)
B(0; 4)
V(2; 0)
C(4; 4)
D(5; 9)
Пример 4
f: R → R
f(x) = -x2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b2 — 4×a×c = 42 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1. $-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
$-\frac{\Delta}{4a}=-\frac{-4}{-4}=-1$
2. f(0) = -5
f(4) = -5 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ -x2 + 4x — 5 = 0,
Δ < 0
У этого уравнения нет решений.
Мы выбрали симметричные значения вокруг 2
A(-1; -10)
B(0; 5)
V(2; -1)
C(4; -5)
D(5; -10)
Если область определения не R (множество действительных чисел), а какой-то интервал, то мы стираем часть графика, которая соответствует тем значениям x, которые не находятся в данном интервале. Необходимо записать конечные точки интервала в таблице.
Пример 5
f: [0; +∞) → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-4$
2. f(0) = -3
f(2) = -3 симметричное 0 значение относительно 1 равно 2)
3. f(x) = 0 ⇒ x2 — 2x — 3 = 0,
Δ = 16
x1 = -1 ∉ [0; ∞)
x2 = 3
A(0; -3)
V(1; -4)
B(2; -3)
C(3; 0)
Чтение графиков функций.
 2 + 2(-1)x + 3\) \(—>\) \(2=-a+3\) \(—>\) \(a=1\)
2 + 2(-1)x + 3\) \(—>\) \(2=-a+3\) \(—>\) \(a=1\)
Ответ: 2)1.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Мария Иванова Мозина
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.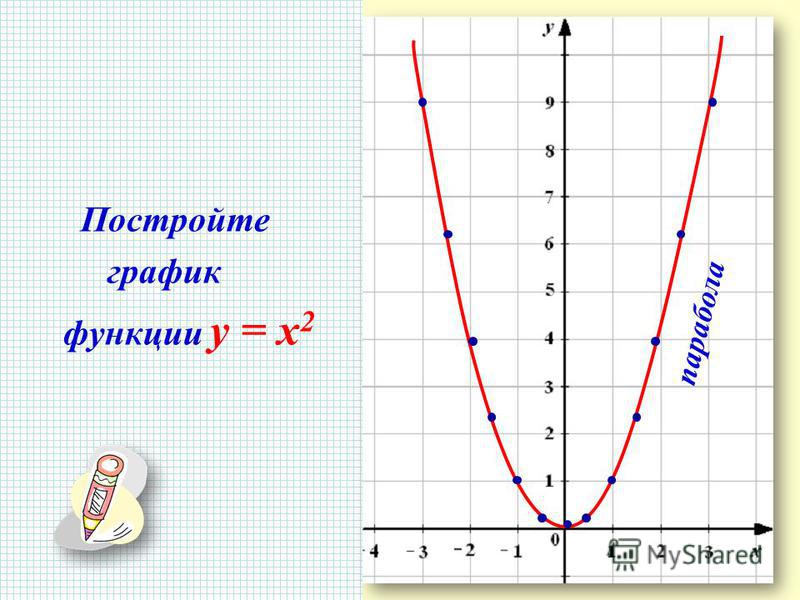 Использую классическую методику преподавания. Мои ученики получают высокие балы по ОГЭ. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Прививаю и поддерживаю интерес детей к предмету.
Использую классическую методику преподавания. Мои ученики получают высокие балы по ОГЭ. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Прививаю и поддерживаю интерес детей к предмету.
Денис Владимирович Нестюк
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы, подготовка к олимпиадам.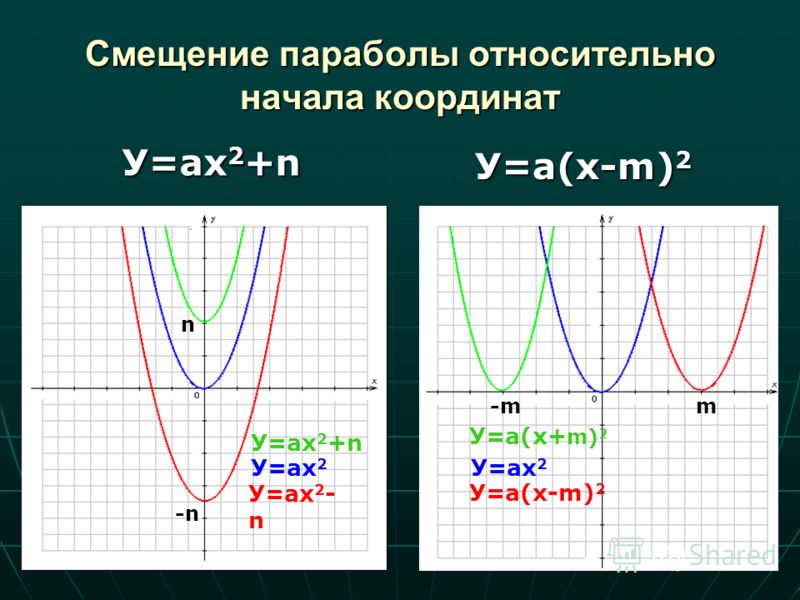 Математика всегда держит наш мозг в тонусе, помогает разобраться во многих вопросах техники, финансовых операциях. Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.
Математика всегда держит наш мозг в тонусе, помогает разобраться во многих вопросах техники, финансовых операциях. Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.
Юрий Павлович Грязнов
Репетитор по математике
Стаж (лет)
Образование:
Донецкий государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Математика двигает человечество вперёд.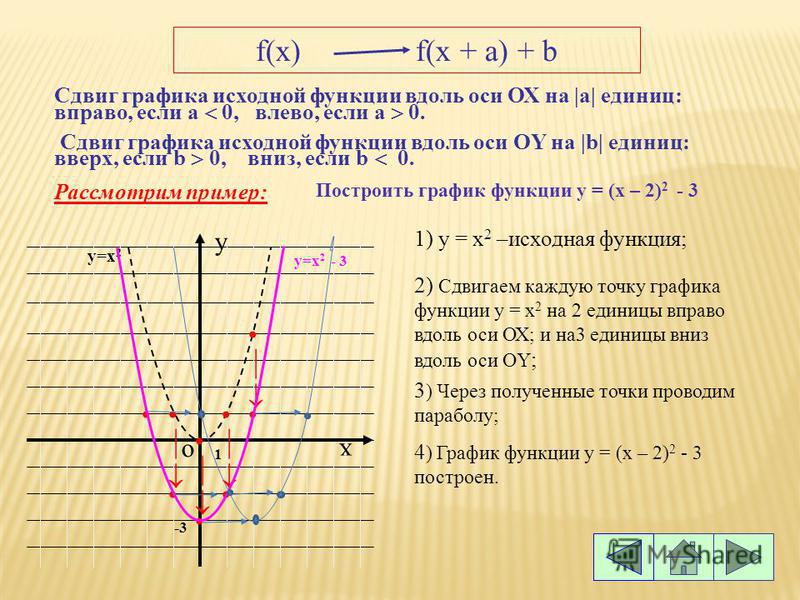 Она помогает учёным познать окружающий мир.
Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума.
Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата.
Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.
Она помогает учёным познать окружающий мир.
Я люблю математику за то, что она дисциплинирует и воспитывает ум. Это очень важно в современном быстроменяющемся мире. Недаром говорят, что математика – это гимнастика ума.
Приоритетом для меня является всестороннее развитие умственных способностей своих учеников, в особенности логического и творческого мышления на основе глубокого знания и понимания предмета. Мне важно видеть реальную позитивную динамику роста моего ученика от урока к уроку, применять индивидуальный подход для достижения необходимого результата.
Самое главное в работе с детьми — настроиться на их волну. Для меня главное, чтобы обучение проходило в непринужденной и доброжелательной атмосфере, чтобы, получая новые знания, ребенок раскрыл и приумножил свои способности, чтобы полученный результат порадовал его и послужил основой для дальнейшего развития.
Похожие статьи
- Жизни математиков (часть 1)
- Декартова прямоугольная система координат, координаты точек
- Примеры решения уравнений: логарифм с переменным основанием
- РУДН: факультет ветеринарии
- РУДН: Физика (факультет)
- Площадь трапеции
- И снова про логарифмические неравенства
- ЕГЭ по математике, базовый уровень.
 Задачи с показательными уравнениями и неравенствами
Задачи с показательными уравнениями и неравенствами
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
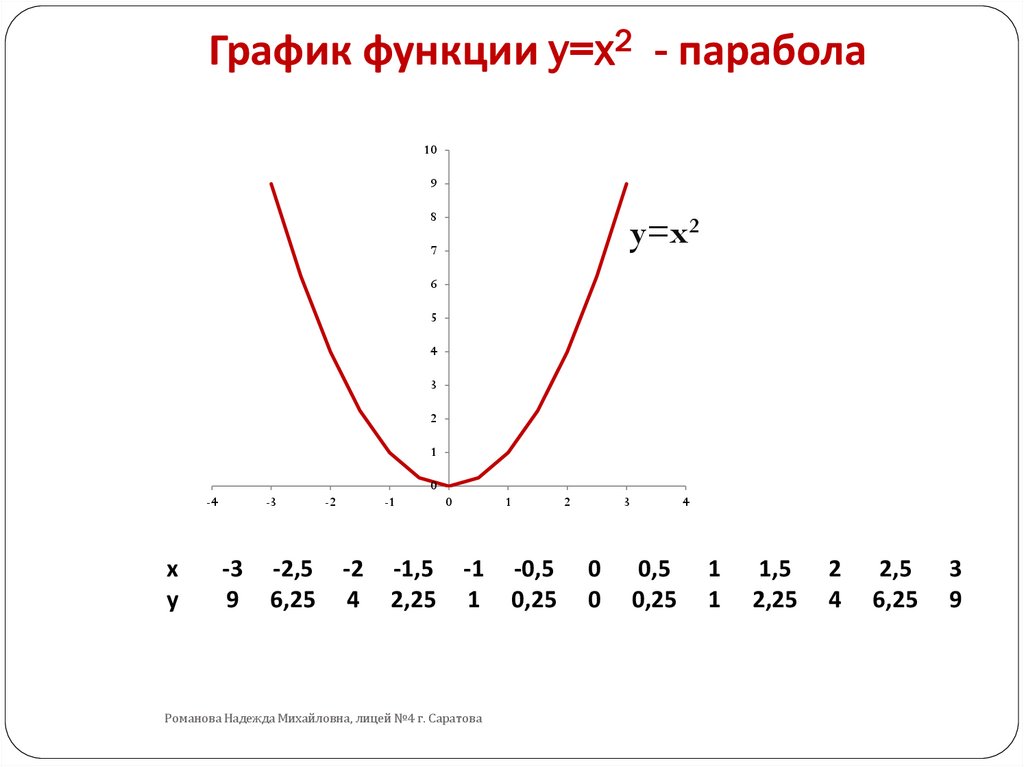
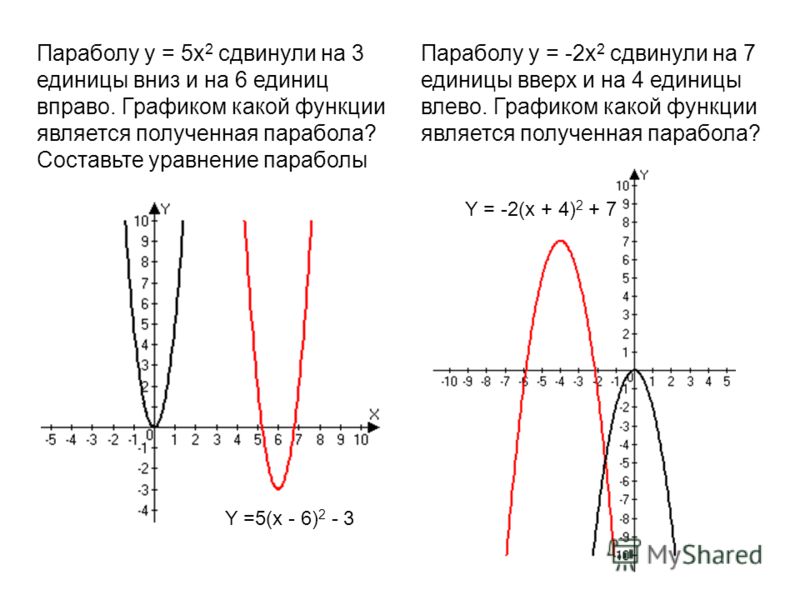
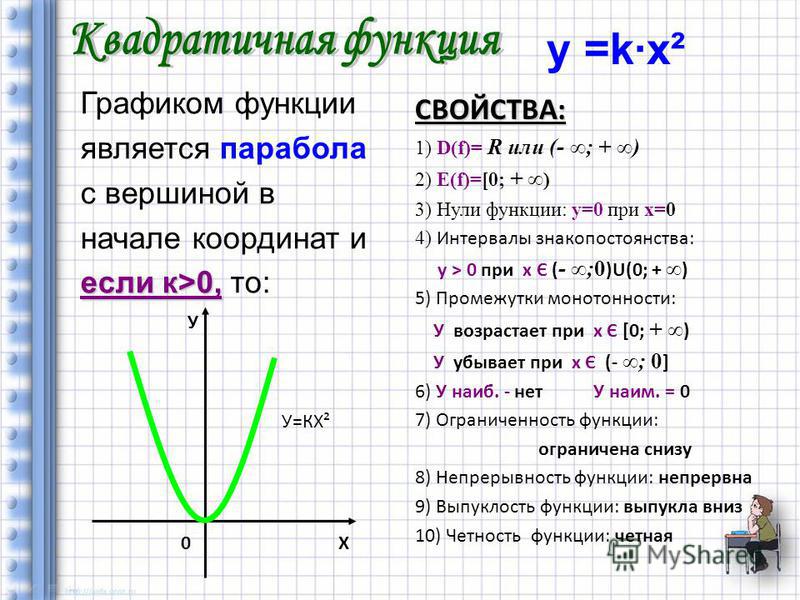
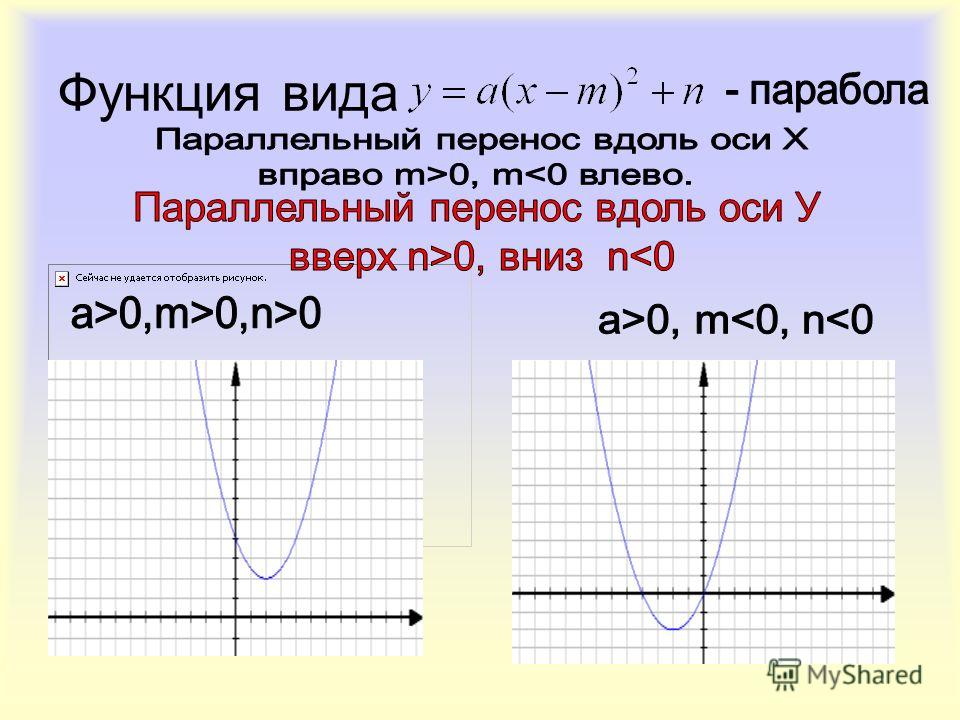
Квадратичная функция и её график
Вершина этой параболы находится в точке (0; 0). И не забудь про то, что ветви параболы бесконечно поднимаются ввысь и не ограничены точками с координатами (3; 9) и (3; -9).
Еще одна стандартная парабола задается функцией y = —x2 (в этом случае а = -1). Для этого графика я тоже напишу табличку:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
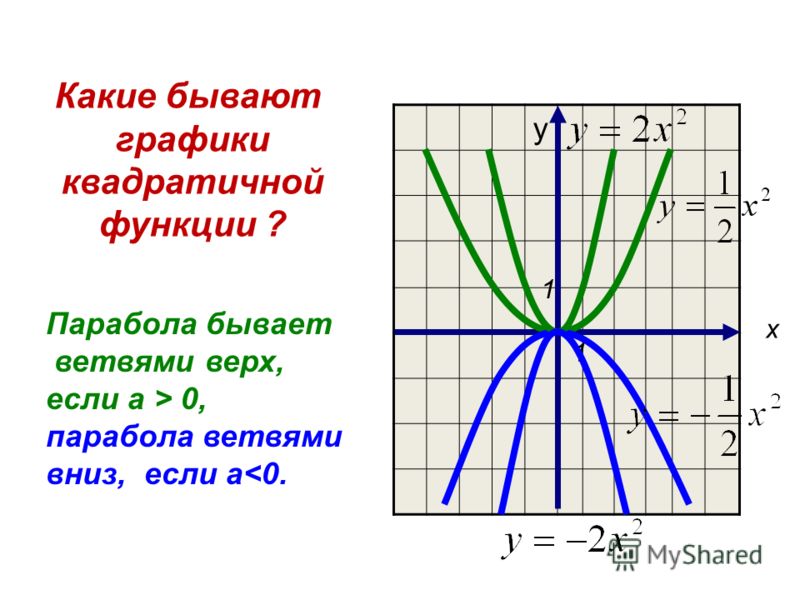
Сразу напрашивается вывод: если перед х2 стоит положительное число, то ветви параболы направлены вверх, если отрицательное — то вниз.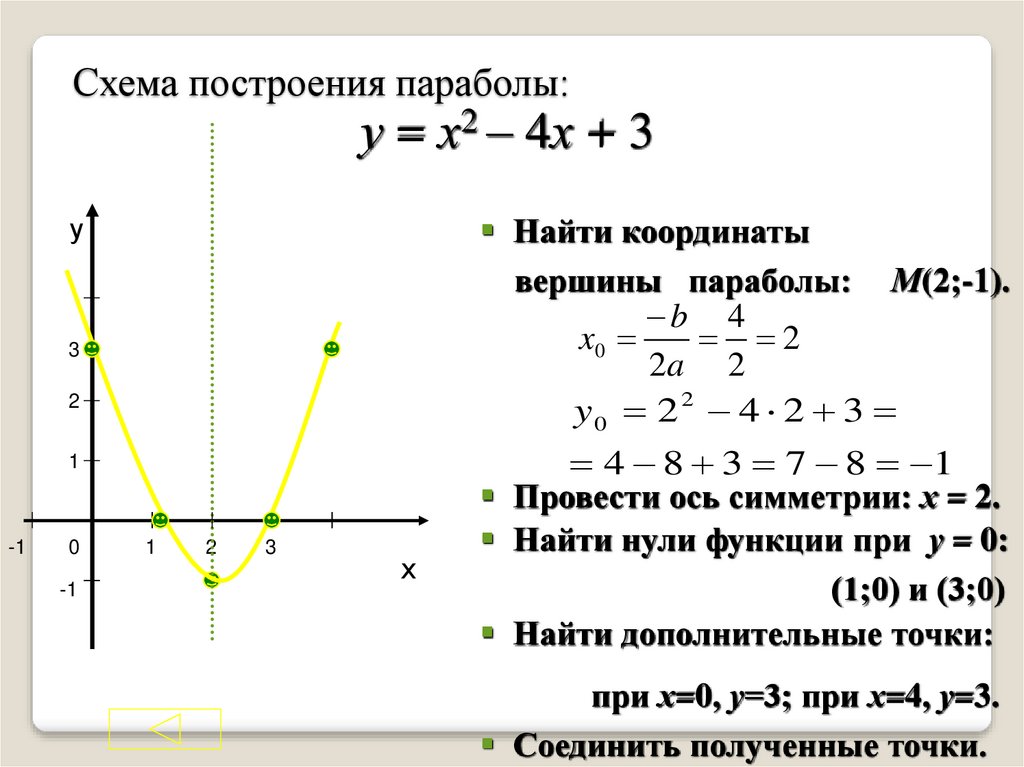
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x2 + bx + c (обязательно коэффициент перед х2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
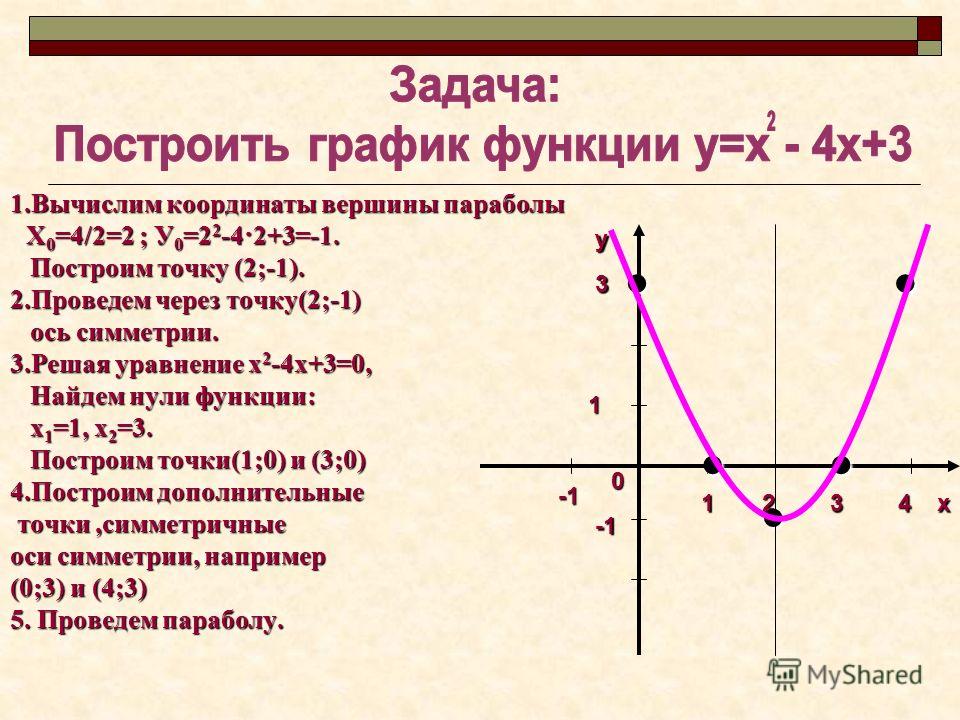
Пример 1.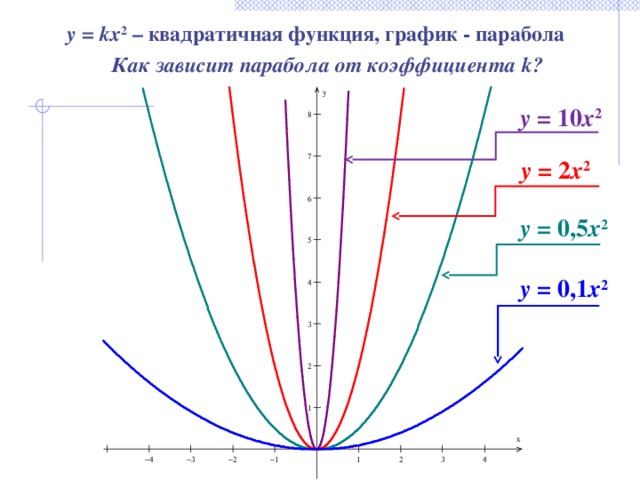
Дана функция y = x2 — 4x + 4. Найдите вершину параболы и постройте график.
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Итак, получили, что О(2; 0) — вершина параболы. Отмечаем ее на координатной плоскости.
Перед х2 стоит положительное число, значит ветви параболы направлены вверх. Наша задача: нарисовать стандартную параболу, представив, что точка О — начало координат. Если тебе это сложно сделать, то необходимо начертить таблицу значений и уже по ней рисовать параболу.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
А если числовой коэффициент лежит в промежутке (-∞; -1) ∪ (1; +∞), то парабола будет прижиматься к оси Оу и занимать меньше места на плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Пусть вершиной первой параболы будет точка А(хА; уА), а вершиной второй параболы — точка B(хB; уB). Вершины буду находить по второму способу (см. выше).
Переходим к таблицам значений.
Голубая парабола.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
Зеленая парабола.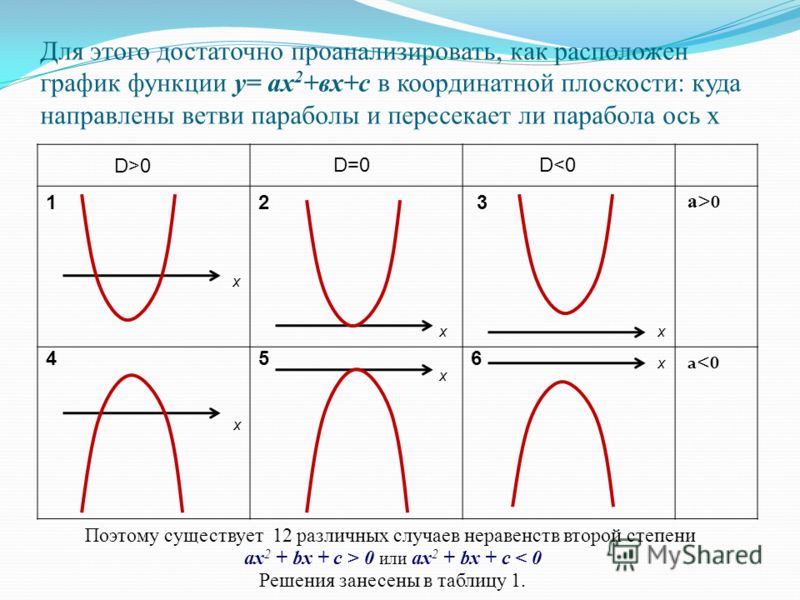
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
А ты заметил, что свободный член в уравнении функции — это точка пересечения графика с осью Оу? В обеих функциях свободный член равен 3 и графики пересекают ось Оу в точке с координатами (0; 3).
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.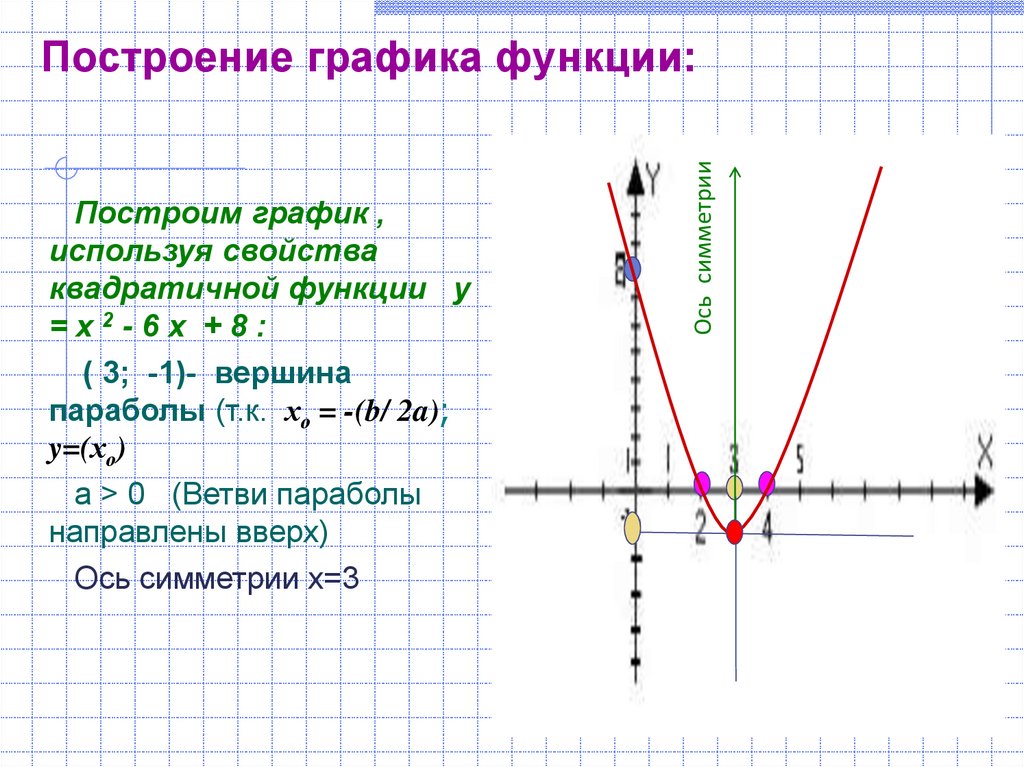
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
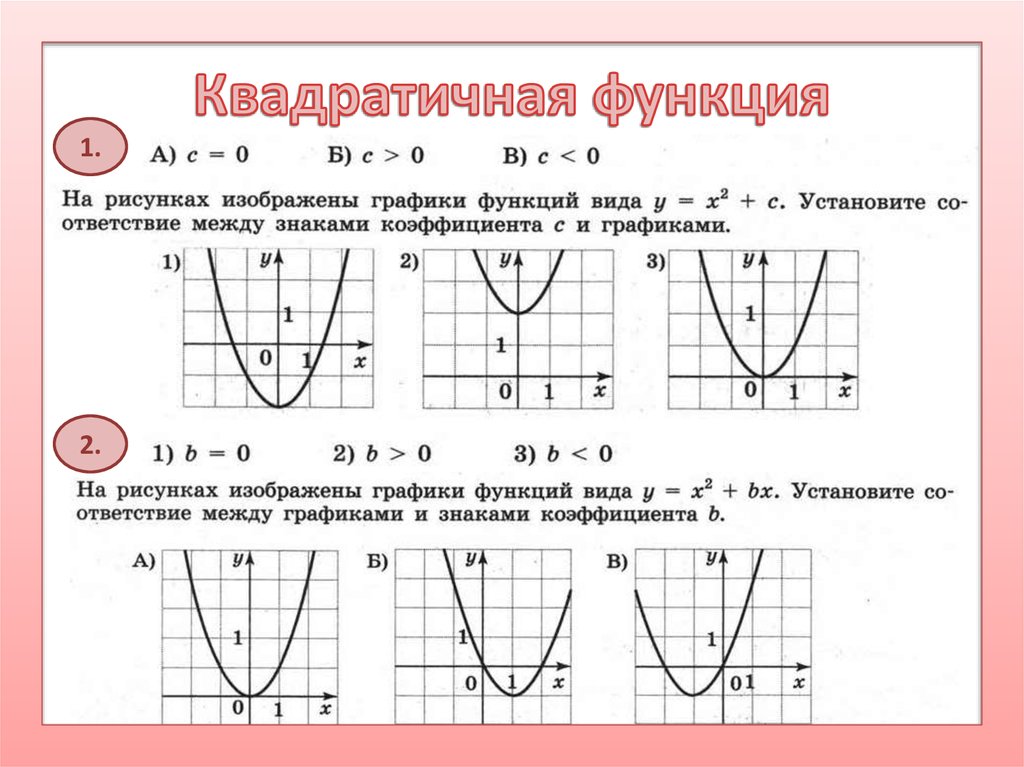
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
Решение. Коэффициент а, стоящий перед х2, отвечает за направление ветвей параболы, а свободный член с — за пересечение графика с осью Оу.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля.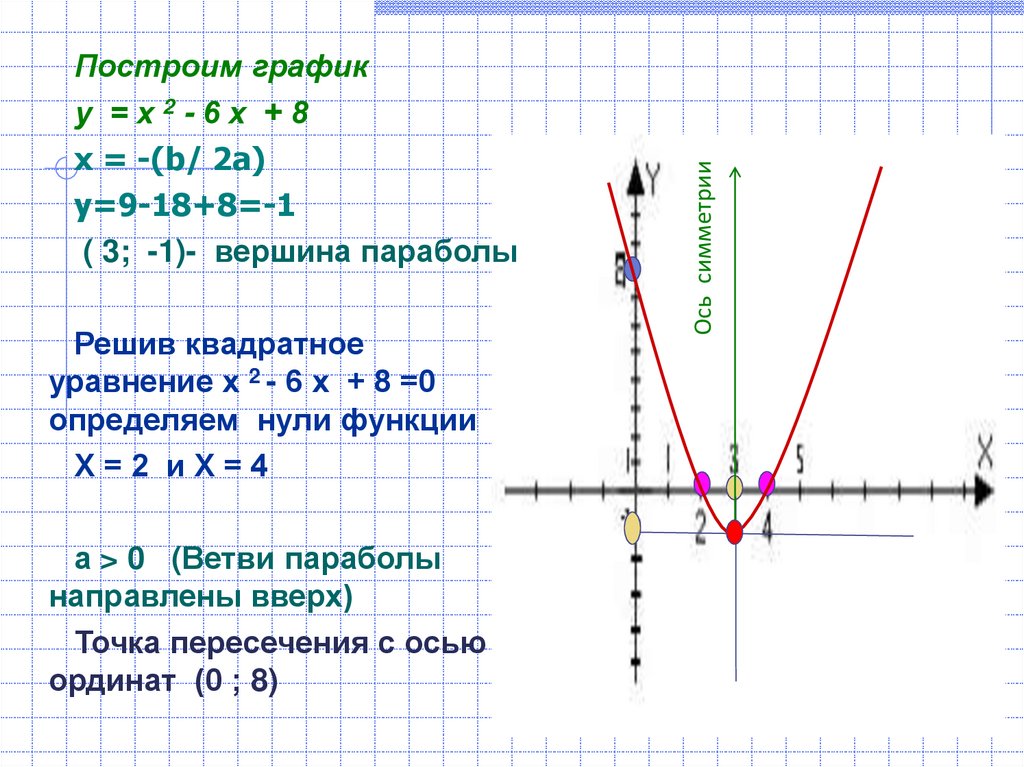 Подходит график 2.
Подходит график 2.
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с < 0. Подходит вариант под номером 1.
В) Ветви направлены вниз, значит а < 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 2.
Задание 3. Установите соответствие между графиками и их функциями.
График В отличается от остальных тем, что его ветви направлены вниз. За направление ветвей отвечает коэффициент перед х2 — он отрицательный.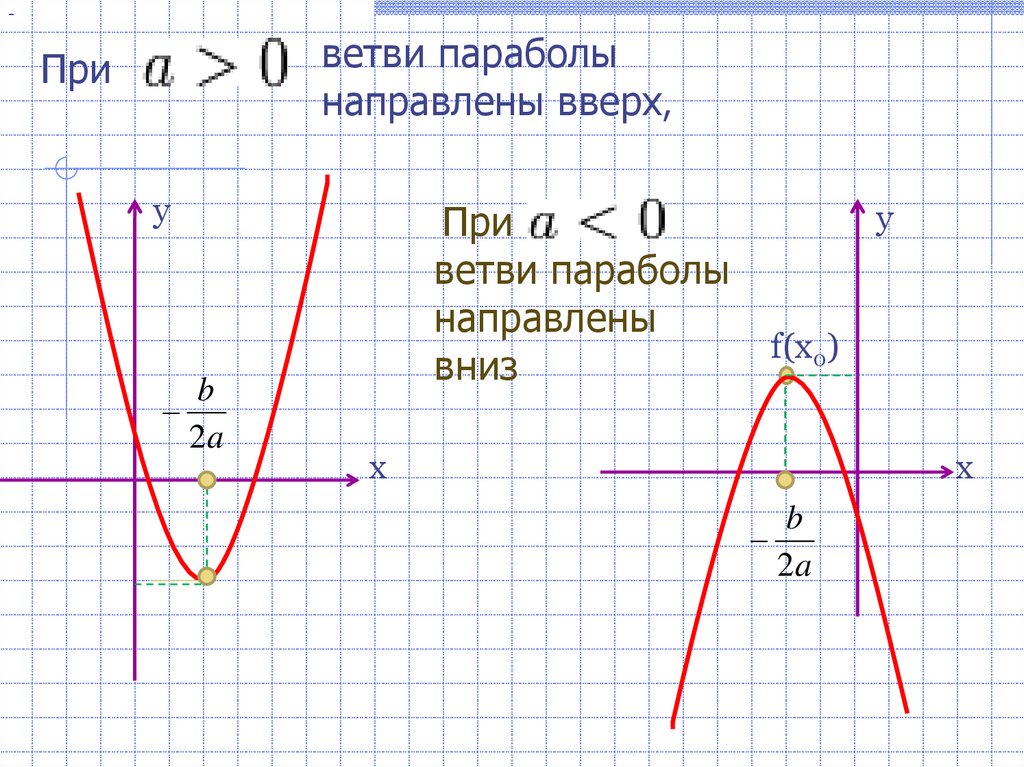 Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Отрицательный коэффициент только в функции под номером 3. Значит В-3.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
Итак, рассматриваем график А и выбираем на нем точку с красивыми координатами (красивые значит не дробные). Мне нравится тут вершина. Ее координаты (4; -3). Даже не спрашивайте почему не прорисованы оси; эти задания взяты с сайта ФИПИ)
Теперь эти координаты подставляем в оставшиеся функции: вместо у подставляем -3, а вместо х подставляем 4.
Подставляем в первую функцию: -3 = 2 · 42 — 16 · 4 + 29; -3 = -3 — верно. Значит, А-1.
И остается Б-2.
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
Очевидно, что В-2.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Подставляем в функцию А: 1 = (-4)2 + 4 · (-4) + 1; 1 = 1 — верно.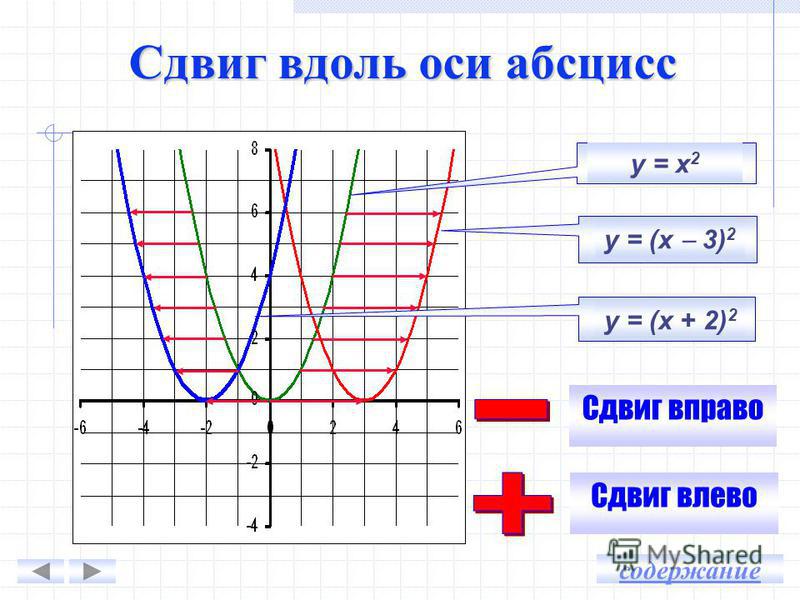 Значит, А-1.
Значит, А-1.
Соответственно, Б-3.
Если ты считаешь, что чего-то не хватает или у тебя есть ещё задания из первой части, связанные с параболами, — напиши мне в VK)
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
 Введите свой запрос: Введите свой запрос: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Является ли парабола функцией? (Плюс 8 других вопросов о параболах) – JDM Educational
Параболы часто встречаются в математике.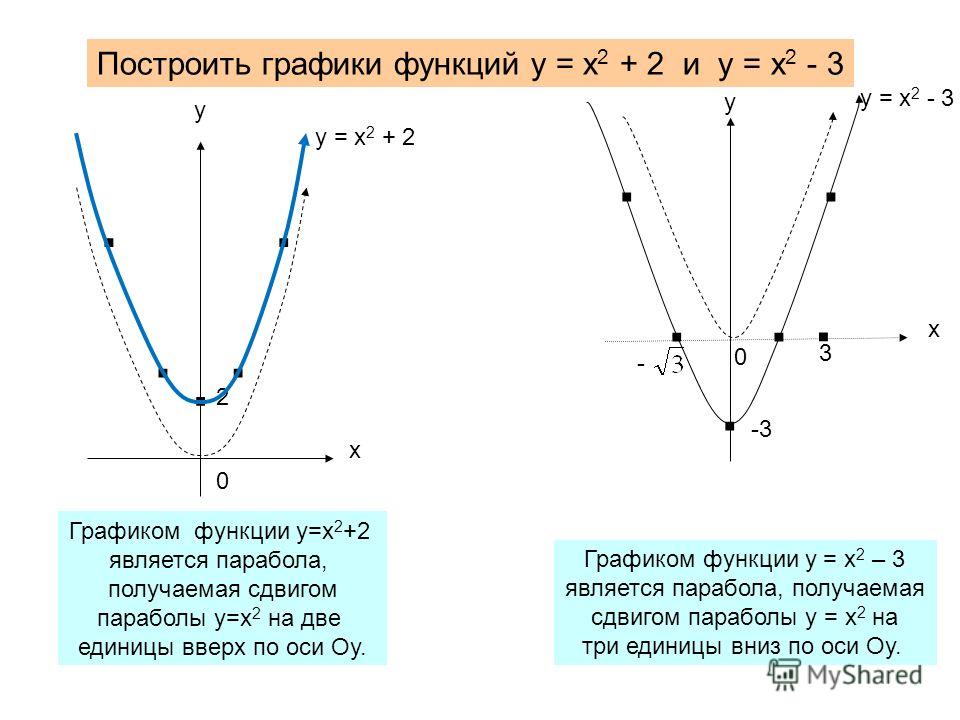 Эти графики имеют красивую симметрию и полезны для решения квадратных уравнений, но являются ли они функциями?
Эти графики имеют красивую симметрию и полезны для решения квадратных уравнений, но являются ли они функциями?
Итак, является ли парабола функцией? Парабола — это график квадратичной функции, если он имеет форму y = ax 2 + bx + c (где a не равно нулю). Однако парабола не является однозначной функцией. Кроме того, «боковая» парабола вида x = ay 2 + by + c не является функцией, так как не проходит тест вертикальной линии.
Конечно, есть много других вопросов о параболах, в том числе о том, как они выглядят и как они могут пересекаться с другими формами.
В этой статье мы поговорим о параболах, отношениях и функциях. Мы также рассмотрим, как применить тест вертикальной линии и тест горизонтальной линии к параболе.
Начнем.
Является ли парабола функцией?
Парабола является функцией, если она имеет вид:
y = ax 2 + bx + c, (где a не равно нулю)
или эквивалент:
f(x) = ax 2 + bx + c, (где a не равно нулю)
Помните, что парабола — это график квадратного уравнения (некоторые параболы — четные функции). Набор упорядоченных пар на графике параболы является отношением, но как мы можем доказать, что это функция?
Набор упорядоченных пар на графике параболы является отношением, но как мы можем доказать, что это функция?
(Чтобы напомнить о разнице между функцией и отношением, прочитайте мою статью здесь).
Мы можем использовать тест на вертикальную линию , чтобы доказать, что парабола является функцией (точнее, парабола является квадратичной функцией). Помните, что тест вертикальной линии применяется при просмотре графика отношения:
- Если мы можем провести вертикальную линию, пересекающую график более одного раза, то отношение не является функцией.
- Если любая вертикальная линия, которую мы можем провести, пересекает график не более одного раза, то отношение является функцией.
В случае с параболой мы видим, что любая вертикальная линия будет пересекать график только один раз.
Любая заданная вертикальная линия будет пересекать параболу только в одной точке, что означает, что парабола проходит тест вертикальной линии и является функцией.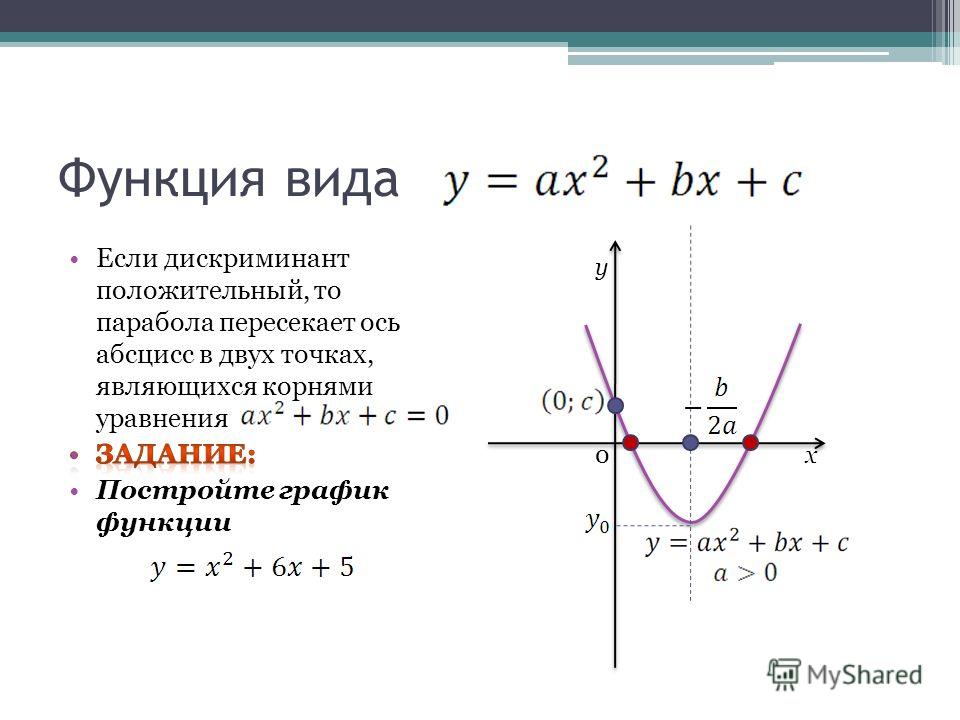
С точки зрения алгебры вертикальная линия имеет форму x = d. Если мы подставим это значение в уравнение параболы, мы получим единственное значение y: в частности, y = ad 2 + bd + c.
Поскольку парабола имеет только один выход для данного входа, это функция.
Является ли парабола взаимно однозначной функцией?
Парабола не является взаимно однозначной функцией, так как она имеет повторяющиеся значения y. Для любой параболы можно найти два значения x (входы), которые приводят к одному и тому же значению y (выходы).
Например, для параболы y = x 2 мы знаем, что входные данные x = 2 и x = -2 оба приводят к результату y = 4. Таким образом, эта парабола не является однозначной.
В более общем случае, если:
- d — координата x вершины параболы (d = -b / 2a), и
- e — любое ненулевое действительное число, тогда:
значения d + e и d – e дадут нам одно и то же значение y, когда мы подставим их вместо x.
Например, парабола y = x 2 – 4x + 4 может быть переписана как y = (x – 2) 2 , что означает, что вершина находится в точке d = 2. Если мы выберем e = 1, то мы можно вычислить, что d – e и d + e равны 1 и 3.
Если мы подставим x = 1 и x = 3, мы получим одно и то же значение y: y = 1.
С визуальной точки зрения мы можем использовать горизонтальные линии, чтобы решить, является ли график функции взаимно однозначным.
Тест горизонтальной линии докажет, что парабола не является однозначной функцией. Помните, что тест горизонтальной линии применяется при просмотре графика отношения:
- Если мы можем провести горизонтальную линию, которая пересекает график более одного раза, то функция не является однозначной.
- Если любая горизонтальная линия, которую мы можем провести, пересекает график не более одного раза, то функция является однозначной.
Например, на графике ниже горизонтальная линия y = 0 (ось x) пересекает параболу y = x 2 + 4x – 5 в двух точках: (-5, 0) и (1, 0).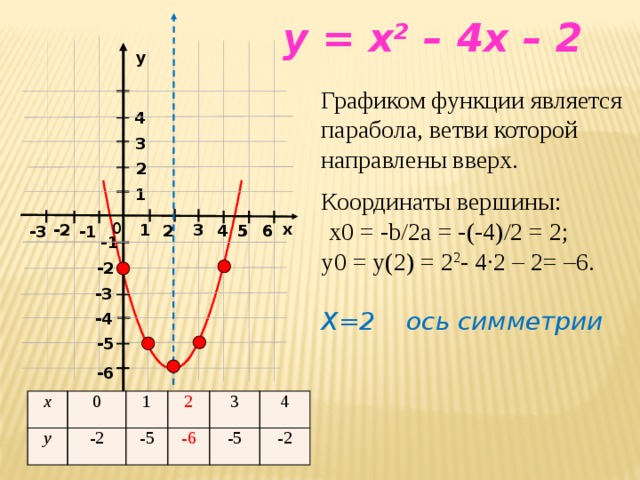
Обратите внимание, что функция «один к одному» обратима. Функция, которая не является взаимно однозначной, необратима.
Однако иногда мы можем ограничить домен, чтобы получить обратимую функцию. Например, если мы рассматриваем параболу f(x) = x 2 для неотрицательных значений x (x >= 0), то функция является взаимно однозначной, а ее обратной является функция квадратного корня с областью определения неотрицательных значений.
Может ли парабола быть боком?
Парабола может быть боковой. Оно имеет вид:
х = ау 2 + by + c (где а не равно нулю)
или его эквивалент:
f(y) = ау 2 + by + c (где а не равна нулю)
Однако «боковая» парабола такого вида не является функцией. Мы можем увидеть это, используя тест вертикальной линии на графике параболы.
Например, при боковой параболе x = y 2 вертикальная линия x = 9 пересечет график дважды:
Боковая парабола x = y 2 пересекает вертикальную линию x = 9 в двух местах: в точках (3, 9) и (-3, 9), что означает, что она не проходит тест вертикальной линии (это не функция).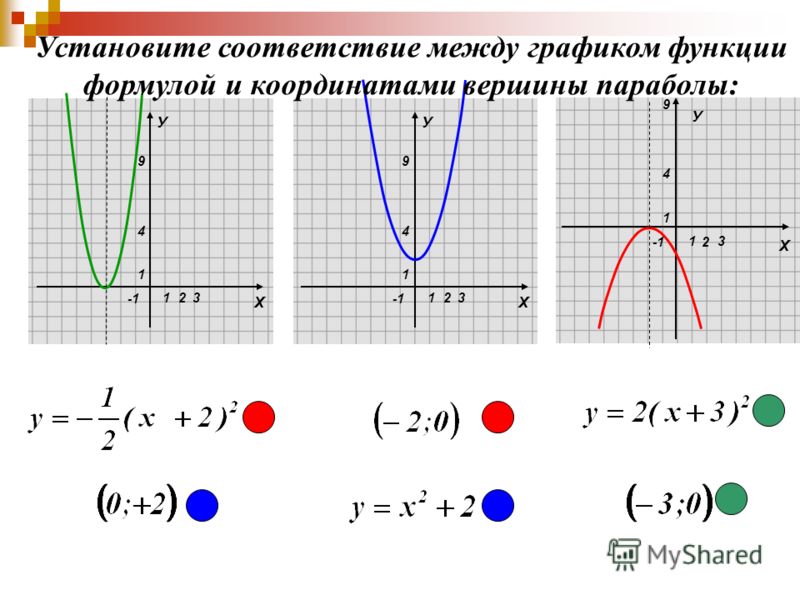
Мы также можем показать это алгебраически:
- x = y 2
- 9 = y 2
- y = +3, -3
Итак, этот график не является отношением.
Может ли парабола быть перевернутой?
Парабола может быть перевернутой (мы также говорим, что она открывается вниз). Это происходит, когда старший коэффициент x 2 , если отрицательный (то есть когда a < 0).
С другой стороны, парабола открывается вверх, если старший коэффициент x 2 положителен (то есть, когда a > 0).
Например, график y = -x 2 представляет собой «перевернутую» параболу, которая открывается вниз. Это потому, что его старший коэффициент -1 (коэффициент x 2 ) отрицателен. (Значения y этого квадратичного выражения всегда отрицательны или равны нулю).
«Перевернутая» парабола y = -x 2 имеет a = -1, что означает, что его старший коэффициент отрицательный, поэтому он открывается вниз.
Может ли парабола быть асимметричной?
Парабола не может быть асимметричной. По определению парабола имеет симметричный график.
Парабола — это график квадратичного уравнения, а квадратное всегда имеет 2 решения, которые находятся на равном расстоянии от линии симметрии параболы (вертикальная линия, проходящая через вершину x = -b / 2a).
Исключением (для действительных чисел) является случай, когда дискриминант отрицателен (два комплексных решения) или равен нулю (одно действительное повторяющееся решение).
Может ли парабола пересекать окружность?
Парабола может пересекать окружность. Однако не каждая парабола пересекает каждую окружность.
Пример 1: Парабола и окружность, пересекающиеся в двух точках
Рассмотрим окружность x 2 + y 2 = 1, которая представляет собой окружность с радиусом 1 и центром в начале координат (0, 0) .
Парабола y = x 2 дважды пересечет окружность – и мы можем решить для этих двух точек:
- x 2 + y 2 = 1 [Оберное уравнение]
- Y + Y 2 = 1 [Заменитель Y = X 2 из уравнения Parabola]
- Y 2007.
 + y – 1 = 0 [найти стандартную форму квадратного уравнения]
+ y – 1 = 0 [найти стандартную форму квадратного уравнения]
Используя квадратичную формулу с a = 1, b = 1 и c = -1, мы получаем:
Два решения квадратной формулы г 2 + г – 1 = 0 .Пример 2. Парабола и окружность, пересекающиеся в одной точке
Рассмотрим окружность x 2 + y 2 = 1, которая представляет собой окружность с радиусом 1 и центром в начале координат (0, 0).
Парабола y = x 2 + 1 пересечет окружность один раз – и мы можем решить для этой точки: x 2 + 1) – 1 + y 2 = 1 [добавьте 1 и вычтите 1 слева, что на самом деле прибавит 0]
Используя квадратичную формулу с a = 1, b = 1 и c = -2, мы получаем:
y = 1 и y = -2
Если мы подставим y = -2 в уравнение окружности, получаем:
- х 2 + у 2 = 1
- х 2 + (-2) 2 = 1
- x 2 + 4 = 1
- x 2 = -3
Это приводит к двум воображаемым ответам, которые не находятся на график.
Однако, если мы подставим y = 1 в уравнение окружности, мы получим x = 0.
Итак, окружность и парабола пересекаются в одной точке: (0, 1). Это вершина (самая низкая точка) параболы и вершина (самая высокая точка) окружности.
Пример 3: Парабола и окружность, не пересекающиеся
Рассмотрим окружность x 2 + y 2 = 1, которая представляет собой окружность с радиусом 1 и центром в начале координат (0, 0).
Парабола y = x 2 + 5 вообще не будет пересекать окружность – и мы можем доказать это алгебраически: (x 2 + 5) – 5 + y 2 = 1 [добавьте 6 и вычтите 6 слева, что на самом деле прибавит 0]
Используя квадратичную формулу с a = 1, b = 1 и c = -6, мы получаем y = -3 и y = 2.
Если мы подставим y = -3 в уравнение окружности, мы получить:
- х 2 + у 2 = 1
- х 2 + (-3) 2 = 1
- x 2 + 9 = 1
- x 2 = -8
Это приводит к двум воображаемым ответам, которых нет на графике.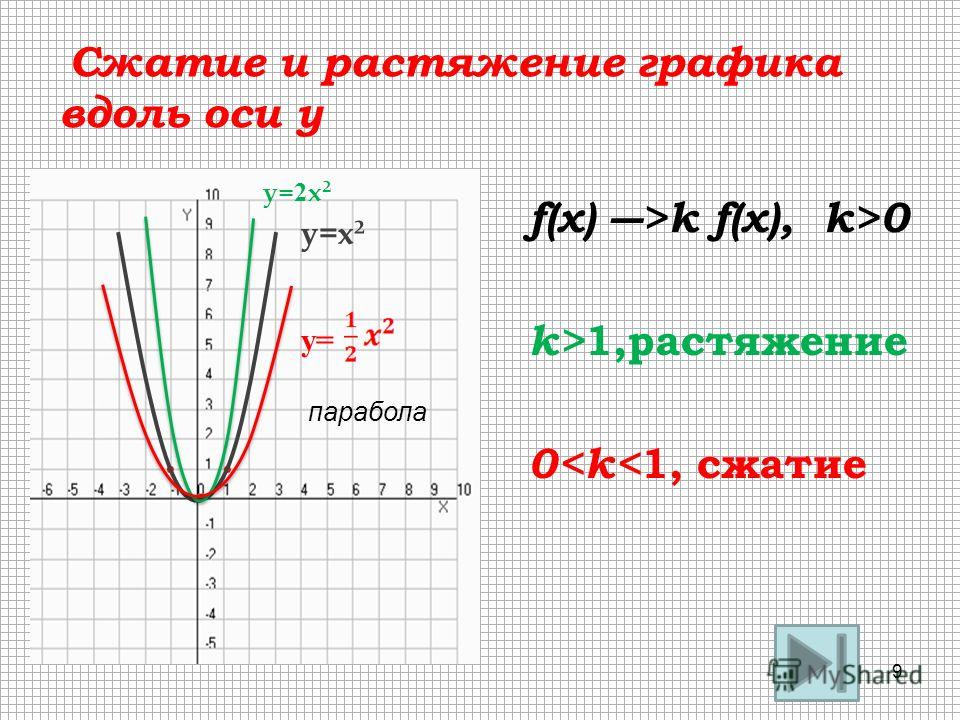
Если мы заменим y = 2 в уравнение круга, мы получаем:
- x 2 + y 2 = 1
- x 2 + (2) 2 = 1
- x 2. + 4 = 1
- x 2 = -3
Это также приводит к двум воображаемым ответам, которых нет на графике.
Итак, окружность и парабола никогда не пересекаются. Вершина (самая низкая точка) параболы находится в точке (0, 5), что на 4 единицы выше вершины (самой высокой точки) круга.
Может ли парабола быть окружностью?
Парабола не может быть окружностью. В их уравнениях есть тонкая разница.
В уравнении круга есть x 2 и y 2 члены . Например:
- x 2 + y 2 = 16 [круг радиусом 4 с центром в начале координат (0, 0)]
С другой стороны, уравнение параболы имеет только один «квадратный» член : либо x 2 , либо y 2 (но не оба). Например:
Например:
- y = x 2
- Y = 2x 2 + 5x — 3
- x = Y 2 — 2y + 1
CAN BAIN A A PARABOLA A BE A A Прямая линия?
Парабола не может быть прямой линией. Парабола — это график квадратичной функции, поэтому она имеет вид:
- y = ax 2 + bx + c, (где a не равно нулю)
тогда как строка имеет вид:
- y = где dx + e или e , может быть нулевым)
Парабола получается из уравнения, в котором член x 2 имеет ненулевой коэффициент (то есть а не равно нулю). Линия получается из уравнения, в котором член x 2 имеет нулевой коэффициент.
Является ли парабола полиномиальной функцией?
Парабола — полиномиальная функция. Парабола — это график квадратичной функции, представляющей собой особый тип полиномиальной функции.
Квадратичная функция — это полиномиальная функция степени 2 (т.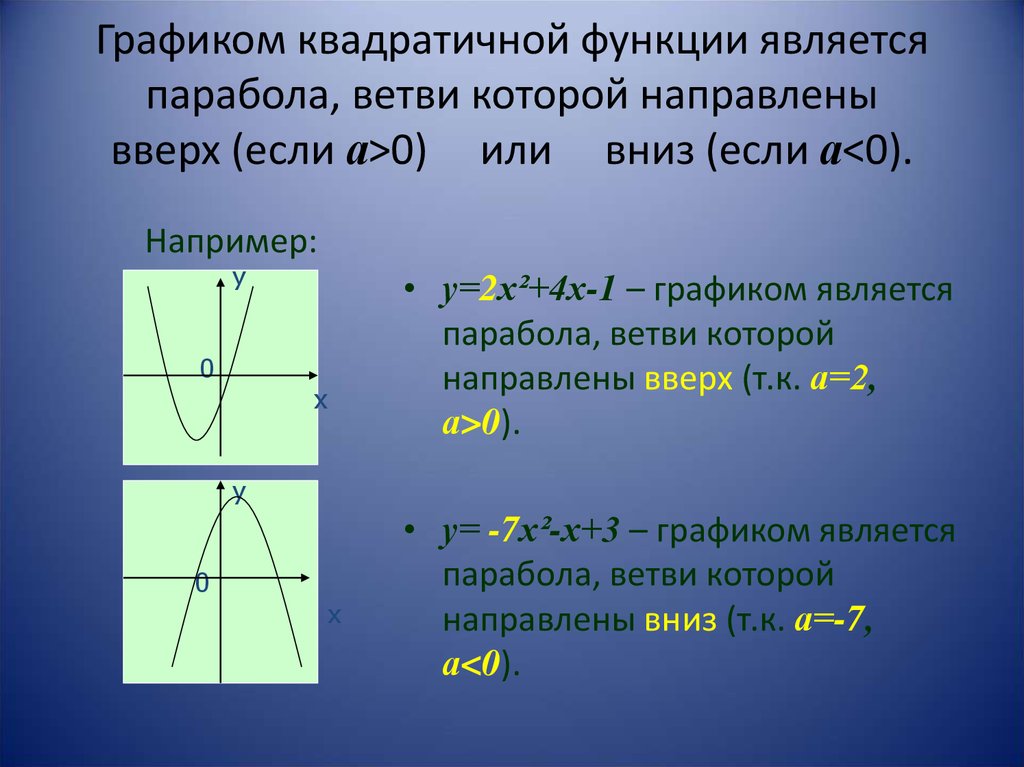 е. наивысшая степень x равна 2).
е. наивысшая степень x равна 2).
Заключение
Теперь вы знаете все о параболах и их классификации (они являются функциями, если они не «боковые», и они не являются взаимно однозначными). Вы также знаете ответы на некоторые другие вопросы о параболах и их значении. выглядит как.
Вы можете узнать о том, как решать и изображать квадратные неравенства в моей статье здесь, или как изменить форму параболы в моей статье здесь.
Вы также можете прочитать мою статью о том, когда квадратное уравнение имеет действительные корни, или мою статью о квадратичном факторизованном виде и о том, что она может вам рассказать.
Вы можете узнать, как найти область определения и диапазон параболы здесь.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
~Джонатон
Графики квадратичных функций | безграничная алгебра |
Части параболы
График квадратичной функции представляет собой параболу, и его части предоставляют ценную информацию о функции.
Цели обучения
Описать составные части и особенности парабол
Ключевые выводы
Ключевые моменты
- График квадратичной функции представляет собой U-образную кривую, называемую параболой.
- Знак перед коэффициентом
aaa
квадратичной функции влияет на то, открывается ли график вверх или вниз. Еслиa<0a<0a<0
, то график нахмурится (развернется вниз), а еслиa>0a>0a>0
, то график улыбнется (развернется). - Крайняя точка (максимум или минимум) параболы называется вершиной, а осью симметрии является вертикальная линия, проходящая через вершину.
- Точки пересечения x — это точки, в которых парабола пересекает ось x . Если они существуют, точки пересечения x представляют собой нули или корни квадратичной функции.
Ключевые термины
- вершина : точка, в которой парабола меняет направление, соответствующее минимальному или максимальному значению квадратичной функции.

- ось симметрии : Вертикальная линия, проведенная через вершину параболы, относительно которой парабола симметрична. 9{2}+bx+cf(x)=ax2+bx+c
.
где
aaa
,
bbb
и
ccc
константы, а
a≠0909a\neq 0a
График квадратичной функции представляет собой U-образную кривую, называемую параболой. Эта форма показана ниже.
Парабола : График квадратичной функции представляет собой параболу.
На графиках квадратичных функций знак перед коэффициентом
aaa
влияет на то, открывается ли график вверх или вниз. Если
a<0a<0a<0
, то график нахмурится (развернется вниз), а если
a>0a>0a>0
, то график улыбнется (развернется).
 Это показано ниже.
Это показано ниже.Направление параболы: Знак перед коэффициентом
ааа
определяет направление параболы.
Характеристики парабол
Параболы имеют несколько узнаваемых особенностей, характеризующих их форму и расположение на декартовой плоскости.
Вершина
Одной из важных особенностей параболы является то, что она имеет крайнюю точку, называемую вершиной. Если парабола раскрывается, вершина представляет собой самую низкую точку на графике или минимальное значение квадратичной функции. Если парабола открывается вниз, вершина представляет собой самую высокую точку на графике или максимальное значение. В любом случае вершина является поворотной точкой на графе.
Ось симметрии
Параболы также имеют ось симметрии, которая параллельна оси Y. Ось симметрии представляет собой вертикальную линию, проведенную через вершину.

гггг
-перехватТочка пересечения y — это точка, в которой парабола пересекает ось y . Таких точек на графике квадратичной функции может быть не более одной. Если бы они были, кривая не была бы функцией, так как было бы два значения
yyy
для одного значения
xxx
, равного нулю.
ххх
-перехватыТочки пересечения x — это точки, в которых парабола пересекает x — ось. Если они существуют, то пересечения x представляют собой нули или корни квадратичной функции, значения
xxx
, при которых
y=0y=0y=0
. Может быть ноль, один или два
xxx
-перехвата. Количество
xxx
-перехватов варьируется в зависимости от расположения графика (см.
 диаграмму ниже).
диаграмму ниже).Возможно
xxx
-пересечения: Парабола может не иметь пересечений по оси x, иметь одно пересечение по оси x или два пересечения по оси xНапомним, что если квадратичная функция равна нулю, то результатом является квадратное уравнение. Решения уравнения называются корнями функции. Это те же самые корни, которые можно наблюдать как
xxx
-пересечения параболы. Обратите внимание, что для парабол с двумя точками пересечения
xxx
вершина всегда попадает между корнями. В связи с тем, что параболы симметричны, координата
xxx
вершины находится точно в середине
xxx
-координаты двух корней.
Графическая интерпретация квадратных решений
Корни квадратичной функции можно найти алгебраически или графически.
: График, показывающий параболу на декартовой плоскости, включая точки, в которых она пересекает ось x. 2-4ac}}{2a })(x=2a−b±b2−4ac 92 — x — 2f(x)=x2−x−2
2-4ac}}{2a })(x=2a−b±b2−4ac 92 — x — 2f(x)=x2−x−2Обратите внимание, что парабола пересекает ось
xxx
в двух точках:
(−1,0)(-1, 0)(−1,0)
и
(2,0)( 2, 0)(2,0)
. Напомним, что
xxx
-пересечения параболы указывают на корни или нули квадратичной функции. Следовательно, есть корни в 92-4(1)(-2)}}{2(1)}x=2(1)−(−1)±(−1)2−4(1)(−2)
Упрощая, имеем:
x=1±92x = \dfrac{1 \pm \sqrt {9}}{2} \\x=21±9
и
x=1±32x = \dfrac{1 \pm 3}{2}x=21±3
Теперь у нас есть два возможных значения для x:
1+32\frac{1+3}{2}21+3
и
1−32\frac{1-3}{2}21−3
.

Уменьшаются до
x=2x = 2x=2
и
x=−1x = — 1x=−1
92 — 4x + 4f(x)=x2−4x+4 .: График вышеуказанной функции с вершиной, помеченной как(2,1)(2, 1)(2,1)
.
Глядя на график функции, замечаем, что он не пересекает
xxx
-ось. Следовательно, у него нет настоящих корней .
Мы можем проверить это алгебраически. Сначала определите значения коэффициентов:
a=1a = 1a=1
,
b=−4b = — 4b=−4
, и 92-4(1)(5)}}{2(1)}x=2(1)−(−4)±(−4)2−4(1)(5)
Упрощая, имеем:
x=4±16−202x=4±42x=\dfrac{4 \pm \sqrt {16-20}}{2} \\ x=\dfrac{4 \pm \sqrt {-4}}{2}x=24±16−20
x=24±−4
Обратите внимание, что у нас есть
−4\ sqrt{-4}−4
в формуле, которая не является действительным числом.
 Следовательно, у данной квадратичной функции нет действительных корней . Мы пришли к тому же заключению, к которому пришли графически.
Следовательно, у данной квадратичной функции нет действительных корней . Мы пришли к тому же заключению, к которому пришли графически.Графики квадратных уравнений в форме вершин
Вершинная форма квадратичной функции позволяет легко найти ее вершину.
Цели обучения
Объясните значения констант
AAA
,
HHH
и
KKK
для квадратичного уравнения в форме вершины
Ключевые Takeaways
. Идентификатор, связанный с инвариантным значением. 92+kf(x)=a(x+h)2+k
, вершина будет
(−h,k).(-h,k).(−h,k).
Коэффициент
aaa
как и прежде контролирует, раскрывается ли парабола вверх или вниз, а также скорость увеличения или уменьшения параболы.

Преобразование вершинной формы в стандартную форму
Если вы хотите преобразовать квадратное число в вершинной форме в квадратное число в стандартной форме, просто умножьте квадрат и объедините одинаковые члены. Например, квадратичный 92×2
(тот, который мы называем
aaa
) равен
111
. В этом случае мы смотрим на коэффициент
xxx
(тот, который мы называем
bbb
) и берем половину от него. Затем возводим это число в квадрат. Таким образом, для этого примера мы делим
444
на
222
, чтобы получить
222
, а затем возводим в квадрат, чтобы получить
9001 2 444.
Затем мы складываем и вычитаем это число следующим образом: 92+2.
 у=(х+2)2+2.
у=(х+2)2+2.Наше уравнение теперь имеет форму вершины, и мы видим, что вершина равна
(−2,2).(-2,2).(−2,2).
Преобразование Когда
a≠1a \neq 1a=1
Чуть сложнее преобразовать стандартную форму в вершинную, когда коэффициент
aaa
не равен
111
. Мы по-прежнему можем использовать этот метод, но сначала нужно выделить
aaa
, как в следующем примере: 92+bx+cy=ax2+bx+c
.
Цели обучения
Explain the meanings of the constants
aaa
,
bbb
, and
ccc
for a quadratic equation in standard form
Key Takeaways
Key Points
Key Terms
- vertex : Максимум или минимум квадратичной функции.

- парабола : Форма, образованная графиком квадратичной функции. 92.у=3х2.
Черная кривая выглядит тоньше, потому что ее коэффициент
aaa
больше, чем у синей кривой.
Открытие параболы вверх или вниз также контролируется
aaa
. При коэффициенте
а>0а>0а>0
парабола открывается вверх, а при коэффициенте
а<0а<0а<0
парабола открывается вниз.
Квадратики открываются вверх или вниз: 92.у=-3×2.
Открывается вниз, так как
a=−3<0.a=-3<0.a=−3<0.
.
Ось симметрии
Коэффициенты
bbb
и
aaa
вместе управляют осью симметрии параболы и
xxx
-координатой вершины.
 Ось симметрии параболы определяется как:
Ось симметрии параболы определяется как:x=−b2ax=-\dfrac{b}{2a}x=−2ab
Например, рассмотрим параболу 92-4x+4.y=2×2−4x+4.
: Ось симметрии представляет собой вертикальную линию, параллельную оси Y в точкеx=1x=1x=1
.
yyy
-пересечение ПараболыКоэффициент
ccc
контролирует высоту параболы. Точнее, это точка пересечения параболы с осью Y. Точка
(0,c)(0,c)(0,c)
является точкой пересечения
yyy
параболы. Обратите внимание, что парабола выше имеет
c=4c=4c=4
и пересекает ось
yyy
в точке
(0,4).(0,4).(0,4).
Лицензии и атрибуты
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка.
 Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
- Бесплатный проект научных текстов для средней школы, функции и графики: парабола (10 класс). . Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Квадратичная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax.
 Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike - Проект бесплатных научных текстов для средней школы, функции и графики: парабола (10 класс). . Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : ОпенСтакс. Лицензия : CC BY: Атрибуция
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Проект бесплатных научных текстов для средней школы, функции и графики: парабола (10 класс).
 . Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike - Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Лицензия : CC BY: Attribution
- Квадратичная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Заполнение квадрата. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Квадратичная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- константа.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - вершина. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- квадратичный. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
- Проект бесплатных научных текстов для средней школы, функции и графики: парабола (10 класс). . Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Квадратичная функция. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Quadratic_function#/media/File:Polynomialdeg2.svg. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Лицензия : CC BY: Attribution
- Квадратичная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- парабола. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- вершина. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- квадратичный.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
- Проект бесплатных научных текстов для средней школы, функции и графики: парабола (10 класс). . Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Квадратичная функция. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предварительное исчисление, квадратичные функции.
 Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution - Оригинальная фигура Марка Вударда. Лицензия CC BY-SA 4.0. Предоставлено : Марк Вудард. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигурка Марка Вударда. Лицензия CC BY-SA 4.0. Предоставлено : Марк Вудард. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Марка Вударда. Лицензия CC BY-SA 4.0. Предоставлено : Марк Вудард. Лицензия : CC BY-SA: Attribution-ShareAlike
- Оригинальная фигура Марка Вударда. Лицензия CC BY-SA 4.0. Предоставлено : Марк Вудард. Лицензия : CC BY-SA: Attribution-ShareAlike 92 + bx + c$$ для некоторых констант $a$, $b$ и $c$.
Нанесение набора точек для некоторых случайно выбранных квадратичных функций раскрывает некоторые интересные свойства, как показано ниже.
 Все квадратичные функции при построении имеют форму буквы «U», хотя иногда эта буква «U» оказывается перевернутой. В результате квадратичные функции имеют либо максимальное, либо минимальное значение, в зависимости от того, перевернута ли буква «U» или перевернута, соответственно. График квадратичной функции (которую мы называем парабола ) иногда кажется «широкой», иногда «узкой», а иногда чем-то средним между этими двумя крайностями. Иногда они пересекают ось $x$, образуя два пересечения $x$. В других случаях коснитесь оси $x$ только один раз или не коснитесь вообще. У них всегда есть $y$-отрезок (конечно, наш график должен быть достаточно большим, чтобы показать его).
Все квадратичные функции при построении имеют форму буквы «U», хотя иногда эта буква «U» оказывается перевернутой. В результате квадратичные функции имеют либо максимальное, либо минимальное значение, в зависимости от того, перевернута ли буква «U» или перевернута, соответственно. График квадратичной функции (которую мы называем парабола ) иногда кажется «широкой», иногда «узкой», а иногда чем-то средним между этими двумя крайностями. Иногда они пересекают ось $x$, образуя два пересечения $x$. В других случаях коснитесь оси $x$ только один раз или не коснитесь вообще. У них всегда есть $y$-отрезок (конечно, наш график должен быть достаточно большим, чтобы показать его).Посмотрим, не сможем ли мы рассмотреть каждую из этих идей более внимательно…
Во-первых, что касается вывода формы графика этой функции из ее уравнения — заметьте, все было бы проще анализировать, если бы мы могли переписать уравнение для функции, используя только одно вхождение $x$.
 2}{4a})$, где происходит максимум или минимум, мы называем 92-4ac$.
2}{4a})$, где происходит максимум или минимум, мы называем 92-4ac$.Как следствие — есть два $x$-перехвата, когда дискриминант положителен; один $x$-перехват, когда дискриминант равен нулю; и нет $x$-перехватов, когда дискриминант отрицательный.
графиков квадратичных функций | Алгебра 1 | Квадратные уравнения и функции | Графики квадратичных функций
Популярные учебные пособия
по графикам квадратичных функцийКак найти ось симметрии квадратичной функции?
Ось симметрии — это вертикальная линия, проходящая через вершину квадратного уравнения. Есть даже формула, которая поможет найти его! В этом уроке вы увидите, как найти ось симметрии для заданного квадратного уравнения.
Как найти вершину квадратичной функции?
Вершина квадратного уравнения – это точка минимума или максимума уравнения. Знаете ли вы, что можно использовать формулу для оси симметрии, чтобы найти вершину квадратного уравнения? Посмотрите этот урок и узнайте, как это делается!
Как составить таблицу для квадратичной функции?
Когда вы пытаетесь построить график квадратного уравнения, очень полезно составить таблицу значений.
 Чтобы выяснить, какие значения x использовать в таблице, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Чтобы узнать, как составить таблицу значений для квадратного уравнения, ознакомьтесь с этим руководством!
Чтобы выяснить, какие значения x использовать в таблице, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Чтобы узнать, как составить таблицу значений для квадратного уравнения, ознакомьтесь с этим руководством!Как построить график квадратичной функции?
Когда вы пытаетесь построить график квадратного уравнения, очень полезно составить таблицу значений. Прежде чем составить таблицу, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Посмотрите этот урок, чтобы узнать, как построить график квадратного уравнения!
Как найти значения a, b и c квадратичной функции?
Когда вы имеете дело с квадратными уравнениями, может быть очень полезно идентифицировать a, b и c.
 Эти значения используются для нахождения оси симметрии, дискриминанта и даже корней по квадратичной формуле. Несомненно, важно знать, как идентифицировать эти значения в квадратном уравнении. Этот урок покажет вам, как!
Эти значения используются для нахождения оси симметрии, дискриминанта и даже корней по квадратичной формуле. Несомненно, важно знать, как идентифицировать эти значения в квадратном уравнении. Этот урок покажет вам, как!Как определить, будет ли вершина квадратичной функции максимумом или минимумом?
Вершина квадратного уравнения является максимумом или минимумом функции. Но как узнать, будет ли это максимум или минимум? Посмотрите этот урок и найдите ответ на этот вопрос!
Что такое вершина квадратичной функции?
Каждое квадратное уравнение имеет либо максимум, либо минимум, а вы знали, что эта точка имеет особое имя? В квадратном уравнении эта точка называется вершиной! Взгляните на вершину квадратного уравнения, просмотрев этот урок.
Что такое ось симметрии квадратичной функции?
Вы когда-нибудь замечали, что левая часть графика квадратного уравнения очень похожа на правую часть графика? На самом деле эти стороны просто зеркальные отражения друг друга! Если бы вы разрезали график квадратного уравнения вертикально пополам в вершине, вы бы получили эти симметричные стороны.
 Та вертикальная линия, которую вы разрезаете, имеет особое имя. Она называется осью симметрии. Чтобы узнать об оси симметрии, посмотрите этот урок!
Та вертикальная линия, которую вы разрезаете, имеет особое имя. Она называется осью симметрии. Чтобы узнать об оси симметрии, посмотрите этот урок!Что такое парабола?
Если построить график линейной функции, получится линия. Если вы начертите квадратичную функцию, вы получите то, что называется параболой. Парабола имеет тенденцию выглядеть как улыбка или хмурый взгляд, в зависимости от функции. Посмотрите этот урок и узнайте больше о параболах!
Что такое максимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум. В этом уроке рассматривается максимум квадратичной функции. Проверьте это!
Что такое минимум квадратичной функции?
Когда вы имеете дело с квадратичными функциями, очень вероятно, что вы встретите максимум и минимум. В этом уроке рассматривается минимум квадратичной функции.
 Проверьте это!
Проверьте это!Что такое квадратичная функция?
Вы не можете пройти алгебру, не видя квадратичных функций. Графики квадратичных функций представляют собой параболы; они имеют тенденцию выглядеть как улыбка или хмурый взгляд. В этом уроке вы познакомитесь с квадратичными функциями, посмотрите на их графики и увидите несколько примеров квадратичных функций!
OpenAlgebra.com: графические параболы
На этом этапе нашего исследования мы должны быть в состоянии найти точки пересечения x и y и решить любое квадратное уравнение. Теперь мы изучим простой метод, используемый для их построения.
Плейлист графических парабол на YouTube
График квадратного уравнения называется параболой.
Одна из наших основных функций
можно изобразить, нанеся точки.
 Мы делаем это, выбирая около пяти x -значений и нахождение соответствующих им y -значений.
Мы делаем это, выбирая около пяти x -значений и нахождение соответствующих им y -значений.График :
Чем больше точек мы наносим, тем легче увидеть, что график имеет U-образную форму. Вершина в данном случае является точкой изменения графика с убывающей на возрастающую, или точкой с наименьшим значением y . Здесь вершина (0, 0), которая также является точкой пересечения x и y . Строка x = 0, ось y является линией симметрии . Это линия, по которой мы могли бы согнуть нашу бумагу, чтобы увидеть, что две стороны графика совпадают.
По заданному графику найдите точки пересечения x и y , вершину, 5-ю точку на графике и линию симметрии.
Линия симметрии: x = 1
точки пересечения x: (-2,0) и (4,0)
точки пересечения y: (0, -8)
Вершина: (1, — 9)
5-й пункт: (2, -8)
Напомним, что две точки определяют прямую — для парабол это не так.
 Параболы требуют минимум 3 точки, но обычно мы хотим найти по крайней мере пять точек, чтобы построить хороший график. Найдите вершину, x — и y — точки пересечения, а также линию симметрии.
Параболы требуют минимум 3 точки, но обычно мы хотим найти по крайней мере пять точек, чтобы построить хороший график. Найдите вершину, x — и y — точки пересечения, а также линию симметрии.График:
Шаг 1 : Найдите точку пересечения y (0, c ).
Шаг 2 : Найдите x — перехватывается путем установки y = 0 и решения для x .
Шаг 3 : Найдите вершину. Вы можете найти значение x вершины, используя вершину x = -b/(2a).
Шаг 4 : Нанесите точки на график и определите ось симметрии.
Область и диапазон вышеуказанной функции можно определить по графику. В предыдущей задаче домен состоит из всех действительных чисел, а диапазон состоит из всех действительных чисел, больших или равных -1.
 Также полезно отметить, что у нас минимум y -значение -1, это будет важным фактом при работе над текстовыми задачами.
Также полезно отметить, что у нас минимум y -значение -1, это будет важным фактом при работе над текстовыми задачами.Совет : осью симметрии любой квадратичной функции будет вертикальная линия
При попытке найти точки пересечения x , где результирующее квадратное уравнение не учитывается, просто используйте квадратную формулу для его решения.
График:
Эта парабола выглядит немного по-другому, обратите внимание, что она открывается вниз, а также обратите внимание, что предыдущая парабола открылась. Есть простой тест, чтобы узнать, как он открывается, еще до того, как мы начнем.
Поэтому, когда вас попросят нарисовать параболу, вы можете получить две важные части информации, не выполняя никакой работы. При осмотре вы можете сказать, открывается ли он вверх или вниз, и вы можете определить и — перехват.

Graph and label all important points :
Graph and label all important points :
Областью предыдущей задачи являются все действительные числа, а диапазон состоит из всех действительных чисел, больших или равных -5. Также обратите внимание, что минимум г -значение равно -5. Оказывается, не все параболы имеют два пересечения x , как можно было бы ожидать. Иногда у них есть только один x -intercept, а иногда и нет.
Пожалуйста, имейте в виду, что все квадратичные функции имеют вершину и точку пересечения и . Кроме того, мы все равно сможем найти другую точку, используя симметрию.
 Поэтому в некоторых случаях допустимо наносить и маркировать только три точки.
Поэтому в некоторых случаях допустимо наносить и маркировать только три точки.Отметьте и обозначьте все важные моменты:
. Сколько времени потребуется, чтобы достичь максимальной высоты? Какая максимальная высота?
Примеры видео на YouTube :
Анализ графиков квадратичных функций
Давайте начнемВведениеИнтерпретация направления и ширины квадратичных функцийИнтерпретация вершин квадратичных функцийИнтерпретация решений квадратичных функцийРезюмеСловарный запасЗанятие в журнале
Давайте исследуем реальные приложения графиков квадратичных функций. Вы будете анализировать графики квадратичных функций и интерпретировать эти графики в контексте ситуации.
Стандарты TEKS и ожидания учащихся
A(7) Квадратичные функции и уравнения.
 Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений. Студент должен:
Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений. Студент должен:A(7)(A) построить график квадратичных функций на координатной плоскости и использовать график для определения ключевых атрибутов, если это возможно, включая x — точку пересечения, y — точку пересечения, нули, максимальное значение, минимальные значения , вершина и уравнение оси симметрии
Ресурс Цели
Имея график ситуации, представленной квадратичной функцией, учащийся анализирует график и делает выводы.
Основные вопросы
Что представляет вершина графа?
Как по графику определить, является ли значение «а» положительным или отрицательным?
Словарь
- Квадратное уравнение
- Парабола
- Константа
- Коэффициент
- y -перехват
- x — перехват
- Вершина
- Линия симметрии
Квадратичные функции повсюду! Посмотрите следующее видео, чтобы просмотреть важные свойства квадратичных функций и увидеть несколько примеров реальных приложений.

Источник
Параболы – краткий обзор, stelladuma, YouTube
Мы собираемся исследовать и анализировать графики квадратичных функций, а затем интерпретировать эти графики в контексте ситуации.
Мы будем анализировать графики квадратичных функций. Сначала давайте сосредоточимся на направлении раскрытия параболы и ширине самой параболы.
Это захватывающе! На твоем лице расцветает улыбка.
График квадратичной функции часто называют параболой с уравнением y = a x 2 + c. Коэффициент «а» описывает направление и ширину параболы, а константа «с» перемещает параболу вверх и вниз.
Посмотрите на картинку ниже, чтобы увидеть параболы в известном маркетинговом символе.
 Используйте пример, чтобы ответить на следующие вопросы. Нажмите на вопрос, чтобы проверить свой ответ.
Используйте пример, чтобы ответить на следующие вопросы. Нажмите на вопрос, чтобы проверить свой ответ.Источник: McDonald’s Golden Arches, The Consumerist, Flickr
Практика
Графики ниже представлены в виде y = a
x 905. Используйте графики, чтобы ответить на вопросы ниже. Чтобы получить подсказку, нажмите на вопрос.Ухмылка или улыбка в стиле Моны Лизы кажется шире, чем парабола, представляющая родительскую функцию. Эта парабола имеет значение «а» между 0 и 1.
Посмотрите видео ниже. При этом обратите внимание на параболы, создаваемые экспериментаторами.
Источник
Диетическая кола + Mentos, zorro13, YouTube
На этом графике представлена зависимость роста дайвера от времени после прыжка дайвера с трамплина.
 Ответьте на следующие вопросы на основе информации.
Ответьте на следующие вопросы на основе информации.Решениями квадратичной функции являются нули. Здесь график квадратичной функции пересекает х – ось.
Пример
В Kemah Boardwalk есть новая игра, в которой игроку, набравшему наибольшее количество очков, предлагается бонус в размере 1000 долларов. Хуан и Мирза решают присоединиться к соревнованию. На конец рычага, лежащего на столе, надевается шарик. Ковши располагаются на разном расстоянии от рычага. Каждый раз, когда вы нажимаете на рычаг, он запускает мяч. Если мяч попадает в ведро, вы зарабатываете очки в зависимости от расстояния, на котором находится ведро от исходной точки.
Цель игры — заработать как можно больше очков. Вот как игрок зарабатывает очки:
- Если мяч не попадает в ведро, начисляется 0 очков.
- Если мяч попадает в первое ведро, начисляется 5 очков.
- Если мяч попадает во второе ведро, начисляется 10 очков.
- Если мяч попадает в третье ведро, начисляется 15 очков.

- Если мяч попадает в четвертое ведро, начисляется 25 очков.
Вот как играть в эту игру:
- Нажмите на рычаг, чтобы выпустить мяч.
- Мяч попадает (надеюсь) в ведро.
- Каждый игрок трижды подбрасывает мяч на свой общий счет.
Воспользуйтесь интерактивным заданием, чтобы имитировать игру, в которую играют Мирза и Хуан. Бросьте мяч, нажав на левый конец рычага. Подбросьте мяч три раза Мирзе, а затем три раза Хосе. Не забудьте записать очки, которые каждый участник заработал за каждый бросок.
Когда Мирза и Хуан играли в ведро, количество заработанных очков зависело от того, где парабола траектории мяча пересекала ось X. На самом деле есть две точки пересечения — первая находится в начале координат, а вторая — в ведре.
Если квадратичная функция имеет вершину на оси x, то существует только одно решение.
Если квадратичная функция не пересекает ось абсцисс, решений с вещественными числами не существует.

Пример
Бернадетт бросает копье для школьной команды по легкой атлетике. На приведенном ниже графике показаны высота и горизонтальное расстояние, пройденное копьем за три тренировочных броска Бернадетт.
Используйте график, чтобы ответить на следующие вопросы.
Вы изучили реальные приложения графиков квадратичных функций. В частности, вы изучили способы интерпретации ширины и направления параболы, вершины параболы и решений параболы.
На приведенном ниже графике показаны важные атрибуты графика параболы, которые можно использовать для анализа и интерпретации графиков квадратичных функций.
Точка пересечения y — точка пересечения параболы с осью y .
Точка пересечения x — это точка или точки, в которых парабола пересекает ось x . Может быть 0, 1 или 2 x -отрезков, в зависимости от параболы.
Вершина — точка поворота параболы. Если парабола открывается вниз, вершина является точкой максимума, а если парабола открывается вверх, вершина является точкой минимума.

- Курирование и доработка.
- vertex : Максимум или минимум квадратичной функции.


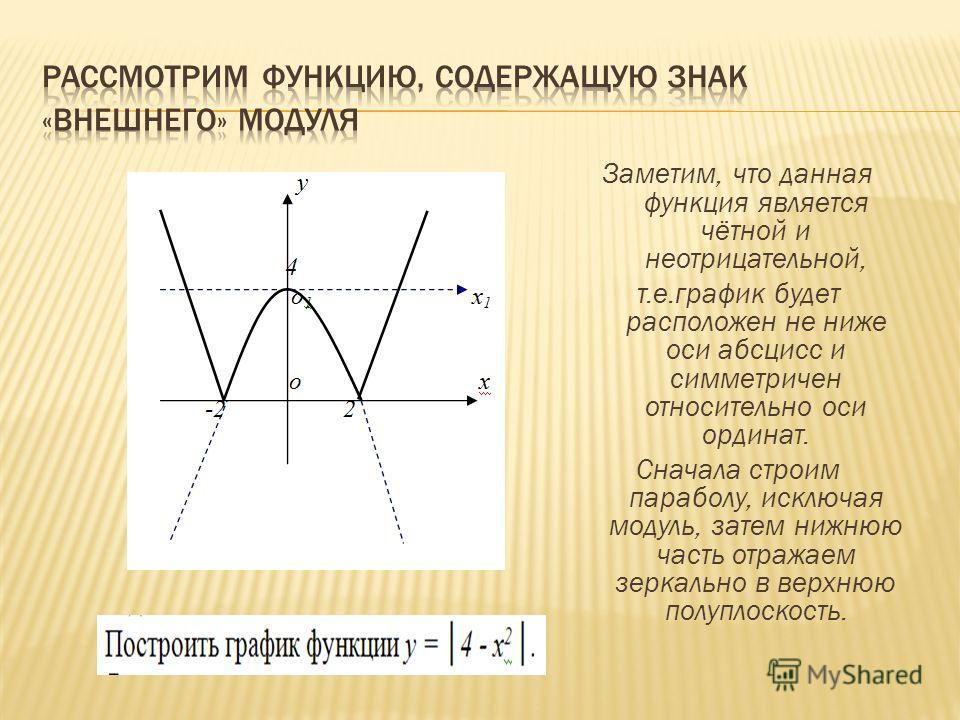 Назовем эти точки и выпишем их координаты.
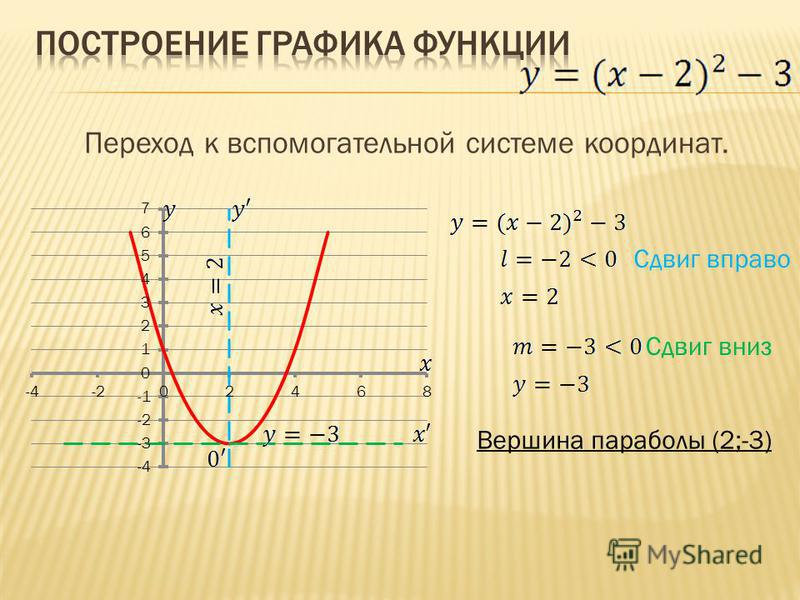
Назовем эти точки и выпишем их координаты.


 2+5x+1\) \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3
2+5x+1\) \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3
 2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))
2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))
 Задачи с показательными уравнениями и неравенствами
Задачи с показательными уравнениями и неравенствами ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет)
ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Графики простейших функций — линейная, параболы, гиперболы, экспоненты, показательные, степенные, логарифмическая, синус, косинус, тангенс, котангенс изучаемых в школе Справочная таблица. Примерно 7-9 класс (13-15 лет) На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций».
Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». ..
..

 + y – 1 = 0 [найти стандартную форму квадратного уравнения]
+ y – 1 = 0 [найти стандартную форму квадратного уравнения]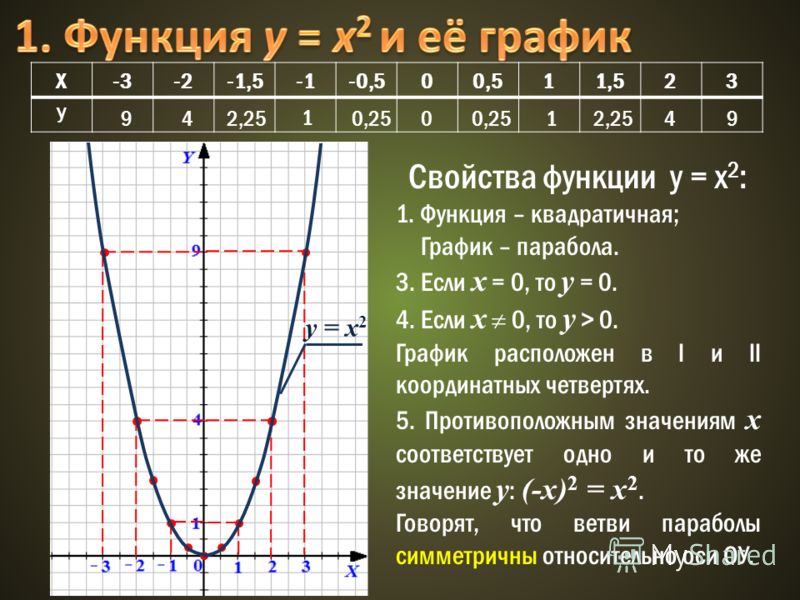
 Это показано ниже.
Это показано ниже.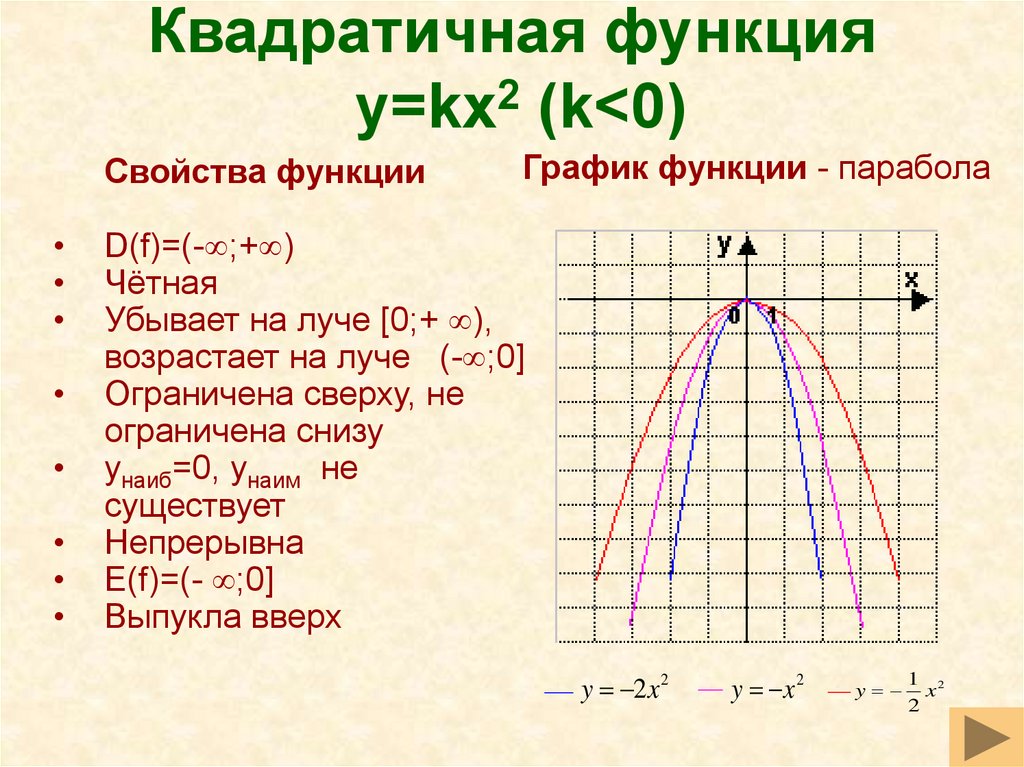
 диаграмму ниже).
диаграмму ниже). 2-4ac}}{2a })(x=2a−b±b2−4ac 92 — x — 2f(x)=x2−x−2
2-4ac}}{2a })(x=2a−b±b2−4ac 92 — x — 2f(x)=x2−x−2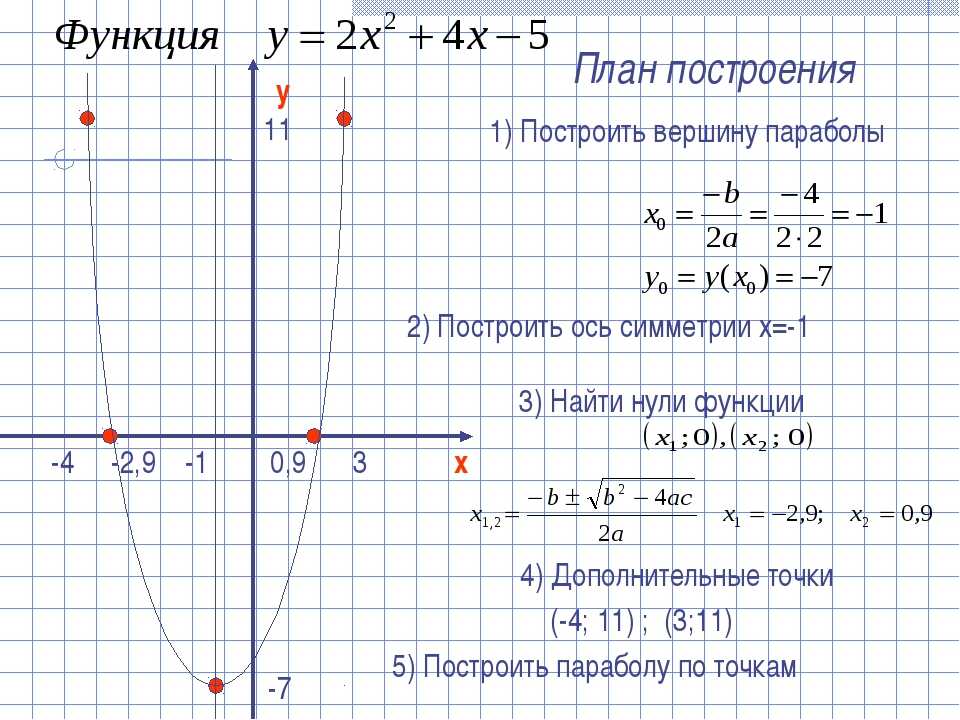
 Следовательно, у данной квадратичной функции нет действительных корней . Мы пришли к тому же заключению, к которому пришли графически.
Следовательно, у данной квадратичной функции нет действительных корней . Мы пришли к тому же заключению, к которому пришли графически.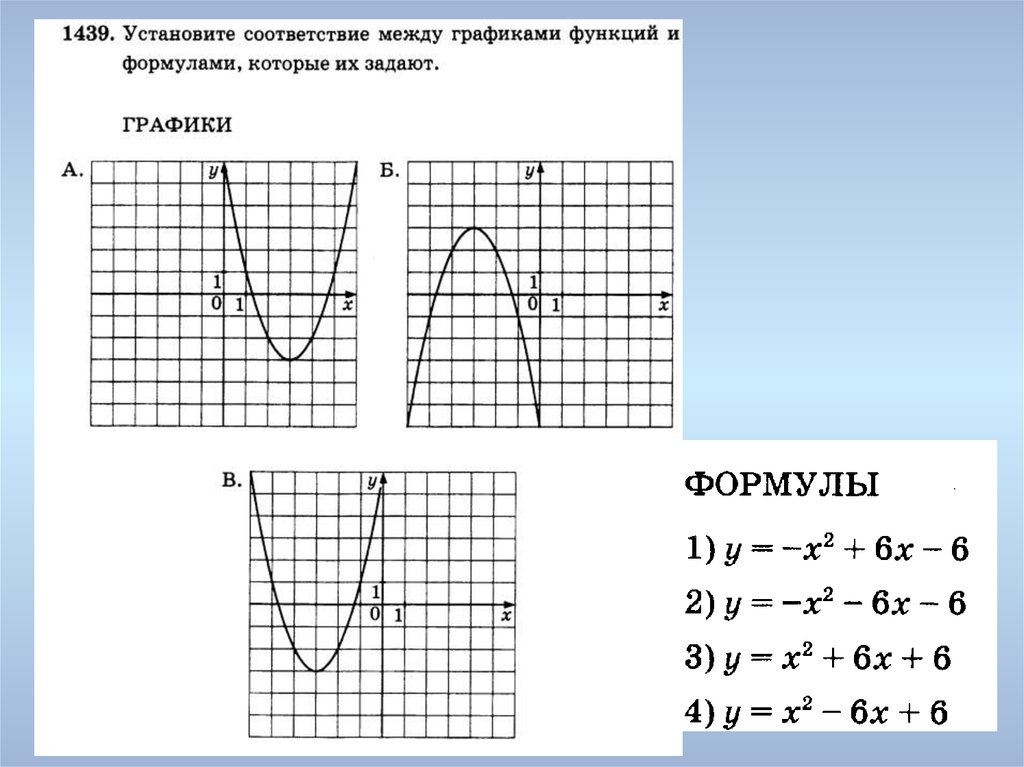
 у=(х+2)2+2.
у=(х+2)2+2.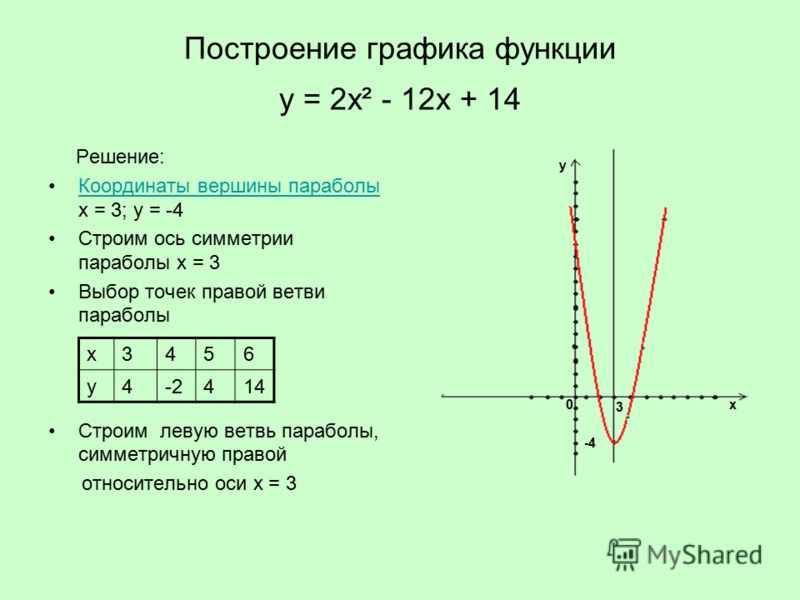
 Ось симметрии параболы определяется как:
Ось симметрии параболы определяется как: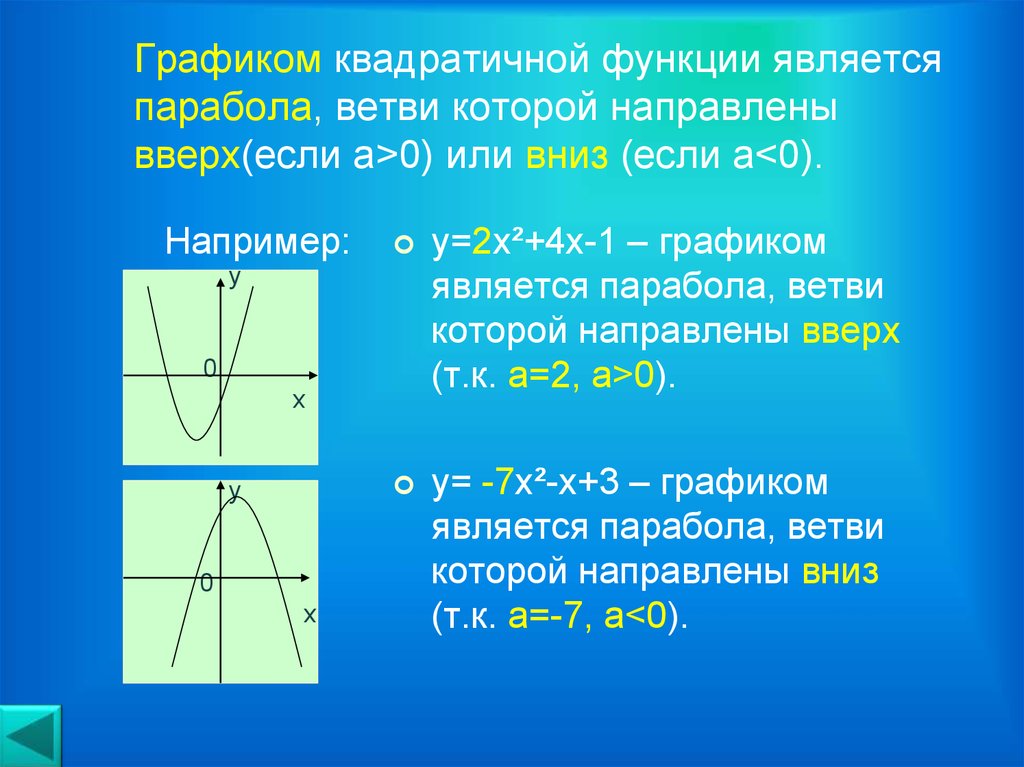 Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права  Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия : CC BY-SA: Attribution-ShareAlike  . Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike 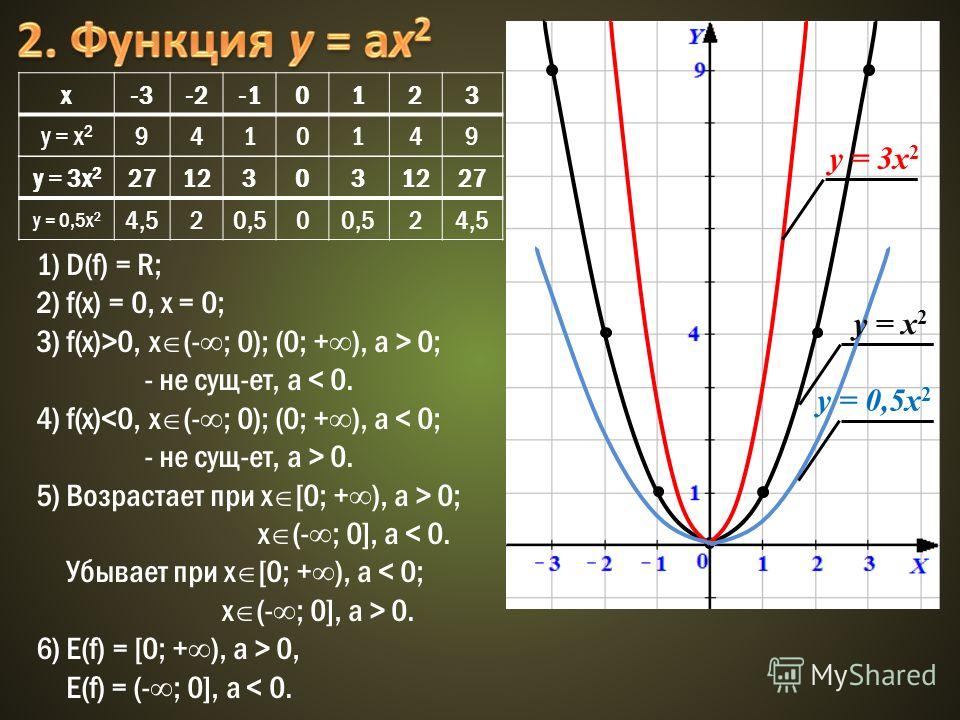 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike 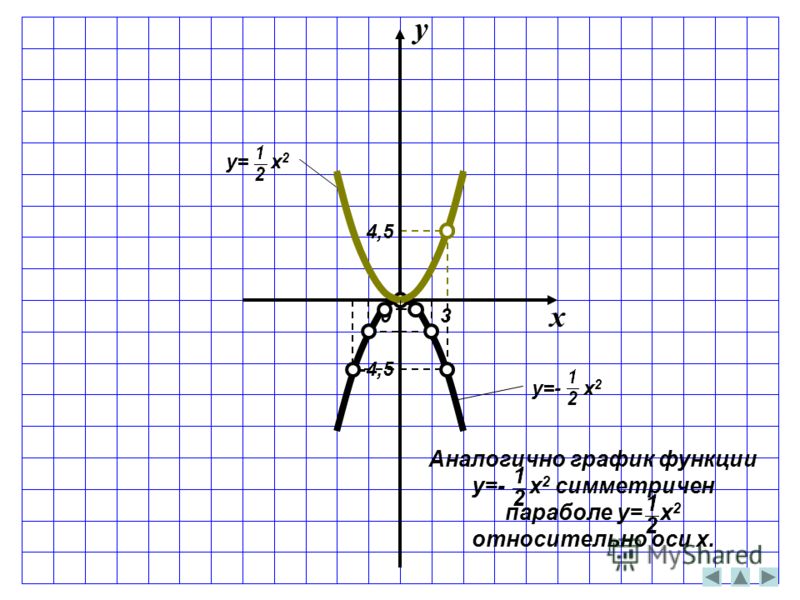 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution 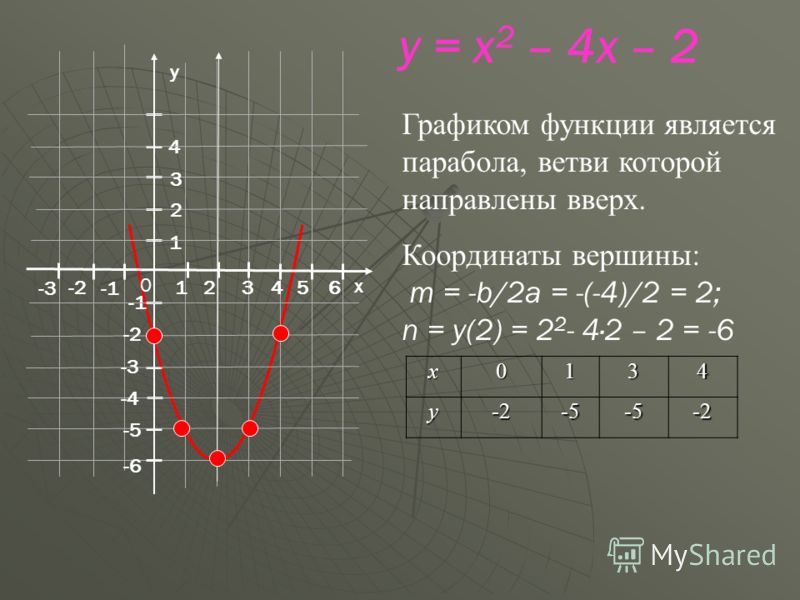 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution 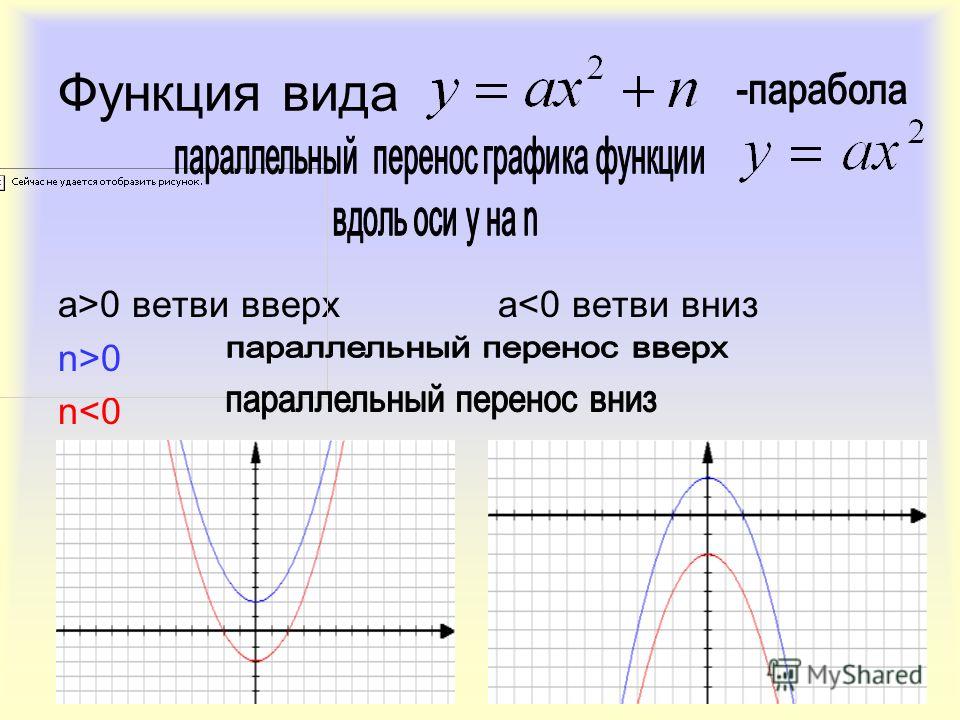 Все квадратичные функции при построении имеют форму буквы «U», хотя иногда эта буква «U» оказывается перевернутой. В результате квадратичные функции имеют либо максимальное, либо минимальное значение, в зависимости от того, перевернута ли буква «U» или перевернута, соответственно. График квадратичной функции (которую мы называем парабола ) иногда кажется «широкой», иногда «узкой», а иногда чем-то средним между этими двумя крайностями. Иногда они пересекают ось $x$, образуя два пересечения $x$. В других случаях коснитесь оси $x$ только один раз или не коснитесь вообще. У них всегда есть $y$-отрезок (конечно, наш график должен быть достаточно большим, чтобы показать его).
Все квадратичные функции при построении имеют форму буквы «U», хотя иногда эта буква «U» оказывается перевернутой. В результате квадратичные функции имеют либо максимальное, либо минимальное значение, в зависимости от того, перевернута ли буква «U» или перевернута, соответственно. График квадратичной функции (которую мы называем парабола ) иногда кажется «широкой», иногда «узкой», а иногда чем-то средним между этими двумя крайностями. Иногда они пересекают ось $x$, образуя два пересечения $x$. В других случаях коснитесь оси $x$ только один раз или не коснитесь вообще. У них всегда есть $y$-отрезок (конечно, наш график должен быть достаточно большим, чтобы показать его). 2}{4a})$, где происходит максимум или минимум, мы называем 92-4ac$.
2}{4a})$, где происходит максимум или минимум, мы называем 92-4ac$.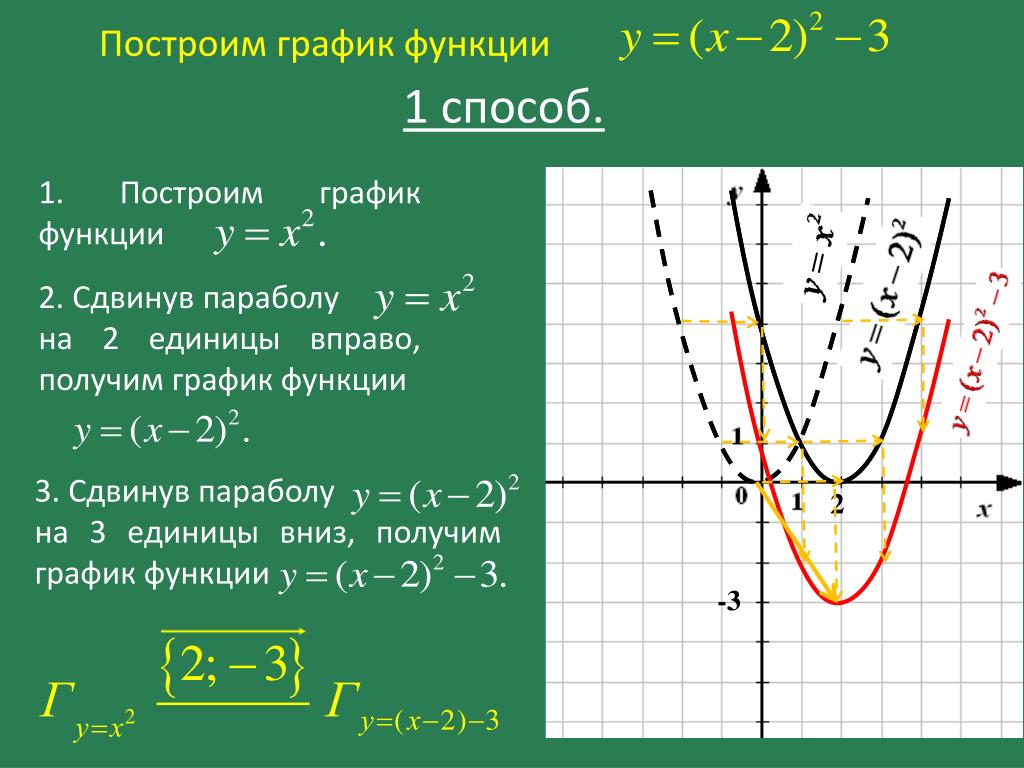 Чтобы выяснить, какие значения x использовать в таблице, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Чтобы узнать, как составить таблицу значений для квадратного уравнения, ознакомьтесь с этим руководством!
Чтобы выяснить, какие значения x использовать в таблице, сначала найдите вершину квадратного уравнения. Таким образом, вы можете выбрать значения с любой стороны, чтобы увидеть, что делает график по обе стороны от вершины. Чтобы узнать, как составить таблицу значений для квадратного уравнения, ознакомьтесь с этим руководством! Эти значения используются для нахождения оси симметрии, дискриминанта и даже корней по квадратичной формуле. Несомненно, важно знать, как идентифицировать эти значения в квадратном уравнении. Этот урок покажет вам, как!
Эти значения используются для нахождения оси симметрии, дискриминанта и даже корней по квадратичной формуле. Несомненно, важно знать, как идентифицировать эти значения в квадратном уравнении. Этот урок покажет вам, как! Та вертикальная линия, которую вы разрезаете, имеет особое имя. Она называется осью симметрии. Чтобы узнать об оси симметрии, посмотрите этот урок!
Та вертикальная линия, которую вы разрезаете, имеет особое имя. Она называется осью симметрии. Чтобы узнать об оси симметрии, посмотрите этот урок! Проверьте это!
Проверьте это! Мы делаем это, выбирая около пяти x -значений и нахождение соответствующих им y -значений.
Мы делаем это, выбирая около пяти x -значений и нахождение соответствующих им y -значений.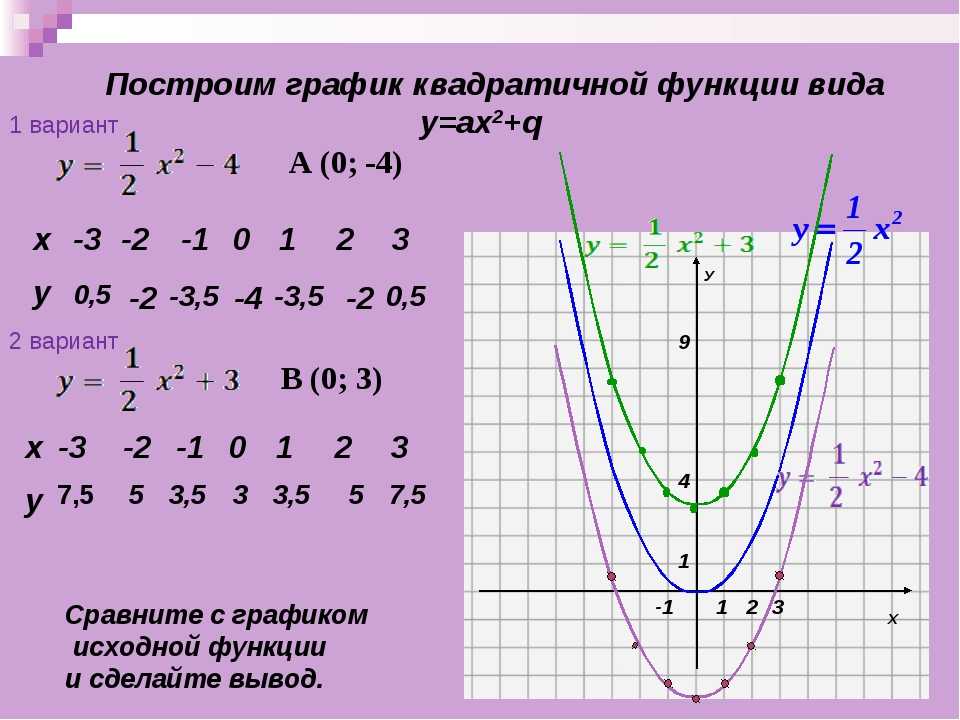 Параболы требуют минимум 3 точки, но обычно мы хотим найти по крайней мере пять точек, чтобы построить хороший график. Найдите вершину, x — и y — точки пересечения, а также линию симметрии.
Параболы требуют минимум 3 точки, но обычно мы хотим найти по крайней мере пять точек, чтобы построить хороший график. Найдите вершину, x — и y — точки пересечения, а также линию симметрии. Также полезно отметить, что у нас минимум y -значение -1, это будет важным фактом при работе над текстовыми задачами.
Также полезно отметить, что у нас минимум y -значение -1, это будет важным фактом при работе над текстовыми задачами.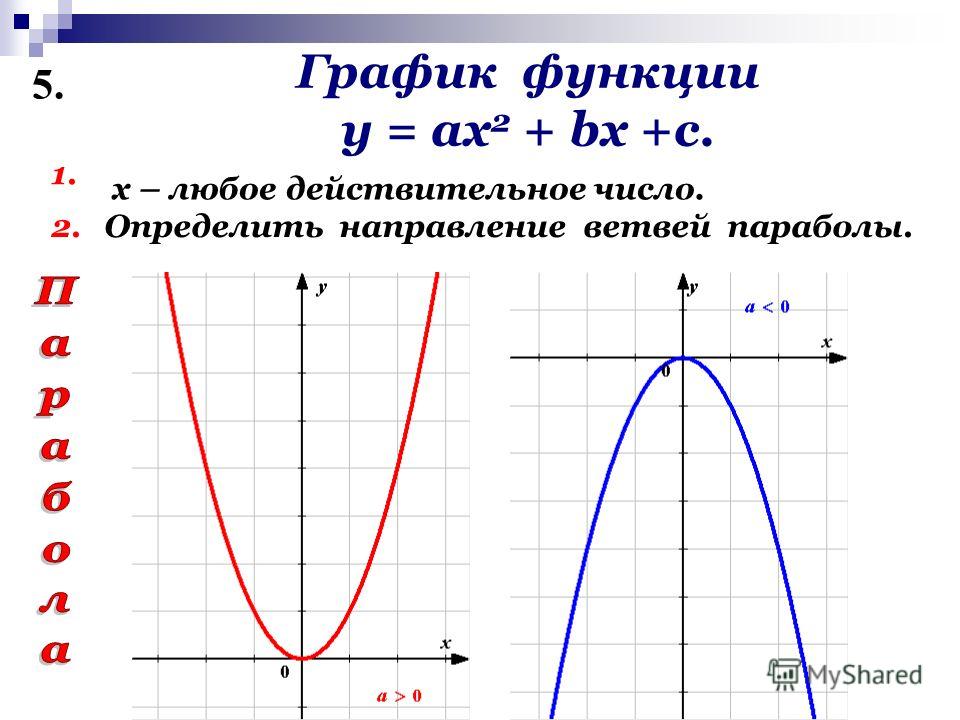
 Поэтому в некоторых случаях допустимо наносить и маркировать только три точки.
Поэтому в некоторых случаях допустимо наносить и маркировать только три точки.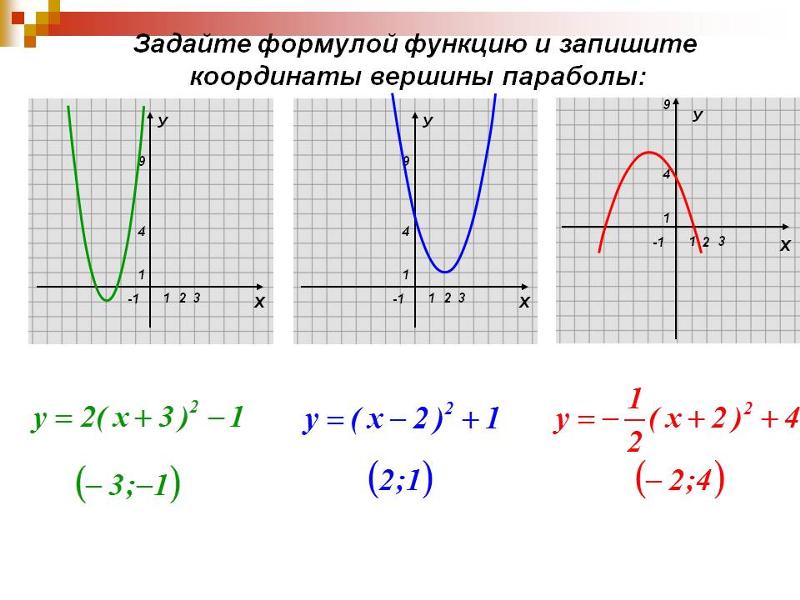 Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений. Студент должен:
Учащийся применяет стандарты математического процесса при использовании графиков квадратичных функций и связанных с ними преобразований для представления различными способами и определения с помощью технологий и без них решений уравнений. Студент должен: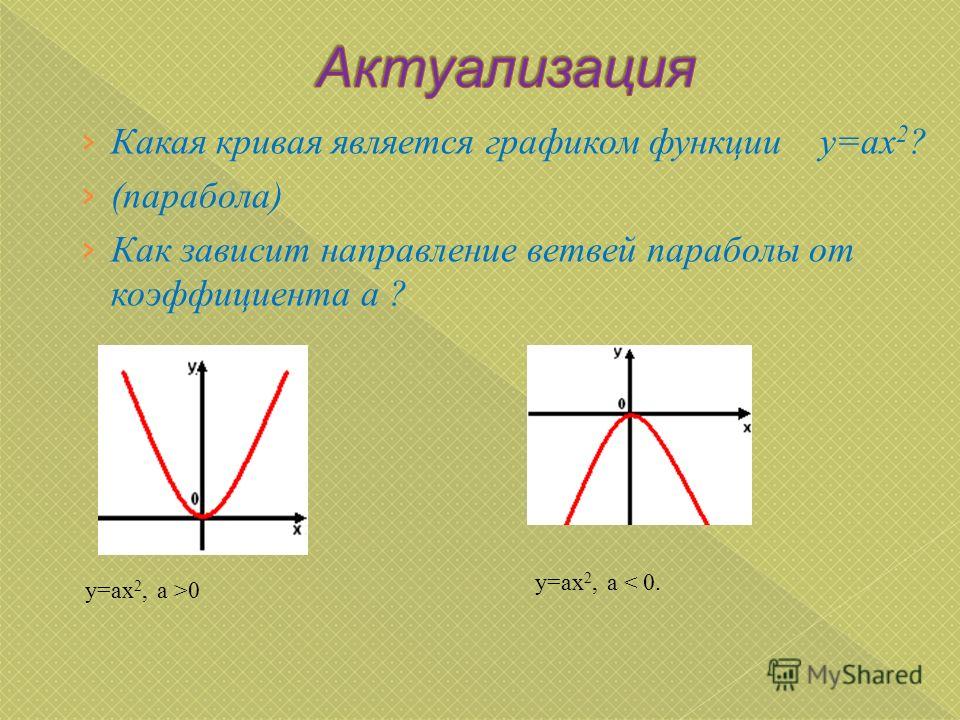
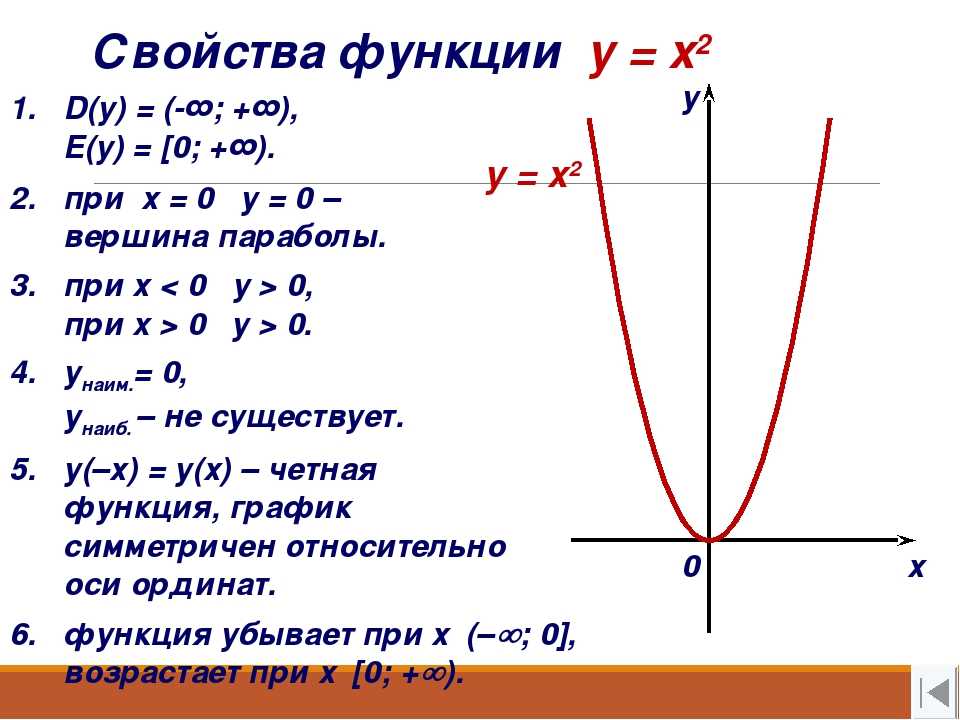 Используйте пример, чтобы ответить на следующие вопросы. Нажмите на вопрос, чтобы проверить свой ответ.
Используйте пример, чтобы ответить на следующие вопросы. Нажмите на вопрос, чтобы проверить свой ответ.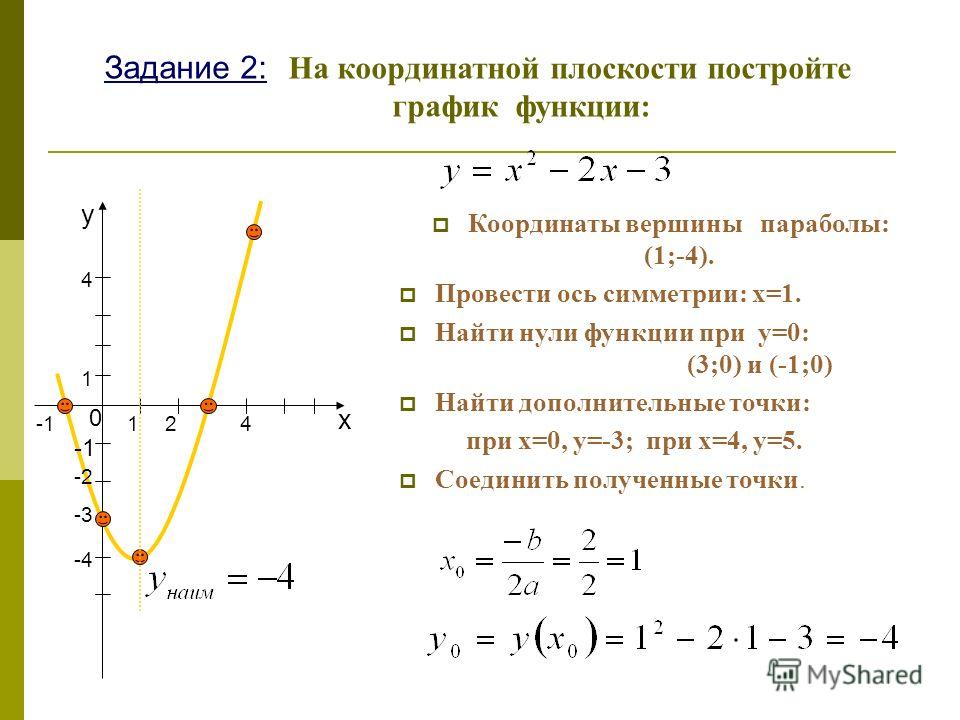 Ответьте на следующие вопросы на основе информации.
Ответьте на следующие вопросы на основе информации.