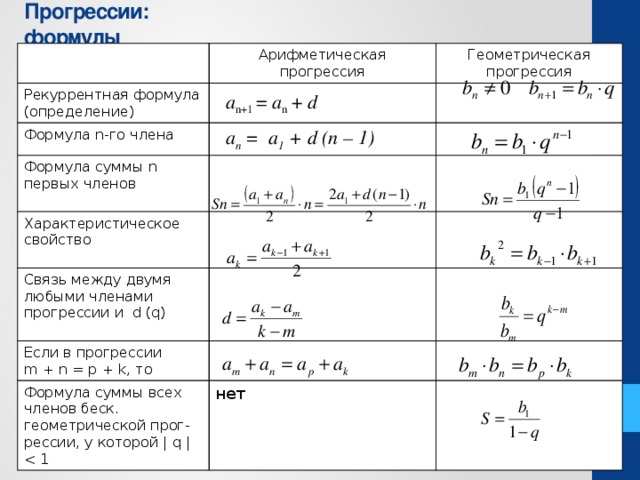
Арифметическая прогрессия
Урок 36. Подготовка к ОГЭ по математике 9 класс
В этом видеофрагменте мы вспомним определение арифметической прогрессии, повторим ее свойство, выведем формулу для вычисления суммы n первых членов арифметической прогрессии.
Конспект урока «Арифметическая прогрессия»
Вопросы занятия:
· повторить определение арифметической прогрессии;
· вспомнить свойство арифметической прогрессии;
· вывести формулу для вычисления суммы n первых членов арифметической прогрессии.
Материал урока
Давайте вспомним определение арифметической прогрессии.
Определение.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом.
Это число
называется разностью арифметической прогрессии.
Давайте попробуем среди предложенных последовательностей определить, какие являются арифметической прогрессией, а какие нет.
Пример.
Как и числовые последовательности, арифметические прогрессии бывают возрастающие и убывающие.
Определение.
Возрастающие – это прогрессии, в которых каждый последующий член больше предыдущего.
Например, примерами возрастающих прогрессий будут прогрессии
Определить возрастающую арифметическую прогрессию нетрудно, достаточно определить разность прогрессии. Если разность арифметической прогрессии больше нуля, то, значит, арифметическая прогрессия возрастающая.
Определение.
Убывающие арифметические прогрессии – это прогрессии, в которых каждое последующий член меньше предыдущего.
Примерами убывающих прогрессий будут прогрессии
У убывающих арифметических прогрессий – разность арифметической прогрессии меньше нуля
.
Рассмотрим пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Теперь давайте рассмотрим задачу.
А давайте теперь найдём х, если арифметическая прогрессия такая: 4024; х; 6072?
Вроде тоже ничего сложного, но здесь при вычислении есть шанс сделать вычислительную ошибку.
Давайте решим это задание в общем виде.
Мы с вами сформулировали основное свойство арифметической прогрессии.
Найдём теперь х из предыдущей задачи с помощью только что доказанной формулы.
Теперь давайте выполним задание.
Пример.
Найти сумму первых девяти членов арифметической прогрессии, состоящей из чётных чисел, записанных в порядке возрастания.
Решение.
Восстановить девять членов этой последовательности нетрудно.
Это будут числа: 2; 4; 6; 8; 10; 12; 14; 16; 18.
Их сумма равна: 2
+ 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 = 90.
Ответ: 90.
А если нам надо найти, например, сумму тысячи первых членов? Как быть? Выписывать тысячу членов прогрессии и все их складывать? Это долго и большая вероятность того, что при нахождении всех чисел, мы допустим ошибку, которая повлечёт за собой ошибку при нахождении суммы.
Давайте выведем формулу, которая поможет нам быстро подсчитать сумму сколько угодно членов арифметической прогрессии.
Эта формула, позволяет находить сумму любого количества первых членов арифметической прогрессии, не вычисляя отдельно их значения.
Теперь давайте вернёмся к нашему примеру и посчитаем сумму девяти членов прогрессии по формуле, которую вывели.
Мы получили такой же результат, только нам не пришлось находить все девять членов прогрессии.
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Есть второй способ
решения такой задачи.
В этом случае, нам не пришлось отдельно вычислять значение тридцать четвёртого члена.
Пример.
Рассмотрим ещё один пример.
Рассмотрим ещё один пример.
Итоги урока
Сегодня на уроке, мы вспомнили определение арифметической прогрессии, повторили свойство арифметической прогрессии, вывели сумму эн первых членов арифметической прогрессии.
Предыдущий урок 35 Числовая последовательность
Следующий урок 37 Геометрическая прогрессия
Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ОГЭ по математике 9 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
100 ballov.
 kz образовательный портал для подготовки к ЕНТ и КТА
kz образовательный портал для подготовки к ЕНТ и КТАЕжегодно Институт образовательных технологий при Открытом университете Великобритании публикует доклад о десяти самых важных трендах в образовании.
По мнению авторов исследования, эти тенденции уже заметны и в будущем могут серьёзно повлиять на мировую систему образования, поэтому заслуживают пристального внимания.
Как эти тренды будут реализованы на постсоветском пространстве и какой отклик они найдут у учащихся? Об этом на международной образовательной конференции Global Impact Conference рассказала Диана Королёва, заведующая лабораторией инноваций в образовании при российской Высшей школе экономики.
Тренд 1. Гибридное обучение
В чём суть. Учащиеся чередуют очные занятия с онлайн-уроками.
Проблемы, выявленные ВШЭ:
- Не везде есть соответствующая инфраструктура.
- Учителя не умеют работать в онлайн-форматах.
Чтобы применять гибридное обучение, должна поменяться методика преподавания. Педагогам нужно будет научиться управлять вниманием учеников и по-новому выстраивать занятия.
Педагогам нужно будет научиться управлять вниманием учеников и по-новому выстраивать занятия.
Лекцию по видеосвязи нельзя считать гибридным обучением. Это должна быть не просто цифровизация, когда мы переносим обычные классные занятия в онлайн-формат, а трансформация всего образовательного процесса. Иначе на уроках будет «говорящая голова» учителя по видео и зевающие ученики.
Тренд 2. Образовательные курсы вместо поступления в вузы
В чём суть. Сегодня не все готовы инвестировать в университетское образование. Вместо этого люди всё чаще выбирают краткосрочные курсы, которые позволяют им быстро получить новые знания, чтобы трудоустроиться или повысить свою квалификацию. Это уже давно распространено в программировании, юриспруденции или психологии. Такая тенденция будет распространяться и на другие сферы.
Проблемы:
- Курсы не смогут заменить долгосрочное образование.
- Выбор курсов большой, поэтому сложно найти нужный, полезный и тот, который впечатлит работодателя.

- Не все умеют планировать своё время. Есть вероятность начать несколько разных курсов и не закончить ни один.
Тренд 3. Совмещение учёбы с практикой
В чём суть. Студенты учатся и одновременно работают на предприятиях или в компаниях по их специализации, чтобы не отставать от всё время меняющихся технологий.
Проблемы:
- В исследовании ВШЭ отмечается, что не все педагоги готовы к такому формату. Одно дело прочитать теоретическую лекцию и спокойно уйти домой, другое – быть постоянно на связи со студентами и менять подход к образованию.
- Не у всех работодателей есть желание учить студентов. Чаще этот тренд распространён в сфере IT – там, где компании знают, что студенты пойдут работать именно к ним.
Тренд 4. Обучение с помощью инфлюенсеров
В чём суть. В последнее время многие блогеры и инфлюенсеры стали предлагать образовательный контент. Это могут быть подкасты о маркетинге или видео в Youtube о законах физики. Они размывают грань между обучением и развлечением, что очень нравится людям.
Они размывают грань между обучением и развлечением, что очень нравится людям.
Проблема: качество такого контента не всегда высокое.
Перспективы: если талантливые учителя научатся использовать соцсети и инструменты инфлюенсеров, они смогут привлечь к себе больше учащихся, сделать процесс обучения доступным и интересным для нового поколения. Это повысит статус учителя, к которому сейчас ученики не всегда относятся с уважением и восхищением, предположили в ВШЭ.
Тренд 5. Индивидуальные образовательные программы
В чём суть. Учащийся сам планирует свою образовательную траекторию – ставит себе цель, выбирает для её достижения дисциплины из списка, в какой последовательности их изучать и с каким темпом, даёт оценку своим результатам.
Это часто практикуется в вузах, но применимо и в школах. К примеру, детям могут на выбор дать задания разной сложности, проекты под их интересы, элективы или темы для изучения (какое произведение из выбранных хотите прочесть?), чтобы лучше раскрыть потенциал и талант ребёнка.
Проблема: когда каждый студент формирует свою уникальную траекторию, сложнее сравнивать уровень знаний учащихся и оценивать их.
Тренд 6. Повышение психологической грамотности учащихся
В чём суть. В школах и вузах вводятся предметы или темы, которые повышают психологическую грамотность учеников, обучают их основам самодиагностики и самопомощи, а также рассказывают, где и когда можно получить помощь.
Проблемы:
- обращение к психологу у нас до сих пор считается чем-то постыдным;
- низкое качество подготовки школьных психологов;
- отсутствие какой-либо психологической помощи учителям.
Тренд 7. Учёт домашней среды во время обучения
В чём суть. При выстраивании образовательного процесса учитель задумывается о том, как обстоят дела в семье ученика, с какими проблемами он сталкивается дома, чему его там учат.
Например, если он знает, что у ребёнка нет родителя, а на уроке будет обсуждаться тема семьи, учитель может скорректировать урок таким образом, чтобы ребёнку было более комфортно.
Или педагог, зная что ученик испытывает дома какую-то проблему (например, плохие отношения с родителями), может затронуть подобную тему на уроке, чтобы помочь ребёнку справиться с ней.
Проблемы:
- нельзя сделать этот процесс персонализированным, учителя могут видеть только общую картину своего класса;
- такие методы обучения должны быть выполнены профессионально, иначе это психологически небезопасно;
- активное вмешательство школы в семейное пространство может навредить отношениям между учениками, родителями и учителями;
- у учеников может появиться чувство, что за ними следят или нарушают их личные границы.
Тренд 8. Совместный просмотр видео
В чём суть. Учащиеся вместе смотрят видео, участвуют в его обсуждении, делятся мнениями, отвечают на вопросы. Это позволяет развить образную грамотность учащегося и развить его коммуникативные навыки.
Возможен и такой формат, когда фильм предлагают посмотреть заранее, в удобное для учащегося время, а потом собраться вместе и обсудить.
Проблемы:
- Ученик при таком подходе остаётся пассивным. Для развития творческих навыков и критического мышления полезнее будет совместное создание видео или подбор видеоматериалов учеником, считают в ВШЭ.
- Ученики часто отвлекаются, поэтому для учёбы удобнее смотреть короткие видео под конкретные цели.
- Не все учителя могут правильно использовать кинопросмотр и выстраивать диалог для обсуждения увиденного.
Тренд 9. Обсуждение острых тем и своих эмоций
В чём суть. Когда учитель на уроках обсуждает с учащимися деликатные темы, вроде социального неравенства, дискриминации, школьной травли, ученики могут открыто говорить о своих чувствах. Вместе с педагогом они стараются исследовать и критически осмысливать эти негативные эмоции, чтобы потом корректировать своё поведение.
Проблемы:
- Дети у нас не привыкли делиться эмоциями, раскрываться перед учителем и другими детьми, и подобного рода обсуждения могут делать их достаточно уязвимым в коллективе.

Тренд 10. Обучение во время прогулок
В чём суть. Родители всё больше обеспокоены тем, что их дети ведут сидячий образ жизни и мало общаются со сверстниками. Поэтому приобретают актуальность прогулки на воздухе, походы и экскурсии вместо обычных занятий в классе.
Проблема: подходит не для всех предметов. Если это урок экологии или истории искусства, то это работает. Но в остальных случаях практически не применяется.
Выводы: в сфере образования стали появляться тренды, которые нацелены на улучшение психологического здоровья учеников и решение социальных конфликтов. На постсоветском пространстве это не очень развито, и есть множество проблем, которые нужно решить, чтобы внедрить такие новшества.
По мнению экспертов из ВШЭ, развитие получат гибридное обучение, совмещение учёбы и практики, всевозможные курсы и проектирование собственного образовательного пути.
Источник: https://informburo.kz
Арифметическая прогрессия — Общая разность и N-й член | Класс 10 Математика
Арифметическая прогрессия — это последовательность чисел, в которой разница между любыми двумя последовательными числами постоянна. Например
1, 3, 5, 7, 9……. находится в ряду, который имеет общую разность (3 – 1) между двумя последовательными членами, равен 2. Если мы возьмем в качестве примера ряды 1, 2, 3, 4…, то общая разность (2 – 1) между двумя последовательными членами равно 1.
Другими словами, арифметическую прогрессию можно определить как « Математическая последовательность, в которой разница между двумя последовательными членами всегда является константой ».
Мы сталкиваемся с разными словами, такими как последовательность, серия и прогрессия в AP, теперь давайте посмотрим, что определяет каждое слово —
- Последовательность — это конечный или бесконечный список чисел, которые следуют определенному шаблону.
Например, 0, 1, 2, 3, 4, 5… — это последовательность, представляющая собой бесконечную последовательность целых чисел.
- Серия — это сумма элементов, которым соответствует последовательность. Например, 1 + 2 + 3 + 4 + 5… это ряд натуральных чисел. Каждое число в последовательности или ряду называется термином. Здесь 1 — термин, 2 — термин, 3 — термин …….
- Прогрессия — это последовательность, в которой общий термин может быть выражен с помощью математической формулы, или Последовательность, в которой используется математическая формула, которую можно определить как прогрессию.
В чем общее отличие AP?
Общая разность в арифметической прогрессии обозначается d . Разница между последующим термином и его предыдущим термином. Она всегда постоянна или одинакова для арифметической прогрессии. Другими словами, мы можем сказать, что в данной последовательности, если общая разность постоянна или одинакова, мы можем сказать, что данная последовательность находится в арифметической прогрессии.
- Формула для нахождения общего различия: d = (a n + 1 – a n ) или d = (a n – a n-1 ) .
- Если общая разность положительна, то AP увеличивается. Например, в примерах 4, 8, 12, 16….. в этих рядах АР увеличивается
- Если общая разность отрицательна, то АР уменьшается. Например, -4, -6, -8……., здесь AP уменьшается.
- Если общая разность равна нулю, то AP будет постоянным. Для примера 1, 2, 3, 4, 5……… здесь AP постоянна.
Последовательность арифметической прогрессии будет похожа на 1 , а 2, а 3 , а 4 ,…
Пример 1: 0, 5, 10, 15, 20, Из приведенного выше примера мы можем сказать, что общая разница равна «5». Пример 2: 0, 7, 14, 21, 28……. Из приведенного выше примера мы можем сказать, что общая разница равна «7». Чтобы найти средний член арифметической прогрессии, нам нужно общее количество членов в последовательности. У нас есть два случая: Четное: Если количество членов в последовательности четное, то у нас будет два средних члена, т. Нечетное: Если число элементов в последовательности нечетное, то у нас будет только один средний член, т.е. (n/2). Пример 1: Пример 2: Чтобы найти n-й член арифметической прогрессии, мы знаем, что ряд A.P имеет вид a, a + d, a + 2d, a + 3d, a + 4d………. Термин n th обозначается T n. Таким образом, чтобы найти n-й член ряда AP, будет: Пример: Найдите 9 -й член данной последовательности AP: 3, 6, 9, 12, 15………..? Шаг 1: Напишите данную серию. Шаг 2 : Теперь запишите значение a и n из данного ряда. Шаг 3: Найдите общую разность d по формуле (a n+1 – a n ) . Шаг 4 : Нам нужно подставить значения a, d, n в формулу (T n = a + (n – 1)d). Следовательно, 9 -й -й член данной серии A.P 3, 6, 9, 12, 15………. это «27». Можно найти формулу для n-го члена для определенного вида последовательности, называемой прогрессией. Наиболее популярной математической прогрессией с простыми формулами является арифметическая прогрессия (АП). Хорошим примером арифметической прогрессии (АР) является последовательность 3, 8, 13, 18, 23, 28, 33…, которая следует шаблону, в котором каждое число получается путем прибавления 5 к предыдущему члену. Рассмотрим понятие арифметической прогрессии, ее формулу, сумму первого n члена и несколько примеров с решениями в этой статье. «Арифметическая прогрессия» (АП) — это ряд чисел, в котором любые два последовательных числа имеют постоянную разность. Арифметическая последовательность — это другое ее название. Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем добавления первого на фиксированное число. Например, в последовательности 4, 7, 10, 13, 16, 19, 22, 25, 28 и 31 первый член равен 4, а общая разница между членами равна 3. Давайте посмотрим на таблицу ниже, чтобы показать общий вид арифметической прогрессии. Предположим, что a — первый термин, n — позиция термина, а d — общая разность. В алгебре арифметическая прогрессия – это такое расположение чисел, при котором существует постоянная разница между членами. Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем прибавления первого к фиксированному числу. Формула для нахождения n-го члена арифметической прогрессии: a n = a + ( n – 1 ) d где a n = n-й член, Формула a n = a + ( n – 1 ) d используется для получения общего члена (или) n-го члена арифметической прогрессии (AP), первый член которой равен a , а общая разница d. Например, у нас есть последовательность 5, 8, 11, 14, 17, 20, 23 и 26. Находя общий член или n-й член, подставим a =5 в качестве первого члена и d = 3 в качестве общей разности в формуле. Итак, имеем a n = a + (n – 1) d Таким образом, общий член последовательности 5, 8, 11, 14, 17, 20, 23, 26,… равен n = 3n + 2. Получение n-го члена арифметики прогрессия полезна для определения значения других членов последовательности, скажем, 30 -й -й термин, 45-й -й -й термин, 90-й -й -й термин, 100 -й -й термин и т. д. без ручного перечисления последовательности. Например, давайте воспользуемся вычисленным общим термином a n = 3n + 2 и идентифицируем 30 й термин, 45 й термин, 90 й термин и 100 й термин. Hence, the 30 th term is 92, the 45 th term is 137, the 90 th term is 272, and the 100 член 302 последовательности 5, 8, 11, 14, 17, 20, 23, 26,… Формула для первых n членов арифметической прогрессия Формула (первые n чисел в AP): S n = n/2 [ 2a + ( n – 1 ) d ] где Sn = сумма n слагаемых , здесь
а 1 = 0, а 2 = 5, поэтому а 2 - а 1 = d = 5 - 0 = 5.
a 3 = 10, a 2 = 5, поэтому a 3 - a 2 = 10 - 5 = 5.
a 4 = 15, a 3 = 10, поэтому a 4 - a 3 = 15 - 10 = 5.
 а 5 =20, а 4 = 15, поэтому a 5 -a 4 = 20 - 15 = 5.
а 5 =20, а 4 = 15, поэтому a 5 -a 4 = 20 - 15 = 5.
здесь,
a 1 = 0, a 2 = 7, поэтому a 2 - a 1 = 7 - 0 = 7
a 3 = 14, a 2 = 7, поэтому a 3 - a 2 = 14 - 7 = 7
a 4 = 21, a 3 = 14, поэтому a 4 - а 3 = 21 - 14 = 7
а 5 = 28, а 4 = 21, поэтому а 5 -а 4 = 28 - 21 = 7
 е. (n/2) и (n/2 + 1).n
е. (n/2) и (n/2 + 1).n Если n = 9, то
Средний член = n/2 = 9/2 = 4.
Если n = 16, то
Первый средний член = n/2 = 16/2 = 8.
Второй средний член = (n/2) + 1 = (16/2) + 1 = 8 + 1 = 9.
Что такое N-й член AP? Данная серия = 3, 6, 9, 12, 15........
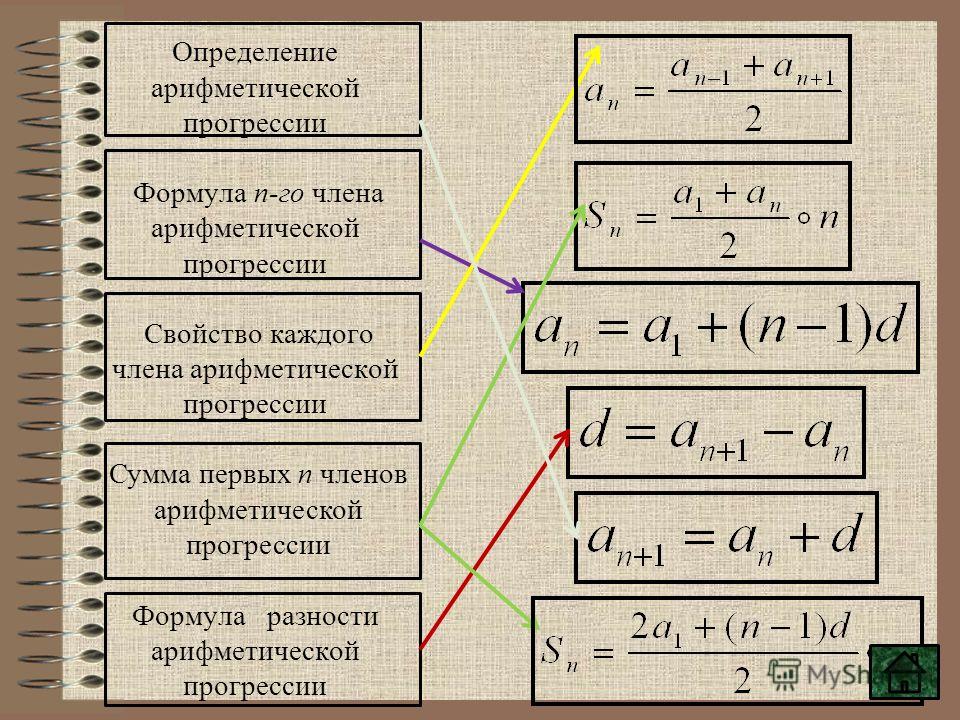
а = 3, п = 9
д = а2 - а1,
здесь а2 = 6 и а1 = 3
поэтому d = (6 - 3) = 3.
Т n = а + (n - 1)d
дано n = 9.
Т 9 = 3 + (9 - 1)3
= 3 + (8)3
= 3 + 24 = 27
Арифметическая прогрессия | Формула, N-й член, сумма и примеры
Введение 
Формула арифметической прогрессии Позиция терминов N-й член Значение N-го члена 1 a 1 a a + ( 1 – 1 ) d 2 a 2 a + d a + ( 2 – 1 ) d 3 a 3 a + 2d a + ( 3 – 1 ) d 4 a 4 a + 3d a + ( 4 – 1 ) d 5 а 5 а + 4d а + ( 5 – 1 ) d 6 a 6 a + 5d a + ( 6 – 1 ) d 7 a 7 a + 6d a + ( 7 – 1 ) д . 
. . . . . . . . . . . н а н a n = a + ( n – 1 ) d
a = 90 d разность,
позиция 0
a n = 5 + (n – 1) 3
a n = 5 + 3n – 3
a n = 3n + 2 при n = 30
a n = 3n + 2
a 30 = 3(30) + 2
a 40 30 90 + 2
A 30 = 92 , когда n = 45
A N = 3N + 2
A 45 = 3 (45) + 2
A 45 = 135 + 2
AST. 45 = 137
45 = 137 when n = 90
a n = 3n + 2
a 90 = 3(90) + 2
a 90 = 270 + 2
a 90 = 272 при n = 100
a n = 3n + 2
a 100 = 3(100) + 2
a 100 = 300 + 2
a 100 = 302
n = общее слагаемое
a = первое слагаемое
d = общая разность
В приведенном примере первый член равен 2 или a = 2; общая разность равна 4 или d = 4, а n = 20. Подставляя данное в формулу, имеем
Подставляя данное в формулу, имеем
S 30 = 30/2 [ 2 (2) + (30 – 1) ( 4 ) ]
S 30 = 15 [ 4 + ( 29 )( 4 ) ]
S 30 = (15) ( 4 + 116)
S 30 = ( 15 ) ( 120 ) 3
S 0
Следовательно, сумма первых 30 чисел в последовательности 2, 6, 10, 14, 18, … равна 1800.
В качестве другого примера предположим, что мы хотим получить сумму первых 50 натуральных чисел.
Арифметическая прогрессия для сценария 1, 2, 3, 4, 5, … 45, 46, 47, 48, 39 50.
Первый член равен 1 или a = 1, общая разность равна 1 или d = 1 и n = 50,
Применение значений к существующей формуле ) ]
S 50 = (25) ( 2 + 49 )
S 50 = ( 25 ) ( 51 )
S 50 = 1275
Когда заданы первый и последний члены формулы сумма первых n членов арифметической прогрессии равна
S n = n/2 (первый член + последний член)
Например, возьмем ранее заданную сумму первых 50 натуральных чисел. Поскольку данное говорит о том, что первый член равен 1, а последний равен 50, решение будет таким:
Поскольку данное говорит о том, что первый член равен 1, а последний равен 50, решение будет таким:
S n = n/2 (первый член + последний член)
S 50 = 50/2 (1 + 50 )
S 50 = 25 ( 51 )
S 50 = 1275
Таким образом, сумма первых 50 натуральных чисел равна 1275.0007
Найдите 25 в каждой из следующих арифметических прогрессий.
(а) 10, 15, 20, 25, 30, 35 …
(б) 12, 20, 28, 36, 44, 52 …
Раствор
(а) 10, 15, 20 , 30, 35 …
Общая разность равна 5 или d = 5, а первый член равен 10 или a = 10.
a n = a + ( n – 1 ) d + ( 25 – 1 ) 5
a 25 = 10 + ( 24 ) 5
a 25 = 10 + 120
a 25 = 130
( b ) 12, 20, 28, 36, 44, 52 …
Общая разность равна 8 или d = 8, а первый член равен 12 или a = 12.
a n = а + ( n – 1 ) d
а 25 = 12 + ( 25 – 1 ) 8
а 25 = 12 + ( 24 ) 8
а + 909 25 3 = 25 = 204
Пример 2
Найдите значение n.
(а) d = 5, а = 4 и а n = 99
(б) d = 9, а = 2, а n = 308
( в ) d = – 2 , а = 25 и а n = -9
Решение
( а ) d = 5, а = 4 , и a n = 99
Подставим данное в формулу.
а + (n – 1) d = a n
4 + (n – 1) 5 = 99
4 + 5n – 5 = 99
5n – 1 = 99
5n = 99 + 1
0 5n
n = 100 / 5
n = 20
(b) d = 9, a = 2, a n = 308
Подставим данное в формулу.
а + (n – 1) d = a n
2 + (n – 1) 9 = 308
2 + 9n – 9 = 308
9n – 7 = 308
9n = 308 + 7 n
9
n = 315 / 9
n = 35
(c) d = – 2 , a = 25, a n = -9
Подставим данное в формулу.
а + ( n – 1 ) d = а n
25 + ( n – 1 ) (-2) = -9
25 – 2n + 2 = -9
-2n + 27 = -9
-2n = -9 – 27
-2n = -36
n = -36 / -2
n = 18
Пример 3
Найдите общий член или явную формулу данной арифметической прогрессии.
(а) -4, 1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, …
(б) -19, -7, 5, 17, 29 , 41, 53, 65, 77, 89, 101, 113, 125, …
(в) 10, 4, -2, -8, -14, -20, -26, -32, 38, -44, — 50,…
Решение
( а ) -4, 1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, 61, …
Возьмем a = -4 и d = 5 в формулу.
а n = а + (n – 1) d
а n = -4 + (n – 1) 5
а n = -4 + 5n – 5
а n 9
( b ) -19, -7, 5, 17, 29, 41, 53, 65, 77, 89, 101, 113, 125, …
Применим a = -19 и d = 12 к формула.
а n = а + ( n – 1 ) d
а n = -19 + ( n – 1 ) 12
а n = -19 + 12n – 12 n 3 а 31
( в ) 10, 4, -2, -8, -14, -20, -26, -32, 38, -44, -50,…
Используем в формуле a = 10 и d = – 6.
а n = а + ( n – 1 ) d
а n = 10 + ( n – 1 ) (-6)
а n = 10 – 6n + 6 9 04
Пример 4
Найдите сумму.
(a) S 30 AP 15, 20, 25, 30, 35, 40,…
(b) S 25 AP 8, 15, 22, 29, 36, 43,…
(в) S 14 АП 20, 17, 14, 11, 8, 5, 2,…
Решение
( a ) S30 АП 15, 20, 25, 30, 35, 40,…
Подставим в формулу a = 15, n = 30, d = 5.
S 30 = 30/2 [ 2 (15) + ( 30 – 1 ) ( 5 ) ]
S 30 = 15 [ 30 + ( 29 )(5 ) ]
S 43 = (9005 ) ( 30 + 145 )
S 30 = ( 15 ) ( 175 )
S 30 = 2625
Подставим в формулу a = 8, n = 25 и d =7.
S 25 = 25/2 [2 (8) + (25 – 1) (7)]
S 25 = 12,5 [16 + (24)(7)]
S 1 9 = 2,9 25 25 ) ( 16 + 168 )
S 25 = ( 12,5) ( 184 )
S 25 = 2300
( в ) S 14 АП 20, 5, 17, 1, 18, 14 ,…
Подставим в формулу a = 17, n = 14 и d = -3.
S 14 = 14/2 [2 (20) + (14 – 1) (-3)]
S 14 = 7 [40 + (13)(-3)]
S 14 = ( 7 ) ( 40 -39 )
S 14 = ( 7 ) ( 1 )
S 14 = 7
Пример 5, 9 5
4 26, 33, 40, 47, 54, 61, 68, 75, …, найти a
45 и S 45.
Решение
Введем заданные значения, a = 5, n = 45, и d = 7, в уравнение.
а n = а + (n – 1) d
а 45 = 5 + (45 – 1) 7
а 45 = 5 + (44) 7
A 45 = 5+ 308
A 45 = 313
| S 45 = 45/2 [2) (45 — 1) (7). = 22,5 [10 + (44) (7)] S 45 = (22,5) (10 + 308) S 45 = (22,5) (318) S 45 = 7155 | 11111111142 45 = 7155 Альтернативное решение S n = n/2 (первый член + последний член) S 45 = 45/2 (5 + 313) S 50 = 22,5 (318) S 50 = 7155 |
Следовательно Резюме
«Арифметическая прогрессия» (АР) – это ряд чисел, в котором любые два следующих друг за другом числа имеют постоянную разницу. Арифметическая последовательность — это другое ее название. Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем добавления первого на фиксированное число.
Арифметическая последовательность — это другое ее название. Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем добавления первого на фиксированное число.
Формула для обнаружения N -го члена арифметической прогрессии дается,
A N = A + (N — 1) D
, где A N = = D
, где A N = D
n-й член,
a = первый член,
n = положение члена
d = общая разность
Задается формулой для первых n членов арифметической прогрессии.
Формула (первые n чисел в AP): S n = n/2 [ 2a + ( n – 1 ) d ]
где S n = сумма n членов
n = общее количество членов
a = первый член
9 d0 = общая разность
Когда заданы первый и последний члены, формула суммы первых n членов арифметической прогрессии имеет вид
Часто задаваемые вопросы об арифметической прогрессии (AP) В чем разница между конечной арифметической последовательностью и бесконечной арифметической последовательностью? Если арифметическая последовательность содержит конечное или ограниченное число членов, она конечна; в противном случае он бесконечен.
Например, {10, 13, 16, 19, 22, 25, 28, 31} является конечной арифметической последовательностью, поскольку она имеет ограниченное количество членов и последний член.
Примером бесконечной арифметической последовательности является { 2, 6, 10, 14, 18, 22, 26, 30, … }
По какой формуле вычисляется арифметическая прогрессия?«Арифметическая прогрессия» (АП) — это ряд чисел, в котором любые два следующих друг за другом числа имеют постоянную разность.
N -й термин арифметической прогрессии можно определить с использованием следующей формулы:
A N = A + (N — 1) D
, где A N = NTH -член первый термин,
n = позиция термина
d = общая разность
В алгебре арифметическая прогрессия (АП) – это такое расположение чисел, при котором существует постоянная разница между терминами. Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем прибавления первого к фиксированному числу.
Арифметическая последовательность — это последовательность чисел, в которой для каждой пары последовательных членов второе число получается путем прибавления первого к фиксированному числу.
Формула для нахождения n-го члена арифметической прогрессии:
a n = a + ( n – 1 ) d
где a n = n-й член,
a = 90 d разность 0,
n
Например, 3, 7, 11, 15, 19, 23,… является арифметической прогрессией с общей разностью 4.
7 – 3 = 4
11 – 7 =4
15 – 11 =4
19 – 15 = 4
Тип последовательности, известный как геометрическая прогрессия (ГП), представляет собой последовательность, в которой каждый последующий член получается путем умножения каждого предыдущего члена на фиксированное число или «общее отношение». Другое название этой прогрессии — геометрическая последовательность чисел.
Следующая формула может быть использована для поиска N-го срока в геометрической прогрессии:
A N = A (R) N-1
, где A N = = = n-й член,
a = первый член,
n = положение члена
r = знаменатель
Например, 2, 6, 18, 54, 162, 486,… — это геометрическая прогрессия со знаменателем 3.
6 / 2 = 3
18 / 6 = 3
54 / 18 = 3
162 / 54 =3
Прямая линия представляет собой график арифметической прогрессии, наклон которой представляет собой общую разность.
Как посчитать сумму первых n чисел в арифметической прогрессии?Сумма первых n членов арифметической прогрессии определяется формулой
(первые n чисел в АП): S n = n/2 [ 2a + ( n – ) г ]
где S n = сумма n членов
n = общее количество членов
a = первый член
d = общая разность
Рассмотрим сложение первых 15 чисел в последовательности, 3, 12, 21, 30 , 39, …
В приведенном примере первый член равен 3 или a = 3, общая разность равна 9 или d = 9, а n = 15. Подставляя данное в формулу, имеем
S 15 = 15/2 [ 2 (3) + ( 15 – 1 ) ( 9 ) ]
S 15 = 7,5 [ 6 + ( 14 )( 9) ]
S 15 = (7,5) ( 6 + 126 )
S 15 = ( 7,5 ) ( 132 )
S 15 = 990
3 , следовательно, сумма чисел в первой последовательности , 12, 21, 30, 39, …
равно 990.



 Например, 0, 1, 2, 3, 4, 5… — это последовательность, представляющая собой бесконечную последовательность целых чисел.
Например, 0, 1, 2, 3, 4, 5… — это последовательность, представляющая собой бесконечную последовательность целых чисел.