Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
вычислите площадь фигуры, ограниченной линиями y=1-x^2, y=0 ( с графиком)
Можно ли подать на апелляцию по части 1 по математике
https://vk. com/doc245577262_450343753?hash=070c1827ac04604427&dl=5341e6ab46d7f1837f 14-й вариант
com/doc245577262_450343753?hash=070c1827ac04604427&dl=5341e6ab46d7f1837f 14-й вариант
Что такое центр симметрии и…
Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
Пользуйтесь нашим приложением
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. 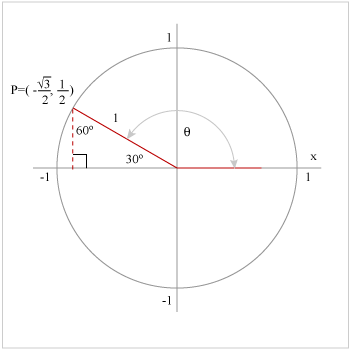 ПЕРИОДИЧЕСКИЕ ДРОБИ ПЕРИОДИЧЕСКИЕ ДРОБИ§ 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10.  РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ§ 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1.  ПОНЯТИЕ ФУНКЦИИ ПОНЯТИЕ ФУНКЦИИ§ 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2.  НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ§ 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6.  § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1.  РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4.  ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙКонтрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3.  СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ§ 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Калькулятор — arctan(sqrt(3)) — Солуматы
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.

- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` | |
| arctan(`-sqrt(3)/3`) | `5*pi/6` | `2*pi/3` |
| arctan(`0`) | `0` | |
| arctan(`sqrt(3)`) | `/3` | |
| arctan(`1`) | `pi/4` | |
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число. 92)`
Предельный арктангенс :
Калькулятор пределов позволяет вычислить пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может строить график функции арктангенса в интервале ее определения.
Свойство функции арктангенс :
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Видео-урок: Обратные тригонометрические функции
Стенограмма видео
В этом видео мы научимся
вычислить точные значения тригонометрических инверсий и оценить композиции
тригонометрические и обратные тригонометрические функции при стандартных углах в радианах. Начнем с того, что вспомним некоторые ключевые
определения и обозначения, относящиеся к обратным функциям вообще. Затем мы углубимся в особенности
как вычислять обратные тригонометрические функции.
Начнем с того, что вспомним некоторые ключевые
определения и обозначения, относящиеся к обратным функциям вообще. Затем мы углубимся в особенности
как вычислять обратные тригонометрические функции.
Функция 𝑓 отображает вход 𝑥 принадлежащий множеству 𝑋, называемому доменом, к выходу 𝑦, равному 𝑓 из 𝑥 принадлежащий множеству 𝑌, называемому диапазоном. Область определения 𝑋 функции 𝑓 есть множество всех возможных входов 𝑥 таких, что 𝑓 из 𝑥 определено. Диапазон 𝑌 функции 𝑓 равен набор всех результатов, которые мы можем получить, применяя 𝑓 к элементам 𝑋.
Функция обратима, если она
один к одному и на функцию. Один к одному или инъективный означает, что
каждый вход имеет один уникальный выход, а онто или сюръективный означает каждый элемент множества.
диапазон может быть записан в виде 𝑓 из 𝑥 для некоторого 𝑥 в домене. Если мы допустим 𝑓, отображение элементов из
𝑋 к 𝑌, — обратимая функция, то обратной к 𝑓 является функция 𝑓
обратный, который отображает элементы из 𝑌 в 𝑋, со свойством 𝑓 из 𝑥 равно 𝑦, если
и только если 𝑓, обратное 𝑦, равно 𝑥.
Проще говоря, инверсия функция обращает исходную функцию. Если 𝑓 обратимо, то 𝑓 отображает вход 𝑥 в уникальный выход 𝑦 и 𝑓 обратное отображение 𝑦 обратно в исходное 𝑥. В результате домен и диапазон обратной функции по существу меняются местами по сравнению с исходной функция. Если домен 𝑓 не равен диапазон обратного 𝑓, мы можем ограничить исходный домен, чтобы гарантировать они совпадают. А теперь вспомним определение составная функция.
Даны две функции 𝑔 от 𝑥 и 𝑓
из 𝑥, мы вычисляем составную функцию 𝑔 из 𝑓 из 𝑥, заменяя каждый экземпляр
из 𝑥 в 𝑔 из 𝑥 на 𝑓 из 𝑥. Например, если 𝑔 из 𝑥 равно двум
𝑥 плюс один и 𝑓 от 𝑥 равно 𝑥 в квадрате, то составная функция 𝑔 от 𝑓 от
𝑥 равно двум 𝑥 в квадрате плюс один. Если функции обратные,
их состав будет иметь очень предсказуемый результат, согласно следующему
правило. Пусть 𝑓 и 𝑔 обратны
функции. Затем, применяя 𝑓 к любому элементу 𝑥
в наборе 𝑋, за которым следует 𝑔, возвращает исходный элемент 𝑥. Точно так же, если мы применим 𝑔 к любому 𝑦
в наборе 𝑌, за которым следует 𝑓, мы возвращаемся 𝑦.
Пусть 𝑓 и 𝑔 обратны
функции. Затем, применяя 𝑓 к любому элементу 𝑥
в наборе 𝑋, за которым следует 𝑔, возвращает исходный элемент 𝑥. Точно так же, если мы применим 𝑔 к любому 𝑦
в наборе 𝑌, за которым следует 𝑓, мы возвращаемся 𝑦.
Теперь, когда мы рассмотрели основные идеи об обратных функциях, мы рассмотрим специальные названия для обратные тригонометрические функции. Во-первых, у нас есть арксинус, который обратная синусу, арккосинус обратная косинусу, арктангенс обратная касательной. Напомним, что тригонометрический функции не однозначны. Это означает, что синус, косинус и касательные необратимы, если мы не ограничим их домены, чтобы убедиться, что каждое значение 𝑘 возвращает ровно одно значение 𝜃.
С соответствующими ограничениями на
𝜃, мы определяем три обратные тригонометрические функции следующим образом.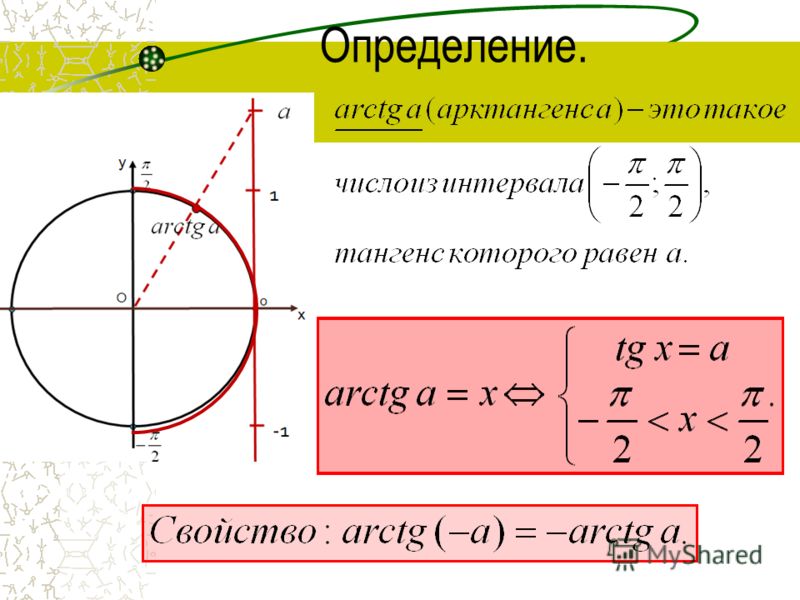 Для синуса и тангенса мы ограничиваем
область в первый и четвертый квадранты единичной окружности. Это интервал от отрицательного
𝜋 больше двух до положительного 𝜋 больше двух радиан. Для косинуса ограничим область определения
на первый и второй квадранты. Это интервал от нуля до
𝜋 радианы. Теперь напомним, что диапазон
синус и косинус уже ограничены значениями, большими или равными отрицательному
единица и меньше или равна положительной единице. И диапазон тангенса — это набор
всех действительных чисел. Далее мы рассмотрим
определения тригонометрических функций в терминах координатных точек.
Для синуса и тангенса мы ограничиваем
область в первый и четвертый квадранты единичной окружности. Это интервал от отрицательного
𝜋 больше двух до положительного 𝜋 больше двух радиан. Для косинуса ограничим область определения
на первый и второй квадранты. Это интервал от нуля до
𝜋 радианы. Теперь напомним, что диапазон
синус и косинус уже ограничены значениями, большими или равными отрицательному
единица и меньше или равна положительной единице. И диапазон тангенса — это набор
всех действительных чисел. Далее мы рассмотрим
определения тригонометрических функций в терминах координатных точек.
Напомним, что когда угол 𝜃 в
стандартное положение проходит через координатную точку 𝑥, 𝑦, мы можем оценить все шесть
тригонометрические функции с использованием 𝑥, 𝑦 и 𝑟 равны квадратному корню из 𝑥 в квадрате
плюс 𝑦 в квадрате согласно следующим определениям. грех 𝜃 равен 𝑦 над 𝑟, где
𝑟 отличен от нуля. cos 𝜃 равен 𝑥 над 𝑟, где
𝑟 также отличен от нуля. И тангенс 𝜃 равен 𝑦 над 𝑥,
где 𝑥 отлично от нуля. По возможности удобно
использовать координатные точки из единичного круга, где 𝑟 равно единице.
грех 𝜃 равен 𝑦 над 𝑟, где
𝑟 отличен от нуля. cos 𝜃 равен 𝑥 над 𝑟, где
𝑟 также отличен от нуля. И тангенс 𝜃 равен 𝑦 над 𝑥,
где 𝑥 отлично от нуля. По возможности удобно
использовать координатные точки из единичного круга, где 𝑟 равно единице.
Стандартные углы в радианах найдены на единичный круг кратен 𝜋 более шести и 𝜋 более четырех между нулем и двумя 𝜋 радианы. Первая схема агрегата кружок показывает приращение 𝜋 более шести. На второй диаграмме показаны приращения из 𝜋 более четырех. Мы включили степень преобразования на схемах. Но мы можем конвертировать между градусами и радианы по мере необходимости, используя тот факт, что 180 градусов равны 𝜋 радианам.
С единичным кругом мы можем использовать
упрощенные определения координат для синуса и косинуса. Чтобы оценить грех 𝜃, мы бы
посмотрите на 𝑦-координату точки, где 𝜃 пересекает единичный круг.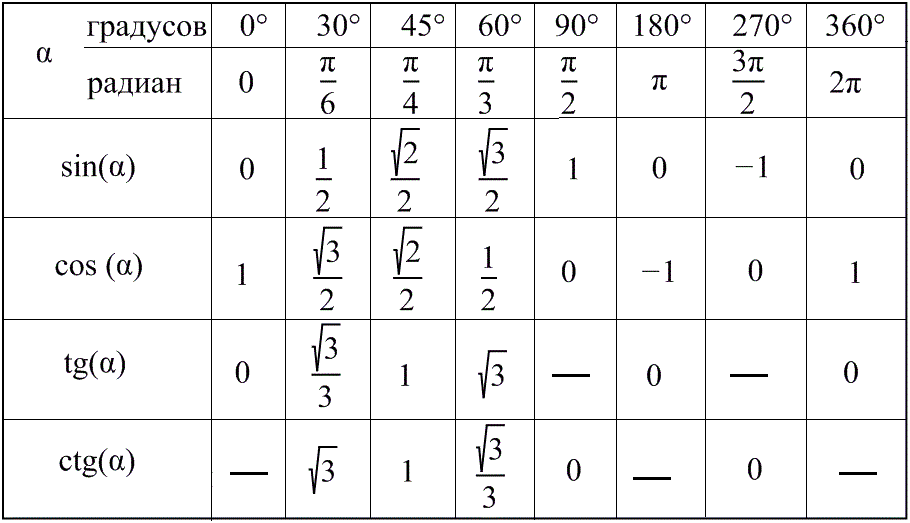 Чтобы оценить cos 𝜃, мы смотрим на
соответствующую 𝑥-координату. Теперь, когда мы рассмотрели, как
вычислить стандартные тригонометрические функции вокруг единичного круга, мы оценим
наша первая обратная тригонометрическая функция.
Чтобы оценить cos 𝜃, мы смотрим на
соответствующую 𝑥-координату. Теперь, когда мы рассмотрели, как
вычислить стандартные тригонометрические функции вокруг единичного круга, мы оценим
наша первая обратная тригонометрическая функция.
Оценить выражение arcsin числа квадратный корень из трех больше двух.
Начнем с того, что вспомним, что арксинус
является обратной тригонометрической функцией синуса. В частности, арксинус 𝑘 дает
нам угол 𝜃 в стандартном положении, для которого синус 𝜃 равен 𝑘, где диапазон
арксинуса 𝜃 больше или равно отрицательному 𝜋 больше двух и меньше или равно
к положительному 𝜋 более чем на два радиана. Это означает, что наш угол 𝜃 должен лежать
где-то в пределах первого или четвертого квадранта на единичной окружности. По словам знакомых CAST
диаграммы, мы знаем, что только косинус положителен в четвертом квадранте.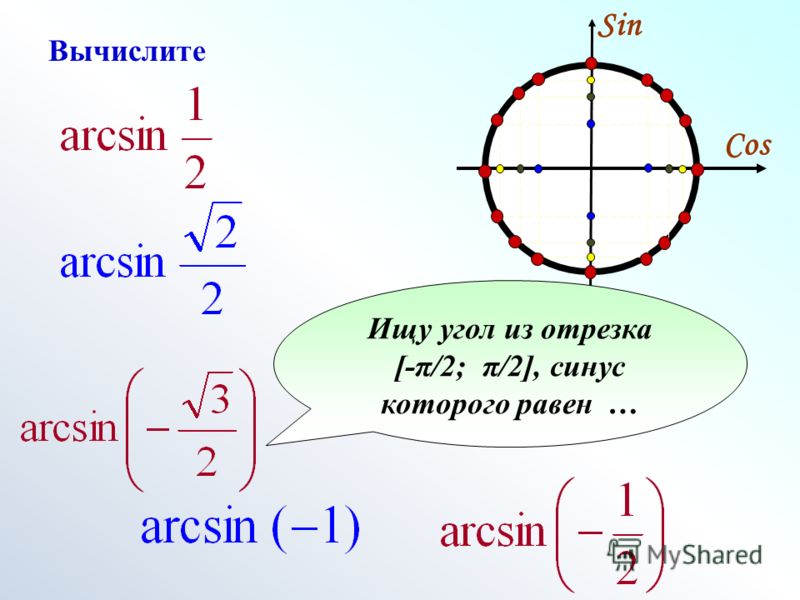 Поскольку мы хотим оценить
обратным синусу при положительном значении, мы можем быть уверены, что 𝜃 будет найдено в
первый квадрант.
Поскольку мы хотим оценить
обратным синусу при положительном значении, мы можем быть уверены, что 𝜃 будет найдено в
первый квадрант.
Теперь вспомним определения тригонометрические функции, выраженные через 𝑥- и 𝑦-координаты от единицы обведите следующим образом. В частности, мы будем использовать определение синуса оценивается в 𝜃, то есть 𝑦. Чтобы оценить арксинус квадрата корень из трех над двумя, нам нужно найти стандартный угол в первой четверти для где синус угла равен квадратному корню из трех над двумя. Поскольку грех 𝜃 равен 𝑦, мы ищем угол, который пересекает единичную окружность по 𝑦-координате квадратный корень из трех больше двух. Итак, смотрим на первый квадрант единичного круга, который показан здесь с шагом 𝜋 более шести и 𝜋 более четыре.
Мы находим точку с 𝑦-значением
квадратного корня из трех на два.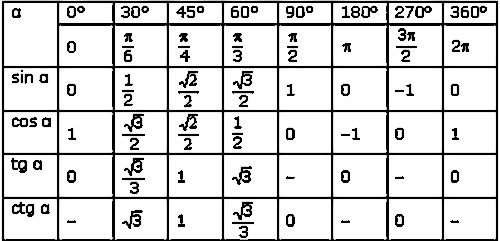 Угол, который пересекает этот
точка на единичной окружности 𝜋 больше трех радиан или 60 градусов. Поскольку грех 𝜋 больше трех равен
квадратный корень из трех из двух и 𝜋 из трех находится в правильном диапазоне для
арксинус, мы заключаем, что арксинус квадратного корня из трех над двумя равен 𝜋
более трех радиан.
Угол, который пересекает этот
точка на единичной окружности 𝜋 больше трех радиан или 60 градусов. Поскольку грех 𝜋 больше трех равен
квадратный корень из трех из двух и 𝜋 из трех находится в правильном диапазоне для
арксинус, мы заключаем, что арксинус квадратного корня из трех над двумя равен 𝜋
более трех радиан.
В некоторых вопросах нас могут спросить вычислить сумму или разность обратных тригонометрических функций. Мы рассмотрим пример этого введите следующий.
Оценить выражение arctan of один минус arcsin от отрицательного.
Во-первых, напомним, что арктангенс равен
инверсия тангенса и арксинуса является инверсией синуса. Чтобы подойти к этой проблеме, мы будем
оцените арктан одного и арксин отрицательного отдельно, затем возьмите их
разница. Начнем с того, что вспомним, что arctan
𝑘 дает нам угол 𝜃 в стандартном положении тогда и только тогда, когда тангенс угла 𝜃 равен
𝑘.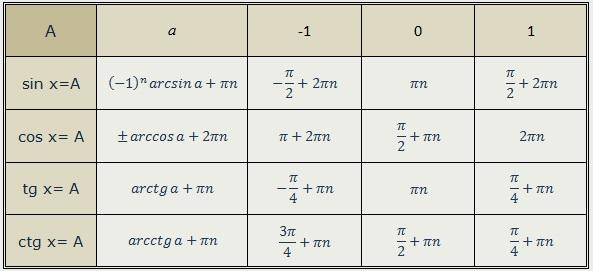 Дальность действия арктана на 𝜃 больше
больше или равно отрицательному 𝜋 в течение двух и меньше или равно положительному 𝜋 в течение двух
радианы. Нам нужно найти стандартный угол
тангенс угла которого равен единице. В терминах 𝑥- и 𝑦-координат
от единичной окружности мы определяем касательную как 𝑦 над 𝑥.
Дальность действия арктана на 𝜃 больше
больше или равно отрицательному 𝜋 в течение двух и меньше или равно положительному 𝜋 в течение двух
радианы. Нам нужно найти стандартный угол
тангенс угла которого равен единице. В терминах 𝑥- и 𝑦-координат
от единичной окружности мы определяем касательную как 𝑦 над 𝑥.
Итак, ищем угол
которая пересекает единичную окружность в точке, где 𝑦, деленное на 𝑥, равно единице. Умножая каждую сторону этого
уравнение на 𝑥, мы имеем 𝑦 равно 𝑥. Это означает, что мы ищем
точка, где 𝑥- и 𝑦-координаты равны. Это происходит только в двух местах
на единичном круге, 𝜋 более четырех и пяти 𝜋 более четырех радиан. Так как пять 𝜋 больше четырех не в
диапазон арктангенса, мы заключаем, что арктангенс единицы не может быть больше пяти 𝜋
четыре. Тем не менее, 𝜋 более четырех находится в
правильный диапазон, а 𝑥- и 𝑦-координаты равны. Итак, мы нашли этот загар 𝜋
больше четырех равняется единице, а это означает, что арктангенс единицы равен 𝜋 больше четырех.
Итак, мы нашли этот загар 𝜋
больше четырех равняется единице, а это означает, что арктангенс единицы равен 𝜋 больше четырех.
Далее нам нужно вычислить арксинус отрицательный. Напомним, что arcsin от 𝑘 дает нам угол 𝜃 в стандартном положении тогда и только тогда, когда грех 𝜃 равен 𝑘. И напомним, что ассортимент арксинус совпадает с диапазоном арктангенса. Так как грех 𝜃 равен 𝑦 на единичной окружности ищем угол, который пересекает единичную окружность в 𝑦-координата отрицательной единицы. Есть только одно место, где мы иметь эту 𝑦-координату на единичной окружности. И это под квадрантным углом три 𝜋 больше двух. Из единичного круга мы видим, что грех трех 𝜋 над двумя равен отрицательной единице. Таким образом, мы ожидаем, что арксинус отрицательный один будет равен трем 𝜋 больше двух.
К сожалению, три 𝜋 больше двух
не в правильном диапазоне для функции арксинуса. У нас есть правильное местоположение на
единичной окружности, но нам нужно найти котерминальный угол с тремя 𝜋 над двумя в
заданный интервал. Чтобы найти котерминальный угол в
радианы, мы прибавляем или вычитаем кратное двум 𝜋. Поскольку три 𝜋 больше двух выше
диапазон арксинуса, мы должны вычесть два 𝜋. Следовательно, после написания обоих терминов
над общим знаменателем двух и нахождением их разности получаем минус 𝜋
больше двух. Следовательно, арксинус отрицательной единицы
равно отрицательному 𝜋 больше двух, потому что отрицательное 𝜋 больше двух находится в правильном диапазоне и
грех отрицательного 𝜋 больше двух равен минус единице.
У нас есть правильное местоположение на
единичной окружности, но нам нужно найти котерминальный угол с тремя 𝜋 над двумя в
заданный интервал. Чтобы найти котерминальный угол в
радианы, мы прибавляем или вычитаем кратное двум 𝜋. Поскольку три 𝜋 больше двух выше
диапазон арксинуса, мы должны вычесть два 𝜋. Следовательно, после написания обоих терминов
над общим знаменателем двух и нахождением их разности получаем минус 𝜋
больше двух. Следовательно, арксинус отрицательной единицы
равно отрицательному 𝜋 больше двух, потому что отрицательное 𝜋 больше двух находится в правильном диапазоне и
грех отрицательного 𝜋 больше двух равен минус единице.
Наконец, мы вычисляем арктангенс одного
минус arcsin отрицательной единицы путем подстановки полученных значений. Вычитание минуса
эквивалентно добавлению положительного. Поэтому с помощью общего
знаменатель четырех, у нас есть три 𝜋 больше четырех.
В заключение мы показали, что арктан единицы минус арксин отрицательной единицы равен трем 𝜋 более четырех радианы.
В нашем последнем примере мы рассмотрим, как оценить композицию стандартных и обратных тригонометрических функции.
Найти точное значение arccos квадратный корень из двух умноженных на отрицательный 𝜋 более шести без использования калькулятор.
Чтобы вычислить это выражение, мы
должны сначала распознать его как композицию функций арккосинуса, обратную
косинус и синус. Давайте вспомним значение слова
композиция двух функций по двум функциям 𝑔 от 𝑥 и 𝑓 от 𝑥. Состав 𝑔 из 𝑓 из 𝑥
вычисляется путем замены каждого экземпляра 𝑥 в 𝑔 из 𝑥 на 𝑓 из 𝑥. В этом случае пусть 𝑔 из 𝑥 будет
arccos из 𝑥 и 𝑓 из 𝑥 будут квадратным корнем из двух умноженных на грех из 𝑥. Чтобы оценить 𝑔 из 𝑓 из 𝑥 в 𝑥
равно отрицательному 𝜋 больше шести, мы сначала оцениваем 𝑓 отрицательного 𝜋 больше шести. Напомним, что синус определяется как
𝑦 на единичной окружности. Итак, мы ищем
𝑦-координата точки, где отрицательный угол 𝜋 больше шести пересекает единицу
круг.
Напомним, что синус определяется как
𝑦 на единичной окружности. Итак, мы ищем
𝑦-координата точки, где отрицательный угол 𝜋 больше шести пересекает единицу
круг.
Круг единицы измерения не отображается
отрицательные угловые меры, поэтому мы должны добавить два 𝜋 радиана, чтобы найти наименьший положительный
котерминальный угол с отрицательным 𝜋 больше шести. Мы можем использовать общий знаменатель
шесть, чтобы найти котерминальный угол. Итак, у нас есть минус 𝜋 больше шести
плюс 12𝜋 больше шести, что равно 11𝜋 больше шести. Мы видим, что 11𝜋 больше шести находится в
четвертый квадрант единичной окружности. В 11𝜋 больше шести мы находим
𝑦-координатная отрицательная половина. Таким образом, мы показали, что грех
отрицательного 𝜋 больше шести равно греху 11𝜋 больше шести, поэтому они оба равны отрицательным
одна половина.
Теперь мы можем оценить 𝑓 из 𝑥 в 𝑥 равно отрицательному 𝜋 больше шести. Используя замену, мы находим, что 𝑓 отрицательного 𝜋 больше шести равняется квадратному корню из удвоенной отрицательной половины. Итак, 𝑓 отрицательных 𝜋 больше шести равно отрицательному квадратному корню из двух больше двух.
Освободим место для следующего
шаг. На данный момент у нас есть 𝑓 отрицательных 𝜋
больше шести равняется отрицательному квадратному корню из двух из двух. Теперь, чтобы оценить 𝑔 из 𝑓 из
отрицательное 𝜋 больше шести, мы должны вычислить 𝑔 отрицательного квадратного корня из двух больше
два. Поскольку 𝑔 из 𝑥 равно arccos из 𝑥,
отсюда следует, что 𝑔 отрицательного квадратного корня из двух больше двух равно arccos
отрицательный квадратный корень из двух больше двух. Наконец, чтобы оценить arccos
отрицательный квадратный корень из двух над двумя, мы еще раз ссылаемся на единичный круг. Напомним, что арккосинус
обратный косинусу, и арккос 𝑘 дает нам угол 𝜃 в стандартном положении,
для которого cos 𝜃 равен 𝑘. В этом случае 𝑘 — это квадратный корень
из двух над двумя.
Напомним, что арккосинус
обратный косинусу, и арккос 𝑘 дает нам угол 𝜃 в стандартном положении,
для которого cos 𝜃 равен 𝑘. В этом случае 𝑘 — это квадратный корень
из двух над двумя.
Определение косинуса, выраженное в координатах единичного круга равно 𝑥. Это означает, что мы ищем стандартный угол с 𝑥-координатой отрицательного квадратного корня из двух из двух. Давайте посмотрим, что еще мы знаем об угле, который мы хотим найти. Напомним, что ассортимент функция арккосинуса ограничена первым или вторым квадрантом, в частности, от от нуля до 𝜋 радиан. Таким образом, мы можем игнорировать все, что ниже 𝑥-ось.
По диаграмме CAST мы
известно, что все тригонометрические функции положительны в первой четверти. Мы хотим оценить обратную
косинус с отрицательным значением, поэтому мы можем быть уверены, что 𝜃 находится во втором квадранте,
где только синус положительный. Во втором квадранте находим
𝑥-координата отрицательный квадратный корень из двух больше двух в 𝜃 равно трем 𝜋 больше
четыре. Это означает, что arccos
отрицательный квадратный корень из двух больше двух равен трем 𝜋 больше четырех.
Во втором квадранте находим
𝑥-координата отрицательный квадратный корень из двух больше двух в 𝜃 равно трем 𝜋 больше
четыре. Это означает, что arccos
отрицательный квадратный корень из двух больше двух равен трем 𝜋 больше четырех.
В заключение мы показали, что arccos квадратного корня из двух, умноженных на sin отрицательного 𝜋 больше шести, равен трем 𝜋 более четырех радиан.
Давайте закончим, подытоживая некоторые важные моменты из этого видео. Три обратных тригонометрических функции арксинус, арккосинус и арктангенс определяются в терминах стандарта тригонометрические функции. Обратная функция синуса называется арксинусом, функция, обратная косинусу, называется арккосинусом, а обратная функция функция тангенса называется арктангенсом.
Тригонометрические функции доступны только
обратимым, когда мы ограничиваем их область таким образом.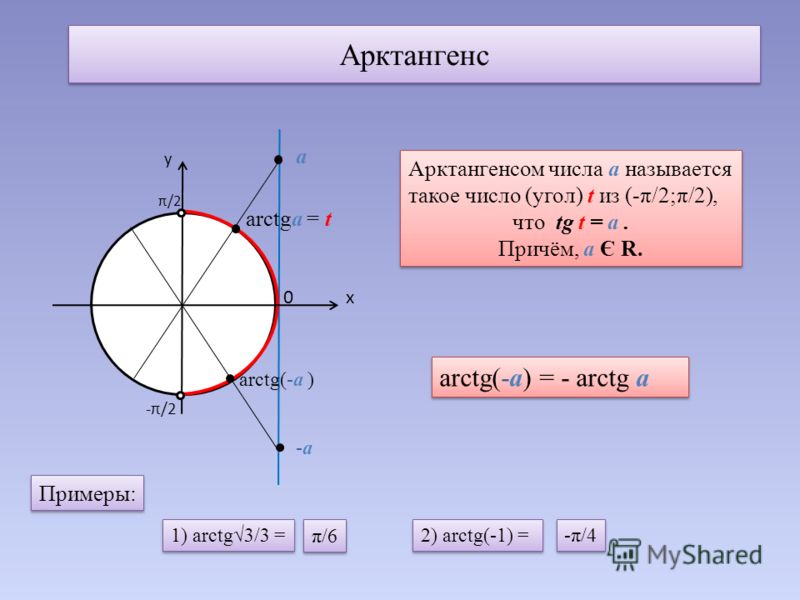 Тогда их можно определить как
следует с точки зрения 𝑘 и 𝜃. Единичный круг – это круг с
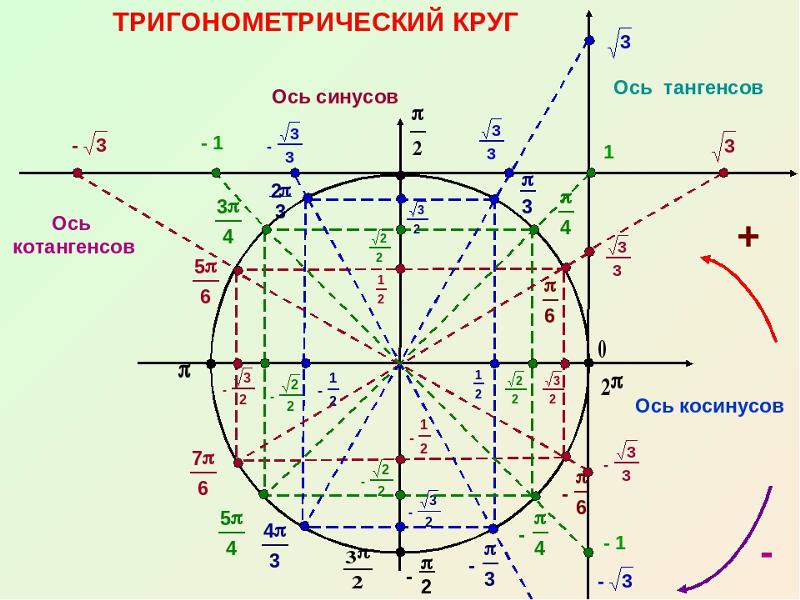
радиус того, центр которого лежит в начале координат плоскости. Стандартные углы в радианах
найденные на единичной окружности кратны 𝜋 более шести и 𝜋 более четырех между нулем
и два 𝜋 радиана. Каждый угол пересекает единицу
окружность в точке координат 𝑥, 𝑦, которая помогает нам определить тригонометрический
работает под этими углами.
Тогда их можно определить как
следует с точки зрения 𝑘 и 𝜃. Единичный круг – это круг с
радиус того, центр которого лежит в начале координат плоскости. Стандартные углы в радианах
найденные на единичной окружности кратны 𝜋 более шести и 𝜋 более четырех между нулем
и два 𝜋 радиана. Каждый угол пересекает единицу
окружность в точке координат 𝑥, 𝑦, которая помогает нам определить тригонометрический
работает под этими углами.
Эти две диаграммы отображают устройство
круг разделен на части 𝜋 более шести и 𝜋 более четырех. Они являются очень полезным ориентиром
при вычислении стандартных или обратных тригонометрических функций. Тригонометрические функции могут быть
определяется через 𝑥- и 𝑦-координаты, показанные на единичной окружности как
следует. Чтобы оценить грех 𝜃, мы смотрим
по 𝑦-координате. Чтобы оценить cos 𝜃, мы смотрим
по 𝑥-координате.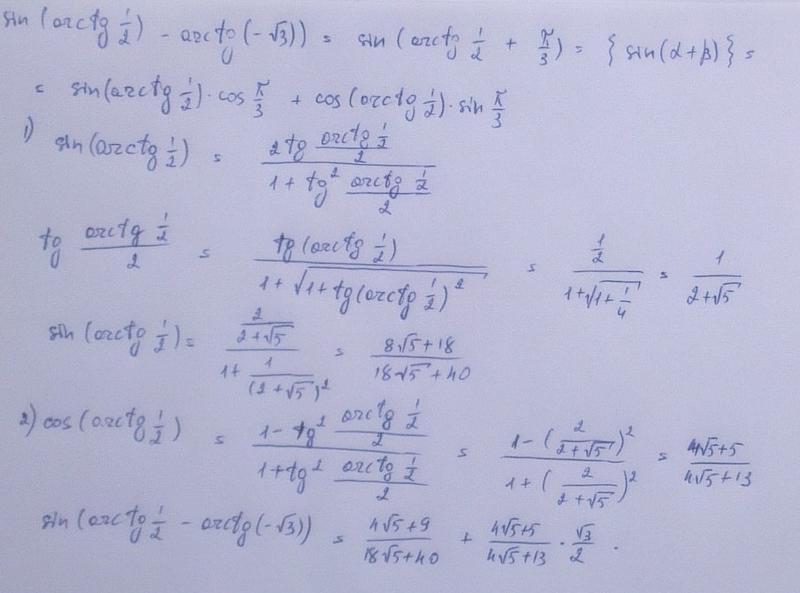

 06.19
06.19 06.19
06.19 К каждому пункту теоретического материала приведены упражнения с решениями и упражнения трех уровней сложности для самостоятельного решения. Она может быть использована при подготовке к экзаменам в высшие учебные заведения.
К каждому пункту теоретического материала приведены упражнения с решениями и упражнения трех уровней сложности для самостоятельного решения. Она может быть использована при подготовке к экзаменам в высшие учебные заведения.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.