Арктангенс посчитать онлайн: Арктангенс — калькулятор онлайн

3 a + b

## [1] 32

Признайся, шалунишка, ты всегда мечтал поделить на ноль?

a <- 1/0
a

## [1] Inf

Что можно делать с бесконечностью?

1/(a - 9)

## [1] 0

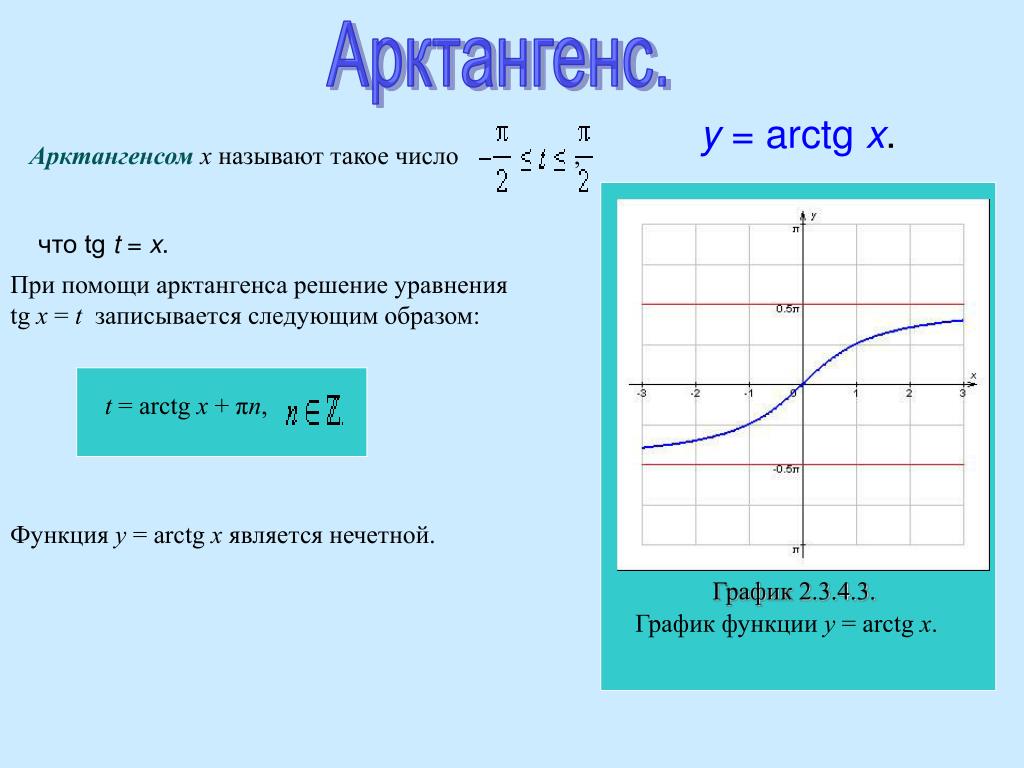
Возьмём арктангенс!

atan(Inf)

## [1] 1.571

Ба! Да это же \( \pi/2 \):

pi/2

## [1] 1.571

Но с неопределенностью ничего не поделаешь

0/0

## [1] NaN

NaN расшифровывается как <>

А теперь векторы

Вектор из чисел по порядку:

a <- 3:10
a

## [1]  3  4  5  6  7  8  9 10

Вектор из одинаковых чисел:

b <- rep(777, times = 5)
b

## [1] 777 777 777 777 777

Вектор из конкретных чисел:

vect <- c(5, -4, 1)

Что можно делать с вектором?

sum(vect)

## [1] 2

Хотите среднее арифметическое?

mean(vect)

## [1] 0.6667

Генерация случайных величин

Хочу 300 случайныхх натуральных чисел от 1 до 5 с повторами! И побыстрее!

h <- sample(1:5, 300, rep = TRUE)

Краткая информация о векторе \( h \) и начало вектора \( h \)

str(h)

##  int [1:300] 2 3 1 1 4 2 2 1 5 1 . ..

head(h)

## [1] 2 3 1 1 4 2

Хочу сгенирировать выборку из 500 значений случайной величины \( X \) с вероятностями:

\( X \)	-2	3	7
\( P() \)	0.1	0.2	0.7

Зададим вектор вектор возможных значений и вектор вероятностей

x.val <- c(-2, 3, 7)
x.pr <- c(0.1, 0.2, 0.7)

Получаем выборку из 500 значений:

s <- sample(x.val, 500, rep = TRUE, x.pr)
str(s)

##  num [1:500] -2 7 3 3 7 7 3 7 3 3 ...

Два простеньких графика

Первое шаманское заклинание, вызывает духов-построителей красивых графиков!

 require(ggplot2)

## Loading required package: ggplot2

Простенькая гистограмма

qplot(factor(s), main = "Гистограмма")

И еще простенький график

x <- rnorm(500)  # 500 нормальных величин со средним 0 и дисперсией 1
y <- rnorm(500)  # 500 нормальных величин со средним 0 и дисперсией 1
qplot(x, y, main = "Точечки")

Отбор значений

Выберем из вектора \( s \) значения больше \( 0 \):

b <- s[s > 0]
b

##   [1] 7 3 3 7 7 3 7 3 3 7 7 7 7 7 7 3 7 7 7 7 7 3 7 7 7 7 7 7 7 7 3 7 7 7 7
##  [36] 7 7 7 3 7 7 7 7 3 7 7 7 3 7 3 3 3 7 7 7 7 3 3 3 7 7 7 7 3 7 3 7 3 7 7
##  [71] 7 7 3 7 3 7 7 7 7 3 7 7 7 3 7 7 7 7 3 7 7 7 7 3 7 3 3 7 7 7 7 3 3 7 7
## [106] 7 7 7 7 7 3 3 3 7 7 7 7 7 7 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7
## [141] 7 7 7 3 3 7 7 7 7 7 3 7 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 3 7 3 3 3 7 3 3
## [176] 7 3 7 7 3 7 7 7 7 7 7 7 7 7 7 7 7 7 3 7 3 3 7 7 3 3 7 7 7 7 7 3 7 3 7
## [211] 7 7 7 3 7 7 3 7 7 7 7 7 7 7 7 7 7 7 3 7 7 7 7 3 3 7 3 3 7 3 7 7 7 3 7
## [246] 7 3 7 7 3 7 7 7 7 3 7 7 7 7 7 7 7 7 3 7 3 7 7 3 7 3 7 7 7 7 7 3 3 3 7
## [281] 7 7 7 7 7 7 3 7 3 7 7 7 7 7 7 7 7 7 7 7 7 7 7 3 7 7 7 7 3 7 7 7 7 7 7
## [316] 7 3 7 3 7 7 7 3 7 7 3 7 7 7 7 7 7 7 7 3 7 7 7 3 7 3 7 7 7 7 3 3 3 7 7
## [351] 3 7 7 7 7 7 7 7 7 7 3 3 7 7 7 7 7 7 7 7 7 3 7 7 7 7 7 3 7 3 7 7 7 7 7
## [386] 3 7 7 3 7 7 3 3 3 3 3 7 3 3 7 3 3 3 7 7 3 7 7 7 7 3 7 7 7 7 7 7 3 7 3
## [421] 7 3 7 7 7 3 3 7 7 7 7 3 7 3 7 7 7 7 7 7 7 7 7 3 7 7 7 3

str(b)

##  num [1:448] 7 3 3 7 7 3 7 3 3 7 . ..

Можно выбрать конкретные \( s \), например с 6-го по 20-ое:

s[6:20]

##  [1]  7  3  7  3  3  7  7  7  7  7  7  3 -2 -2  7

Хочу 5-ое, 7-ое и 13-ое!

s[c(5, 7, 13)]

## [1] 7 3 7

Можно узнать, сколько значений равно 3:

sum(s == 3)

## [1] 115

Еще полезная штучка — количество чисел в векторе

length(b)

## [1] 448

Строительный калькулятор CI Construction Master Pro Trig

Новейший строительный инженерный калькулятор CI Construction Master Pro Trig с возможностью решения тригонометрических функций.

Строительный калькулятор CI Construction Master Pro это призер и новейший калькулятор со встроенными функциями, идеально подходящими для проектирования, планирования, расчета стоимости и оценки. С ним вы сможете осуществлять вычисления со скругленными элементами, спроектировать крышу, лестницу и многое другое. Работает с метрической системой мер, форматом фут-дюйм и десятичными значениями.

Используйте его в офисе или в производственных условиях, чтобы сэкономить время, сократить затраты, избежать переделок, а также извлечь из работы максимум выгоды.

Строительные вычисления:

• Конвертирует и работает со строительными единицами измерения, включая метрическую систему мер.
• Решение тригонометрических функций.
• Нахождение веса на единицу объема.
• Встроенная функция корректировки угла Right-Angle.
• Полное проектирование лестниц.
• Расчет кровли, стропил и каркасов.
• Вычисления со скругленными элементами: арками, окружностями, сферическими поверхностями и многим другим.
• Расчет лестницы — введите высоту лестницы и рассчитайте лестничный пролет.
• Расчет количества распорок на заданную длину.
• Нахождение сложных косых срезов и изогнутых подкосов.
• Операции с равносторонними многоугольниками.

Калькулятор разработан для подрядчиков, архитекторов, инженеров, менеджеров по проектам, сметчиков, чертежников, строителей, плотников, профильных специалистов.

Больше информации с примерами использования в руководстве пользователя

Инструкция к строительному калькулятору CI Construction Master Pro Trig на русском языке

Технические характеристики калькулятора

Размер: 145 мм x 76 мм x 17 мм

Вес изделия: 130 г включая крышку и карманное руководство

Питание: две 1.5-вольтовые долговечные батареи (LR-44/A76)

Тип дисплея: 11 цифр (7 обычных, 4 дроби) с индикаторами

Размеры дисплея: 16 мм x 63.5 мм

Точность: 12 цифр

Автоматическое отключение экономит заряд батареи.

В комплекте: жесткая крышка, устойчивая к пыли, царапинам и влаге, компактное руководство пользователя на английском (полная инструкция на русском языке в эл.виде), две долговечные батареи LR44, гарантия 1 год.

Функции калькулятора

Конвертирует и работает с единицами измерения

Единицы метрической системы (мм, см, м): Есть

Ярды, дробные дюймы, дроби фут-дюйм: Есть

Десятичные футы (10-е, 100-е), дюймы: Есть

Поддержка всех дробных единиц в строительстве: Есть

Конвертация весовой доли: Есть

Работа с правильными углами

Вычисление правильного угла/стропила: Есть

Кнопка нахождения уклона (угол уклона): Есть

Высота, длина, диагональ/стропильная нога: Есть

Угловая стропильная нога/разжелобка, нарожник: Есть

Нестандартная угловая нога/разжелобок, нарожник: Есть

Угол среза стропильной ноги (вертикальный, угловой, ровный): Есть

Ступени (осн. и доп.: лимит подступенка, площадка, толщина пола): Есть

Наклонная стена: Есть

Стойки: нахождение межцентрового расстояния: Есть

Вычисление площади и объема

Квадратные и кубические измерения: Есть

Крыша — партии, кв.метры, листы 4х8, уклон, площадь гориз. сечения: Есть

Гипсокартон, сайдинг и панели — 4х8, 4х9, 4х12: нет

Площадь и объем колонны/конуса: Есть

Основные и дополнительные вычисления с кругами: Есть

Кнопки длины, ширины, высоты, автоматического расчета площади и объема: нет

Блоки, фундамент: нет

Специальные функции калькулятора

Тригонометрические (синус, косинус, тангенс, арксинус, арккосинус, арктангенс): Есть

Борд-футы: Есть

Работа с основными функциями (+, -, х, /, %, π, х², √х): Есть

Пользовательские настройки: Есть

Кнопка редактирования Backspace: Есть

Стоимость единицы (общая стоимость на основе цены единицы): Есть

Равносторонний многоугольник: Есть

Сложные срезы 45о, косые потолочные срезы: Есть

Дополнительные возможности и характеристики

Функция Paperless Tape: Есть

Количество ячеек памяти: 4

Математические измерения и конвертация

Конвертирует и работает со следующими строительными единицами измерения: ярды, дробные и десятичные футы и дюймы, а также единицы метрической системы мер — включая вычисление площади и объема с указанными единицами.

Формат «Градус:минута:секунда» конвертирует в градусы в виде десятичной дроби.

Нахождение веса на единицу объема.

Основные тригонометрические функции: синус, косинус, тангенс, арксинус, арккосинус и арктангенс – упрощают решения сложных дизайнов в строительстве.

Встроенные функции калькулятора, позволяющие экономить время

Полный расчет лестниц — подступенка, ступенек, длины тетивы лестницы и угла наклона.

Введите высоту лестницы, и калькулятор сам подсчитает лестничный пролет.

Встроенная функция выравнивания угла Right-Angle.

Функция расчета кровли служит для нахождения площади, количества и квадратной единицы подшивки 4х8 для плоской или наклонной крыши.

Функция расчета стропил помогает работать со стропилами, простыми и сложными односкатными и многоскатными крышами. Мгновенный расчет угла (боковой грани балки, уровня и отвеса).

Расчет нарожников для одинакового и неодинакового ската крыши. Нахождение подкосов и межцентрового расстояния.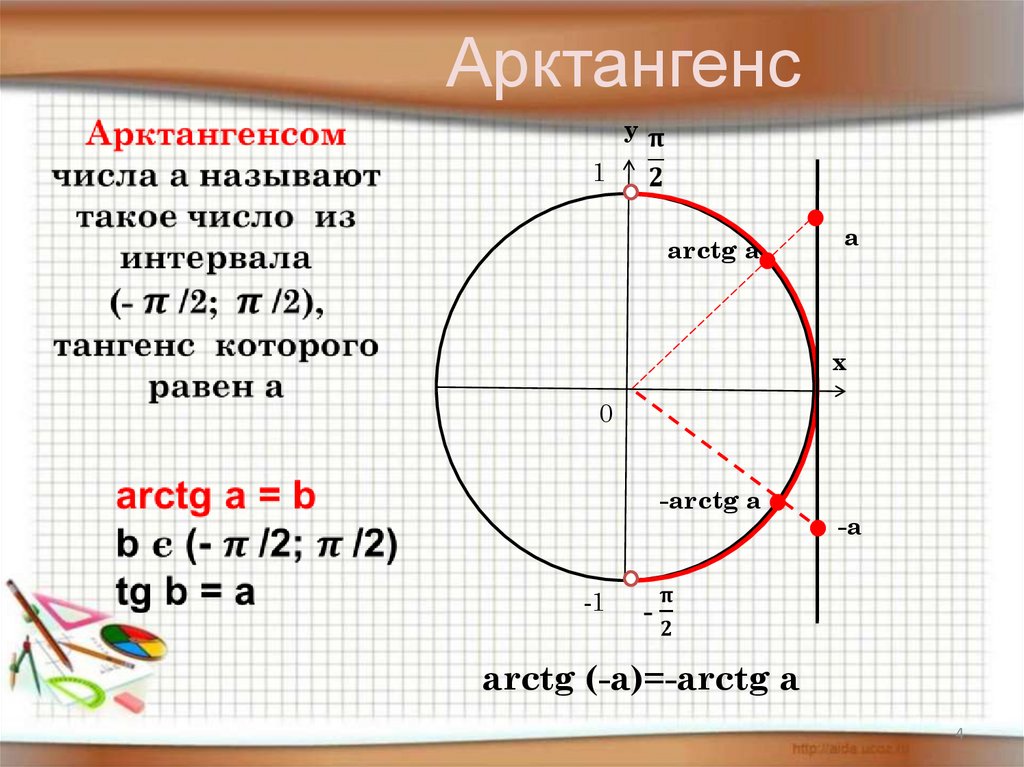

Сложный скос — сохраняйте значение угла свода, а также вводите угол стены, чтобы посчитать угол и положение диска для пилы, если требуется произвести косой срез.

Усовершенствованные решения для скругленных элементов, арок, колонн, подпорок, окон и так далее.

Нахождение изогнутых подкосов с межцентровым расстоянием.

Расчет количества распорок на заданную длину.

Вычисления с равносторонними многоугольниками — расчет угла и биссектрисы, длины стороны, периметра и площади.

Расчет лесоматериалов в досковых футах.

Дополнительные функции калькулятора

Пользовательские настройки: установка пользовательских параметров, например, дроби от 1/2″ до 1/64″, а также высоту лестницы до площадки, градусы в десятичном формате и так далее.

Экспоненциальные значения: ввод и отображение экспоненциальных значений.

Кнопка Backspace легко исправляет последнее введенное значение.

Функция постоянной операции упрощает работу с часто выполняемыми вычислениями.

Быстро рассчитывает себестоимость единицы.

Накопительная память (М+) — дополнительные три хранилища памяти.

Функция «Paperless» Tape позволяет просматривать 20 последних введенных данных для перепроверки вычислений;

Стандартные вычисления

Работает с такими основными математическими действиями как+, -, +/-, x, ÷, %, π, 1/x, x², и √.

Добавить комментарий

Уведомлять меня о новых комментариях по E-mail

Калькулятор — arctan(pi) — Solumaths

Арктан, расчет онлайн

Резюме:

Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.

arctan онлайн

---

Описание:

Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .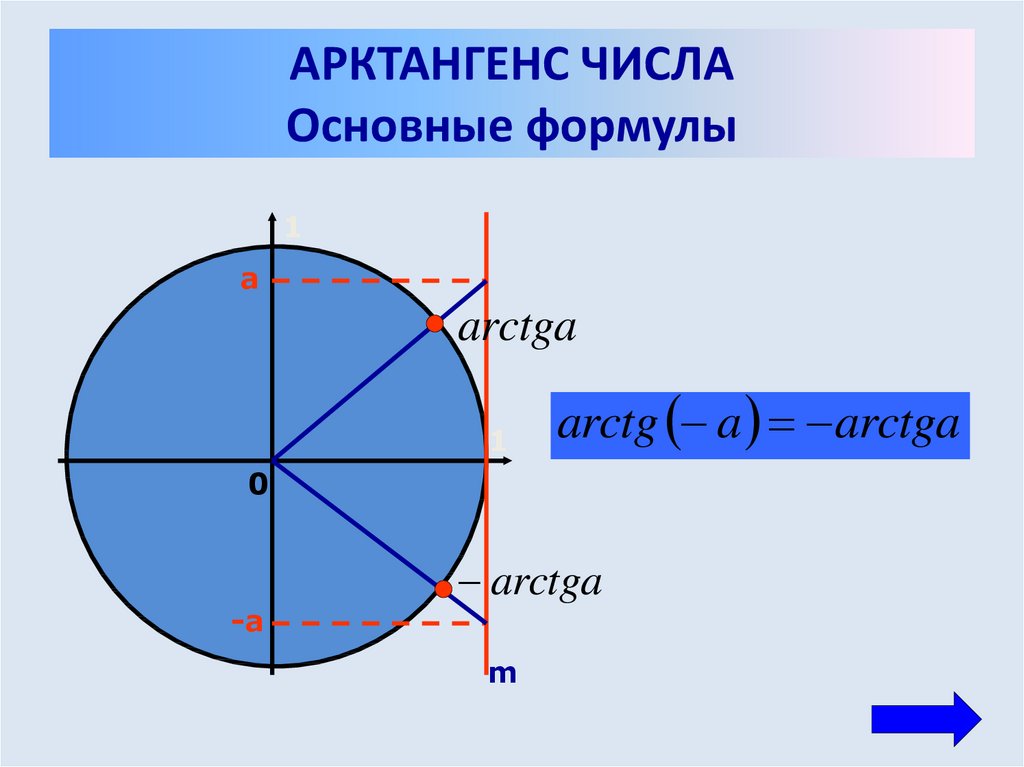

1. Расчет арктангенса

Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.

Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.

2. Пределы арктангенса
Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):

• Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
`lim_(x->-oo)arctan(x)=pi/2`
• Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
`lim_(x->+oo)arctan(x)=-pi/2`

Таблица замечательных значений

arctan (`-sqrt(3)`)

`

arctan(`-1`)	`3*pi/4`
arctan(`-sqrt(3)/3`)	`5*pi/6`	`2*pi/3`
arctan(`0`)	`0`
arctan(`sqrt(3)`)	/3`
arctan(`1`)	`pi/4`
arctan(`sqrt(3)/3`)	`pi/6`

Syntax :

arctan(x) , x — число. 92)`

---

Предельный арктангенс :

Калькулятор пределов позволяет вычислить пределы функции арктангенса.

предел арктангенса(x) is limit(`»arctan»(x)`)

---

Обратная функция арктангенса :

обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.

---

---

Графический арктангенс :

Графический калькулятор может строить график функции арктангенса в интервале ее определения.

---

---

Свойство функции арктангенс :

Функция арктангенса является нечетной функцией.

---

Расчет онлайн с арктангенсом (арктангенсом)

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
• Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
• Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

 

Калькулятор арктангенса

Вычисление функции арктангенса может оказаться довольно сложной задачей: узнайте, как это сделать, и узнайте характеристики этой функции с помощью этого простого инструмента. Продолжайте читать, чтобы узнать:

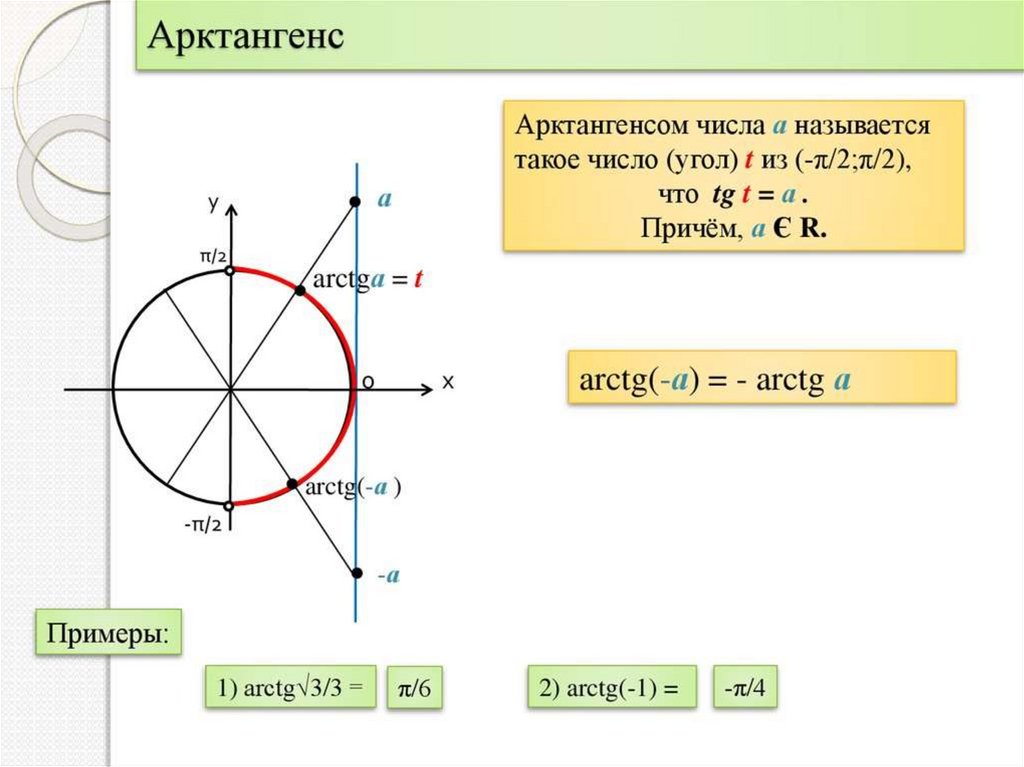
• Что такое арктангенс и как мы его определяем. {-1}(y)x=tan−1(y)

  Тангенс представляет собой периодическую функцию , которая повторяется в диапазоне (−π/2,π/2)(-\pi/2,\pi/2)(−π/2,π/2) со значениями между −∞-\infty−∞ и ∞\infty∞. На изображении ниже вы можете увидеть его график:

  Мы можем инвертировать функцию, взяв отражение относительно диагонали первого квадранта . Однако из-за периодичности функции мы бы нашли что-то, что является , а не совсем функцией , поскольку для каждого значения xxx мы нашли бы бесконечные значения yyy. Чтобы правильно определить функция арктангенса , нам нужно ограничить область определения функции тангенса диапазоном (−π/2,π/2)(-\pi/2,\pi/2)(−π/2,π /2). Сделав это, мы находим один фрагмент функции и можем определить обратную. Вот его график:

  Вы можете ясно видеть, что:

  • Область арктангенса — это вся ось xxx.
  • Диапазон арктангенса ограничен (−π/2,π/2)(-\pi/2,\pi/2)(−π/2,π/2).

  Обратите также внимание на то, что арктангенс больше не является периодическим!

  Как пользоваться нашим калькулятором арктангенса

  Если вы читаете этот текст, то наверняка задаетесь вопросом: «Как вычислить арктангенс?». Ответ прост: используйте калькулятор, так как нет простого способа найти значения этой функции с помощью бумаги и ручки.

  Калькулятор арктангенса Omni является идеальным инструментом для этой цели: введите число в допустимую область арктангенса (то есть всю ось x), и вы получите результат в кратчайшие сроки. Вы также можете использовать наш калькулятор арктангенса в обратном порядке!

  Другой калькулятор арктангенса

  Функция арктангенса известна под разными именами: для каждого из них мы создали отдельный инструмент! Попробуйте наш:

  • Калькулятор арктангенса;
  • Калькулятор арктангенса;
  • Вычислитель Тан-1; и
  • Обратный калькулятор загара!

  Часто задаваемые вопросы

  Где найти арктангенс?

  Арктангенс, даже если он изначально был определен в области тригонометрии, нашел важное применение в машинном обучении, где переключение арктангенса с отрицательного на положительное значение и асимптотическое поведение сделали его хорошим выбором в качестве функция активации .

  No related posts.