Arctan Calculator (обратный касательный) — градусы и радиан
Tan -1 () =
градусов:
—
Радианы:
—
π Радианы:
—
π Радианы:
—
—
.
График арктангенса
Область x все действительные числа .
Диапазон: -π/2 < y < π/2 .
Используйте этот калькулятор, чтобы определить результат арктангенса введенного значения. Ответ будет отображаться в градусах, радианах и π радианах. Рассматривается только диапазон -π/2 < и < π/2.
Вот дополнительная информация о том, как использовать калькулятор арктангенса. Кроме того, вы можете изучить определение, график и важные значения арктангенса.
Как пользоваться калькулятором арктангенса?
Шаг 1: Введите значение x в первое поле ввода.
Вы можете использовать любое реальное значение x .
Шаг 2: Соответствующий угол в градусах будет отображаться на правой панели.
Шаг 3: Угол в радианах и π радианах будет отображаться внизу.
Результат в градусах, радианах и π радианах
Полная окружность дает в общей сложности 360° или 2π радиан. Следовательно, 180° равно π радианам. Если у нас есть угол в градусах и мы хотим преобразовать его в радианы, мы должны разделить его на 180 и умножить на π.
С другой стороны, разница между радианами и π радианами заключается в том, что результат в «радианах» уже включает значение π. Значение π приблизительно равно 3,1415… Например, если у нас есть 0,5 π радиан, это равно 1,571.
Что такое арктангенс?
Арктангенс, также известный как арктангенс, является обратной функцией тангенса. Это означает, что арктангенс меняет действие функции тангенса на противоположное.
Например, тангенс 45° равен 1. Следовательно, арктангенс 1 равен 45°.
Функция арктангенса обозначается как tan -1 (x) или также как arctan(x).
Мы можем использовать арктангенс, чтобы найти угол, если мы знаем отношение сторон прямоугольного треугольника. Например, чтобы найти угол A в треугольнике ниже, мы можем использовать arctan(x), где x равно a/b.
Какие значения x можно использовать для арктангенса?
Арктангенс принимает любое действительное значение x в качестве входных данных. Это потому, что арктангенс является обратной функцией тангенса. Поэтому их домены и диапазоны меняются местами.
Итак, поскольку тангенс имеет диапазон, равный всем действительным числам, область определения арктангенса также равна всем действительным числам.
График арктангенса
График арктангенса можно построить, учитывая, что значения x может быть любым действительным числом, а значения y расположены между -π/2 и π/2 с асимптотами в этих точках.
Область арктангенса
Используя график арктангенса, мы можем видеть, что значения x могут быть любыми значениями без каких-либо ограничений. Следовательно, область определения арктангенса равна всем действительным числам.
Диапазон арктангенса
Из графика арктангенса можно сделать вывод, что выходные значения функции находятся в диапазоне от -π/2 до π/2, не включая эти значения. Тогда его диапазон равен -π/2 < y < π/2.
Table of the inverse tangent of common values
| Value of x | arctan(x)(rad) | arctan(x)(°) |
|---|---|---|
| -∞ | -π/ 2 | -90° |
| -√3 | -π/3 | -60° |
| -1 | -π/4 | -45° |
| -1/√3 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/√3 | π/6 | 30° |
| 1 | π/4 | 45° |
| √3 | π/3 | 60° |
| ∞ | π/2 | 90° |
Связанные калькуляторы:
- Калькулятор Arccos (обратный косинус) – градусы и радианы
- Калькулятор арксинуса (обратный синус) – градусы и радианы
- Калькулятор угловых секунд (арксеканс) – градусы и радианы
- Калькулятор Arccsc (арккосеканс) – градусы и радианы
- Калькулятор Arccot (арккотангенс) – градусы и радианы
Вы можете ознакомиться с другими калькуляторами здесь.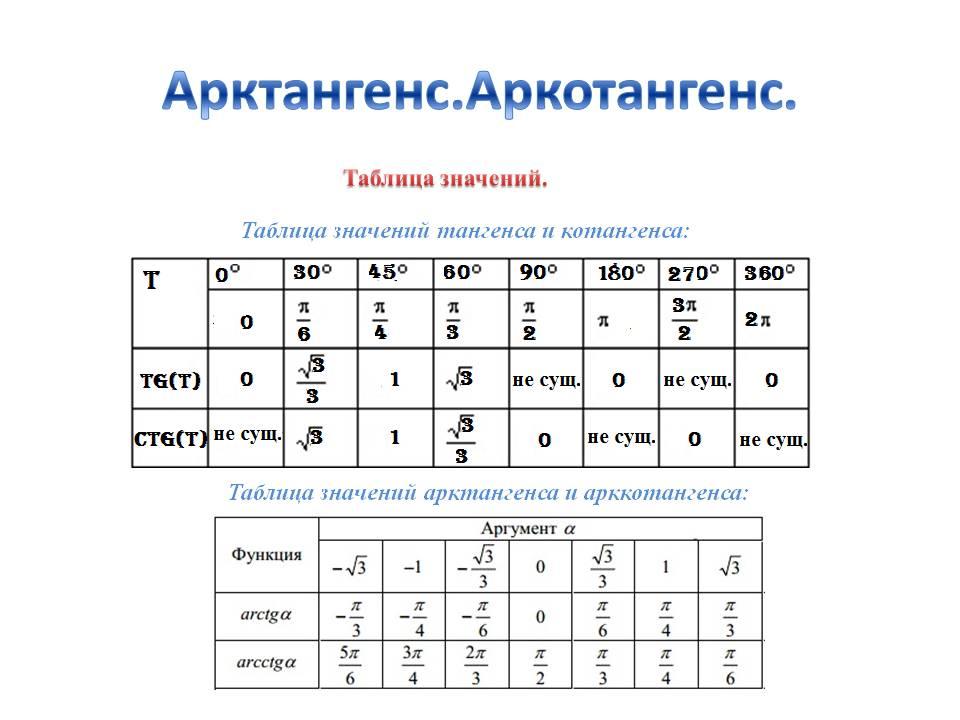
Калькулятор арктангенса | tan(x)
Калькулятор арктангенса
тангенс -1 (x)
Результат:
| 0 | |
| Угол в радианах: | 0 |
Что такое арктангенс?
Арктангенс (или арктангенс) является обратной функцией тангенса. В прямоугольном треугольнике тангенс угла y определяется как отношение стороны, противоположной углу, к прилежащей стороне. Когда мы берем арктангенс этого отношения, мы получаем меру угла y.
Рассмотрим прямоугольный треугольник ниже.
В этом треугольнике прямой угол находится в точке B. Тангенс угла y равен 9{-1} x$$
Выражение y = tan -1 x означает, что tan y = x , когда -π/2
Arctan(x)=y определяется как множество всех углов, tan которых равен x. Здесь следует отметить, что -1 не является показателем степени и, следовательно, тангенс -1 x ≠ 1 / тангенс x .
Свойства функции арктангенса
Ниже приведены некоторые свойства функции арктангенса.
Угол – Угол – это параметр, который рассчитывается, когда известен тангенс, обратный (или арктангенс) угла. 9(-1)х. Это значение равно -π/2
Ниже приведен график функции арктангенса.
На приведенном выше графике ось Y обозначает угол в радианах, а ось X обозначает арктангенс этого угла. Красная кривая обозначает функцию арктангенса. Для любого значения x функция arctan возвращает значение от -π/2 до π/2 радиан (или от -90⁰ до 90⁰).
Например, когда x=1, y=arctan(x) возвращает y= π/4 радиана. Это означает, что тангенс (π/4) = 1,
Если сравнить график арктангенса с графиком тангенса, можно увидеть, что график арктангенса можно получить из графика тангенса, просто поменяв местами горизонтальную и вертикальную оси.
Значения arctan(x)
Ниже приведены некоторые часто используемые значения arctan(x).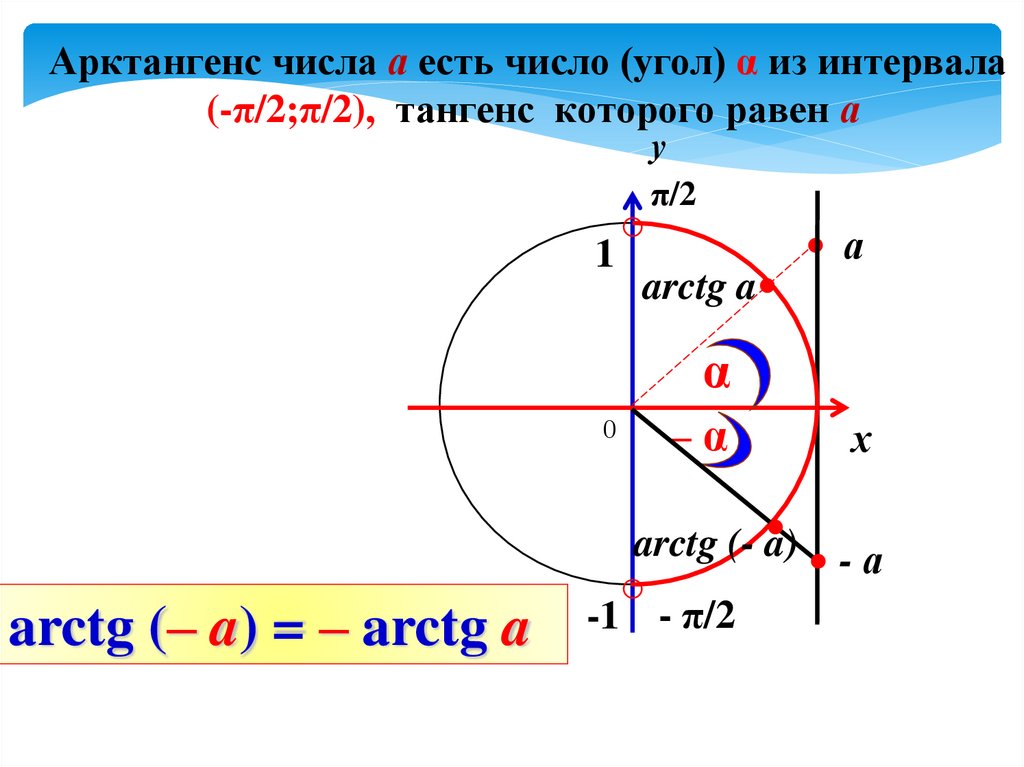
| y=tan -1 x в градусах | y=tan -1 x в радианах | х |
|---|---|---|
| -60 | $$-π\over3$$ | $$-√3$$ |
| -45 | $$-π\over4$$ | -1 |
| -30 | $$-π\over6$$ | $$-1\over\sqrt3$$ |
| 0 | 0 | 0 |
| 30 | $$π\over3$$ | $$1\over\sqrt3$$ |
| 45 | $$π\over4$$ | -1 |
| 60 | $$π\over6$$ | $$\sqrt3$$ |
Значение arctan(x) может быть положительным или отрицательным, в зависимости от значения x. Например, arctan(-1) отрицательный, а arctan(1) положительный.
Это потому, что тангенс -1 (-x) = — тангенс -1 x .
Это показано ниже.
На этом рисунке ось x обозначает значения арктангенса, тогда как ось y обозначает угол θ.
Arctan(x) будет положительным, когда 0≤ θ
Мы также можем отметить, что
tan(tan -1 (x))=x, когда -∞ ≤ x ≤ +∞.
Например, tan(tan -1 (1)) = tan 45 = 1.
Аналогично, tan -1 (tan x) = x, когда -π/2
Например, тангенс -1 (тангенс π/4) = тангенс -1 (1) = π/4.
Если нам нужно найти арктангенс тангенса угла, который не лежит между -π/2 и π/2, правильный угол можно найти, добавляя или вычитая π радиан, пока мы не получим угол в диапазоне от -π/2 до π/2, что является диапазоном функции арктангенса. Это потому, что π — это период функции тангенса. 95} + …, x
Области применения
Тригонометрические функции, а также обратные тригонометрические функции широко используются в технике, геометрии и физике. Они также используются для решения тригонометрических уравнений, описывающих реальные проблемы. Функция обратного тангенса, в частности, довольно широко используется для нахождения углов возвышения и депрессии, что является важной частью науки и техники.
В этом разделе мы рассмотрим несколько примеров задач, связанных с использованием формулы арктангенса.
Ответ: Угол 6π/5 радиан не лежит между -π/2 и π/2, но его можно привести к этому диапазону, добавляя или вычитая π, пока мы не получим угол в диапазоне -π /2 до π/2 радиан, что является диапазоном функции арктангенса.
Для sin и cos мы должны добавить или вычесть 2π радиан, потому что период этих двух функций равен 2π. Для тангенса мы добавляем или вычитаем π радиан, потому что период функции тангенса равен π.
В этом случае 6π/5 радиан можно записать как 6π/5-π=π/5 радиан, что находится между -π/2 и π/2.
Следовательно, тангенс -1 (тангенс (6π/5)) = тангенс -1 (тангенс (π/5)) = π/5
Ответ: Задача может быть представлена в виде ниже.
AB обозначает полюс, а BC — тень, отбрасываемую им. Чтобы найти угол наклона солнца, нам нужно найти тангенс угла y. Здесь АВ = 15 футов, а ВС = 45 футов.