Вторая производная
Всё очень просто. Вторая производная – это производная от первой производной:
Стандартные обозначения второй производной: , или (дробь читается так: «дэ два игрек по дэ икс квадрат»). Чаще всего вторую производную обозначают первыми двумя вариантами. Но третий вариант тоже встречается, причем, его очень любят включать в условия контрольных заданий, например: «Найдите функции…». А студент сидит и битый час чешет репу, что это вообще такое.
Рассмотрим простейший пример. Найдем вторую производную от функции .
Для того чтобы найти вторую производную, как многие догадались, нужно сначала найти первую производную:
Теперь находим вторую производную:
Готово.
Рассмотрим более содержательные примеры.
Пример 11
Найти вторую производную функции
Найдем первую производную:
На
каждом шаге всегда смотрим, нельзя ли
что-нибудь упростить? Сейчас нам предстоит
дифференцировать произведение двух
функций, и мы избавимся от этой
неприятности, применив
известную тригонометрическую
формулу
.
Точнее говоря, использовать формулу
будем в обратном направлении:
:
Находим вторую производную:
Готово.
Можно было пойти другим путём – понизить степень функции еще перед дифференцированием, используя формулу :
Если интересно, возьмите первую и вторую производные снова. Результаты, естественно, совпадут.
Отмечу, что понижение степени бывает очень выгодно при нахождении частных производных функции. Здесь же оба способа решения будут примерно одинаковой длины и сложности.
Как и для первой производной, можно рассмотреть задачу нахождения второй производной в точке.
Например: Вычислим значение найденной второй производной в точке :
Необходимость
находить вторую производную и вторую
производную в точке возникает при
исследовании графика функции на
выпуклость/вогнутость и перегибы.
Пример 12
Найти вторую производную функции . Найти
Это пример для самостоятельного решения.
Аналогично можно найти третью производную, а также производные более высоких порядков. Такие задания встречаются, но встречаются значительно реже.
Решения и ответы:
Пример 2: Найдем производную: Вычислим значение функции в точке
Пример 4: Найдем производную: Вычислим производную в заданной точке:
Пример 6: Уравнение касательной составим по формуле 1) Вычислим значение функции в точке : 2) Найдем производную. Перед дифференцированием функцию выгодно упростить: 3) Вычислим значение производной в точке : 4) Подставим значения , и в формулу :
Пример 8: Преобразуем функцию: Найдем производную: Запишем дифференциал:
Пример 10: Найдем производную:
Запишем дифференциал: Вычислим дифференциал в точке :
Пример 12: Найдем первую производную: Найдем вторую производную: Вычислим:
На
данном уроке мы познакомимся с понятием
функции двух переменных, а также подробно
рассмотрим наиболее распространенное
задание – нахождение частных
производныхпервого
и второго порядка, полного дифференциала
функции.
Студенты-заочники, как правило,
сталкиваются с частными производными
на 1 курсе во 2 семестре. Причем, по моим
наблюдениям, задание на нахождение
частных производных практически всегда
встречается на экзамене.
Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках
Начнем
с самого понятия функции двух переменных,
я постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как
,
при этом переменные
,
называются независимыми
переменными или аргументами.
Пример: – функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Полезно знать геометрический смысл функций. Функции одной переменной соответствует определенная линия на плоскости, например, – всем знакомая школьная парабола. Любая функция двух переменных с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ.
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для
частных производных справедливы все
правила дифференцирования и таблица
производных элементарных функций.
Пример 1
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения: или – частная производная по «икс» или – частная производная по «игрек»
Начнем с . Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).
Решаем. На данном уроке я буду приводить полное решение сразу, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения.
В
данном случае, если Вы где-нибудь
нарисуете «штрих» без
,
то преподаватель, как минимум, может
поставить рядом с заданием
(сразу
откусить часть балла за невнимательность).Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».
(3) Используем табличные производные и .
(4) Упрощаем, или,
как я люблю говорить, «причесываем»
ответ.
Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).
(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.
(2) Используем таблицу производным элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для (да и вообще почти для любой буквы).
В частности, используемые нами формулы выглядят так: и .Итак, частные производные первого порядка найдены
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:
1)
Когда мы находим частную
производную , переменная считается
константой.
2) Когда мы находим частную производную , переменная считается константой.
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения: или – вторая производная по «икс» или – вторая производная по «игрек» или – смешанная производная «икс по игрек» или – смешанная производная «игрек по икс»
В понятии второй производной нет ничего сложного. Говоря простым языком, вторая производная – это производная от первой производной.
Для наглядности я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
Как
видите, всё просто: берем частную
производную
и
дифференцируем ее еще раз, но в данном
случае – уже по «игрек».
Аналогично:
Для практических примеров справедливо следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс». Никаких изобретений, берем и дифференцируем её по «икс» еще раз:
Аналогично:
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для проверки не существует.
Пример 2
Найти частные производные первого и второго порядка функции
Это пример для самостоятельного решения (ответ в конце урока). Если возникли трудности с дифференцированием корней, рекомендую ознакомиться уроком Как найти производную?
При определенном
опыте частные производные из примеров
№№1,2 будут решаться Вами устно.
Переходим к более сложным примерам.
Пример 3
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
Дальнейшие комментарии:
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является .
(2) Под
штрихом у нас осталось произведение
двух функций, следовательно, нужно
использовать правило дифференцирования
произведения
.
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .
Теперь находим смешанные производные второго порядка:
, значит, все вычисления выполнены верно.
Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого порядка функции двух переменных имеет вид:
В данном случае:
То есть, в формулу нужно просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:
Пример 4
Найти
частные производные первого порядка
функции
.
Проверить, что
.
Записать полный дифференциал первого
порядка
.
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5
Найти частные производные первого порядка функции . Записать полный дифференциал .
Решение:
(1) Применяем правило дифференцирования сложной функции . С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение (внутренняя функция) у нас не меняется.
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.
Аналогично:
Запишем полный дифференциал первого порядка:
Пример 6
Найти
частные производные первого порядка
функции
.
Записать
полный дифференциал
.
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Пример 7
Найти частные производные первого порядка функции .
(1) Используем правило дифференцирования суммы
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки».
(Знаете, всегда приятно, когда дробь удается превратить в ноль).
Для
второго слагаемого применяем правило
дифференцирования произведения. Кстати,
в этом смысле ничего бы не изменилось,
если бы вместо была дана функция – важно, что здесь произведение
двух функций, КАЖДАЯ
из которых зависит от «икс»,
а поэтому, нужно использовать правило
дифференцирования произведения.
Для
третьего слагаемого применяем правило
дифференцирования сложной функции.
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: . Второе слагаемое зависит ТОЛЬКО от «икс», значит, считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот
здесь ты ошибаешься, я тебя продифференцирую
по «игрек», так что быть тебе нулем.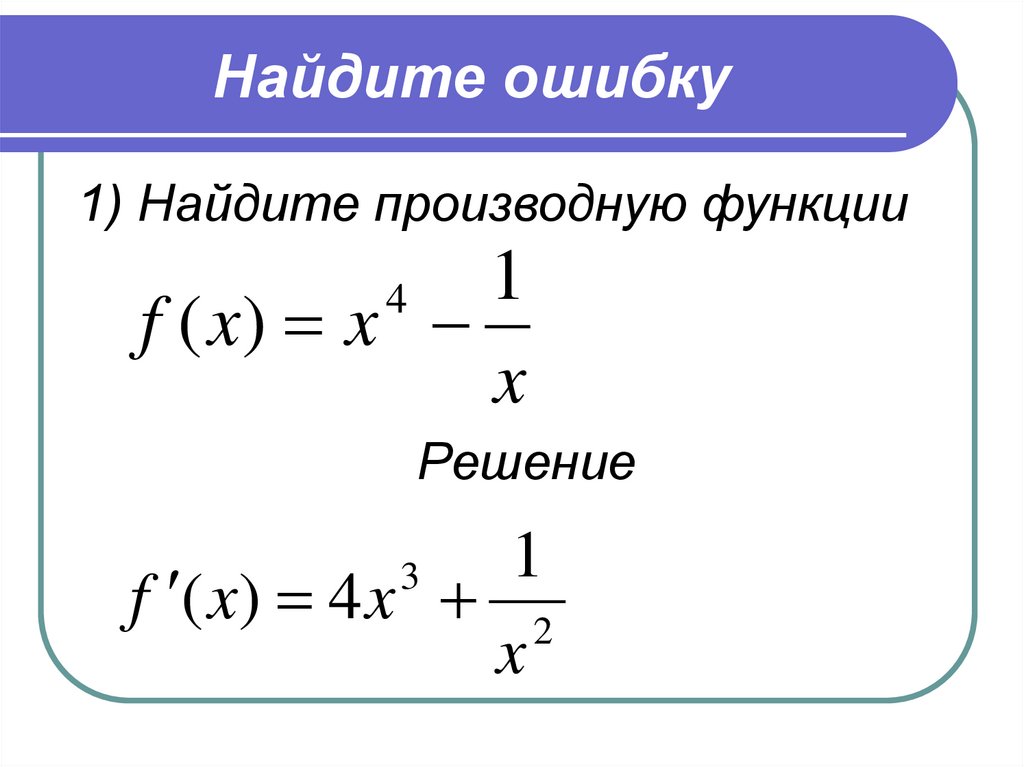
(Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Пример 8
Найти частные производные первого порядка функции .
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.
Пример 9
Дана функция двух переменных . Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Ответы:
Пример 2:
, , ,
Пример
4: Ссылка для просмотра ниже.
Пример 6:
, ,
Тесты по теме Производная онлайн
Тест математика производные
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
Производная. Формулы.
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
Производная функции (высшая математика)
Тест по курсу высшей математики на тему «Производная функции». Тест создан с целью проверки элементарных теоретических знаний производной и умения решать простейшие задачи производной.
Нахождение производной
Тренировочный тест на нахождение производной сложной функции, производная частного и произведения
Производная элементарных функций
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная».
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
Математический анализ. Вычисление производных.
Данный тест рассчитан на выпускников школ и первокурсников ВУЗов. Проверьте свои знания в теории производных.
Производные элементарных функций
Тест рекомендуется использовать при изучении темы «Производные элементарных функций» по учебнику Ю. М. Колягина, 11 класс
Наибольшее и наименьшее значения функций
Контрольный тест по алгебре и началам анализа в 11 классе. По материалам профильного ЕГЭ 2019 года (№12)
Урок №6 «Признаки возрастания и убывания функции»
Данный тест предназначен для закрепления материала по теме «Признак возрастания и убывыания функции». Очень внимательно читайте задание и инструкцию к работе.
Желаю удачи.
Тест «Вторая производная. Физический смысл производной»
Тест «Вторая производная. Физический смысл производной». Тест по теме «Вторая производная. Физический смысл производной» проверяет знание определения первой и второй производной, понимание физического смысла первой и второй производной функции, умения вычислять первую и вторую производные функций. умения вычислять значения производных функций в точке. Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа.
Производная. Геометрический смысл производной.
Алгебра и начала анализа. Тема «Производная» Тест по теме «Производная. Геометрический смысл производной».
Производная функции в школьном курсе математике
Тест состоит из 10 вопросов раскрывающих тему «Производная функции»
Математика тест для 11 класса по теме производная
Тест предназначен для учащихся 11 классов или студентов 1 и 2 курса.
Содержит задания по теме «Производная и её приложения», «Интеграл», «Первообразная», «Пределы». Включает в себя 19 заданий
Тест для обучающихся 11 класс в форме ЕГЭ (профильный уровень)
Тест состоит из 12 вопросов 1 части ЕГЭ профильного уровня обучающихся 11 класса
Вычисление производной
Данный тест может быть использован в качестве контроля знаний учащихся после изучения темы «Производная»
Нахождение производной суммы. Формулы дифференцирования.
Использование формул дифференцирования и правила суммы для нахождения производных.
Дифференцирование алгебраической суммы
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.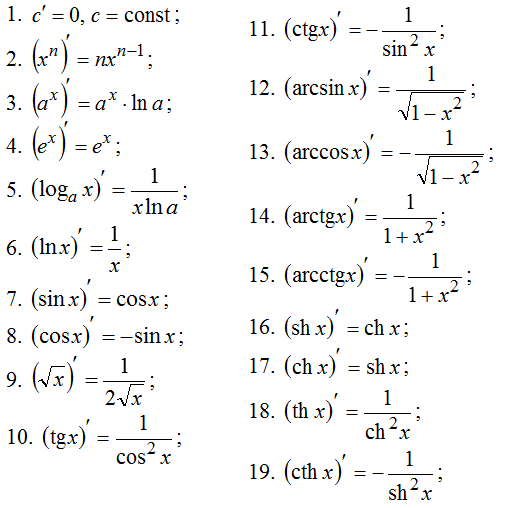
Дифференцирование произведения
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
Нахождение значений производных в точке
Тест направлен на формирования навыков поиска производных различных функций и нахождение значений производных
Дифференцирование частного
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
УД Математика Производная (вариант 2)
Тест по математике «Вычисление производной» для студентов 1 курса СПО
Производная тригонометрической функции
Тест предназначен для проверки зананий по теме «Производная тригонометрических функций и их комбинации с элементарными функциями»
Нахождение значения производной тригонометрической функции в точке
Тест предназначен для проверки зананий по теме «Нахождение значения производной тригонометрической функции в точке»
Производная и ее приложения
Тест предназначен для проверки знания физического и геометрического смысла производной, формул производных элементарных функций, правил вычисления производной, уения применять производную для составления уравнения касательной, исследования функции на монотонность и экстремумы
ОУД.03 Математика. Итоговое тестирование
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части учебной дисциплины математика.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Производная функции
Проверка усвоения учащимися темы «Производная функции», умение применять полученные знания на конкретных примерах и задачам физики и геометрии.
Применение производной к исследованию функций в заданиях ЕГЭ №1
Тест предназначен для обучающихся средней школы для подготовки к ЕГЭ и проверки уровня знаний по теме «Применение производной к исследованию функций и построению графиков».
Выполнение задания №7 формата ЕГЭ (профильный уровень)
В тесте представлены задания на применение геометрического, физического смыслов производной и при исследовании функции
Применение производной к исследованию функций в заданиях ЕГЭ №2
Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Физический, геометрический смысл призводной и применение производной к исследованию функций «.
Производная. Геометрический смысл производной
Данный тест предназначен для проверки знаний обучающихся по теме «Производная. Геометрический смысл производной»
Производная простейших функций
Тест по алгебре и началам математического анализа на применение знаний таблицы производных
Геометрический смысл производной в задачах ЕГЭ
Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Производная. Геометрический смысл производной».
Производные некоторых элементарных функций
Тест по теме «Производные некоторых элементарных функций» предназначен для проверки усвоения указанной темы обучающимися 11 класса
Механический смысл производной
Тест состоит из 7 вопросов по теме «Физический смысл производной», содержит прямые и обратные задания, аналогичные заданию №6 ЕГЭ.
Итоговый тест за 1 четверть, 11 класс, математика
Тест по математике 11 класса за 1 четверть по УМК Алимова Ш.
А. (алгебра и начала анализа) и Атанасяна Л. С. (геометрия). Базовый уровень.
Производные функции
Тест для проработки темы — производная. Предназначен для решения и проработки темы учников и их родителей.
Производная сложной функции
Образовательный тест по теме «Производная сложной функции» позволяет проверить знания школьников или студентов. В тесте требуется как найти сложную функцию из предложенных, так и самостоятельно вычислить производную некоторой сложной функции. Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции. Тест одновариантный, состоит из 14 заданий.
Правила дифференцирования
Тест предназначен для проверки знаний по теме «Правила дифференцирования».
Применение производной к исследованию функций и построению графиков.
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части по теме производная. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Тест по теме «Производная»
Тест по теме «Производная» состоит из четырнадцати вопросов, девять из которых тестовые, остальные с записью ответа
Примеры использования производной для нахождения наилучшего решения в прикладных задачах.
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Начала математического анализа». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Производная. Понятие производной
Алгебра и начала анализа. Тема «Производная» Тест №1 по теме «Понятие производной. Физический смысл производной»
Тест «Правила дифференцирования»
Тест «Правила дифференцирования». Тест по теме «Правила дифференцирования» проверяет знание правил дифференцирования — правило дифференцирования суммы двух функций, правило вынесения постоянного множителя за знак производной, правило нахождения производной произведения функций, частного функций, нахождения производной сложной функции.
Тест содержит 10 вопросов. В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа.
Тест «Производные элементарных функций»
Тест «Производные элементарных функций». Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций. Тест содержит 10 вопросов с единичным верным ответом.
Тест на соответствие «Производные элементарных функций»
Тест на соответствие «Производные элементарных функций». Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, тригонометрических функций, умения вычислять производные функций. Тест содержит 10 функций и 10 производных функций.
При выполнении теста необходимо установить соотвтетствие между функцией и ее производной.
Тест «Геометрический смысл производной. Уравнение касательной и нормали»
Тест по теме «Геометрический смысл производной. Уравнение касательной и нормали» проверяет знание геометрического смысла производной, алгоритм нахождения уравнения касательной и нормали к графику функции в точке; умения составлять уравнение касательной и нормали к графику функции в заданной точке, находить угловой коэффициент касательной к графику функции, угол между касательной к графику и осью Ох. Тест содержит 10 вопросов с выбором единичного и верного ответа, установление верной последовательности и вопросы с вводом верного ответа в виде числа.
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
Данный тест рассчитан на выпускников школ и первокурсников ВУЗов. Проверьте свои знания в теории производных.
Тест по теме Производные некоторых элементарных функций предназначен для проверки усвоения указанной темы обучающимися 11 класса.
Onlinetestpad. com
06.04.2018 16:36:56
2018-04-06 16:36:56
Источники:
Https://onlinetestpad. com/ru/tests/derivative
Задачи на нахождение производных, алгебра, 10 класс » /> » /> .keyword { color: red; }
Тест математика производные
Задачи c решением и ответами к учебнику Мордковича А. Г. на темы: «Правила и формулы нахождение производных»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
1. Найдите производные функций.
$а) y=\frac$;
2.
3$. Найдите ее скорость в момент времени $t=3c$.
5. Найдите все значения x, при которых выполняется неравенство f'(x)
Средство массовой информации сетевое издание «mathematics-tests. com» зарегистрировано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор). Свидетельство о регистрации средства массовой информации ЭЛ № ФС 77 — 63677 от 10 ноября 2015 года. Название — https://mathematics-tests. com.
Учредитель (соучредители) СМИ сетевого издания mathematics-tests. com: Андреев Г. И., главный редактор СМИ: Андреев Г. И., номер телефона редакции: +7 (906) 384-18-43, адрес электронной почты: [email protected] mathematics-tests. com
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
1. Найдите производные функций.
$а) y=\frac$;
2. Найдите производные функций.
А) y=$\frac$;
4.
3$. Найдите ее скорость в момент времени $t=3c$.
5. Найдите все значения x, при которых выполняется неравенство f'(x)
Средство массовой информации сетевое издание «mathematics-tests. com» зарегистрировано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор). Свидетельство о регистрации средства массовой информации ЭЛ № ФС 77 — 63677 от 10 ноября 2015 года. Название — https://mathematics-tests. com.
Учредитель (соучредители) СМИ сетевого издания mathematics-tests. com: Андреев Г. И., главный редактор СМИ: Андреев Г. И., номер телефона редакции: +7 (906) 384-18-43, адрес электронной почты: [email protected] mathematics-tests. com
Прямолинейное движение точки описывается законом t 6-4t 3.
Mathematics-tests. com
12.02.2019 2:31:37
2019-02-12 02:31:37
Источники:
Https://mathematics-tests. com/zadachi-10-klass/algebra-10-klass-zadachi-na-nahozhdenie-proizvodnyh
Тест-зачет по теме Производная функции » /> » /> .
keyword { color: red; }
Тест математика производные
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Знать: Определение производной. Формулы для вычисления производных. Правило составления касательной к графику функции. Исследовать функцию на монотонность и экстремум Уметь: Находить производные, пользуясь формулами. Находить уравнение касательной к графику функции. Применять производную для исследования функции на монотонность и экстремум. Применять производную для отыскания наибольших и наименьших значений функции.
Исследовать функцию на монотонность и экстремум Уметь Находить производные, пользуясь формулами.
Videouroki. net
26.09.2019 12:32:55
2019-09-26 12:32:55
Источники:
Https://videouroki. net/tests/primienieniie-proizvodnoi-1.html
Исчисление
Слово исчисление происходит от латинского слова, означающего «маленький камень».
Потому что это похоже на понимание чего-то, глядя на маленькие кусочки.
Дифференциальное исчисление разрезает что-то на мелкие кусочки, чтобы узнать, как оно меняется.
Интегральное исчисление соединяет (интегрирует) маленькие кусочки вместе, чтобы определить их количество.
Прочитать введение в исчисление или «как быстро прямо сейчас ?»
Ограничения
Пределы приближаются. Иногда вы не можете решить что-то напрямую, но вы можете увидеть, что должно быть, по мере того, как вы подходите все ближе и ближе!
- Введение в ограничения
- Пределы и бесконечность
- Оценка пределов
- Пределы (формальное определение)
- Правило Лопиталя
- Непрерывные функции
Производные (дифференциальное исчисление)
Производная — это «скорость изменения» или наклон функции.
- Введение в деривативы
- Наклон функции в точке (интерактивный)
- Производные как dy/dx
- Производный плоттер (интерактивный)
- Производные правила
- Силовое правило
- Правило продукта
- Вторая производная и вторая производная анимация
- Частные производные
- Дифференцируемый
- Нахождение максимума и минимума с использованием производных
- Вогнутость вверх и вниз и точки перегиба
- Неявное дифференцирование
- Серия Тейлора (используются производные)
- (Дополнительно) Доказательство производных грех, соз и загар
Интеграция (интегральное исчисление)
Интеграциюможно использовать для поиска площадей, объемов, центральных точек и многих других полезных вещей.
- Введение в интеграцию
- Графическое введение в производные и интегралы
- Правила интеграции
- Интеграция по частям
- Интеграция путем замены
- Определенные интегралы
- Длина дуги
- Интегральные приближения
- Калькулятор интегральных приближений и график
- Тела вращения дисков и шайб
- Solids of Revolution от Shells
- Ряд Фурье и графическое устройство ряда Фурье
Дифференциальные уравнения
В нашем мире вещи меняются, и описывает, как они меняются часто заканчивается Дифференциальным Уравнением: уравнением с функцией и один или несколько его производных :
- Введение в дифференциальные уравнения
- Руководство по решению дифференциальных уравнений
- Разделение переменных
- Линейные дифференциальные уравнения первого порядка
- Однородные дифференциальные уравнения (однородные функции)
- Дифференциальное уравнение Бернулли
- Точные уравнения и коэффициенты интегрирования
Дифференциальные уравнения второго порядка:
- Дифференциальные уравнения второго порядка
- Метод неопределенных коэффициентов
- Метод вариации параметров
Если вы хотите осветить больше тем по исчислению, дайте мне знать, какие именно.
Бонусная тема
- Раздвоение
Рабочий лист
производных — Googlesuche
AlleBilderBücherVideosMapsNewsShopping
SUCOOPTIONEN
Bilder
ALLE ANZEIGEN
ALLAR ANZEIGEN
[PDF] MTH 124-005 SS17.
Рабочий лист производных SS17. Название: Цель этого рабочего листа — предоставить возможность попрактиковаться в формулах дифференцирования для раздела 005.
[PDF] МАТЕМАТИКА 171 — Рабочий лист производных Дифференцируйте их для развлечения или …
ic.arc.losrios.edu › ~mirzaam › math500 › DIFFPRACT
MATH 171 — Рабочий лист производных. Различайте их для развлечения или практики, в зависимости от того, что вам нужно. Данные ответы не упрощены. 1. f(x)=4×5.
Рабочий лист производных — Superprof
www.superprof.co.uk › … › Исчисление › Производные
Bewertung 4,0
(8)
Рабочий лист производных $ Упражнение 1) Дифференцируйте следующие функции: f(x) = 5$ 2) $f(x) = -2x$ 3) $f(x) = -2x + 2$ 4)$ f(x) = -2x^2 — 5$ 5) $f (х) .
..
Бесплатные рабочие листы по математике для печати — Kuta Software
www.kutasoftware.com › freeica
Бесплатные рабочие листы по математическому анализу, созданные с помощью Infinite Calculus. … Создавайте нужные рабочие листы с помощью Infinite Calculus. … Приложения дифференциации.
[PDF] Исчисление 12 Имя ______ LG 1 – 3 Пакет рабочих листов
fkss.sd79.bc.ca . Часть A: 1. Найдите первую производную каждой функции: … Используйте производные от sin x и cos x, чтобы проверить производные от ctg x и …
[PDF] Mastering-Derivatives.pdf — Crystal Clear Mathematics
crystalclearmaths.com › wp-content › uploads › 2015/11 › Mastering-…
Страница 1 ~. Исчисление. Искусство измерения формы и вариации! Практические рабочие листы для. Мастерство дифференциации. Грэм Хендерсон …
Рабочие листы по производным — учитесь различать с помощью исчисления College
calculuscollege.