Онлайн-тренажёр «Основы математики для цифровых профессий» от Яндекс Практикум
Большинство цифровых профессий начинаются с математики. Мы сделали бесплатный тренажёр, с помощью которого можно повторить школьную программу и освоить базовые математические навыки для работы маркетологом, разработчиком, аналитиком или специалистом по Data Science.
С чем поможет тренажёр
- Повторить школьную программу по математике и познакомиться с основами работы с данными.
- Освежить знания из теории вероятностей, комбинаторики, логики и теории множеств.
- Повторить базовую математику перед более сложными темами: статистикой, матанализом, линейной алгеброй.
- Потренироваться решать математические задачи перед собеседованиями.
Что вы получите в тренажёре
Онлайн-тренажёр состоит из модулей разного уровня сложности. Базовый уровень: числа, дроби, алгебра. Ближе к миру данных: множества и логика, комбинаторика, теория вероятностей. Внутри модулей — теория в тексте, визуальные интерактивные объяснения и задачи.
Всего более 1600 задач с автоматической проверкой и объяснением хода решения.
База математических навыков
Вы научитесь быстро считать в уме, работать с пропорциями и процентами, решать уравнения и неравенства, совершать операции над множествами, использовать логические операторы, решать комбинаторные задачи и доказывать несложные теоремы.
Аналитическое мышление
Вы научитесь решать задачи с несколькими переменными, корректно интерпретировать данные статистики, видеть ошибки в расчётах и понимать абстракции, которыми в работе оперируют разработчики и аналитики.
Плавный вход в сложный материал
Чтобы работать с данными, нужно понимать статистику и уметь пользоваться инструментами на ее основе. Многим data-специалистам пригодится знать линейную алгебру и матанализ. Погружаться в эти темы не так страшно, если повторить основы математики и теории вероятностей.
Программа обучения
01
Теория вероятностей
• Математическая модель непредсказуемых явлений.
• Геометрическая вероятность.
• Операции над случайными событиями.
• Условная вероятность.
• Теорема Байеса.
• Дискретные случайные величины.
• Характеристики случайных величин.
02
Комбинаторика, Множества, Логика
• Формула включений-исключений.
• Метод математической индукции.
• Мощность множества, булеан.
• Высказывания, логические операторы, булевы функции.
• Визуализация комбинаторного перебора.
• Слова и кортежи с повторениями и без.
• Сочетания, перестановки, лексикографический перебор.
• Биномиальные коэффициенты и бином Ньютона.
03
Числа, Дроби, Алгебра
• Действия с натуральными и целыми числами.
• Простые и составные числа, делимость.
• Лайфхаки быстрых вычислений.
• Обыкновенные дроби.
• Конечные и бесконечные десятичные дроби.
• Проценты, отношения и пропорции.
• Линейные и квадратные уравнения.
• Неравенства, метод интервалов.
Как проходит обучение
Прохождение каждого из модулей занимает 20-30 часов. Все темы и уроки доступны к прохождению сразу. В самом начале вы можете пройти входной тест, чтобы определить, с какого модуля лучше начать. Бесплатный тренажер пополняется новыми темами из основ математики и принципов анализа данных.
От переменных к карьерным переменам
Математика — это универсальный навык для старта и развития в цифровых профессиях. Маркетологам и менеджерам она поможет принимать решения на основе данных. Аналитикам и специалистам по Data Science — понимать, как работают инструменты и алгоритмы и исправлять ошибки в неработающих решениях.
Как понять Геометрию? Основы с нуля
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Математика занимается объектами и делает о них некие заключения, которые называют теоремами.
Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.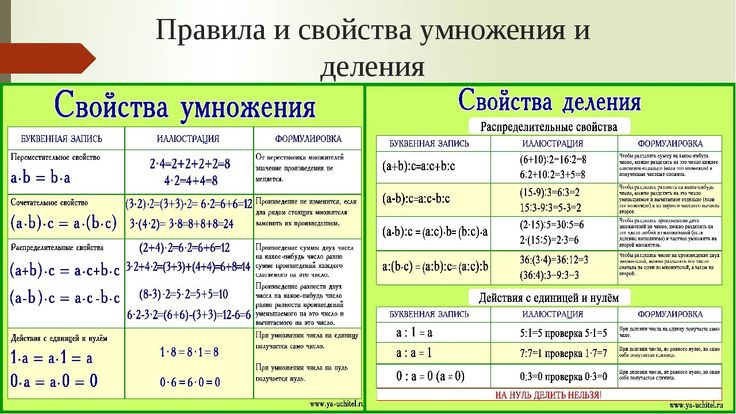
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b, c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
Прямые пересекаются, то есть имеют одну общую точку.
Для записи пересекающихся прямых используют специальный знак — ∩, то есть a∩b (читают: прямая a пересекает прямую b). Чтобы обозначить точку пересечения прямых, пишут a∩b = O (читается: прямая a пересекается с прямой b в точке O).
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — , то есть m n (читают: прямая m не пересекает прямую n). В дальнейшем для обозначения не пересекающихся прямых мы будем использовать знак параллельности ||.
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
-
Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ.
Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы.
По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
Если градусная мера угла меньше 90° — угол острый.
Если градусная мера угла равна 90° — угол прямой.
Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
Если градусная мера угла равна 180° — угол развернутый.
Общая точка, из которой исходят лучи, называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией.
Читайте про вписанные и описанные углы.
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Один из распространенных типов — прямоугольный треугольник.
Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
От правильного треугольника может плавно перейти к правильным многоугольникам.
У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
площадь фигуры
периметр фигуры
площадь прямоугольника
периметр прямоугольника
площадь квадрата
периметр квадрата
параллелограмм
прямоугольный параллелепипед.
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Базовая математика
Базовая математика, предварительная алгебра, геометрия, статистика и алгебра — вот чему вас научит этот веб-сайт. Мы разработали сайт для всех, кто нуждается в базовом или углубленном понимании математических понятий и операций.
Инструкции тщательно выстроены в логическом порядке. Понятия представлены в ясных, простых терминах. Кроме того, каждый раз, когда вводится понятие, будут предоставлены пример или два, иллюстрирующие это понятие.
Пример некоторых интересных тем по математике
Научитесь разлагать числа и трехчлены, такие как квадратные уравнения
Выполняйте домашнее задание по математике с помощью этого очень простого в использовании математического решателя!
Изучение математики может быть сложной задачей, если у вас нет нужных инструментов или материалов, особенно если вы выросли, полагая, что математика сложна и что вы никогда ее не поймете.
Самый первый урок, который я могу преподать, это избавиться от любого негативного мышления, которое ваши учителя, друзья или даже заботливый родственник помогли вам построить на протяжении многих лет, и начать верить в себя.
Другие интересные/сложные темы по математике для изучения на этом сайте
Математика похожа на пирамиду . Каждый новый навык требует понимания предпосылок, чтобы преуспеть. Например, прежде чем научиться складывать трехзначные числа, такие как 256 + 128, важно знать, как складывать числа, содержащие только одну или две цифры, такие как 1 + 5 или 24 + 50.
Точно так же перед изучением начальной алгебры важно хорошо понимать основы математики. И прежде чем изучать алгебру, необходимо твердое понимание предварительной алгебры.
Моя цель и желание — научить вас математике, но прежде всего я хочу научить вас быть свободными и быть вашими лучшими учителями.
Вы заметите, что когда я преподаю урок, я многое объясняю.
Я делаю это, чтобы дать вам глубокое понимание базовой математики и алгебры. Поэтому, если вы ищете быстрый путь, мой веб-сайт не для вас, потому что он разработан, чтобы бросить вам вызов и в значительной степени научить вас.
В конце концов, ваши базовые математические знания будут сильными, и вы будете очень хорошо подготовлены к изучению алгебры или любых других математических курсов более высокого уровня!
Как изучать основы математики, алгебры и геометрии
Следующие советы являются лишь моим советом; Они не абсолютны. Выберите те, которые лучше всего подходят вам.
- Запланируйте регулярное время для занятий
- Выберите тихое место, где вас никто не будет отвлекать.
- Когда вы учитесь, старайтесь изучить весь урок или целую главу.
- Когда вы закончите весь урок или целую главу, у вас может остаться чувство выполненного долга
- Если вы чувствуете сонливость, сделайте небольшой перерыв; вы мало чему научитесь, если не будете бдительны.
- Теперь вы готовы испытать самые полезные усилия прямо здесь, на этом веб-сайте.
Типы треугольников
03, 22 декабря 12:47
Научитесь определять 6 типов треугольников по их сторонам или углам и еще 7 типов по сторонам и углам.
Подробнее
График прямоугольников и усов
18, 22 ноября 08:20
Легко научитесь строить график прямоугольников и усов для набора данных, используя средние и экстремальные значения.
Подробнее
Блог по основам математики
Типы треугольников
03, 22 декабря 12:47
Научитесь определять 6 типов треугольников по их сторонам или углам и еще 7 типов по сторонам и углам.
Подробнее
График прямоугольников и усов
18, 22 ноября 08:20
Легко научитесь строить график прямоугольников и усов для набора данных, используя средние и экстремальные значения.
Подробнее
Двоичная система счисления
17, 22 ноября 10:53
Этот урок познакомит вас с двоичной системой счисления.
Подробнее
Периметр квадрата
16, 22 ноября 02:36
Посмотрите этот урок. Вы обнаружите, что найти периметр квадрата просто и понятно.
Подробнее
Закон косинусов – формула, доказательство и примеры
14, 22 ноября 11:32
Что такое закон косинусов? Посмотрите, как вы можете использовать закон косинусов, чтобы найти одну сторону треугольника.
Подробнее
Сопряжение комплексного числа
12, 22 ноября 10:30
Что такое сопряжение комплексного числа? Определение, объяснение и примеры.
Подробнее
Для чего нужны гистограммы? Определение и примеры
08 ноября, 22 12:56
Этот урок поможет вам четко понять различные типы гистограмм, такие как вертикальная гистограмма, групповая гистограмма и столбчатая гистограмма.
Подробнее
Решение двухшаговых уравнений
7 ноября, 22 14:27
В этом уроке представлены шаги, которые нужно предпринять при решении двухшаговых уравнений или уравнений вида ax + b = c или ax — b = c.
Подробнее
Математические задачи для 6-го класса
5 ноября, 22 18:20
Различные математические задачи для 6-го класса, которые учащиеся должны знать, как решать в 6-м классе.
Подробнее
Математические задачи второго класса
29, 22 октября 09:31
Список важных математических задач второго класса, которые учащиеся должны уметь решать во втором классе
Подробнее
Площадь поверхности сферы – определение, вывод и примеры
26, 22 октября 11:38
Узнайте, как получить и вычислить площадь поверхности сферы.
Урок кристально ясен и точен, но он также показывает, как была получена формула
Подробнее
Площадь поверхности цилиндра — определение, вывод и примеры
24 октября, 22 09:18
Узнайте, как вычислить площадь поверхности цилиндра, наклонного цилиндра и полого цилиндра. Научитесь также выводить формулу.
Подробнее
Сложение целых чисел с помощью числовой строки и правила сложения целых чисел
23, 22 октября 08:17
Сложение целых чисел с использованием числовой строки или правил сложения целых чисел для нахождения суммы положительных и отрицательных целых чисел.
Подробнее
Дроби — определение и примеры из жизни
23 октября 22 07:32
Простое для понимания введение в дроби на примере пиццы из реальной жизни.
Подробнее
Окружность круга — определение, формула, примеры из жизни
21, 22 окт 14:01
Как рассчитать длину окружности по формуле длины окружности.
См. также несколько примеров из реальной жизни, которые легко понять.
Подробнее
Объем сферы – определение, формула, вывод и примеры
20, 22 октября 16:26
Узнайте, как получить объем сферы и объем земли, которая является сферой. Вывод формулы объема с исчислением.
Подробнее
Площадь круга — определение, формула, вывод и примеры
18, 22 октября 10:40
Этот урок научит вас различным способам вычисления площади круга с использованием числа «пи».
Подробнее
Математические задачи третьего класса
13, 22 октября 09:58
Разнообразные математические задачи третьего класса, которые учащиеся должны уметь решать в 3-м классе.
Подробнее
Математические задачи для первоклассников с большим количеством примеров
12, 22 октября 12:05
Разнообразные математические задачи для первоклассников, которые учащиеся должны уметь решать в 1-м классе.
Подробнее
Умножение дробей
11, 22 окт 08:36
Умножение дробей и запись произведения в простейшей форме — цель этого урока.
Подробнее
Математические задачи 5-го класса
06, 22 окт. 12:02
Разнообразные математические задачи 5-го класса, которые учащиеся должны уметь решать в 5-м классе.
Подробнее
Задачи на диаграмму Венна
5 октября, 22 10:58
Эти словесные задачи с диаграммами Венна покажут вам, как использовать диаграммы Венна для решения задач, связанных со счетом.
Подробнее
Задачи на процентные слова
04, 22 октября 11:17
Представляем большое разнообразие задач на процентные слова, которые помогут вам решить любые процентные задачи.
Подробнее
Применение уклона в реальной жизни
03, 22 октября 11:31
Каковы некоторые реальные применения наклона? Наклон имеет множество применений в реальном мире. Исследуйте их здесь!
Подробнее
Задачи на перестановку слов с решениями
30, 22 сентября 16:45
Научитесь решать множество задач на перестановку слов с понятными объяснениями.
Подробнее
Комбинированные словесные задачи с решениями
29, 22 сентября 09:25
Научитесь решать самые разные задачи на сочетания слов с понятными объяснениями.
Подробнее
Задания на геометрическую последовательность
27, 22 сентября 08:34
Разнообразные словесные задачи на геометрическую последовательность, которые помогут вам укрепить свои знания о геометрической последовательности.
Подробнее
Арифметическая последовательность — определение и формула
26, 22 сентября 12:15
Узнайте, как описывать числовые закономерности с помощью арифметической последовательности с помощью кристально ясного урока
Подробнее
Задачи на арифметические последовательности
26, 22 сентября 09:14
Разнообразные словесные задачи на арифметические последовательности, которые помогут вам укрепить свои знания об арифметической последовательности.
Подробнее
Математические понятия для первого класса или учебный план
25, 22 сентября 07:43
Ищете самые важные математические понятия для первого класса? Посмотрите математику, которой учат в первом классе.
Подробнее
Математические концепции для детского сада или учебный план
25 сентября, 22 06:16
Ищете наиболее важные математические концепции для детского сада? Смотрите математические дети должны знать в детском саду.
Подробнее
Добавление полиномов с помощью плиток алгебры по вертикали и горизонтали
24, 22 сентября 12:39
Получите кристально ясное объяснение сложения многочленов с помощью алгебраических плиток по вертикали и горизонтали.
Подробнее
Сложение дробей с одинаковыми или разными знаменателями
23, 22 сентября 08:30
Этот урок научит вас складывать дроби, имеющие одинаковые или разные знаменатели.
Подробнее
Неоднозначный случай закона синусов
22, 22 сент. 18:16
Объяснение неоднозначного случая закона синусов, когда можно образовать ноль, один или два треугольника.
Подробнее
Рассчитайте себестоимость дома, используя цену продажи и процент убытка
19, 22 сентября 05:19
дом.
1) Найдите себестоимость дома 2) Сколько она должна быть
Подробнее
Преобразование метрических единиц
18, 22 сентября 07:09
Научитесь преобразовывать одни метрические единицы в другие, используя простую диаграмму преобразования метрических единиц.
Подробнее
Магазин базовой математики
15, 22 сентября 11:04
Магазин базовой математики предлагает широкий выбор качественных товаров по базовой математике, таких как учебники по математике, математические игры и DVD-диски.
Подробнее
Электронная книга по алгебре
15, 22 сентября 06:20
Получите необходимую помощь по алгебре с помощью этой электронной книги по алгебре. Получите подробный обзор начальных навыков алгебры, которые чрезвычайно важны для достижения успеха в алгебре
Подробнее
Электронная книга по геометрическим формулам
15, 22 сентября 06:19
В этой книге собраны все важные геометрические формулы, используемые в школе, а также хорошо объясненные упражнения и текстовые задачи для этих формул.
Подробнее
Вычисление алгебраических выражений — пошаговое руководство
14, 22 сентября 12:27
Узнайте, как вычислять алгебраические выражения, используя порядок операций.
Подробнее
Четные и нечетные числа — определение и примеры
14, 22 сентября 05:16
Получить четкое представление о четных и нечетных числах. Урок кристально ясен и прямо в точку.
Подробнее
Импульс и столкновения
12, 22 сентября 07:19
Связь между импульсом и столкновениями ясно объясняется законом сохранения импульса и многими примерами из жизни.
Подробнее
Что такое коэффициенты? Определения и примеры
09, 22 сентября 05:50
Определения и реальные примеры соотношений и другие важные вещи, о которых следует помнить.