Решаем неравенство с тангенсом — Сайт Александра Бабаева
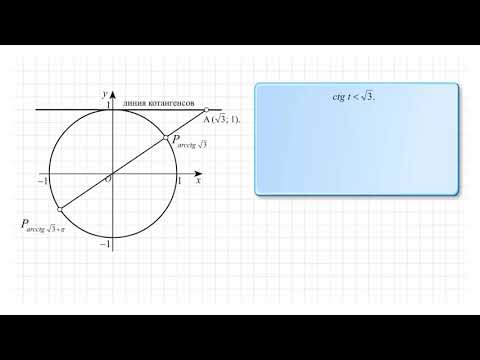
Как с косинусом и синусом, решать неравенства с тангенсом мы будем с помощью единичной окружности.
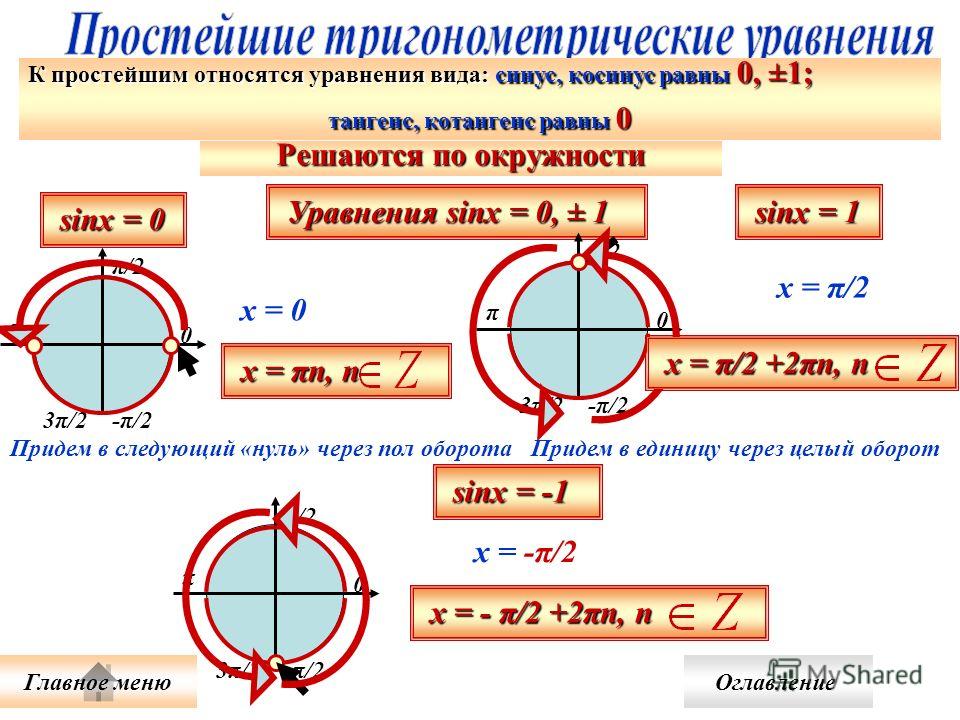
Клише для решений неравенства с тангенсомАлгоритм решения неравенств с тангенсом:
- перерисовываем клише, изображённое на вышестоящем рисунке;
- на линии тангенса отмечаем $a$ и проводим до этой точки из начала координат прямую;
- точка пересечения этой прямой с полуокружностью будет закрашенной, если неравенство нестрогое и не закрашенное, если строгое;
- область будет находится снизу от прямой и до окружности, если неравенство содержит знак «$>$», и снизу прямой и до окружности, если неравенство содержит знак «$<$»;
- для нахождения точки пересечения, достаточно найти арктангенс $a$, т.е. $x_{1}={\rm arctg} a$;
- в ответ выписывается полученный промежуток, добавляя к концам $+ \pi n$.
Примеры решения неравенств с помощью алгоритма.
Пример 1: Решить неравенство:
${\rm tg}{x} \leq 1. $
$
- Копируем клише.
- Отметим на линии тангенса координату $1$.
- Проводим до этой точки из начала координат прямую.
- Отметим точку пересечения. Она будет закрашенной, так как неравенство нестрогое.
- Знак неравенства $\leq$, а, значит, закрашиваем область снизу от прямой, т.е. больший «кусок пирога».
- Находим точку пересечения: $x_{1}={\rm arctg}{1}=\frac{\pi}{4}$.
Таким образом, решение примет вид:
$x \in \left(-\frac{\pi}{2} + \pi n; \frac{\pi}{4} + \pi n\right], \ n \in Z.$
Важно! Точки $-\frac{\pi}{2}$ и $\frac{\pi}{2}$ у тангенса всегда (независимо от знака неравенства) выколоты!
Пример 2: Решить неравенство:
${\rm tg}{x} > — \sqrt{3}.$
Отмечаем на линии тангенса точку $- \sqrt{3}$ и проводим прямую из начала координат до неё. Точка пересечения этой прямой с полуокружностью будет не закрашенной, так как неравенство строгое. Область будет находится выше прямой и до окружности, так как знак неравенства $>$.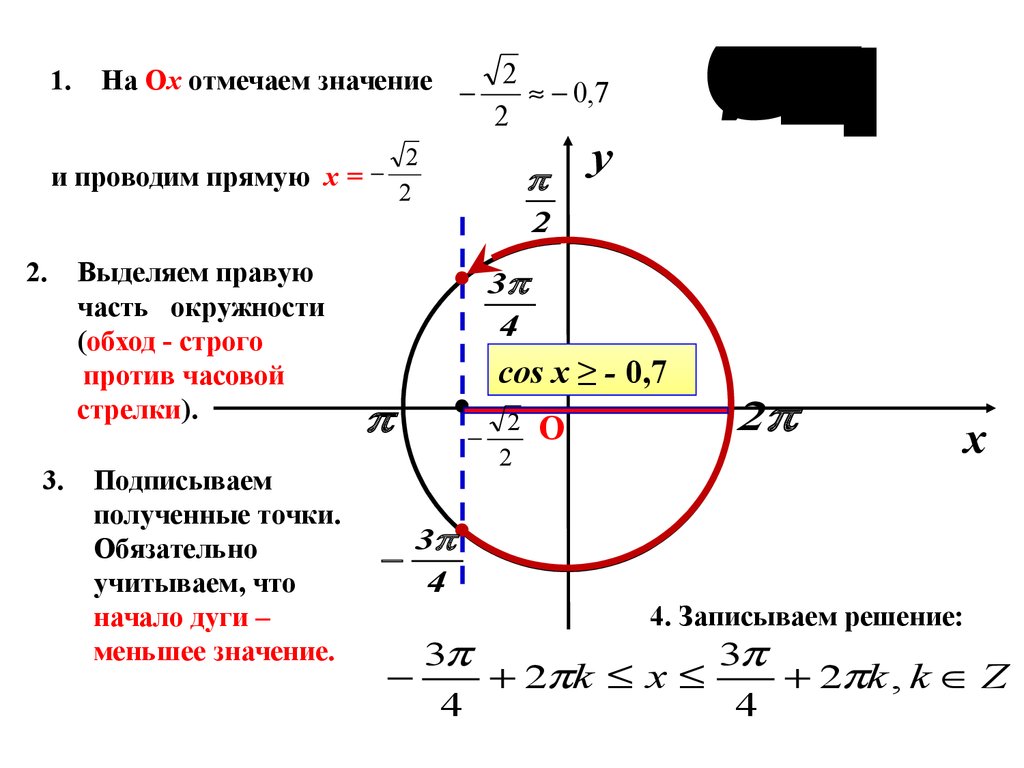
$x_{1} = {\rm arctg}{\left(-\sqrt{3}\right)} = -\frac{\pi}{3}.$
Таким образом, ответом будет:
$x \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right), \ n \in Z.$
Пример 3: Решить неравенство:
${\rm tg}{\left(2x-\frac{\pi}{3}\right)} + \sqrt{3} > 0.$
Сейчас применить алгоритм нельзя. Этот пример похож на пример 3 неравенства с синусом или косинусом. И действовать нужно аналогично. Сначала перенесём всё, что не содержит тригонометрической функции в правую часть.
${\rm tg}{\left(2x-\frac{\pi}{3}\right)} > — \sqrt{3}.$
Теперь же, чтобы применить алгоритм, делаем замену переменной. Всё, что стоит под тригонометрической функцией, обозначаем за новую переменную:
$t=2x-\frac{\pi}{3}$
и получаем неравенство
${\rm tg}{t} > — \sqrt{3},$
которое мы уже решили в примере 2:
$t \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$
Возвращаемся к исходной переменной:
$\left(2x-\frac{\pi}{3}\right) \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right). $
$
Последнее равносильно системе неравенств
$\left\{\begin{array}{c} 2x-\frac{\pi}{3} > -\frac{\pi}{3} + \pi n, \\ 2x-\frac{\pi}{3} < \frac{\pi}{2}+\pi n, \end{array} \right.$
решив которую мы получим ответ. Действительно,
$\left\{\begin{array}{c} 2x > \pi n, \\ 2x < \frac{5 \pi}{6} + \pi n, \end{array} \right.$
$\left\{\begin{array}{c} x > \frac{\pi n}{2}, \\ x < \frac{5\pi}{12}+\frac{\pi n}{2}. \end{array} \right. $
И окончательно получаем:
$x \in \left(\frac{\pi n}{2}; \frac{5\pi}{12} + \frac{\pi n}{2}\right), \ n \in Z.$
**/ ?>10.2.6. Решение тригонометрических неравенств. Часть 6.
Главная » 10 класс. Алгебра. » 10.2.6. Решение тригонометрических неравенств. Часть 6
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 2.5k. Опубликовано
На предыдущих занятиях мы решали тригонометрические неравенства следующих видов:
- sint<a (10.
 2.1. Решение тригонометрических неравенств. Часть 1.)
2.1. Решение тригонометрических неравенств. Часть 1.) - sint>a (10.2.2. Решение тригонометрических неравенств. Часть 2.)
- cost<a (10.2.3. Решение тригонометрических неравенств. Часть 3.)
- cost>a (10.2.4. Решение тригонометрических неравенств. Часть 4.)
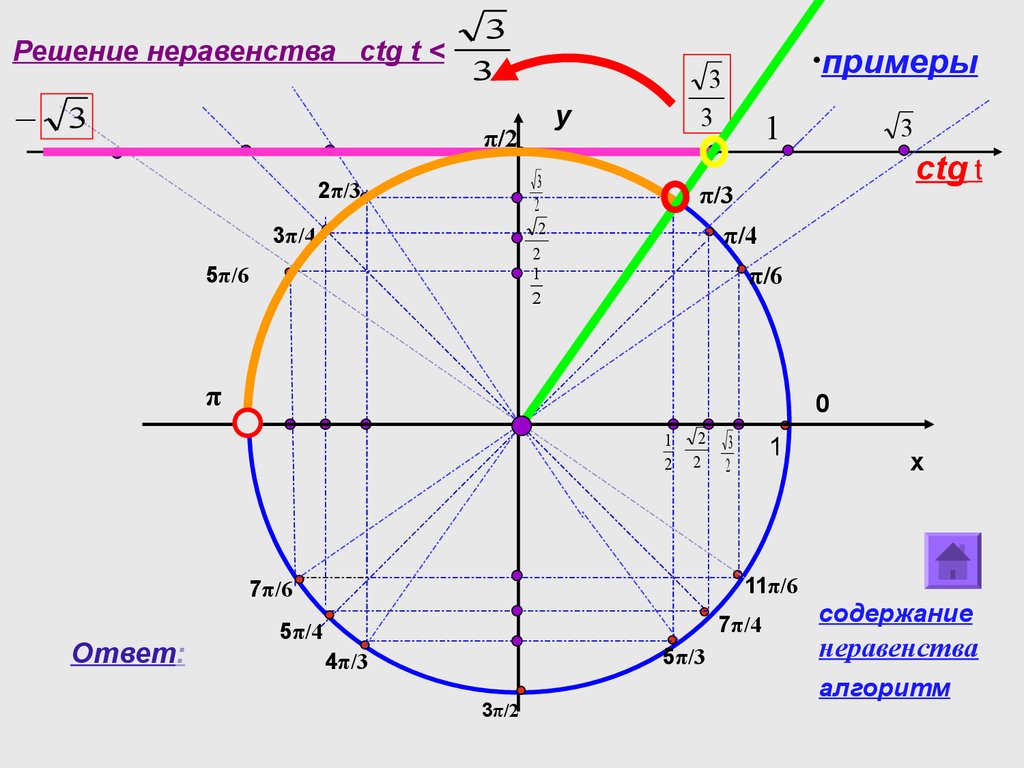
- tgt<a (10.2.5. Решение тригонометрических неравенств. Часть 5.)
На этом занятии мы будем решать неравенства вида tgt>a.
Будем применять следующий алгоритм решения (как на прошлом уроке):
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=tgt и y=a.
3. Находим промежуток значений t, при которых тангенсоида располагается выше прямой у=а.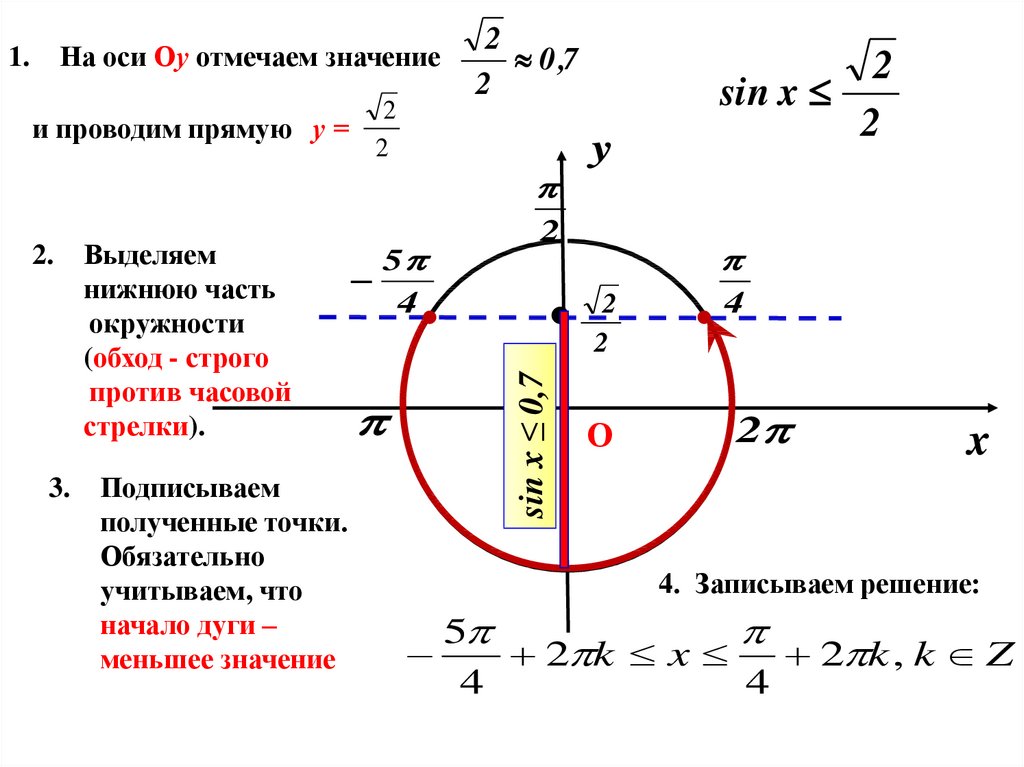 Левая граница этого промежутка arctg a, а правая всегда (π/2)
Левая граница этого промежутка arctg a, а правая всегда (π/2)
4. Записываем двойное неравенство для аргумента t, учитывая наименьший период тангенса Т=π (t будет между абсциссами arctg a и (π/2) ).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Первое неравенство.
Решение.
Разделим обе части неравенства на 3. Сделаем замену данной переменной на t. Тогда получим более простое неравенство.
Определим промежуток значений переменной t, при которых неравенство будет верным. Это абсциссы тех точек графика функции y=tg t, которые лежат выше нашей прямой.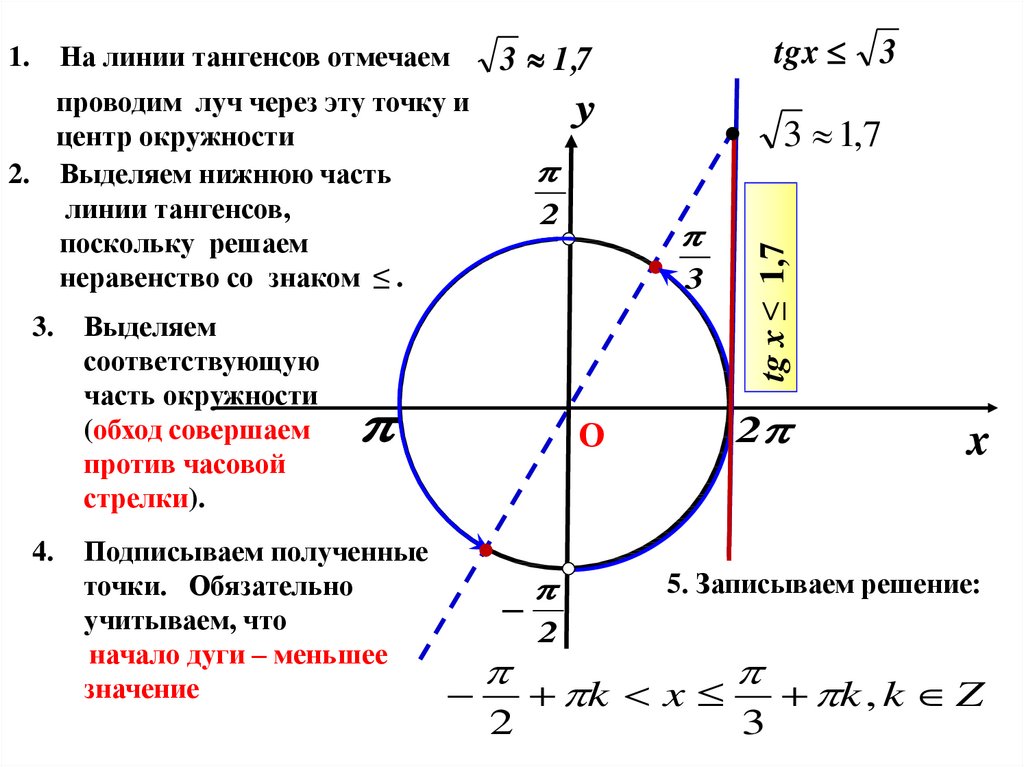 Покажем штриховкой эти значения t. Запишем найденные значения аргумента t в виде двойного неравенства.
Покажем штриховкой эти значения t. Запишем найденные значения аргумента t в виде двойного неравенства.
Второе неравенство.
Решение.
Преобразуем левую часть неравенства по формуле tg (α+β) и получим более простое неравенство. Делаем замену переменной.
Определяем искомый промежуток значений переменной t. Затем выразим х и запишем ответ в виде промежутка. Учтем, что неравенство нестрогое, но что тангенса (π/2) не существует.
Третье неравенство.
Решение.
Применяем правило для формул приведения:
1) перед приведенной функцией ставят знак приводимой; 2) если в записи аргумента (π/2) взято нечетное число раз, то функцию меняют на кофункцию.
Наш аргумент находится в 3-ей четверти, а котангенс в 3-ей четверти имеет знак «плюс», поэтому, знак приведенной функции не поменяется.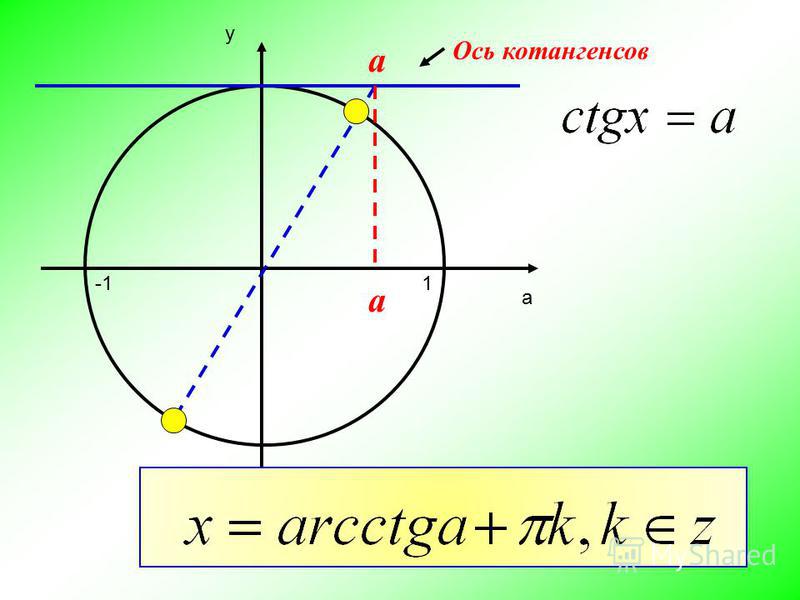 В записи данного аргумента (π/2) взято 3 раза (нечетное число), поэтому функцию котангенс поменяем на кофункцию — тангенс.
В записи данного аргумента (π/2) взято 3 раза (нечетное число), поэтому функцию котангенс поменяем на кофункцию — тангенс.
Теперь данное неравенство приняло вид: tgt≥1. Построим графики функций y=tgt и у=1. Определим промежуток значений аргумента t, при которых неравенство tgt≥1 будет верным. Ответ запишем в виде промежутка. Неравенство у нас нестрогое, но правый конец промежутка не входит в решение неравенства, так как тангенса (π/2) не существует.
Подробные решения этих неравенств смотрите в видео: «10.2.6. Решение тригонометрических неравенств. Часть 6.»
Дорогие друзья! Мы решили неравенства с тангенсом графическим способом, но, конечно, существует и более короткое решение — по формулам.
Если tgt<a, то (- π/2) + πn < t < arctg a + πn, где nєZ.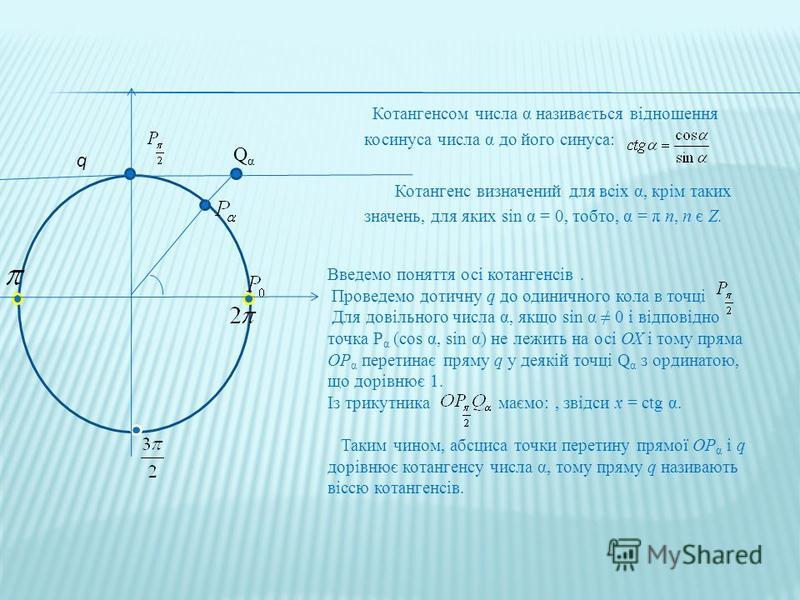
Если tgt>a, то arctg a + πn < t < (π/2) + πn, где nєZ.
Выучите эти формулы, и вы будете решать тригонометрические неравенства с тангенсом быстрее!
видео решение тригонометрических неравенств математика-повторение тригонометрии к ЕНТ и ЕГЭ тригонометрические неравенства с тангенсом
( 1 оценка, среднее 5 из 5 )
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА – ТРИГОНОМЕТРИЯ
Мы можем решить тригонометрические неравенства, глядя на графики основных тригонометрических функций на единичной окружности. Используя следующие шаги, мы можем найти решение любого простого тригонометрического неравенства:
- Найдите область, которая удовлетворяет данному неравенству на единичной окружности.
- Записать границы выделенной области. Мы выделяем границы, двигаясь против часовой стрелки. Помните, что меньшая граница (например, отрицательная граница) всегда должна быть первой границей.

- К sin x и cos x добавьте 2kπ, а к tan x и cot x добавьте kπ.
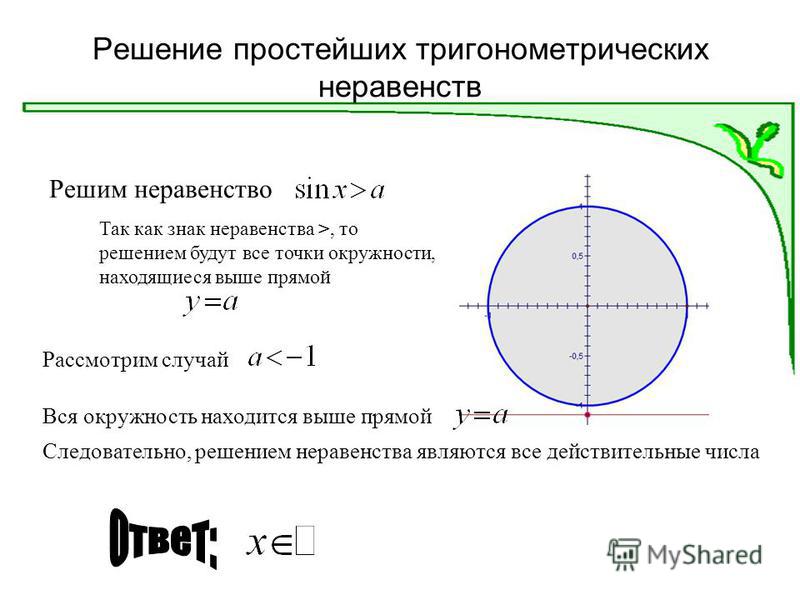
Рассмотрим неравенство sin x > a . Если a > 1 , решения нет (поскольку -1 ≤ sin x ≤ 1 ). Если Рассмотрим неравенство cos х > а.
a < -1 , ответом будут все действительные числа, то есть (-∞, ∞). Если -1 ≤ a ≤ 1 , ответ будет
(arcsin a + 2kπ) < x < (π – arcsin a + 2kπ), k ∈ Z. Мы можем записать это как:
x ∈ (arcsin a + 2kπ, π – arcsin a + 2kπ), k ∈ Z.
Теперь рассмотрим неравенство sin x < a.
Если a < -1 , решения нет.
Если a > 1 , ответом будут все действительные числа, то есть (-∞, ∞).
Если -1 ≤ a ≤ 1 , ответ равен
(-π – arcsin a + 2kπ) < x < (arcsin a + 2kπ), k ∈ Z. x
Если a > 1 решения нет.
Если a < -1 , ответом будут все действительные числа, то есть (-∞, ∞).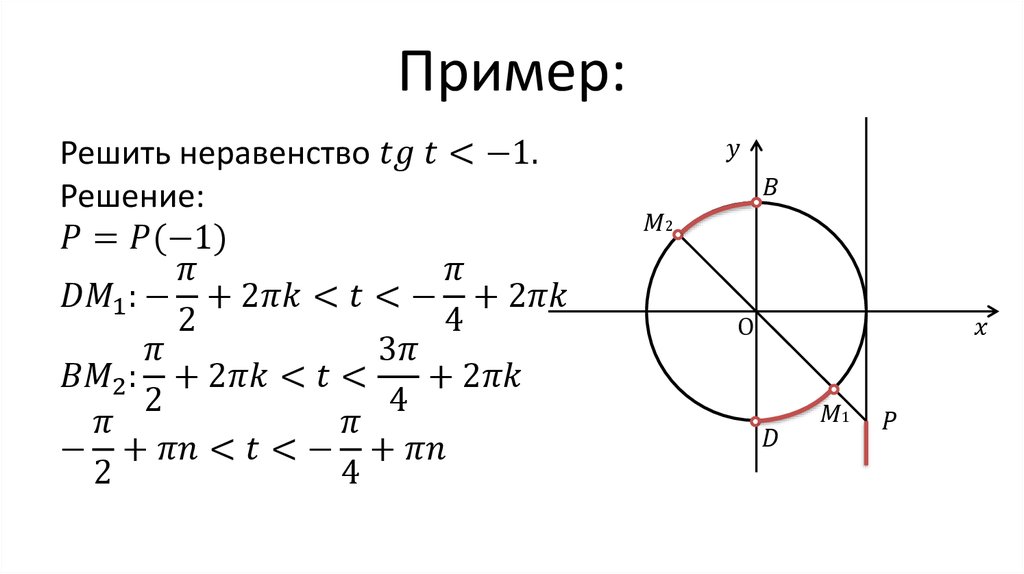
Если -1 ≤ a ≤ 1 , решение будет следующим:
(-arccos a + 2kπ) < x < (arccos a + 2kπ), k ∈ Z.
Теперь рассмотрим неравенство cos x < a.
Если a > -1 решения нет.
Если a < 1 , ответом будут все действительные числа, то есть (-∞, ∞).
Если -1 ≤ a ≤ 1 Ответ:
ARCCOS A + 2Kπ
Как видно из рисунка, решения неравенства симметричны относительно начала координат. Поэтому мы напишем только один ответ и добавим kπ вместо 2kπ , чтобы получить окончательное решение. Итак, решение:
arctan a + kπ < x < π/2 + kπ, k ∈ Z.
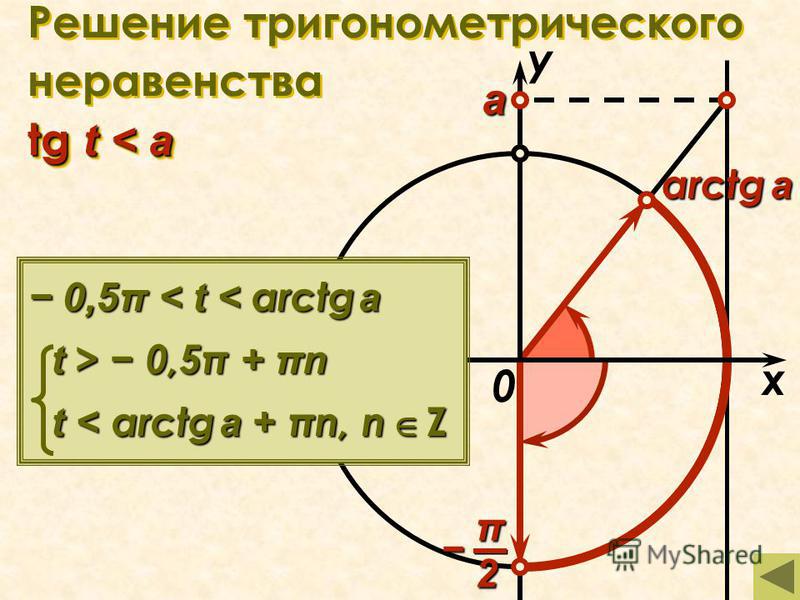
Теперь рассмотрим неравенство tan x < a.
Из рисунка можно получить решение:
-π/2 + kπ < x < (arctan a + kπ), k ∈ Z.
неравенство дано с ≥ или ≤, ответ будет включать арктангенс а, но исключать ±π/2, потому что тангенс (±π/2) не определен. Рассмотрим неравенство cot x > a и посмотрим на рисунок. Мы видим, что неравенство имеет решение: неравенство задано с ≥ или ≤, ответ будет включать arccot a, но исключать 0 и π, поскольку cot 0 и cot π не определены. Подробности и примеры смотрите в видео ниже: Нравится Загрузка. Когда стандартная форма неравенства, такая как R(x) > 0 или R(x) < 0, состоит из 1 или более тригонометрических переменной arc x, то неравенство является тригонометрическим неравенством. Некоторые примеры тригонометрических неравенств: sinx>a, cosx Где значение a — любое действительное число, а x — неизвестная переменная. Решение неравенства заключается в нахождении значения переменной arc x, удовлетворяющего тригонометрическому неравенству. Простыми словами, найти меру угла, удовлетворяющую неравенству. Окружность единичного радиуса с центром в начале координат O называется тригонометрической единичной окружностью. Вращение переменной дуги этой тригонометрической единичной окружности против часовой стрелки дает нам основные тригонометрические функции, а именно: Sec x Мы изучаем тригонометрический единичный круг, потому что он помогает нам решить тригонометрические неравенства с доказательством. Неравенство преобразуется в тригонометрическое уравнение с помощью знака равенства; поэтому заменяем знак неравенства знаком равенства. Сформированное уравнение будет решено, и будет найдено значение угла, лежащее в диапазоне от 0 до 2𝝅(от 0° до 360°). Если угол выходит за пределы 𝝅(180°), то значение угла преобразуется в эквивалентное отрицательное значение. Это делается потому, что значения повторяются на отрицательной стороне начала координат. Между двумя значениями создается базовый интервал. В случае, если функция является асимптотой в пределах развитого интервала, то значение угла, при котором функция является асимптотой, ограничивает значение базового интервала. Наконец, полученное нами решение обобщается. Неравенства sinx sinx>a, sin Если |a|≥1, то неравенство sinx> не имеет решений: x∈∅. Если a<−1, решением неравенства sinx>a является любое действительное число: x∈R. При −1≤a<1 решение неравенства sinx>a выражается в виде arcsina+2𝝅n Если a > 1, неравенство sinx≥a не имеет решений: x∈∅. Если a ≤ −1, решением неравенства sinx≥a является любое действительное число: x∈R. Случай a=1: x = 𝝅/2 + 2𝝅n, n∈Z. При −1 < a < 1 решение нестрогого неравенства sinx≥a включает граничные углы и имеет вид arcsina+2𝝅n ≤ x ≤ π−arcsina+2𝝅n, n ∈Z. Если a > 1, решение неравенства sinx Если a ≤ −1, выполняется неравенство sinx При −1 < a ≤ 1 решение неравенства sin x < a лежит в интервале −𝝅−arcsin a + 2𝝅n < x < arcsin a + 2𝝅n, n∈Z. Если a ≥ 1, решением неравенства sinx≤a является любое действительное число: x∈R. Если a < −1, неравенство sinx≤a не имеет решений: x∈∅. Случай a = −1: x = −(𝝅/2)+2πn, n∈Z. При −1 < a < 1 решение нестрогого неравенства sinx≤a лежит в интервале −𝝅−arcsin a + 2𝝅n ≤ x ≤ arcsin a + 2πn, n∈Z. Если a ≥ 1, неравенство cos x > a не имеет решений: x∈∅. Если a<−1, то решением неравенства cos x > a является любое действительное число: x∈R. При −1≤ a < 1 решение неравенства cosx>a имеет вид -arccos a + 2𝝅n < x < arccos a + 2𝝅n, n∈Z Если a > 1, неравенство cosx≥a не имеет решений: x∈∅. Если a ≤−1, решением неравенства cosx≥a является любое действительное число: x∈R. Случай a = 1: x = 2𝝅n, n∈Z. При −1 < a < 1 решение нестрогого неравенства cosx≥a выражается формулой -arccos a + 2𝝅n ≤ x ≤ arccos a + 2𝝅n, n∈Z x < a Если a > 1, неравенство cosx Если a ≤ −1, неравенство cos x < a не имеет решений: x∈∅. При −1 < a ≤ 1 решение неравенства cos x < a записывается в виде arccos a + 2n < x < 2𝝅 – arccos a + 2𝝅n, n∈Z x ≤ a Если a ≥ 1, решением неравенства cos x ≤ a является любое действительное число: x∈R. Если a < −1, неравенство cosx≤a не имеет решений: x∈∅. Случай a = −1: x = 𝝅 + 2𝝅n, n∈Z. При −1 < a < 1 решение нестрогого неравенства cosx≤a записывается как arccos a + 2𝝅n ≤ x ≤ 2𝝅-arccos a + 2𝝅n, n∈Z Для любого действительного значения a решение строгого неравенства tan x>a имеет вид arctan a + 𝝅n < x < (𝝅/2) + 𝝅n, n∈Z Для любого действительного значения a решение неравенства tan x≥a выражается в виде arctan a + n ≤ x ≤ (𝝅/2) + 𝝅n, n∈Z Для любого значения a решение неравенства tanx -(𝝅/2) + 𝝅n < x < arctan a + 𝝅n, n∈Z Для любого значения a неравенство tanx≤a имеет следующее решение: -(𝝅/2) + 𝝅n < x ≤ arctan a + 𝝅n, n∈Z Для любого значения a решение неравенства cotx >a имеет вид 𝝅n < x < arc cot a + 𝝅n, n∈Z Нестрогое неравенство cotx≥a имеет аналогичное решение: n < x ≤ arc cot a + 𝝅n, n∈Z.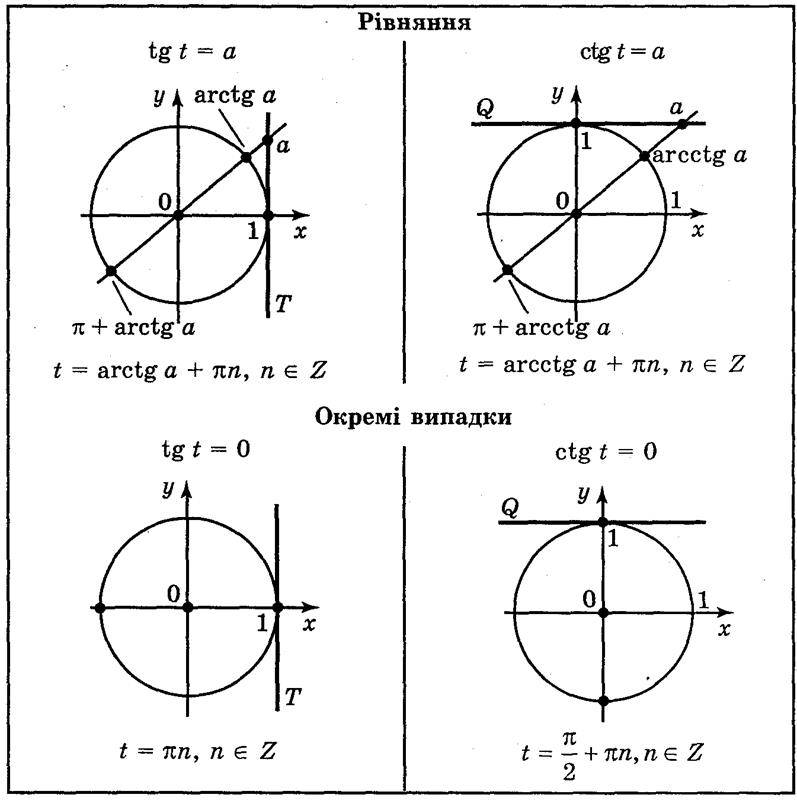 неравенства в кроватке x
неравенства в кроватке x
kπ < x < (arccot a + kπ), k ∈ Z.
Теперь рассмотрим cot x < a.
Из рисунка можно получить решение:
(arccot a + kπ) < x < (π + kπ), k ∈ Z. Нравится:
 ..
.. Подробнее о тригонометрических тождествах и уравнениях-неравенствах
Тригонометрические тождества и уравнениях-неравенствах
Тригонометрическая единичная окружность
Этапы решения тригонометрических неравенств
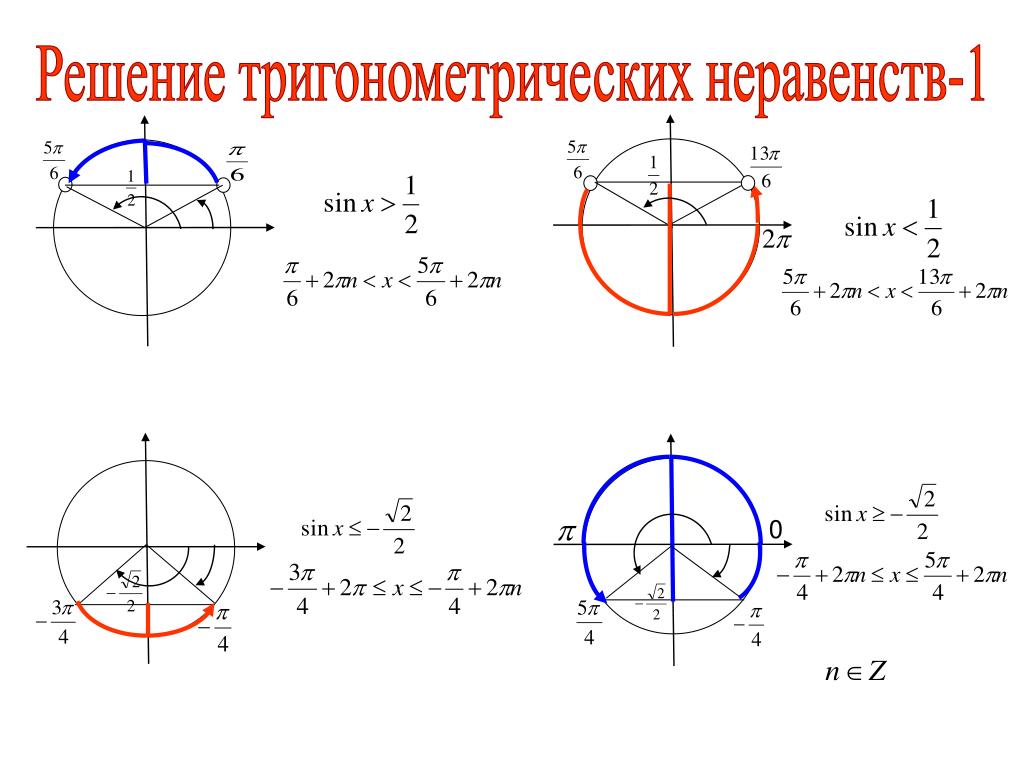
Неравенства Sin x
Sinx>a
Sin x ≥ a
Sin x
< a Sin x ≤ a

Неравенства cosx
Cos x > a
Cosx ≥ a
Неравенства tan x
Tan x > a
Tan x ≥ a
Tan x
< a Tan x ≤ a
Неравенства Cot x
Cot x > a
Cot x ≥ a

 2.1. Решение тригонометрических неравенств. Часть 1.)
2.1. Решение тригонометрических неравенств. Часть 1.)