Решение задач с помощью квадратных уравнений: Решение текстовых задач с помощью квадратных уравнений (8 класс)

alexxlab / / Разное

Решение задач с помощью квадратных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей

Решение задач с помощью квадратных уравнений.

При решении любой задачи необходимо сначала перевести её условие на математический язык, составить нужное уравнение (или не одно, а несколько уравнений – систему уравнений), а затем решить его. Поговорим о таких задачах, в которых уравнения будут получаться не линейные, как это было раньше, а квадратные. Или сводящиеся к квадратным.

Три основных типа текстовых задач в математике – на движение, на работу и на смеси. На смеси очень редко бывают задачи, сводящиеся к квадратным уравнениям, так что о них сейчас говорить не будем. Рассмотрим задачу на движение.

Задача 1. Катер прошел 5 км по течению реки и 8 км по озеру, затратив на весь путь 1 час. Скорость течения равна 3 км/ч. Найти скорость катера по течению.

В подобных задачах лучше всего за х брать то, что спрашивают. Тогда мы не ошибемся, если, найдя х, сразу запишем его в ответ.

Итак, пусть х км/ч – скорость катера по течению. Тогда скорость катера по озеру меньше ровно на скорость течения – ведь в озере течения нет. Значит, по озеру катер двигался со скоростью (х-3) км/ч. При этом мы также знаем пути, которые катер прошёл по реке и по озеру. Вспомним уравнение движения: S = vt. Найдем время по формуле t = s:v. Время движения по озеру 8:(x-3), а по реке 5:x.

Чтобы было удобнее, запишем все данные в следующую таблицу.

 

S, км

v, км/ч

t, ч

По течению

5

x

5x

По озеру

8

x-3

8x-3

 

Теперь вспомним, что в общей сложности катер плыл 1 час, получаем уравнение:

8x-3+5x=1 .

Умножим обе части уравнения на x(x-3) и приравняем числители при условии x(x-3)≠0.

8x+5x-3=x(x-3)

8x+5x-15=x2-3x

x2-16x+15=0

D=(-16)2-4∙1∙15=256-60=196

D=14

x1=—16-142=1

x2=—16+142=15

Первый ответ не подходит, так как скорость катера по течению не может быть меньше скорости течения. Значит, ответ: 15 км/ч.

Универсальный алгоритм для решения текстовых задач:

  1. Переписать условие на математический язык.
  2. Составить уравнение или систему уравнений.
  3. Решить полученное уравнение или систему.
  4. Проанализировать полученное решение и записать ответ.

Так, в рассмотренной задаче про катер получилось два значения неизвестной, и чисто алгебраически оба они являются решениями уравнения (системы). Однако для одного из значений скорость катера против течения реки получается отрицательной – это и есть анализ: в ответ записываем только второе значение.

Задача 2. Бассейн наполняется двумя трубами за 10 часов. За сколько часов наполнит бассейн первая труба, если она это делает на 15 ч быстрее, чем вторая?

Для начала вспомним формулу для вычисления объёма проделанной работы: А = vt. Обрати внимание на то, что здесь есть полное соответствие задачам на движение: путь – объём работы, скорость – производительность, время – время.

Эту задачу можно решить по алгоритму. Сначала перепишем условие на математическом языке.

Работа по наполнению бассейна объёмом A выполнена двумя трубами одновременно с общей скоростью v1+v2 за время t = 10 ч.

Первая труба наполняет бассейн (объём работы A) со скоростью v1 за время t1.

Вторая труба наполняет бассейн (объём работы A) со скоростью v2 за время t2.

Разница между временем t2 и временем t1 равна 15 (t2>t1 на 15 ч).

Обрати внимание на то, что в подобных задачах на совместную работу производительности складывать можно, а времена – нет.

Второй шаг – составляем систему:

A=10v1+v2A=v1t1A=v2t2t2-t1=15

Так как трубы заполняют один и тот же бассейн, то есть выполняют одинаковую работу, то можно принять работу за 1. Обрати внимание, речь не идет об 1 литре или кубометре, 1 в данном случае – это 1 бассейн. Так что и производительность в этом случае будет измеряться не в литрах в час, а в бассейнах в час, то есть какую часть бассейна заполнит труба за час.

Третий шаг – решаем систему:

110=v1+v2A1t1=v1A1t2=v2At2=15+t1

Получаем:

1t1+1t1+15=110

Умножим обе части на 10t1(t1+15)

10t1+15+10t1=t1(t1+15)

10t1+150+10t1=t12+15t1

t12-5t1-150=0

Решая уравнение, получим два корня: 15 и -10.

И теперь анализ: время не может быть отрицательным, так что ответ – 15 часов.

Урок алгебры в 8-м классе по теме «Решение задач с помощью квадратных уравнений»

Тип урока: Урок комплексного применения знаний и способов деятельности.

Цели урока:

  • обеспечить применение учащимися знаний и умений о квадратных уравнениях, способах их решений в разнообразных ситуациях;
  • создать содержательные условия для развития у учащихся умений: анализировать, сравнивать, выделять главное при решении задач с помощью квадратных уравнений;
  • организовать деятельность учащихся по самостоятельному решению разноуровневых задач.

План урока:

  1. Актуализация знаний по теме «Квадратные уравнения».
  2. Составление уравнений к задачам разных типов.
  3. Решение задачи двумя способами.
  4. Знакомство с одним из способов решения квадратного уравнения (через свойства коэффициентов).
  5. Решение задач трёх уровней сложности по вариантам.
  6. Подведение итогов урока и задание на дом.

Оборудование урока:

  1. Компьютер, мультимедийный проектор с экраном.
  2. Карточки с задачами.
  3. Чистый лист бумаги на каждого ученика.
  4. Карточки с домашним заданием.

 

1. Организационный этап

Сообщить учащимся тему, цели и план урока.

2. Этап актуализации комплекса знаний учащихся и способов деятельности

Теоретические вопросы:

  1. Сформируйте определение квадратного уравнения.
  2. Какие вы знаете виды квадратных уравнений?
  3. Какое уравнение называют неполным квадратным уравнением? Приведите примеры.
  4. Какое уравнение называют приведённым квадратным уравнением?

Практические задания:

Корни какого из уравнений обладают свойствами:

  1. сумма корней равна 6, а произведение корней равно ─16;
  2. один из корней равен 6; в) корни равны.

На экране через проектор высвечиваются квадратные уравнения:

х²-6х-16=0,

х²-2х-24=0,

х²-2х+24=0,

х²+6х-16=0,

х²-10х+25=0,

х²-6х=0.

 На основании какой теоремы вы выполняли это задание?

3. Этап самостоятельного применения знаний в сходной и новой ситуациях

Составить уравнения к задачам, при этом корни уравнения находить не надо (7-10 минут).

  1. Найти два последовательных натуральных числа, произведение которых равно 210.
  2. Площадь прямоугольника, одна из сторон которого на 3 см больше другой, равна 54 см². Найти стороны и периметр прямоугольника.
  3. Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найти стороны прямоугольника.
  4. Две машинистки, работая вместе, могут выполнить задание за 3 часа. Сколько времени потребуется для выполнения этого задания первой машинистке, если она может выполнить все задание на 8 часов быстрее второй?
  5. Скорость моторной лодки в стоячей воде 7 км/ч. Время, затраченное на движение лодки на 24 км по течению и на 24 км против течения равно 7 часам. Найти скорость течения реки.

По окончании времени учащиеся выходят к доске и записывают полученные уравнения с комментариями.

Ответы:

  1. х(х + 1) = 210; х2 + х ─ 210 = 0
  2. х(х + 3) = 54; х2 +3х ─ 54 = 0
  3. х2 + (17 ─ х)2 = 169; 2х2 ─ 34х + 120 = 0
  4. + =
  5. + = 7.

Решить задачу двумя способами (использовать алгоритм).

На середине пути между станциями А и В поезд был задержан на 10 минут. Чтобы прибыть в В по расписанию, машинисту пришлось первоначальную скорость поезда увеличить на 12 . Найти первоначальную скорость поезда, если известно, что расстояние между станциями равно 120 км.

У доски выполняет решение один ученик.

Первый способ:

Пусть х скорость поезда на 1-й половине пути.

А так как вторую половину пути поезд прошел на часа быстрее, имеем уравнение.

Второй способ: Учащимся предлагается рассмотреть возможность обозначения за х другой величины.

Пусть х часов время за которое поезд прошел первую половину пути, тогда (х ─ ) ч вторую половину пути. А так как разница скоростей 12 имеем уравнение.

Дополнительный теоретический материал:

С помощью проектора на экране появляется информация:

Даны уравнения: х² ─ 243х+242=0 и 2х² ─7х+5=0. За 20 секунд найти их корни.

─ Существует способ нахождения корней квадратного уравнения через свойство коэффициентов.

Если а+в+с=0, то х1=1, х2= .

Если а-в+с=0, то х

1=1, х2= ─ .

─ Используя эти свойства, приведите пример уравнения и запишите его.

4. Этап контроля и самоконтроля

Учащимся предлагается решить на выбор одну из трех задач.

Вариант 1

На «3» Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?

На «4» Пешеход должен был пройти 9 км с некоторой скоростью, но увеличив эту скорость на 2 км/ч, он прошел 9 км на 45 минут быстрее. Найти истинную скорость пешехода.

На «5» Слесарь должен выполнить заказ за то же время, что и два ученика, работая вместе. За сколько часов может выполнить задание слесарь и каждый из учеников, если слесарь может выполнить заказ на 2 часа быстрее, чем один первый ученик, и на 8 часов быстрее, чем один второй?

Вариант 2

На «3» Знаменатель дроби на 5 больше ее числителя. Если к числителю прибавить 14, а от знаменателя отнять 1, то получиться дробь, обратная данной. Найти первоначальную дробь.

На «4» Велосипедист должен был проехать 40 км с некоторой скоростью, но увеличив эту скорость на 6 км/ч, он проехал 40 км на 20 минут быстрее. Найти истинную скорость велосипедиста.

На «5» Из города А в город В, расстояние между которыми 30 км, выехал грузовой автомобиль, а через 10 минут вслед за ним отправился легковой автомобиль, скорость которого на 20 км/ ч больше скорости грузового. Найти скорость легкового автомобиля, если известно, что он приехал в город В на 5 минут раньше грузового автомобиля.

После того, как учащиеся сдали свои решения, с помощью проектора на экране появляются решения и ответы всех задач. Учащиеся устно воспроизводят свои решения и самостоятельно выполняют проверку.

5. Этап подведения итогов урока и информации о домашнем задании

Дать качественную оценку работы класса и отдельных учащихся.

Задание на дом. Решить задачу:

«Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»

6. Рефлексия

Использование педагогической техники «Координаты»

Приложение 1.

Возраст и числа — Алгебра среднего уровня

Глава 10: Квадратика

Квадратичные текстовые задачи — это третий тип текстовых задач, охватываемых MATQ 1099, причем первый представляет собой линейные уравнения с одной переменной, а второй — линейные уравнения с двумя или более переменными. 2 = 68[/латекс]. Упрощение дает: 92&=&68 \\ &&&&4x&+&4&=&68 \\ &&&&&-&4&&-4 \\ \hline &&&&&&\dfrac{4x}{4}&=&\dfrac{64}{4} \\ \\ &&&&&&&x&=&16 \end {array}[/latex]

Это означает, что два целых числа равны 16 и 18.

Произведение возрастов Салли и Джоуи теперь на 175 больше, чем произведение их возрастов пятью годами ранее. Если Салли на 20 лет старше Джоуи, каков их нынешний возраст? 92&-&10J&& \\ \hline &&\dfrac{10J}{10}&=&\dfrac{100}{10} &&&&&& \\ \\ &&J&=&10 &&&&&& \end{array}[/latex]

Это означает, что Джоуи 10 лет, а Салли 30 лет.

Для вопросов с 1 по 12 напишите и решите уравнение, описывающее взаимосвязь.

  1. Сумма двух чисел равна 22, а произведение этих двух чисел равно 120. Что это за числа?
  2. Разница двух чисел равна 4, а произведение этих двух чисел равно 140. Что это за числа?
  3. Разница двух чисел равна 8, а сумма квадратов этих двух чисел равна 320. Что это за числа?
  4. Сумма квадратов двух последовательных четных целых чисел равна 244. Что это за числа?
  5. Разница квадратов двух последовательных четных целых чисел равна 60. Что это за числа?
  6. Сумма квадратов двух последовательных четных целых чисел равна 452. Что это за числа?
  7. Найдите три последовательных четных числа, произведение первых двух на 38 больше, чем произведение третьего числа.
  8. Найдите три последовательных нечетных числа, произведение первых двух на 52 больше, чем произведение третьего числа.
  9. Произведение возрастов Алана и Терри на 80 больше, чем произведение их возрастов 4 года назад. Если Алан на 4 года старше Терри, каков их текущий возраст?
  10. Произведение возрастов Кэлли и Кэти на 130 меньше, чем произведение их возрастов через 5 лет. Если Кэлли на 3 года старше Кэти, каков их текущий возраст?
  11. Произведение возраста Джеймса и Сьюзен через 5 лет на 230 больше, чем произведение их возраста сегодня. Каков их возраст, если Джеймс на год старше Сьюзен?
  12. Произведение возрастов (в днях) двух новорожденных младенцев Симрана и Джесси через два дня будет на 48 больше, чем произведение их сегодняшних возрастов. Сколько лет малышам, если Джесси на 2 дня старше Симрана?

Даг отправился на конференцию в город в 120 км. На обратном пути из-за ремонта дороги ему пришлось ехать на 10 км/ч медленнее, в результате чего обратный путь занял на 2 часа больше. С какой скоростью он ехал на конференцию?

Первое уравнение: [латекс]r(t) = 120[/латекс], что означает, что [латекс]r = \dfrac{120}{t}[/latex] или [латекс]t = \dfrac{120 }{r}[/латекс].

Во втором уравнении [латекс]r[/латекс] на 10 км/ч медленнее, а [латекс]t[/латекс] на 2 часа дольше. Это означает, что второе уравнение имеет вид [латекс](r — 10)(t + 2) = 120[/латекс].

Мы исключим переменную [латекс]t[/латекс] во втором уравнении путем замены:

[латекс](r-10)(\dfrac{120}{r}+2)=120[/латекс]

Умножьте обе части на [latex]r[/latex], чтобы исключить дробь, которая оставляет нам:

[latex](r-10)(120+2r)=120r[/latex]

Умножение всего дает нам: 92-10r-600&=&0 \\ (r-30)(r+20)&=&0 \\ r&=&30\text{ км/ч или }-20\text{ км/ч (брак)} \end{ массив}[/латекс]

Марк плывет вниз по течению 30 км, затем разворачивается и возвращается на прежнее место. 2&-&60r&-&32&=&0&& \end{массив}[/латекс] 92-15r-8&=&0 \\ (2r+1)(r-8)&=&0 \\ r&=&-\dfrac{1}{2}\text{ км/ч (брак) или }r=8 \text{км/ч} \end{массив}[/latex]

вопросов

Для вопросов с 13 по 20 напишите и решите уравнение, описывающее взаимосвязь.

  1. Поезд проехал 240 км с определенной скоростью. При замене двигателя на усовершенствованную модель скорость увеличилась на 20 км/ч, а время в пути на рейс сократилось на 1 час. Какова была скорость каждого двигателя?
  2. Мистер Джонс регулярно навещает свою бабушку, которая живет в 100 км от него. Недавно открылась новая автострада, и, хотя длина автострады составляет 120 км, он может ехать в среднем на 20 км/ч быстрее и тратит на поездку на 30 минут меньше времени. Какова скорость мистера Джонса как на старом маршруте, так и на автостраде?
  3. Если бы велосипедист ехал на 5 км/ч быстрее, ему потребовалось бы на 1,5 часа меньше времени, чтобы проехать 150 км. Найдите скорость велосипедиста.
  4. Если бы транзитный автобус двигался на 15 км в час быстрее, ему потребовалось бы на 1 час меньше, чтобы проехать 180 км. Какова была средняя скорость этого автобуса?
  5. Велосипедист едет в хижину в 72 км вверх по долине и возвращается через 9 часов. Его скорость возвращения на 12 км/ч больше, чем его скорость движения. Найдите его скорость как на пути, так и на обратном пути.
  6. Велосипедист проехал 120 км и вернулся через 7 часов. На обратном пути скорость увеличилась на 10 км/ч. Найдите скорость этого велосипедиста, движущегося в обе стороны.
  7. Расстояние между двумя автовокзалами 240 км. Если скорость автобуса увеличить на 36 км/ч, то поездка займет на 1,5 часа меньше. Какова обычная скорость автобуса?
  8. Пилот пролетел с постоянной скоростью 600 км. Вернувшись на следующий день, летчик летел против встречного ветра со скоростью 50 км/ч, чтобы вернуться в исходную точку. Если самолет находился в воздухе всего 7 часов, какова была средняя скорость этого самолета?

Найдите длину и ширину прямоугольника, длина которого на 5 см больше ширины, а площадь равна 50 см 2 .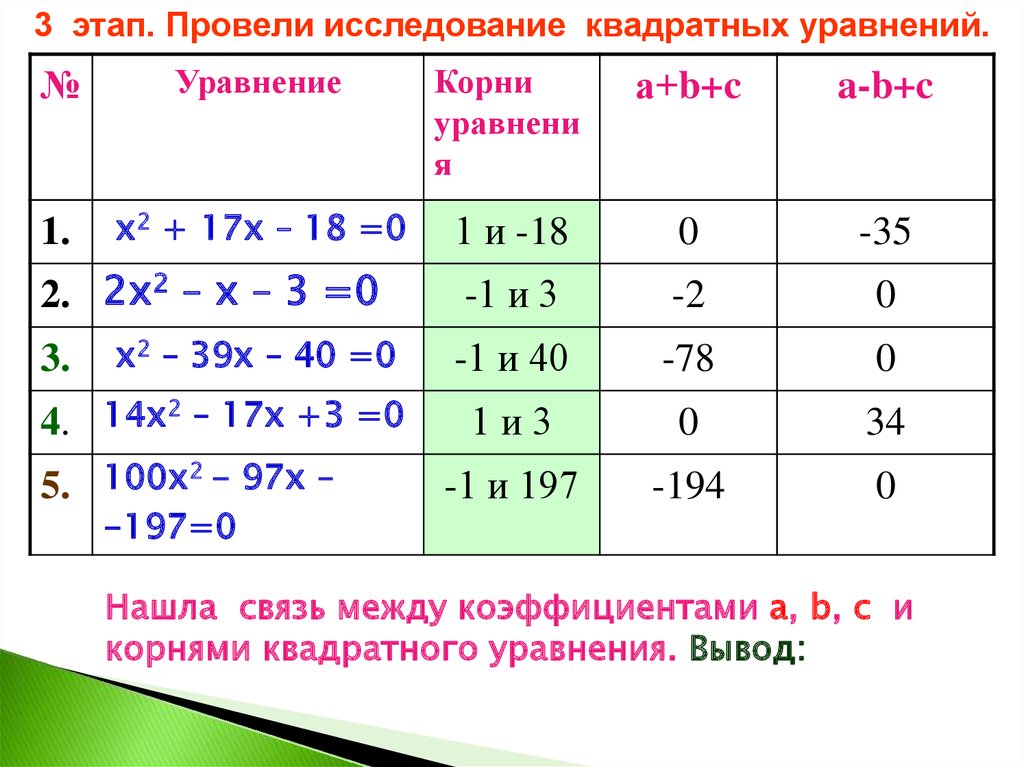 2 [/латекс]. 92-4ac}}{2a},\hspace{0,25in}\text{, где }a=-15, b=24\text{ и }c=144[/latex]

Подстановка этих значений в yields [latex] x = 4[/latex] или [latex]x=-2,4[/latex] (отклонить).

Ник и Хлоя хотят окружить свою свадебную фотографию 60 на 80 см рогожей одинаковой ширины. Полученное фото и паспарту накрыть 1 м 2 листом дорогого архивного стекла. Найдите ширину коврика.

Во-первых, площадь этого прямоугольника равна [латекс]L\times W[/латекс], что означает, что для этого прямоугольника: 92-4(1)(-1300)}}{2(1)}\hspace{0,5 дюйма}x=\dfrac{-70\pm 10\sqrt{101}}{2}[/latex]

[ латекс]x=-35+5\sqrt{101}\hspace{0,75 дюйма} x=-35-5\sqrt{101}\text{(отклонено)}[/latex]

вопросов

Для вопросов с 21 по 28 напишите и решите уравнение, описывающее взаимосвязь.

  1. Найдите длину и ширину прямоугольника, длина которого на 4 см больше ширины, а площадь равна 60 см 2 .
  2. Найдите длину и ширину прямоугольника, ширина которого на 10 см меньше его длины, а площадь равна 200 см 2 .
  3. Большой прямоугольный сад в парке шириной 120 м и длиной 150 м. Призван подрядчик, чтобы добавить кирпичную дорожку вокруг этого сада. Если площадь дорожки 2800 м 2 , то какой ширины дорожка?
  4. Парковый бассейн шириной 10 м и длиной 25 м. Покрытие для бассейна покупается для покрытия бассейна, перекрывая все 4 стороны на одинаковую ширину. Если крытая площадь за пределами бассейна составляет 74 м 2 , насколько широка площадь перекрытия?
  5. В ландшафтном плане прямоугольная клумба запроектирована так, чтобы ее длина была на 4 м больше ширины. Если 60 м 2 нужны для растений на грядке, какие должны быть размеры прямоугольной грядки?
  6. Если сторона квадрата увеличивается на 5 единиц, площадь увеличивается на 4 квадратных единицы. Найдите длину сторон исходного квадрата.
  7. Участок прямоугольной формы имеет длину на 20 м больше ширины и площадь 2400 м 2 . Найдите размеры участка.
  8. Длина комнаты на 8 м больше ширины. Если и длину, и ширину увеличить на 2 м, площадь увеличится на 60 м 9 .0149 2 . Найдите размеры комнаты.

Ключ ответа 10.7

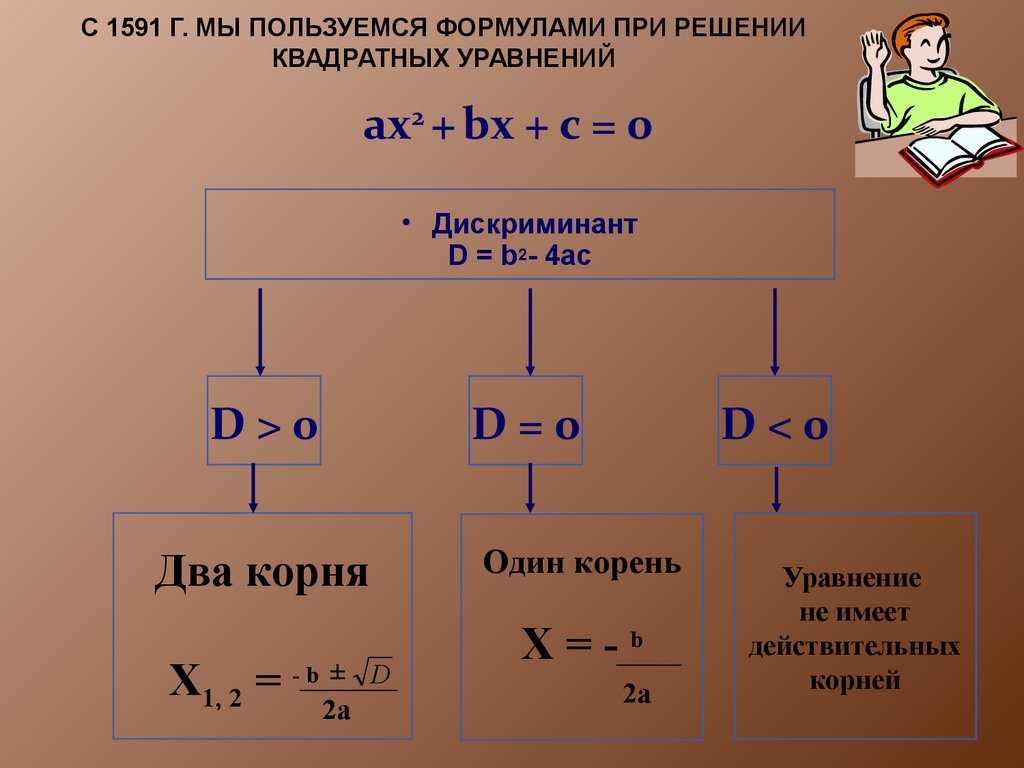
Как решать текстовые задачи в квадратных уравнениях

Мы можем выполнить шаги, указанные ниже, чтобы решить текстовые задачи с помощью квадратных уравнений.

Шаг 1 :

Понимание вопроса важнее всего остального. То есть всегда очень важно понимать информацию, изложенную в вопросе, а не решать.

Шаг 2 :

Если это возможно, мы должны разделить данную информацию. Потому что, когда мы разделяем данную информацию на части, мы можем легко их понять.

Шаг 3 :

Как только мы ясно поймем данную информацию, решение задачи со словами в квадратном уравнении не будет сложной задачей.

Шаг 4:

Когда мы пытаемся решить задачи со словами в квадратных уравнениях, мы должны ввести «x» или какой-либо другой алфавит для неизвестного значения (= ответ на наш вопрос) и составить квадратное уравнение с этим «x». . Наконец, мы должны получить значение для алфавита, которое было введено для неизвестного значения.

Шаг 5 :

Если требуется, мы должны нарисовать картинку для данной информации. Рисунок для данной информации даст нам четкое представление о вопросе.

Шаг 6 :

Используя алфавит, введенный для неизвестного значения, мы должны перевести английское утверждение (информацию), данное в вопросе, как уравнение квадратного уравнения.

При переводе мы должны перевести следующие английские слова как соответствующие математические символы.

из ——> x (умножение)

am, есть, есть, было, были, будут, будет ———> = (равно)

Шаг 7:

Как только мы правильно переведем английское утверждение (информацию), данное в вопросе, в виде квадратного уравнения, 90% работы будет выполнено. Оставшиеся 10% просто получают ответ. Это решение для неизвестного.

Это шаги, наиболее часто используемые при решении текстовых задач в квадратных уравнениях.

Давайте посмотрим, как описанные выше шаги работают при решении текстовых задач с использованием квадратных уравнений.

Задача :

Кусок железного стержня стоил 60 долларов. Если бы стержень был на 2 метра короче, а каждый метр стоил бы на 1 доллар больше, общая стоимость осталась бы неизменной. Какова длина стержня?

Решение:

Шаг 1:

Давайте разберемся в данной информации. В вопросе даны три информации.

1. Кусок железного стержня стоит 60 долларов.

2. Если стержень был на 2 метра короче и каждый метр стоит на 1 доллар больше

3. Общая стоимость останется неизменной.

Шаг 2:

Цель вопроса: Какова длина стержня?

Шаг 3 :

Пусть «x» — длина стержня.

Очевидно, мы должны найти значение «x»

Шаг 4 :

Если стержень короче на 2 метра, длина стержня будет

= (x-2)

Шаг 5 :

Из третьей информации имеем следующие утверждения.

Общая стоимость стержня длиной x метров составляет 60 долларов США.

Общая стоимость стержня длиной (x-2) метра составляет 60 долларов США.

Шаг 6 :

Стоимость 1 метра стержня длиной x метров составляет

=  60 / x  ——(1)

Стоимость 1 метра стержня длиной (x-2) метра составляет

=  60 / (x — 2) ——(2)

Шаг 7 :

Из второй информации получаем можно рассмотреть следующий пример.

То есть, если стоимость 1 метра прута x равна 10$, то стоимость 1 метра прута (x-2) будет 11$.

10 и 11 долларов можно сбалансировать, как показано ниже.

10 + 1  =  11

(это только для примера)

Шаг 8:

Если мы применим ту же логику для (1) и (2), мы получим

(60 / x) + 1 =  60 / (x – 2)

(60 + x) / x =  60 / (x – 2)

(x + 60)(x – 2)  =  60x

x 2 + 58x — 120 = 60x

x 2 — 2x — 120 = 0

(x — 12)(x + 10)  = 0 

x — 12  =  0     или     x + 10  =  0

x  =  12     или      x  = -10

Поскольку длина никогда не может быть отрицательным значением, мы можем игнорировать x = -10.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *