Бесконечная прогрессия: Геометрическая прогрессия. — таблицы Tehtab.ru

Содержание

Геометрическая прогрессия | umath.ru

Определение геометрической прогрессии

Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число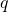

, называется геометрической прогрессией. Число

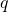называется знаменателем прогрессии.

То есть геометрическая прогрессия определяется рекуррентным соотношением

$b_{n+1} = b_n \cdot q.$

Итак, для n-го члена геометрической прогрессии справедлива формула

$b_n = b_1\cdot q^{n-1}.$

Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:

$b_n^2 = b_{n-1}\cdot b_{n+1}.$

Доказательство. Из определения геометрической прогрессии

$b_n = b_{n-1}\cdot q, \qquad b_{n+1} = b_n \cdot q.$

Следовательно,

$\frac{b_n}{b_{n-1}} = \frac{b_{n+1}}{b_n} = q,$

откуда

$b_n^2 = b_{n-1}\cdot b_{n+1}.$

Обратное утверждение тоже верно. Если для всех членов последовательности 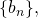$\{b_n\},$ начиная со второго, выполняется равенство 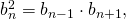$b_n^2 = b_{n-1}\cdot b_{n+1},$ то эта последовательность — геометрическая прогрессия.

Сумма первых n членов геометрической прогрессии

Вычислим сумму первых n членов геометрической прогрессии 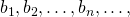$b_1, b_2, \ldots, b_n, \ldots ,$ знаменатель которой $q \ne 0$ :

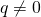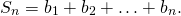
(1) $\begin{equation*}S_n= b_1 + b_2 + \ldots + b_n.\end{equation*}$

Умножим это равенство на :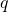

$S_n q = b_1q + b_2q + \ldots + b_nq$

или

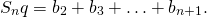
(2) $\begin{equation*}S_n q = b_2 + b_3 + \ldots + b_{n+1}.\end{equation*}$

Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим 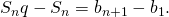$S_n q - S_n = b_{n+1} - b_1.$ Отсюда, так как 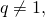$q \ne 1,$ имеем

$S_n = \frac{b_{n+1} - b_1}{q - 1},$

или

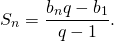
(3) $\begin{equation*}S_n = \frac{b_nq - b_1}{q - 1}.\end{equation*}$

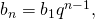
Так как $b_n = b_1q^{n-1},$

то формулу (3) можно переписать в виде

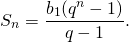
(4) $\begin{equation*}S_n = \frac{b_1(q^n - 1)}{q - 1}.\end{equation*}$

Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.

Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?

Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии

$1, 2, 2^2, 2^3, \ldots , 2^{63}.$

По формуле (3) получаем

$S = \frac{2^{63}\cdot 2 - 1}{2 - 1} = 2^{64} - 1 =$

$= 18\ 446\ 744\ 073\ 709\ 551\ 615.$

Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.

Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.

Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.

Сумма бесконечно убывающей геометрической прогрессии

Рассмотрим геометрическую прогрессию 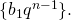$\{b_1q^{n-1}\}.$ Если её знаменатель 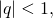$\{b_1q^{n-1}\}.$ то эта последовательность называется бесконечно убывающей геометрической прогрессией.

Сумма бесконечно убывающей геометрической прогресcии выражается формулой

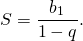
(5) $\begin{equation*}S = \frac{b_1}{1 - q}.\end{equation*}$

Геометрическая прогрессия. Часть 1

Геометрическая прогрессия — это еще один частный случай числовых последовательностей.

Геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

Очевидно, что первый член последовательности, и, следовательно, все ее члены, отличны от нуля.

Число $q={b_k}/{b_{k-1}}$ называется знаменателем геометрической прогрессии.

Основное свойство геометрической прогрессии.

Мы видим, что

$b_k={b_{k-1}}q$

$b_k={b_{k+1}}/q$

Перемножив эти два равенства, получим:

${b_k}^2={b_{k-1}}*{b_{k+1}}$

Итак,

квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних:

${b_k}^2={b_{k-1}}*{b_{k+1}}$

Нетрудно доказать, что

квадрат любого члена геометрической прогрессии, начиная с номера , равен произведению двух соседних:

Формулу n-го члена геометрической прогрессии можно получить аналогично формуле n-го члена арифметической прогрессии, выписав несколько первых членов и установив закономерность.

Формула n-го члена геометрической прогрессии:

ВАЖНО! Зная первый член и знаменатель геометрической прогрессии, можно найти любой ее член.

Несложно получить формулу суммы n членов геометрической прогрессии.

$S_n=b_1+b_1{q}+b_1{q}^2+ b_1{q}^3+$ … $b_1{q}^{n-1}$ (1)

Умножим обе части равенства на

$S_{n}q= b_1{q}+b_1{q}^2+b_1{q}^3+ b_1{q}^4+$ … $b_1{q}^{n}$ (2)

Вычтем из равенства (2) равенство (1). Получим:

$S_{n}q-S_{n}=b_1{q}^{n}-b_1$ (остальные слагаемые в правой части равенства взаимно уничтожатся)

$S_{n}(q-1)=b_1({q}^{n}-1 )$

Отсюда получаем формулу суммы n членов геометрической прогрессии:

$S_{n}(q-1)=b_1({q}^{n}-1 )$ (1)

Бесконечно убывающая геометрическая прогрессия.

Если знаменатель геометрической прогрессии delim{ , то каждый следующий член прогрессии по модулю меньше предыдущего. Если в этой прогрессии бесконечное число членов, то при $n{right}{infty}, ~b_n{right}0$

Такая геометрическая прогрессия называется бесконечно убывающей.

Сумму членов бесконечно убывающей геометрической прогрессии мы находим по формуле:

$n{right}{infty}, ~b_n{right}0$ (2)

ВАЖНО! Формулу суммы членов бесконечно убывающей геометрической прогрессии (2) мы используем только в том случае, если в условии в явном виде указано, что нужно найти сумму бесконечного числа членов. Если указано конкретное число n, то пользуемся формулой (1) суммы n членов, даже если delim{ .

Рассмотрим примеры задач.

1. Дана последовательность . Докажите, что эта последовательность является геометрической прогрессией.

Докажем, что для любого номера n отношение ${c_n}/{c_{n-1}}=const$

$c_{n-1}=5(-2)^{n}$

${c_n}/{c_{n-1}}={5(-2)^{n}} /{5(-2)^{n-1}}=-2$ — мы видим, что отношение ${c_n}/{c_{n-1}}$ не зависит от номера n и равно числу -2, следовательно, данная последовательность является геометрической прогрессией.

2. Дана геометрическая прогрессия

1. Найдите пятый член прогрессии.

2. Найдите сумму первых восьми членов прогрессии.

1. $b_5=2(-3)^{5}=-486$

2. $S_5={b_1(q^5-1)}/{q-1}$

Найдем b_1 и .

$q={b_2}/{b_1}={18}/{-6} =-3$

$S_5={(-6)((-3)^5-1)}/{(-3)-1}={(-6)(-243-1)}/{-4}=-3*122=-366$

Ответ: 1. -162; 2. -366

3. Найдите сумму бесконечной геометрической прогрессии

Сумму бесконечной геометрической прогрессии найдем по формуле $S={b_1}/{1-q}$ . (В задаче в явном виде указано, что мы имеем дело с бесконечной геометрической прогрессией.)

b_1=8 ;

Ответ: 10{2/3}

4. Дана геометрическая прогрессия (c_n) с положительными членами, в которой .

а) Найдите c_1 .

б) Определите количество членов прогрессии, начиная с первого, сумма которых равна 45.

а) Запишем условие задачи, выразив его через c_1 и . Получим систему уравнений:

$delim{lbrace}{matrix{2}{1}{{c_1*q^3=24} {c_1*q^5=96} }}{ }$

Разделим второе уравнение на первое, получим

q^2=4 ; .

По условию наша прогрессия с положительными членами, поэтому q>0 .

Найдем c_1 . Для этого подставим q=2 в первое уравнение системы.

б) По условию S_n=45

$S_n={c_1(q^n-1)}/{q-1}={3(2^n-1)}=45$

2^n=16

n=4

Ответ: а) 3; б) 4.

5. Сумма членов бесконечной геометрической прогрессии (b_n) в три раза больше ее первого члена. Найдите отношение ${b_2}/{b_4}$ .

Выразим условие задачи через b_1 и

$S={b_1}/{1-q}$

Т.к. по условию S=3b_1 , получим

${b_1}/{1-q}=3b_1$ . Отсюда

Нам нужно найти ${b_2}/{b_4}={b_1*q}/{b_1*q^3}=1/{q^2}$ .

$1/{q^2} 1/{(2/3)^2}=9/4=2,25$

Ответ: 2,25

И.В. Фельдман, репетитор по математике.

Геометрическая прогрессия — YouClever.org

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Числовая последовательность

Если ты уже читал тему «Арифметическая прогрессия» ты можешь смело пропускать этот блок и переходить к самой сути. Если нет, то советую ознакомиться, чтобы иметь общее представление о том, что такое прогрессия в целом и с чем ее едят.

Итак, сядем и начнем писать какие-нибудь числа. Например:

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и -ное число) всегда одно.

Число с номером называетмя -ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, ), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: .

В нашем случае:

Самые распространенные виды прогрессии это арифметическая и геометрическая. В этой теме мы поговорим о втором виде – геометрической прогрессии.

Для чего нужна геометрическая прогрессия и ее история возникновения.

Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк, когда сумма процентов начисляется на сумму, скопившуюся на счете за предыдущий период. Иными словами, если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на от исходной суммы, т.е. новая сумма будет равна вкладу, умноженному на . Ещё через год уже эта сумма увеличится на , т.е. получившаяся в тот раз сумма вновь умножится на и так далее. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.

Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил человек, те в свою очередь заразили еще по человека, и таким образом вторая волна заражения – человек, а те в свою очередь, заразили еще … и так далее…

Кстати, финансовая пирамида, та же МММ – это простой и сухой расчет по свойствам геометрической прогрессии. Интересно? Давай разбираться.

Геометрическая прогрессия.

Допустим, у нас есть числовая последовательность:

Ты сразу же ответишь, что это легко и имя такой последовательности — арифметическая прогрессия с разностью ее членов . А как на счет такого:

Если ты будешь вычитать из последующего числа предыдущее, то ты увидишь, что каждый раз получается новая разница ( и т.д.), но последовательность определенно существует и ее несложно заметить – каждое следующие число в раз больше предыдущего!

Такой вид числовой последовательности называется геометрической прогрессией и обозначается .

Геометрическая прогрессия { } — это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число . Это число называют знаменателем геометрической прогрессии.

Ограничения, что первый член { } не равен и не случайны. Допустим, что их нет, и первый член все же равен , а q равно, хм.. пусть , тогда получается:

и так далее.

Согласись, что это уже никакая не прогрессия.

Как ты понимаешь, те же самые результаты мы получим, если будет каким-либо числом, отличным от нуля, а . В этих случаях прогрессии просто не будет, так как весь числовой ряд будут либо все нули, либо одно число, а все остальные нули.

Теперь поговорим поподробнее о знаменателе геометрической прогрессии, то есть о .

Повторим: – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.

Как ты думаешь, каким может быть ? Правильно, положительным и отрицательным, но не нулем (мы говорили об этом чуть выше).

Допустим, что у нас положительное. Пусть в нашем случае , а . Чему равен второй член и ? Ты без труда ответишь, что:

Все верно. Соответственно, если , то все последующие члены прогрессии имеют одинаковый знак – они положительны.

А что если отрицательное? Например, , а . Чему равен второй член и ?

Это уже совсем другая история

Попробуй посчитать член данной прогрессии. Сколько у тебя получилось? У меня . Таким образом, если , то знаки членов геометрической прогрессии чередуются. То есть, если ты увидишь прогрессию, с чередующимися знаками у ее членов, значит ее знаменатель на отрицательный. Это знание может помочь тебе проверять себя при решении задач на эту тему.

Теперь немного потренируемся: попробуй определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической:

Разобрался? Сравним наши ответы:

Геометрическая прогрессия – 3, 6.
Арифметическая прогрессия – 2, 4.
Не является ни арифметической, ни геометрической прогрессиями — 1, 5, 7.

Вернемся к нашей последней прогрессии , а и попробуем так же как и в арифметической найти ее член. Как ты уже догадываешься, есть два способа его нахождения.

Последовательно умножаем каждый член на .

Итак, -ой член описанной геометрической прогрессии равен .

Как ты уже догадываешься, сейчас ты сам выведешь формулу, которая поможет найти тебе любой член геометрической прогрессии. Или ты ее уже вывел для себя, расписывая, как поэтапно находить -ой член? Если так, то проверь правильность твоих рассуждений.

Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии на знаменатель в степени, которая на единицу меньше, чем порядковый номер искомого числа.

Проиллюстрируем это на примере нахождения -го члена данной прогрессии:

Иными словами:

Найди самостоятельно значение члена заданной геометрической прогрессии.

Получилось? Сравним наши ответы:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно умножали на каждый предыдущий член геометрической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

— уравнение членов геометрической прогрессии.

Выведенная формула верна для всех значений — как положительных, так и отрицательных. Проверь это самостоятельно, рассчитав и члены геометрической прогрессии со следующими условиями: , а .

Посчитал? Сравним полученные результаты:

Согласись, что находить член прогрессии можно было бы так же как и член, однако, есть вероятность неправильно посчитать . А если мы нашли уже -ый член геометрической прогрессии, а , то что может быть проще, чем воспользоваться «обрезанной» частью формулы .

Бесконечно убывающая геометрическая прогрессия.

Совсем недавно мы говорили о том, что может быть как больше, так и меньше нуля, однако, есть особые значения при которых геометрическая прогрессия называется бесконечно убывающей.

При – прогрессия называется бесконечно убывающей.

Как ты думаешь, почему такое название?
Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из членов.
Допустим, , а , тогда:

Мы видим, что каждый последующий член меньше предыдущего в раза, но будет ли какое-либо число ? Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.

Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула приобретает следующий вид:

На графиках нам привычно строить зависимость от , поэтому:

Суть выражения не изменилась: в первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера, а во второй записи – мы просто приняли значение члена геометрической прогрессии за , а порядковый номер обозначили не как , а как . Все, что осталось сделать – построить график.
Посмотрим, что у тебя получилось. Вот какой график получился у меня:

Видишь? Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая. Отметим на графике наши точки, а заодно и то, что обозначает координата и :

Попробуй схематично изобразить график геометрической прогрессии при , если первый ее член также равен . Проанализируй, в чем разница с нашим предыдущим графиком?

Справился? Вот какой график получился у меня:

Теперь, когда ты полностью разобрался в основах темы геометрической прогрессии: знаешь, что это такое, знаешь, как найти ее член, а также знаешь, что такое бесконечно убывающая геометрическая прогрессия, перейдем к ее основному свойству.

Свойство геометрической прогрессии.

Помнишь свойство членов арифметической прогрессии? Да, да, как найти значение определенного числа прогрессии, когда есть предыдущее и последующее значения членов данной прогрессии. Вспомнил? Вот это:

— свойство членов арифметической прогрессии.

Теперь перед нами стоит точно такой же вопрос для членов геометрической прогрессии. Чтобы вывести подобную формулу, давай начнем рисовать и рассуждать. Вот увидишь, это очень легко, и если ты забудешь, то сможешь вывести ее самостоятельно.

Возьмем еще одну простую геометрическую прогрессию, в которой нам известны и . Как найти ? При арифметической прогрессии это легко и просто, а как здесь? На самом деле в геометрической тоже нет ничего сложного — необходимо просто расписать по формуле каждое данное нам значение.

Ты спросишь, и что теперь нам с этим делать? Да очень просто. Для начала изобразим данные формулы на рисунке, и попытаемся сделать с ними различные манипуляции, чтобы прийти к значению .

Абстрагируемся от чисел, которые у нас даны, сосредоточимся только на их выражении через формулу. Нам необходимо найти значение, выделенное оранжевым цветом, зная соседствующие с ним члены. Попробуем произвести с ними различные действия, в результате которых мы сможем получить .

Сложение.
Попробуем сложить два выражения и , мы получим:

Из данного выражения, как ты видишь, мы никак не сможем выразить , следовательно, будем пробовать другой вариант – вычитание.

Вычитание.

Как ты видишь, из этого мы тоже не можем выразить , следовательно, попробуем умножить данные выражения друг на друга.

Умножение.

А теперь посмотри внимательно, что мы имеем, перемножая данные нам члены геометрической прогрессии в сравнении с тем, что необходимо найти:

Догадался о чем я говорю? Правильно, чтобы найти нам необходимо взять квадратный корень от перемноженных друг на друга соседствующих с искомым чисел геометрической прогрессии:

Ну вот. Ты сам вывел свойство геометрической прогрессии. Попробуй записать эту формулу в общем виде. Получилось?

, при

Забыл условие при ? Подумай, почему оно важно, например, попробуй самостоятельно просчитать , при . Что получится в этом случае? Правильно, полная глупость так как формула выглядит так:

Соответственно, не забывай это ограничение.

Теперь посчитаем, чему же равно

Правильный ответ – ! Если ты при расчете не забыл второе возможное значение, то ты большой молодец и сразу можешь переходить к тренировке, а если забыл – прочитай то, что разобрано далее и обрати внимание, почему в ответе необходимо записывать оба корня.

Нарисуем обе наши геометрические прогрессии – одну со значением , а другую со значением

Геометрическая прогрессия | Онлайн калькулятор

Геометрическая прогрессия — это числовая последовательность, в которой все ее члены расположены в порядке, подчиняющемся определенной закономерности. Формула геометрической прогрессии определяет, что каждое следующее число будет получено умножением предыдущего на знаменатель прогрессии — постоянное число, не меняющее свое значение в пределах одной последовательности. b_n=b₁ q^(n-1)

В зависимости от знаменателя прогрессии, выписанные члены геометрической прогрессии могут давать различный вид ряда. Если знаменатель является числом положительным, больше 1 (k > 1), тогда он будет увеличивать значение каждого следующего числа. Такая прогрессия будет монотонно возрастать на протяжении всего ряда. Если знаменатель — положительный, но находится между 0 и 1 (0 , тогда он будет каждый раз уменьшать значение следующего члена, и такая прогрессия будет называться бесконечно убывающая геометрическая прогрессия.

Если для все возрастающей последовательности, можно только найти сумму первых членов геометрической прогрессии, то сумма членов бесконечно убывающей прогрессии будет равна вполне конкретному числовому значению, которое может рассчитать калькулятор. Третий случай представлен отрицательным знаменателем (k , тогда прогрессия становится знакочередующейся, то есть первые члены геометрической прогрессии определяют порядок знаков для всей последовательности чисел. Как знаменатель геометрической прогрессии, так и первый член геометрической прогрессии по определению не могут быть равны нулю.

Существует всего несколько формул геометрической прогрессии, из которых можно вывести все необходимые для решения конкретных задач:

• Формула первого члена геометрической прогрессии;

• Формула n члена геометрической прогрессии;

• Формула суммы первых членов геометрической прогрессии;

• Формула суммы бесконечно убывающей геометрической прогрессии;

• Формула знаменателя геометрической прогрессии.

Таким образом, если условиями задана геометрическая прогрессия с хотя бы двумя параметрами из всех выше представленных, для нее можно будет найти любую из всех прочих переменных.

Урок «Бесконечная геометрическая прогрессия»

№ урока – 70. Класс – 9 класс Дата: 14.02.2019

Урок

по алгебре

тема «Бесконечная геометрическая прогрессия.»

Тип урока: урок усвоения новых знаний.

Цели урока: познакомиться с определением бесконечной убывающей геометрической прогрессии и формулу суммы этой прогрессии, учиться применять на практике; развитие самостоятельности, мышления, логики; воспитание активности и аккуратности.

Планируемые результаты:

Предметные: умение работать с текстом, точно и грамотно выражать свои мысли в устной и письменной речи.

Метапредметные УУД:

Коммуникативные: умение формулировать, аргументировать и отстаивать свое мнение.

Познавательные: самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации; структурирование знаний.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

План урока

Организационный момент.-2 мин.
Актуализация опорных знаний – 2-3 мин.
Изучение новой темы.-15 мин.
Физминутка.-1 мин.
Закрепление новых знаний.-20 мин.
Домашнее задание.-2 мин.
Подведение итогов. – 2 мин.

Ход урока

Организационный момент.-2 мин.

Приветствие.
Проверка готовности учащихся к уроку.
Проверка домашнего задания.
Отметить отсутствующих.

Актуализация опорных знаний – 2-3 мин.

Устные упражнения

1. Является ли геометрической прогрессией последовательность чисел:

1) 3; 1; ; ; ;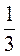

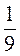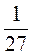2) -3; 1; ; ; ;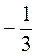

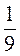3) 1; ; ; ; ; ?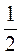

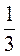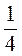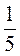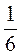Для геометрических прогрессий найдите знаменатель.

2. Как найти сумму первых десяти членов последовательности:
1) (аn): 1; 2; 3; …;

2) (bn): 1; 2; 4; 8; …;

3) (cn): 3; 3; 3; … ?

3. В геометрической прогрессии (dn) d1 = 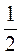; q = 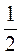.Найдите:

1) d2; 2) d4; 3) d10.

Что можно сказать о ее 100-й член?

Изучение новой темы.

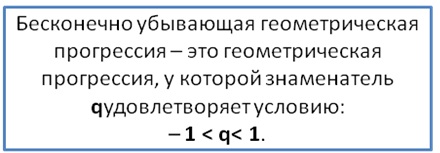
Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q|<1.

Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа.

S= , q≠1

Пример 1: переведи периодическую дробь 0,(8) в обыкновенную дробь.

Решение.

Достаточно очевидно, что 0,(8)=0,8+0,08+0,008+… Мы пришли к сумме членов бесконечно убывающей геометрической прогрессии с первым членом 0,8 и знаменателем S= =

Таким образом, бесконечная периодическая десятичная дробь 0,(8) обращается в обыкновенную дробь .

Пример 2. Найдем сумму бесконечной геометрической прогрессии (bn): 6; -2; … .

Решение

По условию b1 = 6; b2 = -2, следовательно, q = 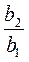= 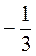. Имеем геометрическую прогрессию, у которой | q | ≠1. По формуле 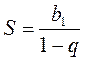находим:

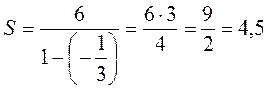Ответ; 4,5.

Пример 3. Найдем сумму бесконечной геометрической прогрессии (bn): 6; -2; … .

РешениеПо условию b1 = 6; b2 = -2, следовательно, q = 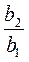= 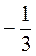. Имеем геометрическую прогрессию, у которой | q | 1. По формуле 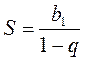находим:

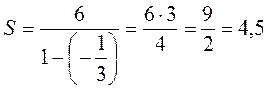Ответ; 4,5.

Пример 4. Запишем число 0,(7) в виде обыкновенной дроби.

Решение

Запись 0,(7) означает бесконечный периодический дробь 0,7777….

Его можно представить как бесконечную сумму + + + … .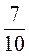

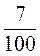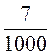Слагаемые этой суммы являются членами бесконечной геометрической прогрессии, у которой b1 = 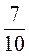, q = 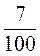: 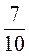= 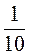, | q | 1. Тогда эта сумма равна:

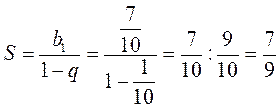. Поэтому 0,(7) = .

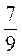Ответ: .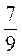

Физминутка.-1 мин.

Нарисуй глазами треугольник.

Теперь его переверни вершиной вниз.

И вновь глазами ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

Зарядка окончилась. Ты – молодец!

Закрепление новых знаний.-20 мин.
1. 1. 1. Сумма первого и пятого членов геометрической прогрессии равна 51, а сумма второго и шестого членов равна 102. Сколько членов этой прогрессии начиная с первого, нужно сложить, чтобы их сумма была равна 3096? (ПРИМЕР 3 СТР229)

Составляем уравнения
1. b1 + b5 = 51
b1 + b1*q^4 = 51
b1 * (1+q^4) = 51
2. b2 + b6 = 102
b1*q + b1*q^5 = 102
b1*q * (1+q^4) = 102
Второе уравнение разделим на первое. Получим
q = 2
Подставляем в первое уравнение и находим b1
b1 * (1+q^4) = 51
b1 * (1+2^4) = 51
b1 * 17 = 51
b1 = 3
Используем формулу суммы n членов
S = b1 * (q^n — 1) / (q — 1)
3 * (2^n — 1) / (2 — 1) = 3069
2^n — 1 = 1023
2^n = 1024
n = 10
Ответ: нужно взять 10 членов, включая первый

1. 1. 1. Обратить десятичную дробь 0, (17) в обыкновенную.

3. Решаем из учебника № 705, 706.

6. Домашнее задание.-2 мин.

п. 27-28, № 703, 710, на повторение № 660 +ОГЭ 15 и 16 вариант.

Подведение итогов. – 2 мин.

1. Бесконечно убывающая геометрическая прогрессия.

2. Сумма бесконечной геометрической прогрессии.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Определение 1. Числовую последовательность

b₁, b₂, … b_k , …

все члены которой отличны от нуля, называют геометрической прогрессией, если справедливы равенства

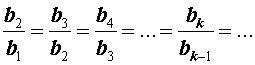
Определение 2. Если последовательность чисел

b₁, b₂, … b_k , …

является геометрической прогрессией, то число q , определенное формулой

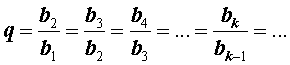
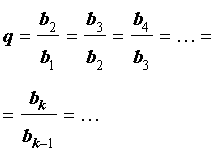
называют знаменателем этой геометрической прогрессии.

Из определений 1 и 2 следует, что для того, чтобы задать геометрическую прогрессию, нужно знать два числа, например, первый член геометрической прогрессии b₁ и знаменатель геометрической прогрессии q . Если числа b₁ и q известны, то все остальные члены прогрессии можно найти по формулам:

b₂ = b₁ q ,

b₃ = b₂ q ,

…

b_k = b_{k – 1} q

…

(1)

По этой причине многие задачи на геометрическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел b₁ и q.

Из формул (1) вытекает общая формула

b_k = b₁q^{k – 1},
k = 1, 2, 3, …

(2)

позволяющая по любому номеру k вычислить член b_k геометрической прогрессии, зная первый член и знаменатель прогрессии. Эта формула носит название формулы общего члена геометрической прогрессии.

Из формулы (2) вытекает утверждение, называемое характеристическим свойством геометрической прогрессии. Это свойство формулируется так: — «Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению своих соседних членов». Таким образом, характеристическое свойство геометрической прогрессии утверждает, что при 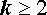справедливо равенство

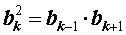(3)

В случае, когда

b₁ > 0 и q > 0

все члены геометрической прогрессии будут положительными, и формулу (3) можно переписать в другом виде:

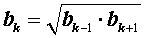(4)

Равенство (4) означает, что каждый член такой геометрической прогрессии, начиная со второго, равен среднему геометрическому своих соседних членов.

Если для суммы первых k членов геометрической прогрессии ввести обозначение

S_k = b₁ + b₂ + … + b_k ,
k = 1, 2, 3, …

то, воспользовавшись равенствами (1), получаем

q S_k =
= b₁q + b₂q + … + b_kq =
= b₂ + b₃ + … + b_{k +1} .

Следовательно,

S_k – q S_k = b₁ – b_{k +1} .

Таким образом , при 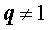будет справедливо равенство

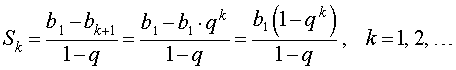
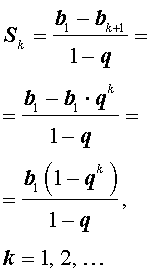
которое называется формулой для суммы первых k членов геометрической прогрессии.

В случае, когда q = 1, все члены геометрической прогрессии равны, что не представляет особого интереса.

Бесконечно убывающая геометрическая прогрессия

Определение 3. Геометрическую прогрессию называют бесконечно убывающей, если её знаменатель удовлетворяет неравенству

| q | < 1 .

В этом случае выполнено равенство

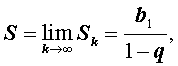
а величину S называют суммой бесконечно убывающей геометрической прогрессии.

Более подробно с понятием предела числовой последовательности можно ознакомиться в в разделе «Пределы числовых последовательностей» нашего справочника.

С примерами решений различных задач по теме «Геометрическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».

Подготовка к ЕГЭ и ОГЭ в учебном центре Резольвента

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Геометрическая прогрессия. — Царство математики

Определение

Геометрическая прогрессия — числовая последовательность, в которой каждый следующий член отличается от предыдущего в определенное количество раз. Частное двух соседних элементов геометрической прогрессии постоянно.

Формула -ого члена геометрической прогрессии

$b_2=b_1 \cdot q$

$b_3=b_2 \cdot q=b_1 \cdot q \cdot q=b_1 \cdot q^2$

$\ldots$

$b_n=b_1\cdot q^{n-1}$

Пример 1. Найдите знаменатель геометрической прогрессии, если третий элемент геометрической прогрессии равен , а -ый — 224 .

Решение.

Третий элемент прогрессии равен $b_3=b_1 \cdot q^2$ , а шестой элемент прогрессии — $b_{6}=b_1 \cdot q^5$ . Сложим данные равенства.

Получим:

$\frac{b_{6}}{b_3}=\frac{q^5}{q^2};$

$q=\sqrt[3]{\frac{224}{28}};$

$q=\sqrt[3]{8};$

$q=2.$

Ответ: .

Сумма геометрической прогрессии

Запишем сумму элементов геометрической прогрессии:

$S_n=b_1+b_2+b_3+\ldots+b_n=b_1+b_1q+b_1q^2+\ldots+b_1q^{n-1}.$

Прибавим к левой и правой части равенства b_1q^n .

Получим:

$S_n+b_1q^n=b_1+b_1q+b_1q^2+\ldots+b_1q^{n-1}+b_1q^n=b_1+q \cdot S_n$

$S_n(1-q)=b_1-b_1q^n$

$S_n=b_1\frac{1-q^n}{1-q}$ , если $q \neq 1.$

Если q=1 , то $S_n=b_1 \cdot n.$

Пример 2. Найдите сумму чисел $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}.$

Решение.

$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=\frac{1}{2}\cdot \frac{1-{\left ( \frac{1}{2}\right )}^5}{1-\frac{1}{2}}=1-\frac{1}{32}=\frac{31}{32}.$

Ответ: $\frac{31}{32}$ .

Бесконечно убывающей геометрической прогрессией называется бесконечная геометрическая прогрессия, знаменатель которой удовлетворяет условию $\frac{31}{32}$ .

При неограниченном возрастании сумма $S_n=b_1\frac{1-q^n}{1-q}$ , первых членов бесконечно убывающей геометрической прогрессии стремится к числу $S=\frac{b_1}{1-q}$ , которое называется суммой бесконечно убывающей геометрической прогрессии.

Пример 3. Переведите бесконечную периодическую дробь 0,(8) в обыкновенную дробь.

Решение.

$0,(8)=\frac{8}{10}+\frac{8}{100}+\frac{8}{1000}+\frac{8}{10000}+\ldots=\frac{0,8}{1-\frac{1}{10}}=\frac{0,8}{0,9}=\frac{8}{9}$

Ответ: $\frac{8}{9}$ .

Характеристическое свойство геометрической прогрессии

$b_n^2=b_{n-1} \cdot b_{n+1}$

Пример 4. Выписано несколько последовательных членов геометрической прогрессии:

$\ldots;189; x; 21; 7; \ldots .$

Найдите .

Решение.

$x^2=189 \cdot 21$

$x^2=13969$

x=63 , так как в данной геометрической прогрессии x>0 .

Ответ: .

Лучшие MMORPG, чтобы прожить свою лучшую фэнтезийную жизнь

Чтобы найти лучшие MMORPG-игры в соответствии с вашими предпочтениями, необходимо точно знать, что вам нравится в жанре. Это большие миры-песочницы? Социальные элементы? Вам нравится открытый мир, PvP с полной добычей или вы предпочитаете решать, когда и когда вы хотите сражаться с другими игроками? Независимо от того, что вы ищете в MMORPG, мы надеемся, что вы найдете в этом списке что-то, что у вас немного порадует.

Мы включили MMORPG из таких крупных франшиз, как The Elder Scrolls и Final Fantasy, а также менее известные MMO, которые, по нашему мнению, заслуживают большего внимания.Погуляйте, позовите друга присоединиться к вам или отправляйтесь в одиночку и найдите новых друзей в своих приключениях.

Лучшие MMORPG-игры всех времен

25. Riders of Icarus

Доступно на: PC

В мире пост-Pokémon Go идея MMO, собирающего монстров, кажется очевидной, и тем не менее, это территория, которую очень мало онлайн-ролевых игр затронули должным образом. Riders of Icarus берет идею сбора карманных монстров и придает ей интересный поворот, превращая всех собираемых вами существ в ездовых животных, которые играют ключевую роль в развитии персонажа.

Бой на лошадях, по понятным причинам, является центральной механикой, и, хотя его сложно освоить, особенно в полете, он также дает некоторые очень приятные и драматические моменты. А в Riders of Icarus полно великолепного редкого снаряжения и квестов, которые часто приятно отклоняются от традиционного шаблона MMO «принеси 15 крысиных шкурок».

24. Defiance 2050

Доступно на: ПК , PlayStation 4, Xbox One

Тот факт, что Defiance — это что-то хорошее, практически чудо.Создание MMO-шутера на основе оригинального телесериала SyFy звучит как рецепт катастрофы, но каким-то образом Trion Worlds удалось создать отличную игру с множеством крутых зацепок. Помогает то, что мир Defiance — интересный, результат любопытного стечения обстоятельств. Земля стала почти неузнаваемой из-за случайного развертывания технологии терраформирования пришельцев, и долгая война с ответственными за это пришельцами поставила обе стороны на грань краха. Фракции разделились, и во многих случаях инопланетяне и люди объединились в отчаянной борьбе за выживание.

В то время как SyFy закрыла телешоу еще в 2015 году, MMO живет, продолжая добиваться успеха благодаря своей боевой механике, удовлетворительному развитию персонажей и огромному арсеналу оружия и снаряжения. Это первая MMO, в которую мы играли, в которой стрельба из оружия в PvE кажется жизнеспособной и увлекательной, и теперь она также включает в себя несколько удивительно эффективного оружия ближнего боя. Перезагруженная версия игры Defiance 2050 доступна на PS4, Xbox One и ПК с классами и деревьями сил, но с тем же миром и квестами — этого недостаточно, чтобы считаться полностью новой игрой, но попробуйте, если вы хотите увидеть мир Defiance свежим взглядом.

23. Black Desert Online

Доступно на : ПК, Xbox One, PS4

Корейская MMO, которая была запущена в США и сопровождалась большой помпой, Black Desert Online в основном способствовала распространению ажиотажа благодаря его быстрые боевые действия и интересные элементы управления недвижимостью. Наряду со стандартным повышением уровня и квестами, BDO предлагает игрокам и гильдиям возможность стать средневековыми лордами трущоб, скупая здания и устанавливая их функции в качестве резиденций или создавая хранилища, или даже взяв под полный контроль целые города.

Хотя некоторые из этих механик были немного неуклюжими или недоступными при запуске, BDO — это игра, в которой в полной мере используются преимущества длительного срока службы большинства MMO и постоянно улучшаются с течением времени. А заявление Microsoft на E3 в этом году о том, что Black Desert появится на Xbox One в качестве эксклюзивной консоли, означает, что больше игроков смогут заполучить этот драгоценный камень для сна.

22. Revelation Online

Доступно на: PC

Говоря о невероятно красивых восточных MMO, Revelation Online доказывает, что красота и сущность не исключают друг друга.Это китайское предложение, недавно появившееся на западе, имеет невероятную глубину с точки зрения создания и развития персонажей, а также обширный, интригующий открытый мир, в котором можно найти добычу и секреты.

Revelation Online — также одна из самых популярных игр, в которой есть возможность выбрать традиционный MMO-бой с нацеливанием на табуляцию или более динамичный боевой бой. Он даже предлагает третий вариант, который представляет собой интригующее (хотя и несколько неуклюже) сочетание обоих. А с возможностью бесплатно изменить характер своего персонажа в любой момент, это простая игра, на которую можно потратить некоторое время, не чувствуя себя скованным своим выбором.

21. Secret Worlds Legends

Доступно на: PC

Еще одна недавно перешедшая в бесплатную модель, Secret World Legends — это игра, во многом определяемая ее сеттингом, который читается, как и все психи из теории заговора сбылась мечта (или сбылся их худший кошмар). Тайные общества, мифологические существа и злые культы определяют мир, окутанный тайнами и полный сверхъестественных ужасов. Сеттинг и сюжет подкрепляют потрясающий звуковой дизайн, который успешно повышает напряжение и придает игровым событиям ощущение драматичности.

Фактически, одна из самых сильных сторон Secret World Legend — это ее преданность рассказу историй. Вместо стандартного метода MMO, позволяющего игрокам выстраивать в очередь практически неограниченное количество квестов — что приводит к множеству бессмысленных захватов и убийств без какого-либо чувства общей цели — The Secret World фокусируется на небольшом количестве квестов одновременно, все с четко определенными целями. Такой узкий фокус помогает подчеркнуть повествование и привлечь внимание к написанию игры и атмосфере, которая имеет довольно однородное высокое качество.

Щелкните «следующую страницу», чтобы увидеть записи 20–11 в нашем обратном отсчете лучших MMORPG.

,Обзор

Endless Space • Eurogamer.net

Одно из преимуществ все более фрагментированного цифрового ландшафта игр заключается в том, что трещины позволяют нишевым играм выделяться в центре внимания, и это доказывает Endless Space. Вход в жанре недостаточно обслуживаемой стратегии 4X, он просит вас исследовать, расширять, эксплуатировать и истреблять, когда вы создаете галактическую империю, стремясь к господству с помощью научных знаний, военной мощи или финансового успеха.

Если вы играли в какую-либо из игр Civilization, то вы знаете, чего ожидать, поскольку давняя классическая серия Сида Мейера остается самым популярным примером стратегии 4X.Тем не менее, с его научно-фантастическим сеттингом Endless Space ориентируется на менее известные источники вдохновения, такие как Master of Orion и Sword of the Stars. На первых порах это увлечение окажется плодотворным, и поклонники жанра будут довольны. Однако в долгосрочной перспективе икоты достаточно, чтобы помешать ему достичь истинного величия.

С самого начала Endless Space определяется готовностью сгибаться, чтобы приспособиться к игроку. Вы можете не только настроить ожидаемые параметры, такие как сложность и продолжительность игры, но также можете указать размер и форму галактики, в которой вы будете играть.Это, в свою очередь, определяет вид звезд и, соответственно, вид планет, доступных для вашего завоевания.

Визуальная изюминка — эпическая кинематографическая анимация боя корабль-корабль.

В игре также есть приятный слой космологической истины. Старая галактика, наполненная красными гигантами и белыми карликами, представляет собой более сложную задачу, чем более молодая галактика, наполненная здоровыми желтыми солнцами в расцвете сил.

На выбор предлагается восемь фракций, предлагающих ожидаемый диапазон специализаций.Объединенная Империя — ваш вариант по умолчанию, экспансионистская человеческая раса с корпоративными устремлениями и кивком в сторону Дюны Фрэнка Герберта, в то время как Паломники обеспечивают более духовную, религиозную мотивацию. Софоны — роботы с научным складом ума, а Сеятели больше ориентированы на инфраструктуру.

«Это все ужасно затягивает. Вы вынуждены нажимать кнопку« конец хода »еще раз, медленно приближаясь к взаимосвязанной паутине различных целей, наблюдая, как ваш домен растет и распространяется.«

Боргоподобные Cravers исполняют роль безжалостных военных завоевателей, а одержимый честью Хиссё аккуратно отображает клингонский архетип. Есть и более странные варианты. Амеба — студенистая раса благородных исследователей, а Горацио — вид, полностью состоящий из клонированных копий тщеславного мании величия. У каждого из них есть свои сильные и слабые стороны и преимущество в различных областях, и если ни одна из них не подходит, вы можете настроить их самостоятельно, используя более 90 черт, чтобы адаптировать игру к вашим точным вкусам.

Оттуда все разворачивается, как и следовало ожидать. Вы начинаете с одной звездной системы и нескольких космических кораблей. Используйте корабль-разведчик, чтобы исследовать близлежащие звезды, и корабли-колонии, чтобы распространить свою империю на планеты, вращающиеся вокруг них. Военные корабли могут быть объединены во флот, состоящий из семи судов, и назначены для защиты любой системы от нападения.

Вы можете настроить игру так, чтобы она автоматически обновляла каждый из ваших кораблей, но вам действительно нужно запастись руками, чтобы максимально использовать свои технологии.

Производство работает на системном уровне, а не на планете за планетой, поскольку вы накапливаете больше кораблей и улучшаете местную среду и доход. На некоторых планетах есть залежи полезных ископаемых, редкая флора или древние артефакты из Бесконечности, предшественницы расы, которая определяет тонкую предысторию, которую может предложить игра. Дипломатия вступает в игру, когда вы сталкиваетесь с другими видами, и вы можете торговать знаниями и ресурсами в обмен на полезные союзы. Все приближает вас к реализации вашего стремления к всеобщему превосходству.

Все это вызывает ужасную зависимость. Вы вынуждены продолжать нажимать кнопку «конец хода» еще раз, медленно приближаясь к взаимосвязанной паутине различных целей, наблюдая, как ваш домен растет и расширяется, звездные системы меняют цвет с нейтрального серого на выбранный вами цвет фракции по мере продвижения. Если вы играли и любили любую предыдущую стратегию 4X, это знакомая радость, которой Endless Space беззастенчиво предается. По крайней мере, вначале часы пролетят незаметно.

Однако в нескольких ключевых областях дела обстоят иначе.Дерево исследований разделено на четыре части, а не следует за одним потоком. Военные улучшения развиваются в одном направлении, а технологии, которые помогают в колонизации, дипломатии и торговле, имеют свои собственные ответвления.

Идея интересная, но не всегда удачная. Отчасти это связано с сеттингом научной фантастики, который может сделать многое в вашем прогрессе довольно абстрактным. Игры Civilization продолжаются благодаря интуитивному развитию. Мы инстинктивно понимаем, как использование алфавита ведет к образованию, которое ведет к улучшению общества.Труднее понять, как и почему «Направленная плазма» предоставит доступ к так называемому «магнитному пульсу», не говоря уже о том, как это является предпосылкой для освоения «Развитой конструкции», которая каким-то образом позволяет вам заполучить «гниющие оболочки».

Цена и наличие

Steam: 22,99 фунтов стерлингов / 29,99 евро / 29,99 долларов США

После того, как вы заселили одну планету в системе, вы можете распространить население на другие, не используя колониальные корабли.

Краткие текстовые описания мало что дают для объяснения реальных преимуществ, поэтому часто приходится гадать, что будет наиболее полезным, а разделение на четыре части исследования означает, что трудно не пренебречь целым рядом потенциальных технологий предложение. Специализация в какой-либо одной области подвергает вас опасной опасности, и поэтому игра подталкивает вас к менее удовлетворительному универсальному пути к власти.

Сражение — еще одна область, где свежая идея спотыкается.Когда военные действия поднимают свою кровавую голову — либо вашими действиями, либо действиями ваших соперников — вы можете выбрать, чтобы битва разыгрывалась автоматически, и в этом случае вы переходите к результатам или вручную. Ручное боевое управление делится на три этапа. Вы можете назначить карту для каждой фазы — большой, средней и близкой — которая будет определять поведение вашего флота.

Это интересная идея, но она на самом деле не меняет фундаментальную природу боя в стратегических играх 4X, а вместо этого придает процессу несколько случайный вид.Влияние этих решений настолько мало, что на самом деле оно влияет только на встречи, в которых комбатанты равны, а этого почти никогда не бывает.

Также усложняет ситуацию тот факт, что замечательные возможности настройки игры означают отсутствие отдельных типов юнитов. Вы можете исследовать и строить новые конструкции кораблей, но у вас есть полная свобода оснащать их любым вооружением и защитой, которые вам нужны. Конечно, ваши враги тоже, а это значит, что вы никогда не будете полностью уверены в том, с чем столкнетесь.Единственный способ гарантировать победу — это направить большую часть своих ресурсов на постоянное совершенствование технологий производства оружия и переоснащение флота за значительные деньги, чтобы гарантировать, что они не будут уничтожены внезапным наплывом подозрительно хорошо вооруженных пиратов — варварского эквивалента игры. ,

Подробнее о бесконечном космосе

Удаленная точка обзора рискует превратить вашу империю в серию точек. Немного больше индивидуальности — возможно, несколько советников — сделало бы его более эмоционально привлекательным.

И хотя игра старается изо всех сил предлагать всплывающие окна, объясняющие большинство функций и значков, слишком много моментов, когда что-то работает не так, как должно, и игра не предлагает никаких объяснений. Почему вы можете колонизировать одну арктическую планету, а другую — нет? Почему недоступны некоторые звездные системы? Ответы есть, но их самостоятельная работа отвлекает от основного игрового процесса и поощряет досадную отрешенность от игры, уже лишенной индивидуальности.

Эта непрозрачность начинает доминировать в игре по мере того, как вы достигаете 200-го хода и далее, при этом ИИ часто действует необъяснимым образом, поскольку необходимость отслеживать десятки звездных систем и флотов смешивается с жонглированием, необходимым для получения максимальной отдачи от вашего исследовательская работа.Игра достаточно оптимизирована, чтобы микроменеджмент никогда не был рутиной, но есть чувство, что для процветания вы все больше полагаетесь на удачу.

Стратегия 4X процветает в долгосрочной перспективе, поэтому очень жаль, что глубоко в игре проявляются мелкие недостатки механизмов Endless Space. Тем не менее, поклонники стратегии не должны сильно расстраиваться. Основы, заложенные здесь, определенно не лишены глубины или развлечения, и вполне возможно, что несколько настроек и балансировок в нужных местах — либо от разработчика, либо от сообщества модов — поднимут Endless Space в жанр, которого он заслуживает. ,

7 / 10

Геометрическая прогрессия | umath.ru

Определение геометрической прогрессии

Сумма первых n членов геометрической прогрессии

Сумма бесконечно убывающей геометрической прогрессии

Геометрическая прогрессия. Часть 1

Геометрическая прогрессия — YouClever.org

Числовая последовательность

Для чего нужна геометрическая прогрессия и ее история возникновения.

Геометрическая прогрессия.

Бесконечно убывающая геометрическая прогрессия.

Свойство геометрической прогрессии.

Геометрическая прогрессия | Онлайн калькулятор

Урок «Бесконечная геометрическая прогрессия»

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Бесконечно убывающая геометрическая прогрессия

Геометрическая прогрессия. — Царство математики

Определение

Формула <img decoding="async" src="/800/600/https/anasta8ia.ru/wp-content/ql-cache/quicklatex.com-11b23897adc487a38e2734cd8483c299_l3.png" alt="n" title="Rendered by QuickLaTeX.com" />-ого члена геометрической прогрессии

Сумма геометрической прогрессии

Характеристическое свойство геометрической прогрессии

Лучшие MMORPG, чтобы прожить свою лучшую фэнтезийную жизнь

Лучшие MMORPG-игры всех времен

25. Riders of Icarus

24. Defiance 2050

23. Black Desert Online

22. Revelation Online

21. Secret Worlds Legends

Endless Space • Eurogamer.net

Цена и наличие

Добавить комментарий Отменить ответ

Формула -ого члена геометрической прогрессии