p — вероятность наступления события;
q=p-1 — вероятность не наступления события
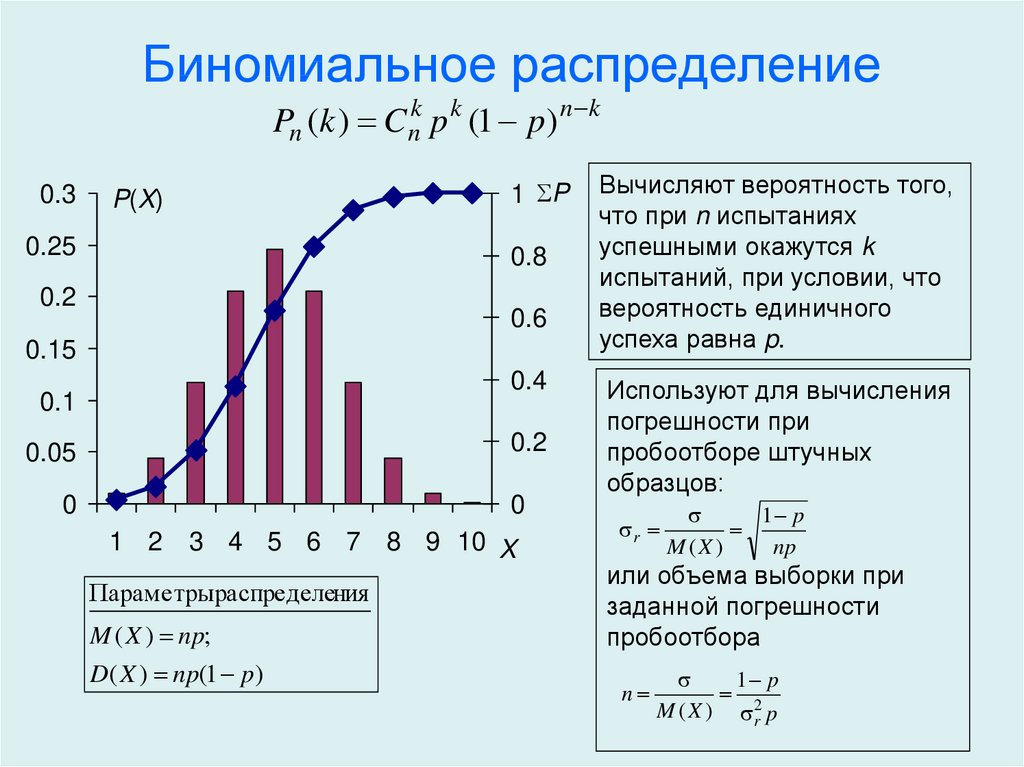
График плотности распределения для биномиального закона распределения СВ.
при k=30, p=0.75
при k=30, p=0.18
при k=30, p=0.5
График функции распределения
Биномиальное распределение относится к дискретному распределению.
Математическое ожидание для этого распределения имеет вид:
M(X)=n⋅p
Дисперсия равна:
D(X)=n⋅p⋅q
Ряд биномиального закона распределения дискретной случайной величины в виде таблицы:
Пример 1
Тракторный завод получает два госзаказа на производство тракторов из 10. Необходимо составить закон распределения вероятностей на производство m тракторов, построить полигон распределения вероятностей.
Решение
Из условия получаем
q=1-p=1-0,2=0,8
n=10
| m | $C_n^m$ | pm | qn-m | Pm,n |
| 0 | 1 | 1,0000000000 | 0,348678 | 0,3486784401 |
| 1 | 10 | 0,1000000000 | 0,38742 | 0,3874204890 |
| 2 | 45 | 0,0100000000 | 0,430467 | 0,1937102445 |
| 3 | 120 | 0,0010000000 | 0,478297 | 0,0573956280 |
| 4 | 210 | 0,0001000000 | 0,531441 | 0,0111602610 |
| 5 | 252 | 0,0000100000 | 0,59049 | 0,0014880348 |
| 6 | 210 | 0,0000010000 | 0,6561 | 0,0001377810 |
| 7 | 120 | 0,0000001000 | 0,729 | 0,0000087480 |
| 8 | 45 | 0,0000000100 | 0,81 | 0,0000003645 |
| 9 | 10 | 0,0000000010 | 0,9 | 0,0000000090 |
| 10 | 1 | 0,0000000001 | 1 | 0,0000000001 |
Полигон распределения вероятностей будет иметь вид:
Пример 2
Производится три выстрела по мишени, вероятность попадания при каждом выстреле равна 0,8.
3} = 0,512$
Представим графически в виде гистограммы
Ряд распределения случайной величины имеет вид:
| X | 0 | 1 | 2 | 3 |
| P | 0.008 | 0.096 | 0.384 | 0.512 |
Проверяем:
∑p=0,008+0,096+0,384+0,512=1
2123
Биномиальное распределение
В настоящей и нескольких следующих заметках мы рассмотрим математические модели случайных событий. Математическая модель — это математическое выражение, представляющее случайную величину. Для дискретных случайных величин это математическое выражение известно под названием функция распределения. [1]
Если задача позволяет явно записать математическое выражение, представляющее случайную величину, можно вычислить точную вероятность любого ее значения.
В этом случае можно вычислить и перечислить все значения функции распределения. В деловых, социологических и медицинских приложениях встречаются разнообразные распределения случайных величин. Одним из наиболее полезных распределений является биномиальное.
Биномиальное распределение используется для моделирования ситуаций, характеризующихся следующими особенностями.
- Выборка состоит из фиксированного числа элементов
- Каждый элемент выборки принадлежит одной из двух взаимоисключающих категорий, исчерпывающих все выборочное пространство. Как правило, эти две категории называют успех и неудача.
- Вероятность успеха р является постоянной. Следовательно, вероятность неудачи равна 1 – р.
- Исход (т.е. удача или неудача) любого испытания не зависит от результата другого испытания. Чтобы гарантировать независимость исходов, элементы выборки, как правило, получают с помощью двух разных методов.
Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.
Каждый элемент выборки случайным образом извлекается из бесконечной генеральной совокупности без возвращения или из конечной генеральной совокупности с возвращением.Скачать заметку в формате Word или pdf, примеры в формате Excel2207
Биномиальное распределение используется для оценки количества успехов в выборке, состоящей из n наблюдений. Рассмотрим в качестве примера оформление заказов. Чтобы сделать заказ клиенты компании Saxon Company могут воспользоваться интерактивной электронной формой и послать ее в компанию. Затем информационная система проверяет, нет ли в заказах ошибок, а также неполной или недостоверной информации. Любой заказ, вызывающий сомнения, помечается и включается в ежедневный отчет об исключительных ситуациях. Данные, собранные компанией, свидетельствуют, что вероятность ошибок в заказах равна 0,1. Компания хотела бы знать, какова вероятность обнаружить определенное количество ошибочных заказов в заданной выборке. Например, предположим, что клиенты заполнили четыре электронных формы.
Какова вероятность, что все заказы окажутся безошибочными? Как вычислить эту вероятность? Под успехом будем понимать ошибку при заполнении формы, а все остальные исходы будем считать неудачей. Напомним, что нас интересует количество ошибочных заказов в заданной выборке.
Какие исходы мы можем наблюдать? Если выборка состоит из четырех заказов, ошибочными могут оказаться один, два, три или все четыре, кроме того, все они могут оказаться правильно заполненными. Может ли случайная величина, описывающая количество неправильно заполненных форм, принимать какое-либо иное значение? Это невозможно, поскольку количество неправильно заполненных форм не может превышать объем выборки n или быть отрицательным. Таким образом, случайная величина, подчиняющаяся биномиальному закону распределения, принимает значения от 0 до n.
Допустим, что в выборке из четырех заказов наблюдаются следующие исходы:
Какова вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, причем в указанной последовательности? Поскольку предварительные исследования показали, что вероятность ошибки при заполнении формы равна 0,10, вероятности указанных выше исходов вычисляются следующим образом:
Поскольку исходы не зависят друг от друга, вероятность указанной последовательности исходов равна: р*р*(1–р)*р = 0,1*0,1*0,9*0,1 = 0,0009.
Если же необходимо вычислить количество вариантов выбора X объектов из выборки, содержащей n элементов, следует воспользоваться формулой сочетаний (1):
где n! = n * (n –1) * (n – 2) * … * 2 * 1 — факториал числа n, причем 0! = 1 и 1! = 1 по определению.
Это выражение часто обозначают как . Таким образом, если n = 4 и X = 3, количество последовательностей, состоящих из трех элементов, извлеченных из выборки, объем которой равен 4, определяется по следующей формуле:
Следовательно, вероятность обнаружить три ошибочных заказа вычисляется следующим образом:
(Количество возможных последовательностей) *
Аналогично можно вычислить вероятность того, что среди четырех заказов окажутся один или два ошибочных, а также вероятность того, что все заказы ошибочны или все верны. Однако при увеличении объема выборки n определить вероятность конкретной последовательности исходов становится труднее.
В этом случае следует применить соответствующую математическую модель, описывающую биномиальное распределение количества вариантов выбора X объектов из выборки, содержащей n элементов.
Биномиальное распределение
где Р(Х) — вероятность X успехов при заданных объеме выборки n и вероятности успеха р, X = 0, 1, … n.
Обратите внимание на то, что формула (2) представляет собой формализацию интуитивных выводов. Случайная величина X
, подчиняющаяся биномиальному распределению, может принимать любое целое значение в диапазоне от 0 до n. Произведение рX(1 – р)n – X представляет собой вероятность конкретной последовательности, состоящей из X успехов в выборке, объем которой равен n. Величина определяет количество возможных комбинаций, состоящих из X успехов в n испытаниях.
Следовательно, при заданном количестве испытаний n и вероятности успеха р вероятность последовательности, состоящей из X успехов, равнаР(Х) = (количество возможных последовательностей) * (вероятность конкретной последовательности) =
Рассмотрим примеры, иллюстрирующие применение формулы (2).
1. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм три окажутся ошибочными? Используя формулу (2), получаем, что вероятность обнаружить три ошибочных заказа в выборке, состоящей из четырех заказов, равна
2. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными? Как показано в предыдущем примере, вероятность того, что среди четырех заполненных форм три окажутся ошибочными, равна 0,0036. Чтобы вычислить вероятность того, что среди четырех заполненных форм не менее трех будут неправильно заполнены, необходимо сложить вероятность того, что среди четырех заполненных форм три окажутся ошибочными, и вероятность того, что среди четырех заполненных форм все окажутся ошибочными.
Вероятность второго события равна
Таким образом, вероятность того, что среди четырех заполненных форм не менее трех окажутся ошибочными, равна
Р(Х > 3) = Р(Х = 3) + Р(Х = 4) = 0,0036 + 0,0001 = 0,0037
3. Допустим, что вероятность неверно заполнить форму равна 0,1. Какова вероятность того, что среди четырех заполненных форм менее трех окажутся ошибочными? Вероятность этого события
Р(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
Используя формулу (2), вычислим каждую из этих вероятностей:
Следовательно, Р(Х < 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.
Вероятность Р(Х < 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х> 3. Тогда Р(Х< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.
По мере увеличения объема выборки n вычисления, аналогичные проведенным в примере 3, становятся затруднительными. Чтобы избегать этих сложностей, многие биномиальные вероятности табулируют заранее.
Рис. 1. Биномиальная вероятность при n = 4, Х = 2 и р = 0,1
Биномиальное распределение можно вычислить с помощью функции Excel =БИНОМ.РАСП() (рис. 2), имеющей 4 параметра: число успехов – Х, число испытаний (или объем выборки) – n, вероятность успеха – р, параметр интегральная, принимающий значения ИСТИНА (в этом случае вычисляется вероятность не менее Х событий) или ЛОЖЬ (в этом случае вычисляется вероятность точно Х событий).
Рис. 2. Параметры функции =БИНОМ.РАСП()
Для вышеприведенных трех примеров расчеты приведены на рис. 3 (см. также Excel-файл). В каждом столбце приведено по одной формуле.
Цифрами показаны ответы на примеры соответствующего номера).
Рис. 3. Расчет биномиального распределения в Excel для n = 4 и p = 0,1
Свойства биномиального распределения
Биномиальное распределение зависит от параметров n и р. Биномиальное распределение может быть, как симметричным, так и асимметричным. Если р = 0,5, биномиальное распределение является симметричным независимо от величины параметра n. Однако, если р ≠ 0,5, распределение становится асимметричным. Чем ближе значение параметра р к 0,5 и чем больше объем выборки n, тем слабее выражена асимметрия распределения. Таким образом, распределение количества неправильно заполненных форм смещено вправо, поскольку p = 0,1 (рис. 4).
Рис. 4. Гистограмма биномиального распределения при n = 4 и p = 0,1
Математическое ожидание биномиального распределения равно произведению объема выборки n на вероятность успеха р:
(3) Μ = Е(Х) = np
В среднем, при достаточно долгой серии испытаний в выборке, состоящей из четырех заказов, может оказаться р = Е(Х) = 4 х 0,1 = 0,4 неправильно заполненных форм.
Стандартное отклонение биномиального распределения
Например, стандартное отклонение количества неверно заполненных форм в бухгалтерской информационной системе равно:
Предыдущая заметка Ковариация и ее применение в финансовом деле
Следующая заметка Гипергеометрическое распределение
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 307–313
Биномиальные случайные величины » Биостатистика » Колледж общественного здравоохранения и медицинских профессий » Университет Флориды
- Биномиальный эксперимент
- Биномиальное распределение вероятностей – использование правил вероятности
- Подсчет результатов
- Среднее и стандартное отклонение биномиальной случайной величины
CO-6: Применять основные понятия вероятности, случайных вариаций и широко используемых статистических распределений вероятностей.
Видео: Биномиальные случайные величины (12:52)
До сих пор в нашем обсуждении дискретных случайных величин мы познакомились с:
- Распределением вероятностей, которое говорит нам, какие значения принимает переменная и как часто это занимает их.
- Среднее значение случайной величины, которое сообщает нам долгосрочное среднее значение, которое принимает случайная величина.
- Стандартное отклонение случайной величины, которое сообщает нам типичное (или долгосрочное среднее) расстояние между средним значением случайной величины и значениями, которые она принимает.
Теперь мы введем специальный класс дискретных случайных величин, которые очень распространены, потому что, как вы увидите, они будут встречаться во многих ситуациях — биномиальных случайных величин.
Вот как мы представим этот материал.
- Сначала мы объясним, какие случайные эксперименты приводят к биномиальной случайной величине и как биномиальная случайная величина определяется в этих типах экспериментов.
- Затем мы представим распределение вероятностей биномиальной случайной величины, которое будет представлено в виде формулы, и объясним, почему эта формула имеет смысл.
- Мы завершим наше обсуждение представлением среднего значения и стандартного отклонения биномиальной случайной величины.
Как мы только что упоминали, мы начнем с описания того, какие случайные эксперименты приводят к биномиальной случайной величине. Мы назовем этот тип случайного эксперимента «биномиальным экспериментом».
Биномиальный эксперимент
LO 6.14: При необходимости примените биномиальную модель для определения вероятностей.
Биномиальные эксперименты — это случайные эксперименты, состоящие из фиксированного числа повторных попыток, таких как 10-кратное подбрасывание монеты, случайный выбор 10 человек, 5-кратное бросание игральной кости и т. д.
Однако эти испытания должны быть независимыми в том смысле, что результат одного испытания не влияет на результат других испытаний.
В каждом из этих повторных испытаний есть один интересующий нас исход (мы называем этот исход «успехом»), и каждое из испытаний идентично в том смысле, что вероятность того, что испытание закончится «успехом ” одинакова в каждом из испытаний.
Так, например, если наш эксперимент подбрасывает монету 10 раз, и нас интересует результат «орел» (наш «успех»), то это будет биномиальный эксперимент, так как 10 испытаний независимы, а вероятность успеха 1/2 в каждом из 10 испытаний.
Подведем итоги и приведем больше примеров.
Требования для того, чтобы случайный эксперимент был биномиальным экспериментом :
- фиксированное количество (n) испытаний
- каждое испытание должно быть независимым от других
- каждое испытание имеет только два возможных исхода, называемых « успех » (исход интереса) и « неудача »
- существует постоянная вероятность (p) успеха для каждого испытания, дополнением которой является вероятность (1 – p) отказа, иногда обозначаемая как q = (1 – p)
В биномиальных случайных экспериментах количество успехов в n испытаниях является случайным.
Может принимать значение от 0, если все попытки заканчиваются неудачно, или до n, если все n попыток завершаются успешно.
Случайная величина X, представляющая количество успехов в этих n испытаниях, называется биномиальной случайной величиной и определяется значениями n и p. Мы говорим: «X биномиально с n = … и p = …»
ПРИМЕР: Случайные эксперименты (биномиальные или нет?)
Рассмотрим несколько случайных экспериментов.
В каждом из них мы решим, является ли случайная величина биномиальной. Если это так, мы определим значения для n и p. Если это не так, мы объясним, почему нет.
Пример A:
Честная монета подбрасывается 20 раз; X представляет количество голов.
X является биномиальным с n = 20 и p = 0,5 .
Пример Б:
Вы бросаете правильный кубик 50 раз; Х — это количество раз, когда вы получаете шесть.
X является биномиальным с n = 50 и p = 1/6 .
Пример C:
Несколько раз бросайте правильный кубик; Х — количество бросков, необходимое для получения шестёрки.
X не является биномиальным, потому что число испытаний не фиксировано .
Пример D:
Вытяните наугад 3 карты, одну за другой, без замены , из набора из 4 карт, состоящих из одной трефы, одной бубны, одной червы и одной пики; X — количество выбранных бриллиантов.
X не является биномиальным, потому что выборки не являются независимыми . (Вероятность (p) успеха не постоянна, так как на нее влияют предыдущие выборы.)
Пример E:
Возьмите 3 случайные карты, одну за другой, с заменой , из набора 4 карты, состоящие из одной трефы, одной бубны, одной червы и одной пики; X — количество выбранных бриллиантов. Выборка с заменой обеспечивает независимость.
X является биномиальным с n = 3 и p = 1/4
Пример F:
Примерно 1 из каждых 20 детей страдает определенным заболеванием.
Пусть X — число детей с заболеванием из случайной выборки из 100 детей. Хотя дети отбираются без замены, предполагается, что мы отбираем образцы из такой обширной совокупности, что выборки практически независимы.
X является биномиальным с n = 100 и p = 1/20 = 0,05 .
Пример G:
Вероятность наличия группы крови B равна 0,1. Выберите 4 человека наугад; X число с группой крови B.
X является биномиальным с n = 4 и p = 0,1 .
Пример H:
Учащийся отвечает на 10 вопросов викторины совершенно случайным образом; первые пять — верно/неверно, вторые пять — множественный выбор, по четыре варианта в каждом. Х обозначает количество правильных ответов.
X не является биномиальным, потому что p изменяется от 1/2 до 1/4 .
Комментарии:
- Пример D выше не был биномиальным, поскольку выборка без замены приводила к зависимому выбору.
- В частности, вероятность того, что вторая карта окажется бубном, сильно зависит от того, была ли первая карта бубном:
- вероятность равна 0, если первой картой была бубна, и 1/3, если первой картой не была бубна.
- В отличие от Пример E было биномиальным, поскольку выборка с заменой приводила к независимым выборкам:
- вероятность того, что любая из 3 карт окажется бубном, равна 1/4, независимо от того, что было выбрано ранее.
- С другой стороны, когда вы берете относительно небольшую случайную выборку испытуемых из большой популяции, даже если выборка не заменяется, мы можем предположить независимость, поскольку математический эффект удаления одного индивидуума из очень большой популяции на следующий выбор незначителен.
- Например, в примере F мы отобрали 100 детей из совокупности всех детей.
- Несмотря на то, что мы отобрали детей без замещения, факт наличия заболевания у одного ребенка на самом деле не влияет на наличие заболевания у другого ребенка.
- То же верно и для Пример (G.) .
Получил ли я это?: Бином или нет?
Биномиальное распределение вероятностей – использование правил вероятности
Теперь, когда мы понимаем, что такое биномиальная случайная величина и когда она возникает, пришло время обсудить ее распределение вероятностей. Мы начнем с простого примера, а затем обобщим его до формулы.
ПРИМЕР: Колода карт
Рассмотрим обычную колоду из 52 карт, в которой по 13 карт каждой масти: червы, бубны, трефы и пики. Выбираем наугад 3 карты с заменой . Пусть X будет количеством карт с бубнами, которые мы получили (из 3).
У нас тут 3 испытания, и они независимые (т.к. отбор с замещением). Исходом каждого испытания может быть либо успех (ромб), либо неудача (не ромб), а вероятность успеха в каждом из испытаний составляет 1/4.
X, таким образом, является биномиальным с n = 3 и p = 1/4.
Давайте построим распределение вероятностей X, как мы это делали в главе о распределениях вероятностей.
Напомним, что мы начинаем с таблицы, в которой мы:
- записываем все возможные исходы в 3 вариантах, где каждый выбор может привести к успеху (ромб, D) или к неудаче (не ромб, N).
- найти значение X, соответствующее каждому результату.
- используют простые принципы вероятности, чтобы найти вероятность каждого исхода.
С помощью принципа сложения мы сконцентрируем информацию в этой таблице, чтобы построить таблицу фактического распределения вероятностей:
Чтобы установить общую формулу для вероятности того, что биномиальная случайная величина X значение x, мы будем искать закономерности в приведенном выше распределении. Из того, как мы построили это распределение вероятностей, мы знаем, что в целом:
Начнем со второй части, вероятности того, что будет x успехов из 3, где вероятность успеха равна 1/4.
Обратите внимание, что доли, умноженные в каждом случае, относятся к вероятности x успехов (где каждый успех имеет вероятность p = 1/4) и оставшихся (3 – x) неудач (где каждая неудача имеет вероятность 1 – p = 3/4).
Итак, в общем:
Давайте поговорим о количестве возможных исходов с x успехами из трех. Здесь сложнее увидеть закономерность, поэтому приведем следующий математический результат.
Подсчет результатов
Рассмотрим случайный эксперимент, состоящий из n испытаний, каждое из которых заканчивается либо успехом, либо неудачей. Количество возможных исходов в выборочном пространстве, которые имеют ровно k успехов из n, составляет:
Обозначение слева часто читается как «n выбирают k». Обратите внимание, что н! читается как «n факториал» и определяется как произведение 1 * 2 * 3 * … * n. 0! определяется как 1.
ПРИМЕР: Пирсинг ушей
Вы выбираете случайным образом 12 студентов мужского пола и записываете, прокололи ли они уши (успешно) или нет. Есть много возможных исходов этого эксперимента (на самом деле, 4,096 из них!).
В скольких возможных исходах этого эксперимента ровно 8 успехов (учащиеся, у которых проколото хотя бы одно ухо)?
Нет никакого способа, чтобы мы начали перечислять все эти возможные результаты.
Приведенный выше результат приходит нам на помощь.
Результат говорит о том, что в подобном эксперименте, когда вы повторяете испытание n раз (в нашем случае мы повторяем его n = 12 раз, по одному разу для каждого выбранного нами учащегося), количество возможных исходов равно 8 успехам ( из 12) составляет:
Я понял?: Подсчет результатов
ПРИМЕР: Повторное посещение карт
Вернемся к нашему примеру, в котором у нас есть n = 3 попытки (выбор 3 карт). Мы видели, что было 3 возможных исхода с ровно 2 успехами из 3. Результат подтверждает это, так как:
В общем, тогда
Сложив все вместе, мы получаем, что распределение вероятностей X, которое является биномиальным с n = 3 и p = 1/4 i
В общем случае число способов получить x успехов (и n – x неудач) в n испытаниях равно
Следовательно, вероятность x успехов (и n – x неудач) в n испытаниях, где вероятность успех в каждом испытании равен p (а вероятность неудачи равна 1 – p) равен количеству исходов, в которых есть x успехов из n испытаний, умноженному на вероятность x успехов, умноженному на вероятность n – x неудач :
Биномиальная формула вероятности для P(X = x)
где x может принимать любое значение 0, 1, …, n.
Давайте рассмотрим другой пример:
ПРИМЕР: Группа крови А
Вероятность наличия группы крови А равна 0,4. Выберите наугад 4 человека и пусть X будет числом с группой крови A.
X — биномиальная случайная величина с n = 4 и p = 0,4.
В качестве обзора давайте сначала найдем распределение вероятностей X по длинному пути: построим промежуточную таблицу всех возможных исходов в S, соответствующих значений X и вероятностей. Затем постройте таблицу распределения вероятностей для X.
Как обычно, правило сложения позволяет нам комбинировать вероятности для каждого возможного значения X:
Теперь давайте применим формулу распределения вероятностей биномиальной случайной величины и увидим, что, используя ее, мы получаем точно что мы получили долгий путь.
Напомним, что общая формула распределения вероятностей биномиальной случайной величины с n испытаниями и вероятностью успеха p:
его распределение вероятностей:
Давайте воспользуемся этой формулой, чтобы найти P(X = 2) и убедимся, что мы получаем точно то же, что и раньше.
Учись на практике: Биномиальные вероятности (с помощью онлайн-калькулятора)
Теперь давайте рассмотрим некоторые действительно практические применения биномиальных случайных величин.
ПРИМЕР: Рейсы авиакомпаний
Прошлые исследования показали, что 90% забронированных пассажиров действительно прибывают на рейс. Предположим, что в маленьком самолете-шаттле 45 мест. Будем считать, что пассажиры прибывают независимо друг от друга. (Это предположение не совсем точно, так как не все люди путешествуют в одиночку, но мы будем использовать его для целей нашего эксперимента).
Много раз авиакомпании « перебронировали » рейсов. Это означает, что авиакомпания продает больше билетов, чем мест в самолете. Это связано с тем, что иногда пассажиры не приходят, и самолет должен лететь со свободными местами. Однако, если они делают избыточное бронирование, они рискуют получить больше пассажиров, чем мест. Так что некоторые пассажиры могут быть недовольны.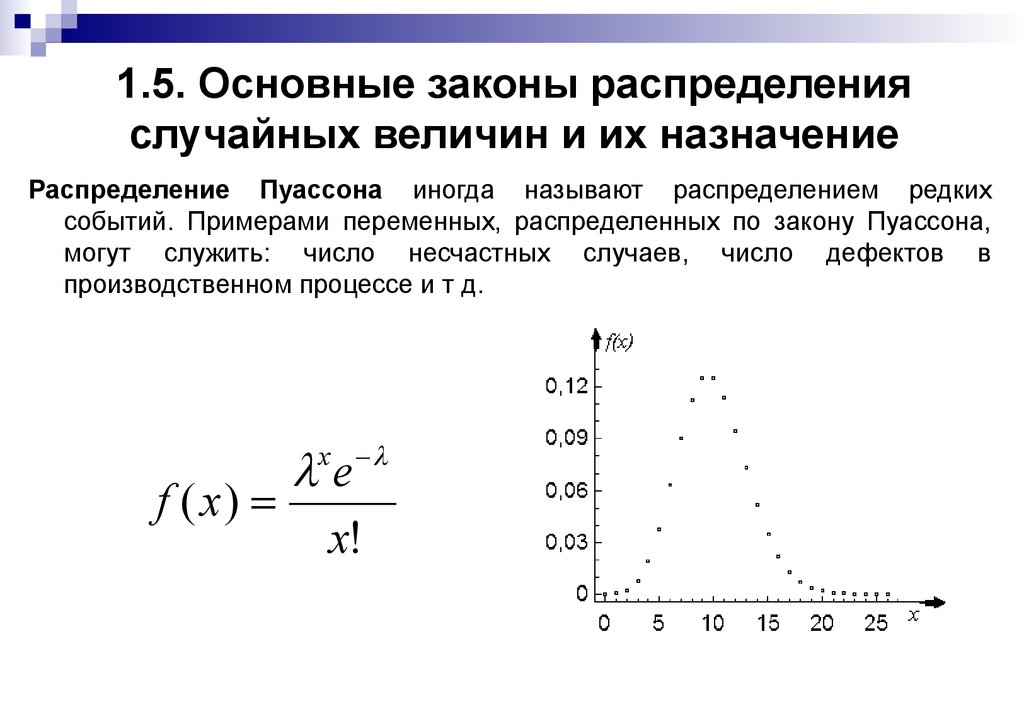
У них также есть дополнительные расходы, связанные с размещением этих пассажиров на другом рейсе и, возможно, с предоставлением жилья.
Помня об этих рисках, авиакомпания решает продать более 45 билетов. Если они хотят, чтобы вероятность появления на рейс более 45 пассажиров была ниже 0,05, сколько билетов они должны продать?
Это биномиальная случайная величина, представляющая количество пассажиров, явившихся на рейс. Он имеет p = 0,90, а n необходимо определить.
Предположим, авиакомпания продает 50 билетов. Теперь у нас есть n = 50 и p = 0,90. Нам нужно знать P(X > 45), что равно 1 – P(X ≤ 45) = 1 – 0,57 или 0,43. Очевидно, что все детали этого расчета не были показаны, так как для расчета ответа использовался пакет статистических технологий. Это, безусловно, больше, чем 0,05, поэтому авиакомпания должна продать меньше мест.
Если мы уменьшим количество проданных билетов, мы сможем уменьшить эту вероятность. Мы рассчитали вероятности в следующей таблице:
| Количество проданных билетов | Р(Х > 45) |
|---|---|
| 50 | 0,43 |
| 49 | 0,26 |
| 48 | 0,13 |
| 47 | 0,04 |
| 46 | 0,008 |
Из этой таблицы видно, что, продав 47 билетов, авиакомпания может снизить вероятность того, что у нее появится больше пассажиров, чем мест, до менее чем 5%.
Примечание. Для практики в нахождении биномиальных вероятностей вы можете проверить один или несколько результатов из приведенной выше таблицы.
Обучение на практике: Биномиальное приложение
Среднее и стандартное отклонение биномиальной случайной величины
LO 6,15: Найти среднее значение, дисперсию и стандартное отклонение биномиальной случайной величины.
Теперь, когда мы поняли, как находить вероятности, связанные с биномиальной случайной величиной X, используя формулу распределения вероятностей или программное обеспечение, мы готовы поговорить о среднем значении и стандартном отклонении биномиальной случайной величины. Начнем с примера:
ПРИМЕР: группа крови B — среднее значение
В целом доля людей с группой крови B составляет 0,1. Другими словами, примерно 10% населения имеют группу крови B.
Предположим, мы выбираем случайным образом 120 человек. В среднем, у скольких из них вы ожидаете иметь группу крови B?
Ответ 12 кажется очевидным; автоматически вы умножаете количество людей, 120, на вероятность группы крови B, 0,1.
Это предлагает общую формулу для нахождения среднего значения биномиальной случайной величины:
Утверждение:
Если X является биномиальным с параметрами n и p, то среднее или ожидаемое значение X равно:
Хотя формула для среднего вполне интуитивно понятна, совсем не очевидно, какими должны быть дисперсия и стандартное отклонение. Оказывается, что:
Претензия:
, если x — биномиальная с параметрами n и p, затем Дисперсия и Стандартное отклонение из X —
Комментарии:
:
:
. среднее значение и дисперсия являются частными случаями наших общих формул для среднего значения и дисперсии любой случайной величины. Очевидно, что гораздо проще использовать представленные выше «сокращенные» формулы, чем вычислять среднее значение и дисперсию или стандартное отклонение с нуля. Предположим, мы случайным образом выбираем 120 человек. Число с группой крови B должно быть около 12, плюс-минус сколько? Другими словами, каково стандартное отклонение числа Х, у которых группа крови В? Поскольку n = 120 и p = 0,1, В случайной выборке из 120 человек мы должны ожидать, что будет около 12 человек с группой крови B, плюс-минус около 3,3. Я понял?: Биномиальное распределение Прежде чем мы перейдем к непрерывным случайным величинам, давайте исследуем форму биномиального распределения. Учись на практике: Формы биномиального распределения Вероятность и статистика имеют огромное применение в науке о данных, поскольку искусственный интеллект и машинное обучение в значительной степени зависят от них. Случайная величина — это переменная, значение которой неизвестно. Он может быть либо дискретным (имеющим определенное значение), либо непрерывным (любое значение в непрерывном диапазоне). Все возможные значения, которые принимает случайная величина, также называются выборочным пространством. Биномиальная случайная величина — это количество успехов в эксперименте, состоящем из N следов. Некоторые из примеров: В биномиальном эксперименте биномиальное распределение представляет собой дискретное распределение вероятностей, которое представляет вероятности биномиальных случайных величин. Возьмем пример. Предположим, вы подбросили монетку. Вероятность выпадения орла или решки равна. Но какова будет вероятность выпадения шести орлов при десяти подбрасываниях монет? Здесь вам понадобится биномиальное распределение. Вы можете рассчитать вероятность выпадения шести орлов при десяти подбрасываниях монеты. Формула биномиального распределения для любой случайной величины X имеет вид P(x, n, P) = nCx * Px * (1 — P)n-x Где, n = количество опытов x = 0, 1, 2, 3, 4, … (общее количество успехов) p = вероятность успеха в одном эксперименте Рассчитаем вероятность выпадения ровно шести решек при десяти подбрасываниях монеты. Мы будем использовать формулу P(x, n, P) = nCx * Px * (1 — P)n-x где n = 10, p = 0,5, x = 6 P(x=6) = 10C6 * 0,56 * 0,54 = 0,205 Среднее значение и дисперсия биномиального распределения: Среднее = np Дисперсия = npq где, p — вероятность успеха q — вероятность отказа (1-р) n — количество испытаний. Свойства биномиального распределения: Давайте проанализируем следующий пример Python, чтобы получить представление о биномиальном распределении. Выходной график, который вы получите после выполнения кода, показан ниже. Если вы посмотрите на приведенный выше график, вероятность успеха составит 0,175.
ПРИМЕР: группа крови B – стандартное отклонение
Что такое биномиальная случайная величина и ее формулы?
В этой статье вы познакомитесь с биномиальным распределением, важной частью функции вероятности. Что такое случайная величина?
Что такое биномиальная случайная величина?
Что такое биномиальное распределение?
Биномиальное распределение — это распределение вероятностей, связанное с биномиальным экспериментом, в котором биномиальная случайная величина указывает количество успешных или неудачных попыток, произошедших в этом пространстве выборки. Среднее значение и дисперсия биномиального распределения
Свойства биномиального распределения
Биномиальное распределение Python: пример
